The critical voltage of a GPL-reinforced composite microdisk covered with piezoelectric layer

Abstract

In this research, electrically characteristics of a graphene nanoplatelet (GPL)-reinforced composite (GPLRC) microdisk are explored using generalized differential quadrature method. Also, the current microstructure is coupled with a piezoelectric actuator (PIAC). The extended form of Halpin–Tsai micromechanics is used to acquire the elasticity of the structure, whereas the variation of thermal expansion, Poisson’s ratio, and density through the thickness direction is determined by the rule of mixtures. Hamilton’s principle is implemented to establish governing equations and associated boundary conditions of the GPLRC microdisk joint with PIAC. The compatibility conditions are satisfied by taking perfect bonding between the core and PIAC into consideration. Maxwell’s equation is employed to capture the piezoelectricity effects. The numerical results revealed the important role of ratios of length scale and nonlocal to thickness, outer-to-inner ratio of radius ($R_{\text{o}} /R_{\text{i}}$), ratio of piezoelectric to core thickness (h_p/h), and GPL weight fraction ($g_{\text{GPL}}$) on the critical voltage of the system. Another important consequence is that by increasing $R_{\text{o}} /R_{\text{i}}$, the critical voltage of the smart structure increases more intensely in comparison with the $g_{\text{GPL}}$.

1 Introduction

Reinforced laminated composites are increasingly used in various applications due to its outstanding features, namely high tensile strength, high modulus, and lightweight [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Because of some important requirements in science and technology for promoting the mechanical response and performance of the systems, reinforcing with GPL attracted the attention of numerous researchers for providing an impressive enhancement in the construction of the practical composite structures. Also, frequency response is more important in many applications [21,22,23,24,25,26,27,28,29,30,31]. Suna et al. [32] performed a study to compare the fracture performance of the functionally graded (FG) cemented carbide in the presence and absence of GPL reinforcement. They concluded that the superb properties of GPLs in the content of nanocomposites can be considered as a barrier in the way of growing microcracks. Also, according to the results of an experimental study, Rafiee et al. [33] asserted that the composites reinforced with GPL present more strength in comparison with the structures employing SWCNT, DWCNT, and MWCNT as the reinforcement. In the current decade, exploring the dynamic response of GPL-reinforced nanostructures becomes the hot topic of many surveys as a consequence of remarkable progress in nanotechnologies. In this field of research, the stability and the vibrational response of a thermo-elastic circular plate are analyzed in Refs [11,12,13,14,15,16, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Vibration, buckling, wave propagation, and bending responses of the nanocomposite-reinforced structures are investigated in Refs. [60,61,62,63,64,65].

High-speed rotation and exposure to the thermal site are considered as the main assumptions in the mathematical modeling of the system to acquire the critical spinning speed of thermos-whirling circular plates. The impressive effect of damping coefficients on the transient forced oscillation and stability of the FG circular plate with viscoelastic boundary edges is revealed by Alipour [66]. Within the framework of classical theory, Ebrahimi and Rastgoo [67] explored solution methods to analyze the vibration performance of the FG circular plate covered with piezoelectric. As another survey, Ebrahimi and Rastgoo [68] studied flexural natural frequencies of FG annular plate coupled with layers made of piezoelectric materials. Shasha et al. [69] introduce a novel exact model on the basis of surface elasticity and Kirchhoff theory to determine the vibration performance of a double-layered microcircular plate. The surface effect is captured in their model as the main novelty. The results obtained with the aid of their modified model showed that the vibration performance of the double-layered microstructure is quite higher than the single-layered one. On the basis of FSD theory, Mohammadimehr et al. [70] conducted a numerical study in the dynamic and static stability performance of a composite circular plate by implementing GDQM. Moreover, they considered the thermo-magnet field to define the sandwich structure model. As another work, Mohammadimehr et al. [71] applied DQM in the framework of MCS to describe stress filed and scrutinize the dynamic stability of an FG boron nitride nanotubes-reinforced circular plate. They claimed that using reinforcement in a higher volume fraction promotes the strength and vibration response of the structure. Nonlinear oscillation and stability of microcircular plates subjected to electrical field actuation and mechanical force are studied by Sajadi et al. [72]. They concluded that pure mechanical load plays a more dominant role on the stability characteristics of the structure in comparison with electromechanical load. Also, they confirmed the positive impact of AC or DC voltage on the stability of the system in different cases of application. In order to determine the critical angular speed of spinning circular shell coupled with sensor at its end, Safarpour et al. [36] applied GDQM to analyze forced and free oscillatory responses of the structure on the base of thick shell theory. Through a theoretical approach, Wang et al. [73] obtained critical temperature and thermal load of a nanocircular shell. Safarpour et al. [44] introduced a numerical technique with high accuracy to study the static stability, forced and free vibration performance of a nanosized FG circular shell in exposure to thermal site. In addition, some researchers showed that some geometrical and physical parameters have important role on the stability or instability of the structures [36,37,38,39, 40,41,42,43,44,45,46,47,48,49,50,51,52, 54, 74,75,77]. Based on the NSG theory, the nonlocal effects on the dynamic and static responses of the micro/nanostructure are presented in Refs. [61, 78,79,80,81,82,83,84,85].

Wang et al. [86] reported the nonlinear dynamic performance of size-dependent circular plates with the piezoelectric actuator in the exposure of a thermal site with the aid of MCS incorporated with surface elasticity theory to consider the size effects. They highlighted the considerable effect of geometrical nonlinearity on the dynamic characteristics of the system. By employing FSDT, NSGT, DQM, and Hamilton’s principle, Mahinzare et al. [87] presented a comprehensive parametric investigation in the size-dependent vibration performance of FG circular plate by considering the electro-elastic, thermal, and rotational effects. They showed the considerable impact of spinning velocity on the natural frequencies of nanosized systems. In another investigation, the same authors [88] studied the size-dependent vibration response of a spinning two-directional FG circular plate integrated with the PIAC on the basis of DQM, Hamilton’s principle, and FSDT. The results confirmed the high dependency of the dynamic performance of the circular plate to spinning load and external applied voltage. In a huge number of researches [79, 89,90,91,92,93,94,95,96], the results of nonlocal elasticity compared with those results by nonlocal strain gradient elasticity.

None of the published articles focused on analyzing the electrically analysis of the GPLRC microdisk joint with PIAC using NSGT. In this survey, the extended model of Halpin–Tsai micromechanics is applied to determine the elastic characteristics of the composite structure. A numerical approach is employed to solve differential governing motion equations for different cases of boundary conditions. Eventually, a complete parametric study is carried out to reveal the impact of $R_{\text{o}} /R_{\text{i}}$, h/h_p, applied voltage, and $g_{\text{GPL}}$ on the critical voltage response of the GPLRC microdisk integrated with PIAC.

2 GPLRC microdisk

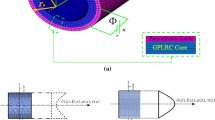
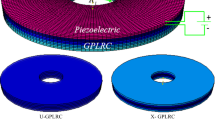
A GPLRC microdisk and coupled with the PIAC is depicted in Fig. 1. The volume fraction for four patterns is described by a specific function as expressed follows [97]:

Fig. 1

GPLRC microdisk covered with piezoelectric layer

$$V_{\text{GPL}} (k) = V_{\text{GPL}}^{*} \quad {\text{GPL-U}}$$

(1)

$$V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} \frac{{\left| { - 1 + 2k - N_{L} } \right|}}{{N_{L} }}\quad {\text{GPL-X}}$$

(2)

$$V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} \left[ {1 - \left( {\frac{{\left| {2k - N_{L} - 1} \right|}}{{N_{L} }}} \right)} \right]\quad {\text{GPL-O}}$$

(3)

$$V_{\text{GPL}} (k) = 2V_{\text{GPL}}^{*} (2k - 1)/N_{L} \quad {\text{GPL-A}}$$

(4)

The parameters participated in Eqs. (1–4) are introduced in Ref. [97] in detail. The explicit relation between $V_{\text{GPL}}^{*}$ and $g_{\text{GPL}}$ can be described by:

$$V_{\text{GPL}}^{*} = \frac{{g_{\text{GPL}} }}{{g_{\text{GPL}} + (\rho_{\text{GPL}} /\rho_{\text{m}} )(1 - g_{\text{GPL}} )}}$$

(5)

in which $\rho_{\text{GPL}}$ and $\rho_{\text{m}}$ are corresponding mass density of GPL and polymer matrix, respectively. The effective elastic modulus of the structure is approximated with the extended model of Halpin–Tsai micromechanics [98]

$$\bar{E} = \left( {\frac{3}{8}\left( {\frac{{1 + \xi_{L} \eta_{L} V_{\text{GPL}} }}{{1 - \eta_{L} V_{\text{GPL}} }}} \right) + \frac{5}{8}\left( {\frac{{1 + \xi_{W} \eta_{W} V_{\text{GPL}} }}{{1 - \eta_{W} V_{\text{GPL}} }}} \right)} \right) \times E_{M}$$

(6)

Also, $\xi_{L} = 2\frac{{L_{\text{GPL}} }}{{t_{\text{GPL}} }}$, $\xi_{W} = 2\frac{{w_{\text{GPL}} }}{{t_{\text{GPL}} }}$, $\eta_{L} = \frac{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{M} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{M} }$}}} \right) - 1}}{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{M} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{M} }$}}} \right) + \xi_{L} }}$ and $\eta_{W} = \frac{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{M} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{M} }$}}} \right) - 1}}{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{M} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{M} }$}}} \right) + \xi_{W} }}$. Finally, by utilizing the well-known rule of mixture, corresponding Poisson’s ratio $\nu_{c}$ and mass density $\rho_{c}$ of the microcomposite consisted of GNP and polymer are approximated as:

$$\begin{aligned} \bar{\nu } & = \nu_{\text{GPL}} V_{\text{GPL}} + \nu_{M} V_{M} , \\ \bar{\rho } & = \rho_{\text{GPL}} V_{\text{GPL}} + \rho_{M} V_{M} . \\ \end{aligned}$$

(7)

2.1 Displacement fields in the circular plate

HOSD theory is chosen to define the corresponding displacement fields of the GPLRC disk according to the subsequent relation [82, 83, 90, 99,100,101,102,103,104,105,106,107,108,109,110,111]:

$$\begin{aligned} & u^{c} (R,z,t) = z^{c} u^{c}_{1} (R,t) + u^{c}_{0} (R,t) - \left[ {u^{c}_{1} (R,t) + \frac{{\partial w^{c}_{0} (R,t)}}{\partial R}} \right]c_{1} z^{c\;3} \\ & v^{c} (R,z,t) = 0 \\ & w^{c} (R,z,t) = w^{c}_{0} (R,t). \\ \end{aligned}$$

(8)

Based on the conventional form of HOSDT [112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129], c₁ is equal to 4/3h².

2.2 Strain–stress of core

According to HOSDT, one can formulate the strain–stress relations as follows:

$$\begin{aligned} & \left\{ \begin{aligned} \sigma^{c}_{RR} \hfill \\ \sigma^{c}_{\,\theta \theta } \hfill \\ \sigma^{c}_{\,rz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {Q_{11} } \hfill & {\quad Q_{12} } \hfill & {\quad 0} \hfill \\ {Q_{12} } \hfill & {\quad Q_{22} } \hfill & {\quad 0} \hfill \\ 0 \hfill & {\quad 0} \hfill & {\quad Q_{55} } \hfill \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon^{c}_{\,RR\,} - \alpha \Delta T \hfill \\ \varepsilon^{c}_{\,\theta \theta \,} \hfill \\ \gamma^{c}_{\,rz\,} \hfill \\ \end{aligned} \right\} \\ & Q_{11} = Q_{22} = \frac{{E^{c} }}{{1 - \nu^{c\;2} }},\quad Q_{12} = \frac{{E_{c} \nu_{c} }}{{1 - \nu^{c\;2} }},\quad Q_{55} = \frac{{E^{c} }}{{2(1 + \nu^{c} )}}, \\ \end{aligned}$$

(9)

and strain components would be written as:

$$\left\{ \begin{aligned} \varepsilon^{c}_{RR} \hfill \\ \varepsilon^{c}_{\theta \theta } \hfill \\ \gamma^{c}_{Rz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {\frac{{z\partial u^{c}_{1} }}{\partial R} + \frac{{\partial u^{c}_{0} }}{\partial R} - z^{3} c_{1} \left( {\frac{{\partial u^{c}_{1} }}{\partial R} + \frac{{\partial^{2} w^{c}_{0} }}{{\partial R^{2} }}} \right)} \hfill \\ {\frac{{u^{c}_{0} }}{R} + z\frac{{u^{c}_{1} }}{R} - z^{c} \;^{3} c_{1} \left( {\frac{{u^{c}_{1} }}{R} + \frac{{\partial w^{c}_{0\,} }}{R\partial R}} \right)} \hfill \\ {\left( {u^{c}_{1} + \frac{{\partial w^{c}_{0} }}{\partial R}} \right)( - 3z^{c} \;^{2} c_{1} + 1)} \hfill \\ \end{array} } \right].$$

(10)

2.3 Piezoelectric displacement fields

On the basis of HOSDT, the piezoelectric microdisk displacement fields can be obtained as follows:

$$\begin{aligned} & u^{p} (R,z,t) = z^{p} u^{p}_{1} (R,t) + u^{p}_{0} (R,t) - \left[ {\frac{{\partial w^{p}_{0} (R,t)}}{\partial R} + u^{p}_{1} (R,t)} \right]c_{1} z^{p\;3} \\ & v^{p} (R,z,t) = 0 \\ & w^{p} (R,z,t) = w^{p}_{0} (R,t). \\ \end{aligned}$$

(11)

2.4 Strain–stress of piezoelectric

The corresponding stress and strain tensors of the PIACs are associated with each other according to the following equations:

$$\left\{ \begin{aligned} \sigma^{p}_{RR} \hfill \\ \sigma^{p}_{\theta \theta } \hfill \\ \sigma^{p}_{Rz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {Q_{11} } \hfill & {\quad Q_{12} } \hfill & {\quad 0} \hfill \\ {Q_{12} } \hfill & {\quad Q_{22} } \hfill & {\quad 0} \hfill \\ 0 \hfill & {\quad 0} \hfill & {\quad Q_{55} } \hfill \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon^{p}_{RR} \hfill \\ \varepsilon^{p}_{\theta \theta } \hfill \\ \gamma^{p}_{Rz} \hfill \\ \end{aligned} \right\} - \left[ {\begin{array}{*{20}l} 0 \hfill & {\quad 0} \hfill & {\quad e_{31} } \hfill \\ 0 \hfill & {\quad e_{32} } \hfill & {\quad 0} \hfill \\ {e_{15} } \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ \end{array} } \right]\left\{ \begin{aligned} E^{p}_{R} \hfill \\ E^{p}_{\theta } \hfill \\ E^{p}_{z} \hfill \\ \end{aligned} \right\}$$

(12)

$$\left\{ \begin{aligned} D^{p}_{\,R\,} \hfill \\ D^{p}_{\,\theta \,} \hfill \\ D^{p}_{\,z\,} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & {e_{15} } \\ 0 & {e_{22} } & 0 \\ {e_{31} } & 0 & 0 \\ \end{array} } \right]\left[ \begin{aligned} \varepsilon^{p}_{\,RR\,} \hfill \\ \varepsilon^{p}_{\,\theta \theta \,} \hfill \\ \varepsilon^{p}_{\,Rz\,} \hfill \\ \end{aligned} \right] + \left[ {\begin{array}{*{20}c} {s_{11} } & 0 & 0 \\ 0 & {s_{22} } & 0 \\ 0 & 0 & {s_{33} } \\ \end{array} } \right]\left\{ \begin{aligned} E^{p}_{\,R\,} \hfill \\ E^{p}_{\,\theta \,} \hfill \\ E^{p}_{\,z\,} \hfill \\ \end{aligned} \right\}$$

(13)

where s_im, e_mij, and Q_ij in order stand for the dielectric and piezoelectric constants, and elasticity matrix. E_m and D_i indicate electric fields strength and electric displacements of the piezoelectric disk, respectively. Corresponding electric and magnetic field strength, i.e., E_x, E_θ, E_z, which are participated in Eqs. (12) and (13), would be formulated as:

$$\begin{aligned} E_{R} & = - \frac{{\partial \tilde{\Phi }}}{\partial R} \\ E_{z} & = - \frac{{\partial \tilde{\Phi }}}{\partial z}. \\ \end{aligned}$$

(14)

Wang [130] explored that the electric potential ($\Phi (x,\theta ,z,t)$) can be accounted as:

$$\Phi (R,z,t) = \frac{{2z\phi_{0} }}{h} - \phi (R,t)\cos (\beta z)$$

(15)

in which β = π/h and $\phi_{0}$ stands for the initial external electric.

2.5 E-compatibility equations

Following relations present mathematical expression for the conditions of compatibility taking perfect bonding between the core and PIAC section and taken into consideration at $z_{\text{p}} = - h_{\text{p}} /2$:

$$\begin{aligned} & \left. {u^{c} } \right|_{{z_{c} = h_{c} /2}} = \left. {u^{p} } \right|_{{z_{\text{p}} = - h_{\text{p}} /2}} , \\ & \left. {w^{c} } \right|_{{z_{c} = h_{c} /2}} = \left. {w^{p} } \right|_{{z_{\text{p}} = - h_{\text{p}} /2}} . \\ \end{aligned}$$

(16)

Based on Eq. (16), the displacement-dependent parameters are related to each other in the PIAC as follows:

$$\begin{aligned} & c_{1} \left( {\frac{{ - h^{c} }}{2}} \right)^{3} \left[ {\frac{{\partial w^{c}_{0} }}{\partial R}} \right] + c_{1} \left( {\frac{{h^{p} }}{2}} \right)^{3} \left[ { + \frac{{\partial w^{p}_{0} }}{\partial R}} \right] = u^{p}_{0} - u^{c}_{0} + u^{c}_{1} \left[ {c_{1} \left( {\frac{{h^{c} }}{2}} \right)^{3} - \frac{{h^{c} }}{2}} \right] - u^{p}_{1} \left[ {c_{1} \left( {\frac{{h^{p} }}{2}} \right)^{3} + \frac{{h^{p} }}{2}} \right], \\ & w^{c}_{0} = w^{p}_{0} . \\ \end{aligned}$$

(17)

2.6 Extended Hamilton’s principle

In order to acquire the governing equations and related boundary conditions, we can utilize Hamilton’s principle as follows:

$$\begin{aligned} & \int_{{t_{1} }}^{{t_{2} }} {(\delta U^{i} - \delta W^{i} )} {\text{d}}t = 0 \\ & i = c,p \\ \end{aligned}$$

(18)

the following relation describes the components involved in the process of obtaining the strain energy of the aforementioned microdisk:

$$\begin{aligned} \delta U^{c} & = \frac{1}{2}\iiint\limits_{V} {\sigma^{c}_{ij\,} \delta \varepsilon^{c}_{ij} {\text{d}}V} \\ & = \int {\left[ {\begin{array}{*{20}l} {\left[ {N^{c}_{RR} \frac{{\partial \delta u^{c}_{0} }}{{\partial R^{c} }} + M^{c}_{RR} \frac{{\partial \delta u^{c}_{1} }}{{\partial R^{c} }} - P^{c}_{RR\,} c_{1} \left( {\frac{{\partial \delta u^{c}_{1} }}{{\partial R^{c} }} + \frac{{\partial^{2} \delta w^{c}_{0} }}{{\partial R^{c2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {N^{c}_{\theta \theta } \frac{{\delta u^{c}_{0} }}{{R^{c} }} + M^{c}_{\theta \theta } \frac{{\delta u^{c}_{1} }}{{R^{c} }} - P^{c}_{\theta \theta } c_{1} \left( {\frac{{\delta u^{c}_{1} }}{{R^{c} }} + \frac{{\partial \delta w^{c}_{0} }}{{R\partial R^{c} }}} \right)} \right]} \hfill \\ {\quad + \left[ {(Q^{c}_{Rz} - 3S^{c}_{Rz} c_{1} )\left( {\delta u^{c}_{1} + \frac{{\partial \delta w^{c}_{0} }}{{\partial R^{c} }}} \right)} \right]} \hfill \\ \end{array} } \right]{\text{d}}R} \\ \end{aligned}$$

(19)

$$\begin{aligned} \delta U^{p} & = \frac{1}{2}\iiint\limits_{V} {\sigma^{p}_{ij} \delta \varepsilon^{p}_{ij} {\text{d}}V} - \iiint\limits_{{V_{\text{piezolayer}} }} {(D^{p}_{R} \delta E^{p}_{R} + D^{p}_{z} \delta E^{p}_{z} ){\text{d}}V_{\text{piezolayer}} } \\ & = \int {\left[ {\begin{array}{*{20}l} {\left[ {N^{p}_{RR} \frac{{\partial \delta u^{p}_{0} }}{{\partial R^{p} }} + M^{p}_{RR} \frac{{\partial \delta u^{p}_{1} }}{{\partial R^{p} }} - P^{p}_{RR} c_{1} \left( {\frac{{\partial \delta u^{p}_{1} }}{{\partial R^{p} }} + \frac{{\partial^{2} \delta w^{p}_{0} }}{{\partial R^{p2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {N^{p}_{\theta \theta } \frac{{\delta u^{p}_{0} }}{{R^{p} }} + M^{p}_{\theta \theta } \frac{{\delta u^{p}_{1} }}{{R^{p} }} - P^{p}_{\theta \theta } c_{1} \left( {\frac{{\delta u^{p}_{1} }}{{R^{p} }} + \frac{{\partial \delta w^{p}_{0} }}{{R^{p} \partial R^{p} }}} \right)} \right]} \hfill \\ {\quad + \left[ {(Q^{p}_{Rz} - 3S^{p}_{Rz} c_{1} )\left( {\delta u^{p}_{1} + \frac{{\partial \delta w^{p}_{0} }}{{\partial R^{p} }}} \right)} \right]} \hfill \\ \end{array} } \right]{\text{d}}R^{p} } \\ & \quad - \int_{0}^{2\pi } {\int_{{R_{i} }}^{{R_{o} }} {\int_{{ - h_{p} /2}}^{{h_{p} /2}} {\left[ {\begin{array}{*{20}l} {D^{p}_{R} \left\{ {\cos (\beta z)\frac{\partial }{{\partial R^{p} }}\delta \phi } \right\}} \hfill \\ {\quad - D^{p}_{z} (\beta \sin (\beta z)\delta \phi )} \hfill \\ \end{array} } \right]} } } R{\text{d}}R{\text{d}}\theta \\ \end{aligned}$$

(20)

where

$$\begin{aligned} & \int_{z} {\left\{ {\sigma^{i}_{RR} ,z\sigma^{i}_{RR} ,z^{3} \sigma^{i}_{RR} } \right\}} {\text{d}}z = \left\{ {N^{i}_{RR} ,M^{i}_{RR} ,P^{i}_{RR} } \right\} = ;\quad i = c,p \\ & \int_{z} {\left\{ {\sigma^{i}_{\theta \theta } ,z\sigma^{i}_{\theta \theta } ,z^{3} \sigma^{i}_{\theta \theta } } \right\}} {\text{d}}z = \left\{ {N^{i}_{\theta \theta } ,M^{i}_{\theta \theta } ,P^{i}_{\theta \theta } } \right\} = ; \\ & \int_{z} {\left\{ {\sigma^{i}_{Rz} ,z^{2} \sigma^{i}_{Rz} } \right\}} {\text{d}}z = \left\{ {Q^{i}_{Rz} ,S^{i}_{Rz} } \right\} = ; \\ \end{aligned}$$

(21)

The first variation of the external work applied by an external electrical load to the structure can be obtained as follows [51]:

$$W_{1} = \frac{1}{2}\int\limits_{z} {\left[ {(N_{i}^{P} )w^{2}_{,x} } \right]{\text{d}}R} ,\quad i = 1,2$$

(22)

where N ^P_i represents the external electric load which could be acquired as follows:

$$N_{i}^{P} = - 2\left( {e_{31} - \frac{{c_{13} e_{33} }}{{c_{33} }}} \right)\phi_{0} .$$

(23)

Eventually, differential equations of motion of the microstructure are extracted as follows:

$$\begin{aligned} & \delta u^{i}_{0} :\\ & \quad \frac{{\partial N^{i}_{RR} }}{\partial R} - \frac{{N^{i}_{\theta \theta } }}{R} = 0, \\ & \delta w^{i}_{0} :\\ & \quad c_{1} \frac{{\partial^{2} P^{i}_{RR} }}{{\partial R^{i2} }} - c_{1} \frac{{\partial P^{i}_{\theta \theta } }}{{R^{i} \partial R^{i} }} + \frac{{\partial Q^{i}_{Rz} }}{{\partial R^{i} }} - 3c_{1} \frac{{\partial S^{i}_{Rz} }}{{\partial R^{i} }} - N_{1}^{p} w^{i}_{{0,x^{2} }} = 0, \\ & \delta u^{i}_{1} :\\ & \quad \frac{{\partial M^{i}_{RR} }}{{\partial R^{i} }} - \frac{{\partial P^{i}_{RR} }}{{\partial R^{i} }}c_{1} - \frac{{M^{i}_{\theta \theta } }}{{R^{i} }} + \frac{{P^{i}_{\theta \theta } c_{1} }}{{R^{i} }} - Q^{i}_{Rz} + 3S^{i}_{Rz} c_{1} = 0, \\ & \delta \phi :\\ & \quad - (X_{11} - 3X_{12} )\left( {u^{p}_{1} \frac{\partial }{{\partial R^{p} }}\delta \phi + \frac{{\partial w^{p}_{0} }}{{\partial R^{p} }}\frac{\partial }{{\partial R^{p} }}\delta \phi } \right) \\ & \quad \; + \frac{\partial }{{\partial R^{p} }}\delta \phi X_{41} \partial \phi /\partial R^{p} \\ & \quad \; + \left( {X_{31} \frac{{\partial u^{p}_{0} }}{\partial R}\delta \phi + X_{32} \frac{{\partial u^{p}_{1} }}{\partial R}\delta \phi - X_{33} \left( {\frac{{\partial u^{p}_{1} }}{\partial R}\delta \phi + \frac{{\partial^{2} w^{p}_{0} }}{{\partial R^{2} }}\delta \phi } \right)} \right) + X_{42} \phi \delta \phi = 0,\quad i = c,p \\ \end{aligned}$$

(24)

where

$$\begin{aligned} N^{i}_{RR} & = \left[ {A^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + B^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - D^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + \left[ {A^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + B^{i}_{12} \frac{{u_{1} }}{R} - D^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ & \quad - X_{31} \phi \\ M^{i}_{RR} & = \left[ {B^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + C^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - E^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + \left[ {B^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + C^{i}_{12} \frac{{u^{i}_{1} }}{{R^{i} }} - E^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ & \quad - X_{32} \phi \\ P^{i}_{RR} & = \left[ {D^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + \left[ {D^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{12} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ & \quad - X_{33} \phi \\ N^{i}_{\theta \theta } & = \left[ {A^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + B^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - D^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + Q^{i}_{22} \left[ {A^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + B^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - D^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ M^{i}_{\theta \theta } & = \left[ {B^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + C^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - E^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + Q^{i}_{22} \left[ {B^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + C^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - E^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ P^{i}_{\theta \theta } & = \left[ {D^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right] + Q^{i}_{22} \left[ {D^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] \\ Q^{i}_{Rz} & = (A^{i}_{55} - 3C^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{11} \partial \phi /\partial R^{i} \\ S^{i}_{Rz} & = (C^{i}_{55} - 3E^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{12} \partial \phi /\partial R^{i} ;\quad i = c,p \\ \end{aligned}$$

(25)

and

$$\left[ {A^{i}_{ij} ,B^{i}_{ij} ,C^{i}_{ij} ,D^{i}_{ij} ,E^{i}_{ij} ,F^{i}_{ij} ,G^{i}_{ij} } \right] = \int\limits_{ - h/2}^{h/2} {Q_{ij} \left[ {1,z^{i} ,z^{i2} ,z^{i3} ,z^{i4} ,z^{i5} ,z^{i6} } \right]} {\text{d}}z;\quad i = c,p$$

(26)

Moreover, the parameters involved in the equation of the PIAC can be given as follows:

$$\begin{aligned} & X_{11} = \int {e_{15} \cos (\beta z)} ,\quad X_{12} = \int {e_{15} z^{2} c_{1} \cos (\beta z)} ,\quad X_{31} = \int {\beta e_{31} \sin (\beta z)} , \\ & X_{32} = \int {z\beta e_{31} \sin (\beta z)} ,\quad X_{33} = \int {z^{3} c_{1} \beta e_{31} \sin (\beta z)} , \\ & X_{41} = \int {s_{11} \left( {\cos (\beta z)} \right)^{2} } ,\quad X_{42} = \int {s_{33} \left( {\beta \sin (\beta z)} \right)^{2} } \\ \end{aligned}$$

(27)

It should be noticed that based on the compatibility relation (Eq. 16), the number of corresponding unknown variables of the core is declined from 5 to 3. Thus, the total number of unknowns in the piezoelectric face sheet and the GPLRC core is reduced to 8.

2.7 NSG theory

In the present article, the size-dependent effects are captured in the mathematical model through NSG theory. According to the theory, corresponding stain and stress tensors of microstructure are correlated with each order as follows:

$$(1 - \mu^{2} \nabla^{2} )t^{i}_{ij} = C^{i}_{ijck} (1 - l^{2} \nabla^{2} )\varepsilon^{i}_{ck} ;\quad i = c,p$$

(28)

where $\nabla^{2} = \partial^{2} /\partial \theta^{2} + \partial /R\partial \theta$, $C_{ijck}$, $\varepsilon_{ck}$, and $t_{ij}$ are tensors of elasticity, strain, and stress of NSGT, respectively. According to NSGT, the tensor of stress would be presented by the subsequent relation [43]:

$$t^{i}_{ij} = \sigma^{i}_{ij} - \nabla \sigma_{ij}^{i\left( 1 \right)} ;\quad i = c,p$$

(29)

Based on Eq. (29), the extended form of the relation between stress and strain would be expressed as follows [131]:

$$(1 - \mu ^{2} \nabla ^{2} )\left\{ \begin{gathered} t^{i} _{{RR}} \hfill \\ t^{i} _{{\theta \theta }} \hfill \\ t^{i} _{{Rz}} \hfill \\ \end{gathered} \right\} = (1 - l^{2} \nabla ^{2} )\left[ {\begin{array}{*{20}l} {\quad Q_{{11}} } \hfill & {\quad Q_{{12}} } \hfill & {\quad 0} \hfill \\ {\quad Q_{{12}} } \hfill & {\quad Q_{{22}} } \hfill & {\quad 0} \hfill \\ {\quad 0} \hfill & {\quad 0} \hfill & {\quad Q_{{55}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\varepsilon ^{i} _{{rr}} - \alpha \Delta T} \hfill \\ {\varepsilon ^{i} _{{\theta \theta }} } \hfill \\ {\gamma ^{i} _{{rz}} } \hfill \\ \end{array} } \right\};\quad i = c,p$$

(30)

Thus, the governing differential equations of motion of the microdisk in thermal environment joint with the PIAC are derived as follows:

$$\begin{aligned} & \delta u^{i}_{0} :\\ & \quad (1 - l^{2} \nabla^{2} )\,\left[ {\frac{{\partial N^{i}_{RR} }}{\partial R} - \frac{{N^{i}_{\theta \theta } }}{R}} \right] = 0, \\ & \delta w^{i}_{0} :\\ & \quad (1 - l^{2} \nabla^{2} )\left[ {c_{1} \frac{{\partial^{2} P^{i}_{RR} }}{{\partial R^{i2} }} - c_{1} \frac{{\partial P^{i}_{\theta \theta } }}{{R^{i} \partial R^{i} }} + \frac{{\partial Q^{i}_{Rz} }}{{\partial R^{i} }} - 3c_{1} \frac{{\partial S^{i}_{Rz} }}{{\partial R^{i} }} - N_{1}^{p} w^{i}_{{0,x^{2} }} } \right] = 0, \\ & \delta u^{i}_{1} :\\ & \quad (1 - l^{2} \nabla^{2} )\left[ {\frac{{\partial M^{i}_{RR} }}{{\partial R^{i} }} - \frac{{\partial P^{i}_{RR} }}{{\partial R^{i} }}c_{1} - \frac{{M^{i}_{\theta \theta } }}{{R^{i} }} + \frac{{P^{i}_{\theta \theta } c_{1} }}{{R^{i} }} - Q^{i}_{Rz} + 3S^{i}_{Rz} c_{1} } \right] = 0, \\ & \delta \phi :\\ & \quad (1 - l^{2} \nabla^{2} )\left( \begin{aligned} + X_{31} \frac{{\partial u^{p}_{0} }}{{\partial R^{p} }} + (X_{11} - 3X_{12} )\frac{{\partial^{2} w^{p}_{0} }}{{\partial R^{p2} }} - X_{33} \frac{{\partial^{2} w^{p}_{0} }}{{\partial R^{p2} }} \hfill \\ \quad - ( - X_{11} + 3X_{12} )\frac{{\partial u^{p}_{1} }}{{\partial R^{p} }} + X_{32} \frac{{\partial u^{p}_{1} }}{{\partial R^{p} }} - X_{33} \frac{{\partial u^{p}_{1} }}{{\partial R^{p} }} \hfill \\ \quad - X_{41} \frac{{\partial^{2} \phi }}{{\partial R^{p2} }} + X_{42} \phi \hfill \\ \end{aligned} \right) = 0;\quad i = c,p \\ \end{aligned}$$

(31)

Eventually, the related boundary conditions would be formulated as follows:

$$\begin{aligned} & \delta u^{i}_{0} = 0\;{\text{or}}\;(1 - l^{2} \nabla^{2} )\left( {N^{i}_{RR} } \right)n^{i}_{R} \\ & \delta w^{i}_{0} = 0\;{\text{or}}\;(1 - l^{2} \nabla^{2} )\,\left( { - P^{i}_{RR} c_{1} + c_{1} \frac{{\partial P^{i}_{RR} }}{{\partial R^{i} }} - \frac{{P^{i}_{\theta \theta } c_{1} }}{{R^{i} }} + (Q^{i}_{Rz} - 3S^{i}_{Rz} c_{1} )} \right)n^{i}_{R} ,\quad i = c,p \\ & \delta u^{i}_{1} = 0\;{\text{or}}\;(1 - l^{2} \nabla^{2} )\left( {M^{i}_{RR} - P^{i}_{RR} c_{1} } \right)n^{i}_{R} , \\ & \delta \phi = 0 \\ \end{aligned}$$

(32)

The governing equations of the smart microstructure are presented in the Appendix section.

2.8 Solution procedure

In order to explore the vibration performance of the microdisk in this survey, a numerical solution approach based on the well-known GDQM is followed. According to this method, the nth-order derivatives of a smooth function f would be obtained by the following expression [132]:

$$\frac{{\partial^{n} f}}{{\partial R^{n} }} = \sum\limits_{m = 1}^{M} {C^{\left( n \right)}_{j,m} f_{m,k} }$$

(33)

The weighting coefficients associated with nth-order derivative along the radius direction is defined as C⁽ⁿ⁾. From Eq. (33), it is apparent that calculating the weighting coefficients is the essential parts of DQM. To estimate the nth-order derivatives of function along radius direction, two forms of DQM developed of GDQM are adopted in this study. Thus, the weighting coefficients are computed from the first-order derivative which is shown as

$$\begin{array}{*{20}l} {C_{ij}^{\left( 1 \right)} = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}} \hfill & {\quad i,j = 1,2, \ldots ,n} \hfill \\ {} \hfill & {\quad i \ne j} \hfill \\ {C_{ij}^{\left( 1 \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( 1 \right)} } } \hfill & {\quad i = j} \hfill \\ \end{array}$$

(34)

here,

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)}$$

(35)

Likewise, the weighting coefficients for higher-order derivatives can be calculated using the shown expressions.

$$\begin{aligned} & C_{ij}^{\left( r \right)} = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right] \\ & i,j = 1,2, \ldots ,n,\;i \ne j \\ & {\text{and}} \\ & 2 \le r \le n - 1 \\ & C_{ii}^{\left( r \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( r \right)} } \\ & i,j = 1,2, \ldots ,n \\ & {\text{and}} \\ & 1 \le r \le n - 1 \\ \end{aligned}$$

(36)

Currently, in this research, a non-uniform batch of seeds is chosen in r axis which is shown as:

$$r_{i} = \frac{{R_{0} - R_{i} }}{2}\left( { - \cos \left( {{{\left( {i - 1} \right)} \mathord{\left/ {\vphantom {{\left( {i - 1} \right)} {\left( {N_{i} - 1} \right)}}} \right. \kern-0pt} {\left( {N_{i} - 1} \right)}}\pi } \right) + 1} \right) + R_{i} \quad i = 1,2,3, \ldots ,N_{i}$$

(37)

Considering the linear motion equations of the structure, we can obtain the total stiffness as follows:

$$\left\{ {\left[ {\begin{array}{*{20}c} {\left[ {K_{dd} } \right]} & {\left[ {K_{db} } \right]} \\ {\left[ {K_{bd} } \right]} & {\left[ {K_{bb} } \right]} \\ \end{array} } \right]} \right\}\left\{ \begin{aligned} \delta_{d} \hfill \\ \delta_{b} \hfill \\ \end{aligned} \right\} = 0$$

(38)

where the subscripts b and d represent the boundary and domain grid points, respectively. Moreover, $\delta$ denotes the vector of displacements. Equation (38) would be transformed into a standard form of eigenvalue problem:

$$\begin{aligned} & [K^{ * } ]\{ \delta_{i} \} = 0, \\ & [K^{ * } ] = [K_{dd} - K_{db} K_{bb}^{ - 1} K_{bd} ] \\ \end{aligned}$$

(39)

2.9 Convergencey

A sufficient number of elements and grid points are essential for obtaining the accurate results in FEM and GDQM [55,56,57,58,59, 133,134,135,136,137,138,139,140,141,142,143,144,145,145]. To guarantee an acceptable accuracy in the results of GDQM, it is crucial to find a sufficient number of grid points. Accordingly, the convergence study is performed for different cases of boundary conditions and also h_p/h ratio. As shown in Table 1, N = 17 as the number of grid points can provide the sufficient accuracy of GDQM results.

Table 1 The effect of the number of grid points on the results convergence for the critical voltage of the GNPRC microdisk with respect to different piezoelectric thickness and boundary conditions (B. Cs) when R_o/R_i = 1.3, h/R = 0.1, l = R/10, pattern 1

2.10 Validation

Numerical results from Table 3, for an isotropic circular plate and different geometrical parameters, were varied with those Ref. [146], to examine the efficiency and validity approach for this study. The maximal discrepancy, as entailed by the reconciliation reported in the table, is relatively 1% (Table 2).

Table 2 Comparison of obtained dynamic response for different h/R_o and boundary conditions with the result of Ref [79]

3 Results

A GPL with a thickness of h_GNP= 1.5 nm and radius of R_GNP = 0.75 μm is used and presented in Table 3. It should be mentioned that the corresponding properties of piezoelectric material are provided in Table 4.

Table 3 Material properties of the epoxy and GPL [80]

Table 4 Material properties of piezoelectric layer which is composed of BiTiO₃–CoFe₂O₄ [81]

Figures 2, 3, and 4 show $g_{\text{GPL}}$ and GPLRC pattern’s effects on the critical voltage of the microdisk under various boundary conditions.

Fig. 2

Effects of different values and various distribution patterns of the GPL on the critical voltage of the GPLRC microdisk covered with a piezoelectric layer for simply–simply boundary conditions

Fig. 3

Effects of different values and various distribution patterns of the GPL on the critical voltage of the GPLRC microdisk covered with a piezoelectric layer for clamped–simply boundary conditions

Fig. 4

Effects of different values and various distribution patterns of the GPL on the critical voltage of the GPLRC microdisk covered with a piezoelectric layer for clamped–clamped boundary conditions

As a typical result which can label Figs. 2, 3, and 4, for S–S, C–S, and C–C boundary conditions and each GPLRC pattern, there is a direct or positive effect from on the critical voltage of the smart microdisk. According to these figures, the best pattern of the GPRC microdisk for having the highest critical voltage at all ranges of the parameter is pattern 3. For all patterns, the relation between parameter and critical voltage is linear, and when the boundary conditions are considered S–S, patterns 4 and 1 have not shown any effect on the critical voltage of the structure. As an astonishing result from Figs. 2, 3, and 4, when the boundary conditions change from S–S to C–C, the influence of GPL pattern on the critical voltage of the smart circular structure in all ranges of the parameter decreases.

Figures 5, 6, and 7 show the effects of different values of $g_{\text{GPL}}$ and ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameters on the critical voltage of the smart microdisk.

Fig. 5

Effects of different values of $g_{\text{GPL}}$ and ${h \mathord{\left/{\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ on the critical voltage of the GPLRC microdisk covered with a piezoelectric sensor for simply–simply boundary conditions

Fig. 6

Effects of different values of $g_{\text{GPL}}$ and ${h \mathord{\left/{\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ on the critical voltage of the GPLRC microdisk covered with a piezoelectric sensor for clamped–simply boundary conditions

Fig. 7

Effects of different values of $g_{\text{GPL}}$ and ${h \mathord{\left/{\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ on the critical voltage of the GPLRC microdisk covered with a piezoelectric sensor for clamped–clamped boundary conditions

Accordion to Figs. 5, 6, and 7, for a specific value of the ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameter and all boundary conditions, by increasing the value of the $g_{\text{GPL}}$, critical voltage of the structure increases linearly. As an astonishing result for the literature, there is a positive and direct relation between ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ and critical voltage of the structure. As a conclusion from Figs. 5, 6, and 7, when the rigidity of the structure increased, the influences of the ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameter on the critical voltage decrease. Besides, having an exact glance to these figures can find out an interesting result which as well as the positive effect from $g_{\text{GPL}}$ on the critical voltage, by increasing $g_{\text{GPL}}$ the positive impact of ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameter on the critical voltage of the structure has been intensified. For greater $g_{\text{GPL}}$ parameter, the effect of ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameter on the critical voltage is more significant in comparison with at the lower value of it.

The main point of Table 5 is a presentation about the influences of the length scale (l/h) and R_o/h parameters on the critical voltage of the simply supported microcircular plate covered with a piezoelectric sensor. According to Table 5, as well as an indirect effect from R_o/h parameter on the frequency, increasing the length scale parameter encounters the structure with a weakness in the dynamic stability of the structure. By having an exact glance at Table 5, the negative effect from R_o/h on the critical voltage of the smart circular plate is much more remarkable in comparison with the same impact from the length scale parameter on the natural property of the structure. As a useful suggestion for applied nanoindustries, by dedicating exact attention to Table 5 can conclude that the highest critical voltage of the composite microdisk is seen when the GPLRC pattern is considered as pattern 1. More on this research, Figs. 8, 9, and 10 have an interview about the impacts of the $g_{\text{GPL}}$ and ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ parameters on the critical voltage of the smart GPLRC microdisk. Correspondent to Figs. 8, 9, and 10, it would be a relevant result which both of $g_{\text{GPL}}$ and ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ parameters have an enhancing effect on the static response or critical voltage of the microstructure. It is evident that the relation between $g_{\text{GPL}}$ and critical voltage is direct and linear. In contrast, the relation between ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ and critical voltage is exponential, polynomial, and exponential for S–S, C–C, and C–S. For more comprehensive, it would be a useful suggestion for the literature, and by increasing the ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$, critical voltage of the smart structure increases more intensely in comparison with the $g_{\text{GPL}}$.

Table 5 Effect of different values of the R_o/h and l/h parameters on the static response of the smart microcircular plate

Fig. 8

Effects of $g_{\text{GPL}}$ and ${{R_{\text{o}} } \mathord{\left/{\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ parameters on the critical voltage of the GPLRC microdisk covered with piezoelectric sensor for simply–simply boundary conditions

Fig. 9

Effects of $g_{\text{GPL}}$ and ${{R_{\text{o}} } \mathord{\left/{\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ parameters on the critical voltage of the GPLRC microdisk covered with piezoelectric sensor for clamped–simply boundary conditions

Fig. 10

Effects of $g_{\text{GPL}}$ and ${{R_{\text{o}} } \mathord{\left/{\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$ parameters on the critical voltage of the GPLRC microdisk covered with piezoelectric sensor for clamped–clamped boundary conditions

4 Conclusion

For the first time, electrically responses of a GPLRC-reinforced microdisk covered with PIAC were explored using the GDQ method and NSG theory. The compatibility conditions were extracted by assuming perfect bonding at the contact interface of the PIAC and the core. Also, the piezoelectricity of the face sheet is modeled with the aid of Maxwell’s equation. The results displayed that $\Delta T$, ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$, different patterns of GPLs, and $g_{\text{GPL}}$ have significant impact on the critical voltage responses of the GPLRC microdisk. The main results are that:

• Changing from S–S to C–C, the influence of GPL pattern on the critical voltage decreases.

• At the greater $g_{\text{GPL}}$ parameter, the effect of ${h \mathord{\left/ {\vphantom {h {R_{\text{o}} }}} \right. \kern-0pt} {R_{\text{o}} }}$ parameter on the critical voltage is more significant in comparison with the lower value of it.

• By increasing the h_p/h, the critical voltage of the GPLRC microdisk covered with PIAC increases.

• By increasing ${{R_{\text{o}} } \mathord{\left/ {\vphantom {{R_{\text{o}} } {R_{\text{i}} }}} \right. \kern-0pt} {R_{\text{i}} }}$, the critical voltage of the smart structure increases more intensely in comparison with the $g_{\text{GPL}}$.

Appendix

The governing equations of the structure are presented as follows:

$$\begin{aligned} & \delta u^{i}_{0} :\\ & \quad (1 - l^{2} \nabla^{2} )\left[ {\begin{array}{*{20}l} {\frac{\partial }{\partial R}\left( {\begin{array}{*{20}l} {\left[ {A^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + B^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - D^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {A^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + B^{i}_{12} \frac{{u_{1} }}{R} - D^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] - X_{31} \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \frac{1}{R}\left( {\begin{array}{*{20}l} {\left[ {A^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + B^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - D^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {A^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + B^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - D^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-1)

$$\begin{aligned} & \delta w^{i}_{0} :\\ & \quad (1 - l^{2} \nabla^{2} )\left[ {\begin{array}{*{20}l} {c_{1} \frac{{\partial^{2} }}{{\partial R^{i2} }}\left( {\begin{array}{*{20}l} {\left[ {D^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {D^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{12} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] - X_{33} \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - c_{1} \frac{\partial }{{R^{i} \partial R^{i} }}\left( {\begin{array}{*{20}l} {\left[ {D^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {D^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad + \frac{\partial }{{\partial R^{i} }}\left( {(A^{i}_{55} - 3C^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{11} \partial \phi /\partial R} \right)} \hfill \\ {\quad - 3c_{1} \frac{\partial }{{\partial R^{i} }}\left( {(C^{i}_{55} - 3E^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{12} \partial \phi /\partial R^{i} } \right) - N_{1}^{p} w^{i}_{{0,x^{2} }} } \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-2)

$$\begin{aligned} & \delta u^{i}_{1} :\\ & \quad (1 - l^{2} \nabla^{2} )\left[ {\begin{array}{*{20}l} {\frac{\partial }{{\partial R^{i} }}\left( {\begin{array}{*{20}l} {\left[ {B^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + C^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - E^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {B^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + C^{i}_{12} \frac{{u^{i}_{1} }}{{R^{i} }} - E^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] - X_{32} \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \frac{{c_{1} \partial }}{{\partial R^{i} }}\left( {\begin{array}{*{20}l} {\left[ {D^{i}_{11} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{11} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{11} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + \left[ {D^{i}_{12} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{12} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right] - X_{33} \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \frac{1}{{R^{i} }}\left( {\begin{array}{*{20}l} {\left[ {B^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + C^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - E^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {B^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + C^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - E^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad + \frac{{c_{1} }}{{R^{i} }}\left( {\begin{array}{*{20}l} {\left[ {D^{i}_{12} \frac{{\partial u^{i}_{0} }}{{\partial R^{i} }} + E^{i}_{12} \frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} - G^{i}_{12} c_{1} \left( {\frac{{\partial u^{i}_{1} }}{{\partial R^{i} }} + \frac{{\partial^{2} w^{i}_{0} }}{{\partial R^{i2} }}} \right)} \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {D^{i}_{22} \frac{{u^{i}_{0} }}{{R^{i} }} + E^{i}_{22} \frac{{u^{i}_{1} }}{{R^{i} }} - G^{i}_{22} c_{1} \left( {\frac{{u^{i}_{1} }}{{R^{i} }} + \frac{{\partial w^{i}_{0} }}{{R^{i} \partial R^{i} }}} \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \left[ {(A^{i}_{55} - 3C^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{11} \partial \phi /\partial R^{i} } \right]} \hfill \\ {\quad + 3c_{1} \left( {S^{i}_{Rz} = (C^{i}_{55} - 3E^{i}_{55} c_{1} )\left( {u^{i}_{1} + \frac{{\partial w^{i}_{0} }}{{\partial R^{i} }}} \right) + X_{12} \partial \phi /\partial R^{i} } \right)} \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-3)

$$\begin{aligned} & \delta \phi :\\ & \quad (1 - l^{2} \nabla^{2} )\left( {\begin{array}{*{20}l} { + X_{31} \frac{{\partial u^{p}_{0} }}{{\partial R^{p} }} + (X_{11} - 3X_{12} )\frac{{\partial^{2} w^{p}_{0} }}{{\partial R^{p2} }} - X_{33} \frac{{\partial^{2} w^{p}_{0} }}{{\partial R^{p2} }}} \hfill \\ {\quad - ( - X_{11} + 3X_{12} )\frac{{\partial u^{p}_{1} }}{{\partial R^{p} }} + X_{32} \frac{{\partial u^{p}_{1} }}{{\partial R^{p} }} - X_{33} \frac{{\partial u^{p}_{1} }}{{\partial R^{p} }}} \hfill \\ {\quad - X_{41} \frac{{\partial^{2} \phi }}{{\partial R^{p2} }} + X_{42} \phi } \hfill \\ \end{array} } \right) = 0 \\ \end{aligned}$$

(P-4)

The GDQ form can be given as follows:

$$\begin{aligned} & \delta u^{i}_{0} :\\ & \quad \left( {1 - l^{2} \left( \begin{aligned} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } + \hfill \\ \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{1}{{R^{i} }} \hfill \\ \end{aligned} \right)} \right)\left[ {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {A^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{0} + B^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} } \hfill \\ {\quad - D^{i}_{11} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } w^{i}_{0} } \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad + \left[ {\begin{array}{*{20}l} { + B^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + A^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }}} \hfill \\ {\quad - D^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right] - X_{31} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \phi_{n} } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \frac{1}{R}\left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {A^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + B^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - D^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {\begin{array}{*{20}l} {A^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{0} }}{{R^{2i} {}_{n}}}} + B^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} } \hfill \\ {\quad - D^{i}_{22} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{w^{i}_{0} }}{{R^{2i} {}_{n}}}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ \end{array} } \right)} \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-5)

$$\begin{aligned} & \delta w^{i}_{0} :\\ & \quad \left( {1 - l^{2} \left( \begin{aligned} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } + \hfill \\ \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{1}{{R_{{}}^{i} }} \hfill \\ \end{aligned} \right)} \right)\left[ {\begin{array}{*{20}l} {c_{1} \left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {D^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } u^{i}_{0} + E^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } u^{i}_{1} } \hfill \\ {\quad - G^{i}_{11} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } u^{i}_{1} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(4)}_{n,v} } w^{i}_{0} } \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad + \left[ {\begin{array}{*{20}l} {D^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + E^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - G^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right] - X_{33} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - c_{1} \left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {D^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + E^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - G^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad + Q^{i}_{22} \left[ {\begin{array}{*{20}l} {D^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R^{2i} {}_{n}}} + E^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} \hfill \\ {\quad - G^{i}_{22} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R^{2i} {}_{n}}}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad + \left( {(A^{i}_{55} - 3C^{i}_{55} c_{1} )\left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } u^{i}_{1} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } w^{i}_{0} } \right) + X_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \phi } \right)} \hfill \\ {\quad - 3c_{1} \left( {\begin{array}{*{20}l} {(C^{i}_{55} - 3E^{i}_{55} c_{1} )\left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } u^{i}_{1} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } w^{i}_{0} } \right)} \hfill \\ {\quad + X_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \phi } \hfill \\ \end{array} } \right) - N_{1}^{p} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } w^{i}_{0} } \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-6)

$$\begin{aligned} & \delta u^{i}_{1} :\\ & \quad \left( {1 - l^{2} \left( \begin{aligned} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } + \hfill \\ \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{1}{{R_{{}}^{i} }} \hfill \\ \end{aligned} \right)} \right)\left[ {\begin{array}{*{20}l} {\left( \begin{aligned} \left[ {B^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{0} + C^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} - E^{i}_{11} c_{1} \left( {\begin{array}{*{20}l} {\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} } \hfill \\ {\quad + \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } w^{i}_{0} } \hfill \\ \end{array} } \right)} \right] \hfill \\ \quad + \left[ {\begin{array}{*{20}l} {B^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + C^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} - } \hfill \\ {E^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right] - X_{32} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \phi \hfill \\ \end{aligned} \right)} \hfill \\ {\quad - c_{1} \left( {\begin{array}{*{20}l} {\left[ {D^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{0} + E^{i}_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} - G^{i}_{11} c_{1} \left( {\begin{array}{*{20}l} {\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } u^{i}_{1} } \hfill \\ {\quad + \sum\limits_{v = 1}^{{N_{n} }} {C^{(3)}_{n,v} } w^{i}_{0} } \hfill \\ \end{array} } \right)} \right]} \hfill \\ {\quad + \left[ {\begin{array}{*{20}l} {D^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + E^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - G^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right] - X_{33} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \phi } \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {B^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + C^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - E^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{0} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad \; + Q^{i}_{22} \left[ {B^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{0} }}{{R^{2i} {}_{n}}}} + C^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} - E^{i}_{22} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{w^{i}_{0} }}{{R^{2i} {}_{n}}}} \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad + c_{1} \left( {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} {D^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{0} }}{{R_{n}^{i} }} + E^{i}_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }}} \hfill \\ {\quad - G^{i}_{12} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{{u^{i}_{1} }}{{R_{n}^{i} }} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \frac{{w^{i}_{1} }}{{R_{n}^{i} }}} \right)} \hfill \\ \end{array} } \right]} \hfill \\ {\quad \; + Q^{i}_{22} \left[ {D^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{0} }}{{R^{2i} {}_{n}}}} + E^{i}_{22} \sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} - G^{i}_{22} c_{1} \left( {\sum\limits_{v = 1}^{{N_{n} }} {\frac{{u^{i}_{1} }}{{R^{2i} {}_{n}}}} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} \frac{{w^{i}_{0} }}{{R^{2i} {}_{n}}}} } \right)} \right]} \hfill \\ \end{array} } \right)} \hfill \\ {\quad - \left[ {(A^{i}_{55} - 3C^{i}_{55} c_{1} )\left( {\sum\limits_{v = 1}^{{N_{n} }} {u^{i}_{0} } I_{v} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} w^{i}_{0} } } \right) + X_{11} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \phi } \right]} \hfill \\ {\quad + 3c_{1} \left( {(C^{i}_{55} - 3E^{i}_{55} c_{1} )\left( {\sum\limits_{v = 1}^{{N_{n} }} {u^{i}_{1} } I_{v} + \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} w^{i}_{0} } } \right) + X_{12} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \phi } \right)} \hfill \\ \end{array} } \right] = 0;\quad i = c,p \\ \end{aligned}$$

(P-7)

$$\begin{aligned} & \delta \phi :\\ & \quad \left( {1 - l^{2} \left( \begin{aligned} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } + \hfill \\ \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } \frac{1}{{R_{{}}^{i} }} \hfill \\ \end{aligned} \right)} \right)\left( {\begin{array}{*{20}l} { + X_{31} \sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } u^{p}_{0} + (X_{11} - 3X_{12} - X_{33} )\sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } w^{p}_{0} } \hfill \\ {\quad - ( - X_{11} + 3X_{12} - X_{32} + X_{33} )\sum\limits_{v = 1}^{{N_{n} }} {C^{(1)}_{n,v} } u^{p}_{1} } \hfill \\ {\quad - X_{41} \sum\limits_{v = 1}^{{N_{n} }} {C^{(2)}_{n,v} } \phi + X_{42} \sum\limits_{v = 1}^{{N_{n} }} \phi I_{v} } \hfill \\ \end{array} } \right) = 0 \\ \end{aligned}$$

(P-8)