1. Introduction

In the last few decades, studying symmetry theory has attracted the attention of many mathematical physicists. A symmetry allows transforming any solution of a partial differential equation (PDE) into a manifold of solutions of the same equation. Local symmetries are defined topologically, and their infinitesimals depend on only the independent variable and finite-order derivatives of the dependent variables. The well-known Lie point symmetries, contact symmetries, and higher-order symmetries are all local [1]–[3]. Because the infinitesimals of a local symmetry have the localization property, local symmetries are just a subset of all symmetries. A symmetry whose infinitesimals depend on integrals of dependent variables is said to be nonlocal. Compared with a local symmetry, a nonlocal symmetry can reflect the global behavior of dependent variables. Considering the absence of a unified approach for seeking nonlocal symmetries, Bluman and Cheviakov proposed a systematic method for finding them using potential systems obtained from conservation laws [4], [5]. Further, a method based on analyzing symmetries of the inverse potential systems was proposed in [6]–[8] for studying nonlocal symmetries of a system of PDEs. It was shown in several studies that in addition to potential systems, nonlocal symmetries can be constructed using a Darboux transformation [9], a Bäcklund transformation [10], a Lax pair [11], and so on.

Painlevé analysis is an effective method for investigating the integrability properties of PDEs [12]. It is known that the residue from a truncated Painlevé expansion is a nonlocal symmetry. Based on this, Lou et al. developed a concise method for constructing nonlocal symmetries of integrable systems[13], [14]. Subsequently, many nonlocal symmetries and interaction solutions of integrable systems such as the (2+1)-dimensional modified Korteweg–de Vries (mKdV)–Calogero–Bogoyavlenkskii–Schiff equation [15], the Gardner equation [16], the (2+1)-dimensional Konopelchenko–Dubrovsky equation [17], the reduced Maxwell–Bloch equations [18], and a (2+1)-dimensional nonlinear system [19] (which can be regarded as a generalized sine-Gordon equation) were investigated using the truncated Painlevé expansion method. Similarly to the truncated Painlevé expansion, we can substitute a consistent Riccati expansion (CRE) in an integrable equation and use it to construct a Bäcklund transformation, which is useful in studying solutions describing the interaction between a solitary wave and another nonlinear wave [20]. If the CRE method is applicable to an integrable equation, then this equation is CRE integrable. It was shown that many integrable systems have CRE integrability, for example, the (2+1)-dimensional KdV equation [21], the modified Kadomtsev–Petviashvili equation [22], and the (2+1)-dimensional Boussinesq equation [23].

As is known, a solitary wave, described by the classical KdV equation

$$u_t+6uu_x+u_{xxx}=0,$$

was first observed in a narrow channel by John Scott Russell in 1834. Later, the bell-shaped solution of the KdV equation was obtained, and the existence of solitary waves was thus proved mathematically. In recent years, more and more studies have shown that the KdV equation plays an important role in analyzing theoretical problems in many disciplines such as plasma physics, astrophysics, biology, ocean waves, and other interdisciplinary subjects.

Here, we consider the (2+1)-dimensional KdV–mKdV equation

$$u_t+u_{xxy}+4uu_y-4u^2u_y+2u_xv=0,\qquad v_x=u_y-2uu_y. $$
(1)

It is a generalization of the KdV equation from the standpoint of dimension and nonlinear terms. Clearly, if \(y=x\), then Eq. (1) is reducible to the KdV–mKdV equation

$$u_t+6uu_x-6u^2u_x+u_{xxx}=0.$$

Analyses of the algebraic, geometric, and also integrability properties of the KdV–mKdV equation can be found in many sources [24]–[27]. Equation (1) first appeared in studying a countable set of conservation laws of a two-dimensional nonlinear equation [28]. The (2+1)-dimensional KdV–mKdV equation is closely related to the (2+1)-dimensional Gardner equation [29]–[31]. A multisymplectic formulation was used in [32] to investigate the generalized (2+1)-dimensional KdV–mKdV equation. In [33], the integrability of Eq. (1) was investigated in the sense of Painlevé analysis, and some exact solutions were found using the Wronskian technique. In [34], traveling wave solutions and conservation laws were obtained for Eq. (1). In solid state physics, the phenomenon of the propagation of a thermal pulse through a single crystal of sodium fluoride can be explained using Eq. (1).

This paper is organized as follows. In Sec. 2, we use the Lie symmetry analysis method to obtain Lie point symmetries of Eq. (1) and derive the group transformations of solutions. In Sec. 3, we construct an optimal system of one-dimensional subalgebras of the Lie algebra using the Ibragimov method, which relies on only the commutator table of the symmetry operators. In Sec. 4, based on the optimal system, we consider similarity reductions and invariant solutions. In Sec. 5, we mainly focus on investigating nonlocal symmetries and Bäcklund transformations using the truncated Painlevé expansion method. In Sec. 6, applying the Bäcklund transformation obtained in Sec. 5, we construct lump-type solutions of Eq. (1). In Sec. 7, we investigate the CRE integrability of Eq. (1). In Sec. 8, we obtain soliton-cnoidal wave solutions. In Sec. 9, we present some conclusions.

2. Lie point symmetries

Proposition 1.

For (2+1)-dimensional KdV–mKdV equation (1), we have the six Lie point symmetries

$$\begin{aligned} \, &X_1=\frac{ \partial }{ \partial t},\qquad X_2=\frac{ \partial }{ \partial x},\qquad X_3=\frac{ \partial }{ \partial y}, \\ &X_4=2 \varphi (t)\frac{ \partial }{ \partial x}+ \varphi '(t)\frac{ \partial }{ \partial v},\qquad X_5=-t\frac{ \partial }{ \partial t}-y\frac{ \partial }{ \partial y}+v\frac{ \partial }{ \partial v}, \\ &X_6=-2t\frac{ \partial }{ \partial t}-2x\frac{ \partial }{ \partial x}- (4t-2y)\frac{ \partial }{ \partial y}+(2u-1)\frac{ \partial }{ \partial u}. \end{aligned} $$
(2)

Proof.

The Lie algebra of the (2+1)-dimensional KdV–mKdV equation is generated by the vector field

$$X=\xi^1(x,y,t,u,v)\frac{ \partial }{ \partial t}+\xi^2(x,y,t,u,v)\frac{ \partial }{ \partial x}+ \xi^3(x,y,t,u,v)\frac{ \partial }{ \partial y}+\eta^1(x,y,t,u,v)\frac{ \partial }{ \partial u}+ \eta^2(x,y,t,u,v)\frac{ \partial }{ \partial v}.$$

The third prolongation of \(X\) for Eq. (1) has the form

$$X^{(3)}_{}=X+\eta_t^{1(1)}\frac{ \partial }{{ \partial u_t}}+\eta_x^{1(1)} \frac{ \partial }{ \partial u_x}+\eta_y^{1(1)}\frac{ \partial }{{ \partial u_y}}+\eta_x^{2(1)} \frac{ \partial }{{ \partial v_x}}+\eta_{xxy}^{1(3)}\frac{ \partial }{ \partial u_{xxy}},$$

where the functions \(\eta_t^{1(1)}\), \(\eta_x^{1(1)}\), \(\eta_y^{1(1)}\), \(\eta_x^{2(1)}\), and \(\eta_{xxy}^{1(3)}\) are determined recursively. The invariance condition is

$$X^{(3)}(\Lambda_1)\big|_{\Delta_1=0}=0,\qquad X^{(3)}(\Lambda_2)\big|_{\Delta_2=0}=0,$$

where

$$\Delta_1=u_t+u_{xxy}+4uu_y-4u^2u_y+2u_xv,\qquad\Delta_2=v_x-u_y+2uu_y.$$

This invariance condition yields an overdetermined system of PDEs. Solving this system, we obtain

$$\begin{aligned} \, &\xi^1=(-2c_2-c_1)t+c_3,\qquad\xi^2=-2c_2x+2 \varphi (t)+c_4,\qquad \xi^3=(-4t+2y)c_2-c_1y+c_5, \\ &\eta^1=2c_2u-c_2,\qquad\eta^2=c_1v+ \varphi '(t). \end{aligned}$$

Therefore, the infinite-dimensional Lie algebra for Eq. (1) is spanned by the vector fields presented in the proposition.

To consider a finite-dimensional Lie algebra spanned by the operators in Proposition 1, we choose an arbitrary function \( \varphi (t)=t\). We then obtain the usual vector fields (2) with \(X_4=2t\, \partial / \partial x+ \partial / \partial v\).

Operators (2) generate a six-dimensional Lie algebra \(L_6\) under the commutators. These commutators are given in Table 1. We obtain the corresponding one-parameter Lie transformation group for \(X_i\) (\(i=1,\dots,6\)) by solving the Cauchy problem for the system of ordinary differential equations

$$\begin{aligned} \, &\frac{dt^*}{d \varepsilon }=\xi^1(t^*,x^*,y^*,u^*,v^*), \\ &\frac{dx^*}{d \varepsilon }=\xi^2(t^*,x^*,y^*,u^*,v^*),\qquad \frac{dy^*}{d \varepsilon }=\xi^3(t^*,x^*,y^*,u^*,v^*), \\ &\frac{du^*}{d \varepsilon }=\eta^1(t^*,x^*,y^*,u^*,v^*),\qquad \frac{dv^*}{d \varepsilon }=\eta^2(t^*,x^*,y^*,u^*,v^*), \\ &t^*|_{ \varepsilon =0}=t,\qquad x^*|_{ \varepsilon =0}=x,\qquad y^*|_{ \varepsilon =0}=y,\qquad u^*|_{ \varepsilon =0}=u,\qquad v^*|_{ \varepsilon =0}=v. \end{aligned}$$

As a result, we obtain six one-parameter groups of symmetries:

$$\begin{alignedat}{3} &G_1\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to(t+ \varepsilon ,x,y,u,v), \\ &G_2\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to(t,x+ \varepsilon ,y,u,v), \\ &G_3\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to(t,x,y+ \varepsilon ,u,v), \\ &G_4\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to(t,2 \varepsilon t+x,y,u,v+ \varepsilon ), \\ &G_5\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to (te^{- \varepsilon },x,ye^{- \varepsilon },u,ve^ \varepsilon ), \\ &G_6\colon&\quad&(t^*,x^*,y^*,u^*,v^*)\to \biggl(te^{-2 \varepsilon },xe^{-2 \varepsilon },te^{-2 \varepsilon }+(-t+y)e^{2 \varepsilon }, \frac{1}{2}+\biggl(u-\frac{1}{2}\biggr)e^{2 \varepsilon },v\biggr). \end{alignedat}$$
Table 1. Commutator table.
Full size table

Theorem 1.

If \(u=f(t,x,y)\) , \(v=g(t,x,y)\) is a solution of the (2+1)-dimensional KdV–mKdV equation, then we can obtain corresponding new solutions of the groups of symmetries as

$$\begin{aligned} \, &u_1=f(t- \varepsilon ,x,y),\qquad v_1=g(t- \varepsilon ,x,y), \\ &u_2=f(t,x- \varepsilon ,y),\qquad v_2=g(t,x- \varepsilon ,y), \\ &u_3=f(t,x,y- \varepsilon ),\qquad v_3=g(t,x,y- \varepsilon ), \\ &u_4=f(t,x-2 \varepsilon t,y),\qquad v_4=g(t,x-2 \varepsilon t,y)+ \varepsilon , \\ &u_5=f(e^ \varepsilon t,x,e^ \varepsilon y),\qquad v_5=e^ \varepsilon g(e^ \varepsilon t,x,e^ \varepsilon y), \\ &u_6=\frac{1}{2}+e^{2 \varepsilon }\biggl[f(e^{2 \varepsilon }t,e^{2 \varepsilon }x, e^{2 \varepsilon }t+e^{-2 \varepsilon }(y-t))-\frac{1}{2}\biggr], \\ &v_6=g(e^{2 \varepsilon }t,e^{2 \varepsilon }x,e^{2 \varepsilon }t+e^{-2 \varepsilon }(y-t)). \end{aligned} $$
(3)

This theorem shows that we can obtain new solutions of Eq. (1) from a seed solution \(f(t,x,y)\), \(g(t,x,y)\) using formulas (3).

3. Optimal systems of subalgebras

The concept of optimal systems of subalgebras of a Lie algebra was first introduced by Ovsyannikov to describe the group of invariant solutions of PDEs. The Ibragimov method for constructing optimal systems of subalgebras is a simple method [35], [36] and relies on only the commutator table of symmetry operators. We previously extended this method to the (2+1)-dimensional Boiti–Leon–Pempinelli system [37], the Heisenberg equation [38], and the AKNS system [39] and studied the optimal systems of subalgebras of the Lie algebra for these equations.

We can write an arbitrary operator of the Lie algebra \(L_6\) expanded in the symmetry operators \(X_i\) (\(i=1,\dots,6\)) as

$$X=l^1X_1+l^2X_2+\dots+l^6X_6. $$
(4)

Obviously, because operator (4) depends on six arbitrary constants \(l^1,l^2,\dots,l^6\), there are infinitely many one-dimensional subalgebras of the Lie algebra \(L_6\). Two subalgebras are similar if they are related by a transformation of the symmetry group. The corresponding invariant solutions in these subalgebras are then related by the same transformation. In this section, we assign similar operators \(X\in L_6\) to one class and choose one representative from each class. The set of representatives comprises an optimal system of one-dimensional subalgebras. The transformations of the symmetry group are equivalent to linear transformations of the vector \(l=(l^1,\dots,l^6)\).

To find the linear transformations of the vector \(l\), we use the generators

$$E_i=c_{ij}^\lambda l^j_{}\frac{ \partial }{ \partial l^\lambda}\quad(i=1,\dots,6), $$
(5)

where \(c_{ij}^\lambda\) is defined by \([X_i,X_j]=c_{ij}^\lambda X_\lambda\). Using Eq. (5) and Table 1, we can write \(E_1,\dots,E_6\) as

$$\begin{aligned} \, &E_1=-(l^5+2l^6)\frac{ \partial }{ \partial l^1}+ 2l^4\frac{ \partial }{ \partial l^2}-4l^6\frac{ \partial }{ \partial l^3}, \\ &E_2=-2l^6\frac{ \partial }{ \partial l^2},\qquad E_3=(-l^5+2l^6)\frac{ \partial }{ \partial l^3}, \\ &E_4=-2l^1\frac{ \partial }{ \partial l^2}+l^5\frac{ \partial }{ \partial l^4},\qquad E_5=l^1\frac{ \partial }{ \partial l^1}+l^3\frac{ \partial }{ \partial l^3}- l^4\frac{ \partial }{ \partial l^4}, \\ &E_6=2l^1\frac{ \partial }{ \partial l^1}+2l^2\frac{ \partial }{ \partial l^2}+ (4l^1-2l^3)\frac{ \partial }{ \partial l^3}. \end{aligned} $$
(6)

To find the transformations given by these generators, we must solve the Lie equations

$$\begin{alignedat}6 &\frac{d \tilde l^1}{da_1}=-( \tilde l^5+2 \tilde l^6),&\qquad &\frac{d \tilde l^2}{da_1}=2 \tilde l^4,&\qquad &\frac{d \tilde l^3}{da_1}=-4 \tilde l^6,&\qquad&\frac{d \tilde l^4}{da_1}=0,&\qquad &\frac{d \tilde l^5}{da_1}=0,&\qquad&\frac{d \tilde l^6}{da_1}=0, \\ &\frac{d \tilde l^1}{da_2}=0,&\qquad&\frac{d \tilde l^2}{da_2}=-2 \tilde l^6,&\qquad &\frac{d \tilde l^3}{da_2}=0,&\qquad& \frac{d \tilde l^4}{da_2}=0,&\qquad &\frac{d \tilde l^5}{da_2}=0,&\qquad&\frac{d \tilde l^6}{da_2}=0, \\ &\frac{d \tilde l^1}{da_3}=0,&\qquad&\frac{d \tilde l^2}{da_3}=0,&\qquad &\frac{d \tilde l^3}{da_3}=- \tilde l^5+2 \tilde l^6,&\qquad &\frac{d \tilde l^4}{da_3}=0,&\qquad&\frac{d \tilde l^5}{da_3}=0,&\qquad &\frac{d \tilde l^6}{da_3}=0, \\ &\frac{d \tilde l^1}{da_4}=0,&\qquad&\frac{d \tilde l^2}{da_4}=-2 \tilde l^1,&\qquad &\frac{d \tilde l^3}{da_4}=0,&\qquad& \frac{d \tilde l^4}{da_4}= \tilde l^5,&\qquad &\frac{d \tilde l^5}{da_4}=0,&\qquad&\frac{d \tilde l^6}{da_4}=0, \\ &\frac{d \tilde l^1}{da_5}= \tilde l^1,&\qquad&\frac{d \tilde l^2}{da_5}=0,&\qquad &\frac{d \tilde l^3}{da_5}= \tilde l^3,&\qquad &\frac{d \tilde l^4}{da_5}=- \tilde l^4,&\qquad&\frac{d \tilde l^5}{da_5}=0,&\qquad &\frac{d \tilde l^6}{da_5}=0, \\ &\frac{d \tilde l^1}{da_6}=2 \tilde l^1,&\qquad &\frac{d \tilde l^2}{da_6}=2 \tilde l^2,&\qquad &\frac{d \tilde l^3}{da_6}=4 \tilde l^1-2 \tilde l^3,&\qquad &\frac{d \tilde l^4}{da_6}=0,&\qquad&\frac{d \tilde l^5}{da_6}=0,&\qquad &\frac{d \tilde l^6}{da_6}=0 \end{alignedat}$$

with the initial condition \( \tilde l|_{a_i=0}=l\) (\(i=1,\dots,6\)). Solving them, we obtain six one-parameter transformations

$$\begin{alignedat}4 &T_1\colon&\quad& \tilde l^1=-a_1l^5-2a_1l^6+l^1,&\qquad & \tilde l^2=2a_1l^4+l^2,&\qquad& \tilde l^3=-4a_1l^6+l^3, \\ &&\quad& \tilde l^4=l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6, \\ &T_2\colon&\quad& \tilde l^1=l^1,&\qquad & \tilde l^2=-2a_2l^6+l^2,&\qquad& \tilde l^3=l^3, \\ &&\quad& \tilde l^4=l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6, \\ &T_3\colon&\quad& \tilde l^1=l^1,&\qquad & \tilde l^2=l^2,&\qquad& \tilde l^3=-a_3l^5+2a_3l^6+l^3, \\ &&\quad& \tilde l^4=l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6, \\ &T_4\colon&\quad& \tilde l^1=l^1,&\qquad & \tilde l^2=-2a_4l^1+l^2,&\qquad& \tilde l^3=l^3, \\ &&\quad& \tilde l^4=a_4l^5+l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6, \\ &T_5\colon&\quad& \tilde l^1={e^{a_5}}l^1,&\qquad & \tilde l^2=l^2,&\qquad& \tilde l^3=e^{a_5}l^3 \\ &&\quad& \tilde l^4=e^{-a_5}l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6, \\ &T_6\colon&\quad& \tilde l^1=e^{2a_6}l^1,&\qquad & \tilde l^2=e^{2a_6}l^2,&\qquad& \tilde l^3=e^{2a_6}l^1+e^{-2a_6}(-l^1+l^3), \\ &&\quad& \tilde l^4=l^4,&\qquad& \tilde l^5=l^5,&\qquad& \tilde l^6=l^6. \end{alignedat}$$

These transformations map the vector \(X\) given by (4) to the vector

$$\tilde X= \tilde l^1X_1+ \tilde l^2X_2+ \tilde l^3X_3+ \tilde l^4X_4+ \tilde l^5X_5+ \tilde l^6X_6.$$

Constructing the optimal system is equivalent to simplifying the vector \(l=(l^1,l^2,\dots,l^6)\) using the transformations \(T_i\) (\(i=1,\dots,6\)).

Theorem 2.

An optimal system of one-dimensional subalgebras of the Lie algebra spanned by the operators \(X_1,X_2,\dots,X_6\) of the (2+1)-dimensional KdV–mKdV equation is provided by the operators

$$\begin{aligned} \, &X_1,\qquad X_2,\qquad X_3,\qquad X_4,\qquad X_5,\qquad X_6, \\ &X_1\pm X_5,\qquad X_1\pm X_6,\qquad X_1\pm X_5\pm X_6, \\ &X_1\pm X_4,\qquad X_1\pm X_4\pm X_6,\qquad X_2\pm X_3, \\ &X_4\pm X_3,\qquad X_5\pm X_2,\qquad X_5\pm X_6,\qquad X_6\pm X_4. \end{aligned}$$

Proof.

We divide the construction of an optimal system of one-dimensional subalgebras of the Lie algebra \(L_6\) into two cases.

Case 1. Let \(l^1\ne0\).

We consider the vector \(l=(l^1,l^2,l^3,l^4,l^5,l^6)\). Taking \(a_4=l^2/2l^1\) in \(T_4\), we reduce this vector to \(l=(l^1,0,l^3,l^4,l^5,l^6)\).

We take \(a_6=(1/4)\log(1-l^3/l^1)\) in \(T_6\) and reduce \(l\) to \(l=(l^1,0,0,l^4,l^5,l^6)\).

Case 1.1. Let \(l^5\ne0\). Then we can use \(T_4\) with \(a_4=-l^4/l^5\) and obtain \( \tilde l^4=0\), and we reduce \(l\) to \(l=(l^1,0,0,0,l^5,l^6)\), which provides the operators \(X_1\pm X_5\) and \(X_1\pm X_5\pm X_6\).

Case 1.2. Let \(l^5=0\). We consider \(l=(l^1,0,0,l^4,0,l^6)\), which yields the operators \(X_1\), \(X_1\pm X_4\), \(X_1\pm X_6\), and \(X_1\pm X_4\pm X_6\).

Case 2. Let \(l^1=0\). We must work with the vector \(l=(0,l^2,l^3,l^4,l^5,l^6)\).

Case 2.1. Let \(l^6\ne0\). Taking \(a_4=l^3/4l^6\) and using \(T_1\), we obtain \(l=(0,l^2,0,l^4,l^5,l^6)\), If we take \(a_2=l^2/2l^6\) and use \(T_2\), then we can further reduce \(l\) to \(l=(0,0,0,l^4,l^5,l^6)\).

Case 2.1.1. Let \(l^5\ne0\). Taking \(a_4=-l^4/l^5\) in \(T_4\), we obtain \(l=(0,0,0,0,l^5,l^6)\), which provides the operators \(X_5\) and \(X_5\pm X_6\).

Case 2.1.2. Let \(l^5=0\). Then we must work with \(l=(0,0,0,l^4,0,l^6)\), which provides the operators \(X_6\) and \(X_6\pm X_4\).

Case 2.2. Let \(l^6=0\). We consider \(l=(0,l^2,l^3,l^4,l^5,0)\).

Case 2.2.1. Let \(l^5\ne0\). Taking \(a_4=-l^4/l^5\) in \(T_4\), we obtain \( \tilde l^4=0\), and \(l\) is mapped to \(l=(0,l^2,l^3,0,l^5,0)\). Similarly, taking \(a_3=-l^3/2l^6\) in \(T_3\) yields \(l=(0,l^2,0,0,l^5,0)\), which provides the operator \(X_5\pm X_2\).

Case 2.2.2. Let \(l^5=0\). Then we must work with \(l=(0,l^2,l^3,l^4,0,0)\). If \(l^4\ne0\), then we take \(a_1=-l^2/2l^4\) in \(T_1\) and transform the vector into \(l=(0,0,l^3,l^4,0,0)\), which provides the operators \(X_4\) and \(X_4\pm X_3\). If \(l^4=0\), then we reduce \(l\) to \(l=(0,l^2,l^3,0,0,0)\), which provides the operators \(X_2\), \(X_2\pm X_3\), and \(X_3\).

4. Similarity reductions and the invariant solutions

Based on the subalgebras of the optimal system in Theorem 2, we investigate the similarity reductions of the (2+1)-dimensional KdV–mKdV equation. Invariant solutions can be obtained by solving the reduced equations. We have the following theorem describing the optimal system of invariant solutions.

Theorem 3.

Some invariant solutions obtained from similarity reductions are described using representatives of the optimal system in the following cases:

$$\begin{alignedat}2 &\textit{Case 1.}&\quad&X_1\colon\;u =f(x,y),\quad v=g(x,y), \\ &&&\textit{where }f_{xxy}+4ff_y-4f^2f_y+2f_xg=0,\quad g_x-f_y+2ff_y=0. \end{alignedat}$$
(7)
$$\begin{alignedat}2 &\textit{Case 2.}&\quad&X_2\colon\;u=f(y,t),\;v=g(y,t), \\ &&&\textit{where }f_t+4ff_y-4f^2f_y=0,\quad f_y(2f-1)=0. \end{alignedat}$$
(8)
$$\begin{alignedat}2 &\textit{Case 3.}&\quad&X_3\colon\;u=f(x,t),\;v=g(x,t), \\ &&&\textit{where }f_t+2f_xg=0,\quad g_x=0. \end{alignedat}$$
(9)
$$\begin{alignedat}2 &\textit{Case 4.}&\quad&X_4\colon\;u=f(y,t),\;v=g(y,t)+\frac{x}{2t}, \\ &&&\textit{where }f_t+4ff_y-4f^2f_y=0,\quad 1-2tf_y+4tff_y=0. \end{alignedat}$$
(10)
$$\begin{alignedat}2 &\textit{Case 5.}&\quad&X_5\colon\;u=f(\xi,\eta),\quad v=\frac{1}{y}g(\xi,\eta),\quad\xi=x,\quad\eta=\frac{t}{y}, \\ &&&\begin{aligned} \, \textit{where }&f_\eta-\eta f_{\xi\xi\eta}- 4\eta ff_\eta+4\eta f^2f_\eta+2f_\xi g=0,\qquad g_\xi+\eta f_\eta-2\eta ff_\eta=0. \end{aligned} \end{alignedat}$$
(11)
$$\begin{alignedat}2 &\textit{Case 6.}&\quad&X_6\colon\;u=\frac{1}{2}+f(\xi,\eta),\quad v=g(\xi,\eta),\quad\xi=\frac{t}{x},\quad\eta=-tx+xy, \\ &&&\begin{aligned} \, \textit{where }&f_\xi+\xi^2f_{\xi\xi\eta}-2\xi\eta f_{\xi\eta\eta}+ \eta^2f_{\eta\eta\eta}+2\xi f_{\xi\eta}- 4f^2f_\eta-2\xi f_\xi g+2\eta f_\eta g-2fg=0, \\ &-\xi g_\xi+\eta g_\eta+2ff_\eta=0. \end{aligned} \end{alignedat}$$
(12)
$$\begin{alignedat}2 &\textit{Case 7.}&\quad&X_1+X_4\colon\;u=f(\xi,\eta),\quad v=t+g(\xi,\eta),\quad\xi=y,\quad\eta={t^2}-x, \\ &&&\textit{where }f_{\xi\eta\eta}+4ff_\xi-4f^2f_\xi-2f_\eta g=0,\quad -g_\eta-f_\xi+2ff_\xi=0. \end{alignedat}$$
(13)
$$\begin{alignedat}2 &\textit{Case 8.}&\quad&X_2+X_3\colon\;u=f(\xi,\eta),\quad v=t+g(\xi,\eta),\quad\xi=t,\;\eta=y-x, \\ &&&\textit{where }f_\xi+f_{\eta\eta\eta}+4ff_\eta-4f^2f_\eta- 2f_\eta g=0,\quad -g_\eta-f_\eta+2ff_\eta=0. \end{alignedat}$$
(14)
$$\begin{alignedat}2 &\textit{Case 9.}&\quad&X_4+X_3\colon\;u=f(\xi,\eta),\quad v=\frac{x}{2t}+g(\xi,\eta),\quad\xi=t,\quad\eta=y-\frac{x}{2t}, \\ &&&\begin{aligned} \, \textit{where }&4\xi^2f_\xi+{f_{\eta\eta\eta}}+ 16\xi^2ff_\eta-16\xi^2f^2f_\eta-4\xi f_\eta g=0, \\ &1-g_\eta-2\xi f_\eta+2\xi ff_\eta=0. \end{aligned} \end{alignedat}$$
(15)
$$\begin{alignedat}2 &\textit{Case 10.}&\quad&X_5+X_6\colon\;u=\frac{1}{2}\biggl(1+ \frac{2f(\xi,\eta)}{x}\biggr),\quad v=\frac{g(\xi,\eta)}{\sqrt x}, \\ &&&{\kern49pt}\xi=\frac{t}{x^{3/2}},\quad\eta=\sqrt{x}\,y-\sqrt{x}\,t, \\ &&&\begin{aligned} \, \textit{where }&-3\xi {g_\xi}+\eta g_\eta-g+4ff_\eta=0, \\ &\begin{aligned} \, 2f_\eta+4f_\xi-16ff_\eta-8fg+9\xi^2f_{\xi\xi\eta}+ 21\xi f_{\xi\eta}-6\xi\eta f_{\xi\xi\eta}+{}& \\ {}+\eta^2f_{\eta\eta\eta}- 3\eta f_{\eta\eta}-12\xi f_\xi g+4\eta f_\eta g&{}=0. \end{aligned} \end{aligned} \end{alignedat}$$
(16)

Remark.

In Theorem 3, we do not list all invariant solutions obtained using representatives of the optimal system because some reduced systems are complicated PDEs with variable coefficients, which are difficult to solve. All invariant solutions of Eq. (1) can be investigated if all 30 operators in Theorem 2 are used. In this section, we mainly presented 10 kinds of similarity reductions, which can be divided into reduced systems with constant coefficients (Cases 1–3) and reduced systems with variable coefficients (Cases 4–10).

In Case 1, system (7) admits the Lie point symmetries

$$X_1=\frac{ \partial }{ \partial x},\qquad X_2=\phi(y)\frac{ \partial }{ \partial y}-\phi(y)v\frac{ \partial }{ \partial v},$$

where \(\phi(y)\) is an arbitrary function of \(y\). In Cases 2 and 3, we can obtain the solutions \(u=c\), \(v=g(y,t)\) and \(u=m(-2n(t)+x)\), \(v=n'(t)\), where \(c\) is an arbitrary constant and \(m\) and \(n\) are arbitrary functions, by solving the reduced systems directly.

It is difficult to directly obtain explicit solutions of the reduced systems with variable coefficients. We can further reduce the dimensions of these systems (Cases 4–10) using symmetries to investigate the exact power series solutions [40], [41].

5. Nonlocal symmetry and Bäcklund transformation

Taking into account that the residue from the truncated Painlevé expansion, as is known, is a nonlocal symmetry, we devote this section to analyzing the nonlocal symmetry and the Bäcklund transformation of Eq. (1). Based on the Painlevé test and analyzing the truncated expansion, we write the expansion for Eq. (1):

$$u=u_0+\frac{u_1}{f},\qquad v=v_0+\frac{v_1}{f}+\frac{v_2}{f^2}, $$
(17)

where \(u_0\), \(u_1\), \(v_0\), \(v_1\), \(v_2\), and \(f\) are functions of \(x\), \(y\), and \(t\). Substituting these expansions in (1) and equating the coefficients of like powers of \(1/f\) to zero, we obtain the solutions for \(u_0\), \(u_1\), \(v_0\), \(v_1\), and \(v_2\):

$$\begin{aligned} \, &u_0=\frac{1}{2}\biggl(1-\frac{f_{xx}}{f_x}\biggr),\qquad u_1=f_x, \\ &v_0=\frac{f_{xx}f_{xy}-f_xf_t-f_xf_y-f_x f_{xxy}}{2f_x^2},\qquad v_1=f_{xy},\qquad v_2=-f_xf_y, \end{aligned} $$
(18)

where \(f\) satisfies the constraint relation

$$f_{xxxy}=\frac{f_xf_{xy}f_{xxx}-f_x^2f_{tx}-f_{xy}f_x^2+ f_{xx}f_xf_y+3f_{xx}f_xf_{xxy}-3f_{xy}f_{xx}^2+f_{xx}f_xf_t}{f_x^2}, $$
(19)

which is equivalent to the Schwarzian form

$$A_x+B_y+C_x=0, $$
(20)

where

$$A=\frac{f_t}{f_x},\qquad B=\frac{f_{xxx}}{f_x}- \frac{3}{2}\frac{{f_{xx}^2}}{f_x^2},\qquad C=\frac{f_y}{f_x}.$$

As a result, we have the following theorems on the Bäcklund transformation, two of which are nonautotransformations and one is an autotransformation.

Theorem 4 (Non-auto-Bäcklund transformation 1).

If a function \(f\) is a solution of Schwarzian equation (20), then

$$u=\frac{1}{2}\biggl(1-\frac{f_{xx}}{f_x}\biggr),\qquad v=\frac{f_{xx}f_{xy}-f_xf_t-f_xf_y-f_x{f_{xxy}}}{2f_x^2} $$
(21)

is a solution of (2+1)-dimensional KdV–mKdV equation (1).

Theorem 5 (Non-auto-Bäcklund transformation 2).

If a function \(f\) is a solution of Schwarzian equation (20), then

$$u=\frac{1}{2}\biggl(1-\frac{f_{xx}}{f_x}\biggr)+\frac{f_x}{f},\qquad v=\frac{f_{xx}f_{xy}-f_xf_t-f_xf_y-f_xf_{xxy}}{2f_x^2}+ \frac{f_{xy}}{f}-\frac{f_xf_y}{f^2} $$
(22)

is a solution of (2+1)-dimensional KdV–mKdV equation (1).

Theorem 6 (Auto-Bäcklund transformation).

If a function \((u_0,v_0)\) is a solution of (2+1)-dimensional KdV–mKdV equation (1), then

$$u=u_0+\frac{f_x}{f},\qquad v=v_0+\frac{f_{xy}}{f}-\frac{f_xf_y}{f^2} $$
(23)

is also a solution of (2+1)-dimensional KdV–mKdV equation (1), where \(f\) satisfies Schwarzian equation (20).

By definition, the residual symmetry of Eq. (1) is written as

$$\sigma^u=f_x,\qquad \sigma^v=f_{xy}. $$
(24)

It is nonlocal because \(\sigma^u\) and \(\sigma^v\) contain the new variable \(f\), which cannot be expressed in terms of \(u\) and \(v\) and their derivatives. It is known that the Schwarzian equation is invariant under the Möbius transformation

$$f\to\frac{a+bf}{c+df}\qquad(ad\ne bc), $$
(25)

and this means that \(f\) has the point symmetry \(\sigma^f=-f^2\), which is easily derived from (25) if we set \(a=0\), \(b=c=1\), and \(d= \varepsilon \). The transformation

$$u=\frac{1}{2}\biggl(1-\frac{f_{xx}}{f_x}\biggr),\qquad v=\frac{f_{xx}f_{xy}-f_xf_t-f_xf_y-f_x f_{xxy}}{2f_x^2} $$
(26)

brings Eq. (1) to Schwarzian form (20). To find the residual symmetry group,

$$u\to \tilde u( \varepsilon )=u+ \varepsilon \sigma^u,\qquad v\to \tilde v( \varepsilon )=v+ \varepsilon \sigma^v,$$

we must solve the Cauchy problem

$$\begin{alignedat}2 &\frac{d \tilde u( \varepsilon )}{d \varepsilon }= \tilde f_x( \varepsilon ),&\qquad & \tilde u( \varepsilon )\big|_{ \varepsilon =0}=u, \\ &\frac{d \tilde v( \varepsilon )}{d \varepsilon }= \tilde f_{xy}( \varepsilon ),&\qquad & \tilde v( \varepsilon )\big|_{ \varepsilon =0}=v, \end{alignedat}$$

where \( \varepsilon \) is an infinitesimal parameter.

To solve the Cauchy problem, we must introduce new variables to convert nonlocal symmetry (24) into a local Lie point symmetry of an extended system. We introduce new variables by setting

$$h_1=f_x,\qquad h_2=f_y,\qquad h_3=h_{1y}, $$
(27)

in which case Eqs. (1), (20), (26), and (27) comprise the extended system. The Lie point symmetry of this system has the form

$$\begin{pmatrix}\sigma^u \\ \sigma^v \\ \sigma^f \\ \sigma^{h_1} \\ \sigma^{h_2} \\ \sigma^{h_3}\end{pmatrix}=\begin{pmatrix} \phantom{-}h_1 \\ \phantom{-}h_3 \\ -f^2 \\ -2fh_1 \\ -2fh_2 \\ -2h_2h_1-2fh_3\end{pmatrix}. $$
(28)

By virtue of Lie’s first theorem, we obtain the corresponding Cauchy problem for the Lie point symmetry

$$\begin{alignedat}2 &\frac{d \tilde u( \varepsilon )}{d \varepsilon }= \tilde h_1( \varepsilon ),&\qquad& \tilde u(0)=u, \\ &\frac{d \tilde v( \varepsilon )}{d \varepsilon }= \tilde h_3( \varepsilon ),&\qquad& \tilde v(0)=v, \\ &\frac{d \tilde f( \varepsilon )}{d \varepsilon }=- \tilde f^2( \varepsilon ),&\qquad& \tilde f(0)=f, \\ &\frac{d \tilde h_1( \varepsilon )}{d \varepsilon }=-2 \tilde f( \varepsilon ) \tilde h_1( \varepsilon ),&\qquad & \tilde h_1(0)=h_1, \\ &\frac{d \tilde h_2( \varepsilon )}{d \varepsilon }=-2 \tilde f( \varepsilon ) \tilde h_2( \varepsilon ),&\qquad & \tilde h_2(0)=h_2, \\ &\frac{d \tilde h_3( \varepsilon )}{d \varepsilon }=-2 \tilde h_2( \varepsilon ) \tilde h_1( \varepsilon )- 2 \tilde f( \varepsilon ) \tilde h_3( \varepsilon ),&\qquad& \tilde h_3(0)=h_3. \end{alignedat} $$
(29)

Solving this initial value problem, we derive a theorem on the symmetry transformation.

Theorem 7.

If \((u,v,f,h_1,h_2,h_3)\) is a solution of extended system (1), (20), (26), (27), then the symmetry transformation maps it to

$$\begin{aligned} \, & \tilde u( \varepsilon )=u+\frac{ \varepsilon h_1}{1+ \varepsilon f},\qquad \tilde v( \varepsilon )=v+ \frac{ \varepsilon h_3}{(1+ \varepsilon f)^2}-\frac{ \varepsilon ^2 h_1h_2}{(1+ \varepsilon f)^2},\qquad \tilde f( \varepsilon )=\frac{f}{1+ \varepsilon f}, \\ & \tilde h_1( \varepsilon )=\frac{h_1}{(1+ \varepsilon f)^2},\qquad \tilde h_2( \varepsilon )=\frac{h_2}{(1+ \varepsilon f)^2},\qquad \tilde h_3( \varepsilon )=\frac{h_3}{(1+ \varepsilon f)^2}-\frac{2 \varepsilon h_1h_2}{(1+ \varepsilon f)^3}, \end{aligned} $$
(30)

and \(\bigl( \tilde u( \varepsilon ), \tilde v( \varepsilon ), \tilde f( \varepsilon ), \tilde h_1( \varepsilon ), \tilde h_2( \varepsilon ), \tilde h_3( \varepsilon )\bigr)\) is also a solution of the extended system.

Theorem 7 is useful for obtaining new solutions of Eq. (1) from a seed solution of Schwarzian form (20). Starting from the form of Eq. (19), we easily obtain \(f=e^{\rho x+\omega y+\kappa t}\). Using symmetry transformation (30), we obtain a new solution of Eq. (1):

$$u=\frac{1}{2}(1-\rho)+\frac{ \varepsilon \rho e^{\rho x+\omega y+\kappa t}} {1+ \varepsilon e^{\rho x+\omega y+\kappa t}},$$
(31)
$$v=-\frac{\kappa+\omega}{2\rho}+\frac{ \varepsilon \rho\omega e^{\rho x+\omega y+\kappa t}}{1+ \varepsilon e^{\rho x+\omega y+\kappa t}}- \frac{ \varepsilon ^2\rho\omega (e^{\rho x+\omega y+\kappa t})^2} {(1+ \varepsilon e^{\rho x+\omega y+\kappa t})^2},$$
(32)

where \(\rho\), \(\omega\), and \(\kappa\) are arbitrary constants. We show this solution with a particular choice of the parameters and \(t=0\) in Fig. 1.

Fig. 1.
figure 1

Kink-type solitary wave (31) and bright soliton (32) with \(\rho=1\), \(\omega=2\), \(\kappa=3\), and \( \varepsilon =0.1\): three-dimensional plots of (a) \(u(x,y,0)\) and (b) \(v(x,y,0)\).

Full size image

Because of the symmetry, all Eqs. (24) are linear in \(f\), and Schwarzian equation (20) has infinitely many solutions. We obtain infinitely many nonlocal symmetries

$$\sigma_n^u=\sum_{i=1}^n \vartheta _if_{i,x},\qquad \sigma_n^v=\sum_{i=1}^n \vartheta _if_{i,xy}, $$
(33)

where \(n\) is an arbitrary constant and \(f_i\) (\(i=1,\dots,n\)) are solutions of the Schwarzian equation

$$\tilde A_x+ \widetilde B_y+ \widetilde C_x=0, $$
(34)

where

$$\tilde A=\frac{f_{i,t}}{f_{i,x}},\qquad \widetilde B=\frac{f_{i,xxx}}{f_{i,x}}- \frac{3}{2}\frac{f_{i,xx}^2}{f_{i,x}^2},\qquad \widetilde C=\frac{f_{i,y}}{f_{i,x}}.$$

Similarly to the \(n{=}1\) case, we introduce new variables to augment Eq. (1) and obtain an extended system such that nonlocal symmetry (33) can be localized and converted into a Lie point symmetry. The new variables are given by

$$h_{1,i}=f_{i,x},\qquad h_{2,i}=f_{i,y},\qquad h_{3,i}=h_{1y,i}. $$
(35)

As a result, nonlocal symmetry (33) becomes the Lie point symmetry

$$\begin{aligned} \, &\sigma_n^u=\sum_{i=1}^n \vartheta _i^{}h_{1,i}^{},\qquad \sigma_n^v=\sum_{i=1}^n \vartheta _i^{}h_{3,i}^{},\qquad \sigma^{f_i}_{}=- \vartheta _i^{}f_i^2-\sum_{j\ne i}^n \vartheta _jf_if_j, \\ &\sigma^{h_{1,i}}=-2 \vartheta _if_ih_{1,i}- \sum_{j\ne i}^n \vartheta _j(f_ih_{1,j}+f_jh_{1,i}), \\ &\sigma^{h_{2,j}}=-2 \vartheta _if_ih_{2,i}- \sum_{j\ne i}^n \vartheta _j(f_ih_{2,j}+f_jh_{2,i}), \\ &\sigma^{h_{3,i}}=-2 \vartheta _i(h_{2,j}h_{1,i}+f_ih_{3,i})-\sum_{j\ne i}^n \vartheta _j(h_{2,j}h_{1,j}+h_{2,j}h_{1,i}+f_ih_{3,j}+f_jh_{3,i}). \end{aligned}$$

We write the corresponding Cauchy problem for the point symmetry as

$$\begin{aligned} \, &\frac{d \tilde u( \varepsilon )}{d \varepsilon }=\sum_{i=1}^n \vartheta _i \tilde h_{1,i}( \varepsilon ), \\ &\frac{d \tilde v( \varepsilon )}{d \varepsilon }=\sum_{i=1}^n \vartheta _i \tilde h_{3,i}( \varepsilon ), \\ &\frac{{d \tilde f_i( \varepsilon )}}{d \varepsilon }=- \vartheta _i \tilde f_i^2( \varepsilon )- \sum_{j\ne i}^n \vartheta _j \tilde f_i( \varepsilon ) \tilde f_j( \varepsilon ), \\ &\frac{d \tilde h_{1,i}( \varepsilon )}{d \varepsilon }=-2 \vartheta _i \tilde f_i( \varepsilon ) \tilde h_{1,i}( \varepsilon )- \sum_{j\ne i}^n \vartheta _j\bigl( \tilde f_i( \varepsilon ) \tilde h_{1,j}( \varepsilon )+ \tilde f_j( \varepsilon ) \tilde h_{1,i}( \varepsilon )\bigr), \\ &\frac{d \tilde h_{2,i}( \varepsilon )}{d \varepsilon }=-2 \vartheta _i \tilde f_i( \varepsilon ) \tilde h_{2,i}( \varepsilon )- \sum_{j\ne i}^n \vartheta _j\bigl( \tilde f_i( \varepsilon ) \tilde h_{2,j}( \varepsilon )+ \tilde f_j( \varepsilon ) \tilde h_{2,i}( \varepsilon )\bigr), \\ &\frac{d \tilde h_{3,i}( \varepsilon )}{d \varepsilon }=-2 \vartheta _i\bigl( \tilde h_{2,i}( \varepsilon ) \tilde h_{1,i}( \varepsilon )+ \tilde f_i( \varepsilon ) \tilde h_{3,i}( \varepsilon )\bigr)-{} \\ &\hphantom{\frac{d \tilde h_{3,i}( \varepsilon )}{d \varepsilon }={}}-\sum_{j\ne i}^n \vartheta _j\bigl( \tilde h_{2,i}( \varepsilon ) \tilde h_{1,j}( \varepsilon )+ \tilde h_{2,j}( \varepsilon ) \tilde h_{1,i}( \varepsilon )+ \tilde f_i( \varepsilon ) \tilde h_{3,j}( \varepsilon )+ \tilde f_j( \varepsilon ) \tilde h_{3,i}( \varepsilon )\bigr) \end{aligned}$$

with the initial conditions

$$\tilde u(0)=u,\qquad \tilde v(0)=v,\qquad \tilde f_i(0)=f_i,\qquad \tilde h_{1,i}(0)=h_{1,i},\qquad \tilde h_{2,i}(0)=h_{2,i},\qquad \tilde h_{3,i}(0)=h_{3,i}.$$

Solving this problem, we establish a theorem on the \(n\)th Bäcklund transformation.

Theorem 8.

If \((u,v,f_i,h_{1,i},h_{2,i},h_{3,i})\) is a solution of extended system (1), (34), (35) and

$$u=\frac{1}{2}\biggl(1-\frac{f_{i,xx}}{f_{i,x}}\biggr),\qquad v=\frac{f_{i,xx}{f_{i,xy}}-f_{i,x}f_{i,t}- f_{i,x}f_{i,y}-f_{i,x}f_{i,xxy}}{2f_{i,x}^2},$$

then \(\bigl( \tilde u( \varepsilon ), \tilde v( \varepsilon ), \tilde f_i( \varepsilon ), \tilde h_{1,i}( \varepsilon ), \tilde h_{2,i}( \varepsilon ), \tilde h_{3,i}( \varepsilon )\bigr)\), where

$$\begin{aligned} \, & \tilde u( \varepsilon )=u+(\log\operatorname{Im})_x,\qquad \tilde v( \varepsilon )=v+(\log\operatorname{Im})_{xy}, \\ & \tilde f_i( \varepsilon )=\frac{\operatorname{Im}_i}{\operatorname{Im}},\qquad \tilde h_{1,i}( \varepsilon )= \tilde f_{i,x}( \varepsilon ),\qquad \tilde h_{2,i}( \varepsilon )= \tilde f_{i,y}( \varepsilon ),\qquad \tilde h_{3,i}( \varepsilon )= \tilde f_{i,xy}( \varepsilon ), \end{aligned}$$

is also a solution of the extended system. Here, \(\operatorname{Im}\) is the determinant

$$\operatorname{Im}=\begin{vmatrix} \vartheta _1 \varepsilon f_1+1& \vartheta _1 \varepsilon \theta_{12}&\cdots& \vartheta _1 \varepsilon \theta_{1n} \\ \vartheta _2 \varepsilon \theta_{21}& \vartheta _2 \varepsilon f_2+1&\ddots&\vdots \\ \vdots&\ddots&\ddots& \vartheta _{n-1} \varepsilon \theta_{n-1,n} \\ \vartheta _n \varepsilon \theta_{1n}&\cdots& \vartheta _n \varepsilon \theta_{n,n-1}& \vartheta _n \varepsilon f_n+1 \end{vmatrix},\qquad \theta_{ij}=\sqrt {f_if_j}, $$
(36)

and \(\operatorname{Im}_i\) is the determinant of the matrix obtained by replacing the \(i\)th row in \(\operatorname{Im}_i\) with

$$\begin{matrix}\theta_{1i}&\cdots&\theta_{i,i-1}&f_i &\theta_{i,i+1}&\cdots&\theta_{in}\end{matrix}.$$

6. Obtaining lump-type solutions using a non-auto-Bäcklund transformation

Lumps, being one kind of rogue wave, arise in many branches of science, for example, in describing waves in shallow water, optical media, and the Bose–Einstein condensate [42]–[44]. It was proved that bilinear functions can be used to construct lump solutions of integrable systems [45]–[49]. The function \(f\) in Theorem 5 satisfies trilinear equation (19), and this suggests the idea to construct a solution in the form of a quadratic function. In [49], a solution of the Kadomtsev–Petviashvili equation was constructed using bilinear forms. Inspired by this work, we use non-auto-Bäcklund transformation 2 can be used to construct lump solitons and similar lump solutions of Eq. (1).

To find a quadratic solution of Eq. (19), we choose

$$f=(a_1x+a_2y+a_3t+a_4)^2+(a_5x+a_6y+a_7t+a_8)^2+a_9, $$
(37)

where \(a_i\) (\(i=1,\dots,9\)) are real parameters to be determined. Substituting (37) in (19) and using symbolic computation, we obtain equations relating the \(a_i\):

$$a_3=-\frac{{-a_1a_5a_7+a_2a_5^2+a_2a_1^2}}{a_5^2},\qquad a_6=-\frac{a_1a_2}{a_5}. $$
(38)

Substituting (37) with (38) in (22) gives the solutions

$$u=\frac{1}{2}\biggl(1-\frac{f_{xx}}{f_x}\biggr)+\frac{f_x}{f},$$
(39)
$$v=\frac{f_{xx}f_{xy}-f_xf_t-f_xf_y-f_xf_{xxy}}{2f_x^2}+ \frac{f_{xy}}{f}-\frac{f_xf_y}{f^2},$$
(40)

where

$$f=\biggl(a_1x+a_2y-\frac{-a_1a_5a_7+a_2a_5^2+a_2a_1^2}{a_5^2}t+ a_4\biggr)^{\!2}+\biggl(a_5x-\frac{a_1a_2}{a_5}y+a_7t+a_8\biggr)^{\!2}+a_9$$

and the \(a_i\) are arbitrary constants. Solutions (39) and (40) can be used to describe nonlinear wave phenomena in oceanography and nonlinear optics.

In Fig. 2, we show the spatial localization of solutions (39) and (40) with certain values of the parameters \(a_i\). In Figs. 2a and 2b, we see a wave falling off on both sides according to the law of inverse proportionality. This is a wave of the lump type because the function \(u\) given by (39) tends to zero as \(f\to\infty\). Compared with the solution \(u\) given by (39), the lump soliton \(v\) given by (40) is a spatially localized wave with a large energy accumulation, which can be seen in Figs. 2c and 2d. The condition \(a_1^2a_2^{}/a_5^{}+a_2^{}a_5^{}\ne0\) ensures the localization of lump solution (40) in all spatial directions, i.e., \(v(x,y,t)\to0\) as \(x^2+y^2\to\infty\) for any \(t\in\mathbb{R}\); the inequality \(a_9>0\) makes the lump solution positive.

Fig. 2.
figure 2

Lump-type wave (39) and lump soliton (40) with \(a_1=a_4=a_5=1\), \(a_2=-2\), \(a_7=1/2\), \(a_8=3\), and \(a_9=4\): (a) three-dimensional plot of \(u(x,y,0)\) and (b) plot of \(u(x,y,0)\) along the \(x\) axis with \(y=0\) (solid), \(y=2\) (dashed), and \(y=4\) (dotted); (c) three-dimensional plot of \(v(x,y,0)\) and (d) plot of \(v(x,y,0)\) along the \(x\) axis with \(y=0\) (solid), \(y=-2\) (dashed), and \(y=-5\) (dotted).

Full size image

7. The CRE integrability

Theorem 9.

If \(w(x,y,t)\) is a solution of the Schwarzian form

$$A'_x +B'_y+C'_x-\delta w_x w_{xy}=0, $$
(41)

where

$$A'=\frac{w_t^{}}{w_x^{}},\qquad B'=\frac{w_{xxx}^{}}{w_x^{}}- \frac{3}{2}\frac{w_{xxx}^2}{w_x^2},\qquad C'=\frac{w_y^{}}{w_x^{}},$$

then

$$\begin{aligned} \, &u=\frac{1}{2}\biggl(1+w_x+\frac{a_1w_{xx}}{w_x}\biggr)+w_xR(w), \\ &v=-\frac{w_x^{}w_y^{}+w_x^{}w_t^{}-w_{xy}^{}w_{xx}^{}+ 2a_0^{}a_2^{}w_y^{}w_x^3+w_x^{}w_{xxy}^{}+a_1^{}w_{xy}^{}w_x^2}{2w_x^2}-{} \\ &{}-(a_2^{}w_{xy}^{}+a_1^{}a_2^{}w_x^{}w_y^{})R(w)-a_2^2w_x^{}w_y^{}R^2(w) \end{aligned} $$
(42)

is a solution of system (1), where \(R(w)\) is a solution of the Riccati equation

$$R(w)_w=a_0+a_1R(w)+a_2R^2(w),\qquad a_0,a_1,a_2=\mathrm{const}. $$
(43)

Proof.

In accordance with the CRE method, we write the solutions of Eq. (1) in the form

$$u=u_0+u_1R(w),\qquad v=v_0+v_1R(w)+v_2R^2(w), $$
(44)

where \(R(w)\) is a solution of Riccati equation (43). Substituting the given expressions for \(u\) and \(v\) in (1) with (43) taken into account and equating the coefficients of like powers of \(R(w)\) to zero, we obtain the relations

$$\begin{aligned} \, &u_0=\frac{1}{2}\biggl(1+w_x+\frac{a_1w_{xx}}{w_x}\biggr),\qquad u_1=w_x, \\ &v_0^{}=-\frac{w_xw_y+w_xw_t-w_{xy}w_{xx}+2a_0^{}a_2^{}w_y^{}w_x^3+ w_x^{}w_{xxy}^{}+a_1^{}w_{xy}^{}w_x^2}{2w_x^2}, \\ &v_1^{}=-a_2^{}w_{xy}^{}-a_1^{}a_2^{}w_x^{}w_y^{},\qquad v_2^{}=-a_2^2w_x^{}w_y^{}, \end{aligned} $$
(45)

and the function \(w(x,y,t)\) satisfies the equation

$$\begin{aligned} \, w_{xxxy}={}&\frac{1}{w_x^2}\bigl(3w_{xx}w_xw_{xxy}-(w_x)^2w_{xy}- (w_x)^2w_{tx}+w_xw_{xy}w_{xxx}-3w_{xy}(w_{xx})^2+{} \nonumber \\ &{}+w_xw_{xx}w_y+w_{xx}w_xw_t+\delta w_x^4w_{xy}\bigr), \end{aligned}$$
(46)

where \(\delta=a_1^2-4a_0a_2\), which is equivalent to (41). The theorem is proved.

8. Soliton-cnoidal wave solutions of Eq. (1)

In this section, we investigate solutions of Eq. (1) with a cnoidal wave form using Theorem 9. For the Riccati equation, we choose

$$w=k_1x+l_1y+h_1t+\psi(\xi),\qquad \xi=k_2x+l_2y+h_2t, $$
(47)

where \(\psi_\xi=d\psi(\xi)/d\xi\) is a solution of the elliptic equation

$$\psi_{\xi\xi}^2=c_0^{}+c_1^{}\psi_\xi^{}+ c_2^{}\psi_\xi^2+c_3^{}\psi_\xi^3+c_4\psi_\xi^4, $$
(48)

where the \(c_i\) (\(i=0,\dots,4\)) are constants. Substituting (47) and (48) in (46), we obtain a set of constraint equations for the coefficients \(c_i\):

$$\begin{aligned} \, &c_0=-\frac{1}{3}\frac{k_1^{}\bigl((-\delta k_1^3+(1+c_2^{}k_2^2)k_1- 2c_1^{}k_2^3)l_2+h_2^{}k_1^{}-k_2^{}(h_1^{}+l_1^{})\bigr)}{l_2^{}k_2^4}, \\ &c_3=\frac{1}{3}\frac{4\delta l_2^{}k_1^3+(2k_2^2l_2^{}c_2^{}-h_2^{}- l_2^{})k_1^{}-k_2^{}(l_2^{}c_1^{}k_2^2-h_1^{}-l_1^{})}{l_2^{}k_1^2k_2}, \qquad c_4=\delta. \end{aligned} $$
(49)

Theorem 9 allows constructing explicit solutions describing the interaction between solutions of Schwarzian equation (41) and solutions of Riccati equation (43). As is known, a solution of the Riccati equation is expressed in terms of the hyperbolic tangent. Based on the analysis presented above, we can conclude that Eq. (41) has a solution written in terms of Jacobi elliptic functions. As a result, we obtain solutions of Eq. (1) of the type of interacting soliton-cnoidal waves.

A simple solution of Eq. (48) is written in terms of the Jacobi elliptic function as

$$\psi_\xi=\mu_0+\mu_1\mathrm{sn}(m\xi,n).$$

We substitute this expression together with (49) in (48) and take the identities \(\mathrm{cn}^2( \,\cdot\, )=1-\mathrm{sn}^2( \,\cdot\, )\) and \(\mathrm{dn}^2( \,\cdot\, )=1-n^2\mathrm{sn}^2( \,\cdot\, )\) for the Jacobi elliptic function into account. We then equate the coefficients of like powers of \(\mathrm{sn}\) to zero. We obtain

$$\begin{aligned} \, &c_1^{}=16\mu_0^3a_2^{}a_0^{}-4\mu_0^3a_1^2+ 2\mu_0^{}m^2_{}n^2_{}+2\mu_0^{}m^2_{}, \\ &c_2^{}=-24\mu_0^2a_2^{}a_0^{}+6\mu_0^2a_1^2-m^2_{}n^2_{}-m^2_{}, \\ &h_1^{}=-\frac{((1+(2n^2_{}-2)m^2_{}k_2^2)l_2^{}+h_2^{}) \sqrt{4m^2_{}\delta}+\delta(h_2^{}\mu_0^{}+l_1^{}+l_2^{}\mu_0)}{\delta}, \\ &k_1^{}=-\frac{(\mu_0^{}a_1^2-4\mu_0^{}a_2^{}a_0^{}+\sqrt{\delta m^2_{}}\,) k_2^{}}{\delta},\qquad\mu_1^{}=\sqrt{\frac{1}{\delta}}mn. \end{aligned} $$
(50)

Using formula (42), we derive a soliton-cnoidal wave solution of Eq. (1):

$$\begin{aligned} \, u={}&\frac{1}{2}\frac{\mu_1^{}mCDk_2^2+k_1^{}+(\mu_0^{}+\mu_1^{}S)k_2^{}+ a_1^{}(k_1^{}+(\mu_0^{}+\mu_1^{}S)k_2^{})^2_{}}{k_1+(\mu_0+\mu_1 S)k_2}+{} \nonumber \\ &{}+\frac{1}{2}(k_1+(\mu_0+\mu_1S)k_2)\Theta, \end{aligned}$$
(51)
$$\begin{aligned} \, v={}&-\frac{1}{2}\bigl[(l_1+(\mu_0+\mu_1S)l_2)(k_1+(\mu_0+\mu_1S)k_2)+{} \nonumber \\ &{}+(k_1^{}+(\mu_0^{}+\mu_1^{}S)k_2^{})(h_1^{}+(\mu_0^{}+ \mu_1^{}S)h_2^{})-\mu_1^2m^2_{}C^2_{}D^2_{}l_2^{}k_2^3+{} \nonumber \\ &{}+2(k_1+(\mu_0+\mu_1S)k_2)^3(l_1+(\mu_0+\mu_1S)l_2)a_0a_2+{} \nonumber \\ &{}+(k_1^{}+(\mu_0^{}+\mu_1^{}S)k_2^{})(-\mu_1^{}m^2_{}D^2_{}S- \mu_1^{}m^2_{}C^2_{}n^2_{}S)l_2^{}k_2^2+{} \nonumber \\ &{}+(k_1+(\mu_0+\mu_1S)k_2)^2\mu_1ml_2k_2a_1CD\bigr] (k_1+(\mu_0+\mu_1S)k_2)^{-2}-{} \nonumber \\ &{}-\frac{1}{2}\frac{(-a_2\mu_1ml_2k_2CD-a_1a_2(k_1+ (\mu_0+\mu_1S)k_2)(l_1+(\mu_0+\mu_1S)l_2))}{a_2}\,\Theta-{} \nonumber \\ &{}-\frac{1}{4}(k_1+(\mu_0+\mu_1S)k_2)(l_1+(\mu_0+\mu_1S)l_2)\Theta^2, \end{aligned}$$
(52)

where

$$\Theta=a_1+\sqrt\delta\tanh\biggl(\frac{1}{2}\sqrt{\delta} \biggl(k_1x+l_1y+h_1t+\int_{\xi_0}^\xi\bigl(\mu_0+ \mu_1\mathrm{sn}(mY,n)\bigr)dY\biggr)\!\biggr),$$

the constants \(a_0\), \(a_1\), \(a_2\), \(\mu_0\), \(k_2\), \(l_1\), \(l_2\), \(h_2\), and \(\xi_0\) are arbitrary, the parameters \(h_1\), \(k_1\), and \(\mu_1\) are given by (50), and

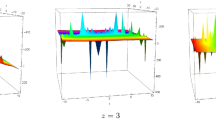
$$\begin{aligned} \, &S=\mathrm{sn}(m(k_2x+l_2y+h_2t),n),\qquad C=\mathrm{cn}(m(k_2x+l_2y+h_2t),n), \\ &D=\mathrm{dn}(m(k_2x +l_2y+h_2t),n). \end{aligned}$$

As can be seen in Fig. 3, the solution \(u\) given by (51) describes an interaction between a kink and a cnoidal wave. We also present a plot of the solution \(v\) given by (52) (see Fig. 4), which describes a soliton traveling along with a cnoidal wave. The solutions \(u\) and \(v\) play an important role in investigating atmospheric dynamics and other physical fields modeled by the (2+1)-dimensional KdV–mKdV equation.

Fig. 3.
figure 3

Soliton-cnoidal wave \(u(x,y,t)\) given by (51) with \(m=1/4\), \(n=1/3\), \(h_2=3\), \(k_2=2\), \(l_1=1\), \(l_2=2\), \(a_0=1\), \(a_1=3\), \(a_2=2\), and \(\xi_0=0\): (a) three-dimensional plot of \(u(x,y,0)\), (b) the wave \(u(x,0,0)\) along the \(x\) axis, (c) the wave \(u(0,y,0)\) along the \(y\) axis, and (d) the wave \(u(0,0,t)\) along the \(t\) axis.

Full size image
Fig. 4.
figure 4

The same plots with the same parameters as in Fig. 3 for the soliton-cnoidal wave \(v(x,y,t)\) given by (52).

Full size image

9. Conclusions

We have focused our attention on investigating the properties of local and nonlocal symmetries of a (2+1)-dimensional KdV–mKdV equation, which describes the propagation of a thermal pulse. We applied the method of Lie symmetry analysis to obtain Lie point symmetries, the group transformation of solutions, and an optimal system of one-dimensional subalgebras of the Lie algebra spanned by the Lie point symmetries. This optimal system contains 30 operators. Using some of these operators, we considered similarity reductions of solutions and invariant solutions. We proved that we can expand Eq. (1) using the truncated Painlevé expansion. Moreover, a nonlocal symmetry is obtained from the term corresponding to the residue. Based on these results, we derived two non-auto-Bäcklund transformations and one auto-Bäcklund transformation. In addition, we wrote the \(n\)th Bäcklund transformation in terms of the determinant. Interestingly, the non-auto-Bäcklund transformation in Theorem 5 can be used to construct the lump and lump-type solutions. The lump-type wave falling off on both sides of the wave maximum describes an inverse proportional dependence. The considered (2+1)-dimensional KdV–mKdV equation is integrable using the CRE method, and this allows obtaining solutions of the type of soliton-cnoidal waves. Using numerical analysis, we investigated the dynamical characteristics of the interaction solutions.