1 Introduction

Nonlinear evolution equations (NLEEs) have wide applications in many branches of physics like quantum field theory, nuclear physics, plasma physics, optical physics, condense matter physics, fluid mechanics and oceanography [1,2,3,4]. Among NLEEs, completely integrable systems are often referred to as exactly solvable models. In \(1+1\) dimensions and \(2+1\) dimensions, there are numerous integrable models, such as the Korteweg–de Vries (KdV) equation, modified KdV equation, Boussinesq equation, nonlinear Schrödinger equation, Camassa–Holm equation, Davey–Stewartson equation, and so on.

Due to the fact that the real physical space is (\(3+1\))-dimensional, the study of higher dimensional NLEEs has attracted considerable attention of mathematicians and physicists. Many higher dimensional NLEEs may provide more beneficial information, and they always possess more abundant explicit solutions, including lump wave, rogue wave, breather as well as quasiperiodic solutions [5,6,7,8,9,10,11,12]. In the past decades, scholars have tried to search for new integrable models using different methods, especially in higher than two space dimensions [13,14,15,16,17]. Until now, nontrivial higher dimensional integrable models are quite a few. There is still a lot of room to establish some methods for constructing new integrable models of higher dimensions.

The (\(4+1\))-dimensional Fokas equation, obtained by extending the Lax pair of (\(2+1\))-dimensional Kadomtsev–Petviashvili (KP) equation to higher dimensions [14], has become a hot research issue in recent years. Yang and Yan derived the point symmetry, potential symmetry and doubly periodic wave solutions [18]. The multiple soliton, rouge wave and lump solutions and singular manifold analysis were given in Refs. [19,20,21,22,23]. The natural and important problem is that are there other (\(4+1\))-dimensional integrable models.

In this paper, we propose a new (\(4+1\))-dimensional model with the form

$$\begin{aligned}&u_{yt}+u_{zt}+u_{st}{+}a u_{xxxy}+au_{xxxz}+au_{xxxs}\nonumber \\&\quad +\,bu_x\,(u_{xy}{+}u_{xz}+u_{xs}){+}b\,u_{xx}\,(u_y+u_z+u_{s}) {=} 0, \nonumber \\ \end{aligned}$$
(1)

with four space variables x, y, z, s and one time variable t; a and b are constant parameters. Equation (1) can be considered as an extension of KdV equation in \(4+1\) dimensions.

For particular choices of parameters, Eq. (1) includes several important (\(2+1\))- and (\(3+1\))-dimensional nonlinear models with physical interests. If \(u=u(x,y,t)\) and \(a=b=-1\), Eq. (1) becomes

$$\begin{aligned} u_{yt} - u_{xxxy} - u_{xx}u_y - \,u_x\,u_{xy} = 0, \end{aligned}$$
(2)

which was first proposed by Boiti et al. [24], hereinafter referred to as BLMP equation. Equation (2) can be used to describe an incompressible fluid and it is closely related to the classic KdV equation. The spectral transform, nonclassical symmetry, Bäcklund transformation (BT) and some explicit solutions have been constructed [24,25,26].

When \(u=u(x,y,t)\), and taking \(a=1\), \(b=-3\), Eq. (1) is reduced to

$$\begin{aligned} u_{yt}+u_{xxxy} - 3\,u_{xx}u_y - 3\,\,u_x\,u_{xy} = 0, \end{aligned}$$
(3)

which is exactly another form of BLMP equation proposed by Gilson et al. [27], and its various exact solutions have been constructed, including Jacobi elliptic function solution, quasiperiodic wave solution and mixed lump–soliton solution [28, 29]. Equation (3) was investigated through Bell polynomial method, and the integrability properties have been presented [30].

If u is independent of the variable s, taking \(a=1\), \(b=-3\), Eq. (1) reduces to the BLMP equation in \(3+1\) dimensions, which reads

$$\begin{aligned}&u_{yt}+u_{zt}+u_{xxxy}+u_{xxxz} - 3\,u_x\,(u_{xy}+u_{xz})\nonumber \\&\quad -\,3\,u_{xx}\,(u_y+u_z) = 0. \end{aligned}$$
(4)

This model has attracted much attention of researchers, and the Painlevé property, Bäcklund transformation, Lax pair, step-like soliton solutions, nontraveling wave solutions, breather waves and lump–kink solutions have been presented by virtue of different methods [31,32,33,34,35,36].

The new model (1) is associated with the BLMP equation in lower dimensions. In what follows, we refer to it as the (\(4+1\))-dimensional BLMP equation. The remaining parts of this work are organized as follows. In Sect. 2, we systematically study the integrable characteristics of Eq. (1) to prove its complete integrability. In Sect. 3, several types of localized wave solutions are constructed through the Hirota’s direct method and then their dynamics are analyzed by some graphs. Finally, this paper concludes in Sect. 4.

2 Integrability of Eq. (1)

In this part, we first perform the singular manifold analysis for Eq. (1) and confirm its Painlevé integrability. Furthermore, we utilize the Bell polynomial method to systematically construct the Hirota’s bilinear representation, Lax pair, bilinear BT as well as infinite conservation laws.

2.1 Painlevé property

Following the WTC-Kruskal method [2], the integrability test of Eq. (1) is made up of three steps. Firstly, we may substitute \(u=u_0\phi ^{\gamma }\) into (1). Balancing the dominant terms, we obtain the values of leading exponent and coefficient, namely \(\gamma =-1\) and \(u_0=6a\phi _x/b\).

The second step is to calculate the values of resonant points, which can be done by inserting the truncated expansion \(u=u_0\,\phi ^{-1}+u_j\,\phi ^{j-1}\) into (1) and balancing the dominant terms. After some calculations, it is found that there are four resonant points, namely \(j=-1\), 1, 4 and 6.

Finally, in order to check whether Eq. (1) passes the integrability or not, we should verify the compatibility conditions at \(j=1\), 4 and 6. For this purpose, the Laurent series may be truncated at the maximum resonant point,

$$\begin{aligned} u = \sum \limits _{j=0}^{6}\,u_j\,\phi ^{j-1}, \end{aligned}$$
(5)

where the Kruskal’s ansatz is used to simplify the involved calculations, i.e., \(\phi =x+\psi (y,z,s,t)\). Note that all the coefficients \(u_j\) in (5) do not depend on the variable x. Inserting (5) into Eq. (1) and collecting the coefficients of \(\phi \) with the same degree, we have

$$\begin{aligned} u_2= & {} \dfrac{\psi _t}{2\,b}+\dfrac{u_{1y}+u_{1z} +u_{1s}}{2(\psi _y+\psi _z+\psi _{s})},\nonumber \\ u_3= & {} \dfrac{\psi _{yt}+\psi _{zt}+\psi _{s\,t}+b(u_{2y}+u_{2z}+u_{2s})}{4\,b\,(\psi _y+\psi _z+\psi _{s})},\nonumber \\ u_5= & {} \left[ (4bu_2u_3-2u_3\psi _t+u_{2t})(\psi _y+\psi _z+\psi _{s})\right. \nonumber \\&\quad \left. +\,(\psi _t-bu_2)(u_{2y}{+}u_{2z}+u_{2s}) {+}u_2(\psi _{yt}{+}\psi _{zt}\right. \nonumber \\&\quad \left. +\,\psi _{s\,t}) - 2\,bu_3(u_{1y}+u_{1z}+u_{1s})-u_{1yt}\right. \nonumber \\&\quad \left. -\,u_{1zt}-u_{1s\,t}\right] \Big /\left[ 24\,a\,(\psi _y+\psi _z+\psi _{s})\right] .\nonumber \\ \end{aligned}$$
(6)

In (6), \(\psi \), \(u_1\), \(u_4\) and \(u_6\) are arbitrary, which indicates that the Laurent series of Eq. (1) admits sufficient number of arbitrary functions. Therefore, the proposed Eq. (1) passes the integrability test and thus it has Painlevé property.

Although there is not a general definition about complete integrable system, it is widely accepted that an integrable model should possess Lax pair, infinite conservation laws, Hamiltonian structure, infinitely many symmetries, bilinear BT as well as N-soliton solutions. Equation (1) is proved to be integrable in the sense of Painlevé, and below we will systematically construct integrable properties using the Bell polynomial method [3].

2.2 Bilinear form

The Painlevé test provides an efficient method to check whether nonlinear models are integrable not. More importantly, it also produces some useful information to further study the integrability properties and various types of explicit solutions.

The singular manifold analysis yields the Painlevé–Bäcklund transformation in the form

$$\begin{aligned} u = \dfrac{6 a}{b}\,(\ln \phi )_{x}+u_1, \end{aligned}$$
(7)

where \(u_1\) is the seed solution of Eq. (1). For the sake of simplicity, we may take \(u_1=0\). Introducing \(q=2\ln \phi \), it follows from (7) that

$$\begin{aligned} u = \dfrac{3 a }{b}\,q_{x}. \end{aligned}$$
(8)

Substituting the transformation (8) into (1), we get

$$\begin{aligned}&q_{xyt}+q_{xzt}+q_{xst} +3a\,\left[ q_{xx}\left( q_{xxy}+q_{xxz}\right. \right. \nonumber \\&\quad \left. \left. +\,q_{xxs}\right) +q_{xxx}(q_{xy}+q_{xz}+q_{xs})\right] \nonumber \\&\quad +\,a\left( q_{xxxxy}+q_{xxxxz}+q_{xxxxs}\right) =0. \end{aligned}$$
(9)

After integrating Eq. (9) once, we easily obtain

$$\begin{aligned}&q_{yt}+q_{zt}+q_{st}+a\,\left( q_{xxxy}+3q_{xx}q_{xy}+q_{xxxz}\right. \nonumber \\&\left. \quad +\,3q_{xx}q_{xz}+q_{xxxs}+3q_{xx}q_{xs}\right) = 0. \end{aligned}$$
(10)

Based on the definition of \(\mathscr {P}\)-polynomial, (10) can be written as

$$\begin{aligned}&\mathscr {P}_{yt}(q)+\mathscr {P}_{zt}(q)+\mathscr {P}_{s t}(q) +a\,\mathscr {P}_{xxxy}(q)\nonumber \\&\quad +\,a\,\mathscr {P}_{xxxz}(q)+a\,\mathscr {P}_{xxxs}(q) = 0. \end{aligned}$$
(11)

Together with \(q=2\ln \,\phi \), from (11) we obtain

$$\begin{aligned}&(D_y D_t+D_z D_t+D_{s} D_t+aD_x^3 D_y\nonumber \\&\quad +\,a\,D_x^3 D_z+a\,D_x^3 D_{s})\,F\,\cdot \,F=0, \end{aligned}$$
(12)

where “D” is the Hirota’s derivative operator [4]. Notice that (12) is exactly the bilinear representation for the (\(4+1\))-dimensional BLMP equation.

2.3 Bilinear Bäcklund transformation and Lax pair

The binary Bell polynomial method provides us a systematic procedure to derive the integrable properties of NLEEs [3]. Based on the results obtained in the above subsection, one can obtain bilinear BT.

Suppose that \(q=2 \ln F\) and \(\bar{q}=2\ln G\) are two solutions of Eq. (10), and we take

$$\begin{aligned} v = \dfrac{\bar{q} - q}{2},\quad w = \dfrac{\bar{q}+q}{2}. \end{aligned}$$
(13)

It follows from Eq. (10) that

$$\begin{aligned}&\dfrac{E(\bar{q})-E(q)}{2}\nonumber \\&\quad = v_{yt}+av_{xxxy}+3aw_{xx}v_{xy}+3aw_{xy}v_{xx}\nonumber \\&\qquad +\,v_{zt}+av_{xxxz}+3aw_{xx}v_{xz}+3aw_{xz}v_{xx}\nonumber \\&\qquad +\,v_{s t}+av_{xxxs}+3aw_{xx}v_{xs}+3aw_{xs}v_{xx} \nonumber \\&\quad =\frac{\partial }{\partial y}\left( \mathscr {Y}_t(v) +a\mathscr {Y}_{xxx}(v,w)\right) +3a(w_{xy}v_{xx}\nonumber \\&\qquad -\,v_xw_{xxy}-v_x^2v_{xy})+\frac{\partial }{\partial z} \left( \mathscr {Y}_t(v)+a\mathscr {Y}_{xxx}(v,w)\right) \nonumber \\&\qquad +\,3a\left( w_{xz}v_{xx}-v_xw_{xxz}-v_x^2v_{xz}\right) \nonumber \\&\qquad +\,\frac{\partial }{\partial s}\left( \mathscr {Y}_t(v) +a\mathscr {Y}_{xxx}(v,w)\right) +3a\left( w_{xs}v_{xx}\right. \nonumber \\&\left. \qquad -\,v_xw_{xxs}-v_x^2v_{xs}\right) . \end{aligned}$$
(14)

To obtain the bilinear BT, we introduce the constraint between v and w with the form

$$\begin{aligned} w_{xy}+v_xv_y+w_{xz}+v_xv_z+w_{xs}+v_xv_{s} = \alpha \,v_x, \end{aligned}$$
(15)

with \(\alpha \) being arbitrary constant, and then Eq. (14) becomes

$$\begin{aligned}&\dfrac{\partial }{\partial y}\left( \mathscr {Y}_t(v)+a\,\mathscr {Y}_{xxx}(v,w)\right) +\dfrac{\partial }{\partial z}(\mathscr {Y}_t(v)\nonumber \\&\quad +\,a\,\mathscr {Y}_{xxx}(v,w))+\dfrac{\partial }{\partial s} \left( \mathscr {Y}_t(v)+a\,\mathscr {Y}_{xxx}(v,w)\right) {=}0. \end{aligned}$$
(16)

Note that (15) can also be expressed as

$$\begin{aligned} \mathscr {Y}_{xy}(v,w)+\mathscr {Y}_{xz}(v,w)+\mathscr {Y}_{xs}(v,w) -\alpha \mathscr {Y}_{x}(v,w)=0. \end{aligned}$$
(17)

The \(\mathscr {Y}\)-polynomials are closely related to the bilinear derivative operators, from (16) and (17), and we get

$$\begin{aligned}&(D_t+a\,D_x^3 - \mu ) F\,\cdot \,G = 0,\nonumber \\&(D_xD_y+D_xD_z+D_xD_{s} - \alpha \, D_x)\,F\cdot G = 0, \end{aligned}$$
(18)

where \(\mu =\mu (t)\) is arbitrary. Equation (18) is just the bilinear BT of Eq. (1).

By setting

$$\begin{aligned} v = \ln \varphi , \quad w = q+\ln \varphi , \end{aligned}$$
(19)

and linearizing the coupled system (16) and (17), the linear differential equations are obtained as

$$\begin{aligned}&\varphi _t+a\,\varphi _{xxx}+b\,u_x\,\varphi _x = 0,\\&\varphi _{xy}+\varphi _{xz}+\varphi _{xs}+\dfrac{b}{3a} (u_y+u_z+u_{s})\varphi -\alpha \varphi _x=0. \end{aligned}$$

It is easy to prove that the above system is just the Lax pair for the (\(4+1\))-dimensional BLMP equation.

2.4 Infinite conservation laws

The concept of infinite conservation laws is a very important property of nonlinear integrable systems. Searching for infinite conservation laws of NLEEs is still an open issue. For the new proposed Eq. (1), the infinite conservation laws can be constructed by virtue of the coupled \(\mathscr {Y}\)-polynomials system (16) and (17).

Introducing the transformation \(\eta = (\bar{q}_x - q_x)/{2}\) and making good use of (13) with \(\alpha =0\), Eqs. (16) and (17) become

$$\begin{aligned}&q_{xy}+q_{xz}+q_{xs}+\eta \,\partial _x^{-1}\eta _y + \eta \,\partial _x^{-1}\eta _z+\eta \,\partial _x^{-1}\eta _{s}\nonumber \\&\quad +\,\eta _{y}+\eta _{z}+\eta _{s} = 0,\nonumber \\&\frac{\partial }{\partial t}\,\left( \partial _x^{-1}\eta _y\right) +\frac{\partial }{\partial x}\,\left[ a\eta _{xz}+a(\eta _x+q_{xx})\partial _x^{-1}\eta _z\right. \nonumber \\&\left. \quad +\,2a\eta (\eta _z+q_{xz})+a\eta ^2\partial _x^{-1}\eta _z\right] +\frac{\partial }{\partial z}\,\left( \partial _x^{-1}\eta _t\right) \nonumber \\&\quad +\,\frac{\partial }{\partial y}\,\left[ a\eta _{xx}+3a\eta (\eta _x+q_{xx}) +a\eta ^3\right] {+}\frac{\partial }{\partial s}\left[ a\eta _{xx}\right. \nonumber \\&\left. \quad +\,a\eta _{xx}+3a\eta (\eta _x+q_{xx})+a\eta ^3+\partial _x^{-1}\eta _t\right] = 0.\nonumber \\ \end{aligned}$$
(20)

The function \({\eta }\) is expanded as the following series,

$$\begin{aligned} {\eta } = \epsilon +\sum \limits _{n=1}^{\infty }\,\mathscr {I}_n \,(q,q_x,\ldots )\,\epsilon ^{-n}. \end{aligned}$$
(21)

Inserting series (21) into the first equation of (20) gives the recursion formula for the conversed densities \(\mathscr {I}_{n}\), namely

$$\begin{aligned}&\mathscr {I}_1 = -\ q_{xx} = -\frac{b}{3a}\,u_x,\nonumber \\&\mathscr {I}_2 = q_{xxx} = \frac{b}{3a}\,u_{xx},\nonumber \\&\partial _x^{-1}\left( \mathscr {I}_{n+1,y} +\mathscr {I}_{n+1,z} +\mathscr {I}_{n+1,s}\right) \nonumber \\&\quad =-\mathscr {I}_{n,y}{-}\mathscr {I}_{n,z}-\mathscr {I}_{n,s}\nonumber \\&\qquad -\,\sum \limits _{k=1}^{n}\,\mathscr {I}_k\,\partial _x^{-1}\left( \mathscr {I}_{n-k,y} {+}\mathscr {I}_{n-k,z}{+}\mathscr {I}_{n-k,s}\right) ,\,n{\ge } 2. \end{aligned}$$
(22)

Using ansatz (21) again, from the second equation of (20), the infinite conservation laws of (1) can be derived as

$$\begin{aligned} \mathscr {L}_{n,t}+\mathscr {F}_{n,x}+\mathscr {G}_{n,y} +\mathscr {H}_{n,z} +\mathscr {M}_{n,s}=0,\,n=1,2,\ldots \end{aligned}$$
(23)

In Eq. (23),

$$\begin{aligned} \mathscr {L}_{n}=\partial _x^{-1} \mathscr {I}_{n,y}, \quad \mathscr {H}_{n}=\partial _x^{-1} \mathscr {I}_{n,t}, \end{aligned}$$

with \(\mathscr {I}_{n}\) being given by (22). The flux \(\mathscr {F}_n\) takes the form

$$\begin{aligned} \mathscr {F}_n= & {} a\mathscr {I}_{n,xz} +aq_{xx}\partial _x^{-1} \mathscr {I}_{n,z}+2a\,q_{xz}\mathscr {I}_{n+1,z} \\&+\,a\partial _x^{-1}\mathscr {I}_{n+2,z}{+}2aq_{xz}\mathscr {I}_{n} {+}a\,\sum \limits _{k=1}^{n}\,\partial _x^{-1}\mathscr {I}_{k,z}\mathscr {I}_{n-k,x}\\&+\,2\,a\sum \limits _{k=1}^{n}\mathscr {I}_{k}\mathscr {I}_{n-k,z} +2\,a\sum \limits _{k=1}^{n+1}\mathscr {I}_{k}\partial _x^{-1}\mathscr {I}_{n-k,z}\\&+\,a\,\sum \limits _{i+j+k=n}\,\mathscr {I}_{i}\mathscr {I}_{k} \partial _x^{-1} \mathscr {I}_{k,z}. \end{aligned}$$

And \(\mathscr {G}_n\) can be expressed as

$$\begin{aligned} \mathscr {G}_n= & {} a\,\,\mathscr {I}_{n,xx}+3\,a\,\mathscr {I}_{n+1,x} +3\,a\,q_{xx}\,\mathscr {I}_{n}\\&+\,3\,a\,\mathscr {I}_{n+2}+3\,a\,\sum \limits _{k=1}^{n} \mathscr {I}_{k}\mathscr {I}_{n-k,x}\\&+\,3\,a\,\sum \limits _{k=1}^{n+1}\mathscr {I}_{k}\mathscr {I}_{n-k} +a\,\sum \limits _{i+j+k=n}\mathscr {I}_{i}\mathscr {I}_{j}\mathscr {I}_{k}. \end{aligned}$$

The fourth fluxes \(\mathscr {M}_n\) read

$$\begin{aligned} \mathscr {M}_n= & {} \partial _x^{-1}\mathscr {I}_{n,t}+a\,\mathscr {I}_{n,xx} +3a\,\mathscr {I}_{n+1,x}+3aq_{xx}\,\mathscr {I}_{n} \\&+\,3a\mathscr {I}_{n+2}+3a\sum \limits _{k=1}^{n}\mathscr {I}_{k}\mathscr {I}_{n-k,x} +3a\sum \limits _{k=1}^{n+1}\mathscr {I}_{k}\mathscr {I}_{n-k}\\&+\,a\sum \limits _{i+j+k=n}\mathscr {I}_{i}\mathscr {I}_{j}\mathscr {I}_{k}. \end{aligned}$$

It is noted that the first member of (23) is proved to be the (\(4+1\))-dimensional BLMP equation (1). In addition, starting from other members of the conservation laws (23), some new integrable models in \(4+1\) dimensions may be generated.

3 Localized wave solutions

The Hirota bilinear method is an efficient and direct tool to study nonlinear evolution models [4], which has been widely applied to investigate integrability properties like bilinear Bäcklund transformation and Lax pairs. In the meanwhile, it also can be used to solve both integrable and nonintegrable NLEEs with important physical interests.

3.1 N-soliton solutions

According to the Hirota’s bilinear method, the key step is to change the original models to bilinear equations with suitable transformations. Through the Painlevé–Bäcklund transformation (7), Eq. (1) can be reduced to

$$\begin{aligned}&\phi _{yt}\phi -\phi _{y}\phi _{t}+\phi _{zt}\phi -\phi _{z}\phi _{t} +\phi _{s\,t}\phi -\phi _{s}\phi _{t}\nonumber \\&\quad +\,a\,\left( \phi _{xxxy}\phi -\phi _{xxx}\phi _y+3\phi _{xx} \phi _{xy} -3\phi _x\phi _{xxy}\right. \nonumber \\&\left. \quad +\,\phi _{xxxz}\phi -\phi _{xxx}\phi _z +3\phi _{xx}\phi _{xz}-3\phi _x\phi _{xxz}\right. \nonumber \\&\left. \quad +\,\phi _{xxxs}\phi -\phi _{xxx}\phi _{s}+3\phi _{xx} \phi _{xs} -3\phi _x\phi _{xxs}\right) =0.\nonumber \\ \end{aligned}$$
(24)

N-soliton solutions may be the fundamental characteristic of integrable nonlinear evolution equations. As discussed in Sect. 2, Equation (1) is integrable in the sense of Painlevé. Following the perturbation method [4], one can obtain the N-soliton solutions with the form

$$\begin{aligned} u = \dfrac{6\,a}{b}\,\cdot \,(\ln \phi )_x, \end{aligned}$$
(25)

and \(\phi \) is given by

$$\begin{aligned}&\phi =1+\sum \limits _{i=1}^{N}\,\mathrm{e}^{\eta _i} +\sum \limits _{i<j}^{N}\,A_{ij}\,\mathrm{e}^{\eta _i+\eta _j}\nonumber \\&\qquad +\sum \limits _{i<j<k}^{N}\,A_{ij}A_{ik}A_{jk} \,\mathrm{e}^{\eta _i+\eta _j+\eta _k}\nonumber \\&\qquad +\cdots +\sum \limits _{1\le i<j \le N}\,A_{ij} \,\mathrm{e}^{\sum \limits _{i=1}^{N}\,\eta _i},\nonumber \\&\eta _i= k_i x+l_i y+p_i z+q_i s +\omega _i t+\eta _{0i},\nonumber \\&\omega _i = -a\,k_i^3,\,\,i=1,\ldots ,N,\nonumber \\&A_{ij} = \dfrac{(k_i-k_j)(l_i+p_i+q_i-l_j-p_j-q_j)}{(k_i+k_j)(l_i+p_i+q_i+l_j+p_j+q_j)}. \end{aligned}$$
(26)

Bidirectional solitons have potential values to simulate ocean waves phenomenon, but they are rare for lower dimensional NLEEs. However, a number of (\(3+1\))-dimensional NLEEs admit bidirectional soliton solutions. The reason is due to the existence of more arbitrary parameters in the dispersion relations. The dispersion relation, given by (26), tells us that there only exist overtaking collisions between solitons along x-direction, while there are both overtaking and head-on collisions between solitons along y-, z- and s-direction. The interactions between multiple solitons are similar to those of the GBS equation [12] and the GNNV equation [37], and thus the interaction analysis is omitted here.

3.2 Periodic soliton solutions

Starting from the N-soliton solutions (25), we can get some interesting periodic soliton solutions by choosing suitable parameters in (26).

Case 1 If taking \(N=2\), from Eq. (26) we have

$$\begin{aligned} \phi = 1+\mathrm{e}^{\eta _1}+\mathrm{e}^{\eta _2}+A_{12}\,\mathrm{e}^{\eta _{1}+\eta _{2}}. \end{aligned}$$
(27)

Together with transformation (25), the two-soliton solution of (1) is then obtained.

For the parametric choices

$$\begin{aligned}&k_1=k_2^{*}=\alpha _1+i\beta _1,\quad l_1=l_2^{*}=\delta _1+i\rho _1,\nonumber \\&p_1=p_2^{*}=\mu _1+i\nu _1,\quad q_1=q_2^{*}=\lambda _1+i\sigma _1,\nonumber \\&\eta _{01}=\eta _{02}=0, \end{aligned}$$
(28)

Equation (27) takes the following form

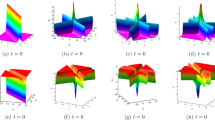
$$\begin{aligned}&\phi = 1+2\,\mathrm{e}^{\alpha _1\,x+\delta _1\,y+\mu _1\,z +\lambda _1\,s\,+\gamma _1\,t}\, \cos (\varTheta )\nonumber \\&\quad +\,A_{12}\,\mathrm{e}^{2(\alpha _1\,x+\delta _1\,y+\mu _1\,z +\lambda _1\,s\,+\gamma _1\,t)},\nonumber \\&\varTheta =\beta _1 x+\rho _1 y+\nu _1 z+\sigma _1 s+\epsilon _1 t,\nonumber \\&\gamma _1=a(3\alpha _1\beta _1^2-\alpha _1^3),\, \epsilon _1 =a(\beta _1^3-3\alpha _1^2\beta _1),\nonumber \\&A_{12}=-\dfrac{\beta _1(\rho _1+\nu _1+\sigma _1)}{\alpha _1(\delta _1+\mu _1+\lambda _1)}. \end{aligned}$$
(29)

Substituting (29) into (25) yields a periodic soliton solution of Eq. (1). Figure 1 shows the interactions between one kinky solitary wave and one periodic wave. Figure 1a–c gives the 3D plots of the periodic solitary wave in x–y plane, x–z plane and x–s plane, respectively. Their contour plots are shown in Fig. 1d–f.

Fig. 1
figure 1

(Color online) Plots of periodic soliton solution given by (25) and (29). a The case of \(z=s=0\) with the parameters \(\alpha _1=\delta _1=0.8\), \(\beta _1=0.4\), \(\rho _1=1\), \(\mu _1=-0.5\), \(\lambda _1=-0.6\), \(\nu _1=\sigma _1=0\), b the case of \(z=s=0\) with the parameters \(\alpha _1=-\mu _1=0.5\), \(\beta _1=0.2\), \(\rho _1=\sigma _1=0\), \(\nu _1=1\), \(\lambda _1=0.4\), c the case of \(y=z=0\) with \(\alpha _1=0.5\), \(\beta _1=0.4\), \(\delta _1=0.8\), \(\rho _1=\nu _1=0\), \(\mu _1=-0.6\), \(\lambda _1=-0.4\), \(\sigma _1=1.2\), d the contour plot in x–y plane, e the contour plot in x–z plane, f the contour plot in x–s plane

Full size image

Case 2 If taking \(N=3\), if follows from Eq. (26) that

$$\begin{aligned} \phi= & {} 1+\mathrm{e}^{\eta _1}+\mathrm{e}^{\eta _2}+\mathrm{e}^{\eta _3} +A_{12}\mathrm{e}^{\eta _{1}+\eta _{2}}+A_{13}\mathrm{e}^{\eta _{1}+\eta _{3}}\nonumber \\&+\,A_{23}\,\mathrm{e}^{\eta _{2}+\eta _{3}} +A_{12}A_{13}A_{23} \,\mathrm{e}^{\eta _1+\eta _{2}+\eta _{3}}. \end{aligned}$$
(30)

Together with transformation (25), one can obtain the three-soliton solution of (1).

For the parametric choices

$$\begin{aligned}&k_1=k_2^{*}=\alpha _1+i\beta _1,\,l_1=l_2^{*}=\delta _1+i\rho _1,\nonumber \\&p_1=p_2^{*}=\mu _1+i\nu _1,\,q_1=q_2^{*}=\lambda _1+i\sigma _1,\nonumber \\&k_3=\alpha _2,\,l_3=\delta _2,\,p_3=\mu _2,\,q_3=\lambda _2,\nonumber \\&\eta _{01}=\eta _{02}=\eta _{03}=0, \end{aligned}$$
(31)

where \(\alpha _1,\alpha _2,\beta _1,\delta _1,\delta _2,\rho _1,\mu _1, \mu _2,\nu _1\) are real constants, Eq. (27) takes the following form:

$$\begin{aligned} \phi= & {} 1+2\,\mathrm{e}^{\xi _1}\,\cos (\varTheta )+A_{12}\,\mathrm{e}^{2\xi _1}\nonumber \\&+\,\mathrm{e}^{\xi _2}\,\left[ 1+2L \mathrm{e}^{\xi _1}\cos (\varTheta +\varPsi ) +A_{12}L^2\,\mathrm{e}^{2\xi _1}\right] ,\nonumber \\ \end{aligned}$$
(32)

where

$$\begin{aligned}&\xi _1=\alpha _1\,x+\delta _1\,y+\mu _1\,z\,+\lambda _1\,s+\gamma _1\,t,\\&\xi _2=\alpha _2\,x+\delta _2\,y+\mu _2\,z\,+\lambda _2\,s - a\alpha _2^3\,t,\\&\varTheta =\beta _1 x+\rho _1 y+\nu _1 z+\sigma _1 s+\epsilon _1 t,\\&\gamma _1=a(3\alpha _1\beta _1^2-\alpha _1^3), \quad \epsilon _1 =a(\beta _1^3-3\alpha _1^2\beta _1),\\&A_{12}=-\dfrac{\beta _1(\rho _1+\nu _1+\sigma _1)}{\alpha _1(\delta _1+\mu _1+\lambda _1)},\\&L\,\mathrm{e}^{i\varPsi } = A_{13}=A_{23}^{*} = \dfrac{(\alpha _1-\alpha _2+i\beta _1)\left[ \delta _1-\delta _2+\mu _1-\mu _2 +\lambda _1-\lambda _2+i(\rho _1+\nu _1+\sigma _1)\right] }{(\alpha _1+\alpha _2+i\beta _1)\left[ \delta _1+\delta _2+\mu _1+\mu _2 +\lambda _1+\lambda _2+i(\rho _1+\nu _1+\sigma _1)\right] }. \end{aligned}$$

Substituting (32) into (25) yields another periodic soliton solution of Eq. (1). Figure 2 depicts the interactions between one periodic wave and two kinky solitary waves. Figure 2a–c gives the 3D plots of the periodic solitary wave in x–y plane, x–z plane and x–s plane, respectively. Their contour plots are shown in Fig. 2d–f.

Fig. 2
figure 2

(Color online) Plots of periodic soliton solution given by (25) and (32). a The case of \(z=s=0\) with \(\alpha _1=\delta _1=-\delta _2=0.8\), \(\alpha _2=-\mu _1=-\mu _2=0.5\), \(\lambda _1=-0.6\), \(\rho _1=-\lambda _2=1\), \(\beta _1=0.4\), \(\nu _1=\sigma _1=0\), b the case of \(y=s=0\) with \(\alpha _1=\delta _1=-\delta _2=0.8\), \(\alpha _2=-\mu _1=0.5\), \(\lambda _1=-0.6\), \(\mu _2=-\lambda _2=1\), \(\nu _1=1.2\), \(\beta _1=0.8\), \(\rho _1=\sigma _1=0\), c the case of \(y=z=0\) with \(\alpha _1=-\delta _1=-\delta _2=0.8\), \(\lambda _1=-\alpha _2=0.6\), \(\mu _1=\mu _2=\beta _1=1\), \(\lambda _2=0.9\), \(\rho _1=\nu _1=0\), \(\sigma _1=1.2\), d the contour plot in x–y plane, e the contour plot in x–z plane, f the contour plot in x–s plane

Full size image

3.3 Mixed lump–kink solutions

In recent years, the study of interactions between lump waves and soliton-like waves has received increasing attention from many scholars, and abundant interesting results have been presented for a number of higher dimensional nonlinear evolution equations. These solutions may be written as combinations of two positive quadratic functions, or two positive quadratic functions plus one exponential function, or two positive quadratic functions plus one hyperbolic cosine function, and so on [38,39,40,41,42,43,44,45,46].

After some tedious computations, it is shown that the (\(4+1\))-dimensional BLMP equation (1) admits more general form of solutions. This new type of solution can be given by transformation (25) and

$$\begin{aligned}&\phi =c_0+{\xi _1}^2+{\xi _1}^2+\sum \limits _{j=1}^{N} \,\left( h_j\mathrm{e}^{\eta _j}+p_j\mathrm{e}^{-\eta _j}\,\right) ,\nonumber \\&\eta _j=k_j x+l_jy+m_jz+n_js+\omega _j t,\nonumber \\&\xi _1=c_1x+c_2y+c_3z+c_4s+c_5 t+c_6,\nonumber \\&\xi _2=c_7x+c_8y+c_9z+c_{10}s+c_{11} t+c_{12}, \end{aligned}$$
(33)

with \(h_j\) and \(p_j\) being arbitrary, and other constant parameters are given by

$$\begin{aligned}&(\mathrm{I})\,c_2=-c_4,\, c_3=c_5=c_7=c_{11}=0,\nonumber \\&\qquad c_i=c_i(i=0,1,4,6,8,9,10,12),\nonumber \\&\qquad l_j=-(m_j+n_j),\,\omega _j=-ak_j^3,\,k_j=k_j,\nonumber \\&\qquad m_j=m_j,\,n_j=n_j,\,j=1,\ldots , N. \end{aligned}$$
(34)
$$\begin{aligned}&(\mathrm{II})\,c_2=-c_4,\, c_3=c_{11}=0,\, c_8=-(c_9+c_{10}),\nonumber \\&\qquad c_i=c_i(i=0,1,4,5,6,7,9,10,12),\nonumber \\&\qquad l_j=-(m_j+n_j),\,k_j=k_j,\,m_j=m_j,\nonumber \\&\qquad n_j=n_j,\,\omega _j=\omega _j,\,j=1,\ldots , N. \end{aligned}$$
(35)
$$\begin{aligned}&(\mathrm{III})\,c_2=-c_3,\,c_4=c_{11}=0,\,c_8=-(c_9+c_{10}),\nonumber \\&\qquad c_i=c_i(i=0,1,3,5,6,7,9,10,12),\nonumber \\&\qquad l_j=-(m_j+n_j),\,k_j=k_j,\,m_j=m_j,\nonumber \\&\qquad \omega _j=-ak_j^3,\,n_j=n_j,\,j=1,\ldots , N. \end{aligned}$$
(36)
$$\begin{aligned}&(\mathrm{IV})\,c_2=-c_3,\, c_4=c_5=c_7=c_{11}=0,\nonumber \\&\qquad c_i=c_i(i=0,1,3,6,8,9,10,12),\nonumber \\&\qquad l_j=-(m_j+n_j),\,\omega _j=-ak_j^3,\,k_j=k_j,\nonumber \\&\qquad m_j=m_j,\,n_j=n_j,\,j=1,\ldots , N. \end{aligned}$$
(37)
$$\begin{aligned}&(\mathrm{V})\,c_2=-\dfrac{c_1c_3+c_1c_4+c_7c_8+c_7c_9+c_7c_{10}}{c_1},\nonumber \\&\qquad c_i=c_i(i=0,1,3,4,6,7,8,9,10,12),\nonumber \\&\qquad c_5=c_{11}=0,\,l_j=-(m_j+n_j),\,\omega _j=-ak_j^3,\nonumber \\&\qquad k_j=k_j,\,m_j=m_j,\,n_j=n_j,\,j=1,\ldots , N. \end{aligned}$$
(38)

Due to the arbitrariness of positive integer N and constant parameters in (34)–(38), different parametric choices lead to different exact solutions for Eq. (1). Here, we only consider six different cases as follows.

Case 1 In (34), taking \(N=1\) and \(p_1=0\), along with (25), the solution with two quadratic functions and one exponential function is obtained

$$\begin{aligned}&u_1 = \dfrac{6a\,(2\,c_1\xi _1+h_1\,k_1\,\mathrm{e}^{\eta _1})}{b\,(c_0+\xi _1^2+\xi _2^2+h_1\mathrm{e}^{\eta _1})},\nonumber \\&\xi _1=c_1 x - c_4y+c_4s+c_6,\nonumber \\&\xi _2=c_8 y+c_9z+c_{10}s+c_{12},\nonumber \\&\eta _1=k_1x-(m_1+n_1)y+m_1z+n_1s-ak_1^3t, \end{aligned}$$
(39)

where \(c_i(i=0,1,4,6,8,9,10,12)\), \(k_1\), \(m_1\), \(n_1\) and \(h_1\) are arbitrary constants.

Case 2 In (35), if \(N=1\) and \(p_1=h_1\) , through transformation (25), we obtain the solution consisting of two quadratic functions and one hyperbolic cosine function

$$\begin{aligned}&u_2 = \dfrac{12a\,[c_1\xi _1+c_7\xi _2+h_1\,k_1\,\sinh (\eta _1)]}{b\,[c_0+\xi _1^2+\xi _2^2+2\,h_1\cosh (\eta _1)]},\nonumber \\&\xi _1=c_1 x - c_4y+c_4s+c_5t+c_6,\nonumber \\&\xi _2=c_7 x - (c_9+c_{10})y+c_9z+c_{10}s+c_{12},\nonumber \\&\eta _1=k_1x-(m_1+n_1)y+m_1z+n_1s+\omega _1\,t, \end{aligned}$$
(40)

where \(c_i(i=0,1,4,5,6,7,9,10,12)\), \(k_1\), \(m_1\), \(n_1\), \(h_1\) and \(\omega _1\) are arbitrary constants.

Case 3 In (35), taking \(N=1\) and \(p_1=-h_1\), from (25) we obtain the solution with two quadratic functions and one hyperbolic sine function

$$\begin{aligned}&u_3 = \dfrac{12a\,\left[ c_1\xi _1+c_7\xi _2+h_1\,k_1\,\cosh (\eta _1)\right] }{b\,\left[ c_0+\xi _1^2+\xi _2^2+2\,h_1\sinh (\eta _1)\right] },\nonumber \\&\xi _1=c_1 x - c_4y+c_4s+c_5t+c_6,\nonumber \\&\xi _2=c_7 x - (c_9+c_{10})y+c_9z+c_{10}s+c_{12},\nonumber \\&\eta _1=k_1x-(m_1+n_1)y+m_1z+n_1s+\omega _1\,t, \end{aligned}$$
(41)

where \(c_i(i=0,1,4,5,6,7,9,10,12)\), \(k_1\), \(m_1\), \(n_1\), \(h_1\) and \(\omega _1\) are arbitrary constants.

Fig. 3
figure 3

Evolution and interaction plots of one lump wave and a pair of kinky waves given by (40) with (45). a\(z=s=0\), \(t=-20\), b\(z=s=0\), \(t=0\), c\(z=s=0\), \(t=20\), d\(y=s=0\), \(t=-30\), e\(y=s=0\), \(t=0\), f\(y=s=0\), \(t=25\), g\(y=z=0\), \(t=-25\), h\(y=z=0\), \(t=0\), i\(y=z=0\), \(t=25\)

Full size image

Case 4 In (36), if \(N=2\), \(p_1=0\) and \(p_2=h_2\), from (25) one obtains the solution in the form

$$\begin{aligned} u_4= & {} 6a\left[ 2c_1\xi _1+2c_7\xi _2+h_1k_1\mathrm{e}^{\eta _1}\right. \nonumber \\&\left. +\,2h_2k_2\sinh (\eta _2)\right] /\left[ b(c_0+\xi _1^2+\xi _2^2\right. \nonumber \\&\left. +\,h_1\mathrm{e}^{\eta _1}+2h_2\cosh (\eta _2))\right] ,\nonumber \\ \xi _1= & {} c_1 x-c_3y+c_3z+c_5t+c_6,\nonumber \\ \xi _2= & {} c_7 x-(c_9+c_{10})y+c_9z+c_{10}s+c_{12},\nonumber \\ \eta _j= & {} k_jx-(m_j+n_j)y+m_jz+n_js-ak_j^3t, \end{aligned}$$
(42)

where \(c_i(i=0,1,3,5,6,7,9,10,12)\), \(k_j\), \(m_j\), \(n_j\), \(h_j\), \(h_j\) and \(\omega _j(j=1,2)\) are arbitrary constants.

Case 5 In (37), taking \(N=2\), \(p_1=h_1\) and \(p_2=h_2\), along with (25), we obtain the solution with two quadratic functions plus one hyperbolic cosine function

$$\begin{aligned} u_5= & {} 12a\left[ c_1\xi _1+h_1k_1\sinh (\eta _1)\right. \nonumber \\&\left. +\,h_2k_2\sinh (\eta _2)\right] /\left[ b(c_0+\xi _1^2+\xi _2^2\right. \nonumber \\&\left. +\,2h_1\cosh (\eta _1)+2h_2\cosh (\eta _2))\right] ,\nonumber \\ \xi _1= & {} c_1x-c_4y+c_4s+c_6,\nonumber \\ \xi _2= & {} c_8y+c_9z+c_{10}s+c_{12},\nonumber \\ \eta _j= & {} k_jx-(m_j+n_j)y+m_jz+n_js-ak_j^3t, \end{aligned}$$
(43)

where \(c_i(i=0,1,4,6,8,9,10,12)\), \(k_j, m_j, n_j, h_j(j=1,2)\) are arbitrary constants.

Case 6 In (38), if \(N=4\) and \(p_1=p_2=p_3=p_4=0\), together with (25), we obtain the solution of the form

$$\begin{aligned}&u_6 = \dfrac{6a\,\left( 2\,c_1\xi _1+2\,c_7\xi _2 +\sum \nolimits _{j=1}^{4}h_j\,k_j\,\mathrm{e}^{\eta _j}\right) }{b\,\left( c_0+\xi _1^2+\xi _2^2+\sum \nolimits _{j=1}^{4}h_j\,\mathrm{e}^{\eta _j}\right) },\nonumber \\&\xi _1=c_1x+c_2\,y+c_3\,z+c_4s+c_6,\nonumber \\&c_2=-\,\dfrac{c_1c_3+c_1c_4+c_7c_8+c_7c_9+c_7c_{10}}{c_1},\nonumber \\&\xi _2=c_7 x+c_8y+c_9z+c_{10}s+c_{12},\nonumber \\&\eta _j=k_jx-(m_j+n_j)y+m_jz+n_js-ak_j^3t, \end{aligned}$$
(44)
Fig. 4
figure 4

Evolution and interaction plots of one lump and four kink waves given by (44) with (46) in x–y plane. a\(t=-5\), b\(t=0.5\), c\(t=6\), d\(t=48\), e\(t=300\), f\(t=1000\)

Full size image

where \(c_i(i=0,1,3,4,6,7,8,9,10,12)\), \(k_j, m_j, n_j, h_j(j=1,2,3,4)\) are arbitrary constants.

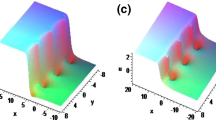
With particular choices of the parameters in (39)–(44), we may obtain abundant interactions between lump wave and kinky solitary waves. Here, solutions (40) and (44) are chosen to illustrate the interesting evolution and interaction phenomenon. Figure 3 gives the three-dimensional plots of evolutions given by (40) with the selection of parameters,

$$\begin{aligned}&a=-1,\,b=3,\,h_1=1,\,c_0=10,\,c_1=20,\nonumber \\&c_4=0.3,\,c_5=0.5,\,c_6=c_{12}=0,\,c_7=25,\nonumber \\&c_9=-0.5,\, c_{10}=0.2,\,k_1=0.8,\,m_1=0.4,\nonumber \\&n_1=0.3,\,\omega _1=0.7. \end{aligned}$$
(45)

Figure 3a–i shows the interaction behaviors between one lump and a pair of kinky solitary waves in x–y plane, x–z plane and x–s plane, respectively. As we can see, the lump wave always lies between these two kinky waves. The amplitude of lump wave first shows a declining trend and then increases gradually with the change of time. As shown in Fig. 3d–i, one can observe that the lump wave has overturned during the evolutions in x–z plane and in x–s plane.

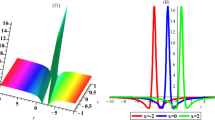
In the following, we select solution (44) to analyze the interesting interactions between one lump wave and four kinky waves by graphs. Taking

$$\begin{aligned}&c_0=c_1=c_8=h_1=h_2=h_3=h_4=1,\nonumber \\&c_3=-c_4=0.5,\,c_6=c_{12}=0,\,c_7=18,\nonumber \\&c_{10}=-c_9=0.6,\,k_1=0.5,\,k_2=1,\,k_3=1.5,\nonumber \\&k_4=2,\,m_1=-0.1,\,m_2=0.5,\,m_3=0.6,\nonumber \\&m_4=-0.2,\,n_1=0.25,n_2=n_3=-0.3,\nonumber \\&n_4=0.7,\,a=1,\,b=3, \end{aligned}$$
(46)

Figure 4 depicts the fission and fusion phenomenon during the evolutions in x–y plane. In Fig. 4a, there is only one kink solitary wave at \(t=-5\). At \(t=0.5\), the lump soliton appears as shown in (b). In (b)–(d), it is easily seen that the kinky wave splits into two, three, and four kinky waves in a short period of time. Meanwhile, the amplitude of the lump soliton has been declined. As shown in Fig. 4d–f, four kinky solitary waves first merge into three, then fuse into two and finally fuse into one kinky solitary wave, which is propagating along the positive x-direction. As shown in Fig. 4b–f, the lump soliton stands at the bottom kinky solitary wave, which depends on the signs of \(k_j(j=1,2,3,4)\) in (44). For the sake of simplicity, the similar analysis in x–z and x–s plane is omitted here.

4 Conclusions

In this paper, we introduce a new integrable nonlinear evolution model in \(4+1\) dimensions, which we call the (\(4+1\))-dimensional BLMP equation. This new equation includes several important NLEEs in \(2+1\) and \(3+1\) dimensions.

By performing the singular manifold analysis, we showed that (\(4+1\))-dimensional BLMP equation passes the Painlevé integrability test. Generally speaking, the positive result in Painlevé test shed light on exploring the N-soliton, Bäcklund and Darboux transformations and Lax pair. Thus, we employed the Bell polynomial approach to further study integrable properties of (\(4+1\))-dimensional BLMP equation and found that it is also integrable under other meanings. The bilinear form, bilinear BT, infinite conservation laws as well as Lax pair are firstly presented.

Based on the Hirota bilinear method, several types of new exact solutions have been constructed, including the N-soliton solutions, periodic soliton solutions and mixed lump–kink wave solutions. The interactions between multiple solitons are unidirectional along x-direction, while the interactions between multiple solitons are bidirectional along y-direction, z-direction and s-direction. In addition, we also studied the interactions between periodic waves and kinky solitary waves. It is noteworthy that Eq. (1) admits a new type of exact solutions composed of two quadratic functions plus N pairs of exponential functions, with N being arbitrary positive integer. The interactions between one lump wave and multiple kinky waves show the characteristics of fusion and fission. For the obtained interesting localized wave solutions, it is very promising to find some potential applications in physical and engineering fields.

We noticed that the contributions of three space variables y, z and s in (1) are the same, so the (\(4+1\))-dimensional integrable BLMP equation may be extended to any dimensions. The more study on Eq. (1) as well as searching for new integrable models in higher dimensions can be investigated in future works.