1 Introduction

Mathematical models play a significant part while dealing with science and engineering problems [1,2,3,4]. As one of the main parts of the mathematical models, the partial differential equations (PDEs) have been widely applied in modern society such as fluid dynamics, plasma physics, soliton theory, hydrodynamics, nonlinear optics, and oceanography. Symmetry analysis method plays an important role in investigating the properties of PDEs [5,6,7,8]. Nowadays classical Lie symmetries have been extended to many general symmetries, such as nonclassical symmetry [9], Lie-Bäcklund symmetry [10], nonlocal symmetry [7]. It is an interesting topic to find the nonlocal symmetries of PDEs. The nonlocal symmetries can yield the new solutions that cannot be obtained from Lie point symmetries. To obtain nonlocal symmetries, Bluman et al.  [11] developed a conservation laws-based method for constructing nonlocally related systems. One can investigate nonlocal symmetries and nonlocal conservation laws by analyzing nonlocally related systems. Furthermore, a symmetry-based method was proposed by Bluman et al. [12] for constructing nonlocally related PDE systems. The symmetry-based method can also be used to construct nonlocal symmetries.

With the development of the theory of nonlocal symmetry, many methods have been found to construct nonlocal symmetries. It is proved that the nonlocal symmetries can be constructed by means of Darboux transformation [13, 14], Bäcklund transformation [15], Lax pair [14, 16] and so on. As we all know, Painlevé analysis technique is an effective method for investigating the integrable properties of PDEs [17,18,19]. It is notable that Lou proved that truncated Painlevé expansion can also be used to construct nonlocal symmetries [20]. Since such type of nonlocal symmetries is the residue of the truncated Painlevé expansion, which is also called residual symmetries. Considering many types of interaction solutions obtained from nonlocal symmetry reduction analysis, Lou developed a more concise consistent Riccati expansion (CRE) method [21] to find the interaction solutions between soliton and other types of waves. This method greatly enriches the types of the solutions of the integrable equations, which are not easily obtained with the aid of Lie symmetry method [22,23,24]. If the CRE method is applicable to an integrable equation, this equation is CRE solvable. There are many CRE solvable integrable equations, for example, the (\(2+1\))-dimensional Korteweg–de Vries equation [25, 26], the coupled Klein–Gordon equations [27], the Bogoyavlenskii coupled KdV system equation [28], the negative-order modified KdV equation [29], supersymmetric mKdV-B equation [30], the (\(2+1\))-dimensional modified KdV–Calogero–Bogoyavlenskii–Schiff equation [31, 32] and the generalized Kadomtsev–Petviashvili equation [33].

In this paper, we consider a (\(2+1\))-dimensional nonlinear system

$$\begin{aligned} \begin{array}{l} {u_{xy}} - 4up + 4q = 0,\\ {u_t} - {q_x} = 0,\\ u{u_y} - {p_x} = 0. \end{array} \end{aligned}$$
(1)

If we set \(q = 0\) in system (1), the system reduces to the sine-Gordon equation

$$\begin{aligned} {v_{xy}} -\, \sin v = 0, \end{aligned}$$

through the changes

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {u = - \,\dfrac{i}{2}{v_x},}\\ {p = \dfrac{1}{4}\cos v.} \end{array}} \right. \end{aligned}$$

Thus this equation can be considered as a generalization of the sine-Gordon equation to \(2+1\) dimensions [34]. Equation (1) can also be trivially written as a modified breaking soliton equation

$$\begin{aligned} 4{u_t} + {u_{xxy}} - 4{u_x}\int {u{u_y}\hbox {d}x} - 4{u^2}{u_y} = 0, \end{aligned}$$

which is an important physical model to describe (\(2+1\))-dimensional interaction of a Riemann wave propagating along the y axis with a long wave along the x axis [35, 36].

The organization of the paper is as follows. In Sect. 2, we obtain the Bäcklund transformation and the residual symmetry of Eq. (1) with the aid of the truncated Painlevé expansion. To localize the residual symmetry to the local Lie point symmetry, an enlarged system of Eq. (1) is introduced. The multiple residual symmetries and the \(n\hbox {th}\) Bäcklund transformation in terms of determinant are also obtained. In Sect. 3, lump and lump-type solutions of Eq. (1) are derived by using the Bäcklund transformation in Sect. 2. In Sect. 4, the CRE solvability of Eq. (1) is investigated. In Sect. 5, the solitary wave solutions and the interaction solutions between soliton and cnoidal periodic wave are investigated systematically. Finally some conclusions are given in the last section.

2 Residual symmetry and Bäcklund transformation

In this section, the residual symmetry of Eq. (1) shall be derived by using the truncated Painlevé expansion. Based on the truncated Painlevé analysis test, Eq. (1) can be expanded to the form

$$\begin{aligned} \begin{array}{l} u = {u_0} + \dfrac{{{u_1}}}{f},\\ p = {p_0} + \dfrac{{{p_1}}}{f}+ \dfrac{{{p_2}}}{f^2},\\ q = {q_0} + \dfrac{{{q_1}}}{f}, \end{array} \end{aligned}$$
(2)

where \({u_0},\;{u_1},\;{p_0},\;{p_1},\;{p_2},\;{q_0},\;{q_1}\) and f are the functions of \(x,\;y\) and t. Substituting (2) into (1) and vanishing all the coefficients of the powers of \(\dfrac{1}{f}\), we have

$$\begin{aligned} {u_0}= & {} \dfrac{{{f_{xx}}}}{{2{f_x}}},\;{u_1} = - \,{f_x},\nonumber \\ {p_0}= & {} \dfrac{{4{f_x}{f_t} + {f_x}{f_{xxy}} - {f_{xx}}{f_{xy}}}}{{4f_x^2}},\;\\ {p_1}= & {} -\, \dfrac{1}{2}{f_{xy}},\;{p_2} = \dfrac{1}{2}{f_x}{f_y},\;\nonumber \\ {q_0}= & {} \dfrac{{{f_{xt}}}}{{2{f_x}}},\;{q_1} = -\, {f_t},\nonumber \end{aligned}$$
(3)

where f satisfies the equation

$$\begin{aligned}&{f_{xxxy}}\nonumber \\&= \dfrac{{{f_x}{f_{xxx}}{f_{xy}} + 3{f_{xx}}{f_{xxy}}{f_x} - 3f_{xx}^2{f_{xy}} - 4{f_{xt}}f_x^2 + 4{f_{xx}}{f_t}{f_x}}}{{f_x^2}},\nonumber \\ \end{aligned}$$
(4)

which is equivalent to the Schwarzian form

$$\begin{aligned} 4{A_x} + {B_y} = 0, \end{aligned}$$
(5)

where

$$\begin{aligned} A = \dfrac{{{f_t}}}{{{f_x}}},\quad B = \dfrac{{{f_{xxx}}}}{{{f_x}}} - \dfrac{3}{2}\dfrac{{f_{xx}^2}}{{f_x^2}}. \end{aligned}$$

Thus, the following Bäcklund transformation theorem for system (1) can be established.

Theorem 1

If function f is a solution of the Schwarzian form (5), then

$$\begin{aligned} \begin{array}{l} u = \dfrac{{{f_{xx}}}}{{2{f_x}}} - \dfrac{{{f_x}}}{f},\\ p = \dfrac{{4{f_x}{f_t} + {f_x}{f_{xxy}} - {f_{xx}}{f_{xy}}}}{{4f_x^2}} - \dfrac{{{f_{xy}}}}{{2f}} + \dfrac{{{f_x}{f_y}}}{{2{f^2}}},\\ q = \dfrac{{{f_{xt}}}}{{2{f_x}}} - \dfrac{{{f_t}}}{f}, \end{array} \end{aligned}$$
(6)

is a solution of system (1).

According to the definition of residual symmetry, the residual symmetry of system (1) can be written as

$$\begin{aligned} {\sigma ^u} = -\, {f_x},\;\;\;{\sigma ^p} = -\, \dfrac{1}{2}{f_{xy}},\;\;\;{} {\sigma ^q} = -\, {f_t}. \end{aligned}$$
(7)

It is a fact that Schwarzian form is invariant under the transformation of Möbius

$$\begin{aligned} f \rightarrow \dfrac{{a + bf}}{{c + df}},\quad \left( {ad \ne bc} \right) \end{aligned}$$
(8)

which means f has the point symmetry

$$\begin{aligned} {\sigma ^f} = -\, {f^2}. \end{aligned}$$
(9)

The symmetry (9) can be simply derived from (8) by making \(a = 0,b = c = 1,d =\varepsilon \). The transformation

$$\begin{aligned} \begin{array}{l} u = \dfrac{{{f_{xx}}}}{{2{f_x}}},\\ p = \dfrac{{4{f_x}{f_t} + {f_x}{f_{xxy}} - {f_{xx}}{f_{xy}}}}{{4f_x^2}},\\ q = \dfrac{{{f_{xt}}}}{{2{f_x}}}, \end{array} \end{aligned}$$
(10)

can change system (1) into the Schwarzian form (5). To find out the residual symmetry group,

$$\begin{aligned} \begin{array}{l} u \rightarrow {\tilde{u}}\left( \varepsilon \right) = u + \varepsilon {\sigma ^u},\\ p \rightarrow {\tilde{p}}\left( \varepsilon \right) = p + \varepsilon {\sigma ^p},\\ q \rightarrow {\tilde{q}}\left( \varepsilon \right) = q + \varepsilon {\sigma ^q}, \end{array} \end{aligned}$$

we should solve the following initial value problem

$$\begin{aligned} \begin{array}{*{20}{l}} {\dfrac{{\hbox {d}{\tilde{u}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, {\tilde{f}}{{\left( \varepsilon \right) }_x},\;\;\;\quad \;{{\left. {{\tilde{u}}\left( \varepsilon \right) } \right| }_{\varepsilon = 0}} = u,}\\ {\dfrac{{\hbox {d}{\tilde{p}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, \dfrac{1}{2}{\tilde{f}}{{\left( \varepsilon \right) }_{xy}},\;\;\;\;{{\left. {{\tilde{p}}\left( \varepsilon \right) } \right| }_{\varepsilon = 0}} = p,}\\ {\dfrac{{\hbox {d}{\tilde{q}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, {\tilde{f}}{{\left( \varepsilon \right) }_t},\;\;\;{{\left. {\quad \;\;{\tilde{q}}\left( \varepsilon \right) } \right| }_{\varepsilon = 0}} = q,} \end{array} \end{aligned}$$

where \(\varepsilon \) is an infinitesimal parameter. However, we find it is hard to solve above initial value problem directly. In order to solve above value problem simply, one can localize the nonlocal symmetry to the local Lie point symmetry for an enlarged system. The new variables are introduced by letting

$$\begin{aligned} {h_1} = {f_x},\quad {h_2} = {f_y},\quad {h_3} = {h_{1y}},\quad {g_1} = {f_t}, \end{aligned}$$
(11)

and then we obtain a prolonged system including (1), (5), (10) and (11). The Lie point symmetry of the prolonged system is

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{\sigma ^u}}\\ {{\sigma ^p}}\\ {{\sigma ^q}}\\ {{\sigma ^f}}\\ {{\sigma ^{{h_1}}}}\\ {\begin{array}{*{20}{l}} {{\sigma ^{{h_2}}}}\\ {{\sigma ^{{h_3}}}} \end{array}}\\ {{\sigma ^{{g_1}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { -\, {h_1}}\\ { -\, {\textstyle {1 \over 2}}{h_3}}\\ { -\, {g_1}}\\ { - \,{f^2}}\\ {\begin{array}{*{20}{l}} { -\, 2f{h_1}}\\ { -\, 2f{h_2}} \end{array}}\\ { -\, 2{h_2}{h_1} - 2f{h_3}}\\ { - \,2f{g_1}} \end{array}} \right) . \end{aligned}$$
(12)

Based on the Lie’s first theorem, the corresponding initial value problem of Lie point symmetry is

$$\begin{aligned}&{\dfrac{{\hbox {d}{\tilde{u}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - \,{{\tilde{h}}_1}\left( \varepsilon \right) ,\quad \quad {\tilde{u}}\left( 0 \right) = u,}\nonumber \\&{\dfrac{{\hbox {d}{\tilde{p}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, \dfrac{1}{2}{{\tilde{h}}_3}\left( \varepsilon \right) ,\;\;\;{\tilde{p}}\left( 0 \right) = p,}\nonumber \\&{\dfrac{{\hbox {d}{\tilde{q}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, {{\tilde{g}}_1}\left( \varepsilon \right) ,\;\;\;\;\;\;{\tilde{q}}\left( 0 \right) = q,} \nonumber \\&\dfrac{{\hbox {d}{\tilde{f}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - \,{\tilde{f}}{\left( \varepsilon \right) ^2},\;\;\;\;\;{\tilde{f}}\left( 0 \right) = f,\nonumber \\&\dfrac{{\hbox {d}{{\tilde{h}}_1}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, 2{\tilde{f}}\left( \varepsilon \right) {{\tilde{h}}_1}\left( \varepsilon \right) ,\;\;\;\quad {{\tilde{h}}_1}\left( 0 \right) = {h_1},\nonumber \\&\dfrac{{d{{\tilde{h}}_2}\left( \varepsilon \right) }}{{d\varepsilon }} = -\, 2{\tilde{f}}\left( \varepsilon \right) {{\tilde{h}}_2}\left( \varepsilon \right) ,\;\;\;\quad {{\tilde{h}}_2}\left( 0 \right) = {h_2},\nonumber \\&\dfrac{{d{{\tilde{h}}_3}\left( \varepsilon \right) }}{{d\varepsilon }} = -\, 2{{\tilde{h}}_2}\left( \varepsilon \right) {{\tilde{h}}_1}\left( \varepsilon \right) - 2{\tilde{f}}\left( \varepsilon \right) {{\tilde{h}}_3}\left( \varepsilon \right) ,\quad {{\tilde{h}}_3}\left( 0 \right) = {h_3},\nonumber \\&\dfrac{{d{{\tilde{g}}_1}\left( \varepsilon \right) }}{{d\varepsilon }} = -\, 2{\tilde{f}}\left( \varepsilon \right) {{\tilde{g}}_1}\left( \varepsilon \right) ,\;\;\;\quad {{\tilde{g}}_1}\left( 0 \right) = {g_1}. \end{aligned}$$
(13)

Solving the above initial problem, we obtain the transformation group that corresponds to the symmetry (12) of the prolonged system (1), (5), (10) and (11)

$$\begin{aligned} \begin{array}{*{20}{l}} {\tilde{u}}\left( \varepsilon \right) = u - \dfrac{{\varepsilon {h_1}}}{{1 + \varepsilon f}},\;{\tilde{p}}\left( \varepsilon \right) = p - \dfrac{{\varepsilon {h_3}}}{{2\left( {1 + \varepsilon f} \right) }}\\ \qquad \qquad + \dfrac{{{\varepsilon ^2}{h_1}{h_2}}}{{2{{\left( {1 + \varepsilon f} \right) }^2}}},\;{\tilde{q}}\left( \varepsilon \right) = q - \dfrac{{\varepsilon {g_1}}}{{1 + \varepsilon f}},\\ {\begin{array}{*{20}{l}} {{\tilde{f}}\left( \varepsilon \right) = \dfrac{f}{{1 + \varepsilon f}},\;{{\tilde{h}}_1}\left( \varepsilon \right) = \dfrac{{{h_1}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}},\;{{\tilde{h}}_2}\left( \varepsilon \right) = \dfrac{{{h_2}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}},\;}\\ {{{\tilde{h}}_3}\left( \varepsilon \right) = \dfrac{{{h_3}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}} - \dfrac{{2\varepsilon {h_1}{h_2}}}{{{{\left( {1 + \varepsilon f} \right) }^3}}},\;{{\tilde{g}}_1}\left( \varepsilon \right) = \dfrac{{{g_1}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}},} \end{array}} \end{array} \end{aligned}$$

where the \(\varepsilon \) is an arbitrary group parameter. Then one has the following finite symmetry transformation theorem for Eq. (1).

Theorem 2

If \(\left\{ {u,p,q,f,{h_1},{h_2},{h_3},{g_1}} \right\} \) is a solution of the prolonged system (1), (5), (10) and (11), then \(\Big \{ {\tilde{u}}\left( \varepsilon \right) ,{\tilde{p}}\left( \varepsilon \right) ,{\tilde{q}}\left( \varepsilon \right) ,{\tilde{f}}\left( \varepsilon \right) ,{{\tilde{h}}_1}\left( \varepsilon \right) ,{{\tilde{h}}_2}\left( \varepsilon \right) ,{{\tilde{h}}_3}\left( \varepsilon \right) ,{{\tilde{g}}_1}\left( \varepsilon \right) \Big \}\) is also a solution of this prolonged system, where \({\tilde{u}}\left( \varepsilon \right) \), \({\tilde{p}}\left( \varepsilon \right) \), \({\tilde{q}}\left( \varepsilon \right) \), \({\tilde{f}}\left( \varepsilon \right) \), \({{\tilde{h}}_1}\left( \varepsilon \right) \), \({{\tilde{h}}_2}\left( \varepsilon \right) \), \({{\tilde{h}}_3}\left( \varepsilon \right) \) and \({{\tilde{g}}_1}\left( \varepsilon \right) \) are given by

$$\begin{aligned}&{\tilde{u}}\left( \varepsilon \right) = u - \dfrac{{\varepsilon {h_1}}}{{1 + \varepsilon f}},\;{\tilde{p}}\left( \varepsilon \right) = p - \dfrac{{\varepsilon {h_3}}}{{2\left( {1 + \varepsilon f} \right) }} \nonumber \\&\qquad \qquad +\, \dfrac{{{\varepsilon ^2}{h_1}{h_2}}}{{2{{\left( {1 + \varepsilon f} \right) }^2}}},\;{\tilde{q}}\left( \varepsilon \right) = q - \dfrac{{\varepsilon {g_1}}}{{1 + \varepsilon f}},\nonumber \\&{{\tilde{f}}\left( \varepsilon \right) = \dfrac{f}{{1 + \varepsilon f}},\;{{\tilde{h}}_1}\left( \varepsilon \right) = \dfrac{{{h_1}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}},\;{{\tilde{h}}_2}\left( \varepsilon \right) = \dfrac{{{h_2}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}},\;}\nonumber \\&{{{\tilde{h}}_3}\left( \varepsilon \right) = \dfrac{{{h_3}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}} - \dfrac{{2\varepsilon {h_1}{h_2}}}{{{{\left( {1 + \varepsilon f} \right) }^3}}},\;{{\tilde{g}}_1}\left( \varepsilon \right) = \dfrac{{{g_1}}}{{{{\left( {1 + \varepsilon f} \right) }^2}}}.} \nonumber \\ \end{aligned}$$
(14)

One can obtain a new solution from any seed solution of system (1) and its Schwarzian form (5) by means of the finite symmetry transformation (14). For example, the Schwarzian form (5) has a solution \(f = {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}\), then \(u = \frac{1}{2}\rho ,\,p = \frac{\kappa }{\rho }\) and \(q = \frac{1}{2}\kappa \) is a solution of system (1). By using the finite symmetry transformations (14), a new solution of system (1) is given by

$$\begin{aligned} \begin{array}{l} {\tilde{u}}\left( \varepsilon \right) = \dfrac{1}{2}\rho - \dfrac{{\varepsilon \rho {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}}}{{1 + \varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}}}},\\ {\tilde{p}}\left( \varepsilon \right) = \dfrac{\kappa }{\rho } - \dfrac{{\varepsilon \rho \omega {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}}}{{2\left( {1 + \varepsilon {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}} \right) }} + \dfrac{{{\varepsilon ^2}\rho \omega {{\left( {{{\mathrm{e}}^{\rho x + \omega y + \kappa t}}} \right) }^2}}}{{2{{\left( {1 + \varepsilon {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}} \right) }^2}}},\;\\ {\tilde{q}}\left( \varepsilon \right) = \dfrac{1}{2}\kappa - \dfrac{{\varepsilon \kappa {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}}}{{1 + \varepsilon {{\mathrm{e}}^{\rho x + \omega y + \kappa t}}}}, \end{array} \end{aligned}$$

where \(\rho ,\,\omega \) and \(\kappa \) are arbitrary constants.

Because the symmetry equations (7) are linear functions and Schwarzian equation (5) has infinitely many solutions, we can obtain infinitely many residual symmetries

$$\begin{aligned} \begin{array}{l} \sigma _n^u = -\, \sum \limits _{i = 1}^n {{\vartheta _i}} {f_{i,x}},\\ \sigma _n^p = - \,\dfrac{1}{2}\sum \limits _{i = 1}^n {{\vartheta _i}} {f_{i,xy}},\\ \sigma _n^q = -\, \sum \limits _{i = 1}^n {{\vartheta _i}} {f_{i,t}}, \end{array} \end{aligned}$$
(15)

where n is an arbitrary constant and \({f_i}\left( {i = 1, \ldots n} \right) \) are the solutions of the Schwarzian equation

$$\begin{aligned} 4{{{\tilde{A}}}_x} + {{\tilde{B}}_{y}} = 0, \end{aligned}$$
(16)

in which

$$\begin{aligned} {\tilde{A}} = \frac{{{f_{i,t}}}}{{{f_{i,x}}}},\;\;\;\;\tilde{B} = \frac{{{f_{i,xxx}}}}{{{f_{i,x}}}} - \frac{3}{2}\frac{{f_{i,xx}^2}}{{f_{i,x}^2}}. \end{aligned}$$

In order to localize the nonlocal symmetries \(\sigma _n^u\), \(\sigma _n^p\) and \(\sigma _n^q\) of (15), one needs to introduce the following new variables

$$\begin{aligned} {h_{1,i}} = {f_{i,x}},\;\; {h_{2,i}} = {f_{i,y}},\;\; {h_{3,i}} = {h_{1y,i}},\;\; {g_{1,i}} = {f_{i,t}}. \end{aligned}$$
(17)

Then the nonlocal symmetry (15) can be localized to a Lie point symmetry

$$\begin{aligned} \sigma _n^u= & {} - \,\sum \limits _{i = 1}^n {{\vartheta _i}} {h_{1,i}},\\ \sigma _n^p= & {} -\, \dfrac{1}{2}\sum \limits _{i = 1}^n {{\vartheta _i}} {h_{3,i}},\\ \sigma _n^q= & {} - \,\sum \limits _{i = 1}^n {{\vartheta _i}} {g_{1,i}},\\ {\sigma ^{{f_i}}}= & {} - \,{\vartheta _i}f_i^2 - \sum \limits _{j \ne i}^n {{\vartheta _j}} {f_i}{f_j},\\ {\sigma ^{{h_{1,i}}}}= & {} -\, 2{\vartheta _i}{f_i}{h_{1,i}} - \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{f_i}{h_{1,j}} + {f_j}{h_{1,i}}} \right) } ,\\ {\sigma ^{{h_{2,i}}}}= & {} - \,2{\vartheta _i}{f_i}{h_{2,i}} - \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{f_i}{h_{2,j}} + {f_j}{h_{2,i}}} \right) } ,\\ {\sigma ^{{h_{3,i}}}}= & {} -\, 2{\vartheta _i}\left( {{h_{2,i}}{h_{1,i}} + {f_i}{h_{3,i}}} \right) \\&-\, \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{h_{2,i}}{h_{1,j}} + {h_{2,j}}{h_{1,i}} + {f_i}{h_{3,j}} + {f_j}{h_{3,i}}} \right) ,}\\ {\sigma ^{{g_{1,i}}}}= & {} -\, 2{\vartheta _i}{f_i}{g_{1,i}} - \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{f_i}{g_{1,j}} + {f_j}{g_{1,i}}} \right) } . \end{aligned}$$

The corresponding initial value problem of Lie point symmetry can be written as

$$\begin{aligned}&{\dfrac{{\hbox {d}{\tilde{u}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - \,\sum \limits _{i = 1}^n {{\vartheta _i}} {{\tilde{h}}_{1,i}}\left( \varepsilon \right) ,}\\&{\dfrac{{\hbox {d}{\tilde{p}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, \dfrac{1}{2}\sum \limits _{i = 1}^n {{\vartheta _i}} {{\tilde{h}}_{3,i}}\left( \varepsilon \right) ,}\\&{\dfrac{{\hbox {d}{\tilde{q}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - \,\sum \limits _{i = 1}^n {{\vartheta _i}} {{\tilde{g}}_{1,i}}\left( \varepsilon \right) ,}\\&{\dfrac{{\hbox {d}{{{\tilde{f}}}_i}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - \,{\vartheta _i}{{\tilde{f}}}_i^2\left( \varepsilon \right) - \sum \limits _{j \ne i}^n {{\vartheta _j}} {{{\tilde{f}}}_i}\left( \varepsilon \right) {{{\tilde{f}}}_j}\left( \varepsilon \right) ,}\\&\dfrac{{\hbox {d}{{\tilde{h}}_{1,i}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - 2{\vartheta _i}{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{1,i}}\left( \varepsilon \right) \\&\qquad \qquad \qquad \quad -\, \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{1,j}}\left( \varepsilon \right) + {{{\tilde{f}}}_j}\left( \varepsilon \right) {{\tilde{h}}_{1,i}}\left( \varepsilon \right) } \right) } ,\\&\dfrac{{\hbox {d}{{\tilde{h}}_{2,i}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - 2{\vartheta _i}{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{2,i}}\left( \varepsilon \right) \\&\qquad \qquad \qquad \quad -\, \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{2,j}}\left( \varepsilon \right) + {{{\tilde{f}}}_j}\left( \varepsilon \right) {{\tilde{h}}_{2,i}}\left( \varepsilon \right) } \right) ,} \\&\dfrac{{\hbox {d}{{\tilde{h}}_{3,i}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = -\, 2{\vartheta _i}\left( {{{\tilde{h}}_{2,i}}\left( \varepsilon \right) {{\tilde{h}}_{1,i}}\left( \varepsilon \right) + {{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{3,i}}\left( \varepsilon \right) } \right) \\&\qquad \qquad \qquad \quad - \,\sum \limits _{j \ne i}^n {\vartheta _j}\left( {{\tilde{h}}_{2,i}}\left( \varepsilon \right) {{\tilde{h}}_{1,j}}\left( \varepsilon \right) \right. \\&\qquad \qquad \qquad \quad \left. +\, {{\tilde{h}}_{2,j}}\left( \varepsilon \right) {{\tilde{h}}_{1,i}}\left( \varepsilon \right) + {{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{h}}_{3,j}}\left( \varepsilon \right) + {{{\tilde{f}}}_j}\left( \varepsilon \right) {{\tilde{h}}_{3,i}}\left( \varepsilon \right) \right) ,\\&\dfrac{{\hbox {d}{{\tilde{g}}_{1,i}}\left( \varepsilon \right) }}{{\hbox {d}\varepsilon }} = - 2{\vartheta _i}{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{g}}_{1,i}}\left( \varepsilon \right) \\&\qquad \qquad \qquad \quad -\, \sum \limits _{j \ne i}^n {{\vartheta _j}\left( {{{{\tilde{f}}}_i}\left( \varepsilon \right) {{\tilde{g}}_{1,j}}\left( \varepsilon \right) + {{{\tilde{f}}}_j}\left( \varepsilon \right) {{\tilde{g}}_{1,i}}\left( \varepsilon \right) } \right) }.\\&{\tilde{u}}\left( 0 \right) = u,\;{\tilde{p}}\left( 0 \right) = p,\;{\tilde{q}}\left( 0 \right) = q,\;{{{\tilde{f}}}_i}\left( 0 \right) = {f_i},\;{{\tilde{h}}_{1,i}}\left( 0 \right) = {h_{1,i}},\\&{{\tilde{h}}_{2,i}}\left( 0 \right) = {h_{2,i}},\;{{\tilde{h}}_{3,i}}\left( 0 \right) = {h_{3,i}},\;{{\tilde{g}}_{1,i}}\left( 0 \right) = {g_{1,i}}. \end{aligned}$$

By solving above initial value problem, one has the following \(n\hbox {th}\) Bäcklund transformation theorem.

Theorem 3

If \(\left\{ {u,p,q,{f_i},{h_{1,i}},{h_{2,i}},{h_{3,i}},{g_{1,i}}} \right\} \) is a solution of the prolonged system (1), (16), (17) and

$$\begin{aligned} \begin{array}{*{20}{l}} {u = \dfrac{{{f_{i,xx}}}}{{2{f_{i,x}}}},}\\ p = \dfrac{{4{f_{i,x}}{f_{i,t}} + {f_{i,x}}{f_{i,xxy}} - {f_{i,xx}}{f_{i,xy}}}}{{4f_{i,x}^2}},\\ {q = \dfrac{{{f_{i,xt}}}}{{2{f_{i,x}}}} ,} \end{array} \end{aligned}$$

then \(({\tilde{u}}\left( \varepsilon \right) ,{\tilde{p}}\left( \varepsilon \right) ,{\tilde{q}}\left( \varepsilon \right) ,{{{\tilde{f}}}_i}\left( \varepsilon \right) ,{{\tilde{h}}_{1,i}}\left( \varepsilon \right) ,{{\tilde{h}}_{2,i}}\left( \varepsilon \right) ,{{\tilde{h}}_{3,i}}\left( \varepsilon \right) ,{{\tilde{g}}_{1,i}}\left( \varepsilon \right) )\) is also the solution of the prolonged system, where \({\tilde{u}}\left( \varepsilon \right) ,{\tilde{p}}\left( \varepsilon \right) ,{\tilde{q}}\left( \varepsilon \right) ,{{\tilde{f}}_i}\left( \varepsilon \right) ,{\tilde{h}_{1,i}}\left( \varepsilon \right) ,{\tilde{h}_{2,i}}\left( \varepsilon \right) ,{\tilde{h}_{3,i}}\left( \varepsilon \right) \) and \({\tilde{g}}_{1,i}\left( \varepsilon \right) \) are given by

$$\begin{aligned} \begin{array}{*{20}{l}} {{\tilde{u}}\left( \varepsilon \right) = u - {{\left( {\ln \wp } \right) }_x},}\\ {{\tilde{p}}\left( \varepsilon \right) = p - \dfrac{1}{2}{{\left( {\ln \wp } \right) }_{xy}},}\\ {{\tilde{q}}\left( \varepsilon \right) = q - {{\left( {\ln \wp } \right) }_t},}\\ {\begin{array}{*{20}{l}} {{{{\tilde{f}}}_i}\left( \varepsilon \right) = \dfrac{{{\wp _i}}}{\wp },\;}\\ {{{\tilde{h}}_{1,i}}\left( \varepsilon \right) = {{{\tilde{f}}}_{i,x}}\left( \varepsilon \right) ,\;{{\tilde{h}}_{2,i}}\left( \varepsilon \right) = {{{\tilde{f}}}_{i,y}}\left( \varepsilon \right) ,}\\ {{{\tilde{h}}_{3,i}}\left( \varepsilon \right) = {{{\tilde{f}}}_{i,xy}}\left( \varepsilon \right) ,{{\tilde{g}}_{1,i}}\left( \varepsilon \right) = {{{\tilde{f}}}_{i,t}}\left( \varepsilon \right) ,} \end{array}} \end{array} \end{aligned}$$

where \({\wp }\) and \({\wp _i}\) are the determinants of two matrices as follows

$$\begin{aligned} \wp= & {} \left| {\begin{array}{*{20}{c}} {{\vartheta _1}\varepsilon {f_1} + 1}&{}{{\vartheta _1}\varepsilon {\theta _{12}}}&{} \cdots &{}{{\vartheta _1}\varepsilon {\theta _{1j}}}&{} \cdots &{}{{\vartheta _1}\varepsilon {\theta _{1n}}}\\ {{\vartheta _2}\varepsilon {\theta _{12}}}&{}{{\vartheta _2}\varepsilon {f_2} + 1}&{} \cdots &{}{{\vartheta _2}\varepsilon {\theta _{2j}}}&{} \cdots &{}{{\vartheta _2}\varepsilon {\theta _{2n}}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{\vartheta _j}\varepsilon {\theta _{1j}}}&{}{{\vartheta _j}\varepsilon {\theta _{2j}}}&{} \cdots &{}{{\vartheta _j}\varepsilon {f_j} + 1}&{} \cdots &{}{{\vartheta _j}\varepsilon {\theta _{jn}}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{\vartheta _n}\varepsilon {\theta _{1n}}}&{}{{\vartheta _n}\varepsilon {\theta _{2n}}}&{} \cdots &{}{{\vartheta _n}\varepsilon {\theta _{jn}}}&{} \cdots &{}{{\vartheta _n}\varepsilon {f_n} + 1} \end{array}} \right| , \end{aligned}$$
(18)
$$\begin{aligned} {\theta _{ij}}= & {} \sqrt{{f_i}{f_j}}, \end{aligned}$$
(19)
$$\begin{aligned} {\wp _i}= & {} \left| {\begin{array}{*{20}{c}} {{\vartheta _1}\varepsilon {f_1} + 1}&{}{{\vartheta _1}\varepsilon {\theta _{12}}}&{} \cdots &{}{{\vartheta _1}\varepsilon {\theta _{1,i - 1}}}&{}{{\vartheta _1}\varepsilon {\theta _{1i}}}&{}{{\vartheta _1}\varepsilon {\theta _{1,i + 1}}}&{} \cdots &{}{{\vartheta _1}\varepsilon {\theta _{1n}}}\\ {{\vartheta _2}\varepsilon {\theta _{12}}}&{}{{\vartheta _2}\varepsilon {f_2} + 1}&{} \cdots &{}{{\vartheta _2}\varepsilon {\theta _{2,i - 1}}}&{}{{\vartheta _2}\varepsilon {\theta _{2i}}}&{}{{\vartheta _2} \in {\theta _{2,i + 1}}}&{} \cdots &{}{{\vartheta _2}\varepsilon {\theta _{2n}}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{\vartheta _{i - 1}}\varepsilon {\theta _{1,i - 1}}}&{}{{\vartheta _{i - 1}}\varepsilon {\theta _{2,i - 1}}}&{} \cdots &{}{{\vartheta _{i - 1}}\varepsilon {f_{i - 1}} + 1}&{}{{\vartheta _{i - 1}}\varepsilon {\theta _{i - 1,i}}}&{}{{\vartheta _{i - 1}}\varepsilon {\theta _{i - 1,i + 1}}}&{} \cdots &{}{{\vartheta _{i - 1}}\varepsilon {\theta _{i - 1,n}}}\\ {{\theta _{1i}}}&{}{{\theta _{2i}}}&{} \cdots &{}{{\theta _{i,i - 1}}}&{}{{f_i}}&{}{{\theta _{i,i + 1}}}&{} \cdots &{}{{\theta _{in}}}\\ {{\vartheta _{i + 1}}\varepsilon {\theta _{1,i + 1}}}&{}{{\vartheta _{i + 1}}\varepsilon {\theta _{2,i + 1}}}&{} \cdots &{}{{\vartheta _{i + 1}}\varepsilon {\theta _{i - 1,i + 1}}}&{}{{\vartheta _{i + 1}}\varepsilon {\theta _{i,i + 1}}}&{}{{\vartheta _{i + 1}}\varepsilon {f_{i + 1}} + 1}&{} \cdots &{}{{\vartheta _{i + 1}}\varepsilon {\theta _{i + 1,n}}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{\vartheta _n}\varepsilon {\theta _{1n}}}&{}{{\vartheta _n}\varepsilon {\theta _{2n}}}&{} \cdots &{}{{\vartheta _n}\varepsilon {\theta _{i - 1,n}}}&{}{{\vartheta _n}\varepsilon {\theta _{in}}}&{}{{\vartheta _n}\varepsilon {\theta _{i + 1,n}}}&{} \cdots &{}{{\vartheta _n}\varepsilon {f_n} + 1} \end{array}} \right| .\qquad \qquad \qquad \qquad \quad \end{aligned}$$
(20)

From Theorem 3, one can construct an infinite number of new solutions from any seed solutions of system (1) and its Schwarzian form (16). For example, for the Schwarzian form (16), it has a special solution

$$\begin{aligned} {f_i} = {{\mathrm{e}}^{\rho x + {\omega _i}y + \kappa t}}. \end{aligned}$$

Then it is obvious that \(u = \frac{1}{2}\rho ,\,p = \frac{\kappa }{\rho }\) and \(q = \frac{1}{2}\kappa \) is a seed solution of system (1). On the basis of theorem 3, one can obtain the following multiple wave solutions for system (1)

$$\begin{aligned} {\tilde{u}}\left( \varepsilon \right)= & {} \dfrac{1}{2} \rho - \dfrac{{{\vartheta _1}\varepsilon \rho {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}}}}{{{\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + 1}},\\ {\tilde{p}}\left( \varepsilon \right)= & {} \dfrac{\kappa }{\rho } - \dfrac{1}{2}\dfrac{{{\vartheta _1}\varepsilon \rho {\omega _1}{{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}}}}{{{\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + 1}}+\dfrac{1}{2}\dfrac{{{\vartheta _1}^2{\varepsilon ^2}\rho {\omega _1}{{\left( {{{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}}} \right) }^2}}}{{{{\left( {{\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + 1} \right) }^2}}},\\ {\tilde{q}}\left( \varepsilon \right)= & {} \dfrac{1}{2}\kappa - \dfrac{{{\vartheta _1}\varepsilon {\omega _1}{{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}}}}{{{\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + 1}}, \end{aligned}$$

for \(n=1\),

$$\begin{aligned} {\tilde{u}}\left( \varepsilon \right)= & {} \dfrac{1}{2}\rho - \dfrac{{{\vartheta _1}\varepsilon \rho {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon \rho {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}}{{1 + {\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}},\\ {\tilde{p}}\left( \varepsilon \right)= & {} \dfrac{\kappa }{\rho } - \dfrac{1}{2}\dfrac{{{\vartheta _1}\varepsilon \rho {\omega _1}{{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon \rho {\omega _2}{{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}}{{1 + {\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}}\\&+ \dfrac{1}{2}\dfrac{{\left( {{\vartheta _1}\varepsilon \rho {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon \rho {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}} \right) \left( {{\vartheta _1}\varepsilon {\omega _1}{{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon {\omega _2}{{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}} \right) }}{{{{\left( {1 + {\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}} \right) }^2}}},\\ {\tilde{q}}\left( \varepsilon \right)= & {} \dfrac{1}{2}\kappa - \dfrac{{{\vartheta _1}\varepsilon \kappa {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon \kappa {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}}{{1 + {\vartheta _1}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _1}y + \kappa t}} + {\vartheta _2}\varepsilon {{\mathrm{e}}^{\rho x + {\omega _2}y + \kappa t}}}}, \end{aligned}$$

for \(n=2\),

$$\begin{aligned}&\vdots \\&{{\tilde{u}}\left( \varepsilon \right) = \dfrac{1}{2}\rho - {{\left( {\ln \wp } \right) }_x},}\\&{{\tilde{p}}\left( \varepsilon \right) = \dfrac{\kappa }{\rho } - \dfrac{1}{2}{{\left( {\ln \wp } \right) }_{xy}},}\\&{{\tilde{q}}\left( \varepsilon \right) = \dfrac{1}{2}\kappa - {{\left( {\ln \wp } \right) }_t},}\\&{{f_i} = 1 + {{\mathrm{e}}^{\rho x + {\omega _i}y + \kappa t}},\;i = 1, \cdots ,n,} \end{aligned}$$

where \(\wp \) is given by (1819) and \(\rho ,\,{\omega _i}\), \(\kappa \) and \({\vartheta _i}\) are arbitrary constants.

3 Lump and lump-type solutions

Lump solutions appear in many physical phenomena, such as plasma, shallow water wave, optic media, Bose–Einstein condensate. Lump wave is one kind of rogue wave [37,38,39]. Based on the bilinear forms, Ma firstly constructed lump solutions of the Kadomtsev–Petviashvili equation [40]. Then this method was further extended to find lump-type solutions of some nonlinear differential equations [41, 42]. Inspired by Ma’s work, we proposed a method for constructing lump and lump-type solutions of integrable equations by means of Bäcklund transformation obtained from the truncated Painlevé expansion [43]. In this section, we shall search lump and lump-type solutions of Eq. (1) with the aid of Bäcklund transformation in Theorem 1.

In order to search quadratic solutions to Eq. (4), we let

$$\begin{aligned} f= & {} {\left( {{a_1}x + {a_2}y + {a_3}t + {a_4}} \right) ^2}\nonumber \\&\quad + {\left( {{a_5}x + {a_6}y + {a_7}t + {a_8}} \right) ^2} + {a_9}, \end{aligned}$$
(21)

where \({a_i},1 \le i \le 9\) are real parameters to be determined. Substituting (21) into (4) with the aid of symbolic computation, we can obtain the following set of constraining equations for \({a_i}\)

$$\begin{aligned} {a_2} = -\, \frac{{{a_5}{a_6}}}{{{a_1}}},\quad {a_7} = \frac{{{a_3}{a_5}}}{{{a_1}}}. \end{aligned}$$
(22)

Substituting (21) with (22) into (6) gives the solutions

$$\begin{aligned} u= & {} \dfrac{{\left( {2 {a_1}^2 + 2 {a_5}^2} \right) }}{2}\left( 2 \left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_1} \right. \nonumber \\&\left. +\, 2 \left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_5} \right) ^{ - 1}\nonumber \\&-\, \left( 2 \left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_1} + 2 \left( {a_5}x + {a_6}y \right. \right. \nonumber \\&\left. \left. +\, \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8} \right) {a_5} \right) \left( {{\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) }^2}\right. \nonumber \\&\left. +\, {{\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) }^2} + {a_9} \right) ^{ - 1}, \end{aligned}$$
(23)
$$\begin{aligned} p= & {} \left( 2\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_3} \right. \nonumber \\&\left. +\, 2\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_3}{a_5}a_1^{ - 1} \right) \nonumber \\&\times \left( 2\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_1}\right. \nonumber \\&\left. +\, 2\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_5} \right) ^{ - 1}\nonumber \\&+\, \dfrac{1}{2}\left( 2\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_1} \right. \nonumber \\&\left. +\, 2\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_5} \right) \nonumber \\&\left( -\, 2\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_6}{a_5}{a_1}^{ - 1} \right. \nonumber \\&\left. +\, 2\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_6} \right) \nonumber \\&\times \left( {{\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) }^2} + \left( {a_5}x + {a_6}y \right. \right. \nonumber \\&\left. \left. +\, \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8} \right) ^2 + {a_9} \right) ^{ - 2}, \end{aligned}$$
(24)
$$\begin{aligned} q= & {} \left( {{a_3}{a_1} + \dfrac{{{a_3}{a_5}^2}}{{{a_1}}}} \right) \left( 2\left( {a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} \right. \right. \nonumber \\&\left. \left. +\, {a_3}t + {a_4} \right) {a_1} + 2 \left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_5} \right) ^{ - 1}\nonumber \\&-\, \left( 2\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) {a_3} \right. \nonumber \\&\left. +\, 2\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) {a_3}{a_5}{a_1}^{ - 1} \right) \nonumber \\&\times \left( {{\left( {{a_1}x - \dfrac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) }^2} \right. \nonumber \\&\left. +\, {{\left( {{a_5}x + {a_6}y + \dfrac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) }^2} + {a_9} \right) ^{ - 1}, \end{aligned}$$
(25)

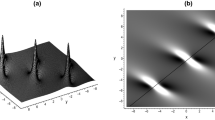
where \({a_1},\,{a_3},\,{a_4},\,{a_5},\,{a_6},\,{a_8}\) and \({a_9}\) are arbitrary constants. The solutions (23), (24) and (25) could be used to describe nonlinear wave phenomena in oceanography and nonlinear optics. Figure 1 shows the dynamic behaviors of solutions (23), (24) and (25) with \({a_1}={a_6}=1,\,{a_3}={a_8}= \frac{1}{2},\,{a_4}={a_5}=-\, 1\) and \({a_9} = 2\). Figure 1d shows the lump solution p (24) maintains property of localization in the \(\left( {x,y} \right) \) plane. The condition \({a_1}{a_6} + \dfrac{{a_5^2{a_6}}}{{{a_1}}} \ne 0\) guarantees the localization of the lump solution (24) in all directions in the space, i.e., \(\mathop {\lim }\nolimits _{{x^2} + {y^2} \rightarrow \infty } p\left( {x,y,t} \right) = 0,\;\forall t \in \mathbb {R}.\) \({a_9} > 0\) makes sure that the lump solution is positive. Figure 1a shows a lump wave residing on a inverse proportional function wave, which is not localized in the \(\left( {x,y} \right) \) plane. The solutions (23) and (25) are lump-type solutions. By observing Fig. 1, we know concentration of energy of lump wave p (24) is more concentrated than lump-type wave u (23) and q (25). Figure 1f exhibits anti-W type solution p in the plane \(\left( {x,t} \right) \). Figure 1g–i illustrates that the dynamic behaviors of lump-type solution q (25) are similar to that of u (23) Fig.1a–c.

Fig. 1
figure 1

(Color online) Lump-type wave (23), (25) and lump wave (24) with \({a_1}={a_6}= 1, {a_3}={a_8}=\frac{1}{2}, {a_4}={a_5}=-\, 1, {a_9}= 2\). a Perspective view of the wave \(u\left( {x,y,0} \right) \). b Perspective view of the wave \(u\left( {0,y,t} \right) \). c Perspective view of the wave \(u\left( {x,0,t} \right) \). d Perspective view of the wave \(p\left( {x,y,0} \right) \). e Perspective view of the wave \(p\left( {0,y,t} \right) \). f Perspective view of the wave \(p\left( {x,0,t} \right) \). g Perspective view of the wave \(q\left( {x,y,0} \right) \). h Perspective view of the wave \(q\left( {0,y,t} \right) \). i Perspective view of the wave \(q\left( {x,0,t} \right) \)

Full size image

Remark 1

Lump solution is rationally localized in all directions in the space. The rational solution that only can be localized in many directions in the space is called lump-type solution [42]. The solution p (24) is rationally localized in all directions in the space. Thus the solution p (24) is a lump solution. The solutions u (23) and q (25) describe a lump wave residing on a inverse proportional function wave, which are not localized in all directions in the space. Strictly speaking, solutions u (23) and q (25) are lump-inverse-proportional wave solutions. All the functions u (23) and q (25) tend to zero when the corresponding sum of squares \({\left( {{a_1}x - \frac{{{a_6}{a_5}y}}{{{a_1}}} + {a_3}t + {a_4}} \right) ^2} + {\left( {{a_5}x + {a_6}y + \frac{{{a_3}{a_5}t}}{{{a_1}}} + {a_8}} \right) ^2} \rightarrow \infty \). But they do not tend to zero in all directions in \({\mathbb {R}^3}\). According to the definition in reference [41], u (23) and q (25) can also be called lump-type solutions.

4 CRE solvability

Based on the CRE method, the solutions of Eq. (1) can be expanded as

$$\begin{aligned} \begin{array}{l} u = {u_0} + {u_1}R\left( w \right) ,\\ p = {p_0} + {p_1}R\left( w \right) + {p_2}R{\left( w \right) ^2},\\ q = {q_0} + {q_1}R\left( w \right) , \end{array} \end{aligned}$$
(26)

where \(R\left( w \right) \) is the solution of the following Riccati equation

$$\begin{aligned} R{\left( w \right) _w} = {a_0} + {a_1}R\left( w \right) + {a_2}R{\left( w \right) ^2}, \end{aligned}$$
(27)

with \({a_0},\,{a_1}\) and \({a_2}\) are arbitrary constants. Substituting the expression (26) with (27) into (1) and collecting all the coefficients of the powers of \(R\left( w \right) \) yields an overdetermined system of PDEs about \({u_0}\), \({u_1}\), \({p_0}\), \({p_1}\), \({p_2}\), \({q_0}\) and \({q_1}\). Solving this system, one has

$$\begin{aligned} \begin{array}{l} {u_0} = \dfrac{1}{2}\dfrac{{{a_1}w_x^2 + {w_{xx}}}}{{{w_x}}},\;{u_1} = {a_2}{w_x},\\ {p_0} {=} \dfrac{{4 {w_x}{w_t} + 2{a_0}{a_2} {w_x}^3{w_y} + {w_x}{w_{xxy}} + {a_1}{w_x}^2{w_{xy}} - {w_{xy}}{w_{xx}}}}{{4{w_x}^2}},\\ {p_1} = \dfrac{1}{2}\left( {{a_2} {w_{xy}} + {a_1}{a_2}{w_x}{w_y}} \right) ,{p_2} = \dfrac{1}{2}a_2^2{w_x}{w_y},\\ \begin{array}{*{20}{l}} {{q_0} = \dfrac{1}{2}\dfrac{{{w_{xt}} + {a_1}{w_x}{w_t}}}{{{w_x}}},\;{q_1} = {a_2}{w_t},}\\ \end{array} \end{array} \end{aligned}$$
(28)

and the function \(w\left( {x,y,t} \right) \) satisfies

$$\begin{aligned} {w_{xxxy}} = \dfrac{{{w_x}{w_{xy}}{w_{xxx}} - 3 {w_{xy}}{w_{xx}}^2 + 4 {w_{xx}}{w_t}{w_x} + 3{w_{xx}}{w_x}{w_{xxy}} - 4 {w_{xt}}{w_x}^2 + \chi {w_x}^4{w_{xy}}}}{{{w_x}^2}}, \end{aligned}$$
(29)

where \(\chi = a_1^2 - 4{a_0}{a_2}\), which is equivalent to the Schwarzian form

$$\begin{aligned} 4{{A'}_x} +{{B'}_y} - \chi w_x {w_{xy}} = 0, \end{aligned}$$
(30)

by introducing notations as

$$\begin{aligned} A'= \dfrac{{{w_t}}}{{{w_x}}},\quad B' = \dfrac{{{w_{xxx}}}}{{{w_x}}} - \dfrac{3}{2}\dfrac{{w_{xx}^2}}{{w_x^2}}. \end{aligned}$$

Then a Bäcklund transformation between the solutions \(u,\;p\) and q of Eq. (1) and \(R\left( w \right) \) of Riccati equation (27) is constructed.

Theorem 4

If function \(w\left( {x,y,t} \right) \) is a solution of Schwarzian form (30), then

$$\begin{aligned} \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {u = \dfrac{1}{2}\dfrac{{{a_1}w_x^2 + {w_{xx}}}}{{{w_x}}} + {a_2}{w_x}R\left( w \right) ,}\\ {p = \dfrac{{4{w_x}{w_t} + 2{a_0}{a_2}{w_x}^3{w_y} + {w_x}{w_{xxy}} + {a_1}{w_x}^2{w_{xy}} - {w_{xy}}{w_{xx}}}}{{4{w_x}^2}}} \end{array}}\\ {\;\;\; \;\;\; +\, \dfrac{1}{2}\left( {{a_2}{w_{xy}} + {a_1}{a_2}{w_x}{w_y}} \right) R\left( w \right) + \dfrac{1}{2}a_2^2{w_x}{w_y}R{{\left( w \right) }^2},}\\ {q = \dfrac{1}{2}\dfrac{{{w_{xt}} + {a_1}{w_x}{w_t}}}{{{w_x}}} + {a_2}{w_t}R\left( w \right) ,} \end{array} \end{aligned}$$
(31)

is a solution of system (1) with \(R\left( w \right) \) which is a solution of the Riccati equation (27).

5 Solitary wave and soliton–cnoidal wave solutions of Eq. (1)

5.1 Solitary wave solutions

To obtain the one soliton solutions of Eq. (1), we choose a tanh-function solution

$$\begin{aligned} R\left( w \right) = -\, \frac{1}{{2{a_2}}}\left[ {{a_1} + \sqrt{\chi } \tanh \left( {\frac{1}{2}\sqrt{\chi } w} \right) } \right] , \end{aligned}$$
(32)

for Riccati equation (27). According to Theorem 4, we let

$$\begin{aligned} w\left( {x,y,t} \right) = kx + ly+ ht , \end{aligned}$$
(33)

and substitute it into (31), then one has

$$\begin{aligned} u= & {} \dfrac{1}{2}{a_1}k + {a_2}kR\left( w \right) , \end{aligned}$$
(34)
$$\begin{aligned} p= & {} \dfrac{{4h + 2{a_0}{a_2}{k^2}l}}{{4k}} + \dfrac{{{a_1}{a_2}kl}}{2}R\left( w \right) + \dfrac{{a_2^2kl}}{2}R{\left( w \right) ^2}, \end{aligned}$$
(35)
$$\begin{aligned} q= & {} \dfrac{{{a_1}h}}{2} + {a_2}hR\left( w \right) , \end{aligned}$$
(36)

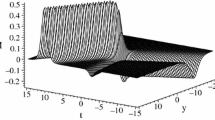
which are the solitary wave solutions of Eq. (1). Figure 2a, c shows the kink-shape solitary waves. The bell-shape dark solitary wave is shown in Fig. 2b.

Fig. 2
figure 2

(Color online) One solitary wave (34), (35) and (36) with \({a_0} =1,\;{a_1} = 3,\;{a_2} = 1,\;{k} =1,\; l=\frac{1}{2},\;h = 2\). a Perspective view of the wave \(u\left( {x,y,0} \right) \). b Perspective view of the wave \(p\left( {x,y,0} \right) \). c Perspective view of the wave \(q\left( {x,y,0} \right) \)

Full size image

5.2 Soliton–cnoidal wave solutions

In order to find the soliton–cnoidal wave interaction solutions of Eq. (1), we let

$$\begin{aligned} w = {k_1}x + {l_1}y + {h_1}t + \psi \left( \xi \right) ,\;\xi = {k_2}x + {l_2}y + {h_2}t, \end{aligned}$$
(37)

where \({\psi _\xi } = \dfrac{{\hbox {d}\psi \left( \xi \right) }}{{\hbox {d}\xi }}\) is a solution of the following elliptic equation

$$\begin{aligned} \psi _{\xi \xi }^2 = {c_0} + {c_1}{\psi _\xi } + {c_2}\psi _\xi ^2 + {c_3}\psi _\xi ^3 + {c_4}\psi _\xi ^4, \end{aligned}$$
(38)

where \({c_i}\left( {i = 0 \cdots 4} \right) \) are constants. Substituting (37) with (38) into (29) yields the following set of constraining equations for \({c_i}\)

$$\begin{aligned} \begin{array}{*{20}{l}} {{c_0} = -\, \dfrac{4}{3}\dfrac{{\left( {\left( {\left( { - {\textstyle {1 \over 4}}\chi } \right) {k_1}^3 + {\textstyle {1 \over 4}}{k_2}^2{c_2}{k_1} - {\textstyle {1 \over 2}}{c_1}{k_2}^3} \right) {l_2} + {h_2}{k_1} - {h_1}{k_2}} \right) {k_1}}}{{{l_2}{k_2}^4}},}\\ {{c_3} = \dfrac{1}{3}\dfrac{{4\chi {l_2}{k_1}^3 + \left( {2{k_2}^2{l_2}{c_2} - 4{h_2}} \right) {k_1} + 4{h_1}{k_2} - {k_2}^3{l_2}{c_1}}}{{{l_2}{k_1}^2{k_2}}},}\\ {{c_4} = \chi .} \end{array} \end{aligned}$$
(39)

Since the general solution of (38) can be written out in terms of Jacobi elliptic functions, one can investigate the explicit interaction solutions between the soliton and the cnoidal periodic wave. In what follows, we offer two special solutions of Eq. (38) to solve Eq. (1).

Fig. 3
figure 3

(Color online) Soliton–cnoidal wave u(x, y, t) (42), p(x, y, t) (43) and q(x, y, t) (44) with \(m = 1,\;n = \frac{1}{2},\;{k_2} = 1,\;{l_1} = 1,\;{l_2} = -\, \frac{3}{2},\;{h_2} = 1,\;{\mu _0} = \frac{1}{2},\;{a_0}= 1\), \(a_1=3\), \(a_2=2\), \({\xi _0}=0\). a The wave along the x axis u(x, 0, 0). b The wave along the y axis u(0, y, 0). c The wave along the t axis u(0, 0, t). d The wave along the x axis p(x, 0, 0). e The wave along the y axis p(0, y, 0). f The wave along the t axis p(0, 0, t). g The wave along the x axis q(x, 0, 0). h The wave along the y axis q(0, y, 0). i The wave along the t axis q(0, 0, t)

Full size image

Case 1

Equation (38) has a simple solution

$$\begin{aligned} {\psi _\xi } = {\mu _0} + {\mu _1}sn\left( {m\xi ,n} \right) . \end{aligned}$$
(40)

Substituting (40) with (39) and conditions \(c{n^2} = 1 - s{n^2}\) and \(d{n^2} = 1 - {n^2}s{n^2}\) into (38) and vanishing all the coefficients of powers of sn, one has

$$\begin{aligned} \begin{array}{*{20}{l}} {{c_1} = -\, 4{\mu _0}^3\chi + 2{\mu _0}{m^2}{n^2} + 2{\mu _0}{m^2},}\\ {{c_2} = 6{\mu _0}^2\chi - {m^2}{n^2} - {m^2}},\\ {{h_1} = \dfrac{{\left( {2{h_2} + \left( { - 1 + {n^2}} \right) {m^2}{l_2}{k_2}^2} \right) m\sqrt{\chi } + 2\chi {h_2}{\mu _0}}}{{ - 2\chi }},}\\ {{k_1} = \dfrac{{\left( {{\mu _0}\chi + m\sqrt{\chi }} \right) {k_2}}}{{ - \chi }},}\\ {{\mu _1} = \sqrt{\dfrac{1}{\chi }} mn.} \end{array} \end{aligned}$$
(41)

Then it leads to the following soliton–cnoidal wave solutions of Eq. (1)

$$\begin{aligned} u= & {} \frac{1}{2}\frac{{{a_1}{{\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) }^2} + {\mu _1}mCD{k_2}^2}}{{{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}}} \nonumber \\&-\, \frac{1}{2}\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) \Xi , \end{aligned}$$
(42)
$$\begin{aligned} p= & {} \dfrac{1}{4}\left( {4\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) \left( {{h_1} + \left( {{\mu _0} + {\mu _1}S} \right) {h_2}} \right) } \right. \nonumber \\&+\, 2{a_0}{a_2}{\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) ^3}\left( {{l_1} + \left( {{\mu _0} + {\mu _1}S} \right) {l_2}} \right) \nonumber \\&+\, \left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) \left( { - {\mu _1}{m^2}{D^2}S - {\mu _1}{m^2}{n^2}{C^2}S} \right) {l_2}k_2^2\nonumber \\&+\, {a_1}{\mu _1}m{l_2}{k_2}CD{\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) ^2} \nonumber \\&{\left. { -\, \mu _1^2{m^2}{l_2}k_2^3{C^2}{D^2}} \right) {{\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) }^{ - 2}}}\nonumber \\&-\, \dfrac{1}{2}\left( \dfrac{1}{2}{\mu _1}m{l_2}{k_2}CD \right. \nonumber \\&\left. +\, \dfrac{1}{2}{a_1}\left( {{l_1} + \left( {{\mu _0} + {\mu _1}S} \right) {l_2}} \right) \left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) \right) \Xi \nonumber \\&{ +\, \dfrac{1}{8}\left( {{l_1} + \left( {{\mu _0} + {\mu _1}S} \right) {l_2}} \right) \left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) {\Xi ^2},} \end{aligned}$$
(43)
$$\begin{aligned} q= & {} \dfrac{1}{2}\dfrac{{{\mu _1}mCD{k_2}{h_2} + {a_1}\left( {{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}} \right) \left( {{h_1} + \left( {{\mu _0} + {\mu _1}S} \right) {h_2}} \right) }}{{{k_1} + \left( {{\mu _0} + {\mu _1}S} \right) {k_2}}}\nonumber \\&-\, \dfrac{1}{2}\left( {{h_1} + \left( {{\mu _0} + {\mu _1}S} \right) {h_2}} \right) \Xi , \end{aligned}$$
(44)

where

$$\begin{aligned} \Xi= & {} \left( {a_1} + \sqrt{\chi } \tanh \left( \dfrac{1}{2}\sqrt{\chi } \left( {k_1}x + {l_1}y + {h_1}t \right. \right. \right. \\&\left. \left. \left. +\, \int _{{\xi _0}}^\xi {\mu _0} + {\mu _1}sn\left( {mY,n} \right) dY \right) \right) \right) , \end{aligned}$$

with \({a_0},\;{a_1},\;{a_2},\;{\mu _0}\), \({k_2}\), \({l_1}\), \({l_2}\), \({h_2}\) and \({\xi _0}\) are arbitrary constants, \({h_1},{k_1}\) and \(\mu _1\) are given by (41), and \(S = sn\left( {m\left( {{k_2}x + {l_2}y+{h_2}t} \right) ,n} \right) ,\) \(C = cn\Big ( m\Big ( {k_2}x +{l_2}y+ {h_2}t \Big ),n \Big )\) and \(D = dn\left( {m\left( {{k_2}x +{l_2}y+ {h_2}t} \right) ,n} \right) \).

Fig. 4
figure 4

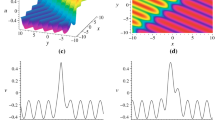
(Color online) Soliton–cnoidal wave with \(m = 1,\;n = \frac{1}{2},\;{k_2} = 1,\;{l_1} = 1,\;{l_2} = -\, \frac{3}{2},\;{h_2} = 1,\;{\mu _0} = \frac{1}{2},\;{a_0}= 1\), \(a_1=3\), \(a_2=2\), \({\xi _0}=0\). a Perspective view of the wave \(u\left( {x,y,0} \right) \). b Perspective view of the wave \(p\left( {x,y,0} \right) \). c Perspective view of the wave \(q\left( {x,y,0} \right) \)

Full size image

Case 2

If we take the solution of (38) as

$$\begin{aligned} {\psi _\xi } = \dfrac{1}{{{b_1} + {b_2}sn{{\left( {m\xi ,n} \right) }^2}}}. \end{aligned}$$
(45)

Substituting (45) with (39) and conditions \(c{n^2} = 1 - s{n^2}\) and \(d{n^2} = 1 - {n^2}s{n^2}\) into (38) and vanishing all the coefficients of powers of sn, we yield

$$\begin{aligned} \begin{array}{l} m = \sqrt{ -\, \dfrac{{\chi {k_1}{b_2}}}{{4 {k_2}^2{k_1}{n^2}{b_2} + 4{k_1}{k_2}^2{b_2} - 4{n^2}{k_2}^3 - 4{k_2}{b_2}^2{k_1}^2}}} {k_1},\\ {b_1} = -\, \dfrac{{{k_2}}}{{{k_1}}},\quad {c_1} = \dfrac{{{k_1}^3\left( { -\chi } \right) {n^2}}}{{{k_2}\left( {{k_2}{k_1}{n^2}{b_2} + {k_1}{k_2}{b_2} - {n^2}{k_2}^2 - {b_2}^2{k_1}^2} \right) }},\\ {c_2} = \dfrac{{\chi {k_1}^2\left( {{k_1}{n^2}{b_2} + {k_1}{b_2} - 3 {k_2}{n^2}} \right) }}{{{k_2}\left( {{k_2}{k_1}{n^2}{b_2} + {k_1}{k_2}{b_2} - {n^2}{k_2}^2 - {b_2}^2{k_1}^2} \right) }},\\ {h_2} = \dfrac{{ 4 {h_1}{k_2}^2{k_1}{n^2}{b_2} + 4 {h_1}{k_2}^2{b_2}{k_1} - 4 {h_1}{k_2}^3{n^2} - 4 {h_1}{k_2}{b_2}^2{k_1}^2 - \chi {k_1}^5{l_2}{b_2}^2}}{{4\left( {{k_2}{k_1}{n^2}{b_2} + {k_1}{k_2}{b_2} - {n^2}{k_2}^2 - {b_2}^2{k_1}^2} \right) {k_1}}}. \end{array} \end{aligned}$$
(46)

Therefore, we obtain the following soliton–cnoidal wave interaction solutions of Eq. (1)

$$\begin{aligned}&u = \dfrac{1}{2}\left( {a_1}{{\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) }^2}-\, \dfrac{{2SCDm{b_2}{k_2}^2}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^2}}} \right) \nonumber \\&\quad \times {\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) ^{ - 1}}-\, \dfrac{1}{2}\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \Theta , \end{aligned}$$
(47)
$$\begin{aligned}&p = \dfrac{1}{4}{\left( {4\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) } \right. ^{ - 1}}\left( {{h_1} + \dfrac{{{h_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \nonumber \\&\quad +2{a_0}{a_2}\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \left( {{l_1} + \dfrac{{{l_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \nonumber \\&\quad +\, {l_2}k_2^2{\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) ^{ - 1}}\nonumber \\&\quad \times \, \left( {\dfrac{{8b_2^2{m^2}{S^2}{C^2}{D^2}}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^3}}} + \dfrac{{2{b_2}{m^2}{S^2}{D^2} + 2{b_2}{m^2}{n^2}{S^2}{C^2} - 2{b_2}{m^2}{C^2}{D^2}}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^2}}}} \right) \nonumber \\&\quad \left. { -\, \dfrac{{2{a_1}{b_2}m{l_2}{k_2}SCD}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^2}}} - {{\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) }^{ - 2}}\dfrac{{4b_2^2{m^2}{l_2}k_2^3{S^2}{C^2}{D^2}}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^4}}}} \right) \nonumber \\&\quad { -\, \dfrac{1}{2}\left( { - \dfrac{{{b_2}m{l_2}{k_2}SCD}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^2}}} + \dfrac{1}{2}{a_1}\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \left( {{l_1} + \dfrac{{{l_2}}}{{{b_1} + {b_2}{S^2}}}} \right) } \right) \Theta }\nonumber \\&\quad { +\, \dfrac{1}{8}\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \left( {{l_1} + \dfrac{{{l_2}}}{{{b_1} + {b_2}{S^2}}}} \right) {\Theta ^2},} \end{aligned}$$
(48)
$$\begin{aligned} {\vspace{15pc}}&q =\dfrac{1}{2}\left( - 2\dfrac{{m{b_2}{k_2}{h_2}SCD}}{{{{\left( {{b_1} + {b_2}{S^2}} \right) }^2}}}{{\left( {{k_1} + \dfrac{{{k_2}}}{{{b_1} + {b_2}{S^2}}}} \right) }^{ - 1}}\right. \nonumber \\&\quad \left. +\, {a_1}\left( {{h_1} + \dfrac{{{h_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \right) -\, \dfrac{1}{2}\left( {{h_1} + \dfrac{{{h_2}}}{{{b_1} + {b_2}{S^2}}}} \right) \Theta , \end{aligned}$$
(49)

where

$$\begin{aligned} \Theta= & {} \left( {a_1} + \sqrt{\chi } \tanh \left( \dfrac{1}{2}\sqrt{\chi } \left( {k_1}x + {l_1}y + {h_1}t \right. \right. \right. \\&\left. \left. \left. +\, \int _{{\xi _0}}^\xi {{{\left( {{b_1} + {b_2}{{\left( {sn\left( {mY,n} \right) } \right) }^2}} \right) }^{ - 1}}} dY \right) \right) \right) , \end{aligned}$$

with \({a_0},{a_1},{a_2},{b _2},{k_1}\), \({k_2}\), \({l_1}\), \({l_2}\), \({h_1}\) and \({\xi _0}\) are arbitrary constants, \({b_1},{h_2}\) and m are given by (46), and \(S = sn\left( {m\left( {{k_2}x + {l_2}y+{h_2}t} \right) ,n} \right) ,\) \(C = cn\big ( m\big ( {k_2}x +{l_2}y+ {h_2}t \big ),n \big )\) and \(D = dn\big ( m\big ( {k_2}x +{l_2}y+ {h_2}t \big ),n \big )\).

The soliton–cnoidal wave solutions describe the solitons moving on the cnoidal wave background. These solutions are useful in studying atmospheric dynamics and other physical fields [14]. In Fig. 3a, b, c, we plot an interaction solution (42) between the kink-shape solitary wave and the cnoidal periodic wave with \(m = 1,\;n = \frac{1}{2},\;{k_2} = 1,\;{l_1} = 1,\;{l_2} = -\, \frac{3}{2},\;{h_2} = 1,\;{\mu _0} = \frac{1}{2},\;{a_0}= 1\), \(a_1=3\), \(a_2=2\) and \({\xi _0}=0\). Figure 3d–f shows that the solution (43) presents a soliton residing on a cnoidal periodic wave. Figure 3g–i exhibits the dynamic behavior of q(x, y, t) (44) is similar to u(x, y, t) (42). To show the interaction between soliton wave and cnoidal periodic wave, three-dimensional plots of u (42), p (43) and q (44) are plotted, which can be seen in Fig. 4a–c, respectively.

6 Conclusions

In this paper, we have analyzed a (\(2+1\))-dimensional nonlinear system, which can be considered as a generalization of the sine-Gordon equation to \(2+1\) dimensions. The residual symmetry and a Bäcklund transformation of this system are obtained by virtue of the truncated Painlevé expansion. The residual symmetry is the nonlocal symmetry. The nonlocal symmetry cannot be used to construct the new solutions directly. Thus a prolonged system is introduced to localize the nonlocal symmetry to a Lie point symmetry. The multiple residual symmetries and the nth Bäcklund transformation in terms of determinant are obtained. Some new multiple wave solutions through the nth Bäcklund transformation have been derived. It is interesting that we have found lump and lump-type solutions by using Bäcklund transformation from the truncated Painlevé expansion. Lump wave can be used to describe nonlinear wave phenomena in oceanography and nonlinear optics. The (\(2+1\))-dimensional nonlinear system is CRE solvable. Two types special solutions of elliptic equation are used to construct soliton–cnoidal wave solutions. Investigating soliton–cnoidal wave interaction solutions is helpful in studying many important physical phenomena, such as tsunami, periodic shallow water waves and fermionic quantum plasma. Applying the truncated Painlevé expansion and CRE method to the high-dimensional systems of differential equations much more difficult than (\(1+1\))-dimensional single equation. It is hopeful that the results of this paper will be useful in understanding and explaining the related physics and the nonlinear dynamics theories.