1 Introduction

Nonlinear partial differential equations (PDEs) play an essential role in the analysis of complex nonlinear phenomena in nonlinear sciences. One needs to obtain explicit closed-form solutions to these nonlinear equations for a clear understanding of these complex nonlinear phenomena characterised by nonlinear PDEs. Nonlinear evolution equations are particular forms of nonlinear PDEs, which describe many nonlinear phenomena in the disciplines of nonlinear sciences and engineering physics such as, optical physics, plasma physics, water waves, chemical physics, fluid dynamics, oceanography, hydrodynamics and so on. For a deep understanding of such complex nonlinear phenomena in nature, seeking exact closed-form solutions of nonlinear PDEs play a crucial role in the study of nonlinear sciences. It is well known that numerous analytical mathematical methods are developed by researchers and mathematicians, to seek closed-form solutions of nonlinear PDEs and each technique is precise for obtaining various forms of exact explicit solutions. Here, our prime objective is to study localised solitary wave solutions that can be described as a travelling wave solution that maintains its shape while propagating at a constant velocity. These solitons/solitary wave solutions are obtained by cancelling dispersive and nonlinear effects in the medium. A variety of efficient mathematical methods such as the auxiliary equation method [1], Bäcklund and Darboux transform [2, 3], Lie symmetry method [4,5,6,7,8,9], the exp-function methods [10, 11], the direct algebraic method and modified extended direct algebraic method [12], the inverse scattering transform [13], the F-expansion method [14], Lax pair [15], Hirota technique [16], Kudryashov method [17], extended simplest equation method [18], bifurcation method [19], the \( ({G'}/{G})\)-expansion method [20], generalised exponential rational function method [21, 22] and so on have been proposed.

In nonlinear sciences, the Kadomtsev and Petviashvili (KP) equation, which describes the nonlinear waves, is introduced by Kadomtsev and Petviashvili [23], has the bilinear form

$$\begin{aligned}&(v_{t}+6 v v_{x}+v_{xxx})_{x}+3 v_{yy}=0 \end{aligned}$$
(1)
$$\begin{aligned}&(D_x D_t+D_{x}^{4}+3D_{y}^{2})f\dot{f}=0. \end{aligned}$$
(2)

The generalised B-type KP (g-BKP) equation in (\(3 + 1\)) dimensions [24,25,26,27] can be furnished as

$$\begin{aligned} v_{ty}-v_{xxxy}-3(v_xv_y)_x+3v_{xz}=0, \end{aligned}$$
(3)

where \(v = v(x, y, z, t)\) is the wave amplitude along with three spatial coordinates and one temporal coordinate and subscripts denote the partial derivatives of v with respect to the respective variables. The g-BKP equation describes the evolution of quasi-one-dimensional shallow water waves, when the effects of viscosity and surface tension are taken to be negligible [27]. The g-BKP equation has a wide range of applications in various fields of mathematical physics such as non-linear optics, oceanography, nonlinear waves, string theory, Bose–Einstein condensation, etc. Wazwaz [24] obtained multiple soliton solutions and multiple singular soliton solutions of the generalised KP equation by utilising the simplified form of Hirota”s method. Wazwaz and El-Tantawy [25] achieved multiple soliton solutions for the g-KP equation via the Hirota method. Ma and Fan [26] constructed N-soliton solutions of the g-BKP equation (3) by using the linear superposition principle of linear exponential travelling waves. Ma and Zhu [27] gained multiple wave solutions of (3) by employing the multiple exp-function algorithms via Hirota’s perturbation scheme. In this paper, we focus on studying a new form of the (\(3+1\))-dimensional generalised B-type KP–Boussinesq (gBKP-B)equation [28,29,30,31] which describes the severe effect on dispersion relation as well as phase shift and enhanced by adding an extra term \((v_{tt})\) to eq. (3) and this is introduced by Wazwaz and El-Tantawy [29]. The gBKP-B equation has the form

$$\begin{aligned} v_{ty}-v_{xxxy}-3(v_xv_y)_x+v_{tt}+3v_{xz}=0. \end{aligned}$$
(4)

Deng et al [28] constructed the rational solution including the semi-rational solutions and breather-type kink soliton solutions of the (\(3+1\))-dimensional B-type KP–Boussinesq equation by using the bilinear method and fusion and fission between lump waves and solitons were also observed. Wazwaz and El-Tantawy [29] applied the simplified Hirota technique and established 1- and 2-soliton solutions, where the coefficients of spatial variables were arbitrary, for the generalised BKP-B equation (4). Gao and Zhang [30] obtained the Lie symmetry reduction with the help of a one-dimensional optimal system. Besides, they solved the reduced equation via the tanh method and established some exact explicit solutions of the gBKP-B equation (4). Recently, Khalique and Moleleki [31] obtained symmetry reductions via the Lie symmetry technique and then they solved the reduced equation through the \({(G'}/{G})\)-expansion method. Besides, conversation laws were derived by applying the multiplier method via the Ibragimov approach.

Lie symmetry technique [32,33,34,35] was pioneered by Sophus Lie (1842–1899), which is one of the best techniques for obtaining exact analytic solutions of nonlinear PDEs Lie symmetry technique is effective, systematic and has been applied to many physical models and nonlinear PDEs [36,37,38,39,40,41,42,43,44,45,46,47,48]. This technique is effective to get group-invariant solutions and dynamics of localised solitary wave solutions of nonlinear PDEs.

The prime objective of this study is to obtain localised solitary wave solutions and exact analytic solutions of the (\(3+1\))-dimensional generalised B-type KP–Boussinesq (gBKP-B) equation by employing the Lie group method. It is remarkable that our newly formed solutions are completely new and never have been reported in the literature. In [31], a few exact solutions were derived with the help of symmetry reductions, direct integration and \(({G'}/{G})\)-expansion method whereas in this work, we obtained abundant exact closed-form solutions under ten symmetry subalgebras via one-dimensional optimal system approach. Therefore, in this article, we attained numerous explicit solutions compared to the solutions obtained in [30, 31]. The generated exact solutions are expressed explicitly including arbitrary independent functional and free parameters which are useful and helpful to describe the internal mechanism of complex nonlinear phenomena. Furthermore, the dynamical analysis of soliton solutions of the gBKP-B equation is discussed physically using their 3D graphics via numerical simulation.

The remaining paper is organised as follows: In §2, we obtain the Lie point symmetries of the (\(3+1\))-dimensional gBKP-B equation. In §3, a one-dimensional optimal system of the governing equation is derived. We obtain numerous closed-form invariant solutions with the aid of symmetry reductions in §4. The dynamical analysis of the gained exact solutions based on numerical simulation is given in §5. Finally, §6 is devoted to the concluding remarks.

2 Lie point symmetries

In this section, we derive Lie point symmetries, infinitesimal generator, commutative table, adjoint table and closed-form invariant solution of the (\(3+1\))-dimensional gBKP-B equation (4). Assume one-parameter Lie group transformations as follows and defined in [32, 33]

$$\begin{aligned} x^*&=x+\epsilon \, \xi (x,y,t,z,v)+O(\epsilon ^2),\nonumber \\ y^*&=y+\epsilon \, \phi (x,y,t,z,v)+O(\epsilon ^2),\nonumber \\ z^*&=z+\epsilon \,\psi (x,y,t,z,v)+O(\epsilon ^2),\nonumber \\ t^*&=t+\epsilon \,\tau (x,y,t,z,v)+O(\epsilon ^2),\nonumber \\ v^*&=v+\epsilon \,\eta (x,y,t,z,v)+O(\epsilon ^2), \end{aligned}$$
(5)

where \(\xi , \phi , \psi , \tau \) and \(\eta \) are infinitesimal generators. Therefore, the associated infinitesimal generator is

$$\begin{aligned} {\mathbf {V}}= \xi \, \partial _x+\phi \, \partial _y+\psi \, \partial _z+\tau \, \partial _t+\eta \, \partial _v. \end{aligned}$$
(6)

The fourth prolongation \(Pr^4\) of \({\mathbf {V}}\) to the gBKP-B (4) equation is

$$\begin{aligned} Pr^4 {\mathbf {V}}&={\mathbf {V}}+ \eta ^x\frac{\partial }{\partial v_x}+\eta ^y\frac{\partial }{\partial v_y}+\eta ^{xx}\frac{\partial }{\partial v_{xx}}\nonumber \\&\quad + \eta ^{xy}\frac{\partial }{\partial v_{xy}} + \eta ^{yt}\frac{\partial }{\partial v_{yt}}+\cdots . \end{aligned}$$
(7)

Utilising this prolongation including invariant conditions to the gBKP-B equation (4), one obtains

$$\begin{aligned}&\eta ^{yt}-\eta ^{xxxy}-3\eta ^{x}v_{xy}-3\eta ^{xy}v_{x}\nonumber \\&\quad -3\eta ^{y}v_{xx}-3\eta ^{xx}v_{y}+\eta ^{tt}+3\eta ^{xz}=0, \end{aligned}$$
(8)

where the extended coefficients \(\eta ^x\), \(\eta ^y\), \(\eta ^{tt}\), \(\eta ^{xx}\), \(\eta ^{xy}\), \(\eta ^{xz}\), \(\eta ^{yt}\), \(\eta ^{xxxy}\) and the total derivative operators \(D_x\), \(D_y\), \(D_z\) and \(D_t\) are described in detail in [32, 33].

We substitute the values of extended coefficients and total derivatives into eq. (8), to obtain the desired determining equation as

$$\begin{aligned}&(\eta )_v=-\frac{1}{5}(\psi )_z, \nonumber \\&(\eta )_x=-(\phi )_z+\frac{1}{2}(\tau )_z, (\eta )_y= -(\xi )_z,\nonumber \\&(\eta )_{tt}=3(\phi )_{zz}-3(\tau )_{zz},\nonumber \\&(\tau )_t=\frac{3}{5}(\psi )_z, (\tau )_y=0, (\tau )_x=0, \nonumber \\&(\xi )_t=-\frac{3}{2}(\tau )_z, (\xi )_v=0, (\xi )_x=\frac{1}{5}(\psi )_z, \nonumber \\&(\xi )_y=0, (\phi )_t=0, (\phi )_v=0, (\phi )_x=0,\nonumber \\&(\phi )_y=\frac{3}{5}(\psi )_z, (\psi )_t = 0, (\psi )_v=0, (\psi )_x=0,\nonumber \\&(\psi )_y=0, (\psi )_{zz}=0. \end{aligned}$$
(9)

Afterwards, we solve the determining equations, the desired infinitesimals generators of gBKP-B equation (4) as follows:

$$\begin{aligned}&\xi = \frac{c_1}{3}x-\frac{3t}{2}f_5'(z)+f_3(z),~~~ \phi = c_1y+f_4(z),~~~ \nonumber \\&\psi =\frac{5c_1}{3} z+c_2,~~~ \tau = c_1 t+f_5(z), \nonumber \\&\eta =-\frac{c_1}{3}v+f_1(z)+t f_2(z)-y f_3'(z)-xf_4'(z)\nonumber \\&\quad +\frac{3}{2}t^2 f_4''(z)+\frac{x}{2}f_5'(z)-\frac{3}{2}t(t-y)f_5''(z). \end{aligned}$$
(10)

Consequently, we obtain the following vector fields of gBKP-B equation (4) with the aid of (10):

$$\begin{aligned}&{\mathbf {V}}_1 = \frac{x}{3}\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+\frac{5z}{3}\frac{\partial }{\partial z}\nonumber \\&\quad ~~~~~~+t\frac{\partial }{\partial t}-\frac{v}{3}\frac{\partial }{\partial v},~~~ \nonumber \\&{\mathbf {V}}_2 =\frac{\partial }{\partial z},~~~ {\mathbf {V}}_3(f_1)= f_1(z)\frac{\partial }{\partial v}, \nonumber \\&{\mathbf {V}}_4(f_2)= t f_2(z)\frac{\partial }{\partial v},~~~~~~\nonumber \\&{\mathbf {V}}_5(f_3) = f_3(z)\frac{\partial }{\partial x}-y f_3'(z)\frac{\partial }{\partial v},~~~~\nonumber \\&{\mathbf {V}}_6(f_4)= f_4(z)\frac{\partial }{\partial y}+\frac{3}{2}t^2f_4''(z)\frac{\partial }{\partial v}-x f_4'(z)\frac{\partial }{\partial v}, \nonumber \\&{\mathbf {V}}_7(f_5)= -\frac{3}{2}tf_5'(z)\frac{\partial }{\partial x}+f_5(z)\frac{\partial }{\partial t}\nonumber \\&\quad ~~~~~~~~~~~~~-\frac{3}{2}t(t-y)f_5''(z)\frac{\partial }{\partial v}+\frac{x}{2} f_5'(z)\frac{\partial }{\partial v}. \end{aligned}$$
(11)
Table 1 Commutator table.
Full size table
Table 2 Adjoint table.
Full size table

3 A one-dimensional optimal system of subalgebras

We follow the same procedure to construct the one-dimensional optimal system of symmetry subalgebras as described in detail in [4, 5, 33, 42]. We construct a one-dimensional optimal system of symmetry subalgebras in this section. By means of commutation relations between seven infinitesimal generators given in table 1, these infinitesimals given in (11) can be written as a linear combination of \({\mathbf {V}}_i\) as follows:

$$\begin{aligned} {\mathbf {V}}&=\alpha _1{\mathbf {V}}_1+\alpha _2{\mathbf {V}}_2+\alpha _3{\mathbf {V}}_3+\alpha _4{\mathbf {V}}_4\nonumber \\&\quad +\alpha _5{\mathbf {V}}_5+\alpha _6{\mathbf {V}}_6+\alpha _7{\mathbf {V}}_7. \end{aligned}$$
(12)

Moreover, we derive the adjoint relations as provided in table 2. Using the Olver technique [33], the adjoint relations of a (\(3+1\))-dimensional gBKP-B equation in table 2 are determined via computerised symbolic computation for the commutator relations of those vector fields.

3.1 Formation of invariants

To attain one-dimensional optimal system of Lie algebra \(\mathbb {R}^7\), thus there is a need to construct the invariant for the suitable selection of representative factors/elements. Thus, the desired matrix representations of ad\(({\mathbf {V}}_i)\) can be furnished as

$$\begin{aligned}&\mathrm {Ad}{(\exp (\epsilon \mathbf{W}))}(\mathbf{{\mathbf {V}}})\nonumber \\&\quad =\mathrm {e}^{-\epsilon \mathbf{W}} {{\mathbf {V}}} \mathrm {e}^{\epsilon \mathbf{W}} = \mathbf{{\mathbf {V}}}-\epsilon [\mathbf{W},\mathbf{{\mathbf {V}}}]\nonumber \\&\qquad + \frac{1}{2!} \epsilon ^2 [\mathbf{W},[\mathbf{W},\mathbf{{\mathbf {V}}}]]-\cdots \nonumber \\&\quad = (\alpha _1 {\mathbf {V}}_1+\dots +\alpha _n {\mathbf {V}}_n)\nonumber \\&\qquad -\epsilon [\beta _1 {\mathbf {V}}_1+\dots +\beta _n {\mathbf {V}}_n, \alpha _1 {\mathbf {V}}_1+\dots \nonumber \\&\qquad +\alpha _n {\mathbf {V}}_n]+O(\epsilon ^2)\nonumber \\&\quad =(\alpha _1 {\mathbf {V}}_1+\dots +\alpha _n {\mathbf {V}}_n)\nonumber \\&\qquad -\epsilon (\Theta _1 {\mathbf {V}}_1+\dots +\Theta _n {\mathbf {V}}_n), \end{aligned}$$
(13)

where \(\Theta = \Theta (\alpha _1,\ldots ,\alpha _n,\beta _1,\ldots ,\beta _n)\) are obtained with the help of symbolic calculations via the commutator table. The commutative relations of the seven-dimensional Lie algebra are expressed in table 1. Putting \(\mathbf{{\mathbf {V}}}= \sum _{i=1}^{7} \alpha _i {\mathbf {V}}_i\) and \(\mathbf{W}= \sum _{j=1}^{7} \beta _j {\mathbf {V}}_j\) in (11)

$$\begin{aligned} \Theta _1&= 0, \,\,\,\,\, \Theta _2 = -\frac{5}{3}\alpha _2\beta _1+\frac{5}{3}\alpha _1\beta _2,~~~~\nonumber \\ \Theta _3&= \frac{1}{3} \alpha _3 \beta _1-\frac{1}{3} \alpha _1 \beta _3+ \alpha _3 \beta _2-\alpha _2 \beta _3\nonumber \\&\quad +\alpha _7 \beta _4-\alpha _4 \beta _7 + \alpha _6 \beta _5-\alpha _5 \beta _6\nonumber \\&\quad +\frac{1}{2}\alpha _7 \beta _5 -\frac{1}{2}\alpha _5 \beta _7,\nonumber \\ \Theta _4&= \frac{5}{3} \alpha _4 \beta _1- \alpha _4 \beta _2-\frac{5}{3} \alpha _1 \beta _4+\frac{3}{2}\alpha _7 \beta _6\nonumber \\&\quad +\alpha _2 \beta _4-\frac{3}{2}\alpha _6 \beta _7,~~~~\nonumber \\ \Theta _5&= \frac{1}{3} \alpha _5\beta _1 +\alpha _5\beta _2-\frac{1}{3} \alpha _1 \beta _5- \alpha _2 \beta _5, \nonumber \\ \Theta _6&= \alpha _6 \beta _1 - \alpha _2 \beta _6 -\alpha _1 \beta _6 +\alpha _6 \beta _2, \nonumber \\ \Theta _7&= \alpha _7 \beta _1 + \alpha _7 \beta _2 - \alpha _2 \beta _7 - \alpha _1 \beta _7. \end{aligned}$$
(14)

For any \(\beta _j, 1 \le j \le 7\), it imposes

$$\begin{aligned}&\Theta _1 \frac{\partial \phi }{\partial \alpha _1} +\Theta _2 \frac{\partial \phi }{\partial \alpha _2} +\Theta _3 \frac{\partial \phi }{\partial \alpha _3} +\Theta _4 \frac{\partial \phi }{\partial \alpha _4} \nonumber \\&\quad +\Theta _5 \frac{\partial \phi }{\partial \alpha _5} +\Theta _6 \frac{\partial \phi }{\partial \alpha _6} +\Theta _7 \frac{\partial \phi }{\partial \alpha _7} =0. \end{aligned}$$
(15)

Equating the various coefficients of different powers of \(\beta _j\) in eq. (15), we obtain seven differential equations with \(\phi (\alpha _1,\alpha _2,\ldots ,\alpha _{7})\) as

$$\begin{aligned}&\beta _1: -\frac{5\alpha _2}{2} \frac{\partial \phi }{\partial \alpha _{2}} \nonumber \\&\quad +\frac{\alpha _3}{3} \frac{\partial \phi }{\partial \alpha _{3}} +\frac{5\alpha _4}{3} \frac{\partial \phi }{\partial \alpha _{4}} +\frac{\alpha _5}{3} \frac{\partial \phi }{\partial \alpha _{5}}\nonumber \\&\quad +\alpha _6 \frac{\partial \phi }{\partial \alpha _{6}}+\alpha _7 \frac{\partial \phi }{\partial \alpha _{7}}=0, \nonumber \\&\beta _2: \frac{5\alpha _1}{3} \frac{\partial \phi }{\partial \alpha _{2}}+ \alpha _3 \frac{\partial \phi }{\partial \alpha _{3}} +\alpha _4 \frac{\partial \phi }{\partial \alpha _{4}}\nonumber \\&\quad + \alpha _5 \frac{\partial \phi }{\partial \alpha _{5}}+\alpha _6 \frac{\partial \phi }{\partial \alpha _{6}}+\alpha _7 \frac{\partial \phi }{\partial \alpha _{7}} =0, \nonumber \\&\beta _3: -\left( \frac{\alpha _1}{3}+\alpha _2 \right) \frac{\partial \phi }{\partial \alpha _{3}}=0,~~~~ \nonumber \\&\beta _4: \alpha _7 \frac{\partial \phi }{\partial \alpha _3} -\left( \frac{5\alpha _1}{3}+\alpha _2 \right) \frac{\partial \phi }{\partial \alpha _4}=0, \nonumber \\&\beta _5: \left( \frac{\alpha _7}{2}+\alpha _6 \right) \frac{\partial \phi }{\partial \alpha _3}- \left( \frac{\alpha _1}{3}+\alpha _2 \right) \frac{\partial \phi }{\partial \alpha _5}=0,~~~~\nonumber \\&\beta _6:-\alpha _5 \frac{\partial \phi }{\partial \alpha _3}+\frac{3\alpha _7}{2}\frac{\partial \phi }{\partial \alpha _7}\nonumber \\&\quad -\left( \alpha _1+\alpha _2\right) \frac{\partial \phi }{\partial \alpha _6}=0, \nonumber \\&\beta _7:-(\frac{\alpha _5}{2} + \alpha _4) \frac{\partial \phi }{\partial \alpha _{3}}\nonumber \\&\quad +\frac{3\alpha _6}{2} \frac{\partial \phi }{\partial \alpha _{4}}-\alpha _1\frac{\partial \phi }{\partial \alpha _{7}}=0. \end{aligned}$$
(16)

Solving system (16), one obtains \(\phi (\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5,\alpha _6,\alpha _7)= F(\alpha _1)\) which is also called the general invariant function of Lie algebra \({\mathbb {R}}^{7}\), where F is an arbitrary function of \(\alpha _1\). As a result, the governing equation (4) has one basic invariant only.

3.2 Calculation of the adjoint transformation matrix

For \(F_i^s:g\rightarrow g\) defined by \({\mathbf {V}}\rightarrow \mathrm {Ad}(\exp (\epsilon _i {\mathbf {V}}_i)\cdot {\mathbf {V}})\) is a linear map, for \(i=1,2,\ldots ,7\). The matrix \(A_i^\epsilon \) of \(F_i^\epsilon , i=1, 2, \ldots , 7\) with respect to basis \(\{ {\mathbf {V}}_1,...,{\mathbf {V}}_{7} \} \) are given and defined in [33, 42] as follows:

$$\begin{aligned}&A_1^\epsilon =\left( \begin{array}{cccccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \mathrm {e}^{\frac{5}{3}\epsilon _1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\frac{\epsilon _1}{3}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\frac{5}{3}\epsilon _1} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\frac{\epsilon _1}{3}} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _1} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _1} \\ \end{array} \right) ,\\&A_2^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad -\dfrac{5}{3} \epsilon _2 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _2} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathrm {e}^{-\epsilon _2} \\ \end{array} \right) ,\\&A_3^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad \dfrac{\epsilon _3}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad \epsilon _3 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) ,~~~\\&A_4^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad \dfrac{5}{3}\epsilon _4 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad \epsilon _4 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \epsilon _4 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) ,~~~~ \\&A_5^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \dfrac{\epsilon _5}{3} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad \epsilon _5 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\epsilon _5 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\dfrac{\epsilon _5}{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) ,\\&A_6^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \epsilon _6 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \epsilon _6 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \epsilon _6 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \dfrac{-3 \epsilon _6}{2} &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) ,~~~~ \\&A_7^\epsilon =\left( \begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \epsilon _7 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \epsilon _7 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \epsilon _7 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \dfrac{\epsilon _7}{2} &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \dfrac{3 \epsilon _7}{2} &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) \end{aligned}$$

Hence, we obtain the global adjoint matrix using these seven matrices as

$$\begin{aligned} A= \left( \begin{array}{ccccccc} 1 &{} -\dfrac{5}{3} \epsilon _2 &{} A_{13} &{} A_{14} &{} \dfrac{\epsilon _5}{3}-\dfrac{5}{3} \epsilon _2 \epsilon _5 &{} \epsilon _6-\dfrac{5}{3}\epsilon _2 \epsilon _6 &{} \epsilon _7-\dfrac{5}{3}\epsilon _2 \epsilon _7 \\ 0 &{} \mathrm {e}^{\frac{5 \epsilon _1}{3}} &{} A_{23} &{} A_{24} &{} \mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _5 &{} \mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _6 &{} \mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _7 \\ 0 &{} 0 &{} \mathrm {e}^{-\frac{\epsilon _1}{3}-\epsilon _2} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \mathrm {e}^{-\frac{5 \epsilon _1}{3}-\epsilon _2} \epsilon _7 &{} \mathrm {e}^{-\frac{5 \epsilon _1}{3}-\epsilon _2} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} A_{53} &{} 0 &{} \mathrm {e}^{-\frac{\epsilon _1}{3}-\epsilon _2} &{} 0 &{} 0 \\ 0 &{} 0 &{} -\mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _5 &{} A_{64} &{} 0 &{} \mathrm {e}^{-\epsilon _1-\epsilon _2} &{} 0 \\ 0 &{} 0 &{} A_{73} &{} -\frac{3}{2} \mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _6 &{} 0 &{} 0 &{} \mathrm {e}^{-\epsilon _1-\epsilon _2} \\ \end{array} \right) , \end{aligned}$$
(17)

where

$$\begin{aligned} A_{13}&=-\frac{1}{3} 5 \epsilon _2 \epsilon _3+\frac{\epsilon _3}{3}+\left( \frac{\epsilon _5}{3}-\frac{5 \epsilon _2 \epsilon _5}{3}\right) \epsilon _6\\&\quad +\left( \frac{5 \epsilon _4}{3}-\frac{5 \epsilon _2 \epsilon _4}{3}\right) \epsilon _7+\frac{1}{2} \left( \frac{\epsilon _5}{3}-\frac{5 \epsilon _2 \epsilon _5}{3}\right) \epsilon _7, \\ A_{23}&=\mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _3+\mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _5 \epsilon _6+\mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _4 \epsilon _7\\&\quad +\frac{1}{2} \mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _5 \epsilon _7,~~~\\ A_{53}&=\mathrm {e}^{-\frac{\epsilon _1}{3}-\epsilon _2} \epsilon _6 +\frac{1}{2} \mathrm {e}^{-\frac{\epsilon _1}{3}-\epsilon _2} \epsilon _7,\\ A_{73}&=\mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _4-\frac{1}{2} \mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _5\\&\quad -\frac{3}{2} \mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _6 \epsilon _7,\\ A_{14}&=-\frac{1}{3} 5 \epsilon _2 \epsilon _4+\frac{5 \epsilon _4}{3} +\frac{3}{2} \left( \epsilon _6-\frac{5 \epsilon _2 \epsilon _6}{3}\right) \epsilon _7, \\ A_{24}&=\mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _4+\frac{3}{2} \mathrm {e}^{\frac{5 \epsilon _1}{3}} \epsilon _6 \epsilon _7,~~~\\ A_{64}&=\frac{3}{2} \mathrm {e}^{-\epsilon _1-\epsilon _2} \epsilon _7. \end{aligned}$$

3.3 One-dimensional optimal system for the gBKP-B equation

The general transformation equation to the generalised gBKP-B equation (4) is

$$\begin{aligned}&(\gamma _1, \gamma _2, \gamma _3, \gamma _4, \gamma _5, \gamma _6, \gamma _7) \nonumber \\&\quad = (\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5,\alpha _6,\alpha _7) \cdot A, \end{aligned}$$
(18)

where A is the global matrix which is already derived above.

$$\begin{aligned} \gamma _1&=\alpha _1,~~~ \gamma _2 =\alpha _2-\epsilon _2,~~~ \gamma _3 =\alpha _3+\frac{2\epsilon _3}{5}, \nonumber \\ \gamma _4&=\alpha _4-\alpha _3 \epsilon _2+\alpha _2 \epsilon _3-\frac{3}{5}\epsilon _4, \nonumber \\ \gamma _5&=\alpha _5 +\frac{5}{2}\alpha _4\epsilon _3+\epsilon _3\epsilon _4+\left( -\frac{5}{2}\epsilon _2\epsilon _3+\frac{5}{2}\epsilon _4\right) \alpha _3 -\frac{\epsilon _5}{5}, \nonumber \\ \gamma _6&=\alpha _6+\frac{1}{8}\alpha _5 \epsilon _3+\frac{6}{5}\epsilon _6, ~~~ \nonumber \\ \gamma _7&=\alpha _7+\alpha _6 \epsilon _2-\frac{1}{8} \alpha _3 \epsilon _5-\frac{1}{20} \alpha _3 \epsilon _5-\epsilon _2\epsilon _6+\frac{\epsilon _7}{5}, \end{aligned}$$
(19)

which must have solutions for \(\epsilon _i\)’s for \(i = 1,2, \dots , 7\) (assuming \(\epsilon _1=0\)).

Case 1: For \(\alpha _1=1\), the representative element \(\tilde{{\mathbf {V}}}= {\mathbf {V}}_1\). Substituting \(\gamma _1=1\) into eq. (19) we get

$$\begin{aligned}&\epsilon _2=\alpha _2,~\epsilon _3=-\frac{1}{2} (5 \alpha _3),~\epsilon _4=-\frac{5}{3} (\alpha _2 \alpha _3-\alpha _4),~\\&\epsilon _5=\frac{5}{4} \left( 25 \alpha _2 \alpha _3^2-25 \alpha _3 \alpha _4+4 \alpha _5\right) ,\\&\epsilon _6=\frac{5}{96} (5 \alpha _3 \alpha _5-16 \alpha _6),~\epsilon _7=5 (\alpha _2 \alpha _6-\alpha _7). \end{aligned}$$

Case 2: Let us consider the representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_1+{\mathbf {V}}_3\). We substitute \(\alpha _1=\alpha _3=1\) and \(\gamma _1=\gamma _3=1\) into eq. (19), to get

$$\begin{aligned}&\epsilon _2 = \alpha _2,~\epsilon _3 = 0,~\epsilon _4 =-\frac{5}{3} (\alpha _2- \alpha _4),~\\&\epsilon _5=-\frac{5}{6} \left( 25\alpha _2- 25\alpha _4-6 \alpha _5\right) ,~~ \epsilon _6 = -\frac{5}{6}\alpha _6,\\&\epsilon _7 = \frac{5}{48} \left( 48 \alpha _2 \alpha _6-125 \alpha _2+125 \alpha _4+30 \alpha _5-48 \alpha _7\right) . \end{aligned}$$

Case 3: Consider the representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_1+{\mathbf {V}}_7\). Substituting \(\alpha _1=\alpha _7=1\) and \(\gamma _1=\gamma _7=1\) into eq. (19), we get

$$\begin{aligned}&\epsilon _2 = \alpha _2,~\epsilon _3 = -\frac{5\alpha _3}{2},~\epsilon _4 =-\frac{5}{3} (\alpha _2\alpha _3- \alpha _4),~\\&\epsilon _5=\frac{5}{4} \left( 25\alpha _2\alpha _3^2- 25\alpha _3\alpha _4+4 \alpha _5\right) ,~~\\&\epsilon _6 = -\frac{5}{96}\left( 5 \alpha _3\alpha _5-16\alpha _6\right) ,~~~~\epsilon _7 = 5 \alpha _2 \alpha _6. \end{aligned}$$

Case 4: We take representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_1+{\mathbf {V}}_2+{\mathbf {V}}_4\). Substituting \(\alpha _1=\alpha _2=\alpha _4=1\) and \(\gamma _1=\gamma _2=\gamma _4=1\) into eq. (19), we get

$$\begin{aligned}&\epsilon _2 = 0,~\epsilon _3 = -\frac{5\alpha _3}{2},~\epsilon _4 =-\frac{25}{3} \alpha _3,~\\&\epsilon _5=-\frac{5}{4} \left( 25\alpha _3-4 \alpha _5\right) ,~~\\&\epsilon _6 = \frac{5}{96}\left( 5 \alpha _3\alpha _5-16\alpha _6\right) ,~~~~\\&\epsilon _7 = -\frac{5}{96} \left( 25 \alpha _3 \alpha _5-80 \alpha _6+96 \alpha _7\right) . \end{aligned}$$

Case 5: For \(\alpha _2=1,\) the representative element \(\tilde{{\mathbf {V}}}= {\mathbf {V}}_2\). By substituting \(\gamma _2=1\) into eq. (19), we get

$$\begin{aligned} \epsilon _3=0,~~~\epsilon _6=-\alpha _7. \end{aligned}$$

Case 6: Select a representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_2+{\mathbf {V}}_3\). Substituting \(\gamma _2=\gamma _3 = 1, \gamma _i = 0, i= 1, 4, 5, 6, 7\) and \(\alpha _2=\alpha _3=1\) into eq. (19), we obtain the solution

$$\begin{aligned}&\epsilon _2=\epsilon _3=-8\frac{\alpha _6}{\alpha _5},~\epsilon _4 = -2 \left( \alpha _5-32 \frac{\alpha _6^2}{\alpha _5^2}\right) , \\&\epsilon _5=0,~\epsilon _6 = \frac{-8 \alpha _6^2-\alpha _5\alpha _7}{\alpha _5}. \end{aligned}$$

Case 7: For \(\alpha _2=\alpha _4=1\), the representative element \(\tilde{{\mathbf {V}}}= {\mathbf {V}}_2+{\mathbf {V}}_4\). By substituting \(\gamma _2=\gamma _4=1\) into eq. (19) we get

$$\begin{aligned} \epsilon _3 =0,~ \epsilon _6 = -\alpha _7. \end{aligned}$$

Case 8: Select a representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_2+{\mathbf {V}}_3+{\mathbf {V}}_5\). Substituting \(\gamma _1 = 0, \gamma _2 =\gamma _3=\gamma _5=1, \gamma _i = 0, i=4,~6,~7\) and \(\alpha _2=\alpha _3=\alpha _5=1\) into eq. (19), we obtain the solution

$$\begin{aligned}&\epsilon _2= \alpha _4-8\alpha _6,~\epsilon _3 =-8\alpha _6,~\epsilon _4 = 64\alpha _6^2,\\&\epsilon _5=0,~\epsilon _6 =(\alpha _4-8\alpha _6)\alpha _6-\alpha _7. \end{aligned}$$

Case 9: Select a representative element \(\tilde{{\mathbf {V}}} = {\mathbf {V}}_2+{\mathbf {V}}_5+{\mathbf {V}}_6\). Substituting \(\gamma _2 =\gamma _5=\gamma _6= 1, \gamma _i = 0, i=1,~3,~4,~7 \) and \(\alpha _2=\alpha _5=\alpha _6=1\) into eq. (19), we obtain the solution

$$\begin{aligned} \epsilon _3=0,~ \epsilon _6 = -\alpha _7+\epsilon _2. \end{aligned}$$

Proceeding as above, we can find the value of \(\epsilon _i\)’s for certain members of optimal system.

Eventually, an optimal system of one-dimensional symmetry subalgebras for a gBKP-B equation is furnished in the following way:

$$\begin{aligned} (\mathrm {i})~~{\mathfrak {T}}_1~&=~{\mathbf {V}}_1 \nonumber \\ (\mathrm {ii})~~{\mathfrak {T}}_2~&=~{\mathbf {V}}_1+{\mathbf {V}}_3 \nonumber \\ (\mathrm {iii})~~{\mathfrak {T}}_3~&=~{\mathbf {V}}_1+{\mathbf {V}}_7 \nonumber \\ (\mathrm {iv})~~{\mathfrak {T}}_4~&=~{\mathbf {V}}_1+{\mathbf {V}}_2+{\mathbf {V}}_4\nonumber \\ (\mathrm {v})~~{\mathfrak {T}}_5~&=~{\mathbf {V}}_2\nonumber \\ (\mathrm {vi})~~{\mathfrak {T}}_6~&=~{\mathbf {V}}_2+{\mathbf {V}}_3\nonumber \\ (\mathrm {vii})~~{\mathfrak {T}}_7~&=~{\mathbf {V}}_2+{\mathbf {V}}_4\nonumber \\ (\mathrm {viii})~~{\mathfrak {T}}_8~&=~{\mathbf {V}}_2+{\mathbf {V}}_3+{\mathbf {V}}_5\nonumber \\ (\mathrm {ix})~~{\mathfrak {T}}_9~&=~{\mathbf {V}}_2+{\mathbf {V}}_5+{\mathbf {V}}_6\nonumber \\ (\mathrm {x})~~{\mathfrak {T}}_{10}~&=~{\mathbf {V}}_2+{\mathbf {V}}_4+{\mathbf {V}}_5 \end{aligned}$$
(20)

4 Exact invariant solutions

This section constructs a variety of closed-form invariant solutions for the corresponding symmetry subalgebras by solving the Lagrange’s characteristic equation [33]

$$\begin{aligned} \frac{\mathrm {d}x}{\xi }=\frac{\mathrm {d}y}{\phi }=\frac{\mathrm {d}z}{\psi }=\frac{\mathrm {d}t}{\tau }=\frac{\mathrm {d}v}{\eta }. \end{aligned}$$
(21)

4.1 Subalgebra \({\mathfrak {T}}_1~{:=}~{\mathbf {V}}_1=\frac{x}{3}\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+\frac{5z}{3}\frac{\partial }{\partial z}+t\frac{\partial }{\partial t}-\frac{v}{3}\frac{\partial }{\partial v}\)

The Langrange’s system (21) becomes

$$\begin{aligned} \frac{\mathrm {d}x}{{x}/{3}}=\frac{\mathrm {d}y}{y}=\frac{dz}{{5z}/{3}}=\frac{\mathrm {d}t}{t}=\frac{\mathrm {d}v}{-{v}/{3}} \end{aligned}$$
(22)

which gives the similarity solution

$$\begin{aligned} v(x,y,z,t)=\frac{V(X,Y,T)}{z^{\frac{1}{5}}} \end{aligned}$$
(23)

with

$$\begin{aligned}X=\frac{x}{z^{\frac{1}{5}}},~Y=\frac{y}{z^{\frac{3}{5}}}\quad \text {and}\quad T=\frac{t}{z^{\frac{3}{5}}} . \end{aligned}$$

Putting (23) into (4), we get

$$\begin{aligned}&V_{XXXY}+3V_XV_{XY}+3V_YV_{XX}+\frac{3}{5}XV_{XX}+\frac{9}{5}(TV_{XT}\nonumber \\&\quad +YV_{XY})+\frac{6}{5}V_X-(V_{TT}+V_{YT})=0. \end{aligned}$$
(24)

To get the group-invariant solution, apply the Lie group method again which results in new infinitesimal generators:

$$\begin{aligned}&\xi _X=-\frac{9}{10}a_1T+a_3,~~~~\xi _Y=a_2,~~~~\xi _T=a_1~~~\nonumber \\&\text {and}~~~\nonumber \\&\eta _V=\frac{18}{50}(a_1-a_2)T^2+\frac{1}{50}(50a_4-18a_1Y)T\nonumber \\&\qquad ~~+\frac{3}{10}a_1X-\frac{3}{5}a_2X -\frac{1}{5}a_3Y+a_5, \end{aligned}$$
(25)

where \(a_i\)’s \((1\le i\le 5)\) are arbitrary constants.

Case (i): When \(a_1 \ne 0\) and other constants are zero

From eq. (25), the associated characteristic equation becomes

$$\begin{aligned}&\frac{\mathrm {d}X}{-({9}/{10})T}=\frac{\mathrm {d}Y}{0}=\frac{\mathrm {d}T}{1}\nonumber \\&\quad =\frac{\mathrm {d}V}{({18}/{50})T^2-({18}/{50})YT+({3}/{10})X}. \end{aligned}$$
(26)

Solving eq. (26), we obtain

$$\begin{aligned} V(X,Y,T)=G(R,S)+\frac{3}{100} T \left( 7 T^2-6 T Y+10 X\right) , \end{aligned}$$
(27)

with

$$\begin{aligned}R=X+\frac{9 T^2}{20},~~S=Y. \end{aligned}$$

Using eq. (27) into (24), we get the following (\(1+1\)) nonlinear partial differential equation:

$$\begin{aligned}&G_{RRRS}+3G_RG_{RS}+3G_SG_{RR}+\frac{3}{5}RG_{RR}+\frac{9}{5}SG_{RS}\nonumber \\&\quad +\frac{3}{10}G_R+\frac{9}{25}S=0. \end{aligned}$$
(28)

Infinitesimals of (28) are

$$\begin{aligned}&\xi _R=-\frac{1}{2}b_1R+b_2,~~~~\xi _S=b_1S\nonumber \\&\text {and}~~~\nonumber \\&\eta _G=-\frac{1}{5}Sb_2+\frac{1}{2}b_1G+b_3. \end{aligned}$$
(29)

On simplifying (29), we obtain

$$\begin{aligned} G(R,S)=S^{\frac{1}{2}}H(w)-\frac{2}{5} \left( A_2 S+5 A_3\right) \end{aligned}$$
(30)

with   \(w=S^{\frac{1}{2}}(R-2 A_2),\) and \( A_2={b_2}/{b_1}\) and \(A_3={b_3}/{b_1}\) are constants. Using eq. (30) into (28), we get

$$\begin{aligned}&25 w H^{(4)}+100H^{(3)}+15H'(7+10H'+10wH'')\nonumber \\&\quad +45 wH''+15(2w+5H)H''+18=0 \end{aligned}$$
(31)

which gives the solutions

$$\begin{aligned} H(w)=\delta _1 -\frac{2}{5}w~~~\text {and}~~H(w)=\frac{\delta _2}{w}-\frac{3}{10}w, \end{aligned}$$
(32)

where \(\delta _1\) and \(\delta _2\) are arbitrary constants.

Accordingly, we derive exact-invariant solution of gBKP-B (4)

$$\begin{aligned} v(x,y,z,t)&=\delta _1 \sqrt{\frac{y}{z}}+\frac{3 t x}{10 z}+\frac{21 t^3-36 t^2 y}{100 z^2}+\frac{2 A_2 y}{5 z^{\frac{4}{5}}}\nonumber \\&\quad -\frac{2}{5}\left( \frac{5 A_3}{\root 5 \of {z}}+\frac{x y}{z}\right) , \end{aligned}$$
(33)
$$\begin{aligned} v(x,y,z,t)&=\frac{21 t^2 (2 t-3 y)}{200 z^2}+\frac{3 x (t-y)}{10 z}+\frac{yA_2}{5z^{\frac{4}{5}}}\nonumber \\&\quad +\frac{20 \delta _2 z}{( x z-40 A_2 z^{\frac{6}{5}}+9 t^2)}-\frac{2A_3}{5z^{\frac{1}{5}}}. \end{aligned}$$
(34)

Case (ii): When \(a_1=a_2 \ne 0\) and other constants are zero

From eq. (25), the associated characteristic equation becomes

$$\begin{aligned}&\frac{\mathrm {d}X}{-({9}/{10})T}=\frac{\mathrm {d}Y}{1}=\frac{\mathrm {d}T}{1}\nonumber \\&\quad =\frac{\mathrm {d}V}{-({18}/{50})YT-({3}/{10})X}. \end{aligned}$$
(35)

Solving eq. (35), we obtain

$$\begin{aligned} V(X,Y,T)=G(R,S)-\frac{3}{100} T \left( T^2+6 T Y+10 X\right) \end{aligned}$$
(36)

with

$$\begin{aligned}R=X+\frac{9 T^2}{20},\,S=Y-T. \end{aligned}$$

Using eq. (36) into (24), we get the following (\(1+1\)) nonlinear partial differential equation:

$$\begin{aligned}&G_{RRRS}+3G_RG_{RS}+3G_SG_{RR}+\frac{3}{5}RG_{RR}+\frac{9}{5}SG_{RS}\nonumber \\&\quad +\frac{3}{10}G_R+\frac{9}{25}S=0. \end{aligned}$$
(37)

Infinitesimals of (37) are

$$\begin{aligned}&\xi _R=-\frac{1}{2}b_1R+b_2,~~~~\xi _S=b_1S\nonumber \\&\text {and}~~~\nonumber \\&\eta _G=-\frac{1}{5}Sb_2+\frac{1}{2}b_1G+b_3. \end{aligned}$$
(38)

On simplifying (38), we get

$$\begin{aligned} G(R,S)=S^{\frac{1}{2}}H(w)-\frac{2}{5} \left( A_2 S+5 A_3\right) , \end{aligned}$$
(39)

with \(w=S^{\frac{1}{2}}(R-2 A_2),\) and \( A_2={b_2}/{b_1}\) and \(A_3={b_3}/{b_1}\) are constants.

Using eq. (39) into (37), we get

$$\begin{aligned}&25 w H^{(4)}+100H^{(3)}+15H'(7+10H'+10wH'')\nonumber \\&\quad +45 wH''+15(2w+5H)H''+18=0 \end{aligned}$$
(40)

which gives the solutions

$$\begin{aligned} H(w)=\delta _3 -\frac{3}{10}w~~~\text {and}~~H(w)=\frac{\delta _4}{w}-\frac{3}{10}w, \end{aligned}$$
(41)

where \(\delta _3\) and \(\delta _4\) are arbitrary constants.

Accordingly, we derive exact invariant solutions of gBKP-B (4) as

$$\begin{aligned} v(x,y,z,t)&=\frac{21t^3}{200z^2}-\frac{63yt^2}{200z^2}-\frac{3xy}{10z}+\delta _3 \sqrt{\frac{y-t}{z}}\nonumber \\&\quad +\frac{(y-t)}{5z^{\frac{4}{5}}}A_2-\frac{2A_3}{z^{\frac{1}{5}}}, \end{aligned}$$
(42)
$$\begin{aligned} v(x,y,z,t)&=\frac{3t}{100z^2}\left( t^2+6ty+10xz\right) \nonumber \\&\quad +\frac{20\delta _4z}{9t^2+20xz-40A_2z^{\frac{4}{5}}}\nonumber \\&\quad -\frac{2(y-t)}{5z^{\frac{4}{5}}}A_2-\frac{3(y-t)}{200z^2}\nonumber \\&\quad \times \left( 9t^2+20xz-40A_2z^{\frac{6}{5}}\right) -\frac{2A_3}{z^{\frac{1}{5}}}. \end{aligned}$$
(43)
Fig. 1
figure 1

Three distinct complex structures of elastic interactions between curve-shaped lumps and oscillating multisolitons for solution (43) with parameters \(A_2=1.7, A_3=31,\delta _4=15.7 \) and \(y=0.7\).

Full size image

4.2 Subalgebra \({\mathfrak {T}}_2\) \(:= {\mathbf {V}}_1+{\mathbf {V}}_3\)

Lagrange’s equation for subalgebra \({\mathfrak {T}}_2\) is

$$\begin{aligned} \frac{\mathrm {d}x}{{x}/{3}}=\frac{\mathrm {d}y}{y} =\frac{\mathrm {d}z}{{5z}/{3}} =\frac{\mathrm {d}t}{t} =\frac{\mathrm {d}v}{f_1(z)-({v}/{3})}. \end{aligned}$$
(44)

On that account, eq. (44) furnishes the similarity form

$$\begin{aligned} v(x,y,z,t)=\frac{V(X,Y,T)}{z^\frac{1}{5}}+\frac{3}{5z^\frac{1}{5}} \int \frac{f_1(z)}{z^\frac{4}{5}} \mathrm {d}z \end{aligned}$$
(45)

with

$$\begin{aligned} X=\frac{x}{z^\frac{1}{5}},\,Y=\frac{y}{z^\frac{3}{5}}\quad \text {and}\quad T=\frac{t}{z^\frac{3}{5}}. \end{aligned}$$

Taking the similarity solution v from (45) into (4), we acquire the newly diminished equation

$$\begin{aligned}&5 (V_{TT}+V_{YT})-6 V_{X}-15 (V_{X} V_{Y})_{X}\nonumber \\&\quad -9 (T V_{XT}+Y V_{XY})- 3 X V_{XX}-5V_{XXXY}=0. \end{aligned}$$
(46)

Again, employing LST on eq. (46), new infinitesimals are given as

$$\begin{aligned} \xi _X&=-\frac{9 a_1}{10}T+a_3,~~~\xi _Y= a_2,~~\xi _T=a_1,~~~ \nonumber \\ \eta _V&=\frac{1}{50} (18 a_1-18a_2)T^2\nonumber \\&\quad +\frac{1}{50} (-18Y a_1+50a_4)T+\frac{3}{10}Xa_1\nonumber \\&\quad -\frac{3}{5}Xa_2-\frac{1}{5}a_3Y+a_5, \end{aligned}$$
(47)

where \(a_i\)’s \( (1\le i\le 5)\) are arbitrary constants.

For \(a_1=a_2\ne 0\) and all other constants are zero. From eq. (47), we get the characteristic system as

$$\begin{aligned} \frac{\mathrm {d}X}{-({9}/{10})T}=\frac{\mathrm {d}Y}{1}=\frac{\mathrm {d}T}{1} =\frac{\mathrm {d}V}{-({18}/{50})YT-({3}/{10})X} \end{aligned}$$
(48)

which gives

$$\begin{aligned} V(X,Y,T)=F(R,S)- \frac{3}{100}T (T^2+10X+6TY) \end{aligned}$$
(49)

with

$$\begin{aligned}R=X+\frac{9T^2}{20},\,S=Y-T. \end{aligned}$$

Using (49) and (46), we have the reduced equation

$$\begin{aligned}&50 F_{RRRS}+150( F_{S} F_{R})_R+30 R F_{RR}\nonumber \\&\quad +15 F_{R}+90 S F_{RS}+18S=0. \end{aligned}$$
(50)

Again, applying the Lie symmetry method on eq. (50), the new infinitesimals are

$$\begin{aligned}&\xi _R=-\frac{1}{2}b_1 R+b_2,~~~\xi _S=b_1 S, ~~~~~\nonumber \\&\eta _F=-\frac{1}{5} S b_2+ \frac{1}{2}b_1 F+b_3, \end{aligned}$$
(51)

where \(b_i\)’s \( (1\le i\le 3)\) are arbitrary constants. The characteristic system for (51) is

$$\begin{aligned}&\frac{\mathrm {d}R}{-({1}/{2}) b_1 R+b_2}=\frac{\mathrm {d}S}{b_1 S}\nonumber \\&\quad =\frac{\mathrm {d}F}{-({1}/{5}) S b_2+ ({1}/{2}) b_1 F+b_3} \end{aligned}$$
(52)

that gives the similarity form

$$\begin{aligned} F(R,S)= \sqrt{S} H(w)- \frac{2}{5} (S B_2 + 5 B_3) \end{aligned}$$
(53)

with \(w= \sqrt{S} (R-2 B_2),\) and \( B_2={b_2}/{b_1}\) and \(B_3={b_3}/{b_1}\) are constants. Using (53) and (50), we get an ODE

$$\begin{aligned}&25 w H^{(4)}+100H^{(3)}+15H'(7+10H'+10wH'')\nonumber \\&\quad +45 wH''+15(2w+5H)H''+18=0. \end{aligned}$$
(54)

On solving (54), we have

$$\begin{aligned}&H(w)=\delta _5- \frac{3}{10} w\nonumber \\&\text {and}~~\nonumber \\&H(w)=\frac{\delta _6}{w}-\frac{3}{10} w , \end{aligned}$$
(55)

where \(\delta _5\) and \(\delta _6\) are any two arbitrary constants.

Accordingly, we obtain the following solutions of the gBKP-B (4):

$$\begin{aligned} v(x,y,z,t)&=\frac{21 t^3}{200 z^2}- \frac{63 t^2 y}{200 z^2}- \frac{3 x y}{10z}\nonumber \\&\quad +\delta _5 \sqrt{\frac{-t+y}{z}}+\frac{(-t+y)B_2}{5 z^{\frac{4}{5}}}\nonumber \\&\quad +\frac{3}{5z^{\frac{1}{5}}} \int \frac{f_1(z)}{z^{\frac{4}{5}}} \mathrm {d}z- \frac{2 B_3}{z^{\frac{1}{5}}}, \end{aligned}$$
(56)
$$\begin{aligned} v(x,y,z,t)&=\frac{3}{5z^{\frac{1}{5}}} \int \frac{f_1(z)}{z^{\frac{4}{5}}} \mathrm {d}z\nonumber \\&\quad -\frac{3t}{100 z^{2}}(t^{2}+6ty+10xz)\nonumber \\&\quad +\frac{20 \delta _6 z}{(9t^{2}+20xz-40z^{\frac{6}{5}}B_{2})} \nonumber \\&\quad -\frac{3(y-t)}{200z^{2}} (9t^{2}+20xz-40z^{\frac{6}{5}}B_{2})\nonumber \\&\quad -\frac{2B_2(y-t)}{5z^{\frac{4}{5}}}-\frac{2B_3}{z^{\frac{1}{5}}}. \end{aligned}$$
(57)
Fig. 2
figure 2

Three distinct complex structures of lump wave solitons for solution (57) with parameters \(a_0=4, B_2=1.7,~B_3=31,~\delta _6=15.7,~ y=11 \) and \(f_1(z)=a_0z\).

Full size image

4.3 Subalgebra \({\mathfrak {T}}_3\) \(:={\mathbf {V}}_1+{\mathbf {V}}_7\) when \( f_5(z)= A z\)

The related Lagrange’s system is interpreted as

$$\begin{aligned} \frac{\mathrm {d}x}{\frac{x}{3}- \frac{3A}{2}t}=\frac{\mathrm {d}y}{y} =\frac{\mathrm {d}z}{\frac{5z}{3}} =\frac{\mathrm {d}t}{t+ A z} =\frac{\mathrm {d}v}{\frac{A}{2} x-\frac{v}{3}}. \end{aligned}$$
(58)

Equation (58) produces

$$\begin{aligned} v(x,y,z,t)&=\frac{V(X,Y,T)}{z^\frac{1}{5}}\nonumber \\&\quad +\frac{3}{64} A (18 A t+16 x- 9 A^2 z), \end{aligned}$$
(59)

with 

$$\begin{aligned} X= & {} \frac{16x+9A(4t-3Az)}{16z^\frac{1}{5}},~~\\ Y= & {} \frac{y}{z^\frac{3}{5}}~~\text {and}\quad T=\frac{2t-3Az}{2z^\frac{3}{5}}. \end{aligned}$$

We obtain a new reduction equation on solving (59) and (4)

$$\begin{aligned}&5 (V_{TT}+V_{YT})-6 V_{X}-15 (V_{X} V_{Y})_{X}-9 (T V_{XT}\nonumber \\&\quad +Y V_{XY})- 3 X V_{XX}-5V_{XXXY}=0. \end{aligned}$$
(60)

By the application of Lie symmetry method on eq. (60), the desired infinitesimals are

$$\begin{aligned} \xi _X&=\frac{-9 a_1}{10}T+a_3,~~~\xi _Y= a_2, ~~~~\xi _T=a_1,~~~\nonumber \\ \eta _V&=\frac{1}{50} (18 a_1-18a_2)T^2+\frac{1}{50} (-18Y a_1+50a_4)T\nonumber \\&\quad +\frac{3}{10}Xa_1-\frac{3}{5}Xa_2-\frac{1}{5}a_3Y+a_5, \end{aligned}$$
(61)

where \(a_i\)’s \( (1\le i\le 5)\) are arbitrary constants.

Suppose \(a_1=a_2\ne 0\) and all other constants are zero. By eq. (61), the characteristic equation becomes

$$\begin{aligned}&\frac{\mathrm {d}X}{-({9}/{10})T}=\frac{\mathrm {d}Y}{1}=\frac{\mathrm {d}T}{1}\nonumber \\&\quad =\frac{\mathrm {d}V}{-({18}/{50})Y T-({3}/{10})X}, \end{aligned}$$
(62)

which provides

$$\begin{aligned} V(X,Y,T)=F(R,S)- \frac{3}{100}T (T^2+10X+6TY), \end{aligned}$$
(63)

with

$$\begin{aligned} R=X+\frac{9T^2}{20},~~S=Y-T. \end{aligned}$$

Using (63) and (60), we get the following equation:

$$\begin{aligned}&50 F_{RRRS}+150( F_{S} F_{R})_R+30 R F_{RR}+15 F_{R}\nonumber \\&\quad +90 S F_{RS}+18S=0. \end{aligned}$$
(64)

Applying Lie symmetry method on eq. (64) again, we get the set of infinitesimals as

$$\begin{aligned} \xi _R&=\frac{-1}{2}b_1 R+b_2,~~~\xi _S=b_1 S,~~\nonumber \\ \eta _F&=\frac{-1}{5} S b_2+ \frac{1}{2}b_1 F+b_3, \end{aligned}$$
(65)

where \(b_i\)’s \( (1\le i\le 3)\) are arbitrary constants. Characteristic equation for (65) is

$$\begin{aligned}&\frac{\mathrm {d}R}{-({1}/{2}) b_1 R+b_2}=\frac{\mathrm {d}S}{b_1 S}\nonumber \\&\quad =\frac{\mathrm {d}F}{-({1}/{5}) S b_2+ \frac{1}{2} b_1 F+b_3} \end{aligned}$$
(66)

which derives the similarity form

$$\begin{aligned} F(R,S)= \sqrt{S} H(w)- \frac{2}{5} (S B_2 + 5 B_3) \end{aligned}$$
(67)

with \(w= \sqrt{S} (R-2 B_2)\), and \( B_2={b_2}/{b_1}\) and \(B_3={b_3}/{b_1}\) are constants. Using (67) and (64), we get an ODE

$$\begin{aligned}&25 w H^{(4)}+100H^{(3)}+15H'(7+10H'+10wH'')\nonumber \\&\quad +45 wH''+15(2w+5H)H''+18=0. \end{aligned}$$
(68)

We solve (68), to get

$$\begin{aligned}&H(w)= \delta _7- \frac{3}{10} w\nonumber \\&\text {and}~~\nonumber \\&H(w)=\frac{\delta _8}{w}-\frac{3}{10} w , \end{aligned}$$
(69)

where \(\delta _7\) and \(\delta _8\) are any two arbitrary constants.

Group-invariant solutions of the gBKP-B equation (4) with the help of back substitution are:

$$\begin{aligned}&v(x,y,z,t)=\frac{9 t^3}{400 z^2}- \frac{63t^2 y}{200 z^2}-\frac{189t^2 A}{400 z}\nonumber \\&\quad +\delta _7 \sqrt{\frac{2(y-t)+3Az}{2z}}+\frac{27At}{400z}(4y+23Az) \nonumber \\&\quad +\frac{\left( 2(y-t)+3Az\right) B_2}{10 z^{\frac{4}{5}}}-\frac{3x}{20}(2y-5Az)\nonumber \\&\quad -\frac{27A^2}{800}(6y+23Az)- \frac{2B_3}{z^{\frac{1}{5}}}, \end{aligned}$$
(70)
$$\begin{aligned}&v(x,y,z,t)=-\frac{27}{32}A^2(t-Az)\nonumber \\&\quad -\frac{1}{320z}(16x-27A^2z+36At)(6t+5z-144Az)\nonumber \\&\quad -\frac{(2y-t+3Az)B_2}{5z^\frac{4}{5}} \nonumber \\&\quad +\frac{20\delta _8z}{(18t^2-27A^2z^2+36Atz+40xz-80B_2z^\frac{6}{5})}\nonumber \\&\quad -\frac{3}{800 z^2}(2t-3Az)^2(2t+6y-3Az)\nonumber \\&\quad -\frac{2B_3}{z^\frac{1}{5}} -\frac{3}{20}\frac{(2y-t+3Az)}{z^\frac{4}{5}}\nonumber \\&\quad \times (18t^2-27A^2z^2+36Atz+40xz-80B_2z^\frac{6}{5}). \end{aligned}$$
(71)
Fig. 3
figure 3

Three distinct complex structures of elastic interactions between curve-shaped lump wave solitons and oscillating multisolitons for solution (71) with parameters \(A=0.16,~B_2=1.37,~B_3=1.2,~\delta _8=5 \) and \(y=0.11\).

Full size image

4.4 Subalgebra \({\mathfrak {T}}_4\) \(:={\mathbf {V}}_1+{\mathbf {V}}_2+{\mathbf {V}}_4\)

The associated Lagrange’s system of \({\mathfrak {T}}_4\) is

$$\begin{aligned} \frac{\mathrm {d}x}{{x}/{3}}&=\frac{\mathrm {d}y}{y} =\frac{\mathrm {d}z}{({5z}/{3})+1} \nonumber \\&=\frac{\mathrm {d}t}{t} =\frac{\mathrm {d}v}{tf_2(z)-({v}/{3})}. \end{aligned}$$
(72)

The similarity form of eq. (72) is

$$\begin{aligned}&v(x,y,z,t)=\frac{V(X,Y,T)}{(3+5z)^\frac{1}{5}}\nonumber \\&\quad +\frac{3t}{(3+5z)^\frac{1}{5}} \int \frac{f_2(z)}{(3+5z)^\frac{4}{5}} \mathrm {d}z~~~~~\nonumber \\&\text {with}\nonumber \\&X=\frac{x}{(3+5z)^\frac{1}{5}},~~Y=\frac{y}{(3+5z)^\frac{3}{5}} \nonumber \\&\text {and}~~\nonumber \\&T=\frac{t}{(3+5z)^\frac{3}{5}}. \end{aligned}$$
(73)

On substitution of v from (73) in (4), we get

$$\begin{aligned}&V_{XXXY}+6 V_{X}+3 (V_{X} V_{Y})_{X}+9 (T V_{XT}+Y V_{XY})\nonumber \\&\quad + 3 X V_{XX}- (V_{TT}+V_{YT})=0. \end{aligned}$$
(74)

For eq. (74), the set of infinitesimals can be provided as

$$\begin{aligned} \xi _X&=\frac{-9 a_1}{2}T+a_3,~~~\xi _Y= a_2,~~~\xi _T=a_1,~~~ \nonumber \\ \eta _V&=\frac{3}{2} ( a_1-2 a_2)X- (9 T a_1+a_3)Y\nonumber \\&\quad +9T^{2}a_1-9T^{2}a_2+Ta_4+a_5, \end{aligned}$$
(75)

where \(a_i\)’s \( (1\le i\le 5)\) are arbitrary constants. Let \(a_1\ne 0\) and the remaining constants are zero.

For eq. (75), the characteristic equation becomes

$$\begin{aligned} \frac{\mathrm {d}X}{-\frac{9 }{2}T}=\frac{\mathrm {d}Y}{0}=\frac{\mathrm {d}T}{1} =\frac{\mathrm {d}V}{({3}/{2}) X-9TY+9T^{2}}. \end{aligned}$$
(76)

Similarity form for eq. (76) is

$$\begin{aligned} V(X,Y,T)=F(R,S)+ \frac{3RT}{2}-\frac{9ST^{2}}{2}+\frac{15T^{3}}{8} \end{aligned}$$
(77)

with

$$\begin{aligned} R=X+\frac{9T^2}{4},~~S=Y. \end{aligned}$$

With the help of (77) and (74), we find a PDE

$$\begin{aligned}&F_{RRRS}+3( F_{S} F_{R})_R+3 R F_{RR}+\frac{3}{2} F_{R}\nonumber \\&\quad +9 S F_{RS}+9S=0. \end{aligned}$$
(78)

Now, apply LSM on eq. (78), then we derive the appropriate infinitesimals

$$\begin{aligned} \xi _R&=-\frac{1}{2}b_1 R+b_2,~~~\xi _S=b_1 S,~~~~ \nonumber \\ \eta _F&=- S b_2+ \frac{1}{2}b_1 F+b_3, \end{aligned}$$
(79)

where \(b_i\)’s \( (1\le i\le 3)\) are arbitrary constants.

For eq. (79), the characteristic equation becomes

$$\begin{aligned} \frac{\mathrm {d}R}{-({1}/{2}) b_1 R+b_2}=\frac{\mathrm {d}S}{b_1 S}=\frac{\mathrm {d}F}{- S b_2+ ({1}/{2}) b_1 F+b_3}. \end{aligned}$$
(80)

Similarity solution for eq. (80) is presented as follows:

$$\begin{aligned} F(R,S)= \sqrt{S} H(w)- \frac{2}{b_{1}} (S b_2 + b_3)\end{aligned}$$
(81)

with

$$\begin{aligned} w= \sqrt{S} \bigg (R-2\frac{ b_2}{b_1}\bigg ). \end{aligned}$$

On combining (81) and (78), we can promptly obtain

$$\begin{aligned}&w H^{(4)}+4 H^{(3)}+6wH'H''+3HH''\nonumber \\&\quad +15wH''+6(H')^2+21H'+18=0. \end{aligned}$$
(82)

On solving (82), we have

$$\begin{aligned}&H(w)=\delta _{9}- \frac{3}{2} w ~~\nonumber \\&\text {and}~~\nonumber \\&H(w)=\frac{\delta _{10}}{w}-\frac{3}{2}w, \end{aligned}$$
(83)

where \(\delta _{9}\) and \(\delta _{10}\) are arbitrary constants.

On solving by substitution, we get the general solutions of the gBKP-B (4):

$$\begin{aligned}&v(x,y,z,t)=\frac{3t}{(3+5z)^{\frac{1}{5}}}\int \frac{f_2(z)}{(3+5z)^{\frac{4}{5}}}\mathrm {d}z\nonumber \\&\quad +\frac{6t(7t^{2}-6ty+2t(3+5z)x)}{8(3+5z)^{2}}+\sqrt{\frac{y}{3+5z}}\delta _{9} \nonumber \\&\quad -\frac{3y}{8(3+5z)^{2}}\left( 9t^{2}+4(3+5z)x+3\frac{b_2}{b_1}(3+5z)^{\frac{6}{5}}\right) \nonumber \\&\quad -\frac{b_2}{b_1}\frac{2y}{(3+5z)^{\frac{4}{5}}}-\frac{b_3}{b_1}\frac{2}{(3+5z)^{\frac{1}{5}}}, \end{aligned}$$
(84)
$$\begin{aligned}&v(x,y,z,t)=\frac{3t}{(3+5z)^{\frac{1}{5}}}\int \frac{f_2(z)}{(3+5z)^{\frac{4}{5}}}\mathrm {d}z\nonumber \\&\quad +\frac{(15t^3-36t^2y)}{8(3+5z)^{2}}+\frac{3t(9t^2+4(3+5z)x)}{8(3+5z)^{\frac{4}{5}}} \nonumber \\&\quad -\frac{b_3}{b_1}\frac{2}{(3+5z)^{\frac{1}{5}}} -\frac{3y}{8(3+5z)^{2}}\nonumber \\&\quad \times \left( 9t^{2}+4(3+5z)x-8\frac{b_2}{b_1}(3+5z)^{\frac{6}{5}}\right) \nonumber \\&\quad -\frac{b_2}{b_1}\frac{2y}{(3+5z)^{\frac{4}{5}}} \nonumber \\&\quad +\frac{4\delta _{10}(3+5z)}{\left( 9t^{2}+4(3+5z)x-8\frac{b_2}{b_1}(3+5z)^{\frac{6}{5}}\right) }. \end{aligned}$$
(85)

4.5 Subalgebra \({\mathfrak {T}}_5\) \(:={\mathbf {V}}_2=\frac{\partial }{\partial z}\)

The associated Lagrange’s system reads as

$$\begin{aligned} \frac{\mathrm {d}x}{0}=\frac{\mathrm {d}y}{0}=\frac{\mathrm {d}z}{1}=\frac{\mathrm {d}t}{0}=\frac{\mathrm {d}v}{0} \end{aligned}$$
(86)

which gives

$$\begin{aligned} v(x,y,z,t)=V(X,Y,T)\end{aligned}$$
(87)

with invariants

$$\begin{aligned} X=x,~~Y=y,~~T=t. \end{aligned}$$

Using (87) into (4), we thus obtain the (\(2+1\))-dimensional reduced nonlinear PDE:

$$\begin{aligned} V_{XXXY}+3V_{X}V_{XY}+3V_{Y}V_{XX}-V_{TT}-V_{YT}=0 \end{aligned}$$
(88)

which has the general solution

$$\begin{aligned}&V(X,Y,T)=c_3\nonumber \\&\quad +2 c_2 \tanh \left( c_1 T+c_2 X-\frac{c_1^2 Y}{c_1-4 c_2^3}+c_4\right) , \end{aligned}$$
(89)

where \(c_1,~ c_2,~ c_3\) and \(c_4\) are constants of integration.

Therefore, the resulting solution of the gBKP-B equation (4) is

$$\begin{aligned}&v(x,y,z,t) =c_3\nonumber \\&\quad +2 c_2 \tanh \left( c_4+c_1 t+c_2 x-\frac{c_1^2 y}{c_1-4 c_2^3}\right) . \end{aligned}$$
(90)

Further, Let us take

$$\begin{aligned} V(X,Y,T)=H(w), \end{aligned}$$
(91)

where \(w=a X+b Y+c T.\)

Here a,  b and c are arbitrary constants. Taking (91) into (88), we have

$$\begin{aligned} a^3 b H^{(4)}+6 a^2 b H'H''-c (b+c)H''=0. \end{aligned}$$
(92)

The primitives are

$$\begin{aligned}&H(w)=\delta _{11}+\delta _{12} w,~~~~H(w)=\delta _{13}+\frac{c (b+c)}{6 a^2 b}w~~~~\nonumber \\&\text {and}\nonumber \\&H(w)=\delta _{14}+\frac{2 a}{w}+\frac{c (b+c)}{6 a^2 b}w, \end{aligned}$$
(93)

where \(\delta _{11}\), \(\delta _{12}\), \(\delta _{13}\) and \(\delta _{14}\) are arbitrary constants.

Hence, we acquire the following exact invariant solutions of gBKP-B (4):

$$\begin{aligned} v(x,y,z,t)&=\delta _{11}+\delta _{12} \left( a x+b y+c t\right) , \end{aligned}$$
(94)
$$\begin{aligned} v(x,y,z,t)&=\delta _{13}+\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t\right) , \end{aligned}$$
(95)
$$\begin{aligned} v(x,y,z,t)&=\delta _{14}+\frac{2 a}{\left( a x+b y+c t\right) }\nonumber \\&\quad +\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t\right) . \end{aligned}$$
(96)

4.6 Subalgebra \({\mathfrak {T}}_6\) \(:={\mathbf {V}}_2+{\mathbf {V}}_3=\frac{\partial }{\partial z}+f_1(z)\frac{\partial }{\partial v}\)

Lagrange’s system reads as

$$\begin{aligned} \frac{\mathrm {d}x}{0}=\frac{\mathrm {d}y}{0}=\frac{\mathrm {d}z}{1}=\frac{\mathrm {d}t}{0}=\frac{\mathrm {d}v}{f_1(z)} \end{aligned}$$
(97)

which gives

$$\begin{aligned} v(x,y,z,t)=V(X,Y,T)+\int f_1(z) \, \mathrm {d}z \end{aligned}$$
(98)

with invariants  \(X=x,~Y=y,~T=t.\)

Substituting (98) into (4), we thus obtain the (\(2+1\))-dimensional reduced nonlinear PDE:

$$\begin{aligned} V_{XXXY}+3V_{X}V_{XY}+3V_{Y}V_{XX}-V_{TT}-V_{YT}=0 \end{aligned}$$
(99)

which has the general solution

$$\begin{aligned}&V(X,Y,T)=c_3\nonumber \\&\quad +2 c_2 \tanh \left( c_1 T+c_2 X-\frac{c_1^2 Y}{c_1-4 c_2^3}+c_4\right) , \end{aligned}$$
(100)

where \(c_1,~c_2,~ c_3\) and \(c_4\) are constants of integration.

Therefore, the resulting solution of the gBKP-B equation (4) is

$$\begin{aligned}&v(x,y,z,t)=c_3+2 c_2 \tanh \nonumber \\&\quad \times \left( c_4+c_1 t+c_2 x-\frac{c_1^2 y}{c_1-4 c_2^3}\right) \nonumber \\&\quad +\int f_1(z)\, \mathrm {d}z. \end{aligned}$$
(101)

Further, we consider that

$$\begin{aligned} V(X,Y,T)=H(w), \end{aligned}$$
(102)

where \(w=a X+b Y+c T.\)

Here, a,  b and c are arbitrary constant parameters. We substitute (102) into (99), to obtain

$$\begin{aligned} a^3 b H^{(4)}+6 a^2 b H'H''-c (b+c)H''=0. \end{aligned}$$
(103)

The primitives are

$$\begin{aligned}&H(w)=\delta _{15}+\delta _{16} w \nonumber \\&\text {and}~~~\nonumber \\&H(w)=\delta _{17}+\frac{2 a}{w}+\frac{c (b+c)}{6 a^2 b}w, \end{aligned}$$
(104)

where \(\delta _{15}\), \(\delta _{16}\) and \(\delta _{17}\) are arbitrary constants.

Hence, we acquire the following exact-invariant solutions of gBKP-B equation (4):

$$\begin{aligned}&v(x,y,z,t)=\delta _{15}+\delta _{16} \left( a x+b y+c t\right) +\int f_1(z)\, \mathrm {d}z, \end{aligned}$$
(105)
$$\begin{aligned}&v(x,y,z,t)=\delta _{17}+\frac{2 a}{\left( a x+b y+c t\right) }\nonumber \\&\quad +\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t\right) +\int f_1(z)\, \mathrm {d}z. \end{aligned}$$
(106)
Fig. 4
figure 4

Three distinct complex structures of lump waves for solution (106) with parameters \(a=191\), \(b=3, c=10.3,\delta _{17}=10, z=0.019\) and \(f_1(z)=z\).

Full size image
Fig. 5
figure 5

Three distinct complex structures of multiple lumps and kinky solitons for solution (116) with parameters \(\delta _{19}=10,~a=10,~b=12,~c=2,~z=1.3\) and \(f_2(z)=z\).

Full size image

4.7 Subalgebra \({\mathfrak {T}}_7\) \(:={\mathbf {V}}_2+{\mathbf {V}}_4\)

Lagrange’s system for \({\mathfrak {T}}_7\) is

$$\begin{aligned} \frac{\mathrm {d}x}{0}=\frac{\mathrm {d}y}{0} =\frac{\mathrm {d}z}{1} =\frac{\mathrm {d}t}{0} =\frac{\mathrm {d}v}{t f_2(z)}. \end{aligned}$$
(107)

Equation (107) provides the following similarity solution:

$$\begin{aligned} v(x,y,z,t)=V(X,Y,T)+t \int f_2(z) \mathrm {d}z \end{aligned}$$
(108)

with invariants \(X=x, \,Y=y \,\text {and}~~T=t.\)

After substitution of (108) into (4), we find a new reduction equation as

$$\begin{aligned} V_{TT}+V_{YT}-3V_XV_{XY}-3V_YV_{XX}-V_{XXXY}=0 \end{aligned}$$
(109)

that provides the general solution

$$\begin{aligned}&V(X,Y,T)= c_3\nonumber \\&\quad +2c_2 \tanh \left( c_2X+c_1T- \frac{c_1^{2}Y}{c_1-4 c_2^{3}}+c_4\right) , \end{aligned}$$
(110)

where \(c_1\), \( c_2\), \(c_3\) and \(c_4\) are arbitrary constants of integration.

Therefore, the resultant solution of the gBKP-B equation (4) is

$$\begin{aligned}&v(x,y,z,t)= c_3\nonumber \\&\quad +2c_2 \tanh \left( c_2x+c_1t- \frac{c_1^{2}y}{c_1-4 c_2^{3}}+c_4\right) \nonumber \\&\quad +t \int f_2(z)\mathrm {d}z. \end{aligned}$$
(111)

Moreover, let

$$\begin{aligned} V(X,Y,T)=H(w), \end{aligned}$$
(112)

where \(w=aX+bY+cT,\) and a,  b and c are arbitrary constant parameters.

Taking (112) into (109), we acquire the following reduced ODE:

$$\begin{aligned} a^3 b H^{(4)}+ 6 a^2 b H' H''- c(c+b) H''=0. \end{aligned}$$
(113)

The primitives are

$$\begin{aligned}&H(w)=\delta _{18}+\frac{c(c+b)}{6a^2 b}w \nonumber \\&\text {and}~~\nonumber \\&H(w)=\frac{2a}{w}+\delta _{19}+\frac{c(c+b)}{6a^2 b}w, \end{aligned}$$
(114)

where \(\delta _{18}\) and \(\delta _{19}\) are arbitrary constants.

Finally, we obtain the following solutions of the gBKP-B equation (4):

$$\begin{aligned} v(x,y,z,t)&=\delta _{18}+\frac{c(c+b)}{6a^2 b}(ax+by+ct)\nonumber \\&\quad +t \int f_2(z) \mathrm {d}z, \end{aligned}$$
(115)
$$\begin{aligned} v(x,y,z,t)&=\delta _{19}+\frac{2a}{(ax+by+ct)}\nonumber \\&\quad +\frac{c(c+b)}{6a^2 b}(ax+by+ct)\nonumber \\&\quad +t \int f_2(z) \mathrm {d}z. \end{aligned}$$
(116)

4.8 Subalgebra \({\mathfrak {T}}_8:={\mathbf {V}}_2+{\mathbf {V}}_3+{\mathbf {V}}_5=f_3(z)\frac{\partial }{\partial x}+\frac{\partial }{\partial z}+(f_1(z)-yf'_3(z))\frac{\partial }{\partial v}\)

For simplification, we assume \(f_1(z)=-a_0f'_3(z)\).

In this case, the related Lagrange’s equation reads as

$$\begin{aligned}&\frac{\mathrm {d}x}{f_3(z)}=\frac{\mathrm {d}y}{0}=\frac{\mathrm {d}z}{1}\nonumber \\&\quad =\frac{\mathrm {d}t}{0}=\frac{\mathrm {d}v}{-(y+a_0)f'_3(z)} \end{aligned}$$
(117)

which gives

$$\begin{aligned} v(x,y,z,t)=V(X,Y,T)-\left( y+a_0\right) f_3(z) \end{aligned}$$
(118)

with invariants \(X=x-\int f_3(z) \, \mathrm {d}z,~~Y=y,~~T=t.\)

Substituting (118) into (4), we thus obtain the (\(2+1\))-dimensional reduced nonlinear PDE:

$$\begin{aligned} V_{XXXY}+3V_{X}V_{XY}+3V_{Y}V_{XX}-V_{TT}-V_{YT}=0 \end{aligned}$$
(119)

which has the general solution

$$\begin{aligned}&V(X,Y,T)=c_3 \nonumber \\&\quad +2 c_2 \tanh \left( c_1 T+c_2 X-\frac{c_1^2 Y}{c_1-4 c_2^3}+c_4\right) , \end{aligned}$$
(120)

where \(c_1,~c_2,~c_3\) and \(c_4\) are integration constants.

Therefore, the resulting solution of gBKP-B equation (4) is

$$\begin{aligned}&v(x,y,z,t)=c_3 +2 c_2 \tanh \nonumber \\&\quad \times \left( c_4+c_1 t+c_2 x-c_2 \int f_3(z) \, \mathrm {d}z-\frac{c_1^2 y}{c_1-4 c_2^3}\right) \nonumber \\&\quad -\left( y+a_0\right) f_3(z). \end{aligned}$$
(121)

Further, we consider that

$$\begin{aligned} V(X,Y,T)=H(w), \end{aligned}$$
(122)

where \(w=a X+b Y+c T\) and a,  b and c are arbitrary constant parameters. Putting (122) into (119), we have

$$\begin{aligned} a^3 b H^{(4)}+ 6 a^2 b H' H''- c(c+b) H''=0. \end{aligned}$$
(123)

Primitives are

$$\begin{aligned}&H(w)=\delta _{20}+\delta _{21} w,~~~~H(w)=\delta _{22}+\frac{c (b+c)}{6 a^2 b}w\nonumber \\&\text {and}~~~~\nonumber \\&H(w)=\delta _{23}+\frac{2 a}{w}+\frac{c (b+c)}{6 a^2 b}w, \end{aligned}$$
(124)

where \(\delta _{20}\), \(\delta _{21}\), \(\delta _{22}\) and \(\delta _{23}\) are arbitrary constants.

Hence, we acquire the following exact invariant solutions of gBKP-B equation (4):

$$\begin{aligned}&v(x,y,z,t)=\delta _{20}\nonumber \\&\quad +\delta _{21} \left( a x+b y+c t-a\int f_3(z) \, \mathrm {d}z\right) \nonumber \\&\quad -\left( y+a_0\right) f_3(z), \end{aligned}$$
(125)
$$\begin{aligned}&v(x,y,z,t)=\delta _{22}\nonumber \\&\quad +\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t-a \int f_3 (z) \, \mathrm {d}z\right) \nonumber \\&\quad -\left( y+a_0\right) f_3(z), \end{aligned}$$
(126)
$$\begin{aligned}&v(x,y,z,t)=\delta _{23}+\frac{2 a}{\left( a x+b y+c t-a \int f_3(z) \, dz\right) }\nonumber \\&\quad +\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t-a \int f_3(z) \, \mathrm {d}z\right) \nonumber \\&\quad -\left( y+a_0\right) f_3(z). \end{aligned}$$
(127)
Fig. 6
figure 6

Three distinct complex structures of elastic interactions between curve-shaped multiple lumps and oscillating multisolitons for solution (127) with parameters \(\delta _{23}=11,~a_0=1,~a=19,~b=5,~c=7,~y=1\) and \(f_3(z)=z\).

Full size image

Again, we use the group-theoretic technique to obtain generators of (119)

$$\begin{aligned} \xi _X&=\frac{a_1}{3}X+a_4,~~ \xi _Y=a_1Y+a_3,~~\nonumber \\ \xi _T&=a_1T+a_2,~~~ \eta _V=-\frac{a_1}{3}V+a_5T+a_6, \end{aligned}$$
(128)

where \(a_i\)’s \( (1\le i \le 6)\) are arbitrary constants.

Then, the associated Lagrange’s system is

$$\begin{aligned}&\frac{\mathrm {d}X}{({a_1}/{3})X+a_4}=\frac{\mathrm {d}Y}{a_1Y+a_3}=\frac{\mathrm {d}T}{a_1T+a_2}\nonumber \\&\quad =\frac{\mathrm {d}V}{-({a_1}/{3})V+a_5T+a_6}. \end{aligned}$$
(129)

Let us suppose \(a_2\) and \(a_5\) are non-zero and others are zero. On solving eq. (129), we have the following similarity form:

$$\begin{aligned} V(X,Y,T)= \frac{a_5 }{2 a_2}T^2+F(R,S) \end{aligned}$$
(130)

with \(R=X \,\text {and}\,S=Y.\)

Substituting (130) into (119), we thus obtain the (\(1+1\))-dimensional PDE as

$$\begin{aligned} F_{RRRS}+3F_RF_{RS}+3F_SF_{RR}-\frac{a_5}{a_2}=0. \end{aligned}$$
(131)

Applying Lie symmetry method on eq. (131) again, the set of infinitesimals is

$$\begin{aligned} \xi _R&=\frac{-1}{4}b_1 R+b_3,~~~\xi _S=b_1 S+b_2,~~ \nonumber \\ \eta _F&=\frac{1}{4} F b_1+ b_4, \end{aligned}$$
(132)

where \(b_i\)’s \( (1\le i\le 4)\) are arbitrary constants.

Suppose \(b_1\ne 0\) and all others are zero. Then, characteristic equation for (132) is

$$\begin{aligned} \frac{\mathrm {d}R}{{-(1}/{4}) R}=\frac{\mathrm {d}S}{ S}=\frac{\mathrm {d}F}{ ({1}/{4}) F} \end{aligned}$$
(133)

which derives the similarity form

$$\begin{aligned} F(R,S)= S^{\frac{1}{4}} H(w)~~~\text {with}~~w=S^{\frac{1}{4}} R. \end{aligned}$$
(134)

Using (134) and (131), we get an ODE

$$\begin{aligned}&w H^{(4)}+4H^{(3)}+6H'(H'+wH'')\nonumber \\&\quad +3HH''-4 \frac{a_5}{a_2}=0 \end{aligned}$$
(135)

which gives

$$\begin{aligned} H(w)=\delta _{24}- \sqrt{\frac{2a_5}{3a_2}}w, \end{aligned}$$
(136)

where \(\delta _{24}\) is an arbitrary constant.

Exact invariant solutions of the gBKP-B equation (4) with the help of back substitution is

$$\begin{aligned}&v(x,y,z,t)=\frac{a_5}{a_2}\frac{t^2}{2}\nonumber \\&\quad +y^{\frac{1}{4}} \left[ \delta _{24}+\sqrt{\frac{2a_5}{3a_2}}y^{\frac{1}{4}}\left( -x+\int f_3(z) \mathrm {d}z\right) \right] \nonumber \\&\quad -(y+a_0)f_3(z). \end{aligned}$$
(137)

4.9 Subalgebra \({\mathfrak {T}}_9\) \(:={\mathbf {V}}_2+{\mathbf {V}}_5+{\mathbf {V}}_6\)

For simplification, in this case, we assume \(f_3(z)=f_4(z).\) Lagrange’s system (21) for \({\mathfrak {T}}_9\) is

$$\begin{aligned} \frac{\mathrm {d}x}{f_4(z)}&=\frac{\mathrm {d}y}{f_4(z)} =\frac{\mathrm {d}z}{1} \nonumber \\&=\frac{\mathrm {d}t}{0} =\frac{\mathrm {d}v}{({3}/{2})t^2 f_4''(z)- (x+y)f_4'(z)}. \end{aligned}$$
(138)

Equation (138) provides the following similarity solution:

$$\begin{aligned} v(x,y,z,t)&=V(X,Y,T)+\frac{3}{2}t^2 f_4'(z)\nonumber \\&\quad - (x+y)f_4(z) \end{aligned}$$
(139)

with \(X=x-\int f_4(z) \mathrm {d}z,\) \(Y=y-\int f_4(z) \mathrm {d}z\) and \(T=t\).

After substitution of (139) into (4), we find a new reduction equation as

$$\begin{aligned} V_{TT}+V_{YT}-3V_XV_{XY}-3V_YV_{XX}-V_{XXXY}=0 \end{aligned}$$
(140)

that provides the general solution

$$\begin{aligned}&V(X,Y,T)= c_3 \nonumber \\&\quad +2c_2\,\mathrm {tanh}\left( c_2X+c_1T- \frac{c_1^{2}Y}{c_1-4 c_2^{3}}+c_4\right) , \end{aligned}$$
(141)

where \(c_1\), \( c_2\), \(c_3\) and \(c_4\) are arbitrary constants of integration. Therefore, the resultant solution of the gBKP-B equation (4) is

$$\begin{aligned}&v(x,y,z,t)= c_3\nonumber \\ {}&\quad +2c_2\, \mathrm {tanh}\left( c_2x+c_1t- \frac{c_1^{2}y}{c_1-4 c_2^{3}}+c_4\right) \nonumber \\&\quad +\frac{3}{2}t^2 f_4'(z)- (x+y)f_4(z). \end{aligned}$$
(142)

Moreover, we consider that

$$\begin{aligned} V(X,Y,T)=H(w),\end{aligned}$$
(143)

where \(w=aX+bY+cT.\) Here, a,  b and c are arbitrary constants.

Putting (143) into (140), one obtains

$$\begin{aligned} a^3 b H^{(4)}+ 6 a^2 b H' H''- c(c+b) H''=0 \end{aligned}$$
(144)

which generates

$$\begin{aligned}&H(w)=\delta _{25}+\delta _{26} w,~~~\nonumber \\&H(w)=\delta _{27}+\frac{c(c+b)}{6a^2 b}w \nonumber \\&\text {and}~~\nonumber \\&H(w)=\frac{2a}{w}+\delta _{28}+\frac{c(c+b)}{6a^2 b}w, \end{aligned}$$
(145)

where \(\delta _{25}\), \(\delta _{26}\), \(\delta _{27}\) and \(\delta _{28}\) are arbitrary constants.

Finally, we derive exact solutions of the gBKP-B equation (4) as

$$\begin{aligned}&v(x,y,z,t)=\delta _{25}-(x+y)f_4(z)\nonumber \\&\quad +\left[ ct+ax+by-(a+b)\int f_4(z)\mathrm {d}z\right] \delta _{26}\nonumber \\&\quad +\frac{3}{2}t^2f_4'(z), \end{aligned}$$
(146)
$$\begin{aligned}&v(x,y,z,t)=\delta _{27}-(x+y)f_4(z)\nonumber \\&\quad +\left[ ct+ax+by-(a+b)\int f_4(z)\mathrm {d}z\right] \frac{c(b+c)}{6a^2b}\nonumber \\&\quad +\frac{3}{2}t^2f_4'(z), \end{aligned}$$
(147)
$$\begin{aligned}&v(x,y,z,t)=\delta _{28}-(x+y)f_4(z)\nonumber \\&\quad +\frac{2a}{\left[ ct+ax+by-(a+b)\int f_4(z)\mathrm {d}z\right] }\nonumber \\&\quad +\frac{3}{2}t^2f_4'(z)\nonumber \\&\quad +\left[ ct+ax+by-(a+b)\int f_4(z)\mathrm {d}z\right] \frac{c(b+c)}{6a^2b}. \end{aligned}$$
(148)
Fig. 7
figure 7

Three distinct complex structures of elastic interactions between curve-shaped lumps and parabolic solitons for solution (148) with parameters \(\delta _{28}=10,~a=11.5,~b=2,~c=0.72,~y=3 \) and \(f_4(z)=1+z^2\).

Full size image

4.10 Subalgebra \({\mathfrak {T}}_{10}\) \(:={\mathbf {V}}_2+{\mathbf {V}}_4+{\mathbf {V}}_5\)

For simplification, we assume \(f_2(z)=a_0f'_3(z).\) As we have demonstrated already, we can find the exact solutions for \({\mathfrak {T}}_{10}\).

The solutions are as follows:

$$\begin{aligned}&v(x,y,z,t)=c_4\nonumber \\&\quad +2 c_2 \tanh \left( c_3+c_2 \left( x- \int f_3(z) \, \mathrm {d}z\right) \right. \nonumber \\&\quad -c_1\left. \left( t- \frac{c_1 y}{c_1-4 c_2^3}\right) \right) \nonumber \\&\quad +\left( -y+t a_0\right) f_3(z), \end{aligned}$$
(149)
$$\begin{aligned}&v(x,y,z,t)=\delta _{29}+\frac{c (b+c)}{6 a^2 b}\nonumber \\&\quad \times \left( a x+b y+c t-a \int f_3(z) \, \mathrm {d}z\right) \nonumber \\&\quad -\left( y- t a_0\right) f_3(z), \end{aligned}$$
(150)
$$\begin{aligned}&v(x,y,z,t)=\delta _{30}+\frac{2 a}{\left( a x+b y+c t-a \int f_3(z) \, dz\right) }\nonumber \\&\quad +\frac{c (b+c)}{6 a^2 b}\left( a x+b y+c t-a \int f_3(z) \,\mathrm { d}z\right) \nonumber \\&\quad -\left( y- t a_0\right) f_3(z), \end{aligned}$$
(151)
$$\begin{aligned}&v(x,y,z,t)=\frac{a_5}{a_2}\frac{t^2}{2}\nonumber \\&\quad + y^{\frac{1}{4}} \left[ \delta _{31}+\sqrt{\frac{2a_5}{3a_2}}y^{\frac{1}{4}}\left( -x+\int f_3(z) \mathrm {d}z\right) \right] \nonumber \\&\quad -(y- t a_0)f_3(z), \end{aligned}$$
(152)

where \(c_1\), \(c_2\), \( c_3\), \( c_4\), \(\delta _{29}\), \( \delta _{30}\) and \(\delta _{31}\) are constants.

5 Physical interpretation of soliton solutions

The nature of mathematical expressions can be made more predictable through their physical analysis. Graphical representation of the explicit solutions are much beneficial to explain the physically meaningful behaviour of the system. Also, it provides vital information to understand the phenomena physically. Numerical simulations have been performed to obtain the best view of graphical representations. Solitons are solitary wave packets and are known for their elastic scattering property that they do not change their shapes and amplitudes after mutual collision. Moreover, they play a prevalent role in the propagation of light in fibre, optical bistability and many other phenomena in plasma and fluid dynamics. In this section, we have analysed solutions (43), (57), (71), (106), (116), (127) and (148) of the g-BKPB equation (4) using their graphical structures. The graphical representations of the generated solutions describe the characteristics of multiple solitons. Various types of solitary wave solutions such as multiwave solitons, parabolic waves, quasiperiodic solitons and lump waves solitons have been exhibited. The choice of arbitrary constants and arbitrary functions contributes to the physically meaningful profiles.

Figure 1 describes curve-shaped elastic multisolitons observed for solution (43). This graphical representation is obtained by taking suitable values to the arbitrary constants as \(A_{2}=1.7\), \(A_{3}=31\), \(\delta _4=15.7\) and \(y=0.7\) for \(-20\le x \le 20\) and \(-10\le t \le 10.\)

Figure 2 depicts lump-type solitons for expression (57). The appropriate values of the introduced arbitrary constants are taken as \(a_0=4\), \(B_2=1.7\), \(B_3=31\), \(\delta _6=15.7\), \(y=11\) and arbitrary function as \(f_1(z)=a_0z,\) for \( -10\le x \le 10 \), \( 1\le t \le 5 \). The study of lump waves has a widespread application in many fields such as oceanographic engineering, non-linear optics, etc.

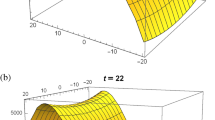
Figure 3 represents the elastic behaviour of curved-shaped multisoliton structure/characteristic of solution (71). The profile is plotted by considering suitable values of parameters as \(y=0.11\), for \(-10\le x \le 10\), \(-10\le t \le 10\), \(A=0.16\), \(B_2= 1.37\), \(B_{3}=1.2\) and \(\delta _{8}=5\).

Figure 4 reveals wave profile of the lump-type solitons in three-dimensional space of solution (106) that was observed via numerical simulation for \( -10\le x \le 10 \), \( -10\le y \le 10 \), \(a=191\), \(b=3\), \(c=10.3\), \(\delta _{17}=10\), \(z=0.019\) and \(f_1(z) = z\).

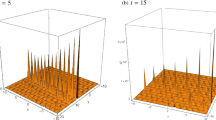
Figure 5 is plotted by choosing suitable arbitrary constants as \( a = 10\), \(b=12\), \(c=2\), \(z=1.3\), \(\delta _{19}=10\) and function as \(f_2(z)=z\) in the particular solution (116). These three figures are traced at \( t=1, 19\) and 35 for \( -50\le x \le 50 \), \( -50\le y \le 50 \). These figures show lump-type soliton behaviour in the spatial profile. Lump-type solitons are localised in almost all directions in space.

Figure 6 shows elastic interactions between curved-shaped multisolitons and lumps are exhibited in this figure for the solution via eq. (127). The profile shows interaction between multisolitons and lumps by taking suitable values of arbitrary functional as \( f_3(z)\) = z and remaining parameters as \(a=19\), \(b=5\), \(c=7\), \(y = 1\), \(\delta _{23} = 11\) and \(a_{0} = 1\). This profile is traced at \( t=0.07\), 5 and 37 for \( -10\le x \le 10 \), \( -10\le z \le 10 \).

Figure 7 represents the annihilation of parabolic curved-shaped profile of eq. (148) in 3D graphics. Interesting intersections of both lump-type solitons and parabolic solitons are observed for v in this figure at \(z=0.75\), \(z=1\) and \(z=1.5\) \(\forall -10\le x \le 10 \), \( -10\le t \le 10 \). This profile is traced by taking the values of constants as \(\delta _{28}= 10\), \(a=11.5\), \(b=2\), \(c=0.72\), \(y = 3\) and arbitrary function as \( f_4(z)\) = \(1+z^{2}\).

6 Conclusion

In summary, we have investigated the generalised BKP–Boussinesq (gBKP-B) equation using the symmetry reduction method, which is a robust, productive, impressive and strong mathematical tool for solving nonlinear PDEs. Lie point symmetries of the gBKP-B equation were considered and then used to derive a one-dimensional optimal system of symmetry subalgebras. Subsequently, three stages of symmetry reductions of the governing equation were carried out using the obtained symmetry subalgebras. The gBKP-B equation was transformed into various nonlinear ODEs which were then solved to attain the exact closed-form solutions of the equation. The solutions obtained have rich localised physical structures as there are five arbitrary independent functions and two parameters that are involved in the infinitesimal generators. The graphical analysis of the newly established solutions has been done by using MATHEMATICA codes via numerical simulation. The different dynamical features and characteristics of multiple solitons of the considered equation are especially analysed based on the suitable selection of arbitrary parameters and arbitrary independent functions. Some of the newly established solutions are more important and useful to explain various nonlinear complex physical phenomena, which makes this work more physically meaningful.