1 Introduction

In real nature, there exist many phenomena that can be properly described by solitons interacted with background nonlinear waves [1,2,3]. For integrable systems, many effective and reliable methods have been developed, such as the Hirota’s bilinear method [4], the Bäcklund transformation (BT) and Darboux transformation (DT) method [5, 6], etc., to derive soliton solutions. However, the interaction solutions of solitons interacted with various nonlinear waves such as cnoidal waves are usually very difficult to be obtained by these traditional methods [7, 8].

As we know, symmetry analysis [9, 10] plays an important role in solving nonlinear problems. Using classical and nonclassical Lie group theory, one can construct abundant reduction solutions of nonlinear differential equations. Nevertheless, these symmetry methods are based on Lie point symmetry group of related equations. Recently, for nonlocal symmetries of some integrable system, Lou found an effective way to localize them into Lie point symmetries by introducing new variables to enlarge the original system. On this basis, various interesting interaction solutions were constructed by using standard Lie symmetry reduction method [11, 12]. Traditionally, nonlocal symmetries of nonlinear systems can be obtained through potential symmetries [13], Lax pair, DT and BT [14], etc. Interestingly, for many Painlevé integrable systems, the residue of truncated Painlevé expansion with respect to singular manifold is actually a nonlocal symmetry, and many interesting interaction solutions were obtained by applying the localization procedure to various nonlinear systems [11, 15]. Furthermore, the truncated Painlevé expansion is extended to consistent Riccati expansion (CRE) by Lou and defined a new integrability of owning CRE property for many nonlinear systems [16,17,18]. More importantly, for CRE integrable systems, solutions of solitons interacted with nonlinear solitary waves can be easily obtained through Riccati expansion [19].

In this paper, we will discuss the (2 \(+\) 1)-dimensional generalization of Boussinesq equation in the form

$$\begin{aligned} u_{tt}-u_{xx}-u_{yy}-(u^2)_{xx}-u_{xxxx}=0 \end{aligned}$$
(1)

by using residual symmetry reduction method and CRE method, respectively. The (2 \(+\) 1)-dimensional Boussinesq equation has important applications in describing the propagation of gravity waves on the surface of water. As for the exact solutions of the (2 \(+\) 1)-dimensional Boussinesq equation, Johnson obtained some different types of solitary-wave solutions by using the Hirota bilinear method [20]; Senthilvelan [21] used the homogeneous balance method to obtain the traveling wave solutions and explored certain new solutions; Chen et al. [22] investigated this equation by using the Riccati equation expansion method and obtained many types of wave solutions.

This paper is organized as follows: In Sect. 2, the residual symmetry of Eq. (1) is obtained from the truncated Painlevé expansion and localized into a Lie point symmetry in a new enlarged system, and then, a new BT is found by solving the corresponding initial value problem. In Sect. 3, the general form of Lie point symmetry group and related symmetry reduction solutions are obtained by applying classical Lie symmetry method to the enlarged (2 \(+\) 1)-dimensional Boussinesq system, from which the interaction solutions are explicitly given for Eq. (1). In Sect. 4, the (2 \(+\) 1)-dimensional Boussinesq equation is found to have CRE integrability property and new BTs of this equation are given through CRE and CTE (consistent tanh expansion) methods. From these BTs, new interaction solutions between solitons and cnoidal waves are explicitly given. The last section contains a discussion and summary.

2 Residual symmetry and related Bäcklund transformation

The truncated Painlevé expansion of the (2 \(+\) 1)-dimensional Boussinesq equation (1) can be easily given by Painlevé analysis, i.e.,

$$\begin{aligned} u=\frac{u_0}{\phi ^2}+\frac{u_1}{\phi }+u_2, \end{aligned}$$
(2)

with \(\phi \) being the singular manifold and \(u_0, u_1, u_2\) being functions of \(x, \,y,\, t\). Substituting (2) into (1) and vanishing the coefficients of all different powers of \(\frac{1}{\phi }\), omitting the details of calculation, we obtain

$$\begin{aligned} u_0= & {} -\,6\phi _x^2,\quad u_1 = 6\phi _{xx}, \end{aligned}$$
(3)
$$\begin{aligned} u_2= & {} -\,\frac{1}{2}\frac{4\phi _x\phi _{xxx}-3\phi _{xx}^2-\phi _t^2+\phi _y^2}{\phi _x^2}-\frac{1}{2}, \end{aligned}$$
(4)

and the Schwarzian form of Eq. (1)

$$\begin{aligned} PP_x-CC_x+P_y-C_t+K_x=0, \end{aligned}$$
(5)

where \(K=\frac{\phi _{xxx}}{\phi _x}-\frac{3}{2}\frac{\phi _{xx}^2}{\phi _x^2}\),  \(C=\frac{\phi _t}{\phi _x}\) and \(P=\frac{\phi _y}{\phi _x}\) are Schwarzian variables. It is obviously that Eq. (5) is invariant under the Möbius transformation

$$\begin{aligned} \phi \rightarrow \frac{a_1\phi +b_1}{a_2\phi +b_2},\, a_1a_2 \ne b_1b_2, \end{aligned}$$
(6)

or in other words, Eq. (5) possesses three symmetries \(\sigma _{\phi }=d_1\), \(\sigma _{\phi }=d_2\phi \) and

$$\begin{aligned} \sigma _{\phi }=d_3\phi ^2 \end{aligned}$$
(7)

with arbitrary constants \(d_1,\,d_2\) and \(d_3.\)

Hereby, by substituting (3) and (4) into (2), the following BT is obtained.

Theorem 1

If \(\phi \) is a solution of the Schwartzian equation (5), then

$$\begin{aligned} u= & {} -\, \frac{12\phi _x^3-12\phi _{xx}\phi _x\phi + \phi _x\phi ^2+4\phi _{xxx}\phi ^2}{2\phi _x\phi ^2}\nonumber \\&+\, \frac{3\phi _{xx}^2+\phi _t^2-\phi _y^2}{2\phi _x^2} \end{aligned}$$
(8)

is a solution u of (1).

The interesting fact is that the residue \(u_1\) of expansion (2) expressed by the singular manifold \(\phi \) in Eq. (3) is a nonlocal symmetry of (1), which can be verified by substituting it into the linearized form of Eq. (1)

$$\begin{aligned}&\sigma _{u,tt}-\sigma _{u,xx}-\sigma _{u,yy}-4u_x \sigma _{u,x}-2\sigma _{u}u_{xx}\nonumber \\&\quad -2u\sigma _{u,xx} -\sigma _{u,xxxx}=0, \end{aligned}$$
(9)

with the BT (8). Apparently, the residual symmetry \(\sigma _u=u_1\) generates the finite transformation (2), and it is related to the symmetry of (7) through the linearized equation of (4).

For nonlocal symmetry, the corresponding finite transformation is hardly to be obtained by using Lie’s first theorem. To overcome this difficulty, the practical way is to localize the residual symmetry

$$\begin{aligned} \sigma _u=6\phi _{xx} \end{aligned}$$
(10)

into a Lie point symmetry in an enlarged system by introducing the following four dependent variables

$$\begin{aligned} g\equiv & {} \phi _x,\,m\equiv \phi _t,\,n\equiv \phi _y, \end{aligned}$$
(11)
$$\begin{aligned} h\equiv & {} g_x. \end{aligned}$$
(12)

To find the symmetries of the enlarged system, we have to solve the linearized equations of (1), (5), (11) and (12), i.e.,

$$\begin{aligned}&\sigma _{u,tt}-\sigma _{u,xx}-\sigma _{u,yy}-4u_x\sigma _{u,x}-2\sigma _{u}u_{xx}\nonumber \\&\quad -\, 2u\sigma _{u,xx}-\sigma _{u,xxxx}=0,\nonumber \\&\quad -\, 2\phi _x\phi _{xxxx}\sigma _{\phi ,x}\nonumber \\&\quad -\,\phi _x^2\sigma _{\phi ,xxxx}+2\phi _x\phi _{tt}\sigma _{\phi ,x}+\phi _x^2\sigma _{\phi ,tt}\nonumber \\&\quad -\, 2\phi _x \phi _{yy}\sigma _{\phi ,x}-\phi _x^2\sigma _{\phi ,yy}+\,4\sigma _{\phi ,x}\phi _{xx}\phi _{xxx}\nonumber \\&\quad +\,4\phi _x\sigma _{\phi ,xx}\phi _{xxx}+4\phi _x\phi _{xx}\sigma _{\phi ,xxx}\nonumber \\&\quad -\, 9\phi _{xx}^2\sigma _{\phi ,xx}-\sigma _{\phi ,xx}\phi _t^2 -\,2\phi _{xx}\phi _t\sigma _{\phi ,t}\end{aligned}$$
(13a)
$$\begin{aligned}&\quad +\,\sigma _{\phi ,xx}\phi _y^2+2\phi _{xx}\phi _y \sigma _{\phi ,y}=0, \end{aligned}$$
(13b)
$$\begin{aligned}&\sigma _{\phi ,x}-\sigma _g=0, \end{aligned}$$
(13c)
$$\begin{aligned}&\sigma _{\phi ,y}-\sigma _n=0, \end{aligned}$$
(13d)
$$\begin{aligned}&\sigma _{\phi ,t}-\sigma _m=0, \end{aligned}$$
(13e)
$$\begin{aligned}&\sigma _{g,x}-\sigma _h=0. \end{aligned}$$
(13f)

By the known solution (10), the solutions of (13) can be easily obtained as

$$\begin{aligned} \sigma _{u}= & {} h, \end{aligned}$$
(14a)
$$\begin{aligned} \sigma _{g}= & {} -\frac{1}{3}g\phi ,\end{aligned}$$
(14b)
$$\begin{aligned} \sigma _{m}= & {} -\frac{1}{3}m\phi ,\end{aligned}$$
(14c)
$$\begin{aligned} \sigma _{n}= & {} -\frac{1}{3}n\phi ,\end{aligned}$$
(14d)
$$\begin{aligned} \sigma _h= & {} -\frac{1}{3}(h\phi +g^2),\end{aligned}$$
(14e)
$$\begin{aligned} \sigma _{\phi }= & {} -\frac{1}{6}\phi ^2, \end{aligned}$$
(14f)

if \(d_3=-\frac{1}{6}\) and \(d_1=d_2=0\) is fixed for \(\sigma _{\phi }\). In other words, the residual symmetry (10) is localized to a Lie point symmetry in the enlarged systems (1), (5), (11) and (12) with the symmetry vector

$$\begin{aligned} V= & {} h\partial _{u}-\frac{1}{3}g\phi \partial _{g}-\frac{1}{3}m\phi \partial _{m}\nonumber \\&-\, \frac{1}{3}n\phi \partial _{n}-\frac{1}{3}(h\phi +g^2)\partial _{h} -\frac{1}{6}\phi ^2\partial _{\phi }. \end{aligned}$$
(15)

Equivalently, the generator of the BT (2) is just a special Lie point symmetry of the enlarged system.

By using Lie’s first theorem, the corresponding finite transformation of symmetry (14) can be obtained by solving the following initial value problem

$$\begin{aligned} \frac{\hbox {d}\hat{u}(\epsilon )}{\hbox {d}\epsilon }= & {} \hat{h}(\epsilon ),\,\quad \hat{u}(0)=u,\end{aligned}$$
(16)
$$\begin{aligned} \frac{\hbox {d}\hat{g}(\epsilon )}{\hbox {d}\epsilon }= & {} -\frac{1}{3}\hat{\phi }(\epsilon )\hat{g}(\epsilon ),\,\quad \hat{g}(0)=g,\end{aligned}$$
(17)
$$\begin{aligned} \frac{\hbox {d}\hat{m}(\epsilon )}{\hbox {d}\epsilon }= & {} -\frac{1}{3}\hat{\phi }(\epsilon )\hat{m}(\epsilon ),\,\quad \hat{m}(0)=m,\end{aligned}$$
(18)
$$\begin{aligned} \frac{\hbox {d}\hat{n}(\epsilon )}{\hbox {d}\epsilon }= & {} -\frac{1}{3}\hat{\phi }(\epsilon )\hat{n}(\epsilon ),\,\quad \hat{n}(0)=n,\end{aligned}$$
(19)
$$\begin{aligned} \frac{\hbox {d}\hat{h}(\epsilon )}{\hbox {d}\epsilon }= & {} -\frac{1}{3}(\hat{g}(\epsilon )^2 +\hat{\phi }(\epsilon )\hat{h}(\epsilon )),\,\quad \hat{h}(0)=h,\end{aligned}$$
(20)
$$\begin{aligned} \frac{\hbox {d}\hat{\phi }(\epsilon )}{\hbox {d}\epsilon }= & {} -\frac{\hat{\phi }(\epsilon )^2}{6},\,\quad \hat{\phi }(0)=\phi . \end{aligned}$$
(21)

Solving out these equations leads to the following BT of the enlarged system, which is stated in the following theorem.

Theorem 2

If \(\{u,g,m,n,h,\phi \}\) is a solution of the enlarged system (1), (5), (11) and (12), then \(\{\hat{u},\hat{g},\hat{m},\hat{n},\hat{h},\hat{\phi }\}\) with

$$\begin{aligned} \hat{u}= & {} u+\frac{6h\epsilon }{\epsilon \phi +6}-\frac{6\epsilon ^2g^2}{(\epsilon \phi +6)^2}, \end{aligned}$$
(22a)
$$\begin{aligned} \hat{g}= & {} \frac{36g}{(\epsilon \phi +6)^2},\end{aligned}$$
(22b)
$$\begin{aligned} \hat{m}= & {} \frac{36m}{(\epsilon \phi +6)^2},\end{aligned}$$
(22c)
$$\begin{aligned} \hat{n}= & {} \frac{36n}{(\epsilon \phi +6)^2},\end{aligned}$$
(22d)
$$\begin{aligned} \hat{h}= & {} \frac{36h}{(\epsilon \phi +6)^2}-\frac{72\epsilon g^2}{(\epsilon \phi +6)^3},\end{aligned}$$
(22e)
$$\begin{aligned} \hat{\phi }= & {} \frac{6\phi }{\epsilon \phi +6}, \end{aligned}$$
(22f)

is also a solution of the system with \(\epsilon \) being an arbitrary group parameter.

3 New symmetry reduction solutions

To seek the symmetry reduction solutions of the (2 \(+\) 1)-dimensional Boussinesq equation related to the residual symmetry, we first investigate Lie point symmetry of the enlarged system in the form

$$\begin{aligned} V= & {} X\frac{\partial }{\partial x}+Y\frac{\partial }{\partial y}+T\frac{\partial }{\partial t}+U\frac{\partial }{\partial u}\nonumber \\&+\,G\frac{\partial }{\partial g}+M\frac{\partial }{\partial m}+N\frac{\partial }{\partial n}+H\frac{\partial }{\partial h}+\Phi \frac{\partial }{\partial \phi }.\nonumber \\ \end{aligned}$$
(23)

In other words, the enlarged systems (1), (5), (11) and (12) are invariant under the transformation

$$\begin{aligned}&\{x,y,t,u,g,m,n,h,\phi \}\nonumber \\&\quad \rightarrow \{x+\epsilon X,y+\epsilon Y,t+\epsilon T,u+\epsilon U,g+\epsilon G,m\nonumber \\&\quad +\, \epsilon M,n+\epsilon N,h+\epsilon H,\phi +\epsilon \Phi \} \end{aligned}$$
(24)

with the infinitesimal parameter \(\epsilon \). Equivalently, the symmetry in form (23) can be written as a function form as

$$\begin{aligned} \sigma _{u}= & {} Xu_{x}+Yu_y+Tu_{t}-U, \end{aligned}$$
(25a)
$$\begin{aligned} \sigma _{g}= & {} Xg_{x}+Yg_y+Tg_{t}-G, \end{aligned}$$
(25b)
$$\begin{aligned} \sigma _{m}= & {} Xm_{x}+Ym_y+Tm_{t}-M, \end{aligned}$$
(25c)
$$\begin{aligned} \sigma _{n}= & {} Xn_{x}+Yn_y+Tn_{t}-N, \end{aligned}$$
(25d)
$$\begin{aligned} \sigma _h= & {} Xh_{x}+Yh_y+Th_{t}-H, \end{aligned}$$
(25e)
$$\begin{aligned} \sigma _{\phi }= & {} X\phi _{x}+Y\phi _y+T\phi _{t}-\Phi . \end{aligned}$$
(25f)

Substituting (25) into (13) and vanishing all the coefficients of the independent partial derivatives of variables u, g, m, n, h and \(\phi \), a system of overdetermined linear equations for \(X, Y, T, U, G, M, N, H, \Phi \) are obtained. Calculated by computer, the desired solutions are

$$\begin{aligned} X= & {} \frac{c_1}{2}x+c_4,\,Y=c_1y+c_3,\, T= c_1t+c_2,\nonumber \\ U= & {} -c_1u+c_5h-\frac{c_1}{2},\,G = -\frac{c_5}{3}g\phi -\frac{c_1}{2}g+gc_6,\nonumber \\ H= & {} -\frac{c_5}{3}h\phi -\frac{c_5}{3}g^2-(c_1-c_6)h,\nonumber \\ M= & {} -\frac{c_5}{3}m\phi -(c_1-c_6)m,\nonumber \\ N= & {} -\frac{c_5}{3}n\phi -(c_1-c_6)n,\nonumber \\ \Phi= & {} -\frac{c_5}{6}\phi ^2+c_6\phi +c_7, \end{aligned}$$
(26)

with \(c_1, c_2, c_3, c_4, c_5, c_6, c_7\) being arbitrary constants. It is interesting that the symmetry of (15) is just a special form of (26) by setting \(c_1=c_2=c_3=c_4=c_6=c_7=0\) and \(c_5=1\).

Substituting (26) into (25), one obtains

$$\begin{aligned} \sigma _{u}= & {} \left( \frac{c_1}{2}x+c_4\right) u_x+(c_1y+c_3)u_y+(c_1t+c_2)u_t\nonumber \\&+\,c_1u-c_5h+\frac{c_1}{2},\nonumber \\ \sigma _{g}= & {} \left( \frac{c_1}{2}x+c_4\right) g_x+(c_1y+c_3)g_y+(c_1t+c_2)g_t\nonumber \\&+\,\frac{c_5}{3}g\phi +\frac{c_1}{2}g-gc_6,\nonumber \\ \sigma _{m}= & {} \left( \frac{c_1}{2}x+c_4\right) m_x+(c_1y+c_3)m_y+(c_1t+c_2)m_t\nonumber \\&+\,\frac{c_5}{3}m\phi +(c_1-c_6)m,\nonumber \\ \sigma _{n}= & {} \left( \frac{c_1}{2}x+c_4\right) n_x+(c_1y+c_3)n_y+(c_1t+c_2)n_t\nonumber \\&+\,\frac{c_5}{3}n\phi +(c_1-c_6)n,\nonumber \\ \sigma _h= & {} \left( \frac{c_1}{2}x+c_4\right) h_x+(c_1y+c_3)h_y+(c_1t+c_2)h_t\nonumber \\&+\,\frac{c_5}{3}h\phi +\frac{c_5}{3}g^2+(c_1-c_6)h,\nonumber \\ \sigma _{\phi }= & {} \left( \frac{c_1}{2}x+c_4\right) \phi _x+(c_1y+c_3)\phi _y+(c_1t+c_2)\phi _t \nonumber \\&+\,\frac{c_5}{6}\phi ^2-c_6\phi -c_7. \end{aligned}$$
(27)

The group invariant solutions of the enlarged system can be obtained by solving (27) under the symmetry constraints \(\sigma _u=\sigma _g=\sigma _m=\sigma _n=\sigma _h=\sigma _{\phi }=0\), alternatively, solving the corresponding characteristic equation

$$\begin{aligned} \frac{\hbox {d}x}{\frac{c_1}{2}x+c_4}= & {} \frac{\hbox {d}y}{c_1y+c_3}=\frac{\hbox {d}t}{c_1t+c_2}\nonumber \\= & {} \frac{\hbox {d}u}{-c_1u+c_5h-\frac{c_1}{2}}\nonumber \\= & {} \frac{\hbox {d}g}{-\frac{c_5}{3}g\phi -\frac{c_1}{2}g+gc_6}\nonumber \\= & {} \frac{\hbox {d}m}{-\frac{c_5}{3}m\phi -(c_1-c_6)m}\nonumber \\= & {} \frac{\hbox {d}n}{-\frac{c_5}{3}n\phi -(c_1-c_6)n} \nonumber \\= & {} \frac{\hbox {d}h}{-\frac{c_5}{3}h\phi -\frac{c_5}{3}g^2-(c_1-c_6)h} \nonumber \\= & {} \frac{\hbox {d}\phi }{-\frac{c_5}{6}\phi ^2+c_6\phi +c_7}. \end{aligned}$$
(28)

Two subcases of symmetry reductions, without loss of generality, are considered in the following.

Case 1 \(c_6=0\) and \(c_i\ne 0\) \((i=1,\,2,\,3,\,4,\,5,\,7)\).

In this case, by solving Eq. (28), the symmetry reduction solutions of the enlarged (2 \(+\) 1)-dimensional Boussinesq system are

$$\begin{aligned} \phi= & {} \frac{\sqrt{6c_7c_5}\tanh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{6c_1}\right) }{c_5},\nonumber \\ \Delta= & {} \sqrt{c_1t+c_2},\end{aligned}$$
(29)
$$\begin{aligned} g= & {} -\frac{2G}{\Delta [\cosh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1}\right) +1]},\end{aligned}$$
(30)
$$\begin{aligned} m= & {} -\frac{2M}{\Delta ^2[\cosh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1} \right) +1]},\end{aligned}$$
(31)
$$\begin{aligned} n= & {} -\frac{2N}{\Delta ^2[\cosh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1}\right) +1]},\end{aligned}$$
(32)
$$\begin{aligned} h= & {} -\frac{2c_5\sqrt{6}\tanh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{6c_1} \right) G^2+6\sqrt{c_7c_5}H}{3\sqrt{c_7c_5}\Delta ^2[\cosh \left( \frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1} \right) +1]}, \end{aligned}$$
(33)
$$\begin{aligned} u= & {} \frac{U}{\Delta ^2}+\frac{2\sqrt{6c_7c_5}H}{\Delta ^2c_7 \left( e^{\frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1}}+1 \right) }\nonumber \\&+\frac{4c_5e^{\frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1}}G^2}{\Delta ^2c_7 \left( e^{\frac{\sqrt{6c_7c_5}(c_1\Phi +\ln \Delta ^2)}{3c_1}}+1\right) ^2}\nonumber \\&+\frac{c_2-\Delta ^2}{2\Delta ^2}, \end{aligned}$$
(34)

where \(U,\, G,\,M,\,N,\, H\) and \(\Phi \) are invariant functions of \(\xi =\frac{c_1x+2c_4}{c_1\sqrt{c_1t+c_2}}\) and \(\eta =\frac{c_1y+c_3}{c_1(c_1t+c_2)}\).

Substituting Eqs.(29)–(34) into the enlarged systems (1), (5), (11), and (12) yields

$$\begin{aligned} G= & {} -\,c_7\Phi _{\xi }, \end{aligned}$$
(35)
$$\begin{aligned} M= & {} c_1c_7 \eta \Phi _{\eta }+\frac{c_1c_7}{2}\xi \Phi _{\xi }-c_7, \end{aligned}$$
(36)
$$\begin{aligned} N= & {} -\,c_7\Phi _{\eta } \end{aligned}$$
(37)
$$\begin{aligned} H= & {} -\,c_7\Phi _{\xi \xi }, \end{aligned}$$
(38)
$$\begin{aligned} U= & {} \frac{1}{24\Phi _{\xi }^2}[12(c_1^2\eta ^2-1)\Phi _{\eta }^2 \nonumber \\&+\,12(c_1^2\Phi _{\xi }\eta \xi -2c_1\eta )\Phi _{\eta }-8c_7c_5\Phi _{\xi }^4\nonumber \\&+\,3(c_1^2\xi ^2 +8\sqrt{6c_7c_5}\Phi _{\xi \xi }-4c_2)\Phi _{\xi }^2\nonumber \\&-\,12(c_1\xi +4\Phi _{\xi \xi \xi })\Phi _{\xi } +36\Phi _{\xi \xi }^2+12], \end{aligned}$$
(39)

where \(\Phi \) satisfies the following reduction equation

$$\begin{aligned}&\Phi _{\xi \xi \xi \xi }\Phi _{\xi }^2 -4\Phi _{\xi \xi }\Phi _{\xi \xi \xi }\Phi _{\xi }\nonumber \\&\quad +\,3\Phi _{\xi \xi }^3 +\left[ -\frac{2}{3}c_7c_5\Phi _{\xi }^4+c_1\xi (c_1\Phi _{\eta }\eta -1)\Phi _{\xi }\right. \nonumber \\&\left. \quad + \, 1+(c_1^2\eta ^2-1)\Phi _{\eta }^2\right. \nonumber \\&\left. \quad -\, 2c_1\Phi _{\eta }\eta \right] \Phi _{\xi \xi } -2\left[ \frac{1}{2}(c_1^2\eta ^2-1)\Phi _{\eta \eta }\right. \nonumber \\&\left. \quad +\, c_1\left( \frac{1}{2}\Phi _{\xi \eta }c_1\xi \eta +c_1\Phi _{\eta }\eta \right. \right. \nonumber \\&\left. \left. \quad +\, \frac{3}{8}c_1\Phi _{\xi }\xi -\frac{1}{2}\right) \right] \Phi _{\xi }^2=0. \end{aligned}$$
(40)

It is natural that once \(\Phi \) is solved out from (40), the explicit solutions of the (2 \(+\) 1)-dimensional Boussinesq equation (1) would be immediately obtained by substituting \(U,\,H,\,G\) and \(\Phi \) into Eq. (34) with Eqs. (35), (38) and (39).

Case 2 \(c_i\ne 0\) \((\hbox {i}=2,\,3,\,4,\,5,\,6,\,7)\) and \(c_1=0\).

In this case, the group invariant solutions of the enlarged system can be obtained with the same logic of case 1, which read

$$\begin{aligned} \phi= & {} \frac{\tanh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) \sqrt{3\Delta _1}+3c_6}{c_5},\nonumber \\ \Delta _1= & {} 2c_5c_7+3c_6^2\end{aligned}$$
(41)
$$\begin{aligned} g= & {} -\, \frac{2g'}{\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{3c_2}\right) +1},\end{aligned}$$
(42)
$$\begin{aligned} m= & {} -\, \frac{2m'}{\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{3c_2} \right) +1},\end{aligned}$$
(43)
$$\begin{aligned} n= & {} -\, \frac{2n'}{\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{3c_2} \right) +1},\end{aligned}$$
(44)
$$\begin{aligned} h= & {} -\,\frac{\sqrt{3}\left( 2c_5g'^2\sinh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) +h'\sqrt{3\Delta _1}\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) \right) }{3\sqrt{\Delta _1}\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) ^3},\end{aligned}$$
(45)
$$\begin{aligned} u= & {} u'-\frac{2c_5\sqrt{3}\sinh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) h'}{\sqrt{\Delta _1}\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) }\nonumber \\&-\frac{2c_5g'^2 \left( \cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2} \right) ^2-1 \right) }{\Delta _1\cosh \left( \frac{\sqrt{3\Delta _1}(\phi '+t)}{6c_2}\right) ^2}, \end{aligned}$$
(46)

where \(u', g',m',n', h', \phi '\) are invariant functions of variables \(x'=\frac{c_2x-c_4t}{c_2}\) and \(y'=\frac{c_2y-c_3t}{c_2}\).

Substituting Eqs. (41), (44), (45) and (46) into the enlarged (2 \(+\) 1)-dimensional Boussinesq system (1), (5), (11) and (12) yields

$$\begin{aligned} g'= & {} - \, \frac{\phi '_{x'}\Delta _1}{2c_2c_5}, \end{aligned}$$
(47)
$$\begin{aligned} m'= & {} -\, \frac{\Delta _1(-c_3\phi '_{y'}-c_4\phi '_{x'}+c_2)}{2c_2^2c_5}, \end{aligned}$$
(48)
$$\begin{aligned} n'= & {} -\, \frac{\phi '_{y'}\Delta _1}{2c_2c_5}, \end{aligned}$$
(49)
$$\begin{aligned} h'= & {} -\, \frac{\phi '_{x'x'}\Delta _1}{2c_2c_5}, \end{aligned}$$
(50)
$$\begin{aligned} u'= & {} -\, \frac{1}{6c_2^2\phi _{x'}'^2}[3(c_2^2-c_3^2)\phi _{y'}'^2-6c_3(c_4\phi _{x'}'-c_2)\phi _{y'}'\nonumber \\&-\, 2\Delta _1\phi _{x'}'^4+3(c_2^2-c_4^2)\phi _{x'}'^2\nonumber \\&+\, 6c_2(2c_2\phi _{x'x'x'}'+c_4)\phi _{x'}'-9c_2^2\phi _{x'x'}'^2-3c_2^2],\nonumber \\ \end{aligned}$$
(51)

where \(\phi '\) satisfies the following reduction equation

$$\begin{aligned}&\left( c_3^2-c_2^2 \right) \phi _{x'x'}'\phi _{y'}'^2 +2 c_3 \left( \phi _{x'x'}'c_4\phi _{x'}' -\phi _{x'x'}'c_2 \right) \phi _{y'}'\nonumber \\&\quad -\, \frac{1}{3}\phi _{x'x'}'\Delta _1\phi _{x'}'^4\nonumber \\&\quad +\, [(c_2^2-c_3^2)\phi _{y'y'}' +c_2^2\phi _{x'x'x'x'}' -2\phi _{x'y'}'c_3c_4]\phi _{x'}'^2\nonumber \\&\quad -\, 2 c_2(2c_2\phi _{x'x'x'}' +c_4)\phi _{x'x'}'\phi _{x'}'\nonumber \\&\quad +\, 3c_2^2\phi _{x'x'}'^3+\phi _{x'x'}'c_2^2=0. \end{aligned}$$
(52)

Similarly to case 1, when \(\phi '\) is solved out by Eq. (52), the solutions of the (2 \(+\) 1)-dimensional Boussinesq equation can be obtained by substituting it into (46) with Eqs. (47), (50) and (51).

From the symmetry reduction Eqs. (40) and (52), one can obtain various nonlinear wave solutions, so the exact solutions of the (2 \(+\) 1)-dimensional Boussinesq equation given by Eqs. (34) and (46) represent the complicated interaction solutions between solitons and background nonlinear waves.

To give out a concrete example, we consider the special solution of Eq. (52) in the form

$$\begin{aligned} \phi '= k_1'\xi +l_1'\eta +c'E_{\pi }(sn(l_2'\eta +k_2'\xi , N'), M', N'),\nonumber \\ \end{aligned}$$
(53)

with arbitrary constants \(k_1',\, l_1',\, c',\, l_2',\, k_2',\, M',\, N'\). Here, \(E_{\pi }\) is the third type of incomplete elliptic integral, while \(sn(l_2'\eta +k_2'\xi , N')\) is a Jacobi elliptic function. Now substitute Eq. (53) into Eq. (52) and vanish different powers of \(sn(l_2'\eta +k_2'\xi , N')\), we get the following conditions

$$\begin{aligned} l_1'= & {} \frac{1}{6c_3^3(M'-1)c'}\left[ 6c_4(c_7c_5+\frac{3}{2}c_6^2)(M'-1)c'k_1^5\right. \nonumber \\&\left. +\, \left[ 12 c_4\left( M'-\frac{3}{2} \right) \left( c_7c_5+\frac{3}{2}c_6^2\right) k_2c'^2\right. \right. \nonumber \\&\left. \left. -\, 2c_3\left( c_7c_5+\frac{3}{2}c_6^2\right) (M'-1)c' \right. \right. \nonumber \\&\left. \left. -\, 36c_3^2c_4k_2(M'-1)^2\right] k_1'^4\right. \nonumber \\&\left. -\, 36\left[ -\left( \frac{1}{6}(M'-3)\right) \left( c_7c_5+\frac{3}{2}c_6^2\right) c'^2\right. \right. \nonumber \\&\left. \left. +\, c_3^2(M'-1)(M'-2)\right] c_4k_2'^2c'k_1'^3\right. \nonumber \\&\left. -\, \left[ 12\frac{1}{2}c_4\left( c_7c_5+\frac{3}{2}c_6^2\right) k'_2c'^3\right. \right. \nonumber \\&\left. \left. -\, \frac{1}{6}(M'-3)c_3\left( c_7c_5+\frac{3}{2}c_6^2 \right) c'^2\right. \right. \nonumber \\&\left. \left. -\, 3c_3^2c_4k'_2(M'-1)c'\right. \right. \nonumber \\&\left. \left. +\, c_3^3(M'-1) (M'-2)\right] k_2'^2c'k_1'^2\right. \nonumber \\&\left. +\, 24\left[ -\frac{1}{6}(c_7c_5+\frac{3}{2}c_6^2)k_2'^3c'^3+c_3^2k_2'^3(M'-1)c'\right. \right. \nonumber \\&\left. \left. -\, \frac{1}{8}c_4c_3(M'-1)\right] c_3c'k'_1+3(M'-1)c_3^3c'\right] , \nonumber \\ \end{aligned}$$
(54)
$$\begin{aligned} l_2'= & {} \frac{k_2'}{c_3^3(M'-1)c'}\left[ 4\left( \left( \frac{1}{12}(-3c_4k'_1+c_3)\right) \left( c_7c_5+\frac{3}{2}c_6^2\right) k_2'^3c'^4\right. \right. \nonumber \\&\left. \left. -\, \frac{1}{6}k'_1(M'-3)\left( c_7c_5+\frac{3}{2}c_6^2\right) k_2'^2\left( -\frac{3}{2}c_4k'_1+c_3\right) c^3\right. \right. \nonumber \\&\left. \left. -\, \frac{1}{2}k'_2\left( -\left( M'-\frac{3}{2}\right) c_4\left( c_7c_5+\frac{3}{2}c_6^2\right) k_1'^3\right. \right. \right. \nonumber \\&\left. \left. \left. +\, c_3(M'-\frac{3}{2}) \left( c_7c_5+\frac{3}{2}c_6^2\right) k_1'^2\right. \right. \right. \nonumber \\&\left. \left. \left. -\, 3c_3^2c_4k_2'^2(M'-1)k'_1+c_3^3k_2'^2(M'-1)\right) c'^2\right. \right. \nonumber \\&\left. \left. +\, \left( \frac{1}{4}c_4\left( c_7c_5+\frac{3}{2}c_6^2\right) k_1'^4\right. \right. \right. \nonumber \\&\left. \left. \left. -\, \frac{1}{3}c_3\left( c_7c_5+\frac{3}{2}c_6^2\right) k_1'^3\right. \right. \right. \nonumber \\&\left. \left. \left. -\, \frac{3}{2}c_3^2c_4k_2'^2(M'-2)k_1'^2+c_3^3k_2'^2(M'-2)k'_1\right. \right. \right. \nonumber \\&\left. \left. \left. -\, \frac{1}{8}c_3^2c_4\right) (M'-1)c'\right. \right. \nonumber \\&\left. \left. +\, \frac{3}{2}c_3^2k_1'^2k'_2(M'-1)^2(-c_4k'_1+c_3)\right) \right] , \end{aligned}$$
(55)

and

$$\begin{aligned} N'^2=\frac{M' \left( -2c_5c_7c'^2-3c_6^2c'^2+12c_3^2M'-12c_3^2 \right) }{12c_3^3(M'-1)}.\nonumber \\ \end{aligned}$$
(56)

Substituting Eq. (53) into Eq. (46) with Eqs. (47), (50) and (51) under conditions (54), (55), (56), we get a special interaction solution between solitons and Jacobi elliptic waves.

4 CRE integrability and new interaction solutions

In this section, we further explore the consistent Riccati expansion (CRE) integrability of the (2 \(+\) 1)-dimensional Boussinesq equation (1). By leading order analysis, the Riccati expansion solution is

$$\begin{aligned} u = v_0+v_1R(w)+v_2R(w)^2, \,(w = w(x,y, t)),\nonumber \\ \end{aligned}$$
(57)

where \(v_0, v_1, v_2\) are functions of (x, y, t) to be determined later and R(w) satisfies the Riccati equation

$$\begin{aligned} R_w=a_0+a_1R+a_2R^2. \end{aligned}$$
(58)

Substituting Eq. (57) with Eq. (58) into Eq. (1) and vanishing all the coefficients of different powers of R(w), we get

$$\begin{aligned} v_2= & {} -\, 6w_x^2a_2^2, \, v_1 = -\, 6a_2(w_x^2a_1+w_{xx}), \end{aligned}$$
(59)
$$\begin{aligned} v_0= & {} -\, \frac{2w_{xxx}}{w_x}+\, \frac{3w_{xx}^2}{2w_x^2}-3a_1w_{xx}+\frac{w_t^2}{2w_x^2}\nonumber \\&-\, \frac{1}{2}-\left( 4a_0a_2+\frac{1}{2}a_1^2\right) w_x^2-\frac{w_y^2}{2w_x^2}, \end{aligned}$$
(60)

leaving four equations for only one dependent variable w. Fortunately, it can be verified that these equations are consistent with each other and the (2 \(+\) 1)-dimensional Boussinesq equation is CRE integrable in this sense [16]. Thus, we obtain the final equation for w

$$\begin{aligned}&\delta w_{xx}w_x-C'_xC'+P'_xP'-C'_t+K'_x+P'_y=0,\nonumber \\&\quad (\delta =4a_0a_2-a_1^2) \end{aligned}$$
(61)

with \(K'=\frac{w_{xxx}}{w_x}-\frac{3}{2}\frac{w_{xx}^2}{w_x^2}\), \(C'=\frac{w_t}{w_x}\) and \(P'=\frac{w_y}{w_x}\).

From the property that these equations derived by vanishing different powers of R(w) in the expansion are consistent with each other, we conclude that the (2 \(+\) 1)-dimensional Boussinesq equation (1) really has CRE integrability and expansion (57) is a CRE expansion. Naturally, the following theorem is ready:

Theorem 3

If w is a solution of

$$\begin{aligned} \delta w_{xx}w_x-C'_xC'+P'_xP'-C'_t+K'_x+P'_y=0 \end{aligned}$$
(62)

then

$$\begin{aligned} u= & {} -6a_2^2w_x^2R(w)^2-6a_2\left( w_x^2a_1+w_{xx}\right) R(w)\nonumber \\&\quad -\, \frac{2w_{xxx}}{w_x}+\frac{3w_{xx}^2}{2w_x^2}\,-\, 3a_1w_{xx}+\frac{w_t^2}{2w_x^2}\nonumber \\&\quad -\, \frac{1}{2}+\left( \frac{1}{2}\delta -6a_0a_2\right) w_x^2 \,-\, \frac{w_y^2}{2w_x^2} \end{aligned}$$
(63)

is a solution of Eq.(1) where \(R=R(w)\) is an arbitrary solution of the Riccati equation (58).

When the Riccati equation (58) takes the special solution \(R = \tanh (w)\), the Riccati expansion (57) becomes

$$\begin{aligned} u = u'_2\tanh (w)^2+u'_1\tanh (w)+u'_0. \end{aligned}$$
(64)

It is natural that any CRE integrable system must also be CTE (consistent tanh expansion) integrable. By using the tanh expansion (64) of the (2 \(+\) 1)-dimensional Boussinesq equation, one could obtain some important explicit solutions, especially the interactions solutions between soliton and nonlinear periodic waves. To this end, we first provide the following nonauto BT.

Theorem 4

If w satisfies the following equation

$$\begin{aligned} 4 w_{xx}w_x+C'C'_x-PP_x'+C'_t-K_x'-P'_y=0 \end{aligned}$$
(65)

then

$$\begin{aligned} u= & {} -6w_x^2\tanh (w)^2+6w_{xx}\tanh (w)\nonumber \\&\quad -\, \frac{2w_{xxx}}{w_x}+\frac{3w_{xx}^2}{2w_x^2}\nonumber \\&\quad +\, \frac{w_t^2}{2w_x^2}-\frac{1}{2}+4w_x^2-\frac{w_y^2}{2w_x^2} \end{aligned}$$
(66)

is a solution of Eq. (1).

To give out some solutions explicitly, we change w to the form

$$\begin{aligned} w = k_1x+l_1y+\omega _1t +g, \end{aligned}$$
(67)

with arbitrary constants \(k_1,\,l_1,\,\omega _1\) and arbitrary function g. By using Theorem 4, we could obtain nontrivial solutions of the (2 \(+\) 1)-dimensional Boussinesq equation from trivial solutions of (65) with Eq. (67). In the following, we give some concrete examples.

Case 1 In Eq. (65), we take a trivial seed solution

$$\begin{aligned} w=kx+ly+\omega t+d, \end{aligned}$$
(68)

with \(k,\,l,\,\omega ,\, d\) being arbitrary constants. By substituting Eq. (68) into Theorem 4, we have the following exact solution for the (2 \(+\) 1)-dimensional Boussinesq equation (1)

$$\begin{aligned} u= & {} -6k^2\tanh (kx+ly+\omega t+d)^2\nonumber \\&+\frac{8k^4-k^2-l^2+\omega ^2}{2 k^2}. \end{aligned}$$
(69)

Case 2 We consider a special solution of (65) in the form

$$\begin{aligned} w= & {} k_1x+l_1y+\omega _1t+W(X),\nonumber \\ X= & {} k_2x+l_2y+\omega _2t, \end{aligned}$$
(70)

with arbitrary constants \(k_1,\, l_1, \, \omega _1,\, k_2,\, l_2,\, \omega _2.\) Substituting (70) into (65), we find that \(W_1(X)\equiv W(X)_X\) satisfies the following elliptic function equation:

$$\begin{aligned} W_{1X}^2 = C_0+C_1W_1+C_2W_1^2+C_3W_1^3+C_4W_1^4 \end{aligned}$$
(71)

with

$$\begin{aligned} {C_0}= & {} \frac{2C_1k_1k_2^5-C_2k_1^2k_2^4+4k_1^4k_2^2-k_1^2l_2^2 +k_1^2\omega _2^2+k_2^2l_1^2-k_2^2\omega _1^2}{3k_2^6},\nonumber \\ C_3= & {} -\frac{C_1k_2^5-2C_2k_1k_2^4-16k_1^3k_2^2+2k_1l_2^2-2k_1\omega _2^2 -2k_2l_1l_2+2k_2\omega _1\omega _2}{3k_1^2k_2^3},\nonumber \\ C_4= & {} 4, \end{aligned}$$
(72)

and arbitrary constants \(C_1\) and \(C_2\). Then the solution of the (2 \(+\) 1)-dimensional Boussinesq equation has the form

$$\begin{aligned} u= & {} -\, 6(W_1k_2+k_1)^2\tanh (k_1x+l_1y+\omega _1t+W)^2\nonumber \\&\quad +\, 6W_{1,X}k_2^2\tanh (k_1x+l_1y+\omega _1t+W)\nonumber \\&\quad +\, \frac{1}{2(W_1k_2+k_1)^2}\big [8W_1^4k_2^4\nonumber \\&\quad + \, 32W_1^3k_1k_2^3+(48k_1^2k_2^2-k_2^2-l_2^2+\omega _2^2)W_1^2\nonumber \\&\quad - \, \left( 4W_{1,XX}k_2^4-32k_1^3k_2+2k_1k_2\right. \nonumber \\&\quad \left. +\, 2l_1l_2-2\omega _1\omega _2\right) W_1+3W_{1,X}^2k_2^4\nonumber \\&\quad -\, 4W_{1,XX}k_1k_2^3+8k_1^4-k_1^2-l_1^2+\omega _1^2\big ]. \end{aligned}$$
(73)

From the form of (73), it is obvious that this solution describes solitons interacted with periodic waves which can be derived from (71). To illustrate this concretely, we consider the cnoidal solution of (71) as

$$\begin{aligned} W_1=\mu _0+\mu _1 sn(M''X,N''), \end{aligned}$$
(74)

with arbitrary constants \(\mu _0,\,\mu _1,\,M''\) and \(N''\). Substituting Eq. (74) with Eq. (72) into Eq. (71) and setting the coefficients of different powers of \(sn(M''X,N'')\) to zero, we get

$$\begin{aligned} {C_1}= & {} 2M^2N^2\mu _0+2M^2\mu _0-16\mu _0^3,\nonumber \\ C_2= & {} -\, M^2N^2-M^2+24\mu _0^2,\nonumber \\ \omega _1^2= & {} -\, \frac{1}{4k_2}(3M^4N^2k2^5-12M^2N^2k_2^5\mu _0^2\nonumber \\&\quad -\, 20M^2N^2k_1k_2^4\mu _0-8M^2N^2k_1^2k_2^3 \end{aligned}$$
(75)
$$\begin{aligned}&\quad -\, 12M^2k_2^5\mu _0^2+48k_2^5\mu _0^4-20M^2k_1k_2^4\mu _0\nonumber \\&\quad +\,160k_1k_2^4\mu _0^3-8M^2k_1^2k_2^3+192k_1^2k_2^3\mu _0^2 \end{aligned}$$
(76)
$$\begin{aligned}&\quad +\, 96k_1^3k_2^2\mu _0+16k_1^4k_2+4k_1l_1l_2\nonumber \\&\quad -\, 4k_1\omega _1\omega _2-4k_2l_1^2), \end{aligned}$$
(77)
$$\begin{aligned} \omega _2^2= & {} \frac{1}{k_1}(M^2N^2k_2^5\mu _0+M^2N^2k_1k_2^4+M^2k_2^5\mu _0\nonumber \\&\quad -\, 8k_2^5\mu _0^3+M^2k_1k_2^4-24k_1k_2^4\mu _0^2\nonumber \\&\quad -\, 24k_1^2k_2^3\mu _0-8k_1^3k_2^2+k_1l_2^2\nonumber \\&\quad -\, k_2l_1l_2+k_2\omega _1\omega _2),\nonumber \\ \mu _1= & {} \frac{MN}{2}. \end{aligned}$$
(78)

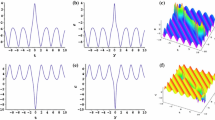
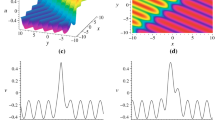
Figures 1, 2 and 3 display the interesting interaction structure between solitons and cnoidal periodic waves in different dimensions. It is shown from Figs. 1b and 3b that a solitary wave propagates on a cnoidal background wave, while Fig. 2b indicates that this interaction is elastic with nonzero phase shifts. For Figs. 1a, c, 2a, c, and 3a, c, respectively, we can give similar conclusions. In consideration of plentiful interacting processes between solitary waves and periodic waves in nature, these interaction solutions can be used to explain related phenomenons.

Fig. 1
figure 1

The soliton–cnoidal wave interaction solution of the (2 \(+\) 1)-dimensional Boussinesq equation given by (73) with (74). The parameters are fixed as \(M'' = 1, N'' = \frac{1}{2}, k_2 = 1, k_1 = \frac{1}{4}, l_1 = 1, l_2 = 1, \mu _0 = \frac{1}{6}, C_1 =\frac{37}{108}, C_2 = -\frac{7}{12}, \omega _2 = \frac{349}{10332}\sqrt{861}, \omega _1 = \frac{499}{13776}\sqrt{861}, C_0 =\frac{5}{162}, C_3 = -\frac{8}{3}, \mu _1 =\frac{1}{4}\): a \(\hbox {t}=0\); b \(\hbox {x}=0\); c \(\hbox {y}=0\)

Full size image
Fig. 2
figure 2

The density plot of interaction solution which is given the same as in Fig. 1 as well as the same parameters fixed: a \(\hbox {t}=0\); b \(\hbox {y}=0\); c \(\hbox {x}=0\)

Full size image
Fig. 3
figure 3

The soliton–cnoidal wave interaction solution which is given the same as in Fig. 1 as well as the same parameters fixed: a \(\hbox {y}=0\), \(\hbox {t}=0\); b \(x=0\), \(\hbox {t}=0\); c \(\hbox {x}=0\), \(\hbox {y}=0\)

Full size image

5 Conclusion and discussion

In summary, the (2 \(+\) 1)-dimensional Boussinesq equation is studied by using residual symmetry reduction method and CRE method, respectively. By applying localization procedure, the residual symmetry is transformed into a Lie point symmetry in a new enlarged system and then the corresponding finite transformation is obtained by solving initial value problem. New interaction solutions of the (2 \(+\) 1)-dimensional Boussinesq equation are obtained by using standard Lie symmetry method, and a concrete example is displayed. Furthermore, the (2 \(+\) 1)-dimensional Boussinesq equation is found to have CRE integrability, and some new BTs are given from this property, from which new interaction solutions are constructed. The concrete interaction solution between soliton and cnoidal waves is explicitly given.

There exist some other methods to investigate interaction solutions between solitons and nonlinear waves. For example, in Ref. [7], by using double commutation method and the inverse scattering transform, the authors investigated soliton solutions of the Toda hierarchy on a quasi-periodic finite-gap background; in Ref. [8], for Sine–Gordon equation, the solitons moving on a cnoidal wave background are obtained by using Darboux transformation method. Compared to these traditional methods, the nonlocal symmetry reduction method and CRE method applied here are more easier to be carried out for more integrable nonlinear systems. Moreover, from different periodic wave solutions of symmetry reduction equations [see, e.g., Eqs. (40), (52)] or CRE Eq. (65), we could easily construct more abundant types of interaction solutions, which could be used to explain related phenomena in nature.

Compared with each other the two kinds of interaction solutions which are derived from symmetry reduction method and CRE method, it is obvious that the former one is more complicated. It needs to investigate the detailed relation between these methods in analyzing relevant physical phenomena in the future.