Computational Modelling and Analysis of Effect of Viscoelastic Materials on Damping and Vibrational Behaviors of Composite Structures—An Extensive Review

Abstract

This article reported an extensive review of computational modelling and analysis on damping and vibrational behaviors of viscoelastic structures, including experimental techniques. viscoelastic materials have emerged as an effective technology for enhancing damping characteristics in composite structures because of their ability to damp vibration and the ability to conserve the geometry of the material after deformation. In structural design viscoelastic material is never employed alone, it is always adhered to the thin-walled structure to form a damping layer of different structural configurations such as sandwich structure configurations and reinforced configurations. It is worth mentioning that viscoelastic materials are quite frequency-dependent meaning that the vibrational properties keep varying with the excitation frequency, accordingly, yielding complex natural frequencies of vibration. This paper provides a primary discussion on the basic forming principles of linear viscoelastic material providing comparisons of different viscoelastic material mathematical models, and applications of viscoelastic material including their effects on composite structure damping and vibrational behaviors. Moreover, different computational methods for dynamic behaviors of viscoelastic sandwich structures including analytical method, finite element method, and mixed method were assessed to provide insights into the limitations of each approach. The drawbacks of each calculation theory for various traditional and recent configurations are systematically presented in engineering structures containing viscoelastic followed by a detailed description and comparison of different modeling methods, their applicability, and their respective comparisons.

1 Introduction

The viscoelastic (VE) material has been extensively used as an efficient vibration suppression technology that can be applied to a variety of applications like electronics [1], automotive [2], aerospace [3], marine [4], and civil engineering [5]. One of the main design directions of modern mechanical applications is lightweight design, which directly leads to thin-walled structures integrated with VE damping layer. Thin-walled structures are represented by thin beams [6,7,8,9,10] thin plates [11,12,13,14] and thin shells [15,16,17,18,19,20]. Accurate modeling of VE material damping characteristics is essential for the vibration-damping structural design process of composite structures thus, many researchers proposed a variety of mathematical models called constitutive models based on traditional differential form [21, 22]. Those models are limited since they are less compatible with measured creep and relaxation behaviors of VE material [23, 24]. Unlike traditional constitutive models, which assume that the material response is instantaneous, fractional constitutive models account for the time-dependent nature of the VE material [25,26,27,28,29]. The VE material dynamic characteristic parameters are not only affected by frequency but temperature provides significant effects on the VE material behaviors which cannot be neglected [30]. In this regard, the mechanical parameters of VE materials are easier to measure in the frequency domain, these models are mathematically represented as complex modulus models, which can accurately simulate the frequency-dependent properties of VE materials in the frequency domain, and capture the creep and relaxation characteristics of VE materials in the time domain [31,32,33]. Those complex models rely on internal dissipation auxiliary coordinates that provide less number of parameters to accurately simulate the frequency dependence behaviors of VE materials such as GHM model and Biot model so that these models are applicable in various engineering applications [34,35,36,37].

VE materials exhibit temperature–frequency equivalence in their mechanical and damping properties [38]. This principle states that the damping characteristics acquired at high temperatures are similar to those found at low frequencies and dynamic mechanical analysis (DMA) parameter curves of VE materials at various temperatures can be adjusted to a reference temperature to derive the master curve [39,40,41]. Ercan and Durmus [42] quantified the VE behaviors of thermoplastic elastomers based on creep tests by using DMA method. Müller-Pabel et al. [43] provided a comprehensive review of recent DMA developments on VE behaviors of Epoxy resins thermosets-based. Mu [44] investigated the VE mechanical behaviors of amorphous plastic composites by using creep and DMA tests. You et al. [45] developed micro-mechanical model to predict the time-dependent mechanical behavior of linear VE particulate composites by utilizing DMA and direct numerical approach.

Nowadays, damping vibration techniques for composite structures using VE material are mainly divided into passive-damping treatment and passive–active damping treatment [46,47,48]. The former refers to damping treatment technique utilizing VE material as a potent passive damping layer, but the latter refers to the combination of actuation scheme of piezoelectric materials and VE materials to augment structural integrity by optimizing the performance of composite structures under various conditions [49, 50]. Kuchak et al. [51] investigated the damping performance of rail damper with rubber layers based on improved FE model and experimental approach. Irazu and Elejabarrieta [52] explored experimentally and numerically the influence of adhesive frequency-independent VE film thickness on the dynamic response of thin sandwich structures. Xing et al. [53] examined the dynamic behaviors of hybrid passive–active lattice sandwich structures with VE-filled corrugated or honeycomb cores imposing periodic boundary conditions. Wang et al. [54] investigated the vibrational damping performance of 3D Kagome lattice truss sandwich panels filled with VE thermosetting polyurethane.

The accurate modeling of VE composite structure is the premise of its vibration analysis therefore, modeling methods of VE composite structure are mainly divided into two categories: analytical method and finite element (FE) method. In addition, some scholars have proposed a modeling method between the first two methods, that is, semi-analytical and semi-numerical modeling methods. It should be mentioned that the application of analytical methods in engineering practice is limited since it requires a solution of higher-order partial differential equations [55]. Park [56] derived the fourth-order differential equation of motion for a damped sandwich beam with a partially VE Layer including transverse deformation and longitudinal shear deformation. Aenlle and Pelayo [57] developed an analytical model for flexural damped vibration of laminated glass beam including the longitudinal inertia effects of VE core. Galuppi and Royer-Carfagni [58] analytically analyzed the time-dependent behavior for VE simply-supported laminated beam and the VE core modeled by prony’s series that incorporated into the modified Maxwell model. Guo et al. [59] performed an analytical study to explore the thermo-VE behaviors for VE laminated sandwich composite structure based on thermo-viscoelasticity theory. Sun et al. [60] developed FE to investigate the dynamics response of VE sandwich beam and the governing equation of motion derived based on virtual work principle. Araújo et al. [61] proposed an FE model to explore the vibration response of active–passive hybrid sandwich plate based on the combination of FSDT and HSDT. Sairajan et al. [62] proposed an FE correlation model to estimate the damping in VE sandwich composite panel. The VE layer was modeled as eight-node hexagonal element while the aluminum face sheets were modeled as four-node quadrilateral shell element. Hernández et al. [63] analyze the uncertainty propagation of design factors and the constitutive parameters of proposed FE model that was formulated based on FSDT for damped VE sandwich beam.. Although FE modelling is extensively used in the dynamic modeling of VE complex sandwich structures, sometimes it is computationally expensive. Thus, some researchers proposed mix model between the analytical method and finite element method (FEM) to improve the calculation efficiency [64]. Eratli et al. [65] used Laplacian mixed FE and Timoshenko beam theory to perform vibrational analysis on VE rod.

At present, many researchers have utilized different damping modelling configurations to achieve high performance in dynamics VE structures. For example, Chen and Liu [66] proposed effective topology optimization design guidelines of constraining layer damping treatment (CLDT) with microstructure VE periodic unit cell. Li et al. [67] analytically and experimentally investigated the damping behaviors of laminated plates embedded with VE considering von Karman nonlinearities effects. Jalaei and Civalek [68] studied the dynamic instability of axially loaded embedded VE porous FGM nanobeams subjected to magnetic field. Kang et al. [69] investigated the forced vibration response of a free–free CLDT beam considering VE frequency-dependent complex parameters based on the combination of analytical and experimental methods. Gupta et al. [70] preformed a comparative study for Active–Passive CLDT of conventional VE material and 0–3 VE symmetric and asymmetric composite sandwich plate. Shahsavari et al. [71] analysis the size-dependent wave propagation response in VE porous FGM curved nanobeam based on HSDT. Youzera et al. [72] developed an analytical model for forced vibration analysis and nonlinear model loss factor of FGM composite beam with VE core by utilizing zig-zag theory coupled with HSDT. Karmi et al. [73] established a numerical model based on a modal stability approach to elaborate the vibro-acoustic response of sandwich beam integrated with frequency and temperature-dependent VE core.

Few scholars reported the recent developments of damping characteristics of VE composite sandwich structures. For example, Trindade and Benjeddou [74] provided a literature review on different modeling approaches of hybrid active–passive damping treatments of beams. Hajianmaleki and Qatu [75] provided a comprehensive review study on the vibrational behaviors of straight and curved laminate composite beams with integral VE layers. Zhou et al. [76] presented a comprehensive review on dynamic and static analysis of sandwich structures containing various VE damping materials. Lewandowski et al. [77] reported the recent achievements of theories for dynamic behaviors of structural elements integrated with VE material. Although research related to VE materials and composite structures is quite broad and covers many different aspects, there is no existing extensive review article in the open literature on computational modelling and analysis of effect of VE materials on damping and vibrational behaviors of composite structures. This work aims to present an organized novel extensive review on the vibration analysis of sandwich composite structures integrated with VE damping materials utilizing computational modelling approaches.

1.1 Literature Research Methodology

The documents assessed in this review article were obtained by using the Scopus database. The first string search was entered as (“viscoelastic” OR “viscoelastic material”) followed by (“damping” OR “vibrational behaviors” OR “dynamic analysis”) then, (“sandwich structure”). Based on the search string keywords, 400 documnets were acquired from the published papers between 1974 and 2023. The results were limited to engineering, material science, mathematics, and energy subject areas then the short surveys and book chapter were excluded from the results while the language was limited to English. The documents were accessible then the search was carried out on on March 12, 2023. Further, many documents were attained from other sources such as ScienceDirect and web of scienece to form recent developments of Computational modelling for VE sandwich structures.

Figure 1 represents statistical data from Scopus of published papers per year from 2000 to 2023. The statistical data in Fig. 1 reveals that there has been a gradual increase in the number of documents published per year between 2014 to 2023. Figure 2 illustrates the statistical data distribution representation of published different document types. The majority of the documents are article-based with 78% and 21% being conference paper, while 1% are review paper. The statistical data representation of published papers by country from Scopus between 2000 and 2023 is displayed in Fig. 3, implying diverse international contributions to the filed of VE modelling and damping methods. Further, It can be pointed out from Fig. 3 that china has a major contribution, which was followed by several other nations. In this review the recent developments VE materials computational modelling and analysis of their implementation on composite sandwich structures were addressed. the paper’s overall structure is organized as follows: The introduction section includes an overview of VE material modelling and testing methods. In Sect. 2 different damping methods and configurations using VE material will be explored. Moreover, the summary of studies reported on VE composite structure’s different modelling approaches including analytical modelling, FEM, and mixed modelling will be presented in Sect. 3.

Fig. 1

A statistical data representation of published papers per year from Scopus by using the following keyword string: (TITLE-ABS-KEY (“viscoelastic” OR “viscoelastic material”)) AND (“damping” OR “vibrational behaviors”) AND (“sandwich structure”) AND (EXCLUDE (LANGUAGE, “Chinese”)

Fig. 2

Pie chart statistical data distribution representation of published different document types from Scopus by using the following keyword string: (TITLE-ABS-KEY (“viscoelastic” OR “viscoelastic material”)) AND (“damping” OR “vibrational behaviors”) AND (“sandwich structure”) AND (EXCLUDE (LANGUAGE, “Chinese”)

Fig. 3

A statistical data bar representation of published papers by country from Scopus by using the following keyword string: (TITLE-ABS-KEY (“viscoelastic” OR “viscoelastic material”)) AND (“damping” OR “vibrational behaviors”) AND (“sandwich structure”) AND (EXCLUDE (LANGUAGE, “Chinese”)

1.2 Theoretical Background of VE Material

The VE material combines two distinct properties when subjected to an external force. The term “elastic” implies the material deforming recovery behavior and pure viscous fluids involve deformation followed by a permanent rearrangement of the fluid molecules [78]. The mechanical properties of materials are commonly investigated using stress–strain behavior but, VE materials form what so-called “hysteresis” loop as shown in Fig. 4a where the area within this loop represents the energy dissipated in the form of heat [79,80,81,82]. Thus, this energy absorption mechanism explains why VE materials are suitable for damping vibration applications [83]. Different parameters may affect the energy dissipation ability of VE materials such as excitation frequencies, applied amplitudes, VE material density, and temperatures Fig. 4b–e [84].

Fig. 4

a Typical hysteresis loop of VE material adapted from [82]. Experimental hysteresis loop Vs different parameters of b excitation frequencies, c applied amplitudes, d VE material density, e temperatures [84]

Another important feature of VE materials is that their mechanical properties are affected by the rate at which they are deformed. Because the molecule’s motion gradually kept up with the external force, the dissipated energy and dynamic stiffness are decreased, as shown in Fig. 5. As a result, the deformation behavior at different deformation rates is represented by a family of curves rather than a single stress–strain curve [85]. Futhuer, temperature influences VE mechanical behaviors because material stiffness varies with temperature so when choosing materials for a certain application, it’s crucial to understand VE materials’ behaviors at a given loading rate and temperature [86]. From Fig. 6, it is seen that the storage modulus, loss factor, equivalent stiffness, and equivalent damping decrease significantly by increasing the temperature [87].

Fig. 5

Dissipated energy damping characteristics variation [85]

Fig. 6

The VE parameters with a displacement of 1.0 mm are as follows: a storage modulus; b loss factor; c equivalent stiffness; d equivalent damping [87]

1.3 Theory of VE Material Modelling

The relationship between the stress–strain of VE materials is called the constitutive relationship, and the equation that describes this behavior is the constative equation [88, 89]. For this purpose, researchers have proposed many mathematical models called constitutive models of VE material. According to different forms of establishment, the constitutive model of a VE material can be divided into a differential type and an integral type. The differential type is based on the constitutive equations established by the spring-damper system and these equations are in differential form while the integral models are based on the measured creep or relaxation function and these equations are in integral form [90,91,92,93,94,95].

1.3.1 Differential Constitutive Models (Classical Models)

The classic constitutive mechanical models consist of spring and damper elements in series and parallel. The spring-dashpot system employs the elastic behavior of the VE material which is represented by the spring element while the VE behavior is represented by the damper element [96]. Typical models include the Maxwell model, Kelvin–Voigt model, and Zener model are shown in Fig. 7. Although these classical models are simple, they cannot simulate the real mechanical behaviors of the VE material [97, 98]. For instance, in the Maxwell model, there is no anelastic recovery which means that the creep response prediction is poor, which is inconsistent with reality while the relaxation response of the Kelvin–Voigt model does not change with time [99]. In addition, the creep and relaxation of the VE material have been improved but the main disadvantage is that it cannot accurately describe the frequency characteristics such as the storage moduli and loss factor [100].

Fig. 7

Classical VE models a Maxwell model, b Kelvin–Voigt model, c Zener model [101]

The following summary can be detected from Table 1: under static load conditions, the storage modulus E of the Maxwell model is zero while the loss factor η approaches infinity. In addition, at high frequencies value the loss factor η is approaching zero. The storage modulus E of Kelvin–Voigt is a constant value and equal to the stiffness of the spring K, while loss factor η is zero and unbound at high frequencies. The Zener model tends to be more realistic than the Maxwell and Kelvin–Voigt models in terms of capturing material dynamic characteristics.

Table 1 Different classical VE models with illustrated various properties behavior

Many scholars have improved the previous classical models such as the standard rheological model which can accurately describe the relaxation response in the frequency domain [104,105,106,107,108,109,110,111]. The main disadvantage is that it needs to obtain the parameters of VE material in a wide frequency range. Bagley et al. [112, 113] proposed a fractional derivative model that can accurately describe the mechanical properties of the VE material in a wide frequency range. Karner et al. [114] developed fractional generalized Maxwell model to anticipate the VE creep behavior of dielectric elastomer actuator. Valvano et al. [115] used Kelvin–Voigt fractional derivative model to explore the frequency-dependent properties of VE sheets in composite plates. The disadvantage of this model is that it is difficult to transform it into time domain, and the calculations are immense when the vibration analysis of the structure is performed, which limits the application of the model [116]. Those classical constitutive models are not compatible with the FEM and are difficult to realize in engineering applications.

1.3.2 Integral Constitutive Models (Complex Models)

The integral constitutive model is a complex modulus model derived from the creep and relaxation functions of VE material. The main standard experiment for VE material is to obtain those mechanical behaviors and the determination of these complex models is based on experimental work, thus they can capture the mechanical properties of VE materials [117]. Furthermore, they simulate the frequency-dependent characteristics of the VE material since these characteristics are easier to measure in the frequency domain. The stress–strain relationship in the integral form can be expressed as [118]:

$$\sigma \left(t\right)=G\left(t\right) {\varepsilon }_{0}+{\int }_{0}^{t}G\left(t-\tau \right)\frac{\partial \varepsilon \left(\tau \right)}{\partial \tau }d\tau$$

(1)

The linear VE material satisfies the Boltzmann Superposition Principle where $\sigma \left(t\right)$ and ${\varepsilon }_{0}$ are the stress relaxation and amplitude of the applied strain respectively, and $G\left(t\right)$ is the shear stress relaxation function, which is a decreasing function representing the energy loss of the VE material [119]. The constitutive stress–strain relationship consists of two parts: initial stress and stress relaxation, the constitutive equation can be obtained in the frequency domain as:

$$\sigma \left(s\right)={G}^{*}\left(s\right) \varepsilon \left(s\right)$$

(2)

where ${G}^{*}\left(s\right)=sG(s)$ is the complex shear stress modulus function of the VE material in the Laplace domain.

1.3.2.1 Complex Constant Modulus Model

The complex constant modulus of VE material G can be expressed as:

$${G}^{*}={G}{\prime}+j{G}^{{\prime}{\prime}}={G}{\prime}\left(1+j\eta \right)$$

(3)

where ${G}{\prime}$ is the real part, also called the storage modulus, and ${G}^{{\prime}{\prime}}$ is the imaginary part which is called the energy dissipation modulus. $\eta = \frac{{G}^{{\prime}{\prime}}}{{G}{\prime}}$ is the loss factor, which is the ratio of the energy dissipation modulus to the storage energy modulus that physically represents the ratio of energy consumed from the VE material to the total energy. Many researchers have used the shear complex modulus, since the frequency variation is not considered, they have obtained a simple dynamic equation by applying a simple harmonic excitation force [120,121,122]. As mentioned above, the shear modulus of VE materials is affected by frequency and temperature, and it is difficult to accurately describe it mathematically. The effect of temperature can be unified with the effect of frequency through the principle of temperature–frequency equivalence, so only the influence of frequency is generally considered in practical applications. It should be pointed out that the complex modulus of VE material is not constant, and it is related to the excitation frequency [123].

1.3.2.2 GHM Model

The GHM (Golla–Hughes–Mctavish) model uses a series of Mini-oscillator functions to represent the complex shear modulus function of VE materials [124, 125]. The mini-oscillator is composed of a virtual spring-mass-damper unit that is connected to the system’s space coordinate x through spatial coordinates z as illustrated in Fig. 8a. The complex shear modulus can expressed as [125, 126]:

$$s\widetilde{G}\left(s\right)={G}^{\infty }\left[1+{\sum }_{k=1}^{N}{\alpha }_{k}\frac{{s}^{2}+2{\widehat{\zeta }}_{k}{\widehat{\omega }}_{k}s}{{s}^{2}+2{\widehat{\zeta }}_{k}{\widehat{\omega }}_{k}s+{{\widehat{\omega }}_{k}}^{2}}\right]$$

(4)

where ${G}^{\infty }$ is the steady-state value of the relaxation function when t = ∞ and s is the Laplace operator. N is the number of terms of Mini-oscillator, and each Mini-oscillator behavior is captured by a second-order rational function determined by three normal parameters {${\alpha }_{k}$, ${\widehat{\omega }}_{k}$, ${\widehat{\zeta }}_{k}$}. If the Mini oscillator takes N, the model has 3N + 1 parameters to determine, which can be obtained by curve fitting to the experimental data through optimization algorithm problem [127]. Due to the efficient computational capacity of GHM model, many researchers used it to capture the frequency-dependent VE behaviors of polymers, composites, and other VE materials under various loading conditions. Gibson et al. [128] implemented GHM into FE model imported from NASTRAN FE solver to represent the frequency-dependent characteristics of VE material. [129, 130]. Huang et al. [131] utilized GHM model to capture the frequency-dependent dynamic characteristics of ZN-1 VE material which were incorporated into the FE model of VE sandwich structure. It can be noticed from Fig. 8b and c that the measured value of ZN-1 complex modulus can be well approximated by the GHM model with relatively low error.

Fig. 8

a GHM model schematic, b GHM Storage modulus fitting results for ZN-1 at 30 °C [131], c GHM Loss modulus fitting results for ZN-1 at 30 °C [131]

1.3.2.3 Biot Model

Biot [132] proposed a complex model that connects a series of micro-vibrators in parallel where these micro-vibrators are parallel with a spring. micro-vibrators elements are coupled to the global coordinates of the system by the internal local coordinates as shown in Fig. 9a to simulate the mechanical dynamic behaviors of VE material. The Biot’s first-order shear relaxation function can be expressed in the frequency domain as [133]:

$${G}^{*}\left(s\right)={G}^{\infty }\left[1+\sum_{i=1}^{N}\frac{{a}_{i}s}{s+{b}_{i}}\right]$$

(5)

where ${G}^{\infty }$ is the equilibrium value of shear stress modulus relaxation of the VE material, s is the Laplace operator, N is the number of micro-vibrators, and if N mini vibrator is selected 3N + 1 must be determined. [a_i, b_i] are positive model parameters determined by the nonlinear curve fitting method using the experimental data of VE material. Few scholars have used the Biot model to study the dynamic behavior of many applications such as composite VE structures. For example, Zhang et al. [134] used Biot model to predict the complex dynamic properties of ZN-1 VE material with different perturbing terms m = 1, m = 2 and then incorporated it into FE model for damping behaviors of VE sandwich structure. It is worth mentioning that the measured value of ZN-1 real and storage modulus and loss modulus can be approximated effectively by the Biot model as shown in Fig. 9c and d respectively. Guo et al. [135] utilized the Biot model to simulate the VE material behavior in the truss damper of the truss sandwich structure. Lin et al. [136, 137] proposed a design methodology to study the vibroacoustic of multi-layered damping beams using Biot damping model. Eugeni et al. [138] and Mastroddi et al. [139] incorporated generalized Biot damping model into FEM for linear structural and aeroelastic systems using Hilbert correction.

Fig. 9

a Biot model, b ADF model schematic adapted from c Biot’s Storage modulus fitting results for ZN-1 at 30 °C [134], d Biot Loss modulus fitting results for ZN-1 at 30 °C [134]

There are also damping models that consider the frequency-dependent complex shear modulus of VE materials. Such as augmenting thermodynamic fields (ATF) [140, 141] and anelastic displacement fields (ADF) [142] shown in Fig. 9b considering both elastic and ADF and Yiu [143] model. Like GHM models and Biot models, they introduce auxiliary coordinates to simulate the frequency dependence of VE materials more accurately.

1.4 Testing of VE Material

1.4.1 Creep/Creep Recovery and Stress Relaxation

The VE properties of many materials can be experimentally evaluated by analyzing the creep, creep recovery, and stress relaxation behaviors of materials such as polymers in many biological applications [144,145,146]. Due to the elastic properties of VE material, creep recovery occurs when a VE deforms under constant load before returning to its original shape where the load is removed Fig. 10a. Accordingly, creep compliance and creep recovery compliance J(t) can be used to express the measured creep and recovery deformation (Fig. 10c), as indicated in Eq. 1. [147]. In addition, stress relaxation occurs under constant strain Fig. 10b where the stress gradually decreases over time [148,149,150] as illustrated in Fig. 10d.

Fig. 10

Illustration of typical VE fresh cement-based materials testing and corresponding response a creep/creep recovery test, b stress relaxation test, c creep/creep recovery behavior, d stress relaxation behavior [147]

$$J\left(t\right)=\frac{\gamma (t)}{{\tau }_{0}}$$

(6)

Moreover, those phenomena are influenced by various parameters such as temperature and stress/strain applied level therefore many researchers investigated the effect of those parameters on the VE material time-dependent behaviors. In this regard, to anticipate time-dependent behaviors, Ornaghi et al. [151, 152] explore the time–temperature creep and stress relaxation response of advanced composites material over material glassy, glass transition, and rubbery states. Further, higher temperatures and stress levels result in greater deformation for creep see Fig. 11a, and the recovery rate is minimal at glass transition temperature T_g as shown in Fig. 11b. Monticeli et al. [153] established an experimental approach based on Taguchi method and analysis of variance to explore the influence of the three VE composite regions on the time-dependent mechanical properties of composite CFR plastic. Sorvari and Malinen [154] proposed numerical model to estimate stress relaxation modulus of linear VE material based on modified Zapas and Phillips model. Song and Wang [155] experimentally investigated stress relaxation, and creep VE behaviors of shape memory polymers including temperature effects, particularly at T_g.

Fig. 11

Experimental data representation of a creep/creep recovery over three composite states. b normalized stress relaxation over three composite states with different strain levels [151], c creep/creep recovery of carbon fiber-reinforced plastic over three composite states, d the variation of relaxation modulus decay with temperature and strain level [153]

1.5 Dynamic Mechanical Analysis (DMA)

DMA is an experimental technique used to characterize the VE mechanical properties such as complex modulus considering wide range of temperatures and frequencies to provide significant facts on the material’s stiffness, strength, toughness, and capacity to resist deformation and fatigue [156, 157]. Many researchers have applied different DMA scientific approaches to capture the frequency-dependent behaviors of VE material. Chia et al. [158] measured the VE damping behavior of plasma spray coatings by using DMA. Singhet et al. [159] presented a novel displacement modulation method for measuring the DMA properties of VE materials with depth-sensing nanoindentation equipment. Melo and Radford [160] presented an experimental method to examine the VE mechanical properties of unidirectional fiber-reinforced composite materials over a range of temperatures and frequencies. Hong et al. [161] used DMA to measure the VE behavior of the ternary graft copolymers at different temperatures. Jrad et al. [162] combined Dahl model with generalized Maxwell model to develop a new visco-tribological model for VE joint while, the identification of VE material characteristics is based on DMA tests. Cheng et al. [163] and Li et al. [164] used time–temperature superposition principle to obtain complex modulus master curve of VE polymers imposing different frequencies and temperatures. Manoharan et al. [107] synergistically investigated the influence of fiber reinforcement on the VE temperature-dependent mechanical properties of hybrid friction composites. Asadian and Shelesh-Nezhad [165] experimentally predicted the VE dynamic behavior of polymer/clay nanocomposite to develop modified generalized Maxwell model that incorporates into FE model. Xu et al. [166] employed dynamic thermomechanical analysis (DTMA) to investigate mechanical performance parameters of VE material including micro effects. To anticipate the nanoscale DMA of composite polymer fluorinated ethylene propylene, Pittenger et al. [167] developed experimental model based on atomic force microscopy approach which could provide more wider range of frequencies up to 20 kHz. The investigated microscopic structure is illustrated in Fig. 12a where the copolymer forms almost circular cross-section area with a diameter of 1 $\upmu$m within the propylene matrix. At room temperature, there is no significant difference between the storage modulus of the propylene matrix and copolymer see Fig. 12b. The damping capacity of copolymer is quite lower than propylene matrix as shown in Fig. 12c. Further, as temperature increases the storage modulus of the two-phase materials keeps decreasing but the divergence rate of Propylene (PP) matrix is higher than the divergence rate of copolymer since the matrix phase since PP softens as it reaches its point of melting at 164 °C. on the other hand, time temperature superposition principle (TTS) used which require a DMA data over range of (0.1–100) Hz with temperature sweeping of (25–130) °C as shown in Fig. 12d to generate the master curve. Wang et al. [168] explored the effect of frequency and temperature on the dynamic performance characteristics of VE damping material by using DMA at frequencies of 1–136 Hz in the temperature range of 50–150 °C, and the relationship between elastic modulus, loss factor of VE material with temperature at different frequencies obtained as shown in Fig. 13. It can be seen from Fig. 13a that as temperature increases the storage modulus gradually decreases, this relationship is valid since, VE materials exhibit solid state at low temperatures in contrast, at high temperatures the VE tends to exhibit rubber state. Likely, when the temperature is lower than T_g the storage modulus increases so the material most likely behaves more elastic and stores the energy rather than dissipates it. On the other hand, Fig. 13b shows an initially increasing in the damping factor then decreases as temperature increases. At the same time, as frequency increases the damping factor decreases, and the T_g increases. At room temperature, as frequency the storage modulus increases Fig. 13c but damping factor show an increasing trend then gradually decreasing trend as depicted in Fig. 13d. The summary of reported studies on VE testing method are presented in Table 2.

Fig. 12

a Storage modulus and loss microscopic maps of polypropylene reinforced with cyclic olefin copolymer (COC), b Storage modulus variation curves of polypropylene matrix and COC at 10 Hz, c loss modulus variation curves of polypropylene matrix and COC at 10 Hz, d DMA coupling with atomic force microscopy approach for polypropylene reinforced with COC over range of (0.1–100) Hz with temperature sweeping of (25–130) °C [167]

Fig. 13

Variation DMA characterizations of VE damping material with frequency and temperature T a storage modulus ${E}{\prime}$ vs T at different frequencies, b damping factor vs T at different frequencies, c storage modulus ${E}{\prime}$ vs f, d damping factor vs f [168]

Table 2 Summary of reported studies on VE testing method

2 VE Material Applications

2.1 Passive Damping Methods Configurations

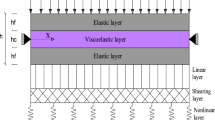
VE materials are widely used to suppress the vibration of thin-walled components. A typical passive damping treatment structure consists of unconstrained treatment as shown in Fig. 14a a VE core sandwiched between the constraining layer and the base beam also called the “Damped layer “as shown in Fig. 14b. The VE core allows the vibration energy to dissipate through a cyclic deformation within it, while the main advantage of the constraining layer is to increase the cyclic shear deformation of the core and withstand high stress, hence directly leading to an increase in the damping energy within the VE core [182, 183]. Those configurations have been utilized in different applications such as automotive and aerospace [3], it has been found that when the constraining and base layers have the same thickness and material properties, the longitudinal shear deformation is maximized [184, 185]. Also, many researchers investigated the damping vibration of railway carriages using passive damping vibration technology to improve the comfort of the passenger interior [186,187,188,189].

Fig. 14

VE passive damping treatment in its most basic configuration forms: a unconstrained treatment (UCLDT), b constrained treatment (CLDT) [190]

2.2 Un-constraining Layer Damping Treatment (UCLD)

The traditional free-damping layer has been utilized by many researchers to achieve optimum passive damping design of vibrational structures. Yi et al. [191] performed a forced vibration analysis of the UCLD plate to explore the efficiency of free damping treatment. The parametric study showed the significant effect of many parameters such as VE layer thickness on the damping behavior of the UCLD plate. Kumar and Panda [192] investigated the passive damping mechanism of UCLD beam integrated with pure VE or with 1–3 VECM, as shown in Fig. 15a using FE model based on Hamilton principle. The model demonstrated the variation in the structural damping capacity with different thicknesses of pure VE Fig. 15b and 1–3 VECM composite material Fig. 15c and a different number of graphite-phase volumes. To show the practical efficiency presented by the conventional UCLD technique, Cortés, and Elejabarrieta [193] elaborated on the damping behavior of the UCLD beam by utilizing different FE models and the FRF extracted using superposition mode. He et al. [194] examined three measures to improve damping in a lightly damped aluminum bridge Fig. 16a using rubber sheet pavements, rubber bearings, and external passive dampers. Experimental comparisons are made to determine their effectiveness in damping increment. The external damper is observed to exhibit the highest efficacy in damping increments followed by rubber bearings and rubber sheet pavements respectively see Fig. 16b. Due to the significant difference in elastic modulus between aluminum and rubber, the rubber sheet exhibits minimal strain during structural vibration, resulting in a lack of internal friction among particles. Consequently, the rubber sheet contributes insignificantly to the overall damping of the material. Additionally, Fig. 16c and d depict the unique free decay oscillation of the bridge when exposed to an external damper with varying liquid viscosity; thus, as expected, the damping vibration is more effective as the viscosity of the liquid increases. Therefore, it is crucial to select a damping material with properties that closely match those of the structure to achieve effective damping. Additionally, the choice of damping material should also consider factors such as durability and compatibility with the surrounding environment to ensure long-term effectiveness.

Fig. 15

a Schematics illustration of (UCLDT) technology, b, c normalized frequency responses of cantilever sandwich beam integrated with pure VE or with 1–3 VECM with different thickness of layer [192]

Fig. 16

Schematic illustration of a experimental setup of aluminum bridge with external damping device, b comparison between three distinct measures of damping increment, c time-free vibration response of aluminum bridge with external damping device, d magnified view of time- free vibration response for aluminum bridge with external damping device [194]

2.3 Constraining Layer Damping Treatment (CLDT)

Another effective conventional way of passive damping of the vibrational structure is CLD treatment, the configuration is way such that the VE is a core layer bonded together with a constraining layer and base layer as shown in. Chen and Huang [195] proposed an effective analytical model to describe the damping vibrations of CLD cylindrical shell strips Fig. 17a, based on the energy approach method which accounts for the compatibility relations between layers Fig. 17b, the discretized equations of motion based on Hamilton principle were obtained considering different transverse modes of the shell. The FRF has been derived analytically from Fig. 17c, to expose the practical validity of the proposed CLD treatment under various parameters. Nayfeh [196] developed FE model for the flexural vibration behavior of sandwich composite beam and the numerical model was validated against the experimental results. In addition, Berthelot [197] investigated the flexural vibration behavior of composite beams and plates by utilizing the Ritz method considering the effect of the beam width, frequency flexural vibration, and boundary condition on the damping vibration behavior of composite sandwich beams and plates. Sher and Moreira [198] performed a dimensionless study analysis of sandwich structure with a single or multi-layer core of VE considering various parameters’ effects to provide design guidelines for CLD treatments. Khalfi and Ross [199] investigated experimentally the transient response of a partially CLD layer sandwich plate using Fourier-Transform with VE frequency-dependent material approximated by Prony series expansions.

Fig. 17

a CLD cylindrical shell strips treatment, b schematics illustrated the system of compatibility relations between layers, c FRF of CLD cylindrical shell with different numbers of strips [195]

Kumar et al. [200] proposed an FE model based on FSDT for augmented CLD with a 0–3 VE composite layer as shown in Fig. 18a, The 0–3 VE composite layer consists of a thin array of rectangular graphite strips including within the VE layer shown in Fig. 18b. The numerical results show a significant improvement in the damping behavior of the composite sandwich plate. To obtain optimal design, a parametric study considers the effects of geometric and mechanical parameters of 0–3 VE composite layer on the model damping factor of the plate as shown in Fig. 18c. On the other hand, FRF is estimated around natural frequency values considering the optimal design of the composite plate, the results show relevant improvement in damping performance in the presence of the proposed 0–3 VE composite layer Fig. 18d.

Fig. 18

a Schematic configuration of sandwich plate integrated with 0–3 VE composite layer, b composite layer of 0–3 VE layer embedded with thin rectangular graphite wafers (c, d) [200]

Duan and Huo [201] proposed a novel pounding tuned mass damper (PTMD) with constrained layer damping (PTMD-CLD) consisting of a VE layer sandwiched between two metal layers, which effectively dissipates vibration energy through internal friction as shown in Fig. 19a. The experimental results show that the PTMD-CLD system significantly reduces the amplitude of free vibrations Fig. 19b and effectively mitigates the pounding force between adjacent structures rather than conventional systems. As depicted in Fig. 19c. Additionally, numerical simulations confirm the effectiveness of the CLD-PTMD in reducing structural vibrations and highlight its potential for practical applications in various engineering fields.

Fig. 19

a A schematic of PTMD-CLD configuration and shear damping mechanism, b steady-state frequency response comparison between the proposed PTMD-CLD and conventional system, c pounding force response comparison between the proposed PTMD-CLD and conventional system [201]

2.4 Hybrid Passive–Active Damping Methods Configuration

By combining the VE passive system and piezoelectric active control, a hybrid damping treatment can effectively address both resonance peaks and lower frequencies, which directly enhance the structure’s dynamic stability [202]. This can be achieved by integrating an active-constrained damping layer (ACLD) made of piezoelectric material into the passive system to increase the shear strain within the core or the induced bending stress of sandwich structures [203, 204]. Accordingly, increase the damping energy of the hybrid passive–active system [205]. therefore, several studies and models, including various configurations, modeling techniques, and parametric investigations are reported. Trindade et al. [206] investigated the dynamic performance of hybrid active–passive damping beam consisting of constraining VE (3M ISD112) layer and piezoelectric (PZT5H) actuator using model strain energy (MSE) method that was implemented into FE model of C–F sandwich beam. Ro and Baz [207] developed an optimization technique to address the optimum design parameters of ACLD patches attached to passively damped plate based on MSE method considering variation of thickness and shear modulus of VE layer. Unlike previous conventional ACLD treatments, Trindade [208] proposed a topological optimization algorithm to maximize the damping performance of C–C beam and simultaneously minimize the aggregated weight added to the structure. Further, the results show that direct active case has the highest damping performance but they also result in a higher mass increase. On the other hand, passive damping treatments offer a lower mass increase but may not be as effective in certain schemes of damping/added mass regions. Therefore, it is crucial to carefully evaluate the specific requirements and constraints of the application before selecting a damping treatment design.

In addition, Kumar and Singh [203] experimentally investigated velocity feedback control of C–F beam exposed to ACLD patches considering the variation in thickness, coverage, and placement for each VE layer. Furthermore, optimizing the position and coverage of the treatment can obtain a more uniform distribution of damping, ensuring consistent damping ratios across all vibration modes. Wang et al. [209] developed analytical model to investigate the stability improvement of VE thin plate with piezoelectric layer subjected to follower force. The analytical model incorporates piezoelectric effects while expressing the differential equation of the plate with uniformly distributed tangential follower forces. The governing equation is derived using the element-free Galerkin method. The obtained results show that, as piezoelectric layer moves closer to the plate’s center, the critical load increases. Further, dimensionless voltage leads to higher critical load, and instability types vary due to surface-bonded piezoelectric layers. Zhai et al. [210] introduced an experimental platform approach for vibration closed-loop control of ACLD aero pipeline system including closed-loop control system and vibration monitoring system to verify the vibration damping performance as depicted in Fig. 20a. The experimental results were validated using the proposed FE numerical model results. Different control voltages were considered to contrast the damping efficacy of ACLD patches. Figure 20b and c show gradual decrease in acceleration time and frequency domain responses respectively, as applied voltage increases However, the acceleration response decreases by 56.93%, but, as voltage keeps increasing, the reduction in vibration reduction per unit voltage becomes smaller, meaning that the effect of ACLD patches on vibration reduction could be limited under certain conditions. Liu et al. [211] investigated the failure mechanism of FGPE-MR as depicted in Fig. 21a by implementing novel fractional feedback equation process parameters optimization based on Grunwald–Letnikov derivative analysis to enhance the efficacy of the control feedback response and mitigate the shortcomings associated with active–passive damping. The actuator layer is a constraining layer, while the sensor layer is a base layer. The actuator layers consist of PZT-4 and PZT-5H. The FGPE-MRE sandwich plate is implemented using a Cartesian coordinate system on a linear orthotropic elastic Pasternak foundation. Figure 21b shows the signal delay curve between expected and actual input voltages for the actuator layers and by incorporating this method, failure characteristics of active–passive damping systems may be obtained more effectively. In addition, this approach allows for the capturing of compressibility behavior of MRE core in a simplified manner by considering the virtual springs as a collective entity see Fig. 21c thus, the proposed method effectively captures the transverse deformation characteristics of the FGPE-MRE.

Fig. 20

a Schematic of ACLD pipeline’s vibration control platform incorporating closed-loop control algorithm, b [210]

Fig. 21

a Schematic illustration of failure mechanism of active–passive FGPE-MRE sandwich structure, b schematic representation of signal delay between actuator layer and sensor layer, c fundamental principle method for compressible MRE core modeled as a collection of virtual springs arranged in parallel [211]

2.5 Recently Embedded Configurations

To attain mankind’s need for new technology development, small-size composite structures with VE material are explored. Lin [6] proposed a numerical model to predict the vibration behavior of nanocomposite beams with VE core reinforced by various sizes of nanofiller particles fraction from 10 to 50 wt%. Guedes et al. [212] investigated experimentally the effect of different multi-walled carbon nanotubes MWCNT fractions on the damping behavior of medical grade ultra-high molecular weight polyethylene. Ansari et al. [213] investigated the nonlinear size-dependent free vibration response of FG microbeams utilizing the strain gradient SGT and Reddy beam theory based on Hamilton’s principle. The developed model considers the material length-scale parameters to demonstrate the influences of size effect on the vibrational response of FGM microbeams. SGT and CT were found to predict the highest and lowest values of non-dimensional natural frequency for all values of dimensionless length among the different microbeam models. Furthermore, it was proven that decreasing non-dimensional natural frequencies results from increasing the material property gradient index. Based on the nonlocal strain gradient theory and high-order refined beam theory, Ebrahimi et al. [214] investigated the hygro-thermal vibrational behavior of VE FG nanobeams. To accurately describe the size-dependency of nanobeams, take into consideration the size-dependent parameters’ influence on the damping frequency. The model has two parameters. and graded material properties modeled according to a power-law model which is assumed to be temperature-dependent. To determine the governing equations and boundary conditions, Hamilton’s principle is used. Karličić et al. [215] analyze the transverse free vibration of the multi-nanoplate system (MNPS) embedded in a VE medium shown in Fig. 22a, considering the small size-dependent parameter effects based on nonlocal theory as Based on the Kirchhoff–Love plate theory. The modified Kelvin–Voigt VE constitutive relation was employed to model the material and nano-scale characteristics of nanoplates. It can be noticed from Fig. 22b and c that as the nonlocal parameter is increased, both components of the complex eigenvalue decrease. This suggests that the small-scale effect decreases the system’s stiffness, resulting in the nanocomposites being “softer.” also, an increase in the system’s nanoplates (m) results in a decrease in the complex natural frequency components. Khaniki et al. [216] investigated the damping vibration behavior of VE DLNPS with moving nanoparticles using Galerkin’s base solution. Kirchhoff–Love plates and D’Alembert’s principle are used to establish the governing equations of motion while the coupling between layers and the size-dependent effects are modeled using Kelvin–Voigt VE theory and Eringen’s non-local elasticity theory.

Fig. 22

a A continuum model nanoplate embedded in VE material The influence of nonlocal (η) and internal VE (T) parameters on complex eigenvalues for different numbers of S–S nanoplates, b damped natural frequencies and c damping ratio [215]

Ansari et al. [217] proposed a fractional nanoscale Euler–Bernoulli beam model reinforced with CNT to study the size-dependent nonlinear free vibration response of VE nanobeams. The governed equation of motion is derived based on the Galerkin bases method to convert it into a fractional ordinary differential equation. To analyze the size effect and fractional behavior in the nanoscale fractional VE structures, respectively, the nonlocal parameter, VE coefficient, and order of fractional derivative were taken into consideration in the proposed model. The rate of decay amplitude was found to decrease as the order of the fractional derivative or nonlocal parameter increased. To illustrate the free vibration response, Arani et al. [218] study the damped free vibration of a VE FG-CNTRC microplate integrated with a piezoelectric sensor and actuator layers subjected to electromagnetic fields embedded in an orthotropic visco-Pasternak foundation. The equation of motion was established based on the Hamilton principle while Kelvin–Voigt model was utilized to model the VE material. Furthermore, the influences of certain significant parameters on the damped free vibration of a system are investigated, including the damping ratio of VE plates, volume fraction of CNT, various types of functionally graded distributions of CNTs, magnetic field, and external voltage. It has been pointed out that, the volume fraction of CNTs and FG distributions of CNT have the main role to increase the whole stiffness of the reinforced micro-composite plate. Oskouie et al. [219] investigated the size-dependent vibration behaviors of VE Euler–Bernoulli nanobeams using fractional derivative and the Gurtin–Murdoch theory. A thorough parametric investigation is carried out to explore the effects of the initial displacement, fractional derivative order, viscoelasticity coefficient, surface elastic modulus, residual surface stress, and thickness-to-length ratio on the nonlinear response of VE nanobeams. Additionally, it is found that surface effects can alter the nanobeam’s stiffness based on the surface elastic modulus and residual surface stress values.

Loghman et al. [220] employed the MCST and the fractional Kelvin– Voigt theory together for nonlinear size-dependent vibration behavior of the fractional VE micro-beam by using FDM coupled with Galerkin bases. the effect of the order of the fractional derivative, the VE model, and the micro-scale parameter on the nonlinear frequency response curve is taken into consideration as shown in Fig. 23. The maximum amplitude of the response can be greatly influenced by the fractional derivative order thus, it can be found that by increasing the order of the fractional derivative, the damping of the VE micro-beam is increased; therefore, the maximum amplitude is decreased as presented in Fig. 23a. Figure 23b shows the influence of the exciting force on the fractional VE micro-frequency beam’s response curve. It is revealed that the resonance frequency amplitude is significantly influenced by the excitation force’s amplitude. When the micro-effect is considered by applying MCST, the maximum amplitude and resonance frequency are seen to decrease and increase, respectively, as shown in Fig. 23c. For investigating the effect of viscous damping on the frequency–response curves of the fractional VE micro-beam, Fig. 23d is shown. It is obvious that viscous damping has a significant effect on the response’s amplitude, and that this influence is strongest close to the resonance. Rahmani et al. [221] proposed a comprehensive mathematical-mechanical model based on nonlocal Eringen’s, theory coupled with MCST by utilizing HSDT and Reddy’s beam theory (RBT) to investigate the wave propagation of a rotating VE nanobeam embedded in a Winkler -Pasternak foundation, as well as the effect of many parameters on the wave propagation frequencies, such as the nonlocal parameter and thermal gradient.

Fig. 23

Parametric representation effects on nonlinear frequency response curve of fractional VE micro-beam a various fractional derivative orders α, b different amplitude of exciting force, c MCST Vs Classical theory, d VE damping ratio [68]

Furthermore, based on NSGT Hajmohammad et al. [222] investigated the dynamic buckling of embedded conical shells composed of sandwich layers of carbon fiber, CNT, and epoxy multiphase nanocomposites resting on the visco-Pasternak foundation. shown in Fig. 24a. The motion equations are constructed by employing FSDT, the energy method, and Hamilton’s principle. and the first dynamic instability region (DIR) of the structure was obtained using the differential quadrature method (DQM) and Bolotin’s method. The first DIR of the structure is explored concerning several parameters, including VE medium, the volume fraction of CNTs, temperature variations, and boundary conditions. Figure 24b. The DIR of the structure for various CNTs weight percentages 0, 1%, 2%, and 3%. It can be stated that as the weight % of CNTs is increased, the DIR of the structure occurs at higher frequencies. because the stiffness and flexibility of the sandwich structure increase with the increase in the weight % of CNTs. In addition, Fig. 24c. represents the effect of temperature variation on the DIR, it makes sense from a physical perspective that the structure becomes less stiff as the difference in temperature increases. Figure 24d. shows the effect of VE medium types on the DIR of the sandwich structure: without VE medium, visco-Winkler, Winkler, visco-Pasternak, and Pasternak. It can be observed that the excitation frequency of the structure is higher in the presence of VE medium, and Visco-Winkler or visco-Pasternak foundations have a lower excitation frequency than Winkler or Pasternak foundations, respectively. Also, the Pasternak foundation’s excitation frequency is higher than the Winkler foundation’s because the Pasternak foundation also considers the medium’s shear constant in addition to the Winkler foundation’s spring constant. Furthermore, Fig. 24e. shows the influence of the sandwich structure’s layer number on the DIR, four-layer numbers of 2, 3, 4, and 5 are taken into consideration, where layer 2 and layer 4 correspond to the anti-symmetric lamina and layers 3 and 5 to symmetrical lamination., the symmetric lamina has a higher DIR than the anti-symmetric lamina due to the stronger structural stability. It is also important to note that since DIR occurs at higher frequencies, layer number 3 is superior to layer number 4 in terms of performance. Yuan et al. [223] performed size-dependent dynamic buckling vibration analysis on truncated conical micro-shells composed of an FGM integrated with magnetostrictive face sheets embedded in a two-parameter Winkler -Pasternak foundation, exhibiting to-size-dependent dynamic stability axial compressive load and a magnetic field are applied to the micro shells as shown in Fig. 25a. while nonlocality and strain gradient size dependencies are maintained. The strain gradient and nonlocal load–frequency responses are compared with the traditional load–frequency responses for the dynamic stability behavior of the system under consideration. It is observed that, during the pre-buckling phase, the strain gradient, and nonlocal forms of size dependency cause, respectively, a decrease and an increase in the frequency of the system under consideration for a given value of the axial compressive load. Al-Furjan et al. [224] developed a mathematical model of size-dependent laminated annular microplates embedded in VE foundation based on non-classical continuum MSCT. The non-classical governing equations of motion and corresponding boundary conditions were established by adding strain gradient rotation using the HSDT and Hamilton’s principle respectively. Summary of several investigated VE embedded configurations are presented in Table 3.

Fig. 24

a An illustration of an embedded sandwich made of conical nanocomposite layers, b effects of various parameter on the sandwich structure’s DIR. b CNTs Weight percentage ${W}_{CNT}$, c temperature change ∆T, d VE medium, e layers number N [222]

Fig. 25

a An illustration of an FGM composite truncated conical micro-shell with magnetostrictive face sheets embedded in nonlinear VE foundations, b FGM truncated conical micro-shells dimensionless classical and nonlocal strain gradient load–frequency response corresponding to different nonlocal parameters [223]

Table 3 Summary of several investigated VE embedded configurations

3 Studies Reported on VE Composite Structures: Theories and Methods

The accurate modeling of the VE sandwich structures is the main key to its vibration analysis. Therefore, a lot of researchers have done a lot of work related to this problem. Nowadays, the modeling of VE sandwich structures is mainly divided into three categories: analytical, FEM, and mixed method. The mixed method proposed by some scholars is semi-analytical and semi-numerical.

3.1 Analytical Models

In 1959, Kerwin [232] developed the first analytical model of VE sandwich structure that defines the relative motion between the three layers of the EVE’s beam structure. Later, based on Kerwin’s works, DiTaranto [233] proposed a sixth-order, homogenous differential equation to study the free vibration of a three-layer beam. The results show that the damping loss factor does not depend on the boundary conditions. Mead and Markus [234, 235] utilized DiTaranto’s model to develop a model that can be applied to various boundary conditions. The Model considered the constrained layer and the base beam as the Euler–Bernoulli beam, neglecting the moment of inertia of the VE layer. According to the Mead-Markus model, the three layers have the same lateral displacement, while the longitudinal displacement of the VE layer can be expressed in terms of the longitudinal displacement of the constrained and base layers. In 2005, Ghinet [236] established a method based on wave theory to analyze the vibration of curved laminate and sandwich composite panels. The previous analytical models assume that damping vibration is only due to the shear deformation assumption of the VE layer. Although this assumption has been widely accepted, some researcher has adapted the compression deformation of the VE layer to be the damping vibration mechanism. In 1997, Douglas and Yang [237] established an analytical model and then proved experimentally the existence of the transverse compression damping mechanism in EVE’s beam in a narrow frequency band centered on the compression resonance frequency of the VE layer. Few scholars like Sylwan [238] established a composite analytical model based on the shear and compression dissipation energy assumption but the model showed an overestimation of the model loss factor in a wide frequency band. Summary of reported studies on VE composite sandwich structures using an analytical solution are presented in Table 4.

Table 4 Summary of reported studies on VE composite sandwich structures using an analytical solution

3.2 FEM Models

In engineering practice, VE composite sandwich structures have complex geometric shapes and boundary conditions. At this time, such problems cannot be solved effectively by the analytical process hence the FE approach is commonly used. There is two main finite element construction for modeling VE sandwich structure, Layered FEM and Direct FEM. The Layered method considers different units for each layer Fig. 26a while Global Direct FE. Considers the displacement of the three layers through nodal element degree of freedom (DOF) Fig. 26b [249]. The layered FEM was used in early commercial software, and it is less efficient. On the other hand, the advantage of Global Direct FE is that it provides less DOF with high accuracy [8]. Based on the shear assumption of damping energy, many researchers have developed FE models such as Johnson and Kienholz [250] and Plouin and Balmms [251] who used triangular shell elements (QUAD4) to discrete the elastic faces and solid elements (HEXA8) for the VE core implemented in NASTRAN commercial software [252]. The traditional shell elements and solid elements have been used to model the core layer. Also, Ma et al. [253] modeled the elastic surface layer and VE layer using shell elements and fully (HEXA8) compatible solid elements.

Fig. 26

Two typical FEM construction methods a layered method, b global element construction method

Arvin et al. [254] reported a numerical FE investigation on the free and forced vibrational response of a composite sandwich beam with a VE core using the Mead and Markus modified model taking into consideration the effects of Young modulus, rotational inertia, and core kinetic energy. Also, a parametric study on the effects of several impressive parameters involving fiber angle, the thickness of faces, and core thickness was investigated. Bilasse et al. [255] reported a study on the investigation of VE sandwich beams Linear and nonlinear vibration response. To elaborate on the linear damping characteristics of VE sandwich structures, Elmoghazy et al. [256] proposed a combined dynamics analysis methodology by utilizing 2D and 3D FE models based on shear deformation theory. The complex eigenmodes of clamped-free and simply-supported VE sandwich structures were explored based on model effective mass approach. In addition, they investigated the effect of core layer thickness and VE material damping factor ${\eta }_{v}$ on the free and forced vibration damped response as shown in. What can be seen from Fig. 27 is there no significat change noticed in natural frequancy but as increasing the VE core damping factor${\eta }_{v}$, the rate of structural damping performance is likely to increase.

Fig. 27

Effects of ${\eta }_{v}$ on the sandwich structure's free vibration response a first mode, b second mode, c third mode [256]

Zhang et al. [257] established electromechanical FE model for analyzing VE cylindrical sandwich smart structures, with a stacking sequence of [PZT/elastic/VE/elastic/PZT] as shown in Fig. 28a based on the zig–zag hypothesis that derived from the Reissner–Mindlin theory, which employs an eight-node element seven different transitional and rotational DOF for each node Fig. 28b. The dynamic equation was derived using Hamilton principle so that the global stiffness contains coupled stiffness matrix, the piezoelectric coupled capacity matrix, and the piezoelectric capacity matrix. To anticipate transient response of the proposed shell cylindrical sandwich smart structures, a step-driving voltage was applied, the vibration of the tip node along the hoop and radial direction (Fig. 28c). Various scenarios are taken into account to display the hoop displacements of the tip node: one involving only structural damping C^s, another involving only VE damping C^v, and a third example that takes into account both structural and VE damping C^s + C^v see Fig. 28d. The results show that the damping provided by the elastic structure has a minimal impact on vibration suppression of the proposed shell cylindrical sandwich smart structures, while the incorporation of VE material substantially enhances the damping ratio.

Fig. 28

a VE cylindrical sandwich smart structure, b quadratic element with seven DOF per node, c transient response of the proposed shell cylindrical sandwich smart structure with a step-driving voltage, d the hoop displacements of the tip node of shell cylindrical sandwich smart structure under different damping conditions [257]

Wang and Inman [258] developed a two-dimension FE model to investigate the dynamic vibration of a composite beam integrated with a VE damping layer. The 10 nodal DOFs of the composite element are shown in Fig. 29a. The FE model assembled based on the Hamilton principle and the VE frequency-dependent material incorporated into the equation of motion of the composite beam through an auxiliary coordinate using the GHM model. Moita et al. [259] proposed FE model for the vibrational response of active–passive damped multi-layered plates consisting of VE and piezoelectric layers. later on, Barbosa and Farage [260] proposed an FE modeling formulation of VE sandwich beam. The FE element (shown in Fig. 29c) consists of seven elements: one four-node plate quadrilateral linear VE element; two-node elastic frame elements; and four rigid connection elements. The proposed model element has 24 physical DOF besides five dissipative DOF of plane stress for VE element resulting in a super element model with 29 DOF. Lin and Rao [136, 261] performed a vibration analysis study of multiple-layered structures with a VE damping layer using FE model. The non-linear behavior of the VE layer was simulated with the Biot damping model. The model showed high accuracy in predicting the time-dependent dissipative energy. Won et al. [262] developed six DOF 2-node beam element model based on Hamilton principle to investigate the damped force vibration of VE three-layered sandwich beam. Kpeky et al. [263] introduced solid-shell FE model (Fig. 29b) coupled with Diamant approach to model the vibration behavior of VE sandwich beam. Eshaghi et al. [264] established FE plate mode ((d)) based on CPT to study the dynamic characteristic of sandwich composite plate. The VE core material was identified as magnetorheological fluids and the experiment characteristics were incorporated into FE model. Ren et al. [264] developed layerwise four-node quadrilateral FE with 17 DOF per node (Fig. 29e) to examine the existence of transverse compression damping for sandwich plate with relatively thick frequency-dependent VE core. The equation of motion derived based virtual work principle in the variation form includes the higher-order variation of the transverse displacement within the VE core.

Fig. 29

Schematic illustration of different FE models for VE composite sandwich structure a five-layer composite nodal degree layered [258], b solid-shell FE element in local coordinate frame [263], c super element DOF [260], d 2D VE sandwich plate element with seven DOF [265], e four-node VE sandwich plate element [264]

3.3 Mixed Models

The FEM has been widely used in the dynamic modeling of complex structures, but some problems are difficult to implement and computationally expensive. Therefore, some researchers try to ensure accurate modeling based on looking for ways to improve computational efficiency, some models between the analytical method and the FEM are proposed type, called semi-analytical semi-numerical method [266]. Daya and Potier-Ferry [267, 268] used the homotopy algorithm and the asymptotic method to solve the nonlinear eigenvalue problem of composite structure with a VE layer and obtain the natural frequency and loss factor. This method can greatly simplify the solution process. Bostrom et.al [269] derived the flexural vibration equations for homogenous, elastic, isotropic pates using displacement field expansion series Koutsawa et al. [270] studied the non-linear behavior of laminated glass beam by applying the asymptotic numerical technique to establish a diamond toolbox. The performance of the diamond toolbox was demonstrated numerically and experimentally. Lampoh et al. [271, 272] performed sensitivity studies on the non-linear mechanical behavior of laminated glass beam. This approach allows for efficient computation of the parameter convergence radius, ensuring accurate sensitivity analysis results. Additionally, by carefully selecting the modeling parameter increase, the sensitivity analysis can provide valuable insights with high precision. Ganguly et al. [273] combined Euler–Bernoulli shaft theory and Maxwell model with finite element formulation to model a damped VE shaft to obtain the vibrational response of the shaft, the results are validated by observing the effect of increasing the number of Maxwell elements on the loss factor and storage elasticity. Zhang et al. [274] conducted a multi-objective optimization of laminated VE composite plates for enhancing sound transmission performance while minimizing the additional mass of a VE damping layer. The design variables include several key parameters, including the thickness, offset position of the damping layer, fiber orientation, maximal first-order modal loss factor (MLF), maximal first sound transmission loss (STL) dip value, and minimal additional mass. Further, to investigate the average sound transmission loss (STL) within the low-frequency range of 10–1 kHz, as well as the STL values at the lowest dip frequencies, particularly the STL value at the first dip frequency, were evaluated. Figure 30a illustrates the STL in the frequency range of 10–1 kHz for plates with three different thicknesses of VE layer. In addition, it is observed that the STL curves of composite plates including a damping layer exhibit three distinct dips. Additionally, Fig. 30b presents the comparisons of the average sound transmission loss (STL) values of the composite plates within the frequency range of 10–1 kHz, as well as their STL values at the three lowest dip frequencies. These comparisons take into consideration the added mass resulting from the increased thickness of the inserted VE layer. The observation reveals a clear correlation between the average STL within the frequency range of 10–1 kHz and the averaged STL at the first three dip frequencies, with both parameters exhibiting an upward trend as the added mass of the VE increases. Summary of reported studies on VE composite sandwich structures using mixed methods and FEM are presented in Table 5.

Fig. 30

a STL curve of VE composite plate with different VE layer thickness, b the STL curve at the first dip frequency of the proposed VE composite plates versus the added VE layer mass, the average STL in 10 to 1 kHz, and the average of the first three STL dips [274]

Table 5 Summary of reported studies on VE composite sandwich structures using mixed methods and FEM

4 Conclusion

This paper presented a comprehensive review of many computational models that were put forth to describe frequency-dependent dynamic properties of VE material, which inherently affected the dynamic response of different VE structural damping configurations using different analysis methods to obtain accurate results. Although passive vibration attenuation of modern mechanical structures is one of the most essential technologies applied to the arsenal of modern mechanical structures, it only efficiently reduces the vibration's amplitude and enhances the overall structure dynamic performance over a limited frequency range. On the contrary, hybrid passive–active damping methods may offer an optimal damping performance of composite structures since they include the ability of both sensing and actuation control. Nonetheless, small-size structures embedded with VE materials are utilized due to humanity's need for innovative multifunctional structures. However, the damping performance of VE composite structures is greatly influenced by the choice of suitable VE materials and their properties. Therefore, additional research and experiments are required to determine the ideal VE material dynamics properties and configurations for composite sandwich structures to achieve the highest damping performance. In the previous article, the research status abroad was summarized from three aspects: VE material constitutive models, VE composites structural modeling, and damping performance research. It can be seen from the literature review that for half a century, scholars have done a lot of work in these three aspects and achieved a lot of results, which greatly promoted the developments of structural dynamics research for VE composites structures, but in the following, there are still some deficiencies, which require further in-depth research:

• The error introduced by traditional differential constitutive relations is too large, which is incompatible with FE modelling and difficult to realize engineering applications; although the complex constant modulus model is simple and easy to solve and reflects some properties of VE materials under the condition of harmonic loading, it cannot truly capture the frequency-dependent characteristics of VE materials. On the other hand, GHM and Biot models describe the frequency-dependent properties of VE materials very well, and they can be integrated into the FEM thus, more applicable in terms of engineering practice.

• Due to the complexity of the constitutive relationship of VE materials, considering the frequency-dependent characteristics of VE materials, the introduction of complex modulus will lead to the complexity of the system matrix.

• Although there are many modeling methods, in general, the analytical method relies on simple mathematical formulations and special boundary conditions, it shows less applicable, limited, and difficult to be used in practical engineering applications; the traditional FEM has many elements, and the calculation work is very difficult. The mathematical models established by the semi-analytic and semi-numerical method is often more complex, and the truncation during the solution will also introduce errors. So how to establish an accurate and efficient FE model needs further research.

• In the study of the damping performance of VE composite sandwich structures, the methods of most scholars are limited to the definition and extraction of both loss factor of VE materials and the model loss factor of the structure so, there is still a lack of in-depth research on the damping mechanism, such as the shear of VE materials during vibration. There are still some controversies on shear energy consumption or compression energy consumption, and there is still a lack of quantitative research on the scope of application of various energy consumption models.

• Various studies on numerical modelling of VE composite structures are reported immensely, yet there exist limited/none reported studies on the implementation of machine learning and deep learning techniques. Thus, further work can be dedicated to these areas.