On the application of fractional calculus for the formulation of viscoelastic Reddy beam

Abstract

The focus of the current work is to present the bending analysis of visco-elastic beams based on Reddy’s third-order shear deformation theory. Fractional calculus is taken into account for dealing with the fractional derivative terms, able to better describe the damping behaviour of any visco-elastic material. Numerical analyses of beams with different boundary conditions have been proposed and discussed following two different approaches, namely the finite element method and the Galerkin method. An assessment of the proposed approach is presented by comparing the computed solutions with those obtained with the classical and first-order shear deformation theories available in the literature.

1 Introduction

In recent years, the scientific community has shown an increasing interest in developing new and more accurate models able to illustrate the internal damping of visco-elastic systems. In this context, special emphasis was placed on to solve the discrepancies observed between the classical viscoelastic models composed to springs and dashpots and the real behaviour of visco-elastic phenomena like relaxation or creep. Inspired by the pioneering works of Nutting [1] and Gemant [2], numerous studies have demonstrated as fractional calculus, i.e. the fractional integration and differentiation introduced by Leibniz in a prophetic letter dated 30 September 1695 to reply to a specific query of the meaning $n = 1/2$ in $d^{n} y\left( x \right)/dx^{n}$ questioned by l’Hôpital (“Thus is follows that $d^{1/2} x$ will be equal to $x\root 2 \of {dx:x}$, an apparent paradox, from which 1 day useful consequences will be drawn” [3]), can be used for the formulation of new visco-elastic constitutive equations, requiring only few parameters to correctly matching experimental data [4].

In this theoretical framework, a link between molecular theories that predict the macroscopic behaviour of viscoelastic media and fractional calculus approach to viscoelasticity was proposed in [5]. Lately, the basic theory of relaxation processes governed by linear differential equations of fractional order were revisited in [6], providing historical notes on the origins of the Caputo derivative and the use of fractional calculus in viscoelasticity. A simple fractional model has been adopted in [7] for modeling viscoelastic behaviour of asphalt mixtures, showing as experimental creep data follow a power decay law rather than an exponential one.

In addition to a constitutive model, structural analysis requires the adoption of a suitable model able to represent appropriately and efficiently the actual behaviour of these structures. In such a context, the simplicity of its mechanical interpretation and the straightforward solution of the corresponding differential equation, the classical beam model proposed by Daniel Bernoulli and Leonhard Euler in about 1750 is by far the most popular [8]. Analysis of visco-elastic beams based on classical beam theory and making use of fractional calculus has been proposed by [9] where, starting from the local fractional visco-elastic relationship between axial stress and axial strain, the authors shown that bending moment, curvature, shear forces and the gradient of curvature involve fractional operators. A new numerical method to solve the constitutive equations of fractional-order viscoelastic Euler–Bernoulli beams was reported in [10]. In [11] the classical Bernoulli beam was reformulated in the Fractional calculus framework, and the constitutive parameters experimentally identified.

Early in the twentieth century, Timoshenko [12] proposed an enhanced beam model that takes into account shear deformation and makes it suitable to describe the behaviour of relatively thick beams. In [13] the authors determined the response of a visco-elastic Timoshenko beam under static loading condition and taking into account fractional calculus. In [14] the authors determined exact linking relationships between elastic Euler–Bernoulli and fractional visco-elastic Timoshenko beam response, providing ready-to-use tables and a straightforward formulation. The response of nonlocal Timoshenko beam modelled by Caputo fractional derivatives and including viscoelastic long-range interactions was also investigated in [15, 16].

Very recently, in order to deal with thick composite beams and to avoid the shear correction factor required in the Timoshenko beam theory to properly represent the strain energy of deformation [17], high-order theories with different shear-strain shape functions (including hyperbolic [18], parabolic [19], trigonometric [20], cubic [21]) have been proposed for both beam and plate modelling.

Among them, the third-order deformation beam theory proposed by Reddy [22, 23] in the early seventies of the last century is certainly one of the most popular. In [24], the author envisioned a sequence of elastic Reddy-type shear deformable beams of increasing order, starting with the Euler–Bernoulli beam (first order) and terminates with the Timoshenko beam (infinite order) and using the principle of virtual power to determine the equilibrium equations and the boundary conditions.

Anisotropic constitutive relation based on a modified couple-stress theory and defined for composite laminated Reddy beam [25], or the buckling analysis of stiffened Reddy composite beams adopting a full Green–Lagrange deformation model instead of the more usual von Karman theory presented in [26, 27], are just a few of the works devoted to the analysis of beams making use of the Reddy model.

In the framework of visco-elastic beams, in [28] the authors proposed a weak form Galerkin finite element model for the nonlinear, quasi-static and fully transient analysis of initial straight visco-elastic Reddy beam. In [29] the authors proposed a vibration and damping analysis of sandwich beams made up of laminated composite face sheets and a viscoelastic core, employing a modified Fourier Ritz method to derive a formulation based on Reddy’s model.

In this paper the problem of visco-elastic Reddy beam in time-domain is addressed within the framework of fractional calculus. The corresponding differential equations are numerically solved considering two different approaches, namely the Galerkin method and the finite element (FE) method, applied to solving simple test cases. A comparison of the computed solutions made with those based on classical and first-order shear deformation theories already available in the literature, assesses accuracy and robustness of the proposed approach and concludes the work.

2 Theoretical background

2.1 Visco-elastic model based on fractional calculus

The constitutive relationship between stress and strain of elastic and viscous materials follows the well-known Hooke’s law of elasticity and Newton’s law of viscosity:

$$\begin{array}{*{20}l} {\sigma = \sigma \left( x \right) = E \cdot \varepsilon = E\left[ {D^{0} \varepsilon } \right]} \hfill \\ {\sigma = \sigma \left( {x,t} \right) = E \cdot \dot{\varepsilon } = \mu \left[ {D^{1} \varepsilon } \right]} \hfill \\ \end{array}$$

(1)

where $D^{0} ,D^{1}$ are the zero-th and the first-order derivatives, $\left( {E,\mu } \right)$ the Young modulus and the viscosity coefficient and $\left( {\varepsilon ,\dot{\varepsilon }} \right)$ are the strain and its rate, respectively.

In uniaxial load conditions, such constitutive behaviours are schematically represented in (Fig. 1a, b). The straightforward generalization of Eq. (1):

$$\sigma = E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \varepsilon } \right)$$

(2)

represented in the literature by the spring-pot element depicted in Fig. 1c, is the fractional law of a visco-elastic material. In Eq. (2) $E_{\alpha }$ contains visco-elastic coefficients and $_{C} D_{{0^{ + } }}^{\alpha }$ is the Caputo’s fractional derivative defined as:

$$\left( {_{C} D_{{0^{ + } }}^{\alpha } \varepsilon } \right)\left( {t_{1} } \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\int_{0}^{{t_{1} }} {\frac{{\dot{\varepsilon }\left( t \right)}}{{\left( {t_{1} - t} \right)^{\alpha } }}dt} \,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le \alpha \le 1$$

(3)

where $\Gamma \left( \bullet \right)$ is the Gamma function. For $\alpha = 0$ and $E_{\alpha } = E$ Eq. (2) returns the Hooke law expressed in Eq. (1a), while for $\alpha = 1$ and $E_{\alpha } = \mu$ Eq. (2) returns Eq. (1b). Any other value of $0 < \alpha < 1$ may describe the viscoelastic constitutive law of any real material. The motivation on the presence of the fractional derivative in the constitutive law instead of derivative of integer order like in the classical Kelvin–Voigt, Maxwell or Burgers models relies on the fact that the creep (or the relaxation) test obeys to power law rather than exponential one [1]. Consequently, by using the Boltzmann superposition principle, the constitutive law expressed in Eq. (2) born in natural way.

Fig. 1

a Purely elastic, b viscous and c generalized visco-elastic spring-pot uniaxial constitutive model

If the stress history is known, the correspondent strain history can be obtained as:

$$\varepsilon = E_{\alpha }^{ - 1} \left( {D_{{0^{ + } }}^{ - \alpha } \sigma } \right)$$

(4)

where $\left( {D_{{0^{ + } }}^{ - \alpha } \sigma } \right)$ is the so-called Riemann–Liouville fractional integral defined as:

$$\left( {D_{{0^{ + } }}^{ - \alpha } \sigma } \right)\left( t \right) = \frac{1}{\Gamma \left( \alpha \right)}\int_{0}^{t} {\left( {t - r} \right)^{\alpha - 1} \sigma \left( r \right)dr}$$

(5)

in terms of the relaxation modulus $\Phi \left( t \right)$ and of the creep compliance $\Psi \left( t \right)$, expressed as:

$$\begin{aligned} \Phi \left( t \right) & = \frac{{E_{\alpha } \,t^{ - \alpha } }}{{\Gamma \left( {1 - \alpha } \right)}} \\ \Psi \left( t \right) & = \frac{{E_{\alpha }^{ - 1} \,t^{\alpha } }}{{\Gamma \left( {1 + \alpha } \right)}} \\ \end{aligned}$$

(6)

The extension of Eqs. (2) and (4) to the case of multiaxial stress and strain is straightforward (see e.g. [30]. and the references reported herein). For sake of simplicity in this work we suppose that the Poisson ratio remain constant over time. In this case only one order of fractional derivative and integral appears, so that Eqs. (2) and (4) may be written as:

$$\begin{aligned} {{\varvec{\upsigma}}} & = {\mathbf{E}}_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } {{\varvec{\upvarepsilon}}}} \right) \\ {{\varvec{\upvarepsilon}}} & = {\mathbf{E}}_{\alpha }^{ - 1} \left( {D_{{0^{ + } }}^{ - \alpha } {{\varvec{\upsigma}}}} \right) \\ \end{aligned}$$

(7)

where ${{\varvec{\upsigma}}}^{T} = \left[ {\sigma_{x} \,\,\,\,\,\sigma_{y} \,\,\,\,\,\sigma_{z} \,\,\,\,\,\tau_{xy} \,\,\,\,\,\tau_{xz} \,\,\,\,\,\tau_{yz} } \right]$, ${{\varvec{\upvarepsilon}}}^{T} = \left[ {\varepsilon_{x} \,\,\,\,\,\varepsilon_{y} \,\,\,\,\,\varepsilon_{z} \,\,\,\,\,\gamma_{xy} \,\,\,\,\,\gamma_{xz} \,\,\,\,\,\gamma_{yz} } \right]$ and ${\mathbf{\rm E}}_{\alpha }$ is a $6 \times 6$ symmetric operator whose elements will be evaluated by best fitting experimental data.

3 Governing equations of fractional visco-elastic Reddy beam

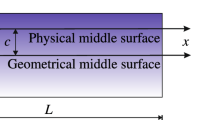
The model assumes that, for the beam pictorially represented in Fig. 2, the axial displacement of a point on the beam cross-section is a cubic function of the beam-thickness coordinate (Fig. 3):

$$\begin{aligned} & s_{x} \left( {x,z;t} \right) = z\phi - \frac{4}{{3h^{2} }}z^{3} \left( {\phi + w,_{x} } \right) \\ & s_{y} = 0 \\ & s_{z} \left( {x,z;t} \right) = w \\ \end{aligned}$$

(8)

in terms of the generalized displacement and rotation:

$${\mathbf{u}}\left( {x,t} \right) = \left[ {w\left( {x;t} \right)\,\,\,\,\,\phi \left( {x;t} \right)} \right]^{T}$$

(9)

of the beam centerline.

Fig. 2

Layout of the beam

Fig. 3

Displacement field of the Reddy beam

The related non-zero strain components are given by:

$${{\varvec{\upvarepsilon}}}\left( {x,z;t} \right) = \left[ \begin{gathered} \varepsilon_{x} \\ \gamma_{xz} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} z & {z^{3} } & 0 & 0 \\ 0 & 0 & 1 & {z^{2} } \\ \end{array} } \right]\left[ \begin{gathered} \chi \\ \eta \\ \gamma \\ \beta \\ \end{gathered} \right] = {\mathbf{b}}\left( z \right){\mathbf{q}}\left( {x;t} \right)$$

(10)

in which the vector:

$${\mathbf{q}}\left( {x;t} \right) = \left[ \begin{gathered} \chi \left( {x;t} \right) \\ \eta \left( {x;t} \right) \\ \gamma \left( {x;t} \right) \\ \beta \left( {x;t} \right) \\ \end{gathered} \right] = \left[ \begin{array}{l} \phi ,_{x} \\ - c_{1} \left( {\phi ,_{x} + w,_{xx} } \right) \\ \left( {\phi + w,_{x} } \right) \\ - c_{2} \left( {\phi + w,_{x} } \right) \\ \end{array} \right]$$

(11)

contains the generalized deformations in Reddy beam theory and $c_{2} = 4/h^{2} ,c_{1} = c_{2} /3$ are constants depending on the height of the beam. The corresponding dual stress vector can be obtained from ${{\varvec{\upsigma}}} = \left[ {\sigma_{x} \,\,\,\,\,\,\tau_{xz} } \right]^{T}$ by invoking the virtual work equivalence:

$$\int_{V}^{{}} {{{\varvec{\upsigma}}}^{T} \cdot \delta {{\varvec{\upvarepsilon}}}dV} = \int_{0}^{L} {\int_{A}^{{}} {{{\varvec{\upsigma}}}^{T} \cdot \delta {{\varvec{\upvarepsilon}}}dAdx} = } \int_{0}^{L} {{\mathbf{Q}}^{T} \delta {\mathbf{q}}dx}$$

(12)

attaining, by substituting (10) in (12), the vector of the generalized Reddy stress:

$${\mathbf{Q}} = \int_{A}^{{}} {{\mathbf{b}}^{T} {{\varvec{\upsigma}}}dA = } \int_{A}^{{}} {\left[ {\begin{array}{*{20}c} z & 0 \\ {z^{3} } & 0 \\ 0 & 1 \\ 0 & {z^{2} } \\ \end{array} } \right]} \left[ \begin{gathered} \sigma_{x} \\ \tau_{xz} \\ \end{gathered} \right] = \left[ \begin{gathered} \int_{A}^{{}} {z\sigma_{x} dA} \\ \int_{A}^{{}} {z^{3} \sigma_{x} dA} \\ \int_{A}^{{}} {\tau_{xz} dA} \\ \int_{A}^{{}} {z^{2} \tau_{xz} dA} \\ \end{gathered} \right] = \left[ \begin{gathered} M \\ P \\ Q \\ R \\ \end{gathered} \right]$$

(13)

The Hamilton’s principle assumes the form:

$$\begin{aligned} & \int_{0}^{T} {\int_{0}^{L} {\left( {\left( {{\mathbf{q}}^{T} \delta {\mathbf{Q}} + p\delta w + m\delta \phi } \right)dx} \right)dt} } \\ & \quad + \int_{0}^{T} {\int_{0}^{L} {\left( {m_{0} \dot{w}\delta \dot{w} + m_{2} \dot{\phi }\delta \dot{\phi } - c_{1} \left( {m_{4} \left( {\dot{\phi }\delta \left( {\dot{\phi } + \dot{w},_{x} } \right) + \left( {\dot{\phi } + \dot{w},_{x} } \right)\delta \dot{\phi }} \right) + c_{1} m_{6} \left( {\dot{\phi } + \dot{w},_{x} } \right)\delta \left( {\dot{\phi } + \dot{w},_{x} } \right)} \right)} \right)} dxdt} = 0 \\ \end{aligned}$$

(14)

The related Euler–Lagrange equations of motion are:

$$\begin{array}{*{20}l} {\left( {\overline{M},_{x} - \overline{Q}} \right) + m = \overline{m}_{2} \ddot{\phi } - c_{1} \overline{m}_{4} \left( {\ddot{\phi } + \ddot{w},_{x} } \right)} \\ {\overline{T},_{x} + p = m_{0} \ddot{w} + c_{1} m_{4} \ddot{\phi },_{x} - c_{1}^{2} m_{6} \left( {\ddot{\phi },_{x} + \ddot{w},_{xx} } \right)} \\ \end{array}$$

(15)

where

$$\begin{aligned} \overline{M} & = M - c_{1} P \\ \overline{Q} & = \left( {Q - c_{2} R} \right) \\ \overline{T} & = \overline{Q} + c_{1} P,_{x} \\ m_{i} & = \int_{A}^{{}} {\rho z^{i} dA} \\ \overline{m}_{i} & = m_{i} - c_{1} m_{i + 2} \\ \end{aligned}$$

(16)

The boundary conditions for bending variables involve one of the following pairs of elements:

$$\begin{array}{*{20}l} {\overline{T} - c_{1} \left( {\overline{m}_{4} \ddot{\phi } - c_{1} m_{6} \ddot{w},_{x} } \right)} & {or} & w \\ {\overline{M}} & {or} & \phi \\ { - c_{1} P} & {or} & {w,_{x} } \\ \end{array}$$

(17)

For visco-elastic material, the not-zero stress components involved in the Reddy beam can be written as:

$$\begin{array}{*{20}l} {\sigma_{x} \left( {x,z;t} \right) = E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \varepsilon_{x} } \right)\left( {x,z;t} \right)} \hfill \\ {\tau_{xz} \left( {x,z;t} \right) = G_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \gamma_{xz} } \right)\left( {x,z;t} \right)} \hfill \\ \end{array} \quad 0 < \alpha < 1$$

(18)

where $\left( {E_{\alpha } ,G_{\alpha } ,\alpha } \right)$ are constants depending on the longitudinal and tangential behaviour of the material.

Combining Eq. (18) with Eqs. (10), (13) and (16) the following stress resultants:

$$\begin{aligned} & \left[ \begin{gathered} M \\ P \\ \end{gathered} \right] = E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } } \right)\left[ {\begin{array}{*{20}l} I & J \\ J & K \\ \end{array} } \right]\left[ \begin{gathered} \chi \\ \eta \\ \end{gathered} \right] \\ & \overline{Q} = G_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } } \right)\left[ {\begin{array}{*{20}c} {\overline{A}} & {\overline{I}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \gamma \\ \beta \\ \end{array} } \right] \\ \end{aligned}$$

(19)

can be obtained in terms of the geometrical parameters:

$$\begin{aligned} & \left( {A,I,J,K} \right) = \int_{A}^{{}} {\left( {1,z^{2} ,z^{4} ,z^{6} } \right)dA} \\ & \overline{A} = A - c_{2} I,\;\;\overline{I} = I - c_{2} J \\ \end{aligned}$$

(20)

To rewrite the equations of motion (15) in terms of the generalized displacements we obtain:

$$\begin{array}{*{20}l} {\hat{I}E_{\alpha } \phi ,_{xx} - c_{1} \hat{J}E_{\alpha } \left( {\left( {\phi ,_{xx} + w,_{xxx} } \right)} \right) - \left( {\overline{A} - c_{2} \overline{I}} \right)G_{\alpha } \left( {\left( {\phi + w,_{x} } \right)} \right) + D_{{0^{ + } }}^{ - \alpha } m = D_{{0^{ + } }}^{ - \alpha } \left( {\overline{m}_{2} \ddot{\phi } - c_{1} \overline{m}_{4} \left( {\ddot{\phi } + \ddot{w},_{x} } \right)} \right)} \\ {\left( {\overline{A} - c_{2} \overline{I}} \right)G_{\alpha } \left( {\left( {\phi ,_{x} + w,_{xx} } \right)} \right) + c_{1} E_{\alpha } \left( {\left( {J\phi ,_{xxx} - c_{1} K\left( {\phi ,_{xxx} + w,_{xxxx} } \right)} \right)} \right) + D_{{0^{ + } }}^{ - \alpha } p = D_{{0^{ + } }}^{ - \alpha } \left( {m_{0} \ddot{w} + c_{1} m_{4} \ddot{\phi },_{x} - c_{1}^{2} m_{6} \left( {\ddot{\phi },_{x} + \ddot{w},_{xx} } \right)} \right)} \\ \end{array}$$

(21)

that is:

$$\begin{array}{*{20}l} {\hat{I}E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \phi ,_{xx} } \right) - c_{1} \hat{J}E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \left( {\phi ,_{xx} + w,_{xxx} } \right)} \right) - \left( {\overline{A} - c_{2} \overline{I}} \right)G_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \left( {\phi + w,_{x} } \right)} \right) + m = \overline{m}_{2} \ddot{\phi } - c_{1} \overline{m}_{4} \left( {\ddot{\phi } + \ddot{w},_{x} } \right)} \\ {\left( {\overline{A} - c_{2} \overline{I}} \right)G_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \left( {\phi ,_{x} + w,_{xx} } \right)} \right) + c_{1} E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } \left( {J\phi ,_{xxx} - c_{1} K\left( {\phi ,_{xxx} + w,_{xxxx} } \right)} \right)} \right) + p = m_{0} \ddot{w} + c_{1} m_{4} \ddot{\phi },_{x} - c_{1}^{2} m_{6} \left( {\ddot{\phi },_{x} + \ddot{w},_{xx} } \right)} \\ \end{array}$$

(22)

or, in a more compact form:

$$\begin{array}{*{20}l} {\tilde{E}\hat{I}\phi ,_{xx} - c_{1} \tilde{E}\hat{J}\left( {\phi ,_{xx} + w,_{xxx} } \right) - \tilde{G}\tilde{A}\left( {\phi + w,_{x} } \right) + m = \overline{m}_{2} \ddot{\phi } - c_{1} \overline{m}_{4} \left( {\ddot{\phi } + \ddot{w},_{x} } \right)} \hfill \\ {\tilde{G}\tilde{A}\left( {\phi ,_{x} + w,_{xx} } \right) + c_{1} \left( {\tilde{E}J\phi ,_{xxx} - c_{1} \tilde{E}K\left( {\phi ,_{xxx} + w,_{xxxx} } \right)} \right) + p = m_{0} \ddot{w} + c_{1} m_{4} \ddot{\phi },_{x} - c_{1}^{2} m_{6} \left( {\ddot{\phi },_{x} + \ddot{w},_{xx} } \right)} \hfill \\ \end{array}$$

(23)

indicating with:

$$\tilde{E} = E_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } } \right),\tilde{G} = G_{\alpha } \left( {_{C} D_{{0^{ + } }}^{\alpha } } \right),\tilde{A} = \left( {\overline{A} - c_{2} \overline{I}} \right),\hat{I} = I - c_{1} J,\hat{J} = J - c_{1} K$$

(24)

4 Quasi static case and corresponding principle

Let us consider a beam in which the applied load varies slowing in time so that the inertial forces in (22) can be neglected. Further, adopting for the known terms the uncoupled form [9]:

$$\begin{aligned} m\left( {x,t} \right) & = \overline{m}\left( x \right)\mu \left( t \right) \\ p\left( {x,t} \right) & = \overline{p}\left( x \right)\psi \left( t \right) \\ \end{aligned}$$

(25)

so that Eq. (22) can be simplified into:

$$\begin{array}{*{20}l} {\hat{I}E_{\alpha } \phi ,_{xx} - c_{1} \hat{J}E_{\alpha } \left( {\left( {\phi ,_{xx} + w,_{xxx} } \right)} \right) - \tilde{A}G_{\alpha } \left( {\phi + w,_{x} } \right) + \overline{m}\left( x \right)\left( {D_{{0^{ + } }}^{ - \alpha } \mu } \right)\left( t \right) = 0} \hfill \\ {\tilde{A}G_{\alpha } \left( {\left( {\phi ,_{x} + w,_{xx} } \right)} \right) + c_{1} E_{\alpha } \left( {J\phi ,_{xxx} - c_{1} K\left( {\phi ,_{xxx} + w,_{xxxx} } \right)} \right) + \overline{p}\left( x \right)\left( {D_{{0^{ + } }}^{ - \alpha } \psi } \right)\left( t \right) = 0} \hfill \\ \end{array}$$

(26)

Since the equation system (26) is linear, it is possible to claim that a visco-elastic Reddy beam in a quasi-static load condition acts like an elastic beam in which the external load varies in time according to the Riemann–Liouville fractional integral of the load amplifier $\left( {\mu \left( t \right),\,\psi \left( t \right)} \right)$. Accordingly, the visco-elastic displacement field can be derived by the elastic one as follows:

$$\begin{aligned} w\left( {x,t} \right) & = \overline{w}_{1} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \psi } \right)\left( t \right) + \overline{w}_{2} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \mu } \right)\left( t \right) \\ \phi \left( {x,t} \right) & = \overline{\phi }_{1} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \psi } \right)\left( t \right) + \overline{\phi }_{2} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \mu } \right)\left( t \right) \\ \end{aligned}$$

(27)

with $\left( {\overline{w}_{i} \left( x \right),\overline{\phi }_{i} \left( x \right)} \right)$ solution of the purely elastic problems:

$$\begin{array}{*{20}l} {\hat{I}E_{\alpha } \overline{\phi }_{1} ,_{xx} - c_{1} \hat{J}E_{\alpha } \left( {\left( {\overline{\phi }_{1} ,_{xx} + \overline{w}_{1} ,_{xxx} } \right)} \right) - \tilde{A}G_{\alpha } \left( {\left( {\overline{\phi }_{1} + \overline{w}_{1} ,_{x} } \right)} \right) = 0} \hfill \\ {\tilde{A}G_{\alpha } \left( {\left( {\overline{\phi }_{1} ,_{x} + \overline{w}_{1} ,_{xx} } \right)} \right) + c_{1} E_{\alpha } \left( {\left( {J\overline{\phi }_{1} ,_{xxx} - c_{1} K\left( {\overline{\phi }_{1} ,_{xxx} + \overline{w}_{1} ,_{xxxx} } \right)} \right)} \right) + \overline{p}\left( x \right) = 0} \hfill \\ \end{array}$$

(28)

and

$$\begin{array}{*{20}l} {\hat{I}E_{\alpha } \overline{\phi }_{2} ,_{xx} - c_{1} \hat{J}E_{\alpha } \left( {\left( {\overline{\phi }_{2} ,_{xx} + \overline{w}_{2} ,_{xxx} } \right)} \right) - \tilde{A}G_{\alpha } \left( {\left( {\overline{\phi }_{2} + \overline{w}_{2} ,_{x} } \right)} \right) + \overline{m}\left( x \right) = 0} \hfill \\ {\tilde{A}G_{\alpha } \left( {\left( {\overline{\phi }_{2} ,_{x} + \overline{w}_{2} ,_{xx} } \right)} \right) + c_{1} E_{\alpha } \left( {\left( {J\overline{\phi }_{2} ,_{xxx} - c_{1} K\left( {\overline{\phi }_{2} ,_{xxx} + \overline{w}_{2} ,_{xxxx} } \right)} \right)} \right) = 0} \hfill \\ \end{array}$$

(29)

respectively. The general strain components can be obtained substituting Eq. (27) in Eq. (11):

$${\mathbf{q}}\left( {x;t} \right) = {\overline{\mathbf{q}}}_{1} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \psi } \right)\left( t \right) + {\overline{\mathbf{q}}}_{2} \left( x \right)\left( {D_{{0^{ + } }}^{\alpha } \mu } \right)\left( t \right)$$

(30)

Which returns the following generalized internal forces:

$$\begin{aligned} & \left[ \begin{gathered} M \\ P \\ \end{gathered} \right] = E_{\alpha } \left[ {\begin{array}{*{20}l} I & J \\ J & K \\ \end{array} } \right]\left[ \begin{gathered} \overline{\chi }_{1} + \overline{\chi }_{2} \\ \overline{\eta }_{1} + \overline{\eta }_{2} \\ \end{gathered} \right] \\ & \overline{Q} = G_{\alpha } \left[ {\begin{array}{*{20}c} {\overline{A}} & {\overline{I}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{\gamma }_{1} + \overline{\gamma }_{2} } \\ {\overline{\beta }_{1} + \overline{\beta }_{2} } \\ \end{array} } \right] \\ \end{aligned}$$

(31)

according to the correspondence principle: “if a visco-elastic beam is subjected to loads which are applied simultaneously at initial time and then held constant, the stresses are the same as those in the purely elastic case under the same load, while strains and displacements depend on time and are derived from the purely elastic case by simply replacing the elastic modulus with the inverse of the creep function”, stated by Flugge in [31].

5 Examples

Equations (28) and (29) represent two linear systems of fractional differential equations in $\overline{\phi }_{i} \left( x \right),\overline{w}_{i} \left( x \right)$. Several numerical procedures have been proposed in the literature for solving Reddy beam equations, see for instance [26]. In this section the previous concepts are applied to two simple examples, represented in Fig. 4, in which the elastic solution is determined following two different approaches, namely a finite element approach and a Galerkin approach.

Fig. 4

Examples: applied loads and boundary conditions

5.1 Finite element approach

To facilitate the direct derivation of a displacement finite element, we use the Hamilton’s principle that, for the Reddy beam theory, is represented by Eq. (14). After some algebraic manipulation, it is possible to represent the internal energy as [32]:

$${\mathbf{q}}^{T} \delta {\mathbf{Q}} = \overline{M}\delta \chi - c_{1} P\delta \eta + \overline{Q}\delta \gamma$$

(32)

that is, in virtue of Eqs. (19), (20) and (24), can be written as:

$${\mathbf{q}}^{T} \delta {\mathbf{Q}} = \left( {\tilde{E}\hat{I}\chi + \tilde{E}\hat{J}\eta } \right)\delta \chi - \tilde{G}\tilde{A}\gamma \delta \gamma - c_{1} \left( {\tilde{E}J\chi + \tilde{E}K\eta } \right)\delta \eta$$

(33)

Replacing in Eq. (33) the generalized deformations represented in Eq. (11), and reordering in terms of:

$${\overline{\mathbf{q}}} = \left[ {\phi ,_{x} \quad w,_{xx} \quad \left( {\phi + w,_{x} } \right)} \right]^{T}$$

(34)

we obtain:

$${\mathbf{q}}^{T} \delta {\mathbf{Q}} = {\overline{\mathbf{q}}}^{T} {\mathbf{D}}\,\delta {\overline{\mathbf{q}}}$$

(35)

with:

$${\mathbf{D}} = \left[ {\begin{array}{*{20}c} {\tilde{E}\hat{I} - c_{1} \tilde{E}\hat{J}} & { - c_{1} \tilde{E}\hat{J}} & 0 \\ { - c_{1} \tilde{E}\hat{J}} & {c_{1}^{2} \tilde{E}K} & 0 \\ 0 & 0 & {\tilde{G}\tilde{A}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{E}\left( {I - 2c_{1} J + c_{1}^{2} K} \right)} & {\tilde{E}\left( {c_{1}^{2} K - c_{1} J} \right)} & 0 \\ {\tilde{E}\left( {c_{1}^{2} K - c_{1} J} \right)} & {c_{1}^{2} \tilde{E}K} & 0 \\ 0 & 0 & {\tilde{G}\left( {A - 2c_{2} I + c_{2}^{2} J} \right)} \\ \end{array} } \right]$$

(36)

Based on Eqs. (34)–(36) it is possible to obtain a stiffness matrix in a straightforward way [33].

Generalized deformation field represented in Eq. (34) requires that the out-of-plane displacement $\overline{w}\left( x \right)$ be twice differentiable and $C^{1}$ continuous, whereas the rotation $\overline{\phi }\left( x \right)$ must be once differentiable and $C^{0}$ continuous. In the present work, a linear interpolation function is used for $\overline{\phi }\left( x \right)$ and the cubic interpolation functions is adopted for $\overline{w}\left( x \right)$ so that, on an element of length $L$:

$$\left[ \begin{gathered} {\overline{\phi }} \\ {\overline{w}} \\ \overline{w},_{x} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} \frac{1}{L} & {\frac{x}{{L^{2} }}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & \frac{x}{L} & {\frac{{x^{2} }}{{L^{2} }}} & {\frac{{x^{3} }}{{L^{3} }}} \\ 0 & 0 & 0 & \frac{1}{L} & {\frac{2x}{{L^{2} }}} & {\frac{{3x^{2} }}{{L^{3} }}} \\ \end{array} } \right] \cdot \left[ \begin{gathered} a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ a_{5} \\ a_{6} \\ \end{gathered} \right];\,\,\,\,\,\,{\mathbf{u}} = {\mathbf{N}}^{*} \cdot {\mathbf{a}}$$

(37)

The generalized deformation field represented in Eq. (34) assumes the form:

$$\left[ \begin{array}{l} \overline{\phi },_{x} \\ \overline{w},_{xx} \\ \left( {\overline{\phi } + \overline{w},_{x} } \right) \\ \end{array} \right] = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{{L^{2} }}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{2}{{L^{2} }}} & {\frac{6x}{{L^{3} }}} \\ \frac{1}{L} & {\frac{x}{{L^{2} }}} & 0 & \frac{1}{L} & {\frac{2x}{{L^{2} }}} & {\frac{{3x^{2} }}{{L^{3} }}} \\ \end{array} } \right] \cdot \left[ \begin{gathered} a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ a_{5} \\ a_{6} \\ \end{gathered} \right];\,\,\,\,\,\,\,\,{\overline{\mathbf{q}}} = {\mathbf{B}}^{*} \cdot {\mathbf{a}}$$

(38)

Collecting the nodal values in a vector:

$$\left[ \begin{gathered} w^{0} \\ w,_{x}^{0} \\ \phi^{0} \\ w^{L} \\ w,_{x}^{L} \\ \phi^{L} \\ \end{gathered} \right] = \frac{1}{L}\left[ {\begin{array}{*{20}c} 0 & 0 & L & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & L & L & L & L \\ 0 & 0 & 0 & 1 & 2 & 3 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ \begin{gathered} a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ a_{5} \\ a_{6} \\ \end{gathered} \right];\,\,\,\,\,\,\,\,{\mathbf{u}}^{n} = {{\varvec{\Gamma}}} \cdot {\mathbf{a}}$$

(39)

it is possible to obtain the shape functions ${\mathbf{N}}$ and ${\mathbf{B}}$ in terms of nodal values as:

$$\begin{aligned} {\mathbf{u}} & = {\mathbf{N}} \cdot {\mathbf{u}}^{n} \\ {\overline{\mathbf{q}}} & = {\mathbf{B}} \cdot {\mathbf{u}}^{n} \\ \end{aligned}$$

(40)

with:

$${\mathbf{N}} = {\mathbf{N}}^{*} \cdot {{\varvec{\Gamma}}}^{ - 1} = \frac{1}{{L^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {L^{2} \left( {L - x} \right)} & 0 & 0 & {L^{2} x} \\ {\left( {L - x} \right)^{2} \left( {L + 2x} \right)} & {L\left( {L - x} \right)^{2} x} & 0 & {\left( {3L - 2x} \right)x^{2} } & {L\left( {x - L} \right)x^{2} } & 0 \\ {6x\left( {x - L} \right)} & {L\left( {L - 3x} \right)\left( {L - x} \right)} & 0 & {6x\left( {L - x} \right)} & {L\left( {3x - 2L} \right)x} & 0 \\ \end{array} } \right]$$

(41)

$${\mathbf{B}} = {\mathbf{B}}^{*} \cdot {{\varvec{\Gamma}}} = \frac{1}{{L^{3} }}\left[ {\begin{array}{*{20}c} 0 & 0 & { - L^{2} } & 0 & 0 & {L^{2} } \\ {6\left( {2x - L} \right)} & {L\left( {6x - 4L} \right)} & 0 & {6\left( {L - 2x} \right)} & {2L\left( {3x - L} \right)} & 0 \\ {6x\left( {x - L} \right)} & {L\left( {L - 3x} \right)\left( {L - x} \right)} & {L^{2} \left( {L - x} \right)} & {6x\left( {L - x} \right)} & {L\left( {3x - 2L} \right)x} & {L^{2} x} \\ \end{array} } \right]$$

(42)

Finally, the stiffness matrix and the vector of nodal forces can be respectively obtained as:

$$\begin{aligned} {\mathbf{K}} & = \int_{0}^{L} {{\mathbf{B}}^{T} \cdot {\mathbf{D}} \cdot {\mathbf{B}}} dx \\ {\mathbf{F}} & = \int_{{L_{1} }}^{{L_{2} }} {{\mathbf{N}}^{T} \cdot p\left( x \right)dx} \\ \end{aligned}$$

(43)

For instance, by considering a rectangular section with dimension $b \times h$, the constitutive matrix (36) becomes:

$${\mathbf{D}} = \left[ {\begin{array}{*{20}c} {\frac{68}{{105}}\tilde{E}I} & { - \frac{16}{{105}}\tilde{E}I} & 0 \\ { - \frac{16}{{105}}\tilde{E}I} & {\frac{1}{21}\tilde{E}I} & 0 \\ 0 & 0 & {\frac{8}{15}\tilde{G}A} \\ \end{array} } \right]$$

(44)

so that:

$${\mathbf{K}} = \frac{{2\tilde{E}I}}{{105L^{3} }}\left[ {\begin{array}{*{20}c} {30} & {15L} & 0 & { - 30} & {15L} & 0 \\ {15L} & {10L^{2} } & { - 8L^{2} } & { - 15L} & {5L^{2} } & {8L^{2} } \\ 0 & { - 8L^{2} } & {34L^{2} } & 0 & {8L^{2} } & { - 34L^{2} } \\ { - 30} & { - 15L} & 0 & {30} & { - 15L} & 0 \\ {15L} & {5L^{2} } & {8L^{2} } & { - 15L} & {10L^{2} } & { - 8L^{2} } \\ 0 & {8L^{2} } & { - 34L^{2} } & 0 & { - 8L^{2} } & {34L^{2} } \\ \end{array} } \right] + \frac{{2\tilde{G}A}}{225L}\left[ {\begin{array}{*{20}c} {72} & {6L} & { - 30L} & { - 72} & {6L} & { - 30L} \\ {6L} & {8L^{2} } & {5L^{2} } & { - 6L} & { - 2L^{2} } & { - 5L^{2} } \\ { - 30L} & {5L^{2} } & {20L^{2} } & {30L} & { - 5L^{2} } & {10L^{2} } \\ { - 72} & { - 6L} & {30L} & {72} & { - 6L} & {30L} \\ {6L} & { - 2L^{2} } & { - 5L^{2} } & { - 6L} & {8L^{2} } & {5L^{2} } \\ { - 30L} & { - 5L^{2} } & {10L^{2} } & {30L} & {5L^{2} } & {20L^{2} } \\ \end{array} } \right]$$

(45)

sum of a bending and a shear contribute.

The FEM analysis requires the solution of:

$${\mathbf{K}} \cdot {\mathbf{u}}^{n} = {\mathbf{F}}^{n}$$

(46)

The nodal force vector ${\mathbf{F}}^{n}$ can be determined by Eq. (43) in terms of the known applied load. For a beam subjected to a uniformly distributed load $\left( {q,m} \right)$, the nodal force vector is:

$${\mathbf{F}}^{n} = \frac{qL}{2}\left[ \begin{array}{l} 1 \\ L/12 \\ 0 \\ 1 \\ - L/12 \\ 0 \\ \end{array} \right] + \frac{mL}{2}\left[ \begin{gathered} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ \end{gathered} \right]$$

(47)

whereas a single force with components $\left( {P,M} \right)$ applied on a point $\overline{x} = \alpha L$ returns a nodal force vector:

$${\mathbf{F}}^{n} = P\left[ \begin{array}{l} \left( {\alpha^{2} - 1} \right)^{2} \left( {1 + 2\alpha } \right) \\ L\left( {\alpha - 1} \right)^{2} \alpha \\ 0 \\ \left( {3 - 2\alpha } \right)\alpha^{2} \\ L\left( {\alpha - 1} \right)\alpha^{2} \\ 0 \\ \end{array} \right] + M\left[ \begin{array}{l} 0 \\ 0 \\ 1 - \alpha \\ 0 \\ 0 \\ \alpha \\ \end{array} \right]$$

(48)

For instance, the clamped-simply supported beam in Fig. 4a loaded by a $\overline{q}\left( t \right) = q\,H\left( t \right)$ returns the displacement and the rotation field represented in Fig. 5.

Fig. 5

Example 1, displacement and rotation field

Figure 6 reports bending moment and shear forces, whereas in Fig. 7 the obtained results are compared with those derived analytically on a Timoshenko beam with dimension ratio $h = b = 0.01L$, a shear factor $\kappa = 5/6$ and following the procedure proposed in [13].

Fig. 6

Example 1, bending moment and shear force

Fig. 7

Example 1, comparison between Reddy and Timoshenko beam results (h = 0.01L, $\kappa$ = 5/6)

Agreement between present numerical results and exact solutions appear very satisfactory and demonstrate the efficiency, accuracy and reliability of the proposed approach and its applicability to a visco-elastic Reddy beam with fractional constitutive relationship. It is also worth noting that the differences between Reddy and Timoshenko models depend on the value assigned to the shear factor $\kappa$, and increase by increasing the $h/L$ ratio, as showed in Fig. 8.

Fig. 8

Example 1, comparison between Reddy and Timoshenko beam results (h = 0.1L, $\kappa$ = 100)

Figure 9 shows the percentage variation

$$\overline{w} = \left| {\frac{{w_{\max }^{R} - w_{\max }^{T} }}{{w_{\max }^{R} }}} \right| \times 100$$

between the maximum displacement obtained by considering the two models.

Fig. 9

Example 1, w_max percentage difference between Bernoulli (in red), Timoshenko and Reddy beam for different values of shear coefficient $\kappa$ and h/L ratio. (Color figure online)

In the same figure is also represented in red the difference $\overline{w}$ obtained by considering the visco-elastic Bernoulli beam model proposed in [9].

Finally, in Fig. 10 is depicted the strain field $\left( {\varepsilon_{x} ,\gamma_{xz} } \right)$ obtained in a generic instant t by substituting in Eq. (10) the generalized ${\overline{\mathbf{q}}}$ represented in Eq. (40).

Fig. 10

Example 1, deformation field

From all these figures it may be asserted that for a slender beam all the beam theories coalesce. However, as soon as the ratio h/L increases, all these theories lead to a quite different results in both displacement field and stress distribution.

5.2 Galerkin approach

Let us consider a visco-elastic, simply supported beam depicted in (Fig. 3b), having length L, section $b \times h$ and forced by an uniformly distributed load

$$\begin{aligned} & p\left( t \right) = pH\left( t \right) \\ & m\left( {x,t} \right) = 0 \\ \end{aligned}$$

(49)

with $H\left( t \right)$ unit step function, for which:

$$\left[ \begin{gathered} E_{\alpha } \\ G_{\alpha } \\ \end{gathered} \right]\left( {D_{{0^{ + } }}^{\alpha } \psi } \right)\left( t \right) = \left[ \begin{gathered} E_{\alpha } \\ G_{\alpha } \\ \end{gathered} \right]\left( {D_{{0^{ + } }}^{\alpha } H} \right)\left( t \right) = \left[ \begin{gathered} \frac{{E_{\alpha } t^{\alpha } }}{{\Gamma \left( {1 + \alpha } \right)}} \\ \frac{{G_{\alpha } t^{\alpha } }}{{\Gamma \left( {1 + \alpha } \right)}} \\ \end{gathered} \right]$$

(50)

Solution of Eq. (29) returns $\overline{w}_{2} \left( x \right) = \overline{\phi }_{2} \left( x \right) = 0$. For $\left( {\overline{w}_{1} \left( x \right),\overline{\phi }_{1} \left( x \right)} \right)$ we assume the following trigonometric series expansions:

$$\begin{aligned} & \tilde{\phi }_{1} \left( x \right) \simeq \overline{\phi }_{1} \left( x \right) = \sum\limits_{n = 1}^{N} {\Phi_{n} \cos \frac{n\pi x}{L}} \\ & \tilde{w}_{1} \left( x \right) \simeq \overline{w}_{1} \left( x \right) = \sum\limits_{n = 1}^{N} {W_{n} \sin \frac{n\pi x}{L}} \\ \end{aligned}$$

(51)

satisfying the natural and essential boundary conditions:

$$\begin{aligned} & w_{0} = w_{L} = 0 \\ & M_{0} = M_{L} = 0 \\ & - c_{1} P_{0} = - c_{1} P_{L} = 0 \\ \end{aligned}$$

(52)

Substitution of Eq. (51) in the equilibrium Eq. (28) returns the residual error:

$$\left[ \begin{gathered} R_{1} \\ R_{2} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} {\sum\limits_{n = 1}^{N} {\left( {c_{1} \tilde{E}\hat{J}\left( {\frac{{\Phi_{n} n^{2} \pi^{2} }}{{L^{2} }} + \frac{{W_{n} n^{3} \pi^{3} }}{{L^{3} }}} \right) - \tilde{E}\hat{I}\frac{{\Phi_{n} n^{2} \pi^{2} }}{{L^{2} }} - \tilde{G}\tilde{A}\left( {\Phi_{n} + \frac{{W_{n} n\pi }}{L}} \right)} \right)\cos \frac{n\pi x}{L} - m} } \\ {\sum\limits_{n = 1}^{N} {\left( {c_{1} \tilde{E}J\frac{{n^{3} \pi^{3} \Phi_{n} }}{{L^{3} }} - \tilde{G}\tilde{A}\left( {\frac{{\Phi_{n} n\pi }}{L} + \frac{{W_{n} n^{2} \pi^{2} }}{{L^{2} }}} \right) - c_{1}^{2} \tilde{E}K\left( {\frac{{\Phi_{n} n^{3} \pi^{3} }}{{L^{3} }} + \frac{{W_{n} n^{4} \pi^{4} }}{{L^{4} }}} \right)} \right)\sin \frac{n\pi x}{L}} - p} \\ \end{array} } \right]$$

(53)

Minimization of the weighted residual:

$$\begin{aligned} & \int_{0}^{L} {R_{1} \left( x \right)\sum\limits_{n = 1}^{N} {\cos \frac{n\pi x}{L}dx} = 0} \\ & \int_{0}^{L} {R_{2} \left( x \right)\sum\limits_{n = 1}^{N} {\sin \frac{n\pi x}{L}} dx = 0} \\ \end{aligned}$$

(54)

returns an algebraic system in the $\left( {\Phi_{n} ,W_{n} } \right)$ unknowns, which solution is:

$$\begin{aligned} & \Phi_{2N} = W_{2N} = 0 \\ & \Phi_{2N - 1} = \frac{{4L^{3} \left( {L^{2} \tilde{G}\tilde{A} - N^{2} c_{1} \tilde{E}\hat{J}\pi^{2} } \right)p}}{{\left( {2N - 1} \right)^{4} \pi^{4} \tilde{E}\left( {L^{2} \tilde{G}\tilde{A}\left( {\hat{I} + c_{1} J} \right) - \left( {2N - 1} \right)^{2} c_{1}^{2} \pi^{2} \tilde{E}\left( {J\hat{J} - \hat{I}K} \right)} \right)}} \\ & W_{2N - 1} = \frac{{4L^{4} \left( {N^{2} \pi^{2} \left( {c_{1} \tilde{E}\hat{J} - \tilde{E}\hat{I}} \right) - L^{2} \tilde{G}\tilde{A}} \right)p}}{{\left( {2N - 1} \right)^{5} \pi^{5} E\left( {L^{2} \tilde{G}\tilde{A}\left( {\hat{I} + c_{1} J} \right) - \left( {2N - 1} \right)^{2} c_{1}^{2} \pi^{2} \tilde{E}\left( {\hat{J}J - \hat{I}K} \right)} \right)}} \\ \end{aligned}$$

(55)

Considering in Eq. (55) $N = 1$, we obtain:

$$\begin{aligned} & \Phi_{1} = \frac{{4L^{3} \left( {L^{2} G_{\alpha } \tilde{A} - c_{1} E_{\alpha } \hat{J}\pi^{2} } \right)p}}{{\pi^{4} E_{\alpha } \left( {L^{2} G_{\alpha } \tilde{A}\left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {J\hat{J} - \hat{I}K} \right)} \right)}} \\ & W_{1} = \frac{{4L^{4} \left( {c_{1} E_{\alpha } \hat{J}\pi^{2} - E_{\alpha } \hat{I}\pi^{2} - L^{2} G_{\alpha } \tilde{A}} \right)p}}{{\pi^{5} E_{\alpha } \left( {L^{2} \tilde{G}A_{\alpha } \left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {\hat{J}J - \hat{I}K} \right)} \right)}} \\ \end{aligned}$$

(56)

that is:

$$\begin{aligned} & w\left( {x,t} \right) = \frac{{\left( {4L^{4} \left( {c_{1} E_{\alpha } \hat{J}\pi^{2} - E_{\alpha } \hat{I}\pi^{2} - L^{2} G_{\alpha } \tilde{A}} \right)p} \right)t^{\alpha } }}{{\pi^{5} E_{\alpha } \left( {L^{2} \tilde{G}A_{\alpha } \left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {\hat{J}J - \hat{I}K} \right)} \right)\Gamma \left( {1 + \alpha } \right)}}\sin \frac{\pi x}{L} \\ & \phi \left( {x,t} \right) = \frac{{\left( {4L^{3} \left( {L^{2} G_{\alpha } \tilde{A} - c_{1} E_{\alpha } \hat{J}\pi^{2} } \right)p} \right)t^{\alpha } }}{{\pi^{4} E_{\alpha } \left( {L^{2} G_{\alpha } \tilde{A}\left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {J\hat{J} - \hat{I}K} \right)} \right)\Gamma \left( {1 + \alpha } \right)}}\cos \frac{\pi x}{L} \\ \end{aligned}$$

(57)

depicted in Figs. 11 and 12 for selected values of time, and compared with finite element results.

Fig. 11

Example 2, displacement field

Fig. 12

Example 2, rotation field

Bending moment and shear forces, reported in Fig. 13, are consequently obtained as:

$$\begin{aligned} & M\left( {x,t} \right) = \frac{{\left( {4L^{4} \left( {c_{1} E_{\alpha } \hat{J}\pi^{2} - E_{\alpha } \hat{I}\pi^{2} - L^{2} G_{\alpha } \tilde{A}} \right)p} \right)}}{{\pi^{5} E_{\alpha } \left( {L^{2} \tilde{G}A_{\alpha } \left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {\hat{J}J - \hat{I}K} \right)} \right)}}\sin \frac{\pi x}{L} \\ & V\left( {x,t} \right) = \frac{{\left( {4L^{3} \left( {L^{2} G_{\alpha } \tilde{A} - c_{1} E_{\alpha } \hat{J}\pi^{2} } \right)p} \right)}}{{\pi^{4} E_{\alpha } \left( {L^{2} G_{\alpha } \tilde{A}\left( {\hat{I} + c_{1} J} \right) - c_{1}^{2} \pi^{2} E_{\alpha } \left( {J\hat{J} - \hat{I}K} \right)} \right)}}\cos \frac{\pi x}{L} \\ \end{aligned}$$

(58)

Fig. 13

Example 2, bending moment and shear force

6 Conclusion

In this paper we investigated the visco-elastic behavior of third-order shear deformation beam in time domain. The spring-pot model with fractional constitutive law has been used to better describe the visco-elastic behavior of the material as intermediate to purely elastic and purely viscous. The paper shows as, for quasi-static loading process, if the applied load can be represented in the uncoupled form ${\mathbf{p}}\left( {z,t} \right) = {\overline{\mathbf{p}}}\left( z \right) \cdot {{\varvec{\uppsi}}}\left( t \right)$, the displacement field can be obtained by amplifying the elastic solution by the Riemann–Liouville fractional integral of the load history ${{\varvec{\uppsi}}}\left( t \right)$. Numerical analyses on simple case examples, achieved by considering both Galerkin and finite element method and in very good agreement with ones available in literature for Timoshenko (first order) shear deformation beam theory, have shown the reliability of the proposed approach.