Introduction

The metal structures exhibit very low damping, responsible for high vibration amplitude. The vibration in the metal structures can be suppressed by providing surface-damping treatments [1]. Constrained layer damping (CLD) is a type of surface damping treatment in which the damping performance is achieved using various viscoelastic materials. Viscoelastic materials are used as dampers to reduce excessive sound and vibration in various engineering applications. The viscoelastic materials are generally used as a core, sandwiched between the base and constraining layers in the case of CLD treatment [2]. In general, the elastic modulus of the viscoelastic material is lower than the elastic moduli of isotropic and orthotropic material of the base and constraining layers of sandwich plates. So the energy dissipation mechanism in these structures is largely based on the shear deformation of the viscoelastic layers. Nowadays, the CLD treatment with viscoelastic material as a core is the most effective passive vibration control technique and finds a large number of applications in aerospace, aeronautics, and transportation engineering [3].

A viscoelastic material possesses both elastic and viscous behaviour. The storage modulus and the loss modulus are the primary properties of the viscoelastic material, which determine its response. The storage modulus represents the amount of energy stored, and the loss modulus represents the energy dissipated in the structure [4]. The mechanical characteristics of viscoelastic materials are varied by combining polymers with various reinforcements and fillers depending on the application, and for this reason, they are often unknown and need to be identified. Some methods for determining the mechanical characteristics of viscoelastic materials have been developed in the past. Dynamic mechanical analysis (DMA), a static testing method, is mainly used to determine the material properties of polymeric materials. Melo and Radford [5] investigated the influence of time and temperature on the viscoelastic properties of a transversely isotropic fibre-reinforced composite using DMA. Jrad et al. [6] performed the DMA test to characterize the non-linear dynamic behaviour of a viscoelastic structure. Performing DMA experiments, Rouleau et al. [7] studied the viscoelastic characteristics of a self-adhesive synthetic rubber using the generalized maxwell and fractional derivative models. Santawisuk et al. [8] obtained the dynamic viscoelastic characteristics of silicone soft liner materials using the DMA test.

The vibration-based material parameter identification is an effective non-destructive approach that has prompted many investigators to research. In many applications, using some empirical relationships, the material parameters of the viscoelastic material can be identified [9]. De Espindola et al. [10] developed an identification technique based on the vibration test to find the parameters of a fractional derivative model of the viscoelastic material. Using the vibration test data, the most common method for identifying the material properties of soft damping materials is the Oberst beam method [11], and the flow process of this identification method is designated at the ASTM E-756 standard. Moreover, based on the ASTM standard, Cortes and Elejabarrieta [12] identified the viscoelastic material properties utilizing the response of a cantilever beam in a free layer damping (FLD) configuration subjected to seismic excitation.

The inverse method of identifying the material parameters is based on the combination of experimental test results and theoretical analysis results. Generally, the structural responses can be determined by proper knowledge of the structure's geometrical and material properties. Thus using an inverse procedure, the measured structural responses may be utilized to identify the material properties of that structure. The inverse method for viscoelastic material parameter identification which is carried out in this study involves the determination of the unknown material parameters by comparing the model predictions with the experimental data. This is achieved by iteratively adjusting the material parameters until the difference between the model and experimental results is minimized. The inverse method relies on numerical optimization algorithms and knowledge of the structural response under various loading conditions. It is an effective way to obtain the material parameters, especially for materials that are difficult to characterize experimentally. However, it is important to note that the accuracy of the inverse method depends on the quality of the experimental data and the accuracy of the FE model used. This approach has the advantage of being able to handle complex loading conditions and can provide accurate results for materials with nonlinear behaviour.

Many researchers have identified the material parameters of different CLD and FLD configured structures using the inverse method. Shi et al. [13] proposed an inverse method for determining the material parameters of a sandwich beam using the measured resonance frequencies based on the Nelder–Mead (NM) simplex optimization approach. The frequency-dependent non-linear mechanical properties of a sandwich beam were obtained using the inverse method by Barkanov et al. [14]; the viscoelastic properties of a 3-M damping layer were determined using the response surface method and a constrained optimization approach. Araujo et al. [15] presented an inverse technique based on a gradient-based optimization method for estimating material parameters in piezoelectric, elastic, and viscoelastic laminated plate structures. The frequency-dependent viscoelastic parameters of laminated sandwich composite plates were also assessed [16]. Kim and Lee [17] identified the fractional-derivative-model parameters of viscoelastic materials using measured frequency response functions (FRFs). The impact test of the FLD beam was conducted in an environmental chamber with cantilever boundary conditions, and the FRFs were constructed at different temperatures. A gradient-based optimization algorithm yielded the optimal parameters of the viscoelastic material. Martinez-Agirre and Elejabarrieta [18] proposed an inverse approach for evaluating the material properties of a high-damping viscoelastic material. The resonance frequencies and FRFs of the cantilever CLD beam were measured from a forced vibration test. The Nelder–Mead simplex algorithm was used to obtain the optimal solution for minimizing the error between the experimental and numerical transfer functions. Schwaar et al. [19] provided a technique for identifying elastic and damping characteristics in a sandwich structure with a moderately stiff core. Elkhaldi et al. [20] presented a gradient approach for determining the viscoelastic behaviour of damped sandwich structures. The technique utilized experimental data, numerical simulations performed using a complex non-linear eigenvalue solver utilizing the asymptotic numerical method, and optimal control for identification of viscoelastic parameters. Allahverdizadeh et al. [21] characterized the material parameters of electrorheological fluid core adaptive sandwich beams. The experimental ASTM E756 method was coupled with the computational particle swarm optimization technique to determine the complex shear modulus of the viscoelastic layer. El-Hafidi et al. [22] presented an identification method based on vibration measurements utilizing sine-sweep excitation to determine the linear viscoelastic characteristics of a flax fibre-reinforced polymer composites. Ledi et al. [23] proposed an inverse technique based on the measured natural frequencies and modal loss factors to identify the material parameters of a three-layered viscoelastic sandwiched beam. The frequency-dependent viscoelastic material properties were identified for each mode of vibration by Hamdaoui et al. [24]. The quadratic error between the finite element model and the experimental modal data was minimized using an adjoint-based gradient technique. Sun et al. [25] characterized the mechanical parameters of a cantilever FLD plate by an inverse technique based on the measured resonance frequencies and FRFs. Two kinds of damping (viscous and material damping) were considered, and the material parameters were obtained using response surface methodology and a constrained optimization approach. For inverse viscoelastic material identification, a parametric model order reduction technique was developed by Xie et al. [26]. Inverse optimization methods for material parameter identification are not limited to viscoelastic sandwich plates. Recently, a new optimization algorithm, Neural network optimization (NNO), was applied for the inverse identification of the constitutive properties of bricks and mortar in unreinforced masonry walls, simulated with the concrete damaged plasticity model, to describe the behaviour of such masonry structures by Albu-Jasim and Papazafeiropoulos [27]. Grosso et al. [28] introduced a new methodology for identifying non-traditional viscoelastic models from vibration data using the circle-fit technique. The proposed method was used to analyse aluminium plates covered with dampening pads and plates composed of quiet aluminium. A theoretical and experimental investigation by Pierro and Carbone [29] was reported to describe the hysteretic characteristics of viscoelastic materials. The mechanical properties of a viscoelastic beam were defined theoretically using an accurate analytical model, and experimental data were fitted to derive the complex modulus. To estimate the frequency-dependent complex modulus of the viscoelastic layer, Kang et al. [30] employed a genetic algorithm to fit the analytical solution of the frequency response function of a free–free viscoelastic sandwich beam. Based on the modal analysis responses, Chandra et al. [31] identified the elastic and damping properties of the carbon-epoxy symmetric cross-ply and angle-ply laminates as a function of temperature. Orta et al. [32] presented an inverse technique based on the three-dimensional surface velocity response to analyse the complex-valued stiffness characteristics of an arbitrary orthotropic viscoelastic plate. Several synthetic data sets were created to represent composite and wood panels, and the developed inversion technique was verified on these data sets, demonstrating their good performance with negligible error.

Viscoelastic materials are mainly employed to reduce structural vibrations effectively. The theoretical study and design of these structures need an understanding of mechanical properties that are primarily dependent on frequency. Accurate determination of the frequency-dependent constitutive parameters of viscoelastic materials is essential for a wide range of engineering applications. The literature discussed above enumerates the parameter identification using structural vibration responses for various polymeric viscoelastic materials. The parameter identification approaches were presented for a similar range of materials. Many inverse identification methods were based on specific model assumptions that may not hold for all materials or systems, leading to limitations in their accuracy and applicability. Other identification techniques are often sensitive to initial conditions, making it difficult to find an optimal global solution for the frequency-dependent material parameters, or are computationally intensive, and, therefore, difficult to implement in real-time or for large data sets. Furthermore, concerted efforts through both experimental and theoretical investigation toward constitutive parameter identification are scarce in literature and far from complete, which needs further attention to get the inversely optimal result regarding the identification of various structural properties. The present study makes an attempt to cover the aforementioned shortcomings. However, to the best of the author’s knowledge, no study in the literature has attempted a material properties identification procedure for natural rubber. There is a significant need for efficient methods to identify the frequency-dependent characteristics of natural rubber to understand its behaviour better and optimize its performance. This study aims to address this research gap by using a novel inverse identification method, the NNO, to accurately determine the viscoelastic material properties of natural rubber, providing new insights into the behaviour of this important material. More specifically, the present study identifies the frequency-dependent shear storage modulus and loss factors of natural rubber using a new metaheuristic approach, known as neural network optimization (NNO), through the concerted efforts of experimental and theoretical investigation. The use of NNO algorithm overcomes the limitations mentioned above by providing a more flexible and efficient way of learning from large amounts of data including both experimental and simulation results, by being insensitive to any initial conditions and finally by being able to be trained to make targeted, accurate predictions of any material’s properties.

To this end, a symmetric three-layered sandwich plate is considered with aluminium as face layers and natural rubber as a core layer. Free vibration tests are performed on the structure using the impact hammer method under a clamped-free boundary condition. The theoretical model confirming the empirical scenario is developed utilizing a finite element technique in MATLAB programming language. The frequency-dependent viscoelastic material properties of natural rubber are identified by minimizing the error between corresponding experimental and numerical structural responses. To minimize the error function, the novel NNO algorithm is used. The proposed inverse technique relies on vibration tests, detailed theoretical modelling, and a convergence criterion for the optimal solution of identified parameters. Besides, the elicited results are successfully validated with experimental results through the DMA test. Apart from the above, the efficiency of the NNO method as an inverse optimizer is shown, and its capability of automatically developing an equivalent neural network of the finite element model under consideration is described in detail. Thereafter, a numerical parametric analysis is performed considering the core's optimized viscoelastic material properties to study the influence of various geometrical factors on the sandwich plate's free vibration response. The use of neural network optimization algorithms can improve the performance of the inverse identification method by reducing the computational time and complexity compared to traditional optimization methods. The algorithm can also provide interpretable results, allowing for a deeper understanding of the behaviour of viscoelastic materials and the optimization process.

The organization of this study is as follows: in "Experimental Investigation", the experimental investigation carried out for the present research work is detailed. In "Finite Element Modelling of the Sandwich Plate", the numerical modelling procedure of the sandwich plate using finite element analysis is presented. In "Identification of Material Parameters", the material parameter identification procedure based on the NNO method is described. In "Results and Discussion", the natural rubber's frequency-dependent shear storage modulus and loss factors are identified using the proposed inverse method and verified with the DMA test results. The numerical parametric analysis is then discussed.

Experimental Investigation

The experimental research work in the present study includes: (1) a free vibration test of the sandwich specimen to obtain its structural responses. (2) a DMA test for determining the viscoelastic material properties of natural rubber. The following sections provide the details of the experimental procedures.

Free Vibration Test

Viscoelastic Sandwich Specimens

Rectangular sandwich plates with viscoelastic cores are fabricated and used as specimens for experimentation. The hand lay-up method is used for fabrication purposes [33]. The proposed sandwich plate is comprised of three layers, i.e., two face layers (top and bottom) and one core layer (middle layer). The faceplates are made of aluminium, and the core is made of natural rubber. The sandwich plates are manually cured by placing heavy iron sheets on them for 72 h at room temperature. The loads are removed after curing, and the plate surfaces are cleaned with acetone to make them free from any impurities. The sandwich plates are then subjected to modal testing employing the impact hammer method.

Impact Hammer Modal Testing

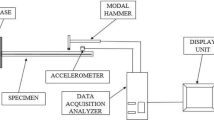
The impact hammer method is a non-destructive vibration testing method for structural analysis. This modal testing technique makes it possible to measure a vibrating structure's frequency response functions. Each FRF is a representation of the spectrum of the vibration that occurs at a single point on the structure, in a specific direction, in response to a unit force that is imparted at some other position on the structure. The block diagram, along with the original photograph of the experimental set-up for the present modal testing, is presented in Figs. 1 and 2. The experimental set-up of the free vibration test relies on the following equipment:

  • FFT analyzer

  • Modal hammer

  • Accelerometer

  • PC with modal analysis software

  • Clamps for holding the specimen

Fig. 1
figure 1

Block diagram of the experimental set-up for modal testing of the sandwich plate under a clamped-free boundary condition

Full size image
Fig. 2
figure 2

Photograph of the experimental set-up for modal testing of the sandwich plate under a clamped-free boundary condition

Full size image

The sandwich plate is fitted to the pre-assembled iron frame with the help of C-clamps to ensure a clamped-free boundary condition. The modal hammer and accelerometer are connected to the FFT analyzer's respective channel, and the FFT analyzer is connected to a PC. The roving hammer technique is adopted for the vibration measurement in which the accelerometer is fixed at one position on the sandwich plate, and the test specimen is excited by moving the modal hammer at different marked points on the sandwich plate. The accelerometer attached to the sandwich plate receives the response generated by the impact of the modal hammer. The FFT analyzer receives a time-varying signal from the accelerometer, converts it into a frequency-based signal known as the frequency response function, and transfers those resulting FRFs to the computer. The modal analysis software Pulse Labshop and ME'scope are used to accomplish experimental modal analysis. The PC with preinstalled Pulse Labshop software captured those FRF spectrums with fine coherence. The impact-testing module of Pulse Labshop software records a series of five impacts at a given point for each testing configuration in accordance with the FRF measurement protocol. The recorded data are further post-processed with ME'scope software to obtain the vibrational characteristics of the sandwich plate. To avoid experimental errors, a substantial number of sandwich plate samples are prepared and tested, and the average of the vibration results is taken into account.

Estimation of Modal Loss Factor

The modal damping associated with a particular eigenmode is usually computed using the half-power bandwidth (HPB) method. The HPB method is quite useful in determining the magnitude of the resonance peak within the recorded FRF corresponding to the selected mode and then assessing the upper (\(\omega_{{{\text{upper}}}}\)) and lower bound (\(\omega_{{{\text{lower}}}}\)) frequencies corresponding to a 3 Db reduction from the peak amplitude of the damped resonant frequency (\(\omega_{{{\text{damped}}}}\)). The calculation for the modal damping ratio (\(\zeta\)) is as follows:

$$\zeta = \frac{{\omega_{{{\text{upper}}}} - \omega_{{{\text{lower}}}} }}{{\omega_{{{\text{damped}}}} }}.$$
(1)

The relationship between the modal loss factor (\(\eta_{{\text{s}}}\)) and modal damping ratio (\(\zeta\)) of a structure can be expressed by [34],

$$\eta_{{\text{s}}} = 2\zeta .$$
(2)

DMA Test

Measurements of frequency-dependent viscoelastic material properties of the natural rubber are carried out on a dynamical mechanical analyzer, DMA-8000. The experimental set-up for the DMA-8000 is presented in Fig. 3. For the measurement, the DMA-8000 is configured in the shear mode for testing. This is achieved by two samples of equal dimensions being sheared between a movable plate and a fixed plate. The natural rubber samples are prepared in line with ASTM D4065 standard, and the sample geometry in the lateral direction is confirmed as 10 mm × 10 mm and a thickness of 2.5 mm. The adhesion between clamps and samples is ensured by applying a compressive pre-strain in a range of 0–10% during the clamping of the specimen in DMA 8000. The viscoelasticity behaviour was observed by taking the samples into account, inducing the dynamic displacement ranging from 1 to 10 μm to a reference frequency of 0–100 Hz and temperature of 23.5 °C. With a temperature ramp phenomenon, the dynamic behaviour of natural rubber is investigated through a multi-frequency test.

Fig. 3
figure 3

Photograph of the experimental set-up of DMA-8000

Full size image

Finite Element Modelling of the Sandwich Plate

To apply the finite element method (FEM) to a three-layered sandwich plate with a viscoelastic core the following steps are egenrally followed: (1) the geometry of the plate is modelled and the kinematic relationships between all layers are defined, (2) the plate is discretized into finite elements which form a system of interconnected nodes, and carry the material and section definitions of the plate, (3) the global stiffness and mass matrices are assembled, which, along with the boundary conditions of the plate, form a system of equations, (4) the system of equations is then solved for the complex eigenvalue problem considered in this study, (5) finally, the natural frequencies and modal loss factors are extracted from the FEM solutions and can be used to characterize the mechanical response of the three-layered sandwich plate. The following subsections provide detailed explanations of the aforementioned steps.

A three-layered sandwich plate with face layers of isotropic elastic material and a core layer of viscoelastic material is shown in Fig. 4. The geometrical outline of the sandwich structure's deformation scheme is represented in Fig. 4b, which depicts the dimensions of the sandwich plate as 'a' and 'b' along its sides in the Cartesian coordinates. \(h_{1} ,h_{2}\) and \(h_{3}\) are the thickness of the elastic base layer, viscoelastic core layer and elastic constraining layer accordingly.

Fig. 4
figure 4

Schematic diagram of the sandwich structure

Full size image

Some basic assumptions are considered for the numerical modelling of the sandwich plate under consideration. First-order shear deformation theory (FSDT) is employed to model the base and constraining layer displacement kinematics. Aspects such as longitudinal and shear deformation of the core are taken into account, making the model more efficient for sandwich structures with thin and thick core layers [35]. The base and constraining layers exhibit transverse displacements independent of each other. The core layer's in-plane and transverse displacements vary linearly throughout its thickness. The absence of sliding movement between layers at their interface ensured perfect continuity. The core material is assumed to be linearly viscoelastic with a complex frequency-dependent shear modulus.

Kinematic Equations

Based on FSDT, the displacement field equations at any point on the elastic base layer are as follows:

$$\begin{aligned} u^{\prime}_{1} & = u_{1} + (z + p^{1} )\theta_{x1} \\ v^{\prime}_{1} & = v_{1} + (z + p^{1} )\theta_{y1} \\ w^{\prime}_{1} & = w_{1} , \\ \end{aligned}$$
(3a)

with \(p^{1} = \frac{{h_{1} + h_{2} }}{2}\) and \(- h_{1} - \frac{{h_{2} }}{2} \le z \le - \frac{{h_{2} }}{2}\), where \(u_{1} ,v_{1}\) and \(w_{1}\) are the mid-displacements of any point on the elastic base layer along the Cartesian coordinates. θx1' and 'θy1' are the rotations of the tangents of the mid-plane of the elastic base layer about the y-axis and x-axis, respectively. Similarly, for the elastic constraining layer, the displacement field equations at any point are:

$$\begin{aligned} u^{\prime}_{3} & = u_{3} + (z - p^{3} )\theta_{x3} \\ v^{\prime}_{3} & = v_{3} + (z - p^{3} )\theta_{y3} \\ w^{\prime}_{3} & = w_{3} , \\ \end{aligned}$$
(3b)

with, \(p^{3} = \frac{{h_{3} + h_{2} }}{2}\) and \(\frac{{h_{2} }}{2} \le z \le \frac{{h_{2} + h_{3} }}{2}\),where \(u_{3} ,v_{3}\) and \(w_{3}\) are the mid-displacements of a point on the elastic constraining layer along Cartesian coordinates. Here the y-axis and x-axis mid-plane rotational tangents of the elastic constraining layers are noted as 'θx3' and 'θy3', respectively.

The kinematic relations of the viscoelastic core layer are obtained from the top and bottom laminae's kinematics. As per the analysis assumptions, the transverse and in-plane displacements are linear in the thickness direction. The displacement field equations for the viscoelastic core layer are as follows:

$$\begin{aligned} u^{\prime}_{2} & = \left[ {\frac{{u_{1} + u_{3} }}{2} + \frac{{h_{1} \theta_{x1} - h_{3} \theta_{x3} }}{4}} \right] + \left[ {\frac{{u_{3} - u_{1} }}{{h_{2} }} - \frac{{h_{1} \theta_{x1} + h_{3} \theta_{x3} }}{{2h_{2} }}} \right]z \\ v^{\prime}_{2} & = \left[ {\frac{{v_{1} + v_{3} }}{2} + \frac{{h_{1} \theta_{y1} - h_{3} \theta_{y3} }}{4}} \right] + \left[ {\frac{{v_{3} - v_{1} }}{{h_{2} }} - \frac{{h_{1} \theta_{y1} + h_{3} \theta_{y3} }}{{2h_{2} }}} \right]z \\ w^{\prime}_{2} & = \left[ {\frac{{w_{1} + w_{3} }}{2}} \right] + \left[ {\frac{{w_{3} - w_{1} }}{{h_{2} }}} \right]z. \\ \end{aligned}$$
(4)

The strain–displacement relationship for the elastic face layers can be expressed as follows:

$$\varepsilon_{kp} = \left[ {\begin{array}{*{20}c} {u^{\prime}_{k,x} } \\ {v^{\prime}_{k,y} } \\ {u^{\prime}_{k,y} + v^{\prime}_{k,x} } \\ \end{array} } \right],$$
(5a)
$$\varepsilon_{kb} = \left[ {\begin{array}{*{20}c} {\theta_{xk,x} } \\ {\theta_{yk,y} } \\ {\theta_{xk,y} + \theta_{yk,x} } \\ \end{array} } \right],$$
(5b)
$$\gamma_{ks} = \left[ {\begin{array}{*{20}c} {\theta_{yk} + w^{\prime}_{k,x} } \\ {\theta_{xk} + w^{\prime}_{k,y} } \\ \end{array} } \right],$$
(5c)

where, \(\varepsilon_{kp}\), \(\varepsilon_{kb}\) and \(\gamma_{ks}\) are the in-plane axial, bending and shear strain vectors for the elastic face layers (k = 1, 3). The notations (),x and (),y signify the partial derivative concerning the 'x' and the 'y' coordinate.

The strain–displacement relationship for the viscoelastic core layer can be expressed as follows:

$$\varepsilon_{2l} = \left[ {\begin{array}{*{20}c} {u^{\prime}_{2,x} } \\ {v^{\prime}_{2,y} } \\ {u^{\prime}_{2,y} + v^{\prime}_{2,x} } \\ \end{array} } \right],$$
(6a)
$$\varepsilon_{2t} = \left[ {w^{\prime}_{2,z} } \right],$$
(6b)
$$\gamma_{2s} = \left[ {\begin{array}{*{20}c} {u^{\prime}_{2,z} + w^{\prime}_{2,x} } \\ {v^{\prime}_{2,z} + w^{\prime}_{2,y} } \\ \end{array} } \right],$$
(6c)

where \(\varepsilon_{2l}\), \(\varepsilon_{2t}\) and \(\gamma_{2s}\) are the longitudinal, transverse and shear strain vectors for the viscoelastic core layer, respectively.

Energy Expressions

Energy expressions for the strain energy (U) and kinetic energy (T) are used to calculate the structure's stiffness and mass matrices. The total strain energy (Ue) of the sandwich plate element is composed of the relative energy contributions of the base layer (U1e), viscoelastic core layer (U2e) and constraining layer (U3e), which can be represented as follows:

$$U^{e} = U_{1e} + U_{2e} + U_{3e} .$$
(7)

The sum of the strain energies caused by the in-plane axial, bending and shear deformation are used to characterize the total strain energy of the elastic face layers. This allows the total strain energy for the face layers (k = 1, 3) to be expressed in mathematical form as follows:

$$U_{ke} = \frac{1}{2}\int\limits_{A} {\left( {\varepsilon_{kp} } \right)^{T} \left( {A_{kij} } \right)} \left( {\varepsilon_{kp} } \right){\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\varepsilon_{kb} } \right)^{T} \left( {D_{kij} } \right)} \left( {\varepsilon_{kb} } \right){\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\gamma_{ks} } \right)^{T} \left( {S_{kij} } \right)} \left( {\gamma_{ks} } \right){\text{d}}A.$$
(8)

The coefficient matrices for the elastic face layers (k = 1, 3) are presented as follows:

$$\begin{array}{*{20}c} {\left( {A_{kij} ,D_{kij} } \right) = \int\limits_{{{\raise0.7ex\hbox{${ - h_{k} }$} \!\mathord{\left/ {\vphantom {{ - h_{k} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${h_{k} }$} \!\mathord{\left/ {\vphantom {{h_{k} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {Q_{kij} (1,z^{2} )\begin{array}{*{20}c} {} \\ \end{array} {\text{d}}z} } & {i,j = 1,2,6} \\ \end{array} ,$$
(9a)
$$(S_{kij} ) = {\text{K}}_{{\text{s}}} \int\limits_{{{\raise0.7ex\hbox{${ - h_{k} }$} \!\mathord{\left/ {\vphantom {{ - h_{k} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${h_{k} }$} \!\mathord{\left/ {\vphantom {{h_{k} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {Q_{kij} \begin{array}{*{20}c} {} \\ \end{array} {\text{d}}z} \begin{array}{*{20}c} {} & {i,j = 4,5} \\ \end{array} ,$$
(9b)

where the stiffness coefficients of the elastic face layers are given as follows:

\(Q_{{k_{11} }} = Q_{{k_{22} }} = \frac{{E_{k} }}{{1 - \upsilon_{k}^{2} }};Q_{{k_{12} }} = \frac{{\upsilon_{k} E_{k} }}{{1 - \upsilon_{k}^{2} }};Q_{{k_{44} }} = Q_{{k_{55} }} = Q_{{k_{66} }} = \frac{{E_{k} }}{{2(1 + \upsilon_{k} )}}\) for k = 1, 3 and Ks is the shear correction factor whose value is taken as 5/6.

The sum of the strain energies resulting from longitudinal, transverse and shear deformation are used to describe the total strain energy of the viscoelastic core layer. This allows the total strain energy for the viscoelastic core layer to be expressed in mathematical form as follows:

$$U_{2e} = \frac{1}{2}\int\limits_{A} {\left( {\varepsilon_{2l} } \right)^{T} \left( {A_{2ij} } \right)} \left( {\varepsilon_{2l} } \right){\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\varepsilon_{2t} } \right)^{T} E_{2} } \left( {\varepsilon_{2t} } \right){\text{d}}A + \frac{1}{2}\int\limits_{A} {\left( {\gamma_{2s} } \right)^{T} \left( {S_{2ij} } \right)} \left( {\gamma_{2s} } \right){\text{d}}A.$$
(10)

The coefficient matrices for the viscoelastic core layer are presented as follows:

$$(A_{{2ij_{1} }} ,A_{{2ij_{2} }} ) = \int\limits_{{{\raise0.7ex\hbox{${ - h_{2} }$} \!\mathord{\left/ {\vphantom {{ - h_{2} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${h_{2} }$} \!\mathord{\left/ {\vphantom {{h_{2} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {Q_{2ij} (1,z_{n}^{2} )\begin{array}{*{20}c} {} \\ \end{array} {\text{d}}z} \begin{array}{*{20}c} {} & {i,j = 1,2,6} \\ \end{array} ,$$
(11a)
$$(S_{{2ij_{1} }} ,S_{{2ij_{2} }} ) = K_{{\text{s}}} \int\limits_{{{\raise0.7ex\hbox{${ - h_{2} }$} \!\mathord{\left/ {\vphantom {{ - h_{2} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${h_{2} }$} \!\mathord{\left/ {\vphantom {{h_{2} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {Q_{2ij} (1,z_{n}^{2} )\begin{array}{*{20}c} {} \\ \end{array} {\text{d}}z} \begin{array}{*{20}c} {} & {i,j = 4,5} \\ \end{array} ,$$
(11b)

where the stiffness coefficients of the viscoelastic core are given as follows:

\(Q_{{2_{11} }} = Q_{{2_{22} }} = \frac{{E_{2} }}{{1 - \upsilon_{2}^{2} }};Q_{{2_{12} }} = \frac{{\upsilon_{2} E_{2} }}{{1 - \upsilon_{2}^{2} }};Q_{{2_{44} }} = Q_{{2_{44} }} = Q_{{2_{66} }} = G_{2}\) and Ks is the shear correction factor whose value is taken equal to 5/6.

In the present analysis, the rheological characteristics of the viscoelastic material are considered according to the complex modulus approach [36]. Thus for the core layer, the complex Young's modulus of the viscoelastic material can be represented as, \(E_{2} = E_{{\text{v}}} (1 + i\beta_{{\text{v}}} )\) and the complex shear modulus can be defined as, \(G_{2} = G_{{\text{v}}} (1 + i\beta_{{\text{v}}} )\), where \(E_{{\text{v}}}\) and \(G_{{\text{v}}}\) represents the storage modulus and \(\beta_{{\text{v}}}\) is the loss factor of the viscoelastic material.

In a similar manner, the total kinetic energy (Te) of the sandwich plate element is defined by the relative energy contributions from the base layer (T1e), the viscoelastic core layer (T2e), and the constraining layer (T3e), which can be expressed as follows:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {T^{e} = T_{1e} + T_{2e} + T_{3e} } & { = \sum\limits_{k = 1}^{3} \frac{1}{2} } \\ \end{array} } \\ \end{array} \int\limits_{v} {\rho_{k} (\dot{u}_{k}^{\prime 2} } + \dot{v}_{k}^{\prime 2} + \dot{w}_{k}^{\prime 2} ){\text{d}}v,$$
(12)

where \(\dot{u}^{\prime}_{k} ,\dot{v}^{\prime}_{k} ,\dot{w}^{\prime}_{k}\) are the 1st derivatives of the displacements with respect to time.

Degrees of Freedom (DOF) and Shape Functions

In the present study, an eight-node, three-layered rectangular sandwich element is proposed for the finite element discretization of the sandwich plate. The nodes are presumed to be located on the sandwich panel's geometrical mid-plane, as shown in Fig. 5. Degrees of freedom are assigned to each node, comprising two axial displacements, one transverse displacement, and two angular rotations of the elastic base layer and the constraining layer, respectively [37].

Fig. 5
figure 5

An eight-node finite sandwich plate element

Full size image

By using iso-parametric mapping, any point (x, y) within the element can be represented as follows:

$$x = \sum\limits_{i = 1}^{8} {N_{i} (\xi ,\eta )x_{i} ,} \quad {\text{and}}\quad y = \sum\limits_{i = 1}^{8} {N_{i} (\xi ,\eta )y_{i} } ,$$
(13)

where \(N_{i}\) is a representation of the shape functions of the second order at the ith node in natural coordinates. At any point within the element, the generalized displacement vector \((\delta )\) may be represented in the following form:

$$\delta = \left\{ {u_{1} ,v_{1} ,w_{1} ,\theta_{x1} ,\theta_{y1} ,u_{3} ,v_{3} ,w_{3} ,\theta_{x3} ,\theta_{y3} } \right\}^{T} .$$
(14)

Expressing Eq. (14) in terms of matrix form as follows:

$$\delta = \sum\limits_{i = 1}^{8} {Nq_{i}^{e} } ,\quad i = 1,...8,$$
(15)

where, N is the shape function matrix and \(q^{e} = \left\{ {\delta_{1} ,\delta_{2} ,\delta_{3} ,....\delta_{8} } \right\}^{T}\) is the elemental displacement vector. The standard second-order serendipity shape functions (\(N_{i}\)) from the shape function matrix are expressed as follows [38]:

$$\begin{aligned} N_{1} & = \frac{1}{4}(1 - \xi )(1 - \eta )( - \xi - \eta - 1),\quad N_{2} = \frac{1}{4}(1 + \xi )(1 - \eta )(\xi - \eta - 1), \\ N_{3} & = \frac{1}{4}(1 + \xi )(1 + \eta )(\xi + \eta - 1),\quad N_{4} = \frac{1}{4}(1 - \xi )(1 + \eta )( - \xi + \eta - 1), \\ N_{5} & = \frac{1}{2}(1 + \xi )(1 - \xi )(1 - \eta ),\quad N_{6} = \frac{1}{2}(1 + \xi )(1 + \eta )(1 - \eta ), \\ N_{7} & = \frac{1}{2}(1 + \xi )(1 - \xi )(1 + \eta ),\quad N_{8} = \frac{1}{2}(1 - \xi )(1 + \eta )(1 - \eta ), \\ \end{aligned}$$
(16)

where \(\xi = {x \mathord{\left/ {\vphantom {x {\text{a}}}} \right. \kern-0pt} {\text{a}}}\) and \(\eta = {y \mathord{\left/ {\vphantom {y {\text{b}}}} \right. \kern-0pt} {\text{b}}}\) are the reduced coordinates used in the above shape function expressions.

The elemental strain–displacement relationships of the face layers from Eq. (5) may be described in terms of the nodal-displacement vector as follows:

$$\left[ {\varepsilon_{kp}^{e} } \right] = \left[ {B_{kp}^{e} } \right]q^{e} ,\;\left[ {\varepsilon_{kb}^{e} } \right] = \left[ {B_{kb}^{e} } \right]q^{e} \;{\text{and}}\;\begin{array}{*{20}c} {\left[ {\gamma_{ks}^{e} } \right] = \left[ {B_{ks}^{e} } \right]q^{e} \quad {\text{for}}\;k = 1,3} \\ \end{array} ,$$
(17)

where \(\left[ {B_{kp}^{e} } \right],\left[ {B_{kb}^{e} } \right]\) and \(\left[ {B_{ks}^{e} } \right]\) are the elemental strain–displacement matrices arising due to the in-plane axial, bending and shear deformation of the elastic face layers. Similarly, the elemental strain–displacement relationships of the viscoelastic core layer from Eq. (6) may be described in terms of the nodal-displacement vector as follows:

$$\left[ {\varepsilon_{2l}^{e} } \right] = \left[ {B_{2l}^{e} } \right]q^{e} ,\;\left[ {\varepsilon_{2t}^{e} } \right] = \left[ {B_{2b}^{e} } \right]q^{e} \;{\text{and}}\;\begin{array}{*{20}c} {\left[ {\gamma_{2s}^{e} } \right] = \left[ {B_{2s}^{e} } \right]q^{e} } \\ \end{array} ,$$
(18)

where \(\left[ {B_{2l}^{e} } \right]\), \(\left[ {B_{2t}^{e} } \right]\) and \(\left[ {B_{2s}^{e} } \right]\) are the elemental strain–displacement matrices arising due to the longitudinal, transverse and shear deformation of the viscoelastic core layer.

The total strain energy for the sandwich plate element may be represented in the form of stiffness matrices, as follows:

$$\begin{aligned} U^{e} & = U_{1e} + U_{2e} + U_{3e} \\ & = \frac{1}{2}\sum\limits_{k = 1,3} {q^{{e^{T} }} \left[ {K_{kp}^{e} + K_{kb}^{e} + K_{k\gamma }^{e} } \right]q^{e} } + \frac{1}{2}q^{{e^{T} }} \left[ {K_{2l}^{e} + K_{2t}^{e} + K_{2\gamma }^{e} } \right]q^{e} \\ & = \frac{1}{2}q^{{e^{T} }} \left[ {K_{1e} + K_{2e} + K_{3e} } \right]q^{e} , \\ \end{aligned}$$
(19)

where \(\left[ {K_{1e} } \right]\), \(\left[ {K_{2e} } \right]\) and \(\left[ {K_{3e} } \right]\) are the elemental stiffness matrices for the elastic base layer, viscoelastic core layer and elastic constraining layer, respectively. As a result, the sandwich plate's element stiffness matrix, \(\left[ {K^{e} } \right]\) may be expressed by summation of the stiffness matrices of the three layers as follows:

$$\left[ {K^{e} } \right] = \left[ {K_{1e} } \right] + \left[ {K_{2e} } \right] + \left[ {K_{3e} } \right].$$
(20)

In its most generic form, the elemental stiffness matrix can be computed as follows:

$$\left[ {K^{e} } \right] = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {B^{T} } \right]} } \left[ D \right]\left[ B \right]{\text{d}}A.$$
(21)

Similarly, the total kinetic energy of the sandwich plate element may be represented in the form of mass matrices as follows:

$$\begin{aligned} T^{e} & = T_{1e} + T_{2e} + T_{3e} \\ & = \sum\limits_{k = 1}^{3} \frac{1}{2} \int\limits_{v} {\rho_{k} (\dot{u^{\prime}}_{k}^{2} } + \dot{v^{\prime}}_{k}^{2} + \dot{w^{\prime}}_{k}^{2} ){\text{d}}v \\ & = \frac{1}{2}\dot{q}^{{e^{T} }} \left[ {M_{1e} + M_{2e} + M_{3e} } \right]\dot{q}^{e} . \\ \end{aligned}$$
(22)

The elemental mass matrices in the above expression are \(\left[ {M_{1e} } \right],\left[ {M_{2e} } \right]\) and \(\left[ {M_{3e} } \right]\) accounted for the elastic base layer, viscoelastic core layer and elastic constraining layer, respectively. As a result, the sandwich plate's element mass matrix,\(\left[ {M^{e} } \right]\) may be expressed as a sum of the mass matrices of the following three layers:

$$\left[ {M^{e} } \right] = \left[ {M_{1e} } \right] + \left[ {M_{2e} } \right] + \left[ {M_{3e} } \right].$$
(23)

In its most generic form, the elemental mass matrix can be computed as follows:

$$\left[ {M^{e} } \right] = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ {N^{T} } \right]} } \left[ I \right]\left[ N \right]{\text{d}}A.$$
(24)

Governing Equations of Motion

Based on Hamilton's principle, the governing equation of motion is derived for the sandwich plate element and can be presented as follows:

$$\int\limits_{\tau 1}^{\tau 2} {\delta \left( {U^{e} - T^{e} } \right)} \;{\text{d}}\tau = 0,$$
(25)

where \(U^{e}\) is the total strain energy and \(T^{e}\) is the total kinetic energy for the sandwich plate element. Substituting the above-discussed energy expressions from Eqs. (19) and (22) in Eq. (25), the equation of motion for the three-layered sandwich plate element is obtained as follows:

$$\left( {K^{e} - \lambda^{e} M^{e} } \right)q^{e} = 0.$$
(26)

For the three-layered sandwich plate, the governing equation of motion in global coordinates can be derived by assembling the element matrices, which take the form as follows:

$$\left( {K - \lambda M} \right)q = 0,$$
(27)

where \(\left[ K \right]\) and \(\left[ M \right]\) are the sandwich plate's global stiffness and mass matrix, respectively, and \(q\) stands for the global displacement vector. To find a substantial non-zero solution for the given expression, the following equation must hold:

$$\left| {K - \lambda M} \right| = 0.$$
(28)

Equation (28) is an eigenvalue problem that may be solved analytically to get the values \(\lambda\). Due to the viscoelasticity of the core material, the value of \(\lambda\) is a complex number, which can be written as follows:

$$\lambda = \omega^{2} \left( {1 + j\eta_{{\text{s}}} } \right),$$
(29)

where \(\omega\) represents the natural frequency and \(\eta_{{\text{s}}}\) represents the modal loss factor for the sandwich plate. The modal loss factor is a measure of the structure's damping capabilities. The modal loss factor signifies energy dissipation owing to the structure's viscoelasticity. The higher the modal loss factor value, the greater the amount of energy absorbed by the sandwich plate and the better the damping properties achieved. The natural frequency and the modal loss factor for the three-layered sandwich plate with a viscoelastic core can be given as follows:

$$\omega = \sqrt {{\text{Real}}(\lambda )} \quad {\text{and}}\quad \eta_{{\text{s}}} = \frac{{{\text{Imag}}(\lambda )}}{{{\text{Real}}(\lambda )}}.$$
(30)

Boundary Conditions

Three cases of boundary conditions have been considered for the sandwich plate as follows:

  1. (a)

    Clamped (C)

    $$u_{1} = v_{1} = w_{1} = \theta_{x1} = \theta_{y1} = u_{3} = v_{3} = w_{3} = \theta_{x3} = \theta_{y3} = 0\quad {\text{at}}\;x\, = \,0,a\;{\text{and}}\;y\, = \,0,b.$$
  2. (b)

    Free (F)

    $$u_{1} = v_{1} = w_{1} = \theta_{x1} = \theta_{y1} = u_{3} = v_{3} = w_{3} = \theta_{x3} = \theta_{y3} \ne 0\quad {\text{at}}\;x\, = \,0,a\;{\text{and}}\;y\, = \,0,b.$$
  3. (c)

    Simply supported (S)

    $$u_{1} = v_{1} = w_{1} = \theta_{y1} = u_{3} = v_{3} = w_{3} = \theta_{y3} = 0\quad {\text{at}}\;x\, = \,0,a,$$
    $$u_{1} = v_{1} = w_{1} = \theta_{x1} = u_{3} = v_{3} = w_{3} = \theta_{x3} = 0\quad {\text{at}}\;y\, = \,0,b.$$

Identification of Material Parameters

Description of the Inverse Optimization Problem

One of the main goals of this study is to find the frequency-dependent constitutive properties of the viscoelastic material which is used as a core in the sandwich plate. The behaviour of the viscoelastic material is characterized by the complex modulus approach. The design variables are the parameters that need to be identified, i.e. the shear storage modulus and the material loss factor of the viscoelastic core. In a forward procedure, the material properties are needed in order to calculate the Eigen characteristics. The opposite task, i.e. the determination of the material properties based on the modal test results of the structure, requires an inverse approach to be accomplished. This inverse approach accepts a numerical model of the structure under consideration (finite element model in our case) and couples it with an optimization algorithm which tries to find the queried material properties (treated as design variables) by minimizing the least square error between the numerically calculated eigenmodes and the eigenmodes observed in experiments. Ideally, if this error is zero, then the result of the optimization algorithm is a candidate solution for the searched material properties. Therefore, the aforementioned procedure works as a calibration tool for the finite element model, which is used for the simulation of the sandwich plate. In the present study, the experimental Eigen frequencies and loss factors are obtained using the impact hammer technique through modal analysis software. The numerical Eigen frequencies and loss factors are taken with the finite element method, which is programmed in integrated, independent code using the MATLAB programming language. The inverse procedure followed in the present study is shown in Fig. 6.

Fig. 6
figure 6

Flow chart of the material properties' identification procedure

Full size image

The Neural Network Optimization (NNO) Algorithm

The NNO algorithm [27] is used for inverse optimization. This algorithm uses a genetic algorithm coupled with an artificial neural network (ANN). The latter reinforces the search for the optimum made by the former, drastically increasing its convergence rate and the quality of the result. Since the NNO algorithmic framework allows for the use of a large variety of alternative optimizers and/or machine learning objects, it can be suitably configured to deal with nearly all optimization problems. A flowchart of the NNO algorithm used in this study is shown in Fig. 7. For more detailed descriptions of the NNO algorithm, the reader is encouraged to refer to references [39, 40].

Fig. 7
figure 7

Flow chart of the NNO algorithm

Full size image

Objective Function and Optimization Space

The objective function is a function that takes any set of design variable values (ANN's input data) and returns the output as the error (ANN's output data). Furthermore, as the algorithm progresses, the training data size increases, the trained ANN gets "better," and the objective function, which is based on this ANN, becomes "better" as well. This signifies that the objective function changes continuously as the algorithm progresses, causing the optimal values of the design variables and the objective function to vary continuously. Within the NNO framework, an ANN tries to mimic the objective function defined by the user, thus playing the role of a "digital twin" of the last. A genetic algorithm is used to optimize this "digital twin" ANN. The original inequality constrained minimization problem can be expressed as follows:

$$\min_{x} \left\{ {\phi_{{{\text{ANN}}}} \left( X \right)} \right\},$$
(31)

subject to:

$$h(X) = \left[ \begin{gathered} {\text{LB}} - X \hfill \\ X - {\text{UB}} \hfill \\ \end{gathered} \right] \le \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right],$$
(32)

where, LB and UB are vectors representing the design variable's lower and upper limits, and X is a vector comprised of the two design variables. The aforementioned limits need to be set so that the search space is both sufficiently large to include the optimal solution and sufficiently small to minimize the computational effort required for the optimization procedure. The values of the design variables may be chosen arbitrarily or by trial and error. The proper selection of the initial values of the design variables is essential to enhance the effectiveness of the inverse technique.

Results and Discussion

Convergence Study and Validation of the Present Finite Element Formulation

To determine the optimal mesh size of the finite element model, a convergence analysis with various levels of discretization is performed for the sandwich plate with a viscoelastic core layer constrained between two isotropic face layers. The convergence of the first three modes of natural frequencies and their corresponding modal loss factors of the sandwich plate under all side clamped boundary conditions over different mesh sizes for an aspect ratio (a/b) = 1 is reported in Table 1. A graphical representation of the convergence analysis is shown in Fig. 8. Observations from Fig. 8 indicate that a mesh size of 10 × 10 produces satisfactory results, and the same mesh size is employed throughout the present analysis.

Table 1 Convergence analysis for the present finite element model
Full size table
Fig. 8
figure 8

Convergence analysis of the finite element model for the first three eigenmodes: a natural frequencies, b modal loss factor

Full size image

For the validation of the proposed finite element formulation, a comparison study is performed with the existing works of literature using the material properties as provided in Table 2 within the equal testing domain. The resulting outcomes, along with a comparison to the present finite element model, are listed in Tables 3 and 4. The first three mode shapes of the sandwich plate for all sides clamped boundary conditions obtained from the developed finite element model are presented in Fig. 9. It can be clearly observed that the values of natural frequencies and modal loss factors obtained from the present finite element analysis are in accordance with the literature results.

Table 2 Geometrical and material properties considered for validation of the proposed finite element model
Full size table
Table 3 Comparison of the first three natural frequencies and modal loss factors of a sandwich plate with viscoelastic core for all sides clamped (CCCC) boundary condition
Full size table
Table 4 Comparison of the first four natural frequencies and modal loss factors of a sandwich plate with viscoelastic core for all sides simply supported (SSSS) boundary condition
Full size table
Fig. 9
figure 9

First three eigenmodes of the plate with fixed boundary conditions along all boundaries showing the displacement along the global Z-axis: a 1st eigenmode, b 2nd eigenmode, c 3rd eigenmode

Full size image

Free Vibration Analysis

Free vibration test is carried out on a symmetric three-layered sandwich plate by taking natural rubbers as viscoelastic core constrained between two aluminium faces. The geometric signatures of the sandwich plate are confirmed through a vernier calliper, taking repeated measurements on the test sample to avoid experimental errors. Table 5 represents the sandwich plate's geometrical and material parameters for all the layers considered for this present study. The overall length of the sandwich plate is 267 mm; 23 mm is taken as the clamping length to ensure rigidity. So 244 mm is the effective length of the sandwich plate for the clamped-free boundary condition. The node points are selected on the surface of the sandwich plate and marked for excitation. The sandwich plate is fixed along one side of the width with the help of C-clamps to the pre-assembled iron frame, ensuring a clamped-free boundary condition. The free vibration test is conducted at room temperature around 23 °C using the impact hammer technique. The experimental modal analysis software ME'scope is used to obtain the sandwich plate's vibrational characteristics. The first five modes of experimental natural frequencies and their corresponding modal loss factors of the sandwich plate are presented in Table 6.

Table 5 Geometrical and material properties of the sandwich plate
Full size table
Table 6 Experimental natural frequencies and modal loss factors of the sandwich plate under a clamped-free boundary condition
Full size table

Identification of Frequency-Dependent Viscoelastic Material Parameters

Considering the viscoelastic core's shear storage modulus and material loss factor as design variables and the difference between experimental and numerical sandwich plate's natural frequencies and modal loss factors as the objective function, the NNO algorithm is used for the identification of the former. For this identification procedure, the upper and lower limits for the shear storage modulus are set as 0.2–1.2 MPa and for the material loss factor as 0.1–0.2 for a frequency range of 1–500 Hz. From the proposed inverse method, the optimal values of shear storage modulus and material loss factor of the viscoelastic core are obtained as 0.94573 MPa and 0.12430, respectively.

Figure 10 shows the evolution of the error between the experimental data and the finite element results during the execution of the proposed NNO algorithm for the user-supplied objective function and for the ANN objective function. It is noted that the size of the initial simulated data (before the iterative procedure begins) is 20, and it is observed that for these first 20 objective function evaluations, the objective values exhibit a random variation, as is expected since these initial samples are selected based on the Latin Hypercube Sampling technique. From the 21st objective function evaluation and forth, it is apparent that the error decreases rapidly in Fig. 10a, ultimately converging to the desired minimum. In Fig. 10b, it is seen that the evolution of the error of the ANN (used as an objective function) shows a similar trend with the variation of the error in Fig. 10a after the 21st objective function evaluation. This observation verifies the fundamental hypothesis that the ANN is trying to mimic the actual user-supplied objective function internally in the NNO algorithm and provides some solid proof of its theoretical soundness. On the other hand, the final error of the objective function and the simulated ANN are close to each other, which implies that the NNO algorithm is successfully applied.

Fig. 10
figure 10

Evolution of the error between the experimental data and the finite element results during the execution of the proposed NNO algorithm: a error of objective function (real), b error of the internal ANN model (simulated)

Full size image

An illustration of the evolution of the NNO algorithm is presented in Fig. 11, which provides a visual representation of the optimization space and the points where the objective function evaluation has taken place until convergence. These points are shown in black dots. It is apparent that the concentration of the black dots near the optimum (illustrated as the red region of the 3D surface) increases compared to other regions of the optimization space. Another significant observation is that, at the initial stage of the NNO algorithm, the initial samples are shown to be uniformly distributed in the optimization space, and this is a result of the Latin Hypercube Sampling methodology used for their selection [41]. This sampling method definitely makes the subsequently trained ANN less biased and more robust as a representative of the true objective function, which highly contributes to the successful solution of the inverse optimization problem.

Fig. 11
figure 11

Optimization space of the inverse problem considered in this study and points where the objective function is evaluated during the execution of the proposed NNO algorithm

Full size image

Verification of the Identified Frequency-Dependent Viscoelastic Material Parameters

Viscoelastic material properties of natural rubber are determined experimentally with the help of a dynamic mechanical analyzer, DMA 8000. The shear test experiments are carried out on DMA-8000, and the viscoelastic material properties are obtained in the frequency domain for a frequency range of 1–100 Hz. The linearity of the viscoelastic behaviour of natural rubber from the DMA test is presented in Table 7.

Table 7 Viscoelastic material properties of natural rubber obtained from the DMA test
Full size table

The summary of the test results shows that the shear storage modulus exhibits an average magnitude of 0.92439 MPa, whereas the associated material loss factor averages 0.12323. In comparison with the results elicited from the proposed NNO algorithm, the DMA test results show a fine resemblance. Quantifying the error, the shear storage modulus and material loss factor exhibit 2.05 and 0.86%, respectively. This excellent agreement clearly shows the robustness of the proposed NNO algorithm, as depicted in Fig. 12.

Fig. 12
figure 12

Validation of the proposed NNO algorithm with the DMA test: a shear storage modulus, b material loss factor

Full size image

Taking these identified viscoelastic material properties of the core from the NNO algorithm as input parameters for the numerical finite element model, the sandwich plate's natural frequencies and modal loss factors are obtained. Table 8 provides the validation of the obtained numerical results for natural frequencies and modal loss factors against the experimental test results. For a comprehensive understanding, an illustrative summarization is presented in Fig. 13. Furthermore, the graphical depiction of modal characters for first, second and third eigenmodes are presented in Figs. 14 and 15 as elicited from the experimentation and numerical simulation, respectively. It is observed from the results that the experimental and numerical outcomes express similitude, which substantiates the effectiveness of the present inverse analysis.

Table 8 Comparison between experimental and numerical free vibration responses for the optimized viscoelastic material properties calculated from the NNO algorithm
Full size table
Fig. 13
figure 13

Validation of the finite element model of the sandwich plate with optimized viscoelastic layer properties for the five first eigenmodes against corresponding experimental data: a natural frequencies, b modal loss factors

Full size image
Fig. 14
figure 14

First three mode shapes of the sandwich plate fixed along the width for a clamped-free boundary condition obtained from the experimental modal analysis: a 1st eigenmode, b 2nd eigenmode, c 3rd eigenmode

Full size image
Fig. 15
figure 15

First three eigenmodes of the sandwich plate fixed along the width for a clamped-free boundary condition showing the displacement along the global Z axis: a 1st eigenmode, b 2nd eigenmode, c 3rd eigenmode

Full size image

Parametric Study

Understanding the resonance phenomenon in the structure may control the vibration range, avoids structural failure. To this end, a parametric study is carried out considering the optimized viscoelastic material properties of the core to investigate the effect of geometrical parameters on the free vibration response of the proposed sandwich plate for different boundary conditions. Furthermore, the sandwich plate's core thickness ratio and aspect ratio are considered as influencing factors of this investigation.

Influence of Different Boundary Conditions

A numerical study is performed considering the following edge conditions: clamped free (FCFF), two opposite short sides clamped (FCFC), all sides simply supported (SSSS), and all sides clamped (CCCC). A detailed summarization of the free vibration response of the sandwich plate under these edge conditions is illustrated in Fig. 16. It is evident from Fig. 16a that the sandwich plate with FCFF boundary condition exhibits the lowest natural frequency, followed by FCFC, SSSS and CCCC in ascending order for all modes of vibration. Because of the constrained effects at the edges of the structure, it becomes stiffer. As a result, its natural frequency increases. Figure 16b shows that the sandwich plate's modal loss factors have the highest value for the FCFF boundary condition, followed by the FCFC, SSSS, and CCCC boundary conditions in descending order for all modes of vibration. This signifies that the amount of damping reduces as the structure stiffens.

Fig. 16
figure 16

Influence of different boundary conditions on the free vibration characteristics of the sandwich plate: a natural frequencies, b modal loss factors

Full size image

The natural frequencies of the sandwich plate are influenced by the type of boundary conditions applied, such as clamped, free, or simply supported edges. The modal loss factors, on the other hand, depend on the viscoelastic properties of the core material and the damping introduced by the boundary conditions. In case of the CCCC boundary condition, the plate is firmly attached at all edges, resulting in high stiffness and low deflection. This leads to the highest natural frequencies and the lowest modal loss factors, with most of the energy concentrated at the edges. In contrast, the FCFF boundary condition results in the lowest natural frequencies but the highest modal loss factors. The SSSS and FCFC boundary conditions provide an intermediate result, balancing the effects of CCCC and FCFF boundary conditions. The influence of boundary conditions on natural frequencies and modal loss factors must be carefully considered when designing the sandwich plate with a viscoelastic core.

Influence of Core Thickness Ratio

The effect of the core thickness ratio (h2/h1) on the free vibration characteristics of the sandwich plate is explored by varying the thickness of the viscoelastic core layer against the thickness of the face layers. Figures 17, 18, 19 and 20 depicts the influence of the core thickness ratio on the natural frequencies of the sandwich plate and the corresponding modal loss factors for various boundary conditions.

Fig. 17
figure 17

Influence of core thickness ratio on the free vibration characteristics of the sandwich plate under FCFF boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 18
figure 18

Influence of core thickness ratio on the free vibration characteristics of the sandwich plate under FCFC boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 19
figure 19

Influence of core thickness ratio on the free vibration characteristics of the sandwich plate under SSSS boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 20
figure 20

Influence of core thickness ratio on the free vibration characteristics of the sandwich plate under CCCC boundary condition: a natural frequencies, b modal loss factors

Full size image

It is evident from Figs. 17a, 18a, 19a and 20a that the natural frequencies of the sandwich plate decrease with an increase in the core thickness ratio for all boundary conditions. This is because as the thickness of the core increases, owing to the viscoelastic material's softness, the plate becomes less stiff, resulting in a reduction in the frequency value. However, the decrease in natural frequency magnitude is not significant for lower modes, but there is a remarkable reduction in the case of higher modes for all boundary conditions. Observations from Fig. 17b indicate that for the FCFF boundary condition, the modal loss factor for mode 1 shows a noticeable increment as the core thickness ratio increases, whereas modal loss factors for modes 2 and 3 first decrease and then gradually increase. As the core thickness ratio rises, the modal loss factor for the higher modes decreases rapidly. Due to the viscoelasticity of the core material, as the core layer thickness increases, damping rises to a limit, beyond which the structure becomes less stiff and more prone to failure. Figures 18b, 19b and 20b show that, for all modes of vibration of the sandwich plate under FCFC, SSSS, and CCCC boundary conditions, the modal loss factors initially decrease rapidly and then gradually rise as the core thickness ratio increases. The trend that the sandwich plate has the highest value of modal loss factor under the FCFF boundary condition and the lowest value of modal loss factor under the CCCC boundary condition is clearly noticeable.

The influence of the core thickness ratio on the free vibration response of the sandwich plate with a viscoelastic core is significant and depends on the specific boundary condition. As the core thickness ratio increases, the natural frequencies of the sandwich plate decrease while the modal loss factors increase. This is due to the fact that a thicker viscoelastic core acts as a more effective damping material, reducing the amplitude of vibrations and, in turn, increasing the modal loss factor. In addition, one of the reasons for the decreased natural frequencies of the plate is that when the core thickness ratio is increased, the mass per square meter of the plate is increased, since the natural frequency is inversely proportional to mass. However, the reduction in natural frequencies can also make the sandwich plate more susceptible to overall structural instability. The optimal balance between reducing the natural frequencies and increasing the modal loss factor should be considered for each boundary condition when designing the sandwich plate with a viscoelastic core.

Influence of Aspect Ratio

In this study, the aspect ratio is defined as the ratio between the sandwich plate's length (a) and width (b), and the length varies against the width. The influence of aspect ratio on the free vibration characteristics of the sandwich plate for different boundary conditions is presented in Figs. 21, 22, 23 and 24.

Fig. 21
figure 21

Influence of aspect ratio on the free vibration characteristics of the sandwich plate under FCFF boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 22
figure 22

Influence of aspect ratio on the free vibration characteristics of the sandwich plate under FCFC boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 23
figure 23

Influence of aspect ratio on the free vibration characteristics of the sandwich plate under SSSS boundary condition: a natural frequencies, b modal loss factors

Full size image
Fig. 24
figure 24

Influence of aspect ratio on the free vibration characteristics of the sandwich plate under CCCC boundary condition: a natural frequencies, b modal loss factors

Full size image

It can be observed from Figs. 21a, 22a, 23a and 24a that as the aspect ratio increases, the sandwich plate's natural frequencies reduce for all modes of vibration across all boundary conditions. With an increase in aspect ratio from 0.5 to 1, the natural frequency value of mode 1 shows a rapid reduction for all boundary conditions. However, further increasing the aspect ratio, the natural frequencies for other modes of vibration decrease gradually. The order of natural frequencies follows the same trend under different boundary conditions. Thus, compared to longer plates (a/b = 2.5 and 3), shorter and wider plates (a/b = 0.5) have a significant impact on increasing natural frequencies. It is evident from Figs. 21b, 22b, 23b and 24b that the FCFF boundary condition yields the highest modal loss factor value, followed by the FCFC, SSSS, and CCCC boundary conditions. Figures 21b, 22b and 23b show that the modal loss factor of mode 1 increases more rapidly than the other modes under the FCFF and SSSS boundary conditions. Figures 21b and 22b indicate that the modal loss factors for higher modes under FCFF and FCFC boundary conditions first increase and then reduce when the aspect ratio is increased from 1.5 to 2. Further increasing the aspect ratio above 2, the modal loss factor increases gradually. However, for the higher modes, complicacy arises due to the complex configuration shapes of the eigenmodes.

The aspect ratio of the sandwich plate with a viscoelastic core can significantly affect its natural frequencies and modal loss factors. In the cases that the plate is vibrating in a predominantly bending deformation, e.g. in the FCFF and FCFC cases where the smaller edges are clamped and for high values of aspect ratio, its natural frequencies tend to be lower, since the plate has increased flexibility in these cases. The effect of increased aspect ratio is that the boundary conditions of the shorter edges of the plate gradually fade away. For increasing aspect ratio the following trends are observed in this study, and should also be expected according to the aforementioned rationale: (a) in the FCFF case since the smaller edges are fixed, natural frequency decreases, (b) in the FCFC case, if the smaller edge is fixed, then the natural frequency decreases, otherwise if the larger edge is fixed, the natural frequency increases, (c) in the SSSS case the natural frequency always decreases and (d) in the CCCC case the natural frequency always decreases. However, the influence of aspect ratio on the natural frequencies and modal loss factors of a sandwich plate with a viscoelastic core is generally complex and depends on the material properties, geometry, and boundary conditions of the plate.

Concluding Remarks

The free vibration characteristics of a three-layered sandwich plate with isotropic face layers of aluminium and a viscoelastic core layer of natural rubber are investigated experimentally and numerically. The experimental modal analysis is performed utilizing the impact hammer method, and the numerical simulations are carried out using the finite element approach. Based on the experimental modal analysis results of the sandwich plate, a neural network optimization (NNO) algorithm is proposed to identify the frequency-dependent viscoelastic material properties of natural rubber.

The viscoelastic material properties of natural rubber are determined experimentally using a dynamic mechanical analyzer, DMA-8000. The identified constitutive parameters of the natural rubber material from the NNO algorithm show an excellent agreement with the experimental DMA test results. This demonstrates that the NNO approach provides an adequately robust and precise inverse optimization technique. In light of this, the suggested NNO algorithm may calibrate viscoelastic material parameters utilizing experimental modal analysis responses without the need for expensive and time-consuming dynamic mechanical analysis experiments.

Furthermore, the optimized viscoelastic material properties obtained from the NNO algorithm are used to explore the effect of various parameters on the free vibration response of the sandwich plate. The numerical parametric study indicates that the edge conditions considerably influence the dynamic performance of the sandwich plate. It is observed that the sandwich plate with one side clamped boundary condition exhibits the lowest natural frequency than other support conditions. In contrast, the observation for the modal loss factor follows the reverse trend. This explains why the largest magnitude of modal loss factor is achieved for the one side clamped boundary condition, whereas the lowest magnitude is observed for all sides clamped boundary condition.

The core thickness ratio significantly affects the sandwich plate's free vibration characteristics. The natural frequencies of each vibration mode of the sandwich plate decrease as the core thickness ratio increases. However, the modal loss factor of the first mode increases, whereas the modal loss factors of higher modes first decrease and then gradually increase as core thickness increases.

The aspect ratio of the sandwich plate has a large impact on its free vibration response. The natural frequencies of the sandwich plate decrease as the aspect ratio increases for all modes of vibration under different boundary conditions. The variations in natural frequency are significantly higher in shorter and wider plates than in longer plates. Concerning the effect of aspect ratio, the sandwich plate exhibits a lower modal loss factor in shorter and wider plates, and the modal loss factor is relatively higher in longer plates.

Knowledge about the material properties is essential for the dynamic analysis of a structure in the vibration reduction technique. Thus the present inverse method is of great significance as it can be applied to characterize the material properties of viscoelastic materials embedded for both FLD and CLD configurations. By calibrating the frequency-dependent material properties of viscoelastic materials, the proposed inverse identification method provides new insights into the behaviour of these materials and their responses to external excitations. The present inverse identification technique is fast and efficient having a high convergence rate for identification of dynamic properties without sacrificing accuracy, and therefore contributes to the advancement of the field of computational materials science by providing a new tool for characterizing and understanding viscoelastic materials utilizing their vibrational dynamic response.