1 Introduction

Passive constrained layer damping (PCLD) is recognized as an effective technique to reduce resonant noise and vibration of structures (Kerwin 1959; Nakra 1998). PCLD has been used widely in surface damping treatments in many engineering fields, including land based vehicles, airplanes, and ships. The efficiency of a constrained layer damping treatment relies on the shear deformation in the viscoelastic layer (Mead and Markus 1969; Rao and Shulin 1993), and this state of shear deformation is the main mechanism by which the vibration energy is dissipated and transformed into heat or other forms of energy. The stiffness, mass and damping of the viscoelastic structure and material have significant effects on the shear deformation in the viscoelastic layer. Thus, design optimization of the structural and material properties plays a very important role in improving the behaviors of PCLD treatments.

Many researchers have suggested different design optimization formulations for damping layout of structures. Studies have primarily focused on designing a constrained layer damping treatment in which the layout of the damping layer is optimized to achieve high damping efficiency for the structure. Zheng et al. (2005) used the Genetic Algorithm (GA) to find optimal locations of damping patches for minimizing the structural vibration response of a cylindrical shell structure. Alvelid (2008) studied the optimal positions and shapes of PCLD patches for minimizing the frequency-averaged response. Several researchers (Ro and Baz 2002; Moreira and Rodrigues 2006; Ling et al. 2011) sought the optimal design of damping treatment for maximizing the modal damping ratios, which was found with a modal strain energy (MSE) approach. More recently, Kim (2011), Kim et al. (2013) proposed topology optimization approaches in order to find an effective partial placement of damping treatment within a given amount of damping material. Kang et al. (2012) studied the optimal distribution of damping material in vibrating structures subject to harmonic excitations by using a topology optimization method.

Despite layout design of damping layer is effective to enhance structural damping performance, the property of viscoelastic materials (i.e. stiffness, damping of viscoelastic material) is another critical factor affected the structural damping performance. Lall et al. (1987) carried out multi-parameter optimum design studies for a sandwich plate with constrained viscoelastic core. Design variables were chosen as shear modulus and thicknesses of viscoelastic layer, with objective functions as modal loss factor and displacement response. They found out that the maximum obtainable modal system loss factor exists at different values of shear modulus for the different modes and for the higher modes it occurs at higher shear modulus values. Then, Al-Ajmi (2004) also indicated that there is a specific value of the shear modulus that maximizes the modal loss factor of damped structures under given mechanical environment. However, different working conditions of structure implies different requirements for optimal damping material properties, and it is very difficult, if not impossible, to implement optimal material properties by choosing the existing viscoelastic damping materials. In fact, this specific shear modulus can be achieved by design optimization of material microstructure through a topology optimization method. Therefore, microstructural design of viscoelastic materials with specially desired properties is a new concept for improving the structural damping effect. Up to now, most of the research regarding any optimal design of PCLD treatment concentrated on the macro scale, i.e. the macro structural layout or damping material distribution, and little work has been devoted to design the micro-structures of the damping materials.

Topology optimization provides a powerful tool for the creative design of structural configurations, which has been used to design the material microstructure for prescribed properties. Topology optimization of microstructure/material was first proposed by Sigmund (1994, 1995). Since then, plenty of work on the basis of this technique has been carried out for different application areas to obtain a material with prescribed or extreme effective material properties (Gibiansky and Sigmund 2000; Huang et al. 2011, 2012; Nomura et al. 2009; Radman et al. 2013). Examples of these materials are elastic composites with maximum bulk or shear modulus, elastic composites with a negative Poisson’s ratio and thermo-elastic composites with negative or zero thermal expansion coefficients, et cetera. The upper bounds on open-cell foam homogenized moduli have been given by Dimitrovová (2005). Furthermore, topology optimization of the microstructure has also been applied to the design of microstructures of viscoelastic composites for optimal damping characteristics (Yi et al. 2000).

This paper focuses on the design of a periodic viscoelastic cellular material with prescribed properties using the topology optimization method and includes an example of the methodology applied to a cantilever beam. It is assumed that the microstructure of the cellular material is composed of regular periodic unit cells (PUCs) and the PUC is discretized into finite elements with periodic boundaries. In Section 2 the homogenization theory is used to calculate the effective properties (i.e., stiffness, damping) of the material. We find that the effective loss factor of the material is independent of the geometrical configuration of the PUC when choosing an isotropic solid material as the matrix material. In Section 3, based upon the SIMP method of topology optimization, the material relative densities of the PUC are considered as the design variables, and the minimization of the difference between the effective and the desired storage shear modulus is selected as the objective of the material design with the isotropy of properties and the volume limit of matrix material as the constraints. Next, the sensitivity analysis is conducted to estimate the effect of individual elements on the variation in objectives and the constraints. The optimization problem is solved using the sequential linear programming (SLP) method. Then in Section 4 several examples of an optimized design are presented to demonstrate the validity of the design approach and methodology. The effectiveness of this design method that enhances the structural modal loss factor and reduces the resonant response is shown by making a comparison between a solid and an optimized cellular viscoelastic material as applied to a cantilever beam with a PCLD treatment. Finally, main conclusions are given in Section 5.

2 Homogenization and linear viscoelasticity

2.1 Linear viscoelasticity in the frequency domain

Suppose that the viscoelastic structural 2-D problem is under steady-state harmonic excitation with isothermal conditions. Using the Correspondence Principle (Christensen 2010), the viscoelastic problem at a fixed frequency ω is as follows:

$$\begin{array}{@{}rcl@{}} \frac{\partial \bar{{\sigma }}_{ij}(x)}{\partial x_{j} }&=&-\omega^{2}\rho \bar{{u}}_{i} ;\\ \bar{{\sigma }}_{ij}( x )&=&G_{ijkl} ( \omega )\bar{{\varepsilon }}_{kl}( x );\\ \bar{{\varepsilon }}_{ij}( x )&=&\frac{1}{2}\left( {\frac{\partial \bar{{u}}_{j}( x )}{\partial x_{i} }+\frac{\partial \bar{{u}}_{i}( x )}{\partial x_{j} }} \right)\\ \end{array} $$
(1)

where ω is the excitation frequency, x i , x j are Cartesian coordinates, ū i , ε̄ ij and σ̄ ij are the spatial part of the displacement, strain, and stress, respectively:

$$\begin{array}{@{}rcl@{}} u( {x,t} )&=&\bar{{u}}( x )e^{i\omega t},\quad \varepsilon_{ij} ( {x,t} )=\bar{{\varepsilon }}_{ij} ( x )e^{i\omega t},\\ \sigma_{ij} ( {x,t} )&=&\bar{{\sigma }}_{ij} ( x )e^{i\omega t} \end{array} $$
(2)

The complex modulus tensor G ijkl (ω) is given by

$$ G_{ijkl} ( \omega )=G_{ijkl}^{\prime} ( \omega )+iG_{ijkl}^{\prime \prime } ( \omega ) $$
(3)

where \(G_{ijkl}^{\prime } (\omega )\in R\), and \(G_{ijkl}^{\prime \prime } (\omega )\in R\) denote the storage and loss modulus, respectively. For isotropic materials with constant Poisson’s ratio, the loss modulus can be expressed in terms of the storage modulus and loss factor as

$$ G_{ijkl}^{\prime \prime } ( \omega )=\eta^{0}( \omega )G_{ijkl}^{\prime} ( \omega ) $$
(4)

where, the storage modulus is expressed in terms of shear modulus C and Poisson’s ratio ν as

$$ G_{ijkl}^{\prime} ( \omega ) = 2C( \omega )\left( {\delta_{ik} \delta_{jl} +\frac{\nu }{1-2\nu }\delta_{ij} \delta_{jl} \delta_{mk} \delta_{ml} } \right) $$
(5)

The complex modulus tensor G ijkl (ω) can be rewritten as follow.

$$ G_{ijkl}( \omega )=G_{ijkl}^{\prime} ( {1+i\eta^{0}( \omega )} ) $$
(6)

2.2 Homogenization method for linear viscoelasticity

In frequency domains, the macroscopic behaviors of a viscoelastic cellular material can be characterized by the effective stress tensor σ͂ ij and strain tensor ε͂ kl over a homogenized medium. They are interrelated by the effective complex modulus tensor, \(G_{ijkl}^{H} ( \omega )\).

$$ \tilde{{\sigma }}_{ij} =G_{ijkl}^{H} ( \omega )\tilde{{\varepsilon }}_{kl} $$
(7)

Where \(G_{ijkl}^{H} (\omega )\) depends upon the volume fraction of solid material and the microstructure of the PUC, and can be obtained by the homogenization theory (Hassani and Hinton 1998a, b; Yi et al. 2000).

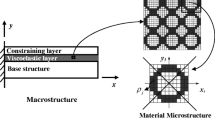
A structure is composed of spatially repeated PUCs and the PUC is very small compared with the size of the structural body as shown in Fig. 1. A micro-scale coordinate system (Y) is introduced to describe the sharp variation of responses and material properties in a near neighborhood of a point (X). The coordinate in Y can be regarded as an amplification of that in X with a positive real parameter δ(y = x / δ, δ < < 1). Based on the idea of homogenization method for viscoelastic materials, the effective complex modulus can be expressed as

$$\begin{array}{@{}rcl@{}} G_{ijkl}^{H} &=&\frac{1}{| Y |}\int_{Y} {G_{pqrs} ( {y,\omega } )} \left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\\ &&\times\left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y \end{array} $$
(8)

where generalized displacement function χ(y) is the periodic solution of the following micro-homogenization problem

$$\begin{array}{@{}rcl@{}} &&\int_{Y} {G_{ijpq} ( {y,\omega } )} \frac{\partial \chi_{p}^{kl} }{\partial y_{q} }\frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y=\int_{Y} {G_{ijkl} ( {y,\omega } )} \frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y, \\ &&{ \forall \mathit{v}\in V_{Y} =\{ {\mathbf{u}\vert y\in Y,\mathbf{u}( y )=\mathbf{u}( {y+Y} )} \}} \\ \end{array} $$
(9)

By solving problem (9) and using (8) the effective complex modulus at a given frequency is obtained. However, the functions in (8) and (9) are complex, thus, to obtain the numerical solutions of the effective complex modulus, a finite element implementation with complex variables are required.

Fig. 1
figure 1

A structure is composed of PUCs

Full size image

In this paper, it is supposed that the viscoelastic material is isotropic and Poisson’s ratio is real constant. Under this assumption, the substitution of (6) into (9), gives

$$\begin{array}{@{}rcl@{}} && {\int_{Y} {( {1+i\eta^{0}( {y,\omega } )} )G_{ijpq}^{\prime} ( {y,\omega } )} \frac{\partial \chi_{p}^{kl} }{\partial y_{q} }\frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y}\\ &=&{\int_{Y} {( {1+i\eta^{0}( {y,\omega } )} )G_{ijpq}^{\prime} ( {y,\omega } )} \frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y} \\ && {\forall \mathit{v}\in V_{Y} =\{ {\mathbf{u}\vert y\in Y,\mathbf{u}( y )=\mathbf{u}( {y+Y} )} \}} \end{array} $$
(10)

If y ∈ Y void (Y void denotes the domain of void), \(G_{ijpq}^{\prime }({y,\omega } ) = 0\). And if y ∈ Y solid (Y solid denotes the domain of solid), η 0(y, ω)=η 0(ω). Therefore, (10) can be simplified as

$$\begin{array}{@{}rcl@{}} && {\int_{Y} {G_{ijpq}^{\prime} ( {y,\omega } )} \frac{\partial \chi_{p}^{kl} }{\partial y_{q} }\frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y=\int_{Y} {G_{ijpq}^{\prime} ( {y,\omega } )} \frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y} \\ && {\forall \mathit{v}\in V_{Y} =\{ {\mathbf{u}\vert y\in Y,\mathbf{u}( y )=\mathbf{u}( {y+Y} )} \}} \end{array} $$
(11)

As the shear storage \(G_{ijpq}^{\prime } (y,\omega )\) is real, the solution of (11) \(\chi _{p}^{kl} \) must be real. Similarly, with the substitution of (6) into (8), the effective complex modulus can be written as follows

$$\begin{array}{@{}rcl@{}} G_{ijkl}^{H} (\omega )&=&\frac{1}{| Y |}\int_{Y} \left( {G_{pqrs}^{\prime} ( {y,\omega } )+iG_{pqrs}^{\prime \prime } ( {y,\omega } )} \right)\\ &&\times \left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y \\ &=&\frac{1}{| Y |}\int_{Y} {\left( {G_{pqrs}^{\prime} ( {y,\omega } )+i\eta^{0}( \omega )G_{pqrs}^{\prime} ( {y,\omega } )} \right)}\\ &&\times {\left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y} \\ &=&\frac{1}{| Y |}\int_{Y} {G_{pqrs}^{\prime} ( {y,\omega } )\left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)}\\ &&\times {\left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y} \\ && +i\eta^{0}( \omega )\frac{1}{| Y |}\int_{Y} {G_{pqrs}^{\prime} ( {y,\omega } )\left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)}\\ &&\times {\left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y} \\ \end{array} $$
(12)

As the solution of the (11) \(\chi _{p}^{kl} \) is real, the real part and the imaginary part of the effective complex modulus in (12) can be expressed as follows.

$$\begin{array}{@{}rcl@{}} G_{ijkl}^{\prime H} ( \omega )&=&\frac{1}{| Y |}\int_{Y} {G_{pqrs}^{\prime} ( {y,\omega } )} \left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\\ &&\times \left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y\end{array}$$
(13)
$$\begin{array}{@{}rcl@{}}G_{ijkl}^{\prime \prime H} ( \omega )&=&\eta^{0}( \omega )\frac{1}{| Y |}\int_{Y} {( {G_{pqrs}^{\prime} ( {y,\omega } )} )} \left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\\ &&\times \left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y \end{array} $$
(14)

\(G_{ijkl}^{\prime \prime H} (\omega ),\) and \(G_{ijkl}^{\prime H} (\omega )\) denote the effective storage modulus (i.e., real part) and loss modulus (i.e., imaginary part), respectively. So, the relation between the effective storage and loss modulus is given as follows:

$$ G_{ijkl}^{\prime \prime H} ( \omega )=\eta^{0}( \omega )G_{ijkl}^{\prime H} ( \omega ), \text{or}, \eta^{H}( \omega )=\frac{G_{ijkl}^{\prime \prime H} ( \omega )}{G_{ijkl}^{\prime H} ( \omega )}=\eta^{0}( \omega ), $$
(15)

The effective complex modulus can be rewritten as:

$$ G_{ijkl}^{H} ( \omega )=( {1+i\eta^{0}( \omega )} )G_{ijkl}^{\prime H} ( \omega ) $$
(16)

Obviously, the effective loss factor of viscoelastic cellular material is same as that of viscoelastic solid matrix material. In other words, the effective loss factor of cellular viscoelastic material is independent of the geometrical configuration of the PUC. As far as we know, it is an original contribution.

In this case, by solving the problem (11) and using (13) the effective storage modulus is obtained. Then, the effective complex modulus of viscoelastic cellular material is easily obtained by (16). Fortunately, the functions in (10) and (12) are real. Thus, for the numerical solutions of the effective complex modulus, we only require a finite element implementation with real variables. Therefore, it is shown that the troubles with the complex operations in (7) and (8) can be avoided.

3 The optimization formulation and sensitivity analysis

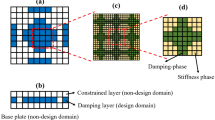
This paper investigates the design of a periodic viscoelastic cellular material with prescribed properties using the topology optimization method. It is assumed that the microstructure of cellular material is composed of PUCs, and the PUC can be discretized into finite elements as shown in Fig. 2. The material distribution of the PUC can be described by the element’s densities (ρ 1, ρ 2, ρ 3,⋯ ,ρ n ), and n is the total number of elements in the PUC. ρ i = 1 (or 0) means that the i-th element is filled by a solid material (or a void). Thus, with the topology optimization process for each iteration, elements within an initial unit cell may change from solid (ρ i = 1) to void (ρ i = 0) or from void to solid. As a result, the PUC topology will be gradually modified until both volume constraint and the convergent criterion are satisfied.

Fig. 2
figure 2

A discretized design domain of the PUC

Full size image

Isotropic materials, in which the properties of the materials are invariant with respect to the material orientation, are the most common materials used in industry and are attractive for engineering applications. It is known that the material is isotropic when the microstructural geometry has 60° symmetry. But this would require a rectangular basic cell in a brick arrangement. It is computationally simpler to work with a square basic cell in a lattice arrangement (Fig. 2), and therefore the isotropy constraints are chosen as a function with respect to modulus (Neves et al. 2000).

$$ f\left( {G_{ijkl}^{\prime} } \right) = 0 $$
(17)

Nevertheless, it is necessary to point out that many potential solutions are disregarded by this choice.

An objective function can be formulated to minimize the difference between the effective storage shear modulus and the prescribed shear modulus \(\left ( {\Pi =\left ( {G_{1212}^{\prime H} -G_{1212}^{\prime \ast } } \right )^{2}} \right )\). The topology optimization problem of viscoelastic cellular material with a prescribed property and with constraints on the isotropic and volume fraction can be expressed as:

$$\begin{array}{@{}rcl@{}} {\mathrm{Find}:} && {\boldsymbol{\uprho} =[ {\rho_{1} ,\rho_{1} ,\cdots ,\rho_{i} ,\cdots \rho_{n} } ]^{T}} \\ {\mathrm{Minimize}:} && {\left( {G_{1212}^{\prime H} -G_{1212}^{\prime \ast } } \right)^{2}+\frac{1}{| Y |} \sum\limits_{i=1}^{n} {\rho_{i} ( {1-\rho_{i} } )} V_{i}} \\ {\mathrm{Subject}\,\,\mathrm{to}:} && {\int\limits_{Y} {G_{ijpq}^{\prime} \frac{\partial \chi_{p}^{km} }{\partial y_{j} }\frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y}}\\ &&{= \int\limits_{Y} {G_{ijkm}^{\prime} \frac{\partial \mathit{v}_{i} }{\partial y_{j} }\mathrm{d}Y} , \forall \mathit{v}, Y-periodic} \\ && {\mathrm{G}_{ijkm}^{\prime H} =\frac{1}{| Y |}\int\limits_{Y} {G_{pqrs}^{\prime} \left( {\delta_{ri} \delta_{sj} -\frac{\partial \chi_{r}^{km} }{\partial y_{s} }} \right)}}\\ &&\times {{\left( {\delta_{pk} \delta_{qm} -\frac{\partial \chi_{p}^{km} }{\partial y_{q} }} \right)\mathrm{d}Y} }\\ && {V^{\ast} -\sum\limits_{i}^{n} {\rho_{i} V_{i} } =0} \\ && {0 < \rho_{\min } \leq \rho_{i} \leq 1,\quad i=1,2,...,n} \\ && {f\left( {G_{ijkl}^{\prime} } \right)=0} \end{array} $$
(18)

Where \(G_{1212}^{\prime H} \) is the effective storage shear modulus and is the prescribed/target storage shear modulus. V i is the volume of the i-th element and V ∗ is the prescribed total volume and n is the total number of elements in the PUC. To avoid singularity in the stiffness matrix, a small value of ρ min, e.g. 0.001, is used to represent the void elements. The term \(\frac{1}{| Y |}{ \sum\limits_{i=1}^{n} \rho_{i} ( {1-\rho_{i} } )} V_{i}\) corresponds to a penalization on the intermediate volume fraction values. This penalty term is intended to reduce the intermediate value of ρ i on the final solution.

In this work, the optimization problem in (16) is solved by the gradient-based sequential linear programming (SLP) method. The sensitivity of the objective function with respect to the element density variable, ρ i is expressed as

$$ \frac{\partial \left( {G_{1212}^{\prime H} -G_{1212}^{\prime \ast } } \right)^{2}}{\partial \rho_{i} } = 2\left( {G_{1212}^{\prime H} -G_{1212}^{\prime \ast } } \right)\frac{\partial G_{1212}^{\prime H} }{\partial \rho_{i} } $$
(19)

Based upon the SIMP model (Bendsøe and Sigmund 1999, 2004), the sensitivity of the storage modulus can be written as:

$$\begin{array}{@{}rcl@{}} \frac{\partial G_{ijkl}^{\prime H} }{\partial \rho_{i} }&=&\frac{p}{| Y |}\int_{Y} {\rho_{i}^{p-1} \Bar{{G}}_{pqrs}^{\prime} } \left( {\delta_{kp} \delta_{lq} -\frac{\partial \chi_{p}^{kl} }{\partial y_{q} }} \right)\\ &&\times \left( {\delta_{ir} \delta_{js} -\frac{\partial \chi_{r}^{ij} }{\partial y_{s} }} \right)\mathrm{d}Y \end{array} $$
(20)

which \(\bar {{G}}_{pqrs}^{\prime } \) is the storage modulus tensor of the viscoelastic solid matrix material, and the exponent p is the penalty exponent that is often chosen to be p = 3 or 4.

The whole optimization procedure can be described by the flowchart in Fig. 3.

Fig. 3
figure 3

Flowchart of the optimization procedure

Full size image

4 Numerical examples and discussions

4.1 Determination of the target shear modulus

In this section, in order to illustrate the influence of the property of viscoelastic materials on the structural damping performance, a cantilever elastic beam covered with a constrained damping layer is considered for the analysis, as shown in Fig. 4. The base beam and constraining layer are made of aluminum and a viscoelastic core is a material with the properties similar to DyAD606 from SOUNDCOAT Company. Thus, the geometric and material properties for the numerical example are given in Table 1.

Fig. 4
figure 4

A three-layered sandwich beam structure

Full size image
Table 1 Geometric and physical parameters of beam structure
Full size table

An energy formulation is used to estimate the modal loss factor of the k-th mode of interest. The modal loss factor is obtained by using MSE method (Ungar and Kerwin 1962)

$$ \varphi_{k} =\frac{\displaystyle\sum\nolimits_{i = 1}^{n} {\eta_{i,k} U_{i,k} } }{U_{total,k} } $$
(21)

where η i, k is the material loss factor of the layer i at mode k, and U i, k is the modal strain energy of the layer iat mode k. U total, k is the total modal strain energy at mode k.

$$ U_{total,k} =\sum\nolimits_{i = 1}^{n} {U_{i,k} } $$
(22)

To study the effect of shear modulus on the modal loss factor of the sandwich beam, the shear modulus of viscoelastic material is varied between 0.2 and 20 MPa. In Fig. 5, the modal loss factor as a function of the shear modulus for the first three modes is presented. For each mode, there is a certain value of the shear modulus that maximizes the modal loss factor in the damping structure. For our research, we are especially interested in the specific shear modulus at which the optimal structural damping performance is achieved. At mode 1, the optimal shear modulus \(C_{\text {opt}}^{1} = 1.2 \text {MPa}\), and the corresponding modal loss factor \(\varphi _{\text {opt}}^{\mathrm {1}} = 0.0374\). At mode 2 with \(C_{\text {opt}}^{2} =5.8 \text {MPa}\), the modal loss factor has the optimal value \(\varphi _{\text {opt}}^{2} = 0.0441\). The optimal shear modulus and modal loss factor are \(C_{\text {opt}}^{\mathrm {3}} = 14.4 \text {MPa}\) and \(\varphi _{\text {opt}}^{3} = 0.0453\) for mode 3.

Fig. 5
figure 5

Optimal shear modulus of viscoelastic layer for maximum modal loss factor

Full size image

It is noticed that the optimal value of shear modulus is not unique and it is dependent on the physical and geometrical properties of the structure. Moreover, the MSE method is an economical approach in dealing with the complex modulus of the damping material. It assumes that the damped structure has similar resonance frequency and the mode shape to those of the undamped structure, which means that the damping material is relatively light and weak.

4.2 Microstructural design

We aim to find the microstructure of a viscoelastic material with storage shear modulus equal to the optimal/target shear modulus for the first three modes in Fig. 5 (i.e., \(C_{\text {opt}}^{1} = 1.2\text {MPa}\) at mode 1, \(C_{\text {opt}}^{\mathrm {2}} =5.8\text {MPa}\) at mode 2, and \(C_{\text {opt}}^{\mathrm {3}} = 14.4\text {MPa}\) at mode 3). A square finite element model of the PUC is discretized into 40 × 40, four-node quadrilateral elements. With the material properties in Table 1, the complex modulus can be written as follows:

$$ G=( {1+0.5i} )G^{\prime} =( {1+0.5i} )\left[ {{\begin{aligned} {76.92} & {36.92} & 0 \\ {36.92} & {76.92}& 0 \\ 0 & 0 & {20.00} \\ \end{aligned} }} \right] $$
(23)

The initial design of the microstructure is given in Fig. 2. A small disturbance of material volume density is introduced into the four corner elements of the design domain to avoid the trivial solution that all elements have the same material volume density in the final design. The volume constraints of solid material are set to be 0.5, 0.7, 0.9 of the design domain for the first, second and third mode respectively, considering the Hashin and Strikman (H-S) upper bounds of the shear modulus \(\left (C_{upper}^{1} =5.4\text {MPa}, C_{upper}^{2} =9.3\text {MPa}, and C_{upper}^{3} = 15.3\text {MPa}\right )\).

As the solid phase is isotropic with constant Posson’s ratio, the damping properties of the designed material are unrelated to the void material. By solving the optimization problem (16), the optimal microstructures with the prescribed shear modulus for the first modes can be achieved. Figure 6 shows the optimal microstructures and corresponding effective complex modulus for the first three modes. The same microstructures in 3 × 3 cells for easier understanding of the designed microstructure are also shown in Fig. 6. It can be seen that the storage shear modulus of the designed microstructures are very close to the optimal/target shear modulus for each mode, and the isotropic requirements of material properties are satisfied.

Fig. 6
figure 6

Unit cell, 3 × 3 cells and effective complex modulus of 2D cellular materials with prescribed shear modulus a mode 1 and volume fraction is 0.5; b mode 2 and volume fraction is 0.7; c mode 3 and volume fraction is 0.9

Full size image

Consider that the sandwich beam in Fig. 4 is excited by a point harmonic force p = Pe iωt at the right end, with P = 1 N (as shown in Fig. 7). The mean displacement of the initial design (solid viscoelastic material layer) and the optimum design (cellular viscoelastic material layer) are compared in Fig. 8 with the unit dB transformed in the following way

$$ \tilde{{U}}( {\text{dB}} ) = 10\;\text{lg}\; \left( {\frac{U}{U_{\text{ref}} }} \right) $$
(24)

where U is the mean displacement of the beam and U ref = 1 m is a reference displacement.

Fig. 7
figure 7

The sandwich beam is excited by a point harmonic force at the right end

Full size image
Fig. 8
figure 8

Comparison of initial design and optimal design results for a cantilever beam for the first three modes. a, c, e Mean displacement; b, d, f vibration amplitude contour of the eigenmode

Full size image

In this paper, it is supposed that a cellular viscoelastic material is composed by a number of spatially repeated periodic unit cell (PUC), and PUC is very small compared with the size of the damping layer. The comparison is conducted by introducing macroscopic properties in the damping layer. For mode 1, the vibration reduction of the resonance peaks is about nearly 5 dB between the initial design and the optimal design, and the mean amplitude is reduced by 70 % by using the optimal cellular damping material. For mode 2, the vibration reduction of the resonance peaks is about nearly 3 dB between the initial design and the optimal design, and the mean amplitude is reduced by 50 %. In mode 3 the vibration reduction of the resonance peak is about 1 dB and the mean amplitude is reduced by 20 %. The frequency of the resonance peaks with the optimal design is shifted down little as the compliance of the whole structure is increased. This confirms the possibility of the topology optimization technique to find the material distribution of viscoelastic microstructure with prescribed property that enhances the modal loss factor and reduces the vibration response of the structure under a given mechanical environment.

5 Conclusions

This paper proposes a topology optimization method for designing a viscoelastic cellular material with prescribed properties, aiming at improving the modal damping performance of the PCLD. In the method, the homogenization method is employed to derive the effective behavior of viscoelastic materials; a topology optimization formulation is presented for microstructure design of the isotropic viscoelastic cellular material with prescribed properties. Based upon the derivation and numerical results we can draw the following conclusions.

  1. 1.

    The effective loss factor of the designed cellular material is just equal to the one of the matrix material, independent of its microstructure configuration, if the matrix is isotropic solid material, thus, only stiffness characteristics of the viscoelastic cellular material can be designed by microstructural geometrical topology.

  2. 2.

    The topology optimization method can formulate the design of a viscoelastic material with prescribed properties, and can determine interesting topological patterns for guiding the viscoelastic cellular material design. Furthermore, microstructure design of viscoelastic material with prescribed properties has a crucial role in improving the damping properties of the macrostructures.