Effective viscoelastic behavior of short fibers composites using virtual DMA experiments

Abstract

May it be for environmental or economic reasons, mass reduction has become one of the main goals in mechanics. The short fiber thermoplastics composite is an interesting possibility since it presents a good compromise between a relatively easy process and mechanical properties. The aim of this work is to estimate and model the viscoelastic behavior at small strain of PC Lexan/Glass fiber composites. To meet this goal, a full field homogenization method based on solving the boundary problem through FFT is used. Virtual DMA experiments are used to build the master curve of the composite. They are later used to identify a macroscopic model for transverse isotropic short fiber composites. Finally, a meta-model is built to estimate the behavior of the composite at any given fiber volume ratio.

1 Introduction

This study is devoted to the overall response of short fibers thermoplastic composites. The mechanical properties (stiffness and strength) of these composites are lower than those reinforced with continuous fibers. For example a 30% short carbon fiber filled PEEK (PolyEtherEtherKetone) has a Young modulus of 20.9 GPa (Solvay 2016), while a unidirectional long carbon fiber/PEEK composite’s modulus is around 140 GPa in the fiber direction (CYTEC 2016). However, they have the great advantage of being formed by injection molding, thus allowing for very short cycle times, which are mandatory in industries involving large volume (like the automotive industry). For mass reduction, the chemical industry focuses on this kind of composite to design some structural part. The complex mechanical behavior of these materials then requires the development of a predictive constitutive model to capture their mechanical properties under realistic solicitations.

The literature shows that a great range of high-end matrices are usually studied: amorphous PC (Polycarbonate) (Haskell et al. 1983; Chrysostomou and Hashemi 1996), PSU (Polysulfone) (Wenz et al. 1990; Demir 2013), or semi-crystalline PEEK (Polyetheretherketone) (Crevel 2014; Garcia-Gonzalez et al. 2015). PC presents the advantage of being already widely used in the industry. PSU composites are less used except for research purposes on amorphous thermoplastics composites. PEEK matrices are spreading fast across the composite industry thanks to their good mechanical, thermal (Solvay 2016) and bio-compatible properties (Morrison et al. 1995). These matrices are reinforced, either by short carbon fibers (e.g. Friedrich et al. 1986; Garcia-Gonzalez et al. 2015; Anuar et al. 2008; Brody and Ward 1971) or short glass fibers (e.g. Demir 2013; Brody and Ward 1971). Thermoplastic polymers exhibit a time dependence, which can be modeled in the framework of viscoelasticity or elasto viscoplasticity (Maurel-Pantel et al. 2015a; Arrieta et al. 2014; Diani et al. 2006; Endo and de Carvalho Pereira 2016; Panoskaltsis et al. 2007). During the past 20 years, a lot of work has been done to model the macroscopic behavior of composite materials with a time dependent behavior. All this work can be separated into two classes.

In the first one, the authors build a so-called phenomenological model by identifying the macroscopic behavior to fit some “well-chosen” experiments (Garcia-Gonzalez et al. 2015). In the case of short fibers, the specimens are obtained by injection molding and the topography of their microstructure can be obtained through micro-tomography (Chrysostomou and Hashemi 1996; Advani and Tucker 1987; Shen et al. 2004; Friedrich et al. 1986). These micro-tomographies exhibit the complexity of the microstructure, and taking their complexity and their effect on the macroscopic behavior to fit the composite law would be too demanding in terms of experiments to be used in an industrial process.

In the second one, the macroscopic behavior is given by homogenization methods (Bornert 2006). These methods integrate directly the effects of the microstructure parameters and the constitutive law of each constituent in the estimated law of the composite. This can be achieved in an analytical way in the case of mean field methods (Kammoun et al. 2015; Despringre et al. 2016) or given as a result of numerical simulations in the case of full field methods (Moulinec and Suquet 1994, 1998; Dirrenberger et al. 2014). In the case of linear viscoelasticity, by using the correspondence principle (Lévesque et al. 2007; Ricaud and Masson 2009), the authors find some estimates in closed form for the macroscopic laws of isotropic composites with microstructures following the Hashin–Shtrikman lower bound. For more complex microstructures, the estimates given by this principle are no longer given in closed form and need some numerical calculations (see Masson and Zaoui 1999; Rougier et al. 1993 in the case of polycrystals). Another limitation of mean field methods is in the complexity of the constituents laws like the nonlinear behavior exhibited by polymer matrices (Lahellec and Suquet 2013; Brassart et al. 2012). Full field methods can handle all this complexity but they only give the response of the composite to the particular loading path used in the modeling.

In this paper, we deal with the behavior of a thermoplastic matrix reinforced by short glass fiber (5 μm of radius and 50 μm length). The objective is to obtain an estimate of the macroscopic behavior of the composite by using an homogenization method. The main problem of such a material is that the microstructure can be really complex, and, to the best of our knowledge there are not so many homogenization methods available to describe such a microstructure. Previous papers usually used the Mori–Tanaka estimates (Kammoun et al. 2015; Despringre et al. 2016) but, as we will see in Sect. 3.2.3, it may give too compliant estimates. To handle this, we use a full field method based on fast Fourier transforms (Moulinec and Suquet 1994, 1998), which has the advantage of being meshless (unlike the finite elements methods) thus evading meshing problems (or a tremendous amount of calculation time to avoid the latter). This method is used to simulate a set of numerical experiments (virtual dynamic mechanical analysis) and to fit a macroscopic law for the composite. The effective composite behavior model is proposed in the viscoelasticity and incompressibility framework. That is why the investigated material is a PC Lexan matrix studied with experiments in small strain at 150 °C. In first approximation the composite is reinforced by short perfectly aligned glass fibers with different volume ratios ranging from 10% to 30%.

This new method to estimate the behavior of composite materials is based on three sequential steps:

• 1. In a first step, the PC Lexan matrix behavior is identified on experimental data obtained with injection molding samples. We performed DMA frequency scans, single cantilever bending, at 15 temperatures, from 50 °C to 190 °C, at each temperature, 10 frequencies are scanned, from 0.1 to 10 Hz. These results are used in order to build the master curve, which is used to model the viscoelastic behavior of the material.

• 2. In a second step, the effective viscoelastic behavior of composite is identified using virtual DMA tests. The numerical tests are run on representative volume elements of the composite, characterized by different fiber volume ratios, with a full field homogenization method. This is controlled by Python scripting which runs FFT full field computations at different frequencies. Generalized Maxwell models with one, two or three branches are then used to fit these virtual measurements. This is done through Mathematica using an evolutionary optimization algorithm (Wolfram 2015).

• 3. At the last step, a meta-model is proposed and validated on prediction of the viscoelastic behavior for any fiber volume ratio within the studied domain ($10\%< c_{f}<30\%$).

In this first study, we used a single spring dashpot Maxwell model as matrix behavior. This allows for a simple validation of the method and also permits a clear evaluation of the reinforcement effect on the composite behavior.

The paper is composed of three sections which are based on the latter enumeration.

2 Matrix behavior

2.1 Dynamic mechanical analysis

To characterize polymers a common way is to use a dynamic mechanical analysis. This method consists in applying sinusoidal loads to material samples, and measuring the lag between strain and stress. By scanning through frequencies, and/or temperature, it is possible to highlight the viscoelastic behavior of the material. When compared to a classic tensile test, this test gives information, such as transition temperatures, and behavior at different strain rates. For isotropic material, at each temperature (or frequency) a DMA tensile test will give two independent parameters: the storage Young modulus (which is often denoted $E'$) representing the stored elastic energy, and the loss Young modulus ($E''$) used to quantize the energy lost by viscosity. When performing a DMA, a sinusoidal strain is imposed as

$$ \varepsilon _{11}(t) = \varepsilon _{0} \sin \biggl( 2\pi f t \biggr), $$

(1)

where $\varepsilon _{11}$ is the strain in the tensile direction, $\varepsilon _{0}$ the amplitude of the strain load, and $f$ is the frequency of that load. As a consequence of this imposed strain comes a lagged sinusoidal stress which can be expressed through

$$ \sigma _{11}(t) = \sigma _{0} \sin \biggl( 2\pi f t +\phi \biggr), $$

(2)

in which the stress amplitude $\sigma _{0}$ and the phase lag $\phi$ are measured. The storage and loss modulus, $E'$ and $E''$, respectively, are defined by

$$ E' = \frac{\sigma _{0}}{\varepsilon _{0}}\cos\phi \quad \mbox{and} \quad E'' = \frac{\sigma _{0}}{\varepsilon _{0}}\sin\phi . $$

(3)

2.2 Matrix characterization

As stated in the introduction, we want to model the polycarbonate at 150 °C. Unfortunately, obtaining a large range of frequencies is impossible with our experimental devices, as showed in Fig. 1. We are thus forced to use the Time–Temperature Superposition (TTS) method (Li 2000; Maurel-Pantel et al. 2015a) to reconstruct a large enough scan. The TTS method uses Eq. (4) (Andrews and Tobolsky 1951) to build the master curve of the material, expressing the storage and loss moduli as a function of an equivalent frequency $f^{*}$ calculated with the so-called WLF equation:

$$ f^{*} = a_{T} \times f = 10^{ ( \frac{-C_{1}(T-T_{\mathit{ref}})}{C _{2}+(T-T_{\mathit{ref}})} ) }\times f . $$

(4)

In this study, the matrix behavior law was obtained through several DMA frequency scans which were used to build the master curve (15 temperatures, from 50 to 190 °C, each time isothermically scanning through 10 frequencies, from 0.1 to 10 Hz). The results of all these experiments are displayed in Fig. 1. Each curve is an isothermal scan through the 10 frequencies. Using the $a_{T}$ variables, it is possible to shift the curves and reconstruct the full master curve, as shown on Fig. 2.

Fig. 1

Experimental DMA results: isothermal frequency scans on pure PC Lexan, from 50 °C to 190 °C

Fig. 2

TTS method illustrated, on the left are displayed the result of a temperature scan DMA, on the right are the $a_{T}$ shifted results which then constitutes the master curve

The results of the $a_{T}$ values at each temperature are displayed on Fig. 3. These results were then used to fit $C_{1}$ and $C_{2}$ as in Eq. (4). They were identified at a reference temperature of 150 °C as $C_{1} = 180$ and $C_{2} = 900$. The black line on Fig. 3 represents this fit. The master curve was then calculated at an equivalent temperature of 150 °C, temperature at which the Polycarbonate is an incompressible material.

Fig. 3

Experimental value of $a_{T}$ obtained with the TTS method and the corresponding best fit to identify the WLF law parameters ($C_{1}$ and $C_{2}$), from 50 °C to 190 °C

To model these master curve, under the isotropy and incompressibility hypotheses, we use a Maxwell model (or single spring dashpot) for which the deviatoric constitutive behavior is given by

$$ \dot{\boldsymbol{\varepsilon }}^{d} = \frac{(\dot{\boldsymbol{\sigma }})^{d}}{2 \mu }+ \frac{\boldsymbol{\sigma }^{d}}{2 \eta }, $$

(5)

with superscript $d$ denoting the deviatoric part of the different tensors, $\mu$ the shear modulus, which is linked to the Young modulus $E$ by $E=3 \mu$ in the case of incompressible and isotropic solids, and $\eta$ the viscous modulus. In Fig. 4, we show the experimental master curve found using the previously described method (circle and cross markers) and the Maxwell model (continuous and dashed lines), with $E=1770~\mbox{MPa}$ and $\eta =31.9~\mbox{MPa}$.

Fig. 4

Spring dashpot model fitted on the 150 °C (the reference temperature) experimental master curve

While being aware that this is a rough modeling, we decided to use it for this first study as it permits the run of a first set of calculations with a viscoelastic matrix quantitatively similar to a real polycarbonate. Having such a simple behavior makes the method building and debugging much easier. Furthermore, it is important to note that this does not affect the quality of the proposed methodology. For future studies, thanks to a modular model architecture, the matrix behavior will be made more complex by using behavior laws based either on a generalized Maxwell model with several relaxation times or on the VENU (ViscoElastic Network Unit, see Maurel-Pantel et al. (2015b) model).

3 Composite effective behavior

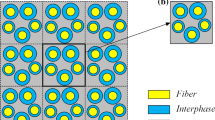
In this section, we model the composite effective behavior with a generalized Maxwell model (in the framework of incompressible, transversely isotropic materials) fitted on virtual DMA testings run on a numerical RVE (Representative Volume Element) like the one presented in Fig. 5. These RVEs are composed of a polycarbonate matrix with the constitutive law given by equation (5) with the material parameters identified in Sect. 2 reinforced by short aligned glass fibers ($E_{f} = 70~\mbox{GPa}$ and $\nu _{f} = 0.33$) with $c_{f}$ varying from 10% to 30% ($c_{f}$ being the fiber volume fraction). These virtual DMA experiments were run at frequencies ranging from 0.01 Hz to 1000 Hz.

Fig. 5

Short fiber RVE used in our computations

3.1 Generalized Maxwell model

The model identified on the virtual experiment results is defined by a generalized Maxwell model which is constructed with several parallel spring dashpots as related in Fig. 6. For this part, let $\mathbf{i}_{2}$, $\boldsymbol{I}$ and $\boldsymbol{I}_{T}$ be, respectively, the second, fourth order and transverse isotropic fourth order identities. We let ⊗ be the tensorial product defined as $(u \otimes v)_{ij}=u_{i} v_{j}$ and $(u \otimes v)_{ijkl}=u_{ij} v _{kl}$ and define

$$ \begin{aligned} & ({i_{2}})_{ij} = \delta _{ij}, \\ & I_{ijkl} = \frac{\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}}{2}, \\ & (I_{T})_{ijkl} = {I}_{ijkl}+n_{i}n_{j}n_{k}n_{l}-\bigl( n_{i}(i_{2})_{jk}n _{l}+n_{k}(i_{2})_{li}n_{j} \bigr) , \end{aligned} $$

(6)

with $\boldsymbol{n}$ the direction of the fibers. Having an incompressible matrix, filled with far stiffer short fibers, we assumed that the composite is also incompressible. For transversely isotropic linear elastic solids, the fourth order tensor of the elastic moduli belongs to a three dimensional vectorial space and can be given as (Bornert 2006)

$$ \boldsymbol{L}=\frac{3}{2}\alpha _{L} \boldsymbol{K}_{E} +\delta _{L} \boldsymbol{K}_{T} + \gamma _{L} \boldsymbol{K}_{L}, $$

(7)

with $\boldsymbol{K}_{T}$, $\boldsymbol{K}_{L}$ and $\boldsymbol{K}_{E}$ three projectors given by

$$ \boldsymbol{K}_{T} = \boldsymbol{I}_{T} - \boldsymbol{J}_{T} , \quad \quad \boldsymbol{K}_{L} = \boldsymbol{K}- \boldsymbol{K}_{T}-\boldsymbol{K}_{E} , \quad\quad \boldsymbol{J} = \frac{1}{3}\mathbf{i}_{2} \otimes \mathbf{i}_{2} , \quad \quad \boldsymbol{K} = \boldsymbol{I}-\boldsymbol{J}, $$

(8)

and

$$ \boldsymbol{K}_{E}= \frac{1}{6} ( 2\boldsymbol{n}\otimes \boldsymbol{n} - \mathbf{i}_{T} ) \otimes (2\boldsymbol{n}\otimes \boldsymbol{n} - \mathbf{i}_{T}) , \quad \quad \boldsymbol{J}_{T} = \frac{1}{2} \mathbf{i}_{T} \otimes \mathbf{i}_{T} , \quad \quad \mathbf{i}_{T} = \mathbf{i}_{2} - \boldsymbol{n} \otimes \boldsymbol{n}. $$

(9)

In Eq. (7), $\alpha _{L}$, $\delta _{L}$ and $\gamma _{L}$ denote the tensile modulus in the fiber direction, the longitudinal and transverse shear moduli, respectively.

Fig. 6

Generalized Maxwell model

Each branch $k$ of the generalized Maxwell model is defined by an elastic moduli tensor $\boldsymbol{L}^{k}$ and a viscous moduli tensor $\boldsymbol{L}_{v}^{k}$ and implies a viscous strain $\boldsymbol{\varepsilon } _{v}^{k}$. To evaluate the total deviatoric stress given by this model, we need to add all the stresses from each branch, which can be written as (let “:” be the double contracted product $(A:\mathbf{B})_{ij}=A _{ijkl}B_{kl}$ or $\mathbf{A}:\mathbf{B}=A_{ik}B_{ik}$):

$$ {\sigma }^{d} = \sum_{k=1}^{N} \bigl({\sigma }^{k} \bigr)^{d} \quad \mbox{and} \quad \bigl({\sigma }^{k} \bigr)^{d}=\boldsymbol{L}^{k} : \bigl( \boldsymbol{\varepsilon }^{d}-\boldsymbol{\varepsilon }_{v}^{k} \bigr); $$

(10)

the evolution of each internal variable $\varepsilon _{v}^{k}$ is given by

$$ \bigl({\sigma }^{k} \bigr)^{d} = \boldsymbol{L}_{v}^{k} : \dot{{\varepsilon }}_{v}^{k}, $$

(11)

with, in the two preceding equations:

$$ \boldsymbol{L}^{k} = \frac{3}{2}\alpha _{L}^{k} \boldsymbol{K}_{E}+\delta _{L}^{k} \boldsymbol{K}_{T} +\gamma _{L}^{k} \boldsymbol{K}_{L} \quad \mbox{and} \quad \boldsymbol{L}_{v}^{k} = \frac{3}{2}\alpha _{\eta }^{k} \boldsymbol{K}_{E}+\delta _{\eta }^{k} \boldsymbol{K}_{T} +\gamma _{\eta }^{k} \boldsymbol{K}_{L}, $$

(12)

with $\alpha _{L}^{k}$, $\delta _{L}^{k}$, $\gamma _{L}^{k}$ the elastic moduli and $\alpha _{\eta }^{k}$, $\delta _{\eta }^{k}$ and $\gamma _{ \eta }^{k}$ the viscous one. $\dot{{\varepsilon }}_{v}^{k}$ can be eliminated with Eqs. (10) and (11) to obtain the final stress–strain relation of the single branch $k$, which can be related to Eq. (5) for transversely isotropic behavior:

$$ \dot{{\varepsilon }}^{d} = { \mathbf{L}^{k}}^{-1}: \bigl( \dot{{\sigma }}^{k} \bigr)^{d}+{\mathbf{L}_{v}^{k}}^{-1}: \bigl( {\sigma }^{k} \bigr)^{d} . $$

(13)

In each branch $k$, using a Laplace–Carson transform, for a time dependent function $f(t)$ given by

$$ \hat{f}(p) = \int _{0}^{+ \infty }e^{-pt}f(t)dt,\quad \mbox{with the nice feature that } \hat{\dot{f}}(p)=p\hat{f}(p), $$

(14)

gives the following expression of the constitutive law (13) in the frequency space:

$$ \bigl(\hat{{\sigma }}^{k} \bigr)^{d}= \hat{\boldsymbol{L}}^{k}_{\mathit{ve}}(p): \hat{{\varepsilon }}^{d}, \quad \text{with } \hat{\boldsymbol{L}}^{k}_{\mathit{ve}}(p) = p \bigl( \bigl(\boldsymbol{L}^{k} \bigr)^{-1}p+ \bigl( \boldsymbol{L}_{v} ^{k} \bigr)^{-1} \bigr) ^{-1}. $$

(15)

For a generalized Maxwell model containing $N$ branches (15), the stress–strain relation in Laplace space is then given by

$$ (\hat{{\sigma }})^{d}=\hat{\boldsymbol{L}}_{\mathit{ve}}(p): \hat{{\varepsilon }}^{d}, \quad \text{with } \hat{ \boldsymbol{L}}_{\mathit{ve}}(p) = \sum_{k=1}^{N} \hat{\boldsymbol{L}}^{k}_{\mathit{ve}}(p) $$

(16)

and

$$ \hat{\boldsymbol{L}}_{\mathit{ve}}(p)=\sum_{k=1}^{N} \bigl( \hat{\alpha }_{\mathit{ve}}(p) \boldsymbol{K}_{E}+\hat{\delta }_{\mathit{ve}}(p)\boldsymbol{K}_{L}+\hat{\gamma }_{\mathit{ve}}(p) \boldsymbol{K}_{T} \bigr) \quad \text{with } \left\{ \textstyle\begin{array}{l} \hat{\alpha }_{\mathit{ve}}(p)= \frac{2 \alpha ^{k}_{\eta }{\alpha ^{k}_{L}} p}{3 (\alpha ^{k}_{L}+\alpha ^{k}_{\eta }p)} \\ \hat{\delta }_{\mathit{ve}}(p)=\frac{\delta ^{k}_{\eta }\delta ^{k}_{L} p}{\delta ^{k} _{L}+\delta ^{k}_{\eta }p} \\ \hat{\gamma }_{\mathit{ve}}(p)=\frac{\gamma ^{k}_{\eta }\gamma ^{k}_{L} p}{\gamma ^{k} _{L}+\gamma ^{k}_{\eta }p}. \end{array}\displaystyle \right. $$

(17)

The complex tensor moduli is given by

$$ \boldsymbol{L}^{*}_{\mathit{ve}}(2\pi f )=\hat{\boldsymbol{L}}_{\mathit{ve}}(i 2\pi f ), $$

which give for each direction the storage and loss moduli which are, respectively, the real and imaginary part of each of the complex moduli $\alpha _{\mathit{ve}}^{*}(2\pi f )$, $\delta _{\mathit{ve}}^{*}(2\pi f )$ and $\gamma _{\mathit{ve}}^{*}(2\pi f )$ defined by

$$ \left\{ \begin{aligned} &\alpha _{\mathit{ve}}^{*}(2\pi f ) = \alpha '_{\mathit{ve}}(2\pi f )+i\alpha ''_{\mathit{ve}}( 2\pi f )= \sum_{k=1}^{N} \biggl( \frac{ 2\alpha ^{k}_{\eta }{\alpha ^{k}_{L}} i 2\pi f }{ 3(\alpha ^{k}_{L}+\alpha ^{k}_{\eta }i 2\pi f )} \biggr) , \\ &\delta _{\mathit{ve}}^{*}(2\pi f ) = \delta '_{\mathit{ve}}( 2\pi f )+i\delta ''_{\mathit{ve}}(2\pi f )=\sum _{k=1}^{N} \biggl( \frac{\delta ^{k}_{\eta }\delta ^{k}_{L} i 2\pi f }{\delta ^{k} _{L}+\delta ^{k}_{\eta }i 2\pi f } \biggr) , \\ &\gamma _{\mathit{ve}}^{*}(2\pi f ) = \gamma '_{\mathit{ve}}( 2\pi f )+i\gamma ''_{\mathit{ve}}(2\pi f )=\sum _{k=1}^{N} \biggl( \frac{\gamma ^{k}_{\eta }\gamma ^{k}_{L} i 2\pi f }{\gamma ^{k} _{L}+\gamma ^{k}_{\eta }i 2\pi f } \biggr). \end{aligned} \right. $$

(18)

3.2 Numerical experiments

3.2.1 Loading conditions

To identify all the material parameters displayed in Eq. (18), we need to numerically simulate DMA along three different loading directions. These directions were chosen parallel to $V_{E}$, $V_{T}$ and $V_{L}$, which are, respectively, eigenvectors of $\boldsymbol{K}_{E}$, $\boldsymbol{K}_{T}$, and $\boldsymbol{K}_{L}$. We have

$$ \left \{ \textstyle\begin{array}{l} V_{E} = -\frac{1}{2}(e_{1}\otimes e_{1}+e_{2}\otimes e_{2})+e_{3} \otimes e_{3}, \\ V_{T} = \frac{1}{2}(e_{1}\otimes e_{1}-e_{2}\otimes e_{2})+e_{2} \otimes e_{1}+e_{1}\otimes e_{2} , \\ V_{L} = e_{3}\otimes (e_{1}+e_{2})+(e_{1}+e_{2})\otimes e_{3}. \end{array}\displaystyle \right . $$

(19)

The numerical values of the storage and loss part of the $\alpha$ modulus, for a given frequency $f$, are computed in the following way.

• 1. The applied strain is

  $$ E(t) = \varepsilon _{0}V_{E}*\sin(2\pi f t), $$

  (20)

  with $\varepsilon _{0}$ chosen as 0.05.

• 2. The macroscopic stress projection $\varSigma :V_{E}$ is then calculated by

  $$ \varSigma (t):V_{E} = \sigma _{0} \sin(2\pi f t + \phi ). $$

  (21)

• 3. Following (3), we find the storage and loss moduli for $\alpha$ by ¹

  $$ \alpha '_{\mathit{ne}}=\frac{3}{2}\frac{\sigma _{0}}{\varepsilon _{0}}\cos\phi \quad \mbox{and} \quad \alpha ''_{\mathit{ne}} = \frac{3}{2} \frac{\sigma _{0}}{\varepsilon _{0}}\sin\phi . $$

  (22)

For the $\delta$ and $\gamma$ moduli, computations are done in exactly the same way by replacing $V_{E}$ by $V_{T}$ and $V_{L}$, respectively, and by replacing Eq. (22) by

$$ \theta '_{\mathit{ne}}=\frac{\sigma _{0}}{\varepsilon _{0}}\cos\phi \quad \mbox{and} \quad \theta ''_{\mathit{ne}} = \frac{\sigma _{0}}{\varepsilon _{0}}\sin \phi , $$

(23)

with $\theta$ being replaced by $\delta$ or $\gamma$.

3.2.2 RVE representativity analysis

To numerically estimate the composite response to the DMA loading, we used a full field homogenization code based on an FFT method (see Moulinec and Suquet 1994, 1998). Contrary to the mean field homogenization methods (e.g. the Mori–Tanaka method; see Appendix A), this code solves exactly (up to the numerical errors) the boundary value problem. From this, we get the estimation of the response of the RVE when subjected to a given loading path (either a macroscopic stress or strain). To avoid numerical inconsistencies, different effects have to be checked.

• As stated in Sect. 2, a DMA test consists in measuring the lag between an imposed sinusoidal strain, and its resulting stress. A too small number of periods might be an issue and thus this needs to be checked.

• The boundary value problem includes time derivatives which are discretized by using a Euler implicit scheme, whose time step needs to be checked.

• The spatial resolution: The numerically generated RVEs are discretized in voxels and the influence of the number of voxels needs to be checked.

• The representativity of the RVE is an issue, which in this case depends on the number of fibers.

These different sensibility studies are done for the computation of $\alpha _{\mathit{ne}}$ for four different frequencies. Only four points were used because of the massive amount of calculation time involved in the calculation of the response of a $600^{3}$ voxel RVE. The calculation time is directly related to the number of voxels; ergo, it increases to the third power of the RVE side.

Number of loading cycles

Having a viscoelastic behavior implies that we need to ensure that it is stabilized when measuring stress and strain. Considering that the first cycles might be different from the stabilized ones, a convergence study was made, from 5 to 20 loading cycles (one cycle being a complete sinus). The phase lag and material parameters are measured only on the five last cycles in every cases (see Fig. 7 for an illustration). Results are shown in Fig. 8. It seems that the number of oscillations has no real effect on the final result of the DMA, and five cycles are enough to accurately represent the behavior. Since the calculation time is only increasing linearly with the number of oscillations, it was decided to use 15 cycles to ensure that the result converged.

Fig. 7

Illustration of the convergence study on loading cycles, $N$ cycles are processed, from 5 to 20, and in every cases the last five cycles are treated (to avoid the stabilization phase)

Fig. 8

Evolution of numerical DMA results on $\alpha '_{\mathit{ne}}$ and $\alpha ''_{\mathit{ne}}$ moduli for four different numbers of cycle (only the five last cycles were processed each time to identify $\alpha '_{\mathit{ne}}$ and $\alpha ''_{\mathit{ne}}$) at four different frequencies

Time steps in one oscillation

Modeling the behavior of materials through FFT implies using time derivatives in the resolution of the boundary problem. To check whether there are enough time steps to have an accurate result, different cases were tested: from 50 points per oscillation to 600 points per oscillation (see Fig. 9). At high frequencies, it seems that even at 50 points per oscillation, the estimated behavior is correct. But as shown in Fig. 9 there is a large dispersion at low frequencies. This means that the point requiring the highest number of time steps will be the first. This is why on Fig. 10 we concentrate on the first frequency. The error rapidly converges under 2% going from 50 time steps to 100. Then the convergence is slow. The calculations were finally made with 500 steps since the relative error seems to be stabilized under 0.5% at this point.

Fig. 9

Numerical DMA results on $\alpha '_{\mathit{ne}}$ and $\alpha ''_{\mathit{ne}}$ moduli for five different numbers of time steps in one oscillation at four different frequencies

Fig. 10

Error on moduli calculation with our numerical DMA as a function of DMA results sampling (considering the result for a sampling of 600 points as reference)

Resolution of the RVE

In order to validate the representativity of the numerically generated microstructure, a first study (with a 50 fibers RVE) was conducted on the voxel resolution, with RVE sizes going from $50^{3}$ voxels to $600^{3}$. In Fig. 11, results of the different calculations were plotted for four frequencies and five resolutions. The maximum dispersion is at the first point. This dispersion is probably induced by the contrast between the very stiff behavior of the fibers and the quasi-fluid-like behavior of the matrix at low frequencies. This implies that a larger resolution is required for this case, so that it can be used to determine the proper RVE size. Figure 12 focuses on this point and gives the relative error (calculated by assuming that the best point, for a $600^{3}$ RVE, is the exact result). Both the storage and the loss moduli have a convergent behavior. A relative error under 10% was determined. Therefore, we chose to use $200^{3}$ voxels RVEs.

Fig. 11

Numerical DMA results on $\alpha '_{\mathit{ne}}$ and $\alpha ''_{\mathit{ne}}$ moduli for different resolutions of numerically generated RVE at four frequencies

Fig. 12

Error on moduli calculation with our numerical DMA as a function of numerically generated RVE resolutions (considering the $600^{3}$ pixels result as reference)

Number of fibers

To validate the representativity of the RVE, we will check that the potential RVE contains enough fibers to be representative (while keeping the same radius in pixel for the fiber). This can be seen as the optical zoom in a picture (see Fig. 13). We need to see how many fibers need to be taken into consideration to accurately represent the behavior of the material. An indicator of the representativity is the dispersion of the results over ten calculations with different generated RVEs. Ten RVEs are generated for each zoom case, and the mean value and the dispersion are compared. The results of the convergence tests are plotted in Figs. 14 and 15, respectively, for the storage and loss moduli. The maximum error (compared to the mean value) in RVEs depends on the frequency at which the error is calculated. Having 200 fibers reduces the dispersion a lot. Therefore, in the rest of this paper, all the results will feature 200 fibers RVEs.

Fig. 13

Effect of the number of fibers (a.k.a zoom) in the RVE

Fig. 14

Mean value and standard deviation (obtained with a set of ten different RVEs) of the $\alpha _{\mathit{ne}}'$ modulus for 50 and 200 fibers and for four frequencies

Fig. 15

Mean value and standard deviation (obtained with a set of ten different RVEs) of the $\alpha _{\mathit{ne}}''$ modulus for 50 and 200 fibers and for four frequencies

3.2.3 Results

Effect of the volume ratio

Figs. 16 and 17 show the evolution of the DMAs for $\alpha _{\mathit{ne}}$ and $\delta _{\mathit{ne}}$, respectively, when the fiber volume ratio goes from 0% to 30%. The case of $\gamma _{\mathit{ne}}$ was omitted here since it presented very similar results to $\delta _{\mathit{ne}}$. Increasing the fibers volume ratio in the RVE naturally increases the moduli while the main relaxation time seems to be decreasing. One could also note that with the addition of fibers, the modulus tends to remain different from 0 at low frequencies; this might be caused by the appearance of a really low relaxation time. Contrary to the $\alpha _{\mathit{ne}}$ DMA (see Fig. 16), the $\delta$ DMA seems to be less affected by the fiber volume ratio. The modulus still increases linearly with the volume ratio. But the relaxation time remains very close to the matrix relaxation time. The overall shear behavior is also significantly closer to a simple 1 spring dashpot model than the fiber axis behavior.

Fig. 16

Numerical DMA results: evolution of $\alpha _{\mathit{ne}}'$ and $\alpha _{\mathit{ne}}''$ moduli with fiber volume ratio change

Fig. 17

Numerical DMA results: evolution of the $\delta _{\mathit{ne}}'$ and $\delta _{\mathit{ne}}''$ with fiber volume ratio change

Model identification

The identification of the different complex viscoelastic moduli $\alpha _{\mathit{ve}}^{*}$, $\delta _{\mathit{ve}}^{*}$ and $\gamma _{\mathit{ve}}^{*}$, defined in equation (18), over the virtual experimental data was made using Mathematica’s differential evolution algorithm, using the usual least squares method; the cost function was defined as follows:

$$ \mathit{Cost} = \sum_{\theta \in \{\alpha ,\delta ,\gamma \}} \sum_{j=1}^{N _{f}} \biggl( \frac{\theta '_{\mathit{ve}} ( 2\pi f_{j} ) -\theta '_{\mathit{ne}} ( 2\pi f_{j} ) }{\theta '_{\mathit{ne}} ( 2\pi f_{j} ) } \biggr) ^{2}+ \biggl( \frac{\theta ''_{\mathit{ve}} ( 2\pi f_{j} ) -\theta ''_{\mathit{ne}} ( 2\pi f_{j} ) }{\theta ''_{\mathit{ne}} ( 2\pi f_{j} ) } \biggr) ^{2}, $$

(24)

in which $\theta$ represents the three different moduli, and $N_{f}= 18$ the number of studied frequencies varying from $10^{-2}$ to $10^{3}~\mbox{Hz}$.

3.3 Number of spring dashpot needed to accurately represent the behavior

Although the matrix behavior is defined as a single spring dashpot (only one relaxation time), it is interesting to note that the composite material behavior law cannot be described accurately with only one spring dashpot. Figures 18 and 19 show the best fit, respectively, on storage and loss moduli, with one, two and three branches of spring dashpot models (and as many relaxation times). The values of the cost function are $C = 9.10$ when only one spring dashpot is used, $C = 0.34$ when two are used, and finally $C =0.1$ when three branches of spring dashpot models define $\alpha _{\mathit{ve}} ^{*}$. Having only one spring dashpot model makes the fitting impossible since on a single spring dashpot model, the storage and loss moduli curves always cross each other at the maximum value of the loss modulus. These figures show that having two parallel spring dashpot branches gives a far better fitting, but the dissipation peak is still not well fitted, especially at its maximum. One could finally conclude that, for this particular case, having a model based on three spring dashpot branches is a good way to achieve an accurate representation since this gives a result extremely close to the virtual experiment result. This setting will be used for the rest of this work. This is not surprising because some authors have already shown that in particular two phases isotropic composites (matrix described by a single spring dashpot and spherical inclusions), exhibit three relaxation times for the effective shear modulus and two for the effective bulk modulus (see Ricaud and Masson 2009). Although this has not been investigated in this work, one might think that if the viscoelastic behavior of the matrix was defined by a generalized Maxwell model, the composite macroscopic behavior should involve even more relaxation times than the matrix.

Fig. 18

Confrontation between storage moduli evolution identified with one, two and three branches of spring dashpot models proposed, the reference values (numerical DMA with a full field method) and the classical MT estimate (numerical DMA with a mean field method)

Fig. 19

Confrontation between loss moduli evolution identified with one, two and three branches of spring dashpot models proposed, the reference values (numerical DMA with a full field method) and the classical MT estimate (numerical DMA with a mean field method)

The three models were compared with Mori–Tanaka estimates (see Figs. 18 and 19). They all give a closer estimation to CraFT results. The Mori–Tanaka (MT) results are failing on different points:

• 1. The high frequency modulus, using a MT estimate leads to an error of 17%, with a value of 5180 MPa for MT and 6192 MPa for the CraFT results.

• 2. When looking at low frequencies, the MT estimates falls off to zero at about 0.1 Hz, while CraFT results never reach zero on the tested frequency range.

• 3. Finally, when looking particularly at Fig. 19, the MT estimate gives good results on high frequencies, where it is actually better than a one and two branches model. But, at lower frequencies (i.e. before the peak) it is the worst model out of the three.

In this section, a model have been developed to avoid going through the whole full field process each time. But, to extend this model to different cases, for example when the fiber volume ratio varies, it was decided to build a meta-model.

4 Meta-modeling the mechanical properties

4.1 Meta-model on the fibers volume ratio

To simplify the modeling process, and gain calculation time, we used a so-called meta-model. This approach permits the prediction of different mechanical parameters within a domain defined by the experimental values used to build the latter. For example, Leh (2013) used a meta-model to accelerate an optimization process on the shape of composite high pressure vessels, and Ghasemi et al. (2014) built a meta-model to represent the mechanical behavior of polymeric nanocomposites. In this work, a simple meta-model was built to be able to predict the behavior of a unidirectional short fiber composite material, having as parameter the fiber volume ratio. The evolution of the six different mechanical parameters ($\alpha _{L},\delta _{L},\gamma _{L},\alpha _{\eta }, \delta _{\eta },\gamma _{\eta }$) of each Maxwell branch were studied for three fiber volume ratios: $c_{f} = 0.1, 0.2 \mbox{ and } 0.3$. A problem was encountered with the first branch, because at lower fiber volume ratio, the behavior becomes closer and closer to a simple Maxwell model. Because of this, for $c_{f} = 0.1$ and 0.2 only two branches were required to fit the macroscopic behavior. Thus, to avoid inconsistencies, it was decided to fit the meta-model over the sums of all branches and the result of the two larger branches. The values identified as best fit can be found in Appendix B. Figure 20 shows the different results of the sums on the elastic parameters. The behavior was assumed linear and the best linear fit is also plotted on this figure. Next, a similar approach was used to explore the evolution of the viscous parameters. It was found that the inverse of the sums had an exponential behavior and, thus, such a fit was used. Figure 21 displays these results and their best exponential fits. Finally, the individual parameters of the two main branches (i.e. the ones with the higher elastic modulus) were fitted in a similar way: linear fit for the elastic parameters, and exponential for the viscous parameter. These results are displayed, respectively, in Figs. 22 and 23. Only the first two main branches were used here because the behavior at low volume ratio is very close to a simple Maxwell model. As a consequence, only two branches are required for the 10% fiber volume ratio case, and this makes the results on the third branch non-consistent. To avoid this inconsistency problem, the parameters of the third branch are calculated last, using the interpolated results of the first two branches and the value of the sums. Figure 24 is a graphical representation of this meta-model. Only one $\delta _{L}^{1}, \delta ^{1}_{\eta }, \gamma ^{1} _{L},\gamma ^{1}_{\eta }$ set is identified, because, as shown in Fig. 17, the shear behavior remains Maxwell-like.

Fig. 20

Evolution of the sums of the elastic parameters with the fiber volume ratio variation, the best linear fit is also plotted

Fig. 21

Evolution of the inverse sums of the viscous parameters with the fiber volume ratio variation, the best exponential fit is also plotted

Fig. 22

Evolution of the $\alpha _{L}$ parameters of the first two branches and best linear fit of it

Fig. 23

Evolution of the $\alpha _{\eta }$ parameters of the first two branches and its best exponential fit

Fig. 24

Framework of the meta-model used to give the estimation of the behavior at a given fiber volume ratio

4.2 Validation of the meta-model

The meta-model gives an estimation of a three branches generalized Maxwell model for any fiber volume ratio in the studied domain (in our case $c_{f} \in [0.1,0.3]$). In order to validate these estimations, two calculations were made under CraFT and compared to the meta-model. Figures 25 and 26 show these comparisons for RVEs made, respectively, of 15% and 25% of glass fiber. The meta-model seems to be able to capture both the change of moduli and the shift in frequency of the moment when the elastic modulus crosses the loss modulus.

Fig. 25

Comparison between the meta-model estimation and reference values obtained through FFT for 15% of fibers

Fig. 26

Confrontation between the identified meta-model estimation and the reference values for 25% of fibers

5 Conclusion

This paper introduces a new method to model the effective linear viscoelastic behavior of composite materials made of a viscoelastic matrix reinforced by elastic fibers. This new method is based on full field calculations which are allowed by the use of an FFT-based method to solve the homogenization problem. As a first step, this new method was applied to short aligned fibers composites, with incompressible matrices modeled by a single spring dashpot model (i.e. Maxwell model). This was used to build a virtual dynamic mechanical analysis data base on which the behavior of the composite was identified following a generalized Maxwell scheme. This data base of a virtual experiment also allowed us to study the influence of the fiber volume ratio on the mechanical parameters. It was found to have an influence on the overall stiffness of the composite and its relaxation times. The proposed model was compared to the usual Mori–Tanaka estimates and we note that it gives a much more accurate estimate for the effective linear viscoelastic behavior.

Finally, this model was used to build a meta-model in order to take into account different fibers volume ratios and it showed promising results. It managed to capture accurately the microstructural effects induced by the addition of fibers in the RVE.

In this paper, the methodology was applied on an idealized matrix behavior since it was assumed to be incompressible and modeled by a single spring dashpot Maxwell model (i.e. with only one relaxation time). These assumptions limit a bit the use of the model but they allowed us to validate the methodology on a very simple case. In future work, these assumptions will be removed and this method will be adapted to a compressible matrix having several relaxation times. The meta-model should also be extended to take into account more microstructural parameters as fiber orientation and fiber length distributions in addition to fiber volume fraction. Finally, it is important to notice that this meta-model can easily be implemented in a FEM code since its formulation is a classical generalized Maxwell model for transversely isotropic material. This implementation could be coupled with other software which provides an estimate for the microstructural parameters (like MoldFlow which gives estimates for the fiber orientation for the injection-molded fiber-reinforced thermoplastics).

Appendices

Appendix A: Hashin–Shrikman lower bound

The aim of this appendix is to derive the Hashin–Shtrikman lower bound for the storage and the loss moduli of the composites described in Sects. 2 and 3. These composites are made of an isotropic and incompressible Maxwellian matrix reinforced by short fibers parallel to the $\mathbf{n}$ direction. The constitutive behavior of the matrix is given by the following differential equation:

$$ \frac{\mathbf{{s}}}{2 \eta }+\frac{\dot{\mathbf{{s}}}}{2 \mu }= \dot{\mathbf{{e}}}, $$

(25)

with $\mathbf {s}$ the deviatoric part of the stress tensor, $\mathbf {e}$ the deviatoric part of the strain tensor, $\mu$ the shear modulus and $\eta$ the viscosity. Equation (25) can be transform by using the Laplace–Carson transform (14) which gives the constitutive behavior in the Laplace domain:

$$ \hat{\mathbf{{s}}}(p)=\mathbf{{L}}_{\mathit{ve}}(p):\hat{\mathbf{{e}}}(p), \quad \text{with } \mathbf{{L}}_{\mathit{ve}}(p)=2\mu _{\mathit{ve}}(p) \mathbf{{K}}, \ \mbox{and} \ \mu _{\mathit{ve}}(p)=\frac{p \mu }{p+ \mu /\eta }. $$

(26)

In this expression, the relation between the strain and the stress is linear (with modulus $\mu _{\mathit{ve}}(p)$) and one can derive the Hashin–Shtrikman lower bound for the macroscopic modulus tensor in the Laplace domain as in Ricaud and Masson (2009). In the case of a matrix, denoted by superscript 2, its modulus tensor and concentration are, respectively, $\mathbf{{L}}_{\mathit{ve}}^{(2)}(p)$ and $c^{(2)}$, reinforced by identical aligned ellipsoidal and stiffer fibers ($\mathbf{{L}}_{\mathit{ve}}^{(1)}(p)$ and $c^{(1)}$); Ponte Castañeda and Willis (1995) give the following expression for the Hashin–Shtrikman lower bound:

$$ \tilde{\mathbf{{L}}}_{\mathit{ve}}^{(\mathit{HS})}(p)=\mathbf{{L}}_{\mathit{ve}}^{(2)}(p)+c^{(1)} \bigl[ \bigl( \mathbf{{L}}_{\mathit{ve}}^{(1)}(p)-\mathbf{{L}}_{\mathit{ve}}^{(2)} \bigr) ^{-1} +c ^{(2)} {\mathbf{{P}}} \bigr] ^{-1}, $$

(27)

in which the microstructural tensor $\mathbf{{P}}$ depends on the shape of the ellipsoidal inclusion and the matrix modulus tensor. When the matrix is isotropic the $\mathbf{{P}}$ tensor is transversely isotropic and if the matrix is also incompressible it can be written

$$ {\mathbf{{P}}}=\frac{3}{2}\alpha _{P} {\mathbf{{K}}}_{E}+ \delta _{P} {\mathbf{{K}}}_{T}+\gamma _{P}{ \mathbf{{K}}}_{L}, $$

(28)

with tensors $\mathbf{{K}}_{E}$, $\mathbf{{K}}_{T}$ and $\mathbf{{K}} _{L}$ already defined in Sect. 2 and scalars $\alpha _{P}$, $\delta _{P}$ and $\gamma _{P}$ defined by

$$\begin{aligned} & h(x)=\frac{x ( x \sqrt{x^{2}-1}-\cosh ^{-1}(x) ) }{ ( x^{2}-1 ) ^{3/2} }\quad \mbox{and} \quad x>1, \end{aligned}$$

(29)

$$\begin{aligned} & \alpha _{P}=\frac{-2 x^{2} h(x)-h(x)+2 x^{2}}{2 \mu ( x^{2}-1 ) }, \end{aligned}$$

(30)

$$\begin{aligned} & \delta _{P}=\frac{2 x^{2}-3 h(x)}{8 \mu ( x^{2}-1 ) }, \end{aligned}$$

(31)

$$\begin{aligned} & \gamma _{P}=\frac{ ( x^{2}+1 ) (3 h(x)-2)}{4 \mu ( x^{2}-1 ) }, \end{aligned}$$

(32)

in the case of spheroidal inclusion defined by the aspect ratio $x=\frac{a_{3}}{a_{1}}=\frac{a_{3}}{a_{2}}$ with $a_{i}$ half of the length of the principal axes. In that case, Eq. (27) shows that $\tilde{\mathbf{{L}}}_{\mathit{ve}}^{(\mathit{HS})}(p)$ is transversely isotropic too and can be written

$$ \tilde{\mathbf{{L}}}_{\mathit{ve}}^{(\mathit{HS})}(p)=\frac{3}{2}\alpha _{L}^{(\mathit{HS})}(p) \mathbf{{K}}_{E}+\delta _{L}^{(\mathit{HS})}(p) \mathbf{{K}}_{T} $$

(33)

with the modulus $\alpha _{L}^{(\mathit{HS})}(p)$, $\delta _{L}^{(\mathit{HS})}(p)$ and ${\gamma }_{L}^{(\mathit{HS})}(p)$ given by Eqs. (27) to (33).

The harmonic effective complex moduli tensor is then given by

$$ \tilde{\mathbf{{L}}}^{*(\mathit{HS})}(2\pi f )=\tilde{\mathbf{{L}}}_{\mathit{ve}}^{(\mathit{HS})}(i 2\pi f )=\tilde{\mathbf{{L}}}^{\prime \,(\mathit{HS})}(2\pi f )+i \tilde{\mathbf{{L}}} ^{\prime\prime \,(\mathit{HS})}(2\pi f ), $$

(34)

with $f$ the frequency, $i$ the imaginary unit, $\tilde{\mathbf{{L}}}^{\prime \,(\mathit{HS})}(2\pi f )$ the storage moduli tensor and $\tilde{\mathbf{{L}}}^{\prime\prime \,(\mathit{HS})}(2\pi f )$ the loss moduli tensor.

Appendix B: Meta-model function values

The different identified functions are specific to the exact case of a material consisting in a short glass fiber reinforced PC matrix, and more specifically when the matrix is supposed to behave like a simple spring dashpot model. Thus these should be used with caution. They are all related in Table 1. The linear functions are written as

$$ f(c_{1}) = Ax+B $$

(35)

and the exponential functions are

$$ f(c_{1}) = Ae^{Bx}. $$

(36)

Table 1 Values of the meta-model functions