Introduction

Structural vibration and acoustic noise problems have become a major preoccupation due to their undesirable effects on the performance of systems and structures. Vibrations can cause dynamic instabilities that can lead to major structural and functional damage. Therefore, the control of vibratory and acoustical phenomena is a very important phase in the design of mechanical systems. The vibration problem can be solved by increasing the damping level of the structure using a passive damping treatment, which involves the incorporation of viscoelastic materials with dissipative properties of vibration energies.

These materials are able to transform vibration energy into thermal energy, there by dissipating deformation energy into heat. Generally, a viscoelastic layer is incorporated between two skins forming a structure called passive constrained layer damping “PCLD” with high damping capacities. The PCLD is widely used in the fields of aviation, aerospace, submarines, vehicles…, because of its low cost, easy implementation and high reliability, especially at low temperatures and high frequencies. The first studies concern sandwich structures with viscoelastic core back to 1959 where Kerwin [1] and Ross [2] used an analytical expression of the loss factor as a function of the characteristics of the structure based on the fourth-order linear ordinary differential equation of the transverse displacement of sandwich beam. A succession of studies has been performed by many researchers, where analytical models have been proposed to characterize the damping properties of sandwich beam with viscoelastic core [3,4,5,6,7]. DiTaranto [8] has defined an equation that describes the damping properties (attenuated pulsation, loss factor) with different boundary conditions.

The frequency independent viscoelastic model has been widely investigated, Rao [9] employed Hamilton’s energy principle to formulate the motion equation, where an analytical resolution has been proposed to characterize the damping properties of sandwich beams. Cai et al. [10] applied an analytical approach to examine the vibration response of the PCLD beam using the Lagrange Energy Method, where the Mead and Markus model [5] has been adopted to describe the kinematic relationships between the three layers. Cai et al. [11] employed for this new study an active treatment (ACLD) which consists in replacing the elastic constraint layer in the PCLD principle by a piezoelectric layer in order to improve the energy dissipation properties of the PCLD treatment, where the same principle was followed with the exception of the adoption of a new admissible function to represent the longitudinal displacements of the piezoelectric constraint layer in the sandwich beam.

However, several numerical approaches based on finite elements have been considered for composite structures to better take into account more complex geometries. Irazu and Elejabarrieta [12] analyzed the influence of design parameters on the dynamic properties of thin sandwich structures. Thus, Daya [13, 14] applied a non-linear theory to study the vibrations of sandwich beams with a viscoelastic core, which the non-linear frequency response of the beam is established using the Harmonic Balance Method coupled to single-mode of Galerkin’s modal basis. Bilasse [15] proposed a simplified and general approaches for analyzing linear and nonlinear vibrations of viscoelastic sandwich beams with various viscoelastic frequency dependent laws using the finite element method. Arvin et al. [16] presented a higher order sandwich theory with composite faces and a viscoelastic core, the transverse displacements are considered independent for the three layers of sandwich. In the same line, another numerical model has been developed by Moita et al. [17] for vibration analysis of multilayer sandwich plates using a hybrid damping treatment, in which the viscoelastic core is sandwiched between an elastic layer and another piezoelectric layer.

Most of the authors have used approximate viscoelastic behavior laws in their studies that are frequency and temperature independent. However, the viscoelastic behavior is highly dependent on frequency as well as temperature, which can be characterized by experimental investigations. Therefore, experimental studies [18, 19] show that for different temperatures and a fixed frequency, the variation in mechanical properties (storage modulus, loss factor) as a function of temperature has the same shape as that obtained in a fixed temperature experiment by varying the frequency, which makes it possible to superpose different curves for various temperatures. The superposition is carried out by a horizontal translation according to a factor called shift factor αT corresponding to a change in frequency scale called reduced frequency \({{\alpha }}_{\mathrm{T}}\upomega \) αTω on the new superposed curve named the master curve. There are several empirical equations to describe the evolution of the shift factor \({\alpha }_{T}\) in logarithmic scale [20]. Moreover, the vibro-acoustic responses of sandwich structures are widely examined, but outside the viscoelastic layer, most authors have studied the responses of sandwich structures with isotropic core materials, while the efficiency of viscoelastic materials can be considerable in reducing acoustic noise. Li and Yu [21] examined the vibrational and acoustic responses of orthotropic sandwich panels in high-temperature environment and under a concentrated harmonic force. The natural frequencies as well as the corresponding modes are obtained under thermal stress by application of low order shear strain theory. The authors proposed an analytical solution validated by a numerical approach using the commercial software “Nastran”. The results shown that the natural frequencies of the sandwich panel decrease with increasing of temperature, however, the vibro-acoustic peaks are very high in the absence of the damping effect in the structure. Jeyaraj et al. [22] applied a numerical method combining finite element method with boundary element method (FEM–BEM) to study vibration and acoustic responses of isotropic plates in thermal environment, it’s concluded that natural frequencies decrease while the displacement response of the structure increases with increasing plate temperature. Zhao et al. [23] also presented a numerical study of fiber-reinforced composite plates in a thermal environment using the classical laminated plate theory, this study showed that resonance amplitudes decrease with temperature increase. An analytical approach was presented by Geng and Li [24] to study the vibrations and acoustic characteristics of an isotropic rectangular thin plate under uniform thermal conditions, the same previous findings were also drawn from which the first natural frequency is more sensitive to temperature variations. Li et al. [25] studied the sound transmission loss (STL) of orthotropic sandwich panels in a thermal environment, where the results of the numerical simulation are validated by experimental studies. The results show that the natural frequencies of the panel decrease and the STL peaks tend to lower frequencies when the temperature increases. Jeyaraj et al. [26] numerically studied the vibration characteristics and acoustic response of a fiber-reinforced composite plate in a thermal environment with consideration of the intrinsic damping properties of the composite material. They found that the vibration response of the structure decreases with uniform temperature increase for both Glass–Epoxy and PEEK/IM7 materials, but the acoustic radiation from the plate decreases only marginally due to the interaction between reduced stiffness and improved damping. Geng and Li [27] studied the acoustic vibration characteristics of a thin rectangular isotropic plate under thermal conditions. The study shows that plate vibration responses and acoustic radiation efficiency tend to low frequencies as the temperature of the structure increases, which is verified by simulations using a combination of the Finite Element Method (FEM) and the Boundary Element Method (BEM).

The development of a reliable and robust vibration control system has become a necessity in the face of the structural functional requirements. Therefore, passive control is very effectively to attenuate structure vibration and acoustic noise. Numerical simulation of structures damped by viscoelastic materials is an important design step to predict the effectiveness of this damping treatment. However, this step requires a good knowledge of the viscoelastic behavior materials and the consideration of all significant factors that affect their behavior. In this work, a numerical approach is presented to study the vibro-acoustic responses of sandwich beams with a viscoelastic core in order to investigate the structural damping provided by the viscoelastic layer taking into account different viscoelastic models described by different laws.

This research investigated the vibroacoustic responses of structures with viscoelastic materials known for their remarkable damping properties. To enhance the study, a Monte Carlo simulation is employed to analyze the variability and stochastic behavior of sandwich beams with randomly varying properties. The frequency responses are evaluated by modal stability procedure (MSP) and asymptotic numerical method (ANM) to estimate the sandwich beam behavior with nonlinear properties. The resolution of the eigenvalues requires the use of a very complex algorithm of the numerical asymptotic method combined with the finite element method given the frequency and temperature dependence of the viscoelastic properties. The MSP formulation is based on the finite element discretization of the equation of motion established by Hamilton’s principle as well as on the ANM to solve the eigenvalue problem, The MSP hypotheses are identified in many research such as [28]. The MSP-MCP formulation applied to the frequency response is used to evaluate the stochastic behavior of a viscoelastic sandwich beam with random properties after validation study by direct comparison with MCS-DFR approach. The vibro-acoustic responses are obtained firstly for different viscoelastic laws describing their mechanical properties and secondly for different structure configurations, precisely the variation of the viscoelastic layer thickness.

Variational Formulation

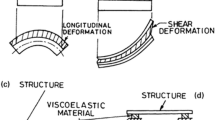
The sandwich beam considered in this work is composed of a viscoelastic layer interposed between two face layers constituting the skins of the sandwich. The assumptions considered by Bilasse [15] are modified to take into account the effect of longitudinal and rotational inertia as well as the asymmetry of the sandwich. The geometrical deformation of the asymmetrical beam considered for this work is shown in Fig. 1a, where h2, h1 and h1 care the thickness of the central layer, upper layer and lower layer, respectively. The displacement field of the viscoelastic sandwich beam is given by Rao’s zigzag model [9] (Fig. 2) based on the first-order deformation theory (Fig. 1b), where Euler–Bernoulli’s theory is applied to the composite sandwich faces and Timoshenko’s theory to the viscoelastic core.

Fig. 1
figure 1

a Sandwich beam configuration. b Displacement field given by Rao’s linear zigzag model [9]

Full size image
Fig. 2
figure 2

Beam element with two nodes

Full size image

Considering these assumptions, the displacement and deformation fields of each face layer are given by:

$$ \begin{array}{*{20}c} {u_{i} \left( {x,z,t} \right) = u_{0i} \left( {x,t} \right) - \left( {z - z_{i} } \right)w_{,x} } \\ {w_{i} \left( {x,z,t} \right) = w\left( {x,t} \right)\quad {\text{with}}\; i = 1,3} \\ {\varepsilon_{ni} \left( {x,z,t} \right) = u_{0i,x} - \left( {z - z_{i} } \right)w_{,xx} } \\ \end{array} $$
(1)

where \(\bullet_{,x}\) the derivative with respect to x, u, w and εn are respectively, longitudinal displacement, transverse displacement and normal deformation adopted for small deformations and defined by the Green–Lagrange formula for each face layer, u0i represent the longitudinal displacement at the middle plane and z is the order of each layer, respectively. For the viscoelastic layer on which Timoshenko’s theorem is applied, the displacement and strain fields are:

$$ \begin{array}{*{20}c} {u_{2} \left( {x,z,t} \right) = u_{0} \left( {x,t} \right) - \left( z \right)\beta } \\ {W_{2} \left( {x,z,t} \right) = w\left( {x,t} \right)} \\ {\begin{array}{*{20}c} {\varepsilon_{n2} \left( {x,z,t} \right) = u_{0,x} + \left( z \right)\beta } \\ {\varepsilon_{s2} \left( {x,z,t} \right) = \beta \left( {x,t} \right) + w_{0,x} } \\ \end{array} } \\ \end{array} $$
(2)

with εs2 is the shear strain of the viscoelastic layer and β is the rotation of the central layer.

The expressions that describe the relationship between the core layer and face layers are given by:

$$ \begin{array}{*{20}c} {u_{01} = u_{0} + \frac{{h_{c} }}{2}\beta - \frac{{h_{1} }}{2}\frac{\partial w}{{\partial x}}} \\ {u_{03} = u_{0} - \frac{{h_{c} }}{2}\beta + \frac{{h_{2} }}{2}\frac{\partial w}{{\partial x}}} \\ \end{array} $$
(3)

with u0 = u02 corresponds to the displacement in the middle plane of the viscoelastic layer. The formulation of equation of motion is established by applying the Hamilton’s principle.

$$ \begin{array}{*{20}c} {\Pi = W_{{\text{p}}} + W_{{\text{c}}} } \\ {W_{{\text{p}}} = \sum\limits_{i = 1}^{3} {\int\limits_{V} {\frac{1}{2}\sigma_{ij} \varepsilon_{ij} {\text{d}}V} } - \int\limits_{V} {f_{i}^{v} w_{i} {\text{d}}V} - \int\limits_{V} {f_{i}^{s} w_{i} {\text{d}}S} } \\ {W_{{\text{c}}} = \sum\limits_{i = 1}^{3} {\frac{1}{2}\int\limits_{V} {\left( {\rho_{i} \dot{u}_{i} \dot{u}_{i} + \rho_{i} \dot{w}_{i} \dot{w}_{i} } \right){\text{d}}V} } } \\ \end{array} $$
(4)

where Wp, Wc are the potential energy and kinetic energy, σ, fv, fs and ρ represent the stress tensor, the volume force, the surface force and the density respectively, Eq. (4) can be rewritten by using the variational formulation, as:

$$ \int\limits_{0}^{T} {\delta \Pi {\text{d}}t} = \int\limits_{0}^{T} {\left( {\delta W_{{\text{p}}} + \delta W_{{\text{c}}} } \right){\text{d}}t} = \int \limits_{0}^{T} \int \limits_{0}^{L} \left[ \begin{gathered} N_{1} \delta u_{1,x} + N_{2} \delta u_{2,x} + N_{3} \delta u_{3,x} + M_{1} \delta w_{,xx} + M_{2} \delta \beta_{,x} \hfill \\ + M_{3} \delta w_{,xx} + T(\delta w_{,x} + \delta \beta ) + \rho_{1} S_{1} \ddot{u}_{1} \delta u_{1} + \ddot{u}_{3} \delta u_{3} \hfill \\ + \rho_{2} S_{2} \ddot{u}_{2} \delta u_{2} + \left( {\rho_{1} S_{1} + \rho_{2} S_{2} + \rho_{3} S_{3} } \right)\ddot{w}\delta w {-}P\left( {x,t} \right)\delta w \hfill \\ \end{gathered} \right]{\text{d}}x{\text{d}}t = 0 $$
(5)

Replacing Eq. (3) in Eq. (5) yields:

$$ \int\limits_{0}^{T} {\int\limits_{0}^{L} {\left[ \begin{gathered} N_{1} \left( {\delta u_{0,x} + \frac{{h_{2} }}{2}\delta \beta_{,x} - \frac{{h_{1} }}{2}\delta w_{,xx} } \right) + N_{2} \delta u_{0,x} + N_{3} \left( {\delta u_{0,x} - \frac{{h_{2} }}{2}\delta \beta_{,x} + \frac{{h_{3} }}{2}\delta w_{,xx} } \right) + M_{1} \delta w_{,xx} + M_{2} \delta \beta_{,x} \hfill \\ + M_{3} \delta w_{,xx} + T_{2} (\delta w_{,x} + \delta \beta ) + \rho_{c} S_{c} \ddot{u}_{0} \delta u_{0} + \rho_{1} S_{1} \left( {\ddot{u}_{0} + \frac{{h_{2} }}{2}\ddot{\beta } - \frac{{h_{1} }}{2}\ddot{w}_{,x} } \right)\left( {\delta u_{0} + \frac{{h_{2} }}{2}\delta \beta - \frac{{h_{1} }}{2}\delta w_{,x} } \right) + \hfill \\ \rho_{3} S_{3} \left( {\ddot{u}_{0} - \frac{{h_{2} }}{2}\beta + \frac{{h_{3} }}{2}\ddot{w}_{,x} } \right)\left( {\delta u_{0} - \frac{{h_{2} }}{2}\delta \beta + \frac{{h_{3} }}{2}\delta w_{,x} } \right) + \left( {\rho_{1} S_{1} + \rho_{3} S_{3} + \rho_{2} S_{2} } \right)\ddot{w}\delta w - P\delta w \hfill \\ \end{gathered} \right]} } {\text{d}}x{\text{d}}t = 0 $$
(6)

Using Hooke’s law to express the normal stress Ni and the bending moment Mi associated to each layer of the sandwich face:

$$ \begin{array}{*{20}c} {N_{i} \left( {x,t} \right) = \int \limits_{{s_{i} }} E_{i} \varepsilon_{ni} {\text{d}}s = E_{i} S_{i} u_{j,x} } \\ {M_{i} \left( {x,t} \right) = \int \limits_{{s_{i} }} \left( {z - z_{i} } \right)E_{j} \varepsilon_{nj} {\text{d}}s = E_{i} I_{i} w_{,xx} } \\ \end{array} i = 1,3 $$
(7)

where Ei and Ii are Young’s modulus and quadratic moment of the cross section of the ith layer, respectively. The normal force N, the bending moment M and the shear force T in the viscoelastic layer are given in the time domain by the following terms:

$$ \begin{array}{*{20}c} {N_{2} \left( {x,t} \right) = \int \limits_{{s_{2} }} E_{2} \dot{\varepsilon }_{n2} {\text{d}}s} \\ {M_{2} \left( {x,t} \right) = \int \limits_{{s_{2} }} \left( {z - z_{2} } \right)E_{2} \dot{\varepsilon }_{n2} {\text{d}}s} \\ \end{array} $$
(8)

The shear force due to the shear stress of the central layer is expressed by:

$$ T\left( {x,t} \right) = \int \limits_{{s_{2} }} \tau_{2} {\text{d}}s{ } $$
(9)

τ2 refers the shear stress into viscoelastic layer.

The Riemann’s convolution product is used to express normal stress, bending moment and shear stress in the form:

$$ \begin{array}{*{20}c} {N_{2} \left( {x,t} \right) = S_{2} E_{2} *\dot{u}_{,x} } \\ {M_{2} \left( {x,t} \right) = I_{2} E_{2} *\dot{w}_{,xx} } \\ {T\left( {x,t} \right) = \frac{{S_{2} }}{{2\left( {1 + \upsilon_{2} } \right)}}E_{2} *\left( {\dot{\beta } + \dot{w}_{,x} } \right)} \\ \end{array} $$
(10)

The Riemann’s convolution product can be replaced by a simple product in the frequency domain using the Laplace transform properties.

$$ \begin{array}{*{20}c} {N_{2} \left( {x,t} \right) = S_{2} E_{2} \left( \omega \right)u_{,x} } \\ {M_{2} \left( {x,t} \right) = I_{2} E_{2} \left( \omega \right)w_{,xx} } \\ {T\left( {x,t} \right) = \frac{{S_{2} }}{{2\left( {1 + \upsilon_{2} } \right)}}E_{2} \left( \omega \right)\left( {\beta + w_{,x} } \right)} \\ \end{array} $$
(11)

with E2(ω) is the frequency-dependent complex Young’s modulus of the viscoelastic layer. Therefore, considering the effect of temperature on the structure, the thermal stress can be expressed for each layer of the sandwich beam as follows [29]:

$$ \begin{array}{*{20}c} {NT_{i} = E_{i} S_{i} \alpha_{x,i} \Delta T} & {{\text{for}}\; i = 1,3} \\ {NT_{2} = E_{2} \left( \omega \right)S_{2} \alpha_{x,2} } & {{\text{for}}\; i = 2} \\ \end{array} $$
(12)

Finite element discretization

The discretization of the equation of motion Eq. (6) by the finite element method and the expression of the displacement field as a function of the nodal displacements Ue make it possible to form the elementary behavior matrices.

$$ \begin{array}{*{20}c} {w = N_{w} U_{e} } \\ {U = N_{u} U_{e} } \\ {\beta = N_{\beta } U_{e} } \\ \end{array} \quad {\text{with}}\quad U_{e} = \left\{ {\begin{array}{*{20}c} {U_{i} } \\ {\beta_{i} } \\ {w_{i} } \\ {\theta_{i} } \\ \end{array} } \right\}i = 1,2 $$
(13)

Nw, Nu and Nβ are the interpolation functions given by:

$$ \begin{array}{*{20}c} {N_{w} = \left[ {0 \, 0 \, \left( {1 + 2\xi^{3} - 3\xi^{2} } \right) \, \left( {\xi^{3} - 2\xi^{2} + \xi } \right)L_{e} \, 0 \, 0 \left( { - 2\xi^{3} + 3\xi^{2} } \right) \, \left( {\xi^{3} - \xi^{2} } \right) \, L_{e} } \right]} \\ {N_{u} = \left[ {\left( {1 - \xi } \right) \, 0 \, 0 \, 0 \, \xi \, 0 \, 0 \, 0} \right]} \\ {N_{\beta } = \left[ {0 \, \left( {1 - \xi } \right) \, 0 \, 0 \, 0 \, \xi \, 0 \, 0} \right] } \\ \end{array} $$
(14)

with ξ = x/le. An element with two nodes is shows in Fig. 2, where the proposed number of degrees of freedom is four (4) for each node, which are the longitudinal displacement u, the transverse displacement w, the shear rotation of the central layer β and the rotation θ = dw/dx.

The elementary matrix system that describes the vibratory behavior of the sandwich beam can be obtained by replacing Eqs. (7–14) in Eq. (6) with:

$$ \left[ M \right]^{e} \left\{ {\ddot{U}_{e} } \right\} + \left[ {K\left( \omega \right)} \right]^{e} \left\{ U \right\}_{e} = \left\{ F \right\}^{e} $$
(15)

where [M]e, [K]e and {F}e are the mass matrix, the stiffness matrix and the nodal force vector, respectively (see Appendix A). The global matrix system describing the vibration behavior of the sandwich beam is obtained after the assembly of the elementary matrix.

Structural Vibration Responses

The expression of the displacement vector as a function of nodal displacements U = U0eiωt and replacing it in Eq. (15) makes it possible to obtain the characteristic equation describing the frequency response of the sandwich beam with viscoelastic core:

$$ \left( { - \omega^{2} \left[ M \right] + \left[ {K\left( \omega \right)} \right]} \right)\left\{ {U_{0} } \right\} = \left\{ F \right\}{ } $$
(16)

with {U0}is the nodal displacement vector.

Acoustic Responses

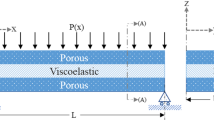
The sound pressure is the physical quantity characterizing the variation of atmospheric pressure that causes a sound impression due to an acoustic source distribution, while the sound power is the transmitted sound energy. In this study, the beam sandwich beam is part of a rigid baffle of infinite length that the bottom of sandwich beam is subject to plane incident pressure wave while the region part above the top layer is an unbounded half-plane fluid domain (Fig. 3). In this region, the pressure distribution can be obtained from the solution of Helmholtz equation [30, 31]:

$$ \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial z^{2} }} + k^{2} } \right)p\left( {x,z,\omega } \right) = 0 $$
(17)
Fig. 3
figure 3

Acoustic radiation field of the sandwich beam

Full size image

The Sommerfeld radiation condition must be satisfy to ensure that the wave amplitude vanishes at infinity:

$$ \mathop {\lim }\limits_{r \to \infty } \left( {\frac{\partial p}{{\partial r}} + \frac{1}{{c_{0} }}\frac{\partial p}{{\partial r}}} \right) = 0 $$
(18)

with the following boundary conditions for rigid walls:

$$ \frac{{\partial p\left( {x,z,\omega } \right)}}{\partial r}|_{{z = - \frac{h}{2}}} = \rho_{0} \omega^{2} v\left( {t,\omega } \right) $$
(19)

where w(rs) refers the normal velocity on the surface of the beam k = ω/c0 is acoustic wave number, ρ and c are the air density and sound velocity, respectively, with |r − rs| is the distance between the surface and the field point. The sound pressure expression in the plane (x, z) of the structure is given in the form:

$$ p\left( r \right) = \frac{{j\omega \rho_{0} }}{2\pi }\int \frac{{v\left( {r_{s} } \right)e^{ - jkR} }}{r}l{\text{d}}x{ } $$
(20)

with v(r) is the complex conjugate of the particle velocity and l represent the width of the sandwich beam. The sound power of the sandwich beam can be obtained by:

$$ W = \frac{1}{2}Re\left( {\int \limits_{0}^{L} p\left( r \right)v^{*} \left( r \right)l{\text{d}}x} \right){ } $$
(21)

.* is the complex conjugate. The transmission loss (TL) generally describes the cumulative decrease in the intensity of the sound energy propagated through the sandwich beam (Absorbed sound power). The acoustic transmission loss is given by:

$$ STL = 10log_{10} \left( {\frac{{W_{i} }}{{W_{T} }}} \right) $$
(22)

where Wi refers the transmitted sound power calculated by Eq. (21) and WT is the sound power given by:

$$ W_{T} = \frac{{AP_{i}^{2} \cos \left( \theta \right)}}{2\rho c}{ } $$

Pi and A are the sound incidence pressure and the contact surface, and θ is incidence angle.

Eigenvalues Problem

In this work, Eq. (16) is solved by the MSP [32] formulation which eigenmodes are obtained by solving the following eigenvalue problem:

$$ \left( {\left[ {K\left( \omega \right)} \right] - \omega^{2} \left[ M \right]} \right)U = 0 $$
(23)

The resolution of the complex problem Eq. (23) can be determined by applying the set of techniques of the asymptotic numerical method starting with the decomposition of the module E2(ω) in the form:

$$ \begin{array}{*{20}c} {E_{2} \left( \omega \right) = E_{0} + E_{c} \left( \omega \right)} \\ \end{array} $$
(24)

with E0 and Ec(ω) are respectively the modulus of delayed elasticity and the dissipation modulus. Consequently, the stiffness matrix can be decomposed into two parts:

$$ \left[ {K\left( \omega \right)} \right] = \left[ {K_{0} } \right] + E\left( \omega \right)\left[ {K_{c} } \right]{ } $$
(25)

The injection of new stiffness matrices into the eigenvalue problem Eq. (23) makes it possible to express the problem in the form:

$$ R\left( {U,\lambda } \right) = \left[ {\left[ {K_{0} \left] { + E\left( \omega \right)} \right[K_{c} } \right] - \omega^{2} \left[ M \right]} \right]U = 0{ } $$
(26)

After the decomposition of the problem, the perturbation technique [33, 34] is applied by writing the resident arguments in the form of a power series:

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {U = U_{0} +\sum \limits_{n = 1}^{N} \left( {\Delta \alpha } \right)^{n} U_{n} } \\ {\lambda = \omega^{2} = \omega_{0}^{2} + \sum \limits_{n = 1}^{N} \left( {\Delta \alpha } \right)^{n} \omega^{2}_{n} } \\ \end{array} } \\ {E\left( \omega \right) = E_{c0} + \sum \limits_{n = 1}^{N} \left( {\Delta \alpha } \right)^{n} E_{n} } \\ \end{array} $$
(27)

where U0, ω0 and Ec0 are the initial parameters of eigenvector, pulsation and dissipative modulus computed for each iteration. Given the complexity of the eigenvalues problem due to the frequency dependence of its parameters, the homotopy procedure is applied by injecting the path parameter (αj + Δα) into the problem Eq. (26), the following new eigenvalue problem is obtained:

$$ R\left( {U,\lambda } \right) = \left[ {K_{0} + \left( {\alpha_{j} + \Delta \alpha } \right)E\left( \omega \right)K_{c} - \lambda M} \right]U = 0 $$
(28)

By replacing the expressions of Eq. (27) into Eq. (28), and arrange them according to the powers of Δα, the following system of linear equations is obtained:

$$ \left[ {A_{0} } \right]\left\{ {U_{n} } \right\} = \left\{ {F_{n} } \right\} $$
$$ \left[ {A_{0} } \right] = \left[ {K_{0} + \alpha_{max} E\left( \omega \right)K_{c} - \lambda M} \right] $$
(29)
$$ F_{n} = - \alpha_{j} \sum \limits_{k = 1}^{n - 1} E_{k} \left[ {K_{c} } \right]\{ U_{n - k} \} - \sum \limits_{k = 0}^{n - 1} E_{k} \left[ {K_{c} } \right]\{ U_{n - k - 1} \} \sum \limits_{k = 1}^{n - 1} \lambda_{k} \left[ M \right]\{ U_{j - k} \} - \alpha_{j} E_{n} \left[ {K_{c} } \right]\{ U_{0} \} + \lambda_{n} \left[ M \right]\left\{ {U_{0} } \right\} $$

The problem Eq. (29) is ill posed because there are (m) equations and (m + 1) unknowns. An additional condition is necessary for each order to solve it. The orthogonality property of the eigenmodes gives another additional solution that can solve the problem Eq. (18):

$$ \left\{ {U_{n} } \right\}^{T} \left\{ {U_{0} } \right\} = 0 $$
(30)

The matrix A0 is non-invertible, which implies that the Eq. (29) at each order n ≥ 1 has no solution only if the following solvency condition is satisfied:

$$ \begin{aligned} \left\{ {F_{n} } \right\}^{T} \left\{ {U_{0} } \right\} = & - \alpha_{j} \sum \limits_{k = 1}^{n - 1} E_{k} \left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{n - k} \} - \sum \limits_{k = 0}^{n - 1} E_{k} \left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{n - k - 1} \} + \sum \limits_{k = 1}^{n - 1} \lambda_{k} \left\{ {U_{0} } \right\}^{T} \left[ M \right]\{ U_{j - k} \} \\ & \quad - \alpha_{j} E_{n} \left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{0} \} + \lambda_{n} \left\{ {U_{0} } \right\}^{T} \left[ M \right]\{ U_{0} \} = 0 \\ \end{aligned} $$
(31)

It is noticed that an implicit equation is appears due to the appearance of the terms λn and En, simultaneously. To solve this type of problem, Faa di Bruno’s recursion formula is used for the high degree differentiation of the composite function Eq. (31). The term En can be decomposed to an equation explicitly dependent on the initial parameters:

$$ E_{n} = \left\{ {E_{{\left. 1 \right|\lambda_{1} = 1}} } \right\}\lambda_{n} + \left\{ {E_{{\left. 1 \right|\lambda_{n} = 0}} } \right\}{ } $$
(32)

The insertion of Eq. (32) in Eq. (31) makes it possible to express after Taylor development of the coefficient λn as a function of lower order terms:

$$ \begin{aligned} \lambda_{n} = & \frac{{\begin{array}{*{20}c} {\alpha_{j} \sum \nolimits_{k = 1}^{n - 1} E_{k} \left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{n - k} \} + \sum \nolimits_{k = 0}^{n - 1} E_{k} \left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{n - k - 1} \} } \\ \end{array} }}{{\left\{ {U_{0} } \right\}^{T} \left[ M \right]\{ U_{0} \} + \alpha_{j} \left\{ {E_{{\left. 1 \right|\lambda_{1} = 1}} } \right\}\left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{0} \} }} \\ & \quad + \frac{{ - \sum \nolimits_{k = 1}^{n - 1} \lambda_{k} \left\{ {U_{0} } \right\}^{T} \left[ M \right]\{ U_{j - k} \} + \alpha_{j} \left\{ {E_{{\left. 1 \right|\lambda_{n} = 0}} } \right\}\left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{0} \} }}{{\left\{ {U_{0} } \right\}^{T} \left[ M \right]\{ U_{0} \} + \alpha_{j} \left\{ {E_{{\left. 1 \right|\lambda_{1} = 1}} } \right\}\left\{ {U_{0} } \right\}^{T} \left[ {K_{c} } \right]\{ U_{0} \} }} \, \\ \end{aligned} $$
(33)

After determination of λn, the n-order Taylor coefficient of vector U can be deduced using Eq. (29). Integrating the Lagrange multiplier χ makes this equation more generic:

$$ \left[ {\begin{array}{*{20}c} {A_{0} } & {U_{0} } \\ {U_{0}^{T} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{n} } \\ \chi \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{n} } \\ 0 \\ \end{array} } \right\} $$
(34)

The problem is solved starting from an initial linear problem R(U, λ) = [[K0] − ω02[M]]U0 for αj = 0 to the nonlinear problem R(U, λ) = [[K0] + En(ω)[Kc] − ω02[M]]U0 for αj = 1. Therefore, a continuation procedure is applied that consists of defining a new step of solution from the starting point (Uj, λj) defined by:

$$ \begin{array}{*{20}c} {U^{j} = \sum \limits_{n = 0}^{N} \left( {\alpha_{max} } \right)^{n} U_{n} } \\ {\lambda^{j} = \sum \limits_{n = 0}^{N} \left( {\alpha_{max} } \right)^{n} \lambda_{n} } \\ \end{array} { } $$
(35)

where αmax is the convergence radius given by [29]:

$$ \alpha_{max} = \left( {\varepsilon \frac{{U_{1} }}{{U_{n} }}} \right)^{{\frac{1}{N - 1}}} { } $$
(36)

with ε is the precision parameter, the continuation process continues for a new iteration with:

$$ a_{j + 1} = a_{j} + a_{max} { } $$
(37)

The process ends when the value of αj+1 > 1, at this step the eigenvalues and the eigenvectors are calculated by:

$$ \begin{array}{*{20}c} {U_{s} = \sum \limits_{n = 0}^{N} \left( {1 - \alpha_{j} } \right)^{n} U_{n} } \\ {\lambda_{s} = \sum \limits_{n = 0}^{N} \left( {1 - \alpha_{j} } \right)^{n} \lambda_{n} } \\ \end{array} $$
(38)

Results and Discussions

The frequency responses of the sandwich beams with a viscoelastic core are obtained for different frequency-dependent viscoelastic laws and for different thermal conditions. Before that, a comparative study is carried out to validate the present numerical approach. The dynamic responses of sandwich beams are studied under the harmonic point load:

$$ P\left( {x,t} \right) = P_{0} \delta \left( {x - x_{0} } \right)e^{i\omega t} $$
(39)

where δ is the Dirac distribution, P0 = 1N is the magnitude force and x0 is the position of the force x0 = {L, L/2} for cantilever and simply supported conditions, respectively.

Free Vibration Validation

The obtained results of the natural frequency and loss factor of the sandwich beam with the two viscoelastic cores PVB and ISD112 27° interposed between two layers of aluminum for the boundary conditions clamped–clamped and clamped–Free are compared with those obtained by Diamond approach of Billasse et al. [15]. The mechanical and geometrical properties of the sandwich beam with viscoelastic core are presented in Table 1. The shear modulus of the viscoelastic material PVB is given by Eq. (40) and the mechanical proprieties of the viscoelastic material ISD112 considered at 27° are reported in Table 1.

$$ G_{c}^{*} \left( \omega \right) = \left[ {G_{\infty } + \left( {G_{0} - G_{\infty } } \right)} \right[1 + \left( {i\omega \tau } \right)^{1 - \alpha } ]^{ - \beta } $$
(40)
$$ G_{0} = 479 \times 10^{3} \;{\text{Pa}} ;\;G_{{{\text{inf}}}} = 2.35 \times 10^{8} \;{\text{Pa}} ; \tau = 0.3979 ;\; \alpha = 0.46 ;\; \beta = 0.1946. $$
Table 1 Mechanical and geometrical properties of the viscoelastic core sandwich
Full size table

It can be seen that the natural frequencies and loss factors presented in Tables 2 and 3 are very close to those obtained by Billasse [15], where residual error is very acceptable.

Table 2 Natural frequencies and loss factor of the sandwich beam with PVB viscoelastic core
Full size table
Table 3 Natural frequencies and loss factor of the sandwich beam with frequency-dependent viscoelastic core in ISD112 at 27°
Full size table

Frequency Responses Validation

In this section, the dynamic responses of the sandwich beam under harmonic point load studied by Cai et al. [10] are obtained by the present approach and compared with their responses [35]. The properties of the sandwich are given in Table 4.

Table 4 Mechanical and geometrical properties of the viscoelastic core sandwich with PCLD Treatment
Full size table

The obtained responses at the tip of the beam are compared for a cantilever beam with two viscoelastic core models “soft” and “hard”, which are shown in Fig. 4a, b.

Fig. 4
figure 4

Comparison of the frequency responses at the tip of the viscoelastic cantilever sandwich beam between present approach and analytical approach [16] (a hard cœur; b soft cœur)

Full size image

It’s noticed that the obtained eigenfrequencies of Cai et al. [10] are underestimated compared for two models of the hard and soft viscoelastic core. In addition, the amplitudes of the frequency responses at the resonance frequencies of the reference [10] for the hard heart are lower than the corresponding results of the present study even at low frequencies. On the other hand, the present obtained amplitudes for second soft-heart model are lower than those obtained by reference [10].

Variability of Beam Frequency Responses

The first two viscoelastic models in the present study are considered frequency-dependent. Two sandwich beams are considered with two different viscoelastic cores, the first operational modulus of the polyvinyl butyral (PVB) viscoelastic material [15, 28] assumed at 20° is described by a fractional derivative model (Eq. 40) and the second of the ISD112 considered at 20° and 27° [36] is described by the generalized Maxwell model (Eq. 41). The mechanical and geometrical properties of the viscoelastic sandwich structure are given in Table 5. The highly frequency-dependent complex Young’s modulus parameters of the viscoelastic material ISD112 considered at 20° and 27° are presented in Table 6.

Table 5 Mechanical and geometrical properties of the PCLD sandwich with a frequency dependent viscoelastic core
Full size table
Table 6 Parameters of viscoelastic Young’s modulus ISD112
Full size table

The modal stability procedure MSP for frequency responses combined to asymptotic numerical method ANM and Monte Carlo Simulation MCS is used here to evaluate the stochastic behavior of a sandwich beam with random properties. A comparative study of the frequency responses between MCS-MSP, MCS-DFR and deterministic modal stability procedure DMSP are discussed in this section. All uncertain mechanical and geometrical parameters of upper face (\({E}_{11}, {E}_{22}, {G}_{12} {\rho }_{1}, {\upsilon }_{1} ,\mathrm{and} {h}_{f})\), lower faces ((\({E}_{11}, {E}_{22}, {G}_{12} {\rho }_{3}, {\upsilon }_{3} ,\mathrm{and} {h}_{3})\), ISD112 viscoelastic core (\({G}_{0}, {\Delta }_{\mathrm{j}}, {\Omega }_{\mathrm{j}}, {\rho }_{2}, {\upsilon }_{2} ,\mathrm{and} {h}_{2})\) and PVB viscoelastic core (\({G}_{0}, {G}_{inf},\uptau ,{\alpha },\upbeta , {\rho }_{2}, {\upsilon }_{2} ,\mathrm{and} {h}_{2})\), are represented by Gaussian distribution fields with a moderate input coefficient variation Cov = 5% in order to test the robustness of the deterministic based in the MSP approach. The MCS are performed with 1000 trials.

The variations of natural frequency and loss factor for sandwich beams with PVB and ISD112 are presented in Figs. 4 and 5 as the first results of this comparative study. It is shown that the variation of the mean natural frequency and loss factors for PVB core obtained by MCS-DFR are very close to MCS-MSP where the relativity errors are less than 1.5% and 1% for the natural frequency and loss factor, respectively. However, for the beam with ISD112 core, the relative error is lower than 1.4% for the natural frequencies and lower than 1% for the loss factors (Fig. 6).

Fig. 5
figure 5

Comparison of natural frequencies (a) and loss factors (b) of the sandwich beam with PVB core for the first six modes between MCS-MSP and DMC

Full size image
Fig. 6
figure 6

Comparison of natural frequencies (a) and loss factors (b) of the sandwich beam with ISD112 core at 27° for the first six modes between MCMS and DMC

Full size image

However, the obtained results of the mean and standard deviation MSP approach for the PVB and ISD112 at 27° sandwich beam cores, presented in Figs. 7 and 8 ((a) mean; (b) standard deviation) respectively, has been validate in this case, the displacements and velocity responses are coincide to those obtained by MCS-DFR. The results of MCS-DFR are always reliable and robust but with a really expensive calculation time. The MCS-MSP is a remarkable and very accurate solution with a very reduced computation time. However, the frequency responses of MCS-MSP are very close to DMSP, where the variability level is lower than 2.64e−4 m and 1.6 e−4 m for the two sandwich beams with PVB and ISD112 viscoelastic cores, respectively.

Fig. 7
figure 7

Comparison of frequency responses of displacement (a) and velocity (b) of the sandwich beam with PVB core between MCS-MPS and DMC

Full size image
Fig. 8
figure 8

Comparison of frequency responses of displacement (a) and velocity (b) of the sandwich beam with ISD112 core at 27° between MCS-MPS and DMC

Full size image

Vibro-Acoustic Responses of PCLD Sandwich Beams

Comparative Study

The obtained results of natural frequency and loss factor of viscoelastic core sandwich beams with the three viscoelastic cores PVB, ISD112 at 20° and ISD112 at 27° are shown in Table 7. The results of the residual error \(R\left( {U,\lambda } \right) = \left( {\left[ K \right] - \omega^{2} \left[ M \right]} \right)U\) illustrate the efficiency of the numerical approach used of which R (U, λ) was generally less than 0.5 × 10–3.

Table 7 Natural frequencies and loss factor of the sandwich beam with frequency-dependent viscoelastic core (PVB, ISD112 at 20° and ISD112 at 27°)
Full size table

The first two viscoelastic models in the present study are considered frequency-dependent. Two sandwich beams are considered with two different viscoelastic cores, the first operational modulus of the polyvinyl butyral (PVB) viscoelastic material [15, 28] assumed at 20° is described by a fractional derivative model (Eq. 40) and the second of the ISD112 considered at 20° and 27° [36] is described by the generalized Maxwell model (Eq. 41). The mechanical and geometrical properties of the viscoelastic sandwich structure are given in Table 5 with viscoelastic core thickness h2 = 0.002 m. The highly frequency-dependent complex Young’s modulus parameters of the viscoelastic material ISD112 considered at 20° and 27° are presented in Table 6.

To examine the importance of the viscoelastic layer in the sandwich structure, the different vibro-acoustic responses of sandwich beams with and without the viscoelastic core are established. The different responses are obtained for the three viscoelastic cores PVB, ISD112 at 27° and ISD112 at 20° and compared with those obtained with a sandwich beam without viscoelastic material, where a simple isotropic material is considered in the core of sandwich with following mechanical properties: E2 = 106 Pa, υ = 0.3, ρ = 40 kg/m3 [21].

The transverse displacement and velocity responses obtained at the observation point (0.3 (m), 0 (m), 0 (m)) are shown in Figs. 9 and 10, respectively. The difference between the responses with and without the viscoelastic core is quite evident especially at the natural frequency where the effect of viscoelastic damping is significant after observing the decrease in amplitude peaks especially for the large natural frequencies, in contrast to responses obtained without viscoelastic damping, which amplitude peaks are very high. This shows the effectiveness of PCLD treatment with the viscoelastic layer. However, comparison of the results of three cores, PVB, ISD112 at 27° and ISD112 at 20° shows that the ISD112 cores are more efficiency in damping, that is because of the very high damping of the ISD112 cores, reflected by the damping factor shown in Table 7.

Fig. 9
figure 9

Frequency displacement responses of the simply supported PCLD beam with and without the viscoelastic core

Full size image
Fig. 10
figure 10

Velocity frequency responses of the simply supported PCLD beam with and without the viscoelastic core

Full size image

The pressure and sound power responses collected at the observation point (0.3 (m), 0 (m), 2 (m)) for the four viscoelastic cores are shown in Figs. 11 and 12, respectively. The results show the damping provided by the viscoelastic layer, especially for the simply supported beam, where the sound pressure magnitudes obtained with the three types of viscoelastic layers (PVB, ISD112 at 27° and ISD112 at 20°) are much lower compared to the results obtained without the viscoelastic core. In addition, the sound pressure response of PCLD sandwich beams with a viscoelastic ISD112 core are lower and more stable compared to those with the PVB core.

Fig. 11
figure 11

Frequency response of the sound pressure level of the simply supported PCLD beam with and without viscoelastic core

Full size image
Fig. 12
figure 12

Frequency response of the sound pressure level of the simply supported PCLD beam with and without viscoelastic core

Full size image

The sound transmission loss responses of different cores are shown in Fig. 13. The results show that the transmission loss for viscoelastic cores are very high compared to the simple isotropic material to core, where the STL values is greater than 17 db.

Fig. 13
figure 13

Frequency responses of the sound transmission loss of the PCLD sandwich beam with and without the viscoelastic core

Full size image

PCLD Sandwich Beam with DYAD606 Viscoelastic Core

In this section, we study the vibration behavior of PCLD sandwich beams under the effect of temperature, whose viscoelastic model is considered frequency and temperature dependent. The operational modulus of the viscoelastic material DYAD606 [15] described by the generalized Maxwell model Eq. (41) is considered for different temperatures T = 10°, 25°, 30° and 38°. The parameters of the viscoelastic Young’s modulus strongly dependent on frequency are given in Table 8. The mechanical and geometrical properties of the sandwich beam are presented in Table 9.

Table 8 Young modulus of the viscoelastic core ISD112
Full size table
Table 9 Mechanical and geometrical properties of the sandwich beam
Full size table

In order to study the effect of temperature on the PCLD sandwich behavior with a viscoelastic core in DYAD606, the different sandwich responses for the simply supported and clamped–free conditions, are obtained for the considered temperatures T = 0°, 25°, 30° and 25°, where the natural frequencies and loss factor are presented in Table 11. The results are illustrated graphically in Figs. 14 and 15. It is observed that the natural frequencies decrease with increasing temperature. This is due to the internal compressive stresses induced by the high temperature increase, which reduces the structural rigidity. On the other hand, the structural damping reflected by the loss factor increases with increasing temperature, thus increasing the structure dissipative capacity.

Table 11 Natural frequencies and loss factor of sandwich beams with frequency–temperature-dependent viscoelastic core DYAD606
Full size table
Fig. 14
figure 14

Natural frequency variation of the PCLD sandwich beam with frequency-temperature-dependent viscoelastic core DYAD606 (a Simply supported; b clamped-free)

Full size image
Fig. 15
figure 15

Loss factor variation of the PCLD sandwich beam with frequency-temperature-dependent viscoelastic core DYAD 606 (a simply supported; b clamped-free)

Full size image

The displacement and velocity responses of the simply supported and cantilever sandwich beam for different temperatures are shown in Figs. 16 and 17. A decrease in amplitudes is observed when the temperature rises, especially at higher frequencies. This explains how the structure becomes highly damping with the high values of the temperatures, whereas the increase in temperature generally causes internal stresses.

Fig. 16
figure 16

Displacement frequency responses of the PCLD Sandwich with frequency–temperature dependent core DYAD606 (a simply supported; b clamped-free)

Full size image
Fig. 17
figure 17

Velocity frequency responses of the PCLD Sandwich with frequency–temperature dependent core DYAD606 (a simply supported; b clamped-free)

Full size image

The sound pressure level and sound power responses of the sandwich beam with viscoelastic core DYAD606 are shown in Figs. 18 and 19, respectively. It is clear to observe the decrease in the amplitudes of different responses for high temperatures. The effect of the damping provided by the viscoelastic layer is very considerable, especially for the viscoelastic core considered at 38°, where amplitudes are very small. In addition, the thermal stress generated by the temperature increase is very low and does not have a significant effect on the vibratory behavior as the temperature range studied is very close to the ambient temperature Tref = 25°.

Fig. 18
figure 18

Sound pressure level responses of the simply supported PCLD Sandwich with frequency–temperature dependent core DYAD606

Full size image
Fig. 19
figure 19

Sound power responses of the simply supported PCLD Sandwich with frequency–temperature dependent core DYAD606

Full size image

Furthermore, the effect of temperature on sound transmission loss responses is shown in Fig. 20 for the same sandwich beam. It can easily be seen that the sound transmission loss increases progressively with increasing temperature, this implies that the structure has more capacity to dampen acoustic noise with the high temperatures of the DAYD606 viscoelastic cores.

Fig. 20
figure 20

Sound transmission loss responses of the simply supported PCLD Sandwich with frequency–temperature dependent core DYAD606

Full size image

Conclusion

In this work, a numerical approach based on a high order theory considering the longitudinal and rotational inertias as well as the asymmetry of viscoelastic core sandwich beams was presented to characterize the vibro-acoustic responses of viscoelastic core sandwich beams. The main objective was to investigate the damping efficiency of viscoelastic materials described by laws of behavior dependent not only on frequency but also on temperature. Therefore, different viscoelastic models have been examined taking into account their specific mechanical properties as well as different configurations of the sandwich structure especially those with PCLD treatment.

Therefore, the finite element method combined with the asymptotic numerical method have been used in this work in order to determine in the first place the damping properties of viscoelastic sandwich beams by solving the complex eigenvalue problem and to obtain in the second place the corresponding structural and frequency acoustic responses to forced vibrations under a point load with unit amplitude. The results obtained have been validated for several cases by comparing these results with other references.

On the basis of these results, the following conclusions can be drawn:

  • The effectiveness of this numerical approach MSP to approximate damping properties and analyze vibro-acoustic responses of sandwich beams with dependent viscoelastic core. The effects of random input parameters of the viscoelastic sandwich on the frequency responses were evaluated by the MSP method combined to MCS. The results calculated by the MCS-MSP are compared with those obtained by the MCS-DFR, and the results are satisfactory given the low computation time compared to the MCS-DFR method.

  • The comparative study of responses without and with the three viscoelastic cores PVB, ISD112 at 27° and ISD112 at 20° showed that the damping provided by the viscoelastic materials is significant particularly for amplitudes corresponding to the high frequencies in contrast to the responses obtained without the viscoelastic layer. In this way, the study illustrated that ISD112 cores are more efficient in terms of damping compared to PVB cores after observing a decrease in the amplitudes of structural and acoustic responses.

  • The behavior of the sandwich beam with DYAD606 viscoelastic core is highly frequency-temperature dependent, therefore the structure becomes softer and more damping of structural vibration and acoustic noise especially for high frequencies with high temperatures.