A Viscoelastic Sandwich Finite Element Model for the Analysis of Passive, Active and Hybrid Structures

Abstract

In this paper we present a finite element model for the analysis of active sandwich laminated plates with a viscoelastic core and laminated anisotropic face layers, as well as piezoelectric sensor and actuator layers. The model is formulated using a mixed layerwise approach, by considering a higher order shear deformation theory (HSDT) to represent the displacement field of the viscoelastic core and a first order shear deformation theory (FSDT) for the displacement field of the adjacent laminated anisotropic face layers and exterior piezoelectric layers. The dynamic problem is solved in the frequency domain with viscoelastic frequency dependent material properties for the core. Control laws are also implemented for the piezoelectric sensors and actuators. The model behaviour in dynamics is assessed with the few solutions found in the literature, including experimental data, and a laminated composite active sandwich application is proposed. In this numerical application, velocity feedback control law is implemented for active control, using co-located piezoelectric patch sensors and actuators.

1 Introduction

Sandwich plates with viscoelastic core are very effective in reducing and controlling vibration response of lightweight and flexible structures, where the soft core is strongly deformed in shear, due to the adjacent stiff layers. Hence, due to this high shear developed inside the core, equivalent single layer plate theories, even those based on higher order deformations, are not adequate to describe the behaviour of these sandwiches, also due to the high deformation discontinuities that arise at the interfaces between the viscoelastic core material and the surrounding elastic constraining layers. The usual approach to analyse the dynamic response of sandwich plates uses a layered scheme of plate and brick elements with nodal linkage. This approach leads to a time consuming spatial modelling task. To overcome these difficulties, the layerwise theory has been considered for constrained viscoelastic treatments, and most recently, Moreira et al. [1, 2], among others, presented generalized layerwise formulations in this scope. From the early 1990s active constrained layer damping became an important subject of research [3, 4]. These hybrid treatments combine the high capacity of passive viscoelastic materials to dissipate vibrational energy at high frequencies with the active capacity of piezoelectric materials at low frequencies. Therefore, in the same damping treatment, a broader control band is achieved [5, 6]. The finite element method has been the main tool of solution for this class of problems, although analytical results have also been obtained for active control of beams and plates [7–10]. An extensive review on recent developments in active and passive constrained layer damping can be found in [11].

To the authors knowledge, few hybrid active-passive sandwich models exist and are mostly limited to beam structures [12]. A very recent exception [13] is a three-node triangular shell sandwich finite element based on the Discrete Kirchhoff Theory, where the viscoelastic sandwich core is modelled according to the first-order shear deformation theory (FSDT) and the elastic and piezoelectric layers according to the classical plate theory. However, this model only allows for isotropic materials, and does not account for composite laminated elastic face layers, as does Trindade et al. [12] for hybrid active-passive beams. Hence, the authors have developed a mixed hybrid active-passive sandwich plate finite element model [14] for optimal design applications [15] and also identification of viscoelastic material parameters [16]. In this model, the viscoelastic core layer is modelled according to a higher order shear deformation theory, adjacent elastic and piezoelectric layers are modelled using the first order shear deformation theory, and all materials are considered to be orthotropic, with elastic layers being formulated as laminated composite plies. Additionally, passive damping is dealt with by using the complex modulus approach, allowing for frequency dependent viscoelastic materials and active damping is incorporated through feedback control laws for co-located control.

Since very few hybrid active-passive sandwich plate results are available in the open literature, the present paper aims at providing new applications in anisotropic laminated sandwich plate structures using piezoelectric sensors and actuators for control, coupled through a velocity feedback law, and a fractional derivative model to account for the viscoelastic material behaviour of the core. The dynamic response of the finite element model is validated using a few reference solutions from the literature, and a new benchmark application is suggested.

2 Mixed Layerwise Hybrid Sandwich Model

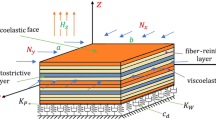
The development of a layerwise finite element model is presented here, to analyse hybrid sandwich laminated plates with a viscoelastic (v) core, laminated anisotropic face layers (e ₁, e ₂) and piezoelectric sensor (s) and actuator (a) layers, as shown in Fig. 1.

Fig. 1

Hybrid sandwich plate

The basic assumptions in the development of the sandwich plate model are:

• 1. All points on a normal to the plate have the same transverse displacement w(x,y,t), where t denotes time, and the origin of the z axis is the mid-plane of the core layer;

• 2. No slip occurs at the interfaces between layers;

• 3. The displacement is C ⁰ along the interfaces;

• 4. Elastic and piezoelectric layers are modelled with first order shear deformation theory (FSDT) and viscoelastic core with a higher order shear deformation theory (HSDT);

• 5. Transverse displacement is constant through the thickness of the sandwich;

• 6. All materials are linear, homogeneous and orthotropic and the elastic layers (e ₁) and (e ₂) are made of laminated composite materials;

• 7. For the viscoelastic core, material properties are complex and frequency dependent;

• 8. Upper and lower layers play the roles of sensor and actuator, respectively, and are connected via feedback control laws, considering co-located control.

The FSDT displacement field of the face layers may be written in the general form:

$$ \begin{array}{lll} \label{eq:disp_FSDT} u^i(x,y,z,t) &=& u_0^i(x,y,t) + (z-z_i) \theta_x^i(x,y,t)\\ v^i(x,y,z,t) &=& v_0^i(x,y,t) + (z-z_i) \theta_y^i(x,y,t)\\ w^i(x,y,z,t) &=& w_0(x,y,t) \end{array} $$

(1)

where $u_0^i$ and $v_0^i$ are the in-plane displacements of the mid-plane of the layer, $\theta_x^i$ and $\theta_y^i$ are rotations of normals to the mid-plane about the y axis (anticlockwise) and x axis (clockwise), respectively, w ₀ is the transverse displacement of the layer (same for all layers in the sandwich), z _i is the z coordinate of the mid-plane of each layer, with reference to the core layer mid-plane (z = 0), and i = s,e ₁,e ₂,a is the layer index.

For the viscoelastic core layer, the HSDT displacement field is written as a second order Taylor series expansion of the in-plane displacements in the thickness coordinate, with constant transverse displacement:

$$ \begin{array}{lll}\label{eq:disp_HSDT} u^v(x,y,z,t) &=& u_0^v(x,y,t) + z \theta_x^v(x,y,t) + z^2 {u_0^*}^v(x,y,t) + z^3 {\theta_x^*}^v(x,y,t)\\ v^v(x,y,z,t) &=& v_0^v(x,y,t) + z \theta_y^v(x,y,t) + z^2 {v_0^*}^v(x,y,t) + z^3 {\theta_y^*}^v(x,y,t)\\ w^v(x,y,z,t) &=& w_0(x,y,t) \end{array} $$

(2)

where $u_0^v$ and $v_0^v$ are the in-plane displacements of the mid-plane of the core, $\theta_x^v$ and $\theta_y^v$ are rotations of normals to the mid-plane of the core about the y axis (anticlockwise) and x axis (clockwise), respectively, w ₀ is the transverse displacement of the core (same for all layers in the sandwich). The functions ${u_0^*}^v$, ${v_0^*}^v$, ${\theta_x^*}^v$ and ${\theta_y^*}^v$ are higher order terms in the series expansion, defined also in the mid-plane of the core layer.

The displacement continuity at the layer interfaces can be written as:

$$ \begin{array}{lll}\label{eq:disp_continuity} u^s\left(x,y,z_s-\frac{h_s}{2},t\right) &=& u^{e_1}\left(x,y,z_{e_1}+\frac{h_{e_1}}{2},t\right)\\ v^s\left(x,y,z_s-\frac{h_s}{2},t\right) &=& v^{e_1}\left(x,y,z_{e_1}+\frac{h_{e_1}}{2},t\right)\\ u^{e_1}\left(x,y,z_{e_1}-\frac{h_{e_1}}{2},t\right) &=& u^v\left(x,y,\frac{h_v}{2},t\right)\\ v^{e_1}\left(x,y,z_{e_1}-\frac{h_{e_1}}{2},t\right) &=& v^v\left(x,y,\frac{h_v}{2},t\right)\\ u^v\left(x,y,-\frac{h_v}{2},t\right) &=& u^{e_2}\left(x,y,z_{e_2}+\frac{h_{e_2}}{2},t\right)\\ v^v\left(x,y,-\frac{h_v}{2},t\right) &=& v^{e_2}\left(x,y,z_{e_2}+\frac{h_{e_2}}{2},t\right)\\ u^{e_2}\left(x,y,z_{e_2}-\frac{h_{e_2}}{2},t\right) &=& u^a\left(x,y,z_a+\frac{h_a}{2},t\right)\\ v^{e_2}\left(x,y,z_{e_2}-\frac{h_{e_2}}{2},t\right) &=& v^a\left(x,y,z_a+\frac{h_a}{2},t\right) \end{array} $$

(3)

where the coordinates of layer mid-planes are:

$$ \begin{array}{lll}\label{eq:z_coord_midlayer} z_s &=& \frac{h_v}{2} + h_{e_1} + \frac{h_s}{2}\\ z_{e_1} &=& \frac{h_v}{2} + \frac{h_{e_1}}{2}\\ z_v &=& 0\\ z_{e_2} &=& -\frac{h_v}{2} - \frac{h_{e_2}}{2}\\ z_a &=& -\frac{h_v}{2} - h_{e_2} - \frac{h_a}{2} \end{array} $$

(4)

Applying the continuity conditions, one obtains:

$$ \begin{array}{lll}\label{eq:final_continuity} u_0^{e_1} &=& \frac{h_{e_1}}{2} \theta_x^{e_1} + u_0^v + \frac{h_v}{2} \theta_x^v + \frac{h_v^2}{4} {u_0^*}^v + \frac{h_v^3}{8} {\theta_x^*}^v\\ v_0^{e_1} &=& \frac{h_{e_1}}{2} \theta_y^{e_1} + v_0^v + \frac{h_v}{2} \theta_y^v + \frac{h_v^2}{4} {v_0^*}^v + \frac{h_v^3}{8} {\theta_y^*}^v\\ u_0^{e_2} &=& - \frac{h_{e_2}}{2} \theta_x^{e_2} + u_0^v - \frac{h_v}{2} \theta_x^v + \frac{h_v^2}{4} {u_0^*}^v - \frac{h_v^3}{8} {\theta_x^*}^v\\ v_0^{e_2} &=& - \frac{h_{e_2}}{2} \theta_y^{e_2} + v_0^v - \frac{h_v}{2} \theta_y^v + \frac{h_v^2}{4} {v_0^*}^v - \frac{h_v^3}{8} {\theta_y^*}^v\\ u_0^s &=& \frac{h_s}{2} \theta_x^s + h_{e_1} \theta_x^{e_1} + u_0^v + \frac{h_v}{2} \theta_x^v + \frac{h_v^2}{4} {u_0^*}^v + \frac{h_v^3}{8} {\theta_x^*}^v\\ v_0^s &=& \frac{h_s}{2} \theta_y^s + h_{e_1} \theta_y^{e_1} + v_0^v + \frac{h_v}{2} \theta_y^v + \frac{h_v^2}{4} {v_0^*}^v + \frac{h_v^3}{8} {\theta_y^*}^v\\ u_0^a &=& - \frac{h_a}{2} \theta_x^a - h_{e_2} \theta_x^{e_2} + u_0^v - \frac{h_v}{2} \theta_x^v + \frac{h_v^2}{4} {u_0^*}^v - \frac{h_v^3}{8} {\theta_x^*}^v\\ v_0^a &=& - \frac{h_a}{2} \theta_y^a - h_{e_2} \theta_y^{e_2} + v_0^v - \frac{h_v}{2} \theta_y^v + \frac{h_v^2}{4} {v_0^*}^v - \frac{h_v^3}{8} {\theta_y^*}^v \end{array} $$

(5)

These relations allow us to retain the rotational degrees of freedom of the face layers, while eliminating the corresponding in-plane displacement ones. Hence, the generalized displacement field has 17 mechanical unknowns.

An obvious limitation of the present model is that the height of the core remains unchanged, i.e. incompressible, making it impossible to capture localised effects and displacements through the depth of soft cores [17]. If these effects are important, the present formulation can be easily generalised [18] to include an expansion of the transverse displacement of the core in the thickness direction in Eq. 2.

We consider that fibre-reinforced laminae in elastic multi-layers (e ₁) and (e ₂), viscoelastic core (v), and piezoelectric sensor (s) and actuator (a) layers are characterized as orthotropic. Furthermore, piezoelectric material is assumed to be mm2 orthorhombic, polarised in the thickness direction. Constitutive equations for each lamina in the sandwich may then be expressed in the principal material directions, and for the zero transverse normal stress situation as [19]:

$$ \begin{array}{lll} \label{eq:piezo_constit_2D} \left\{ \begin{array}{l} \sigma_{11}\\ \sigma_{22}\\ \sigma_{23}\\ \sigma_{13}\\ \sigma_{12} \end{array} \right\} & =& \left[ \begin{array}{ccccc} Q_{11} & Q_{12} & 0 & 0 & 0\\ Q_{12} & Q_{22} & 0 & 0 & 0\\ 0 & 0 & Q_{44} & 0 & 0\\ 0 & 0 & 0 & Q_{55} & 0\\ 0 & 0 & 0 & 0 & Q_{66} \end{array} \right]^E \left\{ \begin{array}{l} \varepsilon_{11}\\ \varepsilon_{22}\\ \gamma_{23}\\ \gamma_{13}\\ \gamma_{12} \end{array} \right\} - \left[ \begin{array}{ccc} 0 & 0 & e_{31}^*\\ 0 & 0 & e_{32}^*\\ 0 & e_{24} & 0\\ e_{15} & 0 & 0\\ 0 & 0 & 0 \end{array} \right] \left\{ \begin{array}{l} E_1\\ E_2\\ E_3 \end{array} \right\}\\ \left\{ \begin{array}{l} D_1\\ D_2\\ D_3 \end{array} \right\} & =& \left[ \begin{array}{ccccc} 0 & 0 & 0 & e_{15} & 0\\ 0 & 0 & e_{24} & 0 & 0\\ e_{31}^* & e_{32}^* & 0 & 0 & 0 \end{array} \right] \left\{ \begin{array}{l} \varepsilon_{11}\\ \varepsilon_{22}\\ \gamma_{23}\\ \gamma_{13}\\ \gamma_{12} \end{array} \right\} + \left[ \begin{array}{ccc} \epsilon_{11} & 0 & 0\\ 0 & \epsilon_{22} & 0\\ 0 & 0 & \epsilon_{33}^* \end{array} \right]^\varepsilon \left\{ \begin{array}{l} E_1\\ E_2\\ E_3 \end{array} \right\} \end{array} $$

(6)

where σ _ij are stress components, ε _ij and γ _ij are strain components, E _i and D _i are the electric field and electric displacement components, respectively, $Q_{ij}^E$ are reduced stiffness coefficients at constant electric field, e _ij and $e_{ij}^*$ are piezoelectric and reduced piezoelectric constants, respectively, and $\epsilon_{ij}^\varepsilon$ and $\epsilon_{33}^{*\varepsilon}$ are dielectric and reduced dielectric constants, measured at constant strain. Expressions for the reduced quantities mentioned above can be found in Araújo et al. [19]. The complete set of equations in (6) is only used for the piezoelectric sensor and actuator layers, while for the remaining elastic and viscoelastic layers, only the first equation is considered, without the piezoelectric part. For the viscoelastic core layer, the reduced stiffness coefficients $Q_{ij}^E$ are complex quantities, since the complex modulus approach was used in this work, using the elastic-viscoelastic principle. In this case, the usual engineering moduli may be represented by complex quantities, considering isothermal conditions:

$$ \begin{array}{lll}\label{eq:complex_engineering} E^*_1(j \omega) &=& E_1(\omega)\big(1 + j \eta_{E_1}(\omega)\big)\\ E^*_2(j \omega) &=& E_2(\omega)\big(1 + j \eta_{E_2}(\omega)\big)\\ G^*_{12}(j \omega) &=& G_{12}(\omega)\big(1 + j \eta_{G_{12}}(\omega)\big)\\ G^*_{23}(j \omega) &=& G_{23}(\omega)\big(1 + j \eta_{G_{23}}(\omega)\big)\\ G^*_{13}(j \omega) &=& G_{13}(\omega)\big(1 + j \eta_{G_{13}}(\omega)\big)\\ \nu^*_{12}(j \omega) &=& \nu_{12}(\omega)\big(1 + j \eta_{\nu_{12}}(\omega)\big) \end{array} $$

(7)

where E ₁, E ₂, G ₁₂, G ₂₃, G ₁₃ and ν ₁₂ denote storage moduli, $\eta_{E_1}$, $\eta_{E_2}$, $\eta_{G_{12}}$, $\eta_{G_{23}}$, $\eta_{G_{13}}$ and $\eta_{\nu_{12}}$ are the corresponding material loss factors, ω represents the angular frequency of vibration and $j=\sqrt{-1}$ is the imaginary unit. Additionally, in Eq. 7, E, G and ν represent Young’s moduli, shear moduli and Poisson’s ratio, respectively.

The equations of motion for the plate are obtained by applying the extended Hamilton’s principle, using an eight node serendipity plate element with 17 mechanical degrees of freedom per node, and one electric potential degree of freedom per piezoelectric layer, assuming that the potential varies linearly in the thickness direction:

$$ \label{eq:global_equilib} \left[ \begin{array}{cc} \mathbf{M}_{uu} & \mathbf{0}\\[4pt] \mathbf{0} & \mathbf{0} \end{array} \right] \left[ \begin{array}{c} \ddot{\mathbf{u}}\\[4pt] \ddot{\boldsymbol{\phi}} \end{array} \right] + \left[ \begin{array}{ll} \mathbf{K}_{uu}(\omega) & \mathbf{K}_{u \phi}\\[4pt] \mathbf{K}_{u \phi}^T & \mathbf{K}_{\phi\phi}\\[4pt] \end{array} \right] \left[ \begin{array}{c} \mathbf{u}\\[4pt] \boldsymbol{\phi} \end{array} \right] = \left[ \begin{array}{c} \mathbf{F}_u\\[4pt] \mathbf{0} \end{array} \right] $$

(8)

where u, $\ddot{\mathbf{u}}$, $\boldsymbol{\phi}$ and $\ddot{\boldsymbol{\phi}}$ are complex mechanical degrees of freedom and corresponding accelerations, electric potential and corresponding second time derivatives, respectively. M _uu and K _uu (ω) are the real mass matrix and complex stiffness matrix, respectively, corresponding to purely mechanical behaviour, while K _ϕϕ is the dielectric stiffness matrix, K _{u ϕ} is the stiffness matrix that corresponds to the coupling between the mechanical and the piezoelectric effects, and F _u is the externally applied complex mechanical load vector.

The feedback control law is based on direct proportional or velocity feedback, and can be written in the following form:

$$ \boldsymbol{\phi}_a = G_d \boldsymbol{\phi}_s + G_v \dot{\boldsymbol{\phi}_s} $$

(9)

where G _d and G _v are the constant displacement and the constant velocity feedback gains, respectively. The vectors of actuator (a) and sensor (s) potentials are $\boldsymbol{\phi}_a$ and $\boldsymbol{\phi}_s$, while $\dot{\boldsymbol{\phi}_s}$ is the vector of sensor potential time derivatives.

Assuming harmonic vibrations, the final equilibrium equations are given by:

$$ \left[ \mathbf{K}^*(\omega)-\omega^2 \mathbf{M}_{uu} \right] \mathbf{u} = \mathbf{F}_u $$

(10)

where the condensed stiffness matrix is written as:

$$ \mathbf{K}^*(\omega) = \mathbf{K}_{uu}(\omega) - \left[ \left( G_d + j \omega G_v\right) \mathbf{K}_{u \phi}^a + \mathbf{K}_{u \phi}^s \right] \mathbf{K}_{\phi \phi}^{s^{-1}} \mathbf{K}_{u \phi}^{s^T} $$

(11)

and K _uu (ω) is a complex matrix.

It is worthwhile noting that when electroded surfaces exist in a given patch or layer, equipotential conditions should be imposed before condensing the electric degrees of freedom.

The forced vibration problem is solved in the frequency domain, which requires the solution of the following linear system of equations for each frequency point:

$$ \label{eq:condensed_eq} \left[ \mathbf{K}^*(\omega) - \omega^2 \mathbf{M}_{uu} \right] \mathbf{u}(\omega) = \mathbf{F}_u(\omega) $$

(12)

where $\mathbf{F}_u(\omega)= \mathcal{F} \left[ \mathbf{F}_u(t) \right]$ is the Fourier transform of the time domain force history F _u (t).

For the free vibration problem, Eq. 12 reduces to the following non-linear eigenvalue problem, due to the frequency dependent nature of the stiffness matrix:

$$\label{eq:free_vibration} \left[ \mathbf{K}^*(\omega) - \lambda_n^* \mathbf{M}_{uu} \right] \mathbf{u}_n = \mathbf{0} $$

(13)

where u _n is a complex eigenvector and $\lambda_n^*$ is the associated complex eigenvalue, which can be written as:

$$ \lambda_n^* = \lambda_n \left( 1 + j \eta_n \right) $$

(14)

and $\lambda_n=\omega_n^2$ is the real part of the complex eigenvalue and η _n is the corresponding modal loss factor.

The non-linear eigenvalue problem is solved iteratively with a shift-invert transformation [20]. Natural frequencies and modal loss factors can also be determined from the frequency domain response [21], but in this work only the complex eigenvalue approach was used.

3 Applications

The validation of the hybrid sandwich plate finite element model has been conducted successfully by comparing eigenfrequencies and associated modal loss factors with the very few reference solutions available in the open literature (mostly for beams and isotropic materials, considering hysteretic damping), and alternatively with commercial finite element solutions. In this paper we present comparative results for passive damping with the ones reported by Rikards at al. [22], which include experimental data. As for hybrid damping, we compare our solutions with the ones reported by Boudaoud et al. [13], which, to the authors’ knowledge, are the only ones available in the literature for hybrid active-passive sandwich plates with co-located control. We further present a benchmark application for a laminated hybrid sandwich plate, considering both frequency and time domain responses, using a fractional derivative [23] constitutive model for the frequency dependent viscoelastic behaviour, and negative velocity feedback control.

3.1 Passive Sandwich Plates

3.1.1 Undamped Sandwich

A symmetric and simply supported rectangular sandwich plate with face layers made of aluminium and a soft orthotropic core is considered [22, 24]. The plate in-plane dimensions (a ×b) are 1.829 m × 1.219 m, the thickness of the face and core layers are $h_{e_1}=h_{e_2}=0.406 \times 10^{-3}$ m, $h_v=0.635 \times 10^{-2}$ m. The aluminium face layers are isotropic with elastic properties E = 7.023 ×10⁴ MPa, ν = 0.3 and material density $\rho=2.82 \times 10^3 \, \textnormal{kg}/\textnormal{m}^3$. The orthotropic soft core is characterized by the following properties (principal material direction 1 is aligned with the x direction): E ₁ = E ₂ = 137 MPa, G ₁₂ = 45.7 MPa, G ₁₃ = 137 MPa, G ₂₃ = 52.7 MPa, ν ₁₂ = 0.5, and $\rho=124.1 \, \textnormal{kg}/\textnormal{m}^3$.

Comparative results for the first ten natural frequencies are presented in Table 1, using a 12 ×10 mesh for both present and reported results [22], where a three node triangular super-element was used. A good agreement can be observed between numerical results and the experimental ones.

Table 1 Natural frequencies (Hz) for the undamped rectangular sandwich plate

3.1.2 Damped Sandwich

A non-symmetric square simply supported sandwich plate with a thick damping core is considered [22, 25]. The material properties and geometry of the plate are characterized by non-dimensional quantities. The plate in-plane dimensions are (a ×a) with a = 100, the thickness of the face and core layers are $h_{e_1}=0.4$, $h_{e_2}=0.28$, h _v  = 4. The face layers are isotropic with elastic properties E = 10⁵, ν = 0.3 and material density ρ = 1. The isotropic soft core is characterized by the following non-dimensional properties: G = 1, ν = 0.3, ρ = 0.5, and η _G  = 0.5 (material loss factor associated with shear modulus).

Comparative results for the first three modal loss factors are presented in Table 2, using a 12 ×12 mesh for both present and reported [22, 25] results, where a good agreement can be observed. The approximate nature of the energy method used by Rikards et al. [22] to calculate the modal loss factor might explain the deviations observed.

Table 2 Modal loss factors for the square damped sandwich plate

3.2 Hybrid Damping

3.2.1 Comparative Analysis

The validation of the hybrid sandwich plate finite element has been conducted by comparison with the few reproducible reported results found in the literature [13]. Only direct proportional feedback control has been reported.

The problem consists of a simply supported beam with overall thickness h = 10 mm and length L = 500 mm. Since the width of the beam does not influence the flexural modes of vibration, a value of l = 50 mm was used. Isotropic elastic layer thicknesses are $h_{e_1}=h_{e_2}=\frac{6}{15} h$ and the isotropic viscoelastic and piezoelectric layer thicknesses are $h_v=h_a=h_s=\frac{h}{15}$. Material densities are $\rho_{e_1}=\rho_{e_2}=2040 \, \textnormal{kg/m}^3$, $\rho_{v}=1200 \, \textnormal{kg/m}^3$ and $\rho_s=\rho_a=7500 \, \textnormal{kg/m}^3$. Elastic shear modulus is 25 GPa and viscoelastic shear modulus assumes three different values: 2.5 MPa, 25 MPa and 2500 MPa. The material loss factor for the viscoelastic layer was η = 0.5. As for the sensor and actuator layers, PZT4 was considered, with properties: E ₁ = E ₂ = 81.3 GPa, G ₁₂ = 30 GPa, G ₁₃ = G ₂₃ = 25.6 GPa, $e_{31}^*=-11.75$ N/Vm, $e_{32}^*=-7.36$ N/Vm, and $\epsilon_{33}^{*\varepsilon}=9.14 \times 10^{-9}$ F/m. Reduced piezoelectric and dielectric constants are obtained from the 3D elasticity matrix, by imposing ν ₁₂ = ν ₂₃ = 0 for compatibility with the beam theory. For the same reason, the elastic and the viscoelastic material’s in-plane Poisson’s ratios were also set to zero.

In Table 3 the fundamental resonant frequency and corresponding modal loss factor is presented using a 30 ×1 mesh, for three different values of the viscoelastic core shear modulus and direct proportional feedback gain G _d , and for G _v  = 0. It can be observed that present results show a good agreement with the reported ones. The missing values in Table 3 are found to be in error in [13].

Table 3 Simply supported hybrid sandwich beam: fundamental natural frequency (f ₁) and corresponding modal loss factor (η ₁)

3.2.2 Laminated Hybrid Sandwich Plate

To illustrate the effect of frequency dependent material properties, a laminated hybrid sandwich plate is considered with a viscoelastic core described by a fractional derivative constitutive law, and with four pairs of surface bonded co-located sensor-actuator patches, using the negative velocity feedback control law.

The plate is a 300 mm × 200 mm laminated sandwich with all edges simply supported and made of carbon fibre plies and a central isotropic viscoelastic damping material core. The stacking sequence for carbon fibre laminates is $\left[0^\circ / 90^\circ / +45^\circ\right]$ for (e ₁) and $\left[+45^\circ / 90^\circ / 0^\circ\right]$ for (e ₂). The thickness of each carbon fibre ply is 0.5 mm, and the viscoelastic core is 2.5 mm thick.

Material properties for the isotropic viscoelastic damping polymer are described by a five parameter fractional derivative constitutive model [23], where ν = 0.49 and ρ = 1300 $\textnormal{kg}/\textnormal{m}^3$, have been assumed here. The expression for the complex shear modulus is as follows:

$$ G(j \omega) = G_0 + G_0 (d-1) \frac{(j \omega \tau)^\alpha}{1+(j \omega \tau)^\beta} $$

(15)

where G ₀ = 0.8 MPa is the static shear modulus, d = 1570, α = 0.566, β = 0.558, and τ = 7.23 ×10^− 10 s is the relaxation time.

For the carbon fiber plies, material properties are E ₁ = 130.8 GPa, E ₂ = 10.6 GPa, G ₁₂ = 5.6 GPa, G ₁₃ = 4.2 GPa, G ₂₃ = 3.0 GPa, ν ₁₂ = 0.36, and ρ = 1543 $\textnormal{kg}/\textnormal{m}^3$.

Four pairs of surface electroded 50 mm × 50 mm × 0.9 mm piezoelectric patches are also bonded to the upper and lower surface of the plate, as illustrated in Fig. 2.

Fig. 2

Laminated viscoelastic sandwich plate with piezoelectric patch positions (dimensions in mm)

Material properties for the piezoelectric patches were taken as E ₁ = 50.9 GPa, E ₂ = 46.1 GPa, G ₁₂ = 14.3 GPa, G ₁₃ = 8.0 GPa, G ₂₃ = 20.6 GPa, ν ₁₂ = 0.29, ρ = 7800 $\textnormal{kg}/\textnormal{m}^3$, $e^*_{31}=-17.0$ N/Vm, $e^*_{32}=-12.2$ N/Vm, and $\epsilon_{33}^{*\varepsilon}=1.549 \times 10^{-8}$ F/m.

Both sets of material data for the carbon fibre plies and the piezoelectric patches were obtained through parameter estimation techniques using laminated carbon fibre specimens with surface bonded piezoelectric patches, using the methodology presented by Araújo et al. [19].

The first five flexural natural frequencies of free vibration of the plate and corresponding modal loss factors are presented in Table 4 for three different electrode configurations: SC (Short Circuit—top and bottom electroded surfaces of each patch have the same electric potential), OC (Open Circuit—top and bottom electroded surfaces of each patch have independent electric potentials), and G _v  = − 0.01 (negative velocity feedback). A 12 ×8 finite element mesh was used with a total of 4,497 mechanical degrees of freedom (DOF) and 8 electric potential DOF.

Table 4 First five natural frequencies and modal loss factors for the simply supported hybrid sandwich laminated plate

The influence of the negative velocity feedback control law in natural frequencies and modal loss factors can be observed from Table 4, where a significant increase in some modal loss factors is observed, as well as some increase in resonant frequencies. Also, the magnitude of the frequency response of the central point of the plate is presented in Fig. 3, due to a central 10 N force applied at t = 0. Resonances in Fig. 3 correspond to modes 1, 4 and 5. The time domain response of the central point of the plate, obtained by the inverse Fourier transform of the frequency response, is displayed in Fig. 4.

Fig. 3

Frequency response of the simply supported laminated viscoelastic sandwich plate

Fig. 4

Time response of the simply supported laminated viscoelastic sandwich plate

4 Conclusions

A new hybrid sandwich plate finite element model has been developed for the analysis of the dynamic response of plate structures with active-passive damping. The model is capable of handling a wide variety of layer configurations and direct proportional and velocity feedback control laws have been implemented. The complex modulus approach was used, along with frequency domain response analysis, allowing for frequency dependent material data. The developed eight node finite element model presents a good behaviour with passive and hybrid damping, when compared to reference solutions, and a benchmark application is suggested in this paper. The response of the model has also been compared with experimental data available in the literature, showing excellent agreement.

Although the current finite element model may not present significant advantages over 3D ones regarding the number of degrees of freedom, due to its 2D nature it is especially adequate for optimization applications that use thickness design variables, as constant re-meshing is no longer required. Also it presents obvious advantages for modelling, analysis, control, and optimization of hybrid active-passive laminated sandwich structures relative to the current state of the art commercial finite element codes.