Keywords

1 Introduction

The flexibility of beam elements leads to their large amplitude nonlinear vibrations under different kind of loads and thereby causes their fracture/fatigue failure. Hence, a substantial amount of research is conducted on the vibration control of linear and nonlinear vibrations of beam elements under various loadings [1,2,3,4,5]. One of the popular technique is the constrained layer damping (CLD) treatment of the structure, where the vibrational energy is dissipated through the transient deformation of viscoelastic material by constraining it between the elastic substrate/face layers. For the design of an effective damping treatment, the accurate optimization studies of geometrically complex damping treatments [6, 7] may be necessary. Hence, for this purpose, finite element (FE) method is commonly used that provides accurate nonlinear dynamics compared to other alternative methods.

To conduct nonlinear dynamic analysis especially in conjunction with optimization, the use of time integration may be inappropriate and expensive due to the requirement of response for large number of geometrical parameters and excitation frequency [2, 3]. Hence, to directly evaluate the steady-state frequency response without requiring time integration method, the harmonic balance method (HBM) is popularly used in literature [3, 8, 9]. Although it is computationally efficient compared to time integration, it needs high computational time and memory [1, 3, 8,9,10] mainly due to the large number of degree of freedom associated with FE discretization, Fourier expansion of HBM and especially, additional internal variables/degree of freedom to model viscoelasticity. Therefore, various reduced-order FE models (ROMs) had been developing in literature that are majorly limited to elastic structures [11,12,13]. Hence, the objective of the present work is to derive the reduced-order FE model in conjunction with HBM to evaluate the nonlinear steady-state frequency response of viscoelastic sandwich (VS) beam.

Most of the nonlinear dynamic studies in the literature were neglected the frequency-dependency of stiffness/damping of viscoelastic material by considering Kelvin-Voigt model [2, 14, 15]. However, the variation of nonlinear resonant frequency with the amplitude of vibration and the presence of frequency dependent damping may significantly affect the resonant amplitude of the vibration. So, the main objective is decided to investigate the effect of frequency-dependent viscoelasticity on the steady-state nonlinear response by comparing the response evaluated using fractional Zener viscoelastic model with that evaluated using an equivalent Kelvin-Voigt model.

2 Reduced-Order FE Model of Viscoelastic Sandwich Beam

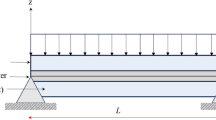
Figure 1 shows the schematic diagram of a VS beam, where the thickness of substrate and viscoelastic core layer are denoted by \(h_s\) and \(h_v\), respectively. The length and width of the beam are denoted by \(L\) and \(b\), respectively. Since it as a plane stress problem [3] in two dimensional \(xz\)-plane, the state of stress and state of strain at any point in the \(xz\)-plane can be written as,

$$ \begin{aligned} {\user2{\sigma }} & = \{ \begin{array}{*{20}c} {\sigma _x } & {\sigma _z } & {\tau _{xz} } \\ \end{array} \} ^{\text{T}} ,{\user2{\varepsilon }} = \{ \begin{array}{*{20}c} {\varepsilon _x } & {\varepsilon _z } & {\gamma _{xz} } \\ \end{array} \} ^{\text{T}} ,{\user2{\varepsilon }} = {\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n , \\ {\user2{\varepsilon }}_l & = {\user2{L}}\,\,{\user2{d}}_s ,{\user2{\varepsilon }}_n = {\user2{L}}_n ({\user2{d}}_s )\,\,{\user2{d}}_s ,{\user2{d}}_s = \{ u\,\,\,\,\,w\} ^{\text{T}} \\ \end{aligned} $$
(1)
Fig. 1
figure 1

Schematic diagram of a viscoelastic sandwich beam

Full size image

where, \( {\user2{\varepsilon }}_l \) and \({{\user2{\varepsilon}}}_n\) are the linear and nonlinear counterpart of Green–Lagrange strain, respectively, while \({{\user2{L}}}\) and \({{\user2{L}}}_n\) are the corresponding operator matrices; \(u\) and \(w\) are the displacements along \(x\) and \(z\) directions respectively. However, to derive the incremental FE model, the incremental forms of state variables (\(\Delta {{\user2{d}}}_s\),\(\Delta \omega\)) about a reference state (\({}^i{{\user2{d}}}_s\),\(\omega_i\)) can be given as in Eq. (2). The corresponding expressions of strain and stress vectors can be given as in Eq. (3).

$$ {{\user2{d}}}_s = {}^i{{\user2{d}}}_s + \Delta {{\user2{d}}}_s ,\omega = \omega_i + \Delta \omega $$
(2)
$$ \begin{aligned} {{\user2{\varepsilon}}}_l & = {}^i{{\user2{\varepsilon}}}_l + \Delta {{\user2{\varepsilon}}}_l ,{{\user2{\varepsilon}}}_n = {}^i{{\user2{\varepsilon}}}_n + \Delta {{\user2{\varepsilon}}}_{n1} + \Delta {{\user2{\varepsilon}}}_{n2} ,{{\user2{\sigma}}} = {}^i{{\user2{\sigma}}} + \Delta {{\user2{\sigma}}}, \\ {}^i{{\user2{\varepsilon}}}_l & = {{\user2{L}}}\,\,{}^i{{\user2{d}}}_s ,\Delta {{\user2{\varepsilon}}}_l = {{\user2{L}}}\,\,\Delta {{\user2{d}}}_s ,{}^i{{\user2{\varepsilon}}}_n = ({1 / 2})\,{}^i{{\user2{L}}}_n \,{}^i{{\user2{d}}}_s ,\Delta {{\user2{\varepsilon}}}_{n1} = {}^i\,{{\user2{L}}}_n \,\Delta {{\user2{d}}}_s , \\ \Delta {{\user2{\varepsilon}}}_{n2} & = ({1 / 2})\,\,\Delta {{\user2{L}}}_n \,\Delta {{\user2{d}}}_s ,{}^i{{\user2{L}}}_n = \,{{\user2{L}}}_n ({}^i{{\user2{d}}}_s ),\Delta {{\user2{L}}}_n = {{\user2{L}}}_n (\Delta {{\user2{d}}}_s ) \\ \end{aligned} $$
(3)

where, pre-superscript \(i\) denotes the variable about the reference state of vibration. The incremental governing equation of VS beam subjected to transverse harmonic point load (\(p_t^o \cos \omega \,t\))/axial compressive harmonic load (\(p_a^o (1 + \lambda \cos 2\omega t)\)) can be obtained by following Hamilton’s principle and Eqs. (1)–(3) as,

$$ \int_A {\left\langle {\begin{array}{*{20}l} {(\delta \Delta {\user2{\varepsilon }}_l + \delta \Delta {\user2{\varepsilon }}_{n1} )^{\text{T}} ({}^i{\user2{\sigma }} + \Delta {\user2{\sigma }}) + (\delta \Delta {\user2{\varepsilon }}_{n2} )^{\text{T}} \,{}^i{\user2{\sigma }}} \hfill \\ { + (\delta \Delta {\user2{d}}_s )^{\text{T}} \rho ({}^i{{\ddot{\user2{d}}}}_s + \Delta {\ddot{\user2{d}}}_s ) - \,(\{ 0\,\,\,1\} \,\left. {\delta \Delta {\user2{d}}_s } \right|_{(x_l ,z_l )} )^{\text{T}} ({{p_t^o } / b})\cos \omega t} \hfill \\ { - ({\user2{L}}_g \,\delta \Delta {\user2{d}}_s )^{\text{T}} ({{p_a^o } / {bh_s }})(1 + \lambda \cos 2\omega \,t)\,{\user2{L}}_g ({}^i{\user2{d}}_s + \Delta {\user2{d}}_s )} \hfill \\ {} \hfill \\ \end{array} } \right\rangle } bdA = 0 $$
(4)

where, \(p_t^o\) is amplitude of transverse harmonic point load; \((x_l ,z_l ) = (L/4,\,0)\) is the location of point load; \({{\user2{L}}}_g\) is the linear operator of strain vectors associated with geometric stiffness term due to pre-stress;\(p_a^o\) and \(\lambda\) are the static counterpart and dynamic load parameter of axial harmonic load, respectively; \(\omega\) and \(2\omega\) are the frequency of excitation of harmonic point load and axial periodic load, respectively. In Eq. (4), the last term with \(p_a^o\) vanishes for viscoelastic material mainly due to the negligible axial pre-stress induced in it.

Now, for the implementation of HBM, the response is assumed following the Fourier series with finite number (\(H\)) of harmonic terms as,

$$ {{\user2{d}}}_s = {{\user2{d}}}_s^o + \sum_{m = 1}^H {{{\user2{d}}}_{sm}^c \cos (m\omega t) + {{\user2{d}}}_{sm}^s \sin (m\omega t)} $$
(5)

where, \({{\user2{d}}}_s^o\), \({{\user2{d}}}_{sm}^c\) and \({{\user2{d}}}_{sm}^s\) are the Fourier coefficient vectors of displacement (\({{\user2{d}}}_s\)) corresponding to the constant, \(m{\text{th}}\) cosine and \(m{\text{th}}\) sine terms of Fourier series, respectively. The corresponding Fourier series of stress vector in terms of strain can be given in through the constitutive relation of viscoelastic material in frequency-domain as,

$$ \begin{aligned} {\user2{\sigma }} & = ({\user2{\sigma }})^o + \sum_{m = 1}^{2H} {({\user2{\sigma }})_m^c \cos (m\omega t) + ({\user2{\sigma }})_m^s \sin (m\omega t)} , \\ ({\user2{\sigma }})_m^s & = {\user2{C}}\left\langle {f_m^c ({\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n )_m^s - f_m^s ({\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n )_m^c } \right\rangle ,({\user2{\sigma }})_m^c = {\user2{C}}\left\langle {f_m^c ({\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n )_m^c + f_m^s ({\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n )_m^s } \right\rangle \\ ({\user2{\sigma }})^o & = {\user2{C}}({\user2{\varepsilon }}_l + {\user2{\varepsilon }}_n )^o ,f_m^c = E^R (m\omega )/E_o ,f_m^s = E^I (m\omega )/E_o \\ \end{aligned} $$
(6)

where, \(E_o\) is the relaxed elastic modulus; \({{\user2{C}}}\) is the stiffness matrix in terms of \(E_o\) and Poisson ratio; \(E^R\)/\(E^I\) are the frequency-dependent storage/loss moduli of the viscoelastic material. In this work, the frequency dependent viscoelasticity is modelled using fractional Zener viscoelastic model [10]. The relation in Eq. (6) also represent the constitutive relation for an elastic material when \(f_m^c = 1,\,\,f_m^s = 0\). However, to consider frequency-independent property for viscoelastic material, an equivalent Kelvin-Voigt model in a specified frequency range (\([\omega_1 \,\,\omega_2 ]\)) is used, where the corresponding constitutive relation can be given in time-domain as,

$$ \begin{aligned} {\user2{\sigma }} & = {\user2{C}}(\,{\user2{\varepsilon }} + \tau _v \,{{\dot{\user2{\varepsilon }}}}), \\ \tau _v & = \frac{1}{{\omega _2 - \omega _1 }}\int_{\omega _1 }^{\omega _2 } {\frac{{\eta (\omega )}}{{\omega \,\,}}} d\omega ,\,\eta (\omega ) = E^I (\omega )/E^R (\omega ) \\ \end{aligned} $$
(7)

where, the relaxation time (\(\tau_v\)) is evaluated by averaging the ratio of frequency-dependent loss factor (\(\eta (\omega )\)) and frequency (\(\omega\)) in the interval \([\omega_1 \,\,\omega_2 ]\) [15]. The corresponding constitutive relation in frequency-domain can be obtained similar to Eq. (6) with \(f_m^c = 1\) and \(f_m^s = \tau_v \,m\,\omega\). To derive the FE model, the \(xz\)-plane of VS beam (Fig. 1) is discretized with nine-node isoparametric quadrilateral element. Subsequently, considering the reduce-order transformation using a reduction basis (RB) (\({{\user2{\varPhi}}}\)), the displacement and strain expressions at any point in a typical element can be written as,

$$ \begin{aligned} {}^i{{\user2{d}}}_s & = {{\user2{N}}}\,{{\user2{\varPhi}}}^e \,{}^i{{\user2{V}}},\Delta {{\user2{d}}}_s = {{\user2{N}}}\,{{\user2{\varPhi}}}^e \,\Delta \,{{\user2{V}}} \\ {}^i{{\user2{\varepsilon}}}_l & = {{\user2{B}}}_l {{\user2{\varPhi}}}^e {}^i{{\user2{V}}},\Delta {{\user2{\varepsilon}}}_l = {{\user2{B}}}_l {{\user2{\varPhi}}}^e \Delta {{\user2{V}}},{}^i{{\user2{\varepsilon}}}_n = ({1 / 2})\,{{\user2{B}}}_n {{\user2{\varPhi}}}_I^e {}^i{{\user2{V}}}_I {}^i{{\user2{V}}},\Delta {{\user2{\varepsilon}}}_{n1} = {{\user2{B}}}_n {{\user2{\varPhi}}}_I^e {}^i{{\user2{V}}}_I \Delta {{\user2{V}}} \\ {{\user2{\varPhi}}}_I^e & = {{\user2{\varPhi}}}^e \otimes {{\user2{\varPhi}}}^e ,{}^i{{\user2{V}}}_I = {}^i{{\user2{V}}} \otimes {{\user2{I}}}_{N_r } \\ \end{aligned} $$
(8)

where, \({{\user2{N}}}\) is the shape function matrix; \({{\user2{N}}}_r\) is the number of basis vectors in RB; \({{\user2{B}}}_n\) is a linear matrix corresponding to the operator \({{\user2{L}}}_n\)(Eq. 3) that is obtained by separating space-dependent and displacement dependent terms;\({{\user2{\varPhi}}}^e\) is the RB at element level; \({}^i{{\user2{V}}}\)/\(\Delta {{\user2{V}}}\) are the incremental forms of reduced coordinate vector. Thus, substituting Eqs. (5)–(8) in Eq. (4) and applying Galerkin method, the reduced-order FE governing equation of motion in frequency-domain can be obtained using the orthogonality of Fourier basis functions as,

$$ \begin{gathered} {{\user2{K}}}_t \,\Delta {{\user2{X}}} = {{\user2{R}}} + {{\user2{R}}}_\omega \,\Delta \omega , \hfill \\ {{\user2{R}}} = {{\user2{P}}} - {{\user2{K}}}_m \,{}^i{{\user2{X}}},{{\user2{R}}}_\omega = {{ - (\partial \,{{\user2{K}}}_m } / {\partial \omega_i }}){}^i{{\user2{X}}} \hfill \\ \end{gathered} $$
(9)

where, \({{\user2{K}}}_m\)/\({{\user2{K}}}_t\) are the effective reduced-order stiffness/tangent stiffness; \({{\user2{R}}}\) is residue vector; \({{\user2{R}}}_\omega\) is the force vector per unit increment of frequency;\({{\user2{P}}}\) is external load vector. However, the corresponding full-order FE governing equation can be obtained by taking \({{\user2{\varPhi}}}^e\) as a unit matrix. Thus, the solution of Eq. (9) using continuation method provides the frequency response of VS beam under harmonic point load/axial compressive harmonic load. However, the RB is constructed by taking first 4 modes obtained using modal strain energy method (MSE) [16] and corresponding 10 static derivatives [17].

3 Numerical Results and Discussion

In this section, the numerical results are presented to show the effect of frequency-dependent viscoelastic property on the forced and parametric resonant response of clamped–clamped VS beam. However, initially, the validation for the accuracy of the ROM against full-order model is presented. The geometrical properties of VS beam are considered as \(L\) = 0.4 m, \(b\) = 12 mm and \(h_s\) = 2 mm. The substrate layers are considered to be made of Aluminum (\(E\) = 70.3 GPa, \(\nu\) = 0.345, \(\rho\) = 2690 kg/m3 [10]) and viscoelastic core is made of ISD 112 (\(\nu\) = 0.499, \(\rho\) = 1600 kg/m3) with its fractional Zener viscoelastic model parameters [10] as \(E_o\) = 1.5 MPa, \(E_\infty\) = 69.9495 MPa, \(\alpha\) = 0.7915 and \(\tau = 1.4052 \times 10^{ - 5}\) s.

Initially, to validate the full-order FE model, the frequency response associated with forced resonance of clamped–clamped VS beam (with Kelvin-Voigt viscoelastic model) is evaluated by solving Eq. (9) using continuation method and compared in Fig. 2a with the similar results in Ref. [1]. Next, to verify the modelling of frequency-dependent properties and axial compressive harmonic load, the parametric instability region is constructed using Eq. (9) [3]. This region is compared in Fig. 2b with similar result in Ref. [18]. The good agreement shown in Fig. 2 with the similar reference results, validates the formulation of full-order FE model and solution method.

Fig. 2
figure 2

Validation for the evaluation of a frequency response of sandwich beam with viscoelastic core modelled by Kelvin-Voigt model (Ref. [1]), b parametric instability region of frequency-dependent viscoelastic beam (\(E_o\) = 425.72 MPa, \(E_\infty\) = 5954.6 MPa, \(\alpha\) = 0.2255 and \(\tau\) = 0.6338 s) for a load parameter of 0.6 (Ref. [18])

Full size image

Next, to validate the reduced-order FE model, the frequency response associated with parametric resonance of VS beam is evaluated by using ROM as well as full-order FE model. The corresponding responses are depicted in Fig. 3a, where also the axial load parameters are mentioned. The Fig. 3a illustrates that the frequency response evaluated using ROM reasonably agrees with that evaluated using full-order FE model. It is to be noted that RB is evaluated without considering the effect of static counterpart of axial load that significantly reduces the linear stiffness of beam. For further validation of such RB, the similar frequency response for an axial load near to the critical buckling load (331.2745 N) is evaluated and shown in Fig. 3b. It reveals that the accuracy of response is almost independent of the value of static counterpart of axial load. Thus, the present ROM and its RB with MSE method accurately evaluates the frequency response of frequency-dependent VS beam.

Fig. 3
figure 3

Validation of reduced-order FE model for the evaluation of frequency response (\(H\) = 7) of VS beam (\(h_v\) = 4 mm) under axial compressive periodic load (\(\lambda\) = 0.7) with its static counterpart as a \(p_a^o\) = 231.96215 N and b\(p_a^o\) = 298.14705 N

Full size image

To investigate the effect of frequency-dependent viscoelastic property on the forced /parametric resonant response of VS beam, the corresponding frequency response is compared with the similar responses evaluated using an equivalent Kelvin-Voigt model. Considering a limited frequency range around the twice of natural frequency (100–1500 rad/s, Eq. 7), the frequency response of VS beam under axial periodic load is evaluated by using Kelvin-Voigt model. The corresponding response along with the response evaluated using frequency dependent property (fractional Zener viscoelastic model) are presented in Fig. 4a. Similarly, the frequency response of VS beam under transverse harmonic point load is evaluated using Kelvin-Voigt model by considering a limited frequency range around the natural frequency (100–900 rad/s). The corresponding response along with the response evaluated using frequency dependent property are presented in Fig. 4b. Thus, from the Fig. 4 it can be observed that the effect of frequency dependent property on the forced/parametric resonant response is very less since an equivalent Kelvin-Voigt model provides nearly same response. However, to investigate the same for a wide frequency range (100–3000 rad/s), the frequency response of VS beam under harmonic transverse point load is evaluated using Kelvin-Voigt model and presented in Fig. 5 along with the response evaluated using frequency-dependent property (fractional Zener viscoelastic model). Here, Fig. 5 shows a significantly higher inaccuracy of frequency-independent property (Kelvin-Voigt model) in the representation of resonant peak amplitudes. Thus, from Figs. 4 and 5, it can be concluded that the consideration of frequency-independent property (ie. Kelvin-Voigt model) may be accurately valid when the different properties (i.e. parameters of Kelvin-Voigt model parameters) are used around each modal natural frequency.

Fig. 4
figure 4

Comparison of frequency response (\(H\) = 7) of VS beam using fractional Zener viscoelastic model and Kelvin-Voigt viscoelastic model for the a parametric resonance (\(p_a^o\) = 298.23705 N, \(h_v\) = 4 mm), and b forced resonance (\(p_t^o\) = 6 N, \(h_v\) = 2 mm)

Full size image
Fig. 5
figure 5

Comparison of forced resonant response (\(H\) = 7) of VS beam in a wide frequency range using Fractional Zener viscoelastic model and Kelvin-Voigt viscoelastic model (\(p_t^o\) = 6 N, \(h_v\) = 2 mm)

Full size image

4 Conclusions

In this work, the effect of frequency-dependent viscoelastic property on the forced/parametric resonant amplitude of viscoelastic sandwich beam is investigated by deriving a reduced-order finite element model (ROM) in frequency domain. The forced and parametric excitations were separately considered by applying transverse harmonic point load and axial periodic load respectively. The frequency-dependent viscoelasticity is modelled using fractional Zener model and the corresponding responses of sandwich beam are compared with that are derived using an equivalent Kelvin-Voigt model. The ROM in frequency domain is derived by implementing harmonic balance method prior to the finite element discretization and reduced-order transformation. Whereas the reduction basis is constructed using first four eigen modes through modal strain energy method and their corresponding static derivatives. The comparison of frequency responses evaluated using ROM and full-order FE model revealed that the ROM with aforesaid reduction basis evaluates the frequency response of frequency-dependent viscoelastic sandwich beam with reasonable accuracy. Further, the frequency dependent viscoelastic property has shown a significant effect on the resonant amplitudes when compared with the frequency-dependent property approximated in a wide frequency range using Kelvin-Voigt model. Thus, the results suggest that the nonlinear frequency response analysis of viscoelastic layered beams using Kelvin-Voigt model may be reasonably accurate when the different model parameters are considered around each modal natural frequency.