Optical soliton solutions to the fractional nonlinear Fokas–Lenells and paraxial Schrödinger equations

Abstract

In nonlinear optics, photonics, plasma, condensed matter physics, and other domains, the space–time fractional nonlinear Fokas–Lenells and paraxial Schrödinger equations associated with beta derivative have significant applications. The fractional wave transformation has been used to turn the space–time fractional nonlinear equations into integer order equations. To obtain optical soliton solutions relating to exponential, trigonometric, and hyperbolic functions and their integration with free parameters, the improved Bernoulli sub-equation function (IBSEF) scheme has been exploited. Different shapes of solitons have been extracted from the attained solutions, including kink, periodic, bell-shaped, anti-kink, dark-bright soliton, single kink type soliton, etc. A kink soliton is an optical shock front that keeps its shape while traveling through optical fibers. The characteristics of the solitons have been studied by describing profiles in 3D, 2D, contour, and density plots. The results imply that the IBSEF technique is simple, efficient, and capable of generating comprehensive soliton solutions of nonlinear models related to telecommunication and optics.

1 Introduction

The fractional nonlinear Schrödinger equation (FNSE) is crucial in optics. Nonlinear optics, which interprets the amplification of short pulses in optical fiber and is vital in ultra-fast signal routing, telecommunication systems, and other applications, is one of the main concerns. The nonlinear mathematical models in nonlinear optics, condensed matter physics and quantum mechanics are significantly influenced by the fractional nonlinear Schrödinger equation (Wang et al. 2022; Rezazadeh et al. 2018; Das and Saha Ray 2022). Solitons are used in optics to distinguish optical fields that do not change in size or shape during propagation due to a balanced combination between linear and nonlinear impacts of the medium. Therefore, analytical soliton solutions to the FNSE are put to use frequently in a broad range of nonlinear fields, such as optics, signal processing, control theory, plasma physics, astrophysics, probability, image processing, system identification and other areas (Akram et al. 2022; Mirzazadeh et al. 2021; Hashemi et al. 2017). Thus, several approaches, notably, the reproducing kernel discretization technique (Arqub et al. 2020), the modified Kudryashov scheme (Darvishi et al. 2021), the tanh-coth method (Zulfiqar and Ahmad 2022), the new Kudryashov extension (Rezazadeh et al. 2021), the Hirota bilinear scheme (Wang et al. 2021), the directed extended Riccati method (Islam et al. 2022), the rational sine–Gordon expansion approach (Yel et al. 2022), the improved Bernoulli sub-equation function (IBSEF) procedure (Islam and Akbar 2020, 2021; Demirbileko et al. 2021), the Lie group approach (Pashayi et al. 2017), the Nucci’s reduction approach (Hashemi et al. 2014; Hashemi 2021; Xia et al. 2022), etc., have been developed and exploited by physicists and mathematicians to determine the soliton solutions to the FNSE in the literature.

The space–time fractional nonlinear Fokas–Lenells (FL) equation (Zafar et al. 2021a) is:

$$i{D}_{t}^{\mu }v+{n}_{1}{D}_{xx}^{2\alpha }v+{n}_{2}{D}_{t}^{\mu }{D}_{x}^{\alpha }v+{\left|v\right|}^{2}\left(sv+ir{D}_{x}^{\alpha }v\right) = i\beta {D}_{x}^{\alpha }v+i\gamma {D}_{x}^{\alpha }\left({\left|v\right|}^{2n}v\right)+iv{D}_{x}^{\alpha }{\left|v\right|}^{2n},$$

(1)

where $0<\mu ,\alpha \le 1$, $i=\sqrt{-1}$ is the imaginary unit, $v=v\left(x,t\right)$, $x$ is the spatial coordinate and $t$ be temporal variable, ${n}_{1}$, $\beta$, ${n}_{2}$, $\delta$ and $\gamma$ are the coefficients which represents the spatiotemporal dispersion (STD), inter-modal dispersion (IMD), group velocity dispersion (GVD), nonlinear dispersion (ND) coefficient and self-steepening perturbation term respectively and $i{D}_{t}^{\mu }v$ be the linear fractional temporal evolution of the pulses in the nonlinear optics. The full nonlinearity is represented by the parameter $n$. Equation (1) is called the original Fokas–Lenells equation if $\mu =\alpha =1$ (Biswas et al. 2018a, b; Demiray and Bulut 2015). The classical form of Eq. (1) has been investigated by means of several approaches, such as, the modified simple equation and trial equation approach (Biswas et al. 2018a), the extended trial function scheme (Demiray and Bulut 2015; Biswas et al. 2018b), the generalized exponential function procedure (Osman and Ghanbari 2018), the sine–Gordon expansion process (Ali et al. 2020), the generalized Kudryashov method (Barman et al. 2021), etc. Further, the fractional form of the Eq. (1) has also been investigated by putting into use several methods, such as the fractional dual-function method (Wang et al. 2020), the extended sinh-Gordon equation expansion scheme (Bulut et al. 2018), the extended direct algebraic method (Sajid and Akram 2019), the simplest Riccati equation scheme (Zafar et al. 2021b), the ${\phi }^{6}$-model expansion method (Sajid and Akram 2021), etc.

The space–time fractional nonlinear paraxial Schrödinger equation in the Kerr media (Tariq et al. 2021) is:

$$i{D}_{z}^{\alpha }v+\frac{q}{2}{D}_{tt}^{2\mu }v+\frac{r}{2}{D}_{yy}^{2\alpha }v+s{\left|v\right|}^{2}v=0,$$

(2)

where $v\left(y,z,t\right)$ is the function of complex wave envelope, $q$, $r$ and $s$ represent evolution, diffraction, and Kerr nonlinearity, respectively. If $q r>0$, then Eq. (2) is called elliptical nonlinear Schrödinger equation (NSE) and Eq. (2) is called hyperbolic NSE for $q r<0$. To our optimal knowledge, the classical form of Eq. (2) has been investigated by making use of the several approaches, such as, the Hirota bilinear method (Rizvi et al. 2021), the extended trial equation method (Ali et al. 2019), the Lie symmetry scheme (Rizvi et al. 2019), the modified $(1/G{^{\prime}}$)-expansion and modified Kudryashov approach (Durur and Yokuş 2021), etc. Furthermore, the fractional form of Eq. (2) has been examined using several techniques, such as the modified simple equation method and auxiliary equation method (Tariq et al. 2021), the modified exponential function (Gao et al. 2019), etc.

To the foremost of our review, the IBSEF approach has not formerly been exploited to assess Eqs. (1) and (2) in the sense of beta derivative. Therefore, our focus is to ascertain typical and broad-ranging stable optical soliton solutions to the above-stated nonlinear fractional model through the IBSEF technique (Islam and Akbar 2020). Through this approach, we ascertain the exponential, trigonometric, hyperbolic, and rational form of solutions from which kink, periodic, bell-shaped multi-periodic, anti-kink, breathing, bright soliton, and other solitons are established with rich physical characteristics. The characteristics of the solitons have been studied by describing profiles in 3D, 2D, contour, and density plots.

The layout of the article is organized as: The introduction is described in Sect. 1. The Beta derivative is discussed in Sect. 2 of this article. The method is described in Sect. 3, and the extraction of solutions is presented in Sect. 4. To show the novelty of the attained results, we compared them in Sect. 5. The results and discussion are presented in Sect. 6, and conclusions are presented in the last section.

2 Beta derivative

Many academics have presented the definition of fractional derivative (Miller and Ross 1993; Kumar et al. 2020; Khalil et al. 2014; Hashemi and Baleanu 2020). Most of them do not follow the chain rule; the derivative of a constant is zero, and the Leibnitz rule. Atangana et al. (Atangana et al. 2016) proposed a significant and advanced definition of the fractional derivative, called the beta derivative. This definition behaves well and fulfills all the properties of classical calculus, including Leibniz and chain rules (Atangana and Alqahtani 2016).

Definition: Let $a \epsilon {\mathbb{R}}$ and $g$ be a function such that $g:\left[a, \infty \right)\to {\mathbb{R}}$. Then the $\beta$-operator on $g$ is defined as (Atangana and Alqahtani 2016):

$${D}_{y}^{\beta }g\left(y\right)=\left\{\begin{gathered}\begin{gathered}\mathrm{lim}\\ \varepsilon \to 0\end{gathered}\frac{g\left(y+\varepsilon {\left(y+\frac{1}{\Gamma (\beta )}\right)}^{1-\beta }\right)-g(y)}{\varepsilon }, y\ge 0, 0<\mu \le 1\\ g\left(y\right), \; y\ge 0, \mu =0\end{gathered}\right.$$

From the definition, we have ${D}_{y}^{\beta }g\left(y\right)=\frac{d}{dy}g(y)$ for $\beta =1$.

Theorems: Consider $g(y)$ and $h(y)$ are $\beta$-order differentiable for all $y>0$ and ${b}_{1}$ and ${b}_{2}$ are real constants. Then the subsequent characteristics are satisfied by this definition (Ismael et al. 2021).

• 1. ${D}_{y}^{0} g\left(y\right)=g(y)$.

• 2. ${D}_{y}^{\beta }\left({b}_{1}g\left(y\right)+{b}_{2} h\left(y\right)\right)={b}_{1} {D}_{y}^{\beta }\left(g\left(y\right)\right)+{b}_{2} {D}_{y}^{\beta }(h\left(y\right))$.

• 3. ${D}_{y}^{\beta }\left(g\left(y\right)h(y)\right)=g\left(y\right) {D}_{y}^{\beta }\left(h\left(y\right)\right)+h\left(y\right) {D}_{y}^{\beta }\left(g\left(y\right)\right)$.

• 4. ${D}_{y}^{\beta }\left({g}^{-1}\left(y\right)\right)=-\frac{{D}_{y}^{\beta }\left(g\left(y\right)\right)}{{g}^{2}\left(y\right)}$.

• 5. ${D}_{y}^{\beta }\left(\frac{g\left(y\right)}{h\left(y\right)}\right)=\frac{h\left(y\right) {D}_{y}^{\beta }\left(g\left(y\right)\right)-g\left(y\right) {D}_{y}^{\beta }\left(h\left(y\right)\right)}{{h}^{2}(y)}$.

• 6. ${D}_{y}^{\beta }\left((goh)(y)\right)={D}_{y}^{\beta }\left(g(h\left(y\right))\right)h{^{\prime}}(y)$.

• 7. ${D}_{y}^{\beta }\left(g(y)\right)={\left(y+\frac{1}{\Gamma (\beta )}\right) }^{1-\beta }\frac{dg(y)}{dy}$.

Because of its accessibility, simplicity, and usefulness, many researchers have employed this remarkable fractional derivative definition in many physical applications (Ismael et al. 2021; Islam et al. 2021; Al-Amin et al. 2021).

3 The method

The main features of the improved Bernoulli sub-equation function (IBSEF) approach are briefly described (Islam and Akbar 2021; Demirbileko et al. 2021) in the underneath:

3.1 Step 1:

The nonlinear fractional equation is presumed as the subsequent form:

$$\mathcal{Z}{(v,D}_{t}^{\mu }v,{D}_{x}^{\alpha }v,{D}_{tt}^{2\mu }v,{D}_{xt}^{\alpha \mu }v,{D}_{xx}^{2\alpha }v,\dots .)=0,$$

(3)

where $\mathcal{Z}$ is a polynomial of $v$, ${D}_{t}^{\mu }$ be the fractional derivative of $\mu$-order and $v\left(x,t\right)$ is an implicit function of coordinates $x$ and $t$. The purpose is to transform (3) into the nonlinear equation using a suitable fractional transformation. The fractional wave transformation is considered as:

$$v\left(x,t\right)=V\left(\zeta \right),\quad \zeta =\frac{s}{\alpha }{\left(x+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }+\frac{\omega }{\mu }{\left(t+\frac{1}{\Gamma \left(\mu \right)}\right)}^{\mu },$$

(4)

where $\omega$ be the wave velocity, $s$ be the wave number, $\zeta$ be the wave variable, $\mu$ be the order of time fractional derivative and $\alpha$ be the order of space fractional derivative.

Introducing the wave transformation (4) into the fractional nonlinear Eq. (3), we attain the subsequent nonlinear equation of integer order:

$${\rm T}\left(V,{V}^{{^{\prime}}},{V}{^{\prime\prime} },{V}^{\prime\prime\prime},\dots .\right)=0.$$

(5)

3.2 Step 2:

As per this method, the trial solution of the Eq. (5) can be assumed as:

$$V\left(\zeta \right)=\frac{\sum_{i=0}^{m}{a}_{i}{P}^{i}\left(\zeta \right)}{\sum_{j=0}^{l}{b}_{j}{P}^{j}\left(\zeta \right)}=\frac{{a}_{0}+{a}_{1}P\left(\zeta \right)+{a}_{2}{P}^{2}\left(\zeta \right)+\dots +{a}_{m}{P}^{m}\left(\zeta \right)}{{b}_{0}+{b}_{1}P\left(\zeta \right)+{b}_{2}{P}^{2}\left(\zeta \right)+\dots +{b}_{l}{P}^{l}\left(\zeta \right)},$$

(6)

where $P=P\left(\zeta \right)$ is the solution to the improved Bernoulli equation, ${a}_{0}$, ${a}_{1}$, ${a}_{2}$,$\dots$,${a}_{m}$ and ${b}_{0},{b}_{1},{b}_{2},\dots {b}_{l}$ are later determined coefficients. $l\ne 0$, $m\ne 0$ are arbitrary constants that can be determined through the balance principle. The general form of the improved Bernoulli equation can be presented as follows:

$${P}^{{^{\prime}}}\left(\zeta \right)=dP\left(\zeta \right)+h{P}^{L}\left(\zeta \right), \quad d\ne 0, h\ne 0, L\in R-\left\{0,\mathrm{1,2}\right\}.$$

(7)

The homogeneous balancing of the highest order linear term with the highest order nonlinear term of the Eq. (4) can be used to determine the value of the unknown parameters $l$ and $m$. This procedure yields the following $l$ and $m$ values.

Introducing solution (4) into (3) with the aid of Eq. (5), it provides an equation of polynomial $\mathcal{B}(P(\zeta ))$ of $P\left(\zeta \right)$:

$$\mathcal{B}(P\left(\zeta )\right)={\alpha }_{s}{P\left(\zeta \right)}^{s}+{\alpha }_{s-1}{P\left(\zeta \right)}^{s-1}+\dots +{\alpha }_{1}P\left(\zeta \right)+{\alpha }_{0}=0.$$

(8)

3.3 Step 3:

An algebraic system of equations can be gained by equalizing each coefficient of $\mathcal{B}(P\left(\zeta )\right)$ coefficients to zero:${\alpha }_{k}=0$, $k=0$, $\dots$, $s$.

We can attain the values of ${a}_{0}$, ${a}_{1}$,$\dots$, ${a}_{m}$ and ${b}_{0}$, ${b}_{1}$,$\dots$, ${b}_{l}$ by unraveling this system algebraic equation.

3.4 Step 4:

We obtain the ensuing two conditions and solutions to Eq. (7) based on the values of $d$ and $h$:

$$P\left(\zeta \right)={\left[-\frac{h}{d}+\frac{E}{{e}^{d\left(L-1\right)\zeta }}\right]}^{\frac{1}{1-L}}, \quad d\ne h.$$

(9)

$$P\left(\zeta \right)={\left[\frac{\left(E-1\right)+\left(E+1\right)\mathrm{tanh}\left(\frac{d\left(1-L\right)\zeta }{2}\right)}{1-\mathrm{tanh}\left(\frac{d\left(1-L\right)\zeta }{2}\right)}\right]}^{\frac{1}{1-L}}, \quad d=h,$$

(10)

where $E\in {\mathbb{R}}$, be an integrating constant.

The analytical solutions of Eq. (5) are accomplished with the aid of Maple software program and categorize the analytical solutions to Eq. (5) using a whole distinction system for polynomial of $P\left(\zeta \right)$.

4 Extraction of solutions

The objective of this module is to obtain the stable, broad-ranging, and typical soliton solutions to the space–time fractional nonlinear Schrödinger Fokas–Lenells and the fractional nonlinear paraxial Schrödinger equations using the IBSEF approach, from which some existing solutions can be re-established.

4.1 The space–time fractional nonlinear Fokas–Lenells (Wazwaz 2009) equation

Consider the complex wave transformation.

$$v\left(x,t\right)=V\left(\zeta \right){e}^{i\varphi },$$

(11)

where $\zeta =\frac{1}{\alpha }{(x+\frac{1}{\Gamma \left(\alpha \right)})}^{\alpha }-\frac{c}{\mu }{(t+\frac{1}{\Gamma \left(\mu \right)})}^{\mu }$,

and $\varphi =-\frac{k}{\alpha }{(x+\frac{1}{\Gamma \left(\alpha \right)})}^{\alpha }+\frac{\omega }{\mu }{(t+\frac{1}{\Gamma \left(\mu \right)})}^{\mu }+{\varphi }_{0}$, where $c$ is the wave velocity, $k$ be the frequency, $\omega$ be the wave number and ${\varphi }_{0}$ be the phase parameter.

The wave transformation (11) remodels Eq. (1) into a nonlinear equation and equating real and imaginary parts, we attain.

$$\left({n}_{1}-c{n}_{2}\right){V}^{{^{\prime}}{^{\prime}}}+\left({n}_{2}k\omega -{n}_{1}{k}^{2}-\omega -\beta k\right)V+\left(s+rk\right){V}^{3}-k\gamma {V}^{2n+1}=0,$$

(12)

and

$$\left(c+2{n}_{1}k+\beta -{n}_{2}\left(\omega +ck\right)-r{V}^{2}+\left(2n\gamma +\gamma +2n\delta \right){V}^{2n}\right){V}^{{^{\prime}}}=0.$$

(13)

Setting $n=1$, to Eq. (1), Eqs. (12) and (13) become (Pashayi et al. 2017):

$$i{D}_{t}^{\mu }v+{n}_{1}{D}_{xx}^{2\alpha }v+{n}_{2}{D}_{t}^{\mu }{D}_{x}^{\alpha }v+{\left|v\right|}^{2}\left(sv+ir{D}_{x}^{\alpha }v\right) = i\beta {D}_{x}^{\alpha }v+i\gamma {D}_{x}^{\alpha }\left({\left|v\right|}^{2}v\right)+iv{D}_{x}^{\alpha }{\left|v\right|}^{2}$$

(14)

$$\left(c+2{n}_{1}k+\beta -{n}_{2}\left(\omega +ck\right)+\left(3\gamma +2\delta -r\right){V}^{2}\right){V}^{{^{\prime}}}=0,$$

(15)

$$\left({n}_{1}-c{n}_{2}\right){V}^{{^{\prime}}{^{\prime}}}+\left({n}_{2}k\omega -{n}_{1}{k}^{2}-\omega -\beta k\right)V+\left(s+rk-k\gamma \right){V}^{3}=0.$$

(16)

From Eq. (15), we achieve.

$$r=3\gamma +2\delta \quad {\rm and} \quad c=\frac{\beta +2{n}_{1}k-\omega {n}_{2}}{{n}_{2}k-1},$$

(17)

since ${V}^{2}{V}{^{\prime}}\ne 0$ and ${V}{^{\prime}}\ne 0$, where ${n}_{2}k\ne 1$, $c$ be the wave velocity and $\beta$ represents a coupled constraints relation between the parameters.

Balancing between ${V}^{{^{\prime}}{^{\prime}}}$ and ${V}^{3}$ appearing in Eq. (16), we attain following relation.

$$l+L=m+1.$$

Considering $l=1$, $L=3$, it is found $m=3$.

Therefore, the trial solution of Eq. (16) can be written as.

$$V\left(\zeta \right)=\frac{{a}_{0}+{a}_{1}P\left(\zeta \right)+{a}_{2}{P}^{2}\left(\zeta \right)+{a}_{3}{P}^{3}(\zeta )}{{b}_{0}+{b}_{1}P(\zeta )},$$

(18)

where ${P}{^{\prime}}\left(\zeta \right)=dP\left(\zeta \right)+h{P}^{3}\left(\zeta \right)$, ${a}_{3}\ne 0$, ${b}_{1}$ or ${b}_{0}\ne 0$, $d\ne 0$, $h\ne 0$.

Equation (16) becomes a polynomial in $P$ when solution (18) and Eq. (7) are introduced, and a group of over-determined processes is resulted by setting each coefficient to zero. We attain the coefficient values listed below by using Maple to unravel the group of algebraic equations.

4.2 Set 1:

$$\begin{gathered}{a_0} = \pm \sqrt {\frac{{{n_1} + \beta {n_2}}}{{{n_2}r - \gamma {n_2} + sn_2^2}}} {b_0},\quad {a_1} = \pm \sqrt {\frac{{{n_1} + \beta {n_2}}}{{{n_2}r - \gamma {n_2} + sn_2^2}}} {b_1},\quad {a_2} = \pm 2\sqrt {\frac{{{n_1} + \beta {n_2}}}{{{n_2}r - \gamma {n_2} + sn_2^2}}} {b_0},\\{a_3} = \pm 2\sqrt {\frac{{{n_1} + \beta {n_2}}}{{{n_2}r - \gamma {n_2} + sn_2^2}}} {b_1},\quad k = \frac{1}{{{n_2}}},\quad c = \frac{1}{2}\frac{{2n_2^2{n_1}{d^2} + \beta {n_2} + {n_1}}}{{n_2^3{d^2}}}.\end{gathered}$$

(19)

4.3 Set 2:

$$\begin{gathered}{a_0} = \frac{1}{2}\frac{{{a_3}d{b_0}}}{{{b_1}h}},\quad {a_1} = \frac{1}{2}\frac{{{a_3}d}}{h},\quad {a_2} = \frac{{{a_3}{b_0}}}{{{b_1}}},\\k = \frac{{\left( {sa_3^2 - 8c{n_2}{h^2}b_1^2 + 8{n_1}{h^2}b_1^2} \right)}}{{a_3^2\left( { - r + \gamma } \right)}},\\\omega = \frac{{A\left( {r - \gamma } \right) - B\left( {c{n_2} - {n_1}} \right) - {n_1}{s^2}a_3^4}}{{a_3^2\left( {\gamma - r} \right)(a_3^2\left( {\gamma - r - {n_2}s) + 8{n_2}{h^2}b_1^2(c{n_2} - {n_1})} \right)}}\end{gathered}$$

(20)

where ${a}_{3}$, ${b}_{0}$ and ${b}_{1}$ are arbitrary parameters, $A=8\beta {a}_{3}^{2}{h}^{2}{b}_{1}^{2}\left({n}_{1}-c{n}_{2}\right)+\beta {a}_{3}^{4}s,$,

$$B=64{{n}_{1}h}^{4}{b}_{1}^{4}\left(c{n}_{2}-{n}_{1}\right)-16{n}_{1}s{a}_{3}^{2}{h}^{2}{b}_{1}^{2}+4{d}^{2}{a}_{3}^{4}r\gamma -2{d}^{2}{a}_{3}^{4}\left({r}^{2}+{\gamma }^{2}\right).$$

Case 1: For $d\ne h$

We attain the exponential function solution to the space–time fractional nonlinear Fokas–Lenells model by introducing the estimations of the parameters indicated in (19) into solution (18), along with (9), the solution of the improved Bernoulli equation, and transformation (11):

$$v\left(x,t\right)=\pm \sqrt{\frac{{n}_{1}+\beta {n}_{2}}{{n}_{2}(r-\gamma +s{n}_{2})}}(1+\frac{2h{e}^{d\zeta }}{-h{e}^{ d\zeta }+d{Ee}^{-d\zeta }}){e}^{i\varphi },$$

(21)

where

$$\begin{gathered}\zeta = \frac{1}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } - \frac{c}{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu }, \varphi = - \frac{k}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } + \frac{\omega }{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu } + {\varphi _0}.\end{gathered}$$

The obtained results in Eq. (17) are connected to rewrite solution (21) as:

$${v}_{1}\left(x,t\right)=\pm \sqrt{\frac{{n}_{1}+(c{n}_{2}k-c-2{n}_{1}k+\omega {n}_{2}){n}_{2}}{(2\gamma +2\delta +s{n}_{2}){n}_{2}}}(1+\frac{2h{e}^{d\zeta }}{-h{e}^{ d\zeta }+d{Ee}^{-d\zeta }}){e}^{i\varphi },$$

(22)

where

$$\begin{gathered}\zeta = \frac{1}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } - \frac{c}{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu },\\{\rm{and}} \; \varphi = - \frac{k}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } + \frac{\omega }{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu } + {\varphi _0}.\end{gathered}$$

Simplifying (22), the hyperbolic function form solution is obtained as:

$${v}_{11}\left(x,t\right)=\pm R\left(\frac{\left(h+dE\right)\mathrm{cosh}\left(d\zeta \right)+\left(h-dE\right)\mathrm{sinh}\left(d\zeta \right)}{\left(h-dE\right)\mathrm{cosh}\left(d\zeta \right)+\left(h+dE\right)\mathrm{sinh}\left(d\zeta \right)}\right){e}^{i\varphi },$$

(23)

where $R=\sqrt{\frac{{n}_{1}+\left(c{n}_{2}k-c-2{n}_{1}k+\omega {n}_{2}\right){n}_{2}}{\left(2\gamma +2\delta +s{n}_{2}\right){n}_{2}}}$, and $d$, $E$, $\omega$, ${\varphi }_{0}$ are nonzero parameters.

Since $E$ is an subjective constraint, we can choose its values intuitively in terms of $d$ and $h$, the coefficients of the improved Bernoulli equation, to attain further simple form solutions. This is explained in detail below:

We attain from solution (23) for $E=h/12d,$

$${v}_{12}\left(x,t\right)=\pm R \left(\frac{13\mathrm{cosh}\left(d\zeta \right)+11\mathrm{sinh}\left(d\zeta \right)}{11\mathrm{cosh}\left(d\zeta \right)+13\mathrm{sinh}\left(d\zeta \right)}\right){ e}^{i\varphi },$$

(24)

In particular, we perceive the subsequent form of the solution (23) for $E=-h/d$,

$${v}_{13}\left(x,t\right)=\pm R\mathrm{ tanh}\left(d\zeta \right){e}^{i\varphi }.$$

(25)

For $E=h/d$, we attain the subsequent form of the solution (23).

$${v}_{14}\left(x,t\right)=\pm R\mathrm{ coth}(d\zeta ){e}^{i\varphi }.$$

(26)

Other relevant solutions can be obtained from the same general solution (23) by modifying the values of the parameter $E$, however such solutions are not stated for brevity.

Case 2: For $d=h$

Assigning the values of the parameters listed in (19) to solution (18) along with (10), the solution of the modified Bernoulli equation, we obtain the ensuing exponential function solution to the space–time fractional nonlinear Fokas–Lenells model.

$${v}_{2}\left(x,t\right)=\pm \sqrt{\frac{{n}_{1}+\beta {n}_{2}}{{n}_{2}(r-\gamma +s{n}_{2})}}(\frac{\left(E-1\right)\mathrm{tanh}\left(\mathrm{d\zeta }\right)-(E+1)}{\left(E+1\right)\mathrm{tanh}\left(\mathrm{d\zeta }\right)-(E-1)}){e}^{i\varphi },$$

(27)

Solution (27) can be presented as follows using Eq. (17):

$${v}_{21}\left(x,t\right)=\pm \sqrt{\frac{{n}_{1}+\left(c{n}_{2}k-c-2{n}_{1}k+\omega {n}_{2}\right){n}_{2}}{\left(2\gamma +2\delta +s{n}_{2}\right){n}_{2}}}(\frac{\left(E-1\right)\mathrm{tanh}\left(d\zeta \right)-(E+1)}{\left(E+1\right)\mathrm{tanh}\left(d\zeta \right)-(E-1)}){e}^{i\varphi },$$

(28)

where

$$\begin{gathered}\zeta = \frac{1}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } - \frac{{\rm{c}}}{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu },\\{\rm{and}}\\\varphi = - \frac{k}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } + \frac{\omega }{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu } + {\varphi _0}.\end{gathered}$$

We can choose further values of $E$, since $E$ is an integrating constant.

For $E=\sqrt{13}$, we found from solution (28).

$${v}_{22}\left(x,t\right)=\pm \sqrt{\frac{{n}_{1}+\left(c{n}_{2}k-c-2{n}_{1}k+\omega {n}_{2}\right){n}_{2}}{\left(2\gamma +2\delta +s{n}_{2}\right){n}_{2}}}\left(\frac{\left(\sqrt{3}-1\right)\mathrm{tanh}\left(d\zeta \right)-\left(\sqrt{3}+1\right)}{\left(\sqrt{3}+1\right)\mathrm{tanh}\left(d\zeta \right)-\left(\sqrt{3}-1\right)}\right){e}^{i\varphi }.$$

(29)

Changing arbitrarily the value of the free parameter $E$, we might establish a broad-spectrum soliton solution to the fractional nonlinear Fokas–Lenells model. For the sake of conciseness, only a few solutions are recorded.

It can be derived further analytical wave solutions by interleaving the coefficients sorted out in set (2) into solution (18), along with the solutions (9) and (10). For $d\ne h$, we attain the exponential function solution to the space–time fractional nonlinear Schrödinger FL equation by including the values of the parameters mentioned in (20) into solution (18), and (9), the estimation of the modified Bernoulli equation as follow:

$${v}_{3}\left(x,t\right)=\frac{{a}_{3}d}{{b}_{1}h} \left(\frac{1}{2}+\frac{\mathrm{h}{e}^{d\zeta }}{-\mathrm{h}{e}^{d\zeta }+{\mathrm{dEe}}^{-\mathrm{d}\zeta }}\right) {e}^{i\varphi },$$

(30)

where

$$\begin{gathered}\zeta = \frac{1}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } - \frac{c}{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu }, \varphi = - \frac{k}{\alpha }{(x + \frac{1}{{\Gamma \left( \alpha \right)}})^\alpha } + \frac{\omega }{\mu }{(t + \frac{1}{{\Gamma \left( \mu \right)}})^\mu } + {\varphi _0}.\end{gathered}$$

Diverse typical wave solutions can be originated from the general solution for specific values of the parameters, but these solutions are not specified here for terseness.

4.4 The space–time fractional nonlinear paraxial Schrödinger (Wazwaz 2009) equation

Consider the wave transformation.

$$v\left(y,z,t\right)=V\left(\zeta \right){e}^{ik\zeta },$$

(31)

where

$$\zeta =\frac{1}{\alpha }{\left(y+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }+\frac{1}{\alpha }{\left(z+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }-\frac{\omega }{\mu }{\left(t+\frac{1}{\Gamma \left(\mu \right)}\right)}^{\mu }.$$

Wave variable (31) remodels Eq. (2) into a single variable nonlinear equation and separating real and imaginary parts, we found.

$$\left(a{\omega }^{2}+b\right){V}{^{\prime\prime} }-\left(2k+a{k}^{2}{\omega }^{2}+b{k}^{2}\right)V+2c{V}^{3}=0,$$

(32)

$$\left(1+bk+ak{\omega }^{2}\right){V}^{{^{\prime}}}=0.$$

(33)

Since

$$V{^{\prime}}\ne 0 , \quad {\rm therefore}, \quad b=\frac{-1-ak{\omega }^{2}}{k}.$$

(34)

Inserting the value of $b$ into (32) and after some simple calculation, we obtain.

$${V}{^{\prime\prime} }+{k}^{2}V-2ck{V}^{3}=0,$$

(35)

Balancing between ${V}{^{\prime\prime} }$ and ${V}^{3}$, we obtain the relationship among $l$, $L$ and $M$ as follows:

$$l+L=m+1.$$

(36)

Choosing $l=1$, $L=4$, we obtain $m=4$.

The solution to the Eq. (35) can be presented as,

$$V\left(\zeta \right)=\frac{{a}_{0}+{a}_{1}P\left(\zeta \right)+{a}_{2}{P}^{2}\left(\zeta \right)+{a}_{3}{P}^{3}\left(\zeta \right)+{a}_{4}{P}^{4}(\zeta )}{{b}_{0}+{b}_{1}P(\zeta )},$$

(37)

where ${P}{^{\prime}}\left(\zeta \right)=dP\left(\zeta \right)+h{P}^{4}\left(\zeta \right)$, ${a}_{4}\ne 0$, ${b}_{1}$ or ${b}_{0}\ne 0$, $d\ne 0$, $h\ne 0$.

Introducing solution (37) and (7) into Eq. (35) generates a polynomial in $P$, and setting each coefficient to zero yields an over-determined group of equations. We determine the subsequent values of the coefficients by unraveling the algebraic group of equations with the help of Maple:

$$\begin{gathered}{a_0} = \pm \frac{{{2^{1/4}}\sqrt 3 }}{2}\sqrt {d/s} {b_0},\quad {a_1} = \pm \frac{{{2^{1/4}}\sqrt 3 }}{2}\sqrt {d/s} {b_1},\quad {a_2} = 0,\\{a_3} = \pm \frac{{{2^{1/4}}\sqrt 3 }}{{\sqrt {ds} }}h{b_0},\quad {a_4} = \pm \frac{{{2^{1/4}}\sqrt 3 }}{{\sqrt {ds} }}h{b_1},\quad k = \frac{{3d}}{{\sqrt 2 }},\end{gathered}$$

(38)

where ${b}_{0}$ and ${b}_{1}$ are arbitrary parameters.

Case 1: For $d\ne h$

Interleaving the values of the parameters accumulated in (38) and (9), the solution of the modified Bernoulli equation into solution (37), the exponential function solution to the space–time fractional nonlinear paraxial Schrödinger equation in Kerr media is attained as follows:

$$v\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\left\{\frac{h{e}^{\frac{3}{2}d\zeta }+dE{e}^{-\frac{3}{2}d\zeta }}{-h{e}^{\frac{3}{2}d\zeta }+dE{e}^{-\frac{3}{2}d\zeta }}\right\} {e}^{ik\zeta },$$

(39)

where

$$\zeta =\frac{1}{\alpha }{\left(y+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }+\frac{1}{\alpha }{\left(z+\frac{1}{\Gamma \left(\alpha \right)}\right)}^{\alpha }-\frac{\omega }{\mu }{\left(t+\frac{1}{\Gamma \left(\mu \right)}\right)}^{\mu }.$$

After simplifying solution (39), the hyperbolic function form of solution is attained as.

$${v}_{1}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\left\{\frac{\left(dE+h\right)\mathrm{cosh}\left(\frac{3}{2}d\zeta \right)-(dE-h)\mathrm{sinh}\left(\frac{3}{2}d\zeta \right)}{\left(dE-h\right)\mathrm{cosh}\left(\frac{3}{2}d\zeta \right)-(dE+h)\mathrm{sinh}\left(\frac{3}{2}d\zeta \right)}\right\} {e}^{ik\zeta },$$

(40)

where $E$, $d$, $s$ and $h$ are nonzero parameters.

Inasmuch as $E$ is an integral constant, one can pick out its value arbitrarily. Therefore, when $E=4h/d$, from the solution (46), we attain.

$${v}_{11}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\left\{\frac{5\mathrm{cosh}\left(\frac{3}{2}d\zeta \right)-3\mathrm{sinh}\left(\frac{3}{2}d\zeta \right)}{3\mathrm{cosh}\left(\frac{3}{2}d\zeta \right)-5\mathrm{sinh}\left(\frac{3}{2}d\zeta \right)}\right\}{e}^{ik\zeta }.$$

(41)

Particularly, the solution (40) takes the subsequent form for $E=-h/d$,

$${v}_{12}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\mathrm{tanh}\left(\frac{3}{2}d\zeta \right){e}^{ik\zeta }.$$

(42)

When $E=h/d$, from solution (46), we extract.

$${v}_{13}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\mathrm{coth}\left(\frac{3}{2}d\zeta \right){e}^{ik\zeta }.$$

(43)

Other forms of relevant solutions can be obtained by changing the values of the parameter $E$ from the same general solution (40) but, for the sake of conciseness, these solutions are not presented.

Case 2: For $d=h$

By combining the values of the parameters stated in (38) into solution (37), and (10), the solution of the improved Bernoulli equation, the hyperbolic function solution of Eq. (2) is originated as.

$${v}_{2}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\{\frac{\left(E+1\right)-\left(E-1\right)\mathrm{ tanh}\left(\frac{3}{2}d\zeta \right)}{\left(E-1\right)-\left(E+1\right)\mathrm{tanh}\left(\frac{3}{2}d\zeta \right)}\} {e}^{ik\zeta },$$

(44)

where

$$\zeta =\frac{1}{\alpha }{(y+\frac{1}{\Gamma \left(\alpha \right)})}^{\alpha }+\frac{1}{\alpha }{(z+\frac{1}{\Gamma \left(\alpha \right)})}^{\alpha }-\frac{\omega }{\mu }{(t+\frac{1}{\Gamma \left(\mu \right)})}^{\mu }.$$

We can randomly choose the values of $E$ as it is an integrating constant. Therefore, we gained from solution (44) for $E=\sqrt{13}$,

$${v}_{21}\left(y,z,t\right)=\pm \frac{{2}^{1/4}\sqrt{3}}{2}\sqrt{d/s}\{\frac{\left(\sqrt{13}+1\right)-\left(\sqrt{13}-1\right)\mathrm{ tanh}\left(\frac{3}{2}d\zeta \right)}{\left(\sqrt{13}-1\right)-\left(\sqrt{13}+1\right)\mathrm{tanh}\left(\frac{3}{2}d\zeta \right)}\} {e}^{ik\zeta }.$$

(45)

Other sorts of solutions to Eq. (2) can be obtained by arbitrarily picking different values of the arbitrary parameter $E$. But, for simplicity, only a few are displayed.

5 Comparison of the results

We compare the results of the space–time fractional nonlinear Fokas–Lenells (FL) and paraxial Schrödinger equations obtained in this study using the IBSEF approach with the solutions reachable in the existing literature to show the novelty of the established solutions. We compare the obtained results of the space–time fractional nonlinear FL equation in Table 1 to those of Bulut et al. (2018) solutions and the solutions of the space–time fractional paraxial Schrödinger equation with the solutions attained by Gao et al. (Gao et al. 2019) in Table 2. It is observed that some of the achieved results are similar to the results developed previously by other methods and some solutions are fresh.

Table 1 Comparison of the obtained solutions to the space–time fractional nonlinear FL equation with the solutions found by Bulut et al. in (Bulut et al. 2018)

Table 2 Comparison of the obtained solutions to the space–time fractional paraxial Schrödinger equation with the solutions found Gao et al. (2019)

It is noteworthy to observe that the attained solutions ${v}_{13}\left(x,t\right)$, ${v}_{14}\left(x,t\right)$ and ${v}_{12}\left(x,t\right)$ of the space–time fractional FL equation are similar to some solutions of Bulut et al. (2018) for definite values of arbitrary constants, whereas the other solutions, ${v}_{1}\left(x,t\right)$, ${v}_{11}\left(x,t\right)$, ${v}_{2}\left(x,t\right)$, ${v}_{21}\left(x,t\right)$ and ${v}_{3}\left(x,t\right)$ are new and might be significant to analyze the tangible phenomena.

From the above Table 2, we see that the obtained solutions ${v}_{12}\left(y,z,t\right)$ and ${v}_{13}\left(y,z,t\right)$ of the space–time fractional paraxial Schrödinger equation are similar to some solutions of Gao et al. (2019) But, the soliton solutions ${v}_{1}\left(y,z,t\right)$, ${v}_{11}\left(y,z,t\right)$, ${v}_{2}\left(y,z,t\right)$ and ${v}_{21}\left(y,z,t\right)$, of the space–time fractional paraxial Schrödinger equation are not found in the prior literature. The achieved solutions might be useful in nonlinear optics, signal processing, control theory, plasma physics, image processing, system identification, etc.

6 Results and discussion

Using the symbolic computation tool Mathematica, the characteristic of the obtained analytical solutions for different parametric values have been explored and illustrated through the graphics in this section.

6.1 The sketch and explanation of the solutions to the fractional nonlinear FL equation

This section discusses the graphical representations of the derived solutions to the fractional nonlinear Fokas–Lenells equation for various parametric variables. There are two components to the solutions that have been found: real and imaginary parts.

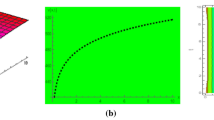
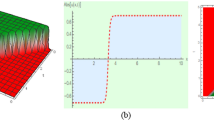
The 3D graph in Fig. 1a depicts the kink shape soliton attained for the absolute component of the solution (22) for the parametric values${n}_{1}=-4.55$,${n}_{2}=-1.2$,$d=8.25$,$h=-3.5$,$E=10$,$\delta =-6.05$,$\gamma =-1.5$,$k=-5.1$,$s=-1.4$,$\omega =-1.7$,$\alpha =0.6$, $\mu =0.9$ with wave velocity $c=0.7$ between the intervals$0\le x\le 10$,$0\le t\le 10$; the 2D plot for t = 5.5 is presented in Fig. 1b, and the contour graph in Fig. 1c. Kink solitons are solitons that change asymptotic states. Kink waves are further stable as they get closer to infinity (Hashemi and Baleanu 2020). The kink soliton, in the concept of optical fibers, is an optical shock front that maintains its form while propagating through the fiber (Atangana et al. 2016). Furthermore, by only altering the value of $h$ from $-3.5$ to$0.1$, the singular kink type soliton is generated for the modulus of same solution (22) as shown in Fig. 2. Furthermore, when$E=-10$, this singular soliton may be shown. We ignore it for brevity. The real part of the solution (22) illustrates the periodic bell shape soliton with distinct amplitudes for the values${n}_{1}=-0.41$,${n}_{2}=-0.61$,$d=-0.52$,$h=-0.305$,$\alpha =0.57$,$\mu =0.55$,$e=-2$,$\gamma =-2$,$\delta =-2$,$k=-2$,$s=-2$,$\omega =2$, ${\phi }_{0}=-2$ with wave velocity $c=-2$ throughout the intervals$0\le x\le 10$, $0\le t\le 10$ as shown in the 3D graph in Fig. 3a; the 2D graph for $t=6$ is given in Fig. 3b and the contour graph in Fig. 3c. The 3D, 2D, and contour plots of the real portion of the solution (22) are displayed the periodic soliton with small wavelength or large frequency, shown in Fig. 4 for the fractional order $\alpha =0.99$ and$\mu =0.99$, assuming other parameters remain unchanged. It is compatible with the classical solution i.e.; the fractional form solution is converted to the classical form solution (Zafar et al. 2021a). Assuming that others are the same, the breathing type soliton for $c=1.2$ of the real part of solution (22) is constructed, and shown in Fig. 5. The imaginary part of the solution (22) illustrates the parabolic soliton (Hashemi and Baleanu 2020) for${n}_{1}=2.16$,${n}_{2}=-3.72$,$d=-3.24$,$h=3$, E$=-2.24$,$\gamma =-2.24$,$\delta =-2.24$,$k=0.05$,$s=-1.7$,$\omega =\text{.83}$,${\phi }_{0}=-4.49$,$\alpha =0.67$, $\mu =0.61$ with travelling wave velocity $c=-0.2$ within the same intervals as shown in Fig. 6. Further, Fig. 6b: 2D plot is attained for$t=3.25$. The periodic type soliton is illustrated for$c=1.31$, $\mu =0.9$ and $\alpha =0.9$ of the imaginary part of solution (22) as presented in Fig. 7. By increasing the value of frequency k, we get multi-periodic soliton of the imaginary part of the solution (22) that is not presented here for brevity. In particular, Fig. 8 depicts the singular periodic soliton formed by the real part of the solution (24) for${n}_{1}=-0.41$,${n}_{2}=-0.61$,$d=-0.52$,$\alpha =0.8$,$\mu =0.79,$

Fig. 1

Graph displaying the solution (22)'s absolute part

Fig. 2

Graph presenting the solution (22)'s absolute part

Fig. 3

Graph displaying the solution (22)'s real part

Fig. 4

Graph displaying the solution (22)'s real part

Fig. 5

Graph displaying the solution (22)'s real part

Fig. 6

Graph displaying the solution (22)'s imaginary part

Fig. 7

Graph displaying the solution (22)'s imaginary part

Fig. 8

Graph portraying the solution (24)'s real part

Fig. 9

Graph displaying the solution (24)'s imaginary part

Fig. 10

Graph displaying the solution (28)'s real part

Fig. 11

Graph displaying the solution (28)'s imaginary part

Fig. 12

Graph displaying the solution (30)'s absolute part

Fig. 13

Graph displaying the solution (30)'s absolute part

Fig. 14

Graph displaying the solution (30)'s absolute part

Fig. 15

Graph displaying the solution (30)'s real part

Fig. 16

Graph displaying the solution (30)'s real part

Fig. 17

Graph displaying the solution (30)'s imaginary part

For the sake of brevity and to avoid the duplication of analogous solitons, other derived solutions to this equation generate identical solitons for varying values of the free parameters, which are not displayed. The soliton changes form primarily depends on the values of fractional order, phase shift, wave number, and velocity as shown in the previous illustration of the soliton profiles. The other coefficients of this solution to the equation have no effect on the wave's speed in this case, but the Bernoulli parameters $d$ and $h$, as well as the integrating constants, often do (Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17).

6.2 The sketch and explanation of the solutions to the fractional paraxial Schrödinger equation

The graphical representations of the instigated solutions to the fractional nonlinear paraxial Schrödinger equation for various parametric variables are discussed in this section. Real and imagined parts combine with the solutions that have been established.

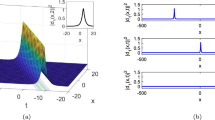
The modulus of the solution (39) represents the kink type soliton for $\omega =1.4$, $E=-5$, $d=-0.28$, $h=-5$, $z=1$, $s=-0.28$, $\alpha =0.85$, $\mu =0.85$ within intervals $0\le y\le 10$, $0\le t\le 10$ and displayed in Fig. 18. Also, 18b: 2D plot is portrayed for $t=3.45$. By varying the values of $\omega$, various kink shape soliton could be drawn and by altering the values of $E$, several singular shape solitons can be illustrated. For brevity, the figure is not illustrated. The periodic soliton is depicted of the real part of the solution (39) for $E=-3.59$, $d=-0.46$, $h=-\text{.8}$, $z=1$, $s=-0.28$, $\alpha =0.775$, $\mu =0.775$ $k=-2$ with travelling wave velocity $\omega =-1.18$ throughout the intervals $0\le y\le 10$, $0\le t\le 10$ and shown in Fig. 19. Further, 19b: 2D graph is displayed for $t=3.45$. Simply, increasing the value of the travelling wave velocity $\omega$ from $-1.18$ to $-0.26$, the periodic soliton is attained of the real part of (39) shown in Fig. 20, others shapes are same as Fig. 19. Figure 21 represents periodic soliton with large frequency of the real part of the solution (39) for $\omega =1.5$ preserving the monotony of others. The compacton like soliton is illustrated of the imaginary part of the solution (39) for $k=-\text{.62}$ preserving the sameness of others as Fig. 19 as depicted in Fig. 22. Further, the 2D plot is displayed for $t=5.02$. The compacton soliton for $k=0.14$ and the periodic bell shape soliton for $k=1.5$ is depicted of the imaginary part of the solution (39) respectively as portrayed in Figs. 23 and 24.The 2D graph is attained at $t=3.45$ as shown in Figs. 23b and 24b respectively.

Fig. 18

Graph displaying the solution (45)'s absolute part

Fig. 19

Graph displaying the solution (45)'s real part

Fig. 20

Graph displaying the solution (45)'s real part

Fig. 21

Graph displaying the solution (45)'s real part

Fig. 22

Graph displaying the solution (45)'s imaginary part

Fig. 23

Graph displaying the solution (45)'s imaginary part

Fig. 24

Graph displaying the solution (45)'s imaginary part

Other resulting solutions to this equation produce similar solitons for varied values of the free parameters, which have been omitted strategically. As demonstrated in the preceding representation of the soliton profiles, the values of fractional order, phase shift, and wave velocity influence how the soliton changes form. In this context, the remaining coefficients in this equation's solution have no influence on the waves speed, but the Bernoulli coefficients $d$ and $h$, as well as $E$ contribute.

7 Conclusions

In this article, the optical soliton solutions to the space–time fractional nonlinear Fokas–Lenells and the space–time fractional Schrödinger equations, which are of interest to physicists, mathematicians, and engineers, have been successfully originated through the IBSEF approach. The Bernoulli equation of order 3 and 4 has effectively been exploited for the considered models. The portrayal of the solutions comprises the anti-kink, kink, singular-periodic, periodic, breather, singular kink type soliton, dark-bright soliton, and some other distinctive solitons that may be used in research on nonlinear optics, plasmas, photonics, condensed matter physics, etc. We have instigated Maple software package to compute the related computational operations and Wolfram Mathematica has been used to portray the 2D, density or contour and 3D surfaces. All the solutions obtained in this article for suitable parameter values are useful to characterize the physical characteristics of the phenomena. This research demonstrates that the IBSEF approach is effective, straightforward, and rationally capable and can be used to establish optical soliton solutions to other fractional nonlinear Schrödinger type equations in optics, quantum physics, and engineering.