1 Introduction

Researchers are constantly exploring the various phenomena that occur in nature in the language of mathematics called mathematical models by successfully presenting a well-thought-out research plan. Among these, scholars have preferred the nonlinear partial differential equation as an important means of expressing the most widely accepted. In that context, scientists have been solving the problems by explaining those mathematical models through various methods (Kudryashov 2019; Khan and Akbar 2013a, 2013b; Barman et al. 2021; Abdelrahman et al. 2015; Islam et al. 2021a, 2020; Hosseini et al. 2020, 2019; Mirzazadeh et al. 2015; Yokus et al. 2018; Zhang et al. 2020; Baskonus et al. 2019; Yépez-Martíneza et al. 2018; Islam and Akbar 2020a; Iqbal et al. 2020; Helal et al. 2014; Kundu et al. 2021; Chu et al. 2021; Khater et al. 2019; Li et al. 2019; Kumar et al. 2021; Ding et al. 2019; Chen et al. 2021; Raza et al. 2020; Osman and Ali 2020; Malik et al. 2021; Tahir et al. 2021; Kayum et al. 2021; Ali et al. 2020; Osman 2017) have been exposed to solve the mathematical problems, the solutions from each schemes of which have given various solutions and research on these is ongoing. Among the above methods, very detailed results are found in these two methods namely, improved Bernoulli sub-equation function (IBSEF) method (Islam and Akbar 2020b; Islam et al. 2021b) and the new auxiliary equation (NAE) method (Akbar et al. 2019) which can be enriched further by conducting this study.

In today's human evolution, communication, on the other hand, plays an essential role. The invention and development of amplifiers erbium-doped fiber (Agrawa 1989) and optical directional couplers generate the revolution in telecommunications fiber. This new-fangled all-optical equipment, which associates the norm of issue inspired in erbium with the controlling assets of the fiber, allows, without the conversion steps optical-electronic and electronic-optical growth rates of transmission (Chiang 1992). The fiber can be an optical amplifier, an optical switch converter wavelength, solitons in a source, a compressor noise, an optical memory etc. Breeding in a directional coupler is modeled by the system of equation of coupled nonlinear Schrödinger equation (NLSE) (Agrawal 2001) and the dual-core optical fibers equation (Younis et al. 2015; Abdelrahman and Moaaz 2020; Nair et al. 2018; Baskonus et al. 2018; Shamseldeen et al. 2017) is one of them. As per our knowledge, few researchers has been studied the dual-core optical fibers equation via different schemes namely, Younis et al. (Younis et al. 2015) through the \((G^{\prime}/G)\)-expansion method, Abdelrahman and Moaaz (Abdelrahman and Moaaz 2020) used Riccati-Bernoulli sub-ODE method, Nair et al. (Nair et al. 2018) via modulational instability (MI) analysis, Baskonus et al. (Baskonus et al. 2018) via the extended sinh-Gordon equation expansion method, Shamseldeen et al. (Shamseldeen et al. 2017) via linear stability analysis. The IBSEF and NAE approaches, however, have not been implemented to investigate the stated equation. Therefore, the objective of this study is to establish wide-ranging and adequate definitive soliton solutions to the dual-core optical fibers equation through setting in use the suggested methods. Besides, we analyze the various types of soliton like solutions for the different value free parameters of the obtained solutions illustrated in 3D plot via Matlab and marked out the significant role of the value of wave number and velocity of the solutions to changing the nature of the soliton in wave profile.

2 Description of two proposed methods

This section introduces and analyzes the improved Bernoulli sub-equation function method and the new auxiliary equation method in details.

2.1 The IBSEF method

In order to illustrate the IBSEF method, we take into consideration the NLEE associated with two independent variables \(x\) and \(t\) of the form.

$$R\left( {u,\frac{\partial u}{{\partial t}},{ }\frac{\partial u}{{\partial x}},{ }\frac{{\partial^{2} u}}{\partial x\partial t},\frac{{\partial^{2} u}}{{\partial t^{2} }},{ }\frac{{\partial^{2} u}}{{\partial x^{2} }}, \ldots } \right) = 0,$$
(2.1.1)

wherein \(u=u(x,t)\) is the number of waves, \(R\) is a polynomial of the variable \(u\) and \(\frac{\partial u}{\partial x},\frac{\partial u}{\partial t},\dots\) be the partial derivatives with respect to \(t,x,\dots\) etc.

Under the travelling wave variable

$$u\left( {x,t} \right) = u\left( \eta \right),\;\eta = \alpha x - ct,$$
(2.1.2)

wherein \(\alpha\) is the wave number and \(c\) is the vector speed of the soliton, by the action of the wave variable (2.1.2), the NLEE (2.1.1) reduces to the subsequent nonlinear differential equation.

$$T\left( {u, \frac{du}{{d\eta }}, \frac{{d^{2} u}}{{d\eta^{2} }}, \ldots } \right) = 0,$$
(2.1.3)

wherein \(T\) is a polynomial of the variable \(u(\eta )\) and its derivatives. In accordance with the improved Bernoulli sub-equation function method, the solution of Eq. (2.1.3) can be formulated as.

$$u\left( \eta \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{n} p_{i} H^{i} }}{{\mathop \sum \nolimits_{j = 0}^{m} q_{j} H^{j} }} = \frac{{p_{0} + p_{1} H + p_{2} H^{2} + { } \cdots + p_{n} H^{n} }}{{q_{0} + q_{1} H + q_{2} H^{2} + q_{3} H^{3} + { } \cdots + q_{m} H^{m} }},$$
(2.1.4)

where \(H=H(\eta )\) satisfies the improved Bernoulli equation.

$$H^{\prime} = \alpha H + \beta H^{P} ,\;\alpha \ne 0,\;\beta \ne 0,\;P \in {\mathbb{R}} - \left\{ {0,1,2} \right\}$$
(2.1.5)

The value of \(m\) and \(n\) of the undefined parameters can be determined by considering the balancing principle of the highest order linear term with the maximum order nonlinear term. This technique provides the values of \(m,n\) and \(P\). Introducing solution (2.1.4) along with the improved Bernoulli equation into Eq. (2.1.3) yields a polynomial equation \(\Omega \left(H\right)\) of \(H:\)

$${\Omega }\left( H \right) = \sigma_{s} H^{s} + { } \cdots + \sigma_{1} H + \sigma_{0} = 0.$$
(2.1.6)

Equalizing the coefficients of \(\Omega (\mathrm{H})\) to zero provides a system of algebraic equations:

$$\sigma_{k} = 0,\;k = 0, \ldots s$$
(2.1.7)

With Mathematica software, we can solve the system of algebraic equations to determine the values of \({p}_{0},{p}_{1},\dots ,{p}_{n}\) and \({q}_{0},{q}_{1},\dots ,{q}_{m}\). The solutions of the improved nonlinear Bernoulli equation depend on the values of the parameters \(\alpha\) and \(\beta\). The two types of solutions of the improved Bernoulli’s equation are as follows:

$$H\left( \eta \right) = \left\{ { - \frac{\beta }{\alpha } + \frac{\tau }{{e^{{\alpha \left( {P - 1} \right)\eta { }}} }}} \right\}^{{\frac{1}{1 - P}}} ,\;\alpha \ne \beta ,$$
(2.1.8)
$$H\left( \eta \right) = \left\{ {\frac{{\left( {\tau - 1} \right) + \left( {\tau + 1} \right)\tanh \left( {\frac{{\alpha \left( {1 - P} \right)\eta }}{2}} \right)}}{{1 - \tanh \left( {\frac{{\alpha \left( {1 - P} \right)\eta }}{2}} \right)}}} \right\}^{{\frac{1}{1 - P}}} ,\;\alpha = \beta ,\;\tau \in {\mathbb{R}}.$$
(2.1.9)

Thus, embedding the values of the parameters \({p}_{i}(i=0, 1, 2, \dots , n)\), \({q}_{j} (j=0, 1, 2, \dots , m)\) and the solutions of the improved Bernoulli Eq. (2.1.5) together with wave variable, further general and some acknowledged solutions accessible in the literature for the definite values of the subjective parameters to the nonlinear evolution Eq. (2.1.1) can be ascertained.

2.2 The new auxiliary equation method

Consider the nonlinear evolution equation.

$${\mathcal{L}}\left( {q,q_{t} ,q_{x} ,q_{y} ,q_{z} ,q_{xx} , \ldots \ldots \ldots } \right) = 0,$$
(2.2.1)

where \(\mathcal{L}\) is a function of \(q(x,y,z,t)\) which is a wave function.

  • Step 1 To format into nonlinear differential equation of NLEE (2.2.1), we need to choose a wave variable as

    $$q\left( {x,y,z,t} \right) = Q\left( \tau \right),\;\tau = \alpha x + \beta y + \gamma z - \delta t$$
    (2.2.2)

    and the transformed nonlinear ODE is

    $${\mathcal{M}}\left( {Q,Q^{\prime},Q^{\prime\prime},Q^{\prime\prime\prime}, \ldots } \right) = 0$$
    (2.2.3)

    wherein prime means for the derivative with respect to \(\tau\).

  • Step 2 In harmony with the new auxiliary equation method, the exact soliton solution of Eq. (2.2.3) is guessed to be

    $$Q\left( \mu \right) = \mathop \sum \limits_{k = 0}^{L} S_{k} a^{kg\left( \tau \right)}$$
    (2.2.4)

    Here \({S}_{0},{S}_{1},{S}_{2},\dots ,{S}_{L}\) are unknown parameter to be calculated wherein \({S}_{L}\ne 0\) and \(g(\tau )\) is the solution of the nonlinear equation.

    $$g^{\prime}\left( \tau \right) = \frac{1}{\ln a}\left\{ {pa^{ - g\left( \tau \right)} + q + ra^{g\left( \tau \right)} } \right\}$$
    (2.2.5)

  • Step 3 The balancing principle need to apply to find the value of positive integer \(L\) in Eq. (2.2.4).

  • Step 4 Eq. (2.2.3) provides a polynomial of \({a}^{kg\left(\tau \right)}\), \(\{k=\mathrm{0,1},2,\dots \}\) by substituting the solution (2.2.4) together with (2.2.5). Furthermore, we attain a system of algebraic equation by conveying each coefficient of the resulting polynomials to zero.

    The values of \({S}_{k},p,q,r\) obtained from step 4 and evoke the solution \(g(\tau )\) which attained in (2.2.5) making use various cases in details (Chen et al. 2021) into Eq. (2.2.4) provides ample soliton solution to the evolution Eq. (2.2.1).

3 Soliton solutions analysis

In this part, we have established the standard and broad-ranging explicit soliton solution through above stated methods of the dual core optical fiber equations which is of the following form:

$$\begin{array}{*{20}c} {p\phi_{tt} + i\left( {\phi_{x} + q\psi_{t} } \right) + r\left| \phi \right|^{2} \phi + s\psi = 0,} \\ {p\psi_{tt} + i\left( {\psi_{x} + q\phi_{t} } \right) + r\left| \psi \right|^{2} \psi + s\phi = 0} \\ \end{array}$$
(3.1)

where \(p,q,r,s\) are free constants.

Based on the linear stability analysis (Baskonus et al. 2018), we attaining the traveling wave velocity for non-oscillatory soliton-form solutions. Let us consider.

$$\phi \to \overline{\phi } \left( {z,t} \right),$$
$$\psi \to \overline{\psi }\left( {z,t} \right),$$

where \(\left(z,t\right)=(x-lt,t)\) is the travelling wave coordinates and \(l\) is the vector speed. Therefore, the Eqs. (3.1) tends to its homogenous steady state appears as \(\phi ,\psi \to 0\). The partial derivatives for traveling wave coordinates are:

$$\frac{\delta }{\delta x}\to \frac{\delta }{\delta z}$$
$$\frac{\delta }{\delta t} \to \frac{\delta }{\delta t} - l\frac{\delta }{\delta z},$$

then the system (3.1) is linearized near its steady state in the coordinates and performs as.

$$\omega \left( {\overline{\phi },\overline{\psi }} \right) = 0,$$
$$\omega \left( {\overline{\psi },\overline{\phi }} \right) = 0,$$

where \(\overline{\phi }\) and \(\overline{\psi }\) are the perturbation of \(\phi\) and \(\psi\) close the stable state and.

$$\omega \left( {K_{1} ,K_{2} } \right) = p\left( {\frac{\delta }{\delta t} - l\frac{\delta }{\delta z}} \right)^{2} K_{1} + i\left( {\frac{\delta }{\delta z}K_{1} + q\left( {\frac{\delta }{\delta t} - l\frac{\delta }{\delta z}} \right)K_{2} } \right) + \delta K_{2}$$

Choosing the Fourier form of the modifying traveling wave perturbation be \(\overline{\phi }=\overline{\psi }=\epsilon {e}^{(\xi z-i\mu t)}\), where \(\xi\) is complex parameter \(\mu\) is real modulating frequency constant and \(\epsilon \ll 1\) and the characteristic equation is of the form.

$$pl^{2} \xi^{2} + i\left( {1 - ql + 2pl\mu } \right)\xi + s + q\mu - p\mu^{2} = 0$$

If we consider \(1-ql+2pl\mu =0\), the eigenvalues of \(\xi\) are only real. Consequently, system (3.1) supports a soliton like solutions with a velocity \({l}_{p}=1/(q-2p\mu )\) is the transition speed.

To convert the Eq. (3.1) into nonlinear differential equation, the wave transformation is used as follow

$$\begin{array}{*{20}c} {\phi \left( {x,t} \right) = u\left( \eta \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,} \\ {\psi \left( {x,t} \right) = v\left( \eta \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,} \\ \end{array}$$
(3.2)
$${\text{Where}}\;\eta = \gamma x - \delta t$$
(3.3)

For real parameters \({\sigma }_{1},{\sigma }_{2},\gamma ,\delta\). By replacing (3.2) into system (3.1) gives

$$\begin{array}{c}\theta \left(u\left(\eta \right),v\left(\eta \right)\right)=0,\\ \theta \left(v\left(\eta \right),u\left(\eta \right)\right)=0,\end{array}$$
(3.4)

where

$$\theta \left( {K_{1} ,K_{2} } \right) = p\delta ^{2} K_{1}^{{''}} + i\left( {\gamma + 2p\delta \sigma _{2} } \right)K_{1}^{'} - iq\delta K_{2}^{'} + rK_{1}^{3} - \left( {\sigma _{1} + p\sigma _{2}^{2} } \right)K_{1} + \left( {s + q\sigma _{2} } \right)K_{2}$$

By setting the complex parts in system (3.4) to zero, we attain

$$\begin{array}{*{20}c} {\left( {\gamma + 2p\delta \sigma _{2} } \right)u^{\prime} - q\delta v' = 0,} \\ {\left( {\gamma + 2p\delta \sigma _{2} } \right)v^{\prime} - q\delta u' = 0,} \\ \end{array}$$
(3.5)

This implies that.

$$\left( {\begin{array}{*{20}c} {\gamma + 2p\delta \sigma_{2} } & { - q\delta } \\ { - q\delta } & {\gamma + 2p\delta \sigma_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {u^{\prime}} \\ {v^{\prime}} \\ \end{array} } \right) = 0$$

By integrating, system (3.5) gives.

$$\left( {\begin{array}{*{20}c} {\gamma + 2p\delta \sigma_{2} } & { - q\delta } \\ { - q\delta } & {\gamma + 2p\delta \sigma_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) = 0,$$
(3.6)

where the integration constants are zero and this procedure does not affect the generality, Therefore, when.

$$det\left( {\begin{array}{*{20}c} {\gamma + 2p\delta \sigma_{2} } & { - q\delta } \\ { - q\delta } & {\gamma + 2p\delta \sigma_{2} } \\ \end{array} } \right) = 0,$$
(3.7)

i.e., \(\gamma +2p\delta {\sigma }_{2}=q\delta\), the system (3.6) has a nontrivial envelope solution \(u=v\). Thus, by means of (3.5), the system (3.4) becomes.

$$p\delta^{2} u^{\prime\prime} + ru^{3} - Lu = 0,$$
(3.8)
$${\text{Where}}\;L = \left( {\sigma_{1} + p\sigma_{2}^{2} } \right) - \left( {s + q\sigma_{2} } \right)$$
(3.9)

Besides, we get the relation from (3.7) as.

$$\frac{\delta }{\gamma } = \frac{1}{{q - 2p\sigma_{2} }} = l$$
(3.10)

Therefore, in order to locate the solitary wave solution of the considered Eq. (3.1), it would be sufficient to examine the Eq. (3.8).

3.1 Soliton solutions through IBSEF method

We gain a correspondence among \(m\), \(n\) and \(P\) by means of the balancing principle between \(u''\) and \({u}^{3}\) in Eq. (3.8) regarding to the IBSEF method:

$$n - m - P + 1 = 0$$

Here \(m\) and \(P\) are free parameters, thus assigning \(m=1\), \(P=3\) provide \(n=3.\) Thus, the interim solution (2.1.4) becomes.

$$u\left( \eta \right) = \frac{{p_{0} + p_{1} H\left( \eta \right) + p_{2} H^{2} \left( \eta \right) + p_{3} H^{3} \left( \eta \right)}}{{q_{0} + q_{1} H\left( \eta \right)}},$$
(3.1.1)

where \(H(\xi )\) is the solution of the improved Bernoulli Eq. (2.1.5).

Substituting solution (3.1.1) together with the assistance of the improved Bernoulli Eq. (2.1.5) into (3.8) yields a polynomial in \(H\). Unraveling the system of the algebraic equations, we secure the subsequent set of solutions of the parameters:

$$\delta = \pm \frac{{\sqrt { - 2p\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)} }}{2p\alpha },\;p_{1} = \pm q_{1} \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} ,\;p_{3} = \pm \frac{{2q_{1} \beta \sqrt {r\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)} }}{r\alpha },\;p_{0} = \frac{{p_{2} \alpha }}{2\beta },\;q_{0} = \pm \frac{{p_{2} \alpha r}}{{2\beta \sqrt {r\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)} }}$$
(3.1.2)

  • Case 1 Since the solutions of the improved Bernoulli equation depend on \(\alpha\) and \(\beta\), first we consider \(\alpha \ne \beta\):

    Making use the values stated in (3.1.2) along with (2.1.8) into (3.8), we establish the exponential function solution as below:

    $$u\left( {x,t} \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \frac{{\left( {\beta e^{2\alpha \eta } + \alpha \tau } \right)}}{{\left( {\beta e^{2\alpha \eta } - \alpha \tau } \right)}},$$
    (3.1.3)

    which implies the general solution of dual core optical fiber Eq.  (3.1.1) belongs with (3.2) is.

    $$\phi_{1} \left( {x,t} \right) = \psi_{1} \left( {x,t} \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \frac{{\left( {\beta e^{2\alpha \eta } + \alpha \tau } \right)}}{{\left( {\beta e^{2\alpha \eta } - \alpha \tau } \right)}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
    (3.1.4)

    where \(\alpha \ne \beta\) and \(\eta =(\gamma x-\delta t)\). Restructuring the solution (3.1.4) to hyperbolic form, we attain.

    $$\phi_{1} \left( \eta \right) = \psi_{1} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \left\{ {\frac{{\left( {\beta + \alpha \tau } \right)\cosh \left( {\alpha \eta } \right) + \left( {\beta - \alpha \tau } \right)\sinh \left( {\alpha \eta } \right)}}{{\left( {\beta - \alpha \tau } \right)\cosh \left( {\alpha \eta } \right) + \left( {\beta + \alpha \tau } \right)\sinh \left( {\alpha \eta } \right)}}} \right\} e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
    (3.1.5)

    where \(\eta =(\gamma x-\delta t)\).

    Setting \(\beta =2\alpha \tau\) into (3.1.5), we ascertain the following impactful and inclusive soliton solution.

    $$\phi _{{11}} \left( \eta \right) = \psi _{{11}} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma _{2}^{2} - q\sigma _{2} - s + \sigma _{1} }}{r}~} \left\{ {\frac{{3\cosh \left( {\alpha \eta } \right) + \sinh \left( {\alpha \eta } \right)}}{{\cosh \left( {\alpha \eta } \right) + 3\sinh \left( {\alpha \eta } \right)}}} \right\}~e^{{i\left( {\sigma _{1} x - \sigma _{2} t} \right)}}$$
    (3.1.6)

    Introducing \(\beta =-\alpha \tau\) into (3.1.5), we attain the kink shape soliton.

    $$\phi_{12} \left( \eta \right) = \psi_{13} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \tanh \left( {\alpha \eta } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
    (3.1.7)

    On the other hand, for \(\beta = \alpha \tau\), from solution (3.1.5), we obtain.

    $$\phi_{13} \left( \eta \right) = \psi_{12} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \coth \left( {\alpha \eta } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
    (3.1.8)

    where \(\eta =(\gamma x-\delta t)\). Modifying the values of the free parameter \(\beta\), scores of further important solutions can be obtained from the same general solution (3.1.5), but such solutions are not recorded for brevity.

    Case 2 Now, we consider the case \(\alpha =\beta\):

    Substituting the values of the parameters arranged in (3.1.2) along with (2.1.2) and (2.1.9) into solution (3.1.1), we attain the exponential function solution the dual-core optical fiber equation in the exponential form as:

    $$\phi_{2} \left( {x,t} \right) = \psi_{2} \left( {x,t} \right) = \pm \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \frac{{\left( {\tau - 1} \right)\tanh \left( {\alpha \eta } \right) - \left( {\tau + 1} \right)}}{{\left( {\tau + 1} \right)\tanh \left( {\alpha \eta } \right) - \left( {\tau - 1} \right)}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
    (3.1.9)

    where \(\alpha = \beta\) and \(\eta = \left( {\gamma x - \delta t} \right)\).

    Solution (3.1.9) can be written as,

    $$\phi_{2} \left( \eta \right) = \psi_{2} \left( \eta \right) = \pm \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \frac{{\left( {\tau - 1} \right)\sinh \left( {\alpha \eta } \right) - \left( {\tau + 1} \right)\cosh \left( {\alpha \eta } \right)}}{{\left( {\tau + 1} \right)\sinh \left( {\alpha \eta } \right) - \left( {\tau - 1} \right)\cosh \left( {\alpha \eta } \right)}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
    (3.1.10)

    When we choose various values of the real constant \(\tau\) such as \(\tau =4\), then (3.1.10) turns out to.

    $$\phi_{{2_{1} }} \left( \eta \right) = \psi_{{2_{1} }} \left( \eta \right) = \pm \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \frac{{3\sinh \left( {\alpha \eta } \right) - 5\cosh \left( {\alpha \eta } \right)}}{{5\sinh \left( {\alpha \eta } \right) - 3\cosh \left( {\alpha \eta } \right)}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
    (3.1.11)

    Choosing the free parameter \(\tau =-1\), solution (3.1.10) gives.

    $$\phi_{{2_{2} }} \left( \eta \right) = \psi_{{2_{2} }} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \tanh \left( {\alpha \eta } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$

    Again considering \(\tau = 1\), from solution (3.1.10) turns out to be.

    $$\phi_{3} \left( \eta \right) = \psi_{{2_{3} }} \left( \eta \right) = \mp \sqrt {\frac{{p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} }}{r} } \coth \left( {\alpha \eta } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$

    where \(\eta =(\gamma x-\delta t)\).

    It is significant to note that the wave solutions of the dual core optical fibers equation found here are effective, resourceful and were not established in the earlier research.

3.2 Soliton solutions through the new auxiliary equation method

In order to establish soliton solutions to the stated dual-core optical model through the new auxiliary equation method, it need the value of \(L\). We gain \(L=1\) based on balancing principle between \(u''\) and \({u}^{3}\) presented in Eq. (3.8).

By means of the NAE method, substituting the value of \(L\) into (2.2.4) the solution shape is of the form:

$$u\left( {x,t} \right) = a_{0} + a_{1} a^{g\left( \tau \right)} ,$$
(3.2.1)

where, \(g(\tau )\) is the estimation of the nonlinear Eq. (2.2.5).

Based on the solution (3.2.1) with help of (2.2.5) from Eq. (3.8), we assert

$$\left( {2p\delta^{2} A_{1} n^{2} + rA_{1}^{3} } \right)\left\{ {a^{g\left( \tau \right)} } \right\}^{3} + \left( {3\delta^{2} mnpA_{1} + 3rA_{0} A_{1}^{2} } \right) \left\{ {a^{g\left( \tau \right)} } \right\}^{2} + \left( {2\delta^{2} lnpA_{1} + \delta^{2} m^{2} pA_{1} - pA_{1} \sigma_{2}^{2} + 3rA_{0}^{2} A_{1} + qA_{1} \sigma_{2} + sA_{1} - A_{1} \sigma_{1} } \right)\left\{ {a^{g\left( \tau \right)} } \right\} + \delta^{2} lmpA_{1} - pA_{0} \sigma_{2}^{2} + rA_{0}^{3} + qA_{0} \sigma_{2} + sA_{0} - A_{0} \sigma_{1} = 0$$
(3.2.2)

Equalizing like power of \(\{{a}^{g(\tau )}\}\) form Eq. (3.2.2) yields a system of algebraic equations and unraveling the obtained system provides the results as follow:

$$\delta = \pm \sqrt {\frac{{2\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{{p\left( {4ln - m^{2} } \right)}}} ,\;A_{0} = \mp m\sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{{ - r\left( {4ln - m^{2} } \right)}}} ,\;A_{1} = \pm 2n\sqrt {\frac{{ - \left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{{r\left( {4ln - m^{2} } \right)}}}$$
(3.2.3)

Based on the above values of the parameters, we achieve the subsequent solution functions to the dual-core Eq. (3.1) as follow:

When \({m}^{2} - 4ln < 0\) and \(n\ne 0,\)

Inserting the values of the constants arranged in (3.2.3) align with (2.2.5) into solution (3.2.1), we attain the solution of the dual-core optical fiber Eq. (3.1) through (3.2) as.

$$\phi_{31} = \psi_{31} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{ - r}} \tan \left( {\frac{{\sqrt {4ln - m^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.4)

or

$$\phi_{32} = \psi_{32} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{ - r}} \cot \left( {\frac{{\sqrt {4ln - m^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.5)

where \(\tau =(\gamma x-\delta t)\).When \({m}^{2} - 4 ln> 0\) and \(n\ne 0,\)

Exerting (3.2.3) together with (2.2.5) into (3.2.1), we achieve the solution of stated Eq. (3.1) through (3.2.1) and (3.8) as follows,

$$\phi_{41} = \psi_{41} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tanh \left( {\frac{{\sqrt {m^{2} - 4ln } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.6)

or.

$$\phi_{42} = \psi_{42} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \coth \left( {\frac{{\sqrt {m^{2} - 4ln } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.7)

where \(\tau = \left( {\gamma x - \delta t} \right)\).

When \({m}^{2}+ 4 {l}^{2}< 0\), \(n\ne 0\) and \(n=-l,\)

We achieve the solution of (3.1) employing (3.2.3) together with (2.2.5) into (3.2.1) given in the underneath.

$$\phi_{51} = \psi_{51} = \sqrt {\frac{{ - \left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tan \left( {\frac{{\sqrt { - m^{2} - 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.8)

or.

$$\phi_{52} = \psi_{52} = \sqrt {\frac{{ - \left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \cot \left( {\frac{{\sqrt { - m^{2} - 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.9)

where \(\tau =(\gamma x-\delta t)\).When \({m}^{2}+ 4 {l}^{2}> 0\), \(n\ne 0\) and \(n=-l\),

Introducing (3.2.3) together with (2.2.5) into solution (3.2.1), we secure the solution of stated dual-core Eq. (3.1) through (3.2.1) and (3.8) as.

$$\phi_{61} = \psi_{61} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tanh \left( {\frac{{\sqrt {m^{2} + 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.10)

or

$$\phi_{62} = \psi_{62} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \coth \left( {\frac{{\sqrt {m^{2} + 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.11)

where \(\tau = \left( {\gamma x - \delta t} \right)\).

When \({m}^{2}- 4 {l}^{2}< 0\), and \(n=l,\)

Appling (3.2.3) along with (2.2.5) into Eq. (3.2.1), we found.

$$\phi_{71} = \psi_{71} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{ - r}} \cot \left( {\frac{{\sqrt {4l^{2} - m^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.12)

or

$$\phi_{72} = \psi_{72} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{ - r}} \cot \left( {\frac{{\sqrt {4l^{2} - m^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.13)

where \(\tau =(\gamma x-\delta t)\).

When \({m}^{2}- 4 {l}^{2}> 0\), \(n\ne 0\) and \(n=l,\)

Setting (3.2.3) together with (2.2.5) into solution (3.2.1), we derive the solutions of (3.1) from Eq. (3.2.1) and (3.5), we attain

$$\phi_{81} = \psi_{81} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tanh \left( {\frac{{\sqrt {m^{2} - 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.14)

or

$$\phi_{82} = \psi_{82} = \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \coth \left( {\frac{{\sqrt {m^{2} - 4l^{2} } }}{2}\tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.15)

where \(\tau = \left( {\gamma x - \delta t} \right)\).

When \(ln<0\), \(m=0\) and \(n\ne 0\),

By means of (3.2.3) together with (2.2.5) and the solution (3.2.1), we gain the solutions of (3.1) from Eq. (3.2.1) and (3.5) provided in the ensuing

$$\phi_{91} = \psi_{91} = \mp \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tanh \left( {\sqrt { - ln} \tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.16)

or

$$\phi_{92} = \psi_{92} = \mp \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \coth \left( {\sqrt { - ln} \tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.17)

where \(\tau = \left( {\gamma x - \delta t} \right)\)

When \(m=0\) and \(l=-n\), we secure the solutions of (3.1) by putting (3.2.3) and (2.2.5) into Eq. (3.2.1) and (3.5) as follows.

$$\phi_{10} = \psi_{10} = \mp \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \frac{{\left( {1 + e^{ - 2n \tau } } \right)}}{{ \left( { - 1 + e^{ - 2n \tau } } \right)}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}}$$
(3.2.18)

where \(\tau = \left( {\gamma x - \delta t} \right)\)

When \(m = n = K\), \(l = 0\),

By means of the parametric values stated in (3.2.3), from (3.2.1) and (3.5), we derive the subsequent solution

$${\phi }_{11}={\psi }_{11}=\pm \sqrt{\frac{\left(p{\sigma }_{2}^{2}-q{\sigma }_{2}-s+{\sigma }_{1}\right)}{r}}\frac{\left(1+{e}^{K \tau }\right)}{ \left(-1+{e}^{K \tau }\right)} {e}^{i\left({\sigma }_{1}x-{\sigma }_{2}t\right)}$$
(3.2.19)

where \(\tau =(\gamma x-\delta t)\).

When \(m=(l+n)\),

Placing the values assigned in (3.2.3) with (2.2.5) into solution (3.2.1), we ascertain.

$$\phi_{12} = \psi_{12} = \pm \sqrt {\frac{{\left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \frac{{\left( {{ }ne^{{\left( {l{ } - { }n} \right){ }\tau }} + 1} \right)}}{{\left( {ne^{{\left( {l{ } - { }n} \right){ }\tau }} - 1} \right){ }}}e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.20)

where \(\tau =(\gamma x-\delta t)\).

When \(m=-(l+n)\),

We get the succeeding solution of the dual-core optical fiber Eq. (3.1) with the assistance of (3.2) and setting the values of the constants assembled in (3.2.3) into solution (3.2.1)

$${\phi }_{13}={\psi }_{13}=\pm \sqrt{\frac{\left(p{\sigma }_{2}^{2}-q{\sigma }_{2}-s+{\sigma }_{1}\right)}{r}}\frac{\left( {e}^{\left(l - n\right) \tau }+n\right)}{\left({e}^{\left(l - n\right) \tau }-n\right) }{e}^{i\left({\sigma }_{1}x-{\sigma }_{2}t\right)}$$
(3.2.21)

where \(\tau =(\gamma x-\delta t)\).

When \(l=0\),

With the aid of (3.2) and setting the values of the constants assembled in (3.2.3) into solution (3.2.1), we get the following solution of the dual-core optical fiber Eq. (3.1),

$${\phi }_{14}={\psi }_{14}=\pm \sqrt{\frac{\left(p{\sigma }_{2}^{2}-q{\sigma }_{2}-s+{\sigma }_{1}\right)}{r}}\frac{\left( n{e}^{m \tau }+1\right)}{\left( n{e}^{m \tau }-1\right) }{e}^{i\left({\sigma }_{1}x-{\sigma }_{2}t\right)}$$
(3.2.22)

where \(\tau =(\gamma x-\delta t)\).

When \(n=m=l\ne 0\),

We attain the next solution of (3.1) by considering (3.2.3) and (2.2.5) into (3.2.1) and (3.5) as follows

$${\phi }_{{15}_{1}}={\psi }_{{15}_{1}}=\mp \sqrt{\frac{-\left(p{\sigma }_{2}^{2}-q{\sigma }_{2}-s+{\sigma }_{1}\right)}{r}} \mathrm{tan}\left(\frac{\sqrt{3}l \tau }{2}\right){e}^{i\left({\sigma }_{1}x-{\sigma }_{2}t\right)}$$
(3.2.23)

Or

$${\phi }_{{15}_{2}}={\psi }_{{15}_{2}}=\mp \sqrt{\frac{\left(p{\sigma }_{2}^{2}-q{\sigma }_{2}-s+{\sigma }_{1}\right)}{r}} \mathrm{tanh}\left(\frac{\sqrt{-3}l \tau }{2}\right){e}^{i\left({\sigma }_{1}x-{\sigma }_{2}t\right)}$$
(3.2.24)

where \(\tau =(\gamma x-\delta t)\).

When \(=l\),\(m=0\), we obtain the following solution.

$$\phi_{16} = \psi_{16} = \mp \sqrt {\frac{{ - \left( {p\sigma_{2}^{2} - q\sigma_{2} - s + \sigma_{1} } \right)}}{r}} \tan \left( {l \tau } \right)e^{{i\left( {\sigma_{1} x - \sigma_{2} t} \right)}} ,$$
(3.2.25)

where \(\tau =(\gamma x-\delta t)\).

From the above investigation, we have found various types of solutions of the dual-core optical fiber equation such as hyperbolic, trigonometric, exponential functions solution and rational solutions.

4 Physical explanation to the travelling wave solutions

In this section, the obtained soliton solutions of the dual-core optical fibers equation are depicted in the figures and discussed the natures of these solitons for diverse values of the free parameters with the aid of software Matlab.

4.1 Graphical explanation to the attained solutions using the IBSEF method

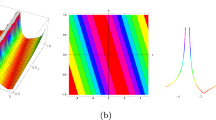
The obtained solutions using the IBSEF method are involved with two parts such as the real part and the imaginary part. Furthermore, these solutions associated with the velocity and wave number of the travelling wave denoted by \(\delta\), \({\sigma }_{2}\) and \(\gamma\), \({\sigma }_{1}\) respectively which play very impactful role on wave profile. Starting the values of the free parameters \(\gamma ,{\delta ,\sigma }_{1},{\sigma }_{2}\) very nearer to zero as \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=.001\), the solution \({{\phi }_{1}}_{2}\) represents a peakon for real part and a singular soliton for imaginary part asserted in Fig. 1a. Only a little increase of the values of velocity as \(\delta ={\sigma }_{2}=1\) without change the values of wave number and vice versa, the same solution function depicts anti-bell shape soliton for real part and spike type singular soliton for imaginary part with singularity at \((\mathrm{0,0},0)\) shown in Fig. 1b. Consequently, extending these values to large number like, \(\gamma =.001,\delta =10,{\sigma }_{1}=.001,{\sigma }_{2}=10\), then \({{\phi }_{1}}_{2}\) demonstrates spike type singular wave for real and unequal periodic wave illustrated in Fig. 1c. When we increase these values together by a larger margin such \(\gamma =10,\delta =10,{\sigma }_{1}=10,{\sigma }_{2}=10\), then both real and imaginary part display the dissipating periodic soliton asserted in Fig. 1d.

Fig. 1
figure 1

a For\(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=.001\), b: For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1\), c For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =.001,\delta =10,{\sigma }_{1}=.001,{\sigma }_{2}=10\), c For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=10\)

Full size image

Using the same values of the free parameters considered previously, we will discuss the wave profile for the solution \({{\phi }_{1}}_{3}\left(x,t\right)={{\psi }_{1}}_{3}(x,t)\). The solution \({{\phi }_{1}}_{3}\left(x,t\right)={{\psi }_{1}}_{3}(x,t)\) demonstrates a compacton soliton for real part and oblique plane for imaginary part outlined in Fig. 2a for \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=.001\). For \(p=1\), \(q=2\), \(r=3\), \(s=4\), \(\alpha =0.001\), \(\beta =1\), \(\gamma =0.001\), \(\delta =1\), \({\sigma }_{1}=0.001\), \({\sigma }_{2}=1\) within the limit \(-2\le x,t<2\), the shape of the real part is an ideal bell-shape soliton and the imaginary portrays a dark-bright soliton traced in Fig. 2b. Only increasing the interval as \(-5\le x,t<5\) the same solution \({{\phi }_{1}}_{3}\left(x,t\right)={{\psi }_{1}}_{3}(x,t)\) depicts w-shaped soliton and two soliton portrayed in Fig. 2c for real part and imaginary part respectively. Proceeding the same way and only by increasing the value of velocity as \(\delta =10,{\sigma }_{2}=10\), the real and imaginary part belong an irregular periodic wave asserted in Fig. 2d. Furthermore, extending the values of the wave number and vector speed in big amount like, \(p=1\), \(q=2\), \(r=3\), \(s=4\), \(\alpha =0.001\), \(\beta =1\), \(\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=10\), both real and imaginary part represent periodic soliton shown in Fig. 2e.

Fig. 2
figure 2

a For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=.001\), b For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1\) with \(-2\le x,t\le 2\), c For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1\) with \(-5\le x,t\le 5\), d For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =.001,\delta =10,{\sigma }_{1}=.001,{\sigma }_{2}=10\) with \(-5\le x,t\le 5\), e For \(p=1, q=2,r=3,s=4,\alpha =.001, \beta =1,\gamma =\delta ={\sigma }_{1}={\sigma }_{2}=10\).

Full size image

The other results obtained through the IBSEF method and the NAE method represent similar wave profiles for different values of free parameters and thus not presented here for simplicity. From the above illustration of the wave profiles, it might be concluded that the soliton profile changes their shape depending on the values of the wave number and velocity mostly. Here the coefficients \(p,q,r,s\) of the dual-core optical fibers equation do not play a major role in changing the speed of the wave but the Bernoulli parameters \(\alpha\) and \(\beta\) contribute a little.

4.2 Physical illustration of the solutions obtained by the auxiliary equation method

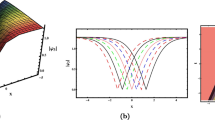
The exact solution \({{\phi }_{3}}_{1}\left(x,t\right)={{\psi }_{3}}_{1}(x,t)\) represent compacton for real part and oblique plane for imaginary part sketched in Fig. 3a for \(p=1\), \(q=2\), \(r=3\), \(s=4\), \(\gamma =0.001\), \(\delta =0.001\), \({\sigma }_{1}=0.001\), \({\sigma }_{2}=0.001\), \(l=1\), \(m=1\), \(n=1\). Behalf of the scheduled condition \({m}^{2} - 4ln < 0\), \(n\ne 0,\) and increasing the values of the other free parameters specially the vector speed as \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=1,m=1,n=1\), the same solution depicts double soliton for both real and imaginary part asserted in Fig. 3b. Moreover, the solution \({{\phi }_{3}}_{1}\) represents irregular periodic soliton shown in Fig. 3c by increasing the values of \(l,m,n\) but unchanging the other values as \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=5,m=1,n=5\).

Fig. 3
figure 3

a For \(p=1, q=2,r=3,s=4,\gamma =.001,\delta =.001,{\sigma }_{1}=.001,{\sigma }_{2}=.001,l=1,m=1,n=1\), b For \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=1,m=1,n=1\), c For \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=5,m=1,n=5\)

Full size image

If we choose the values of the arbitrary parameters as before \(p=1, q=2,r=3,s=4,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1,l=1,m=1,n=1\) associated to the condition \({m}^{2} - 4ln<0\), \(n\ne 0\), the closed form solution \({{\phi }_{3}}_{2}(x,t)\) display anti-bell shape soliton with singularity at (0,0,0) and non-topological soliton graphed in Fig. 4a for real and imaginary part respectively. Subsequently, ascending the value of velocity \({\sigma }_{1}=10,{\sigma }_{2}=10\) with parallel values of other parameters as before, the solution function portrays singular and non-topological soliton for both parts sketched in Fig. 4b. If we increase the value of all parameters in large amount the solution spectacles periodic soliton traced in Fig. 4c for \(p=10, q=3,r=5,s=7,\gamma =20,\delta =.001,{\sigma }_{1}=10,{\sigma }_{2}=10,l=1,m=1,n=1\).

Fig. 4
figure 4

a For \(p=1, q=2,r=3,s=4,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1,l=1,m=1,n=1\), b For \(p=1, q=2,r=3,s=4,\gamma =.001,\delta =1,{\sigma }_{1}=10,{\sigma }_{2}=10,l=1,m=1,n=1\), c For \(p=10, q=3,r=5,s=7,\gamma =20,\delta =.001,{\sigma }_{1}=10,{\sigma }_{2}=10,l=1,m=1,n=1\)

Full size image

For the values of the arbitrary parameters \(p=1, q=2, r=3, s=4, \gamma =.001, \delta =1, {\sigma }_{1}=.001, {\sigma }_{2}=1,l=2,m=2,n=-2\), the solution \({{\phi }_{5}}_{1}(x,t)\) illustrates a bell-shaped soliton for the real part and dark-bright soliton for the imaginary part asserted in Fig. 5

Fig. 5
figure 5

Plot of \({{\phi }_{5}}_{1}(x,t)\) using \(p=1, q=2,r=3,s=4,\gamma =.001,\delta =1,{\sigma }_{1}=.001,{\sigma }_{2}=1,l=2,m=2,n=-2\)

Full size image

On the other hand, the solution \({{\phi }_{6}}_{1}(x,t)\) represents \(W\)-shaped soliton for real part and a dark-bright soliton for imaginary part outlined in Fig. 6 for \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=-10,m=5,n=10\).

Fig. 6
figure 6

Plot of \({{\phi }_{6}}_{1}(x,t)\) for \(p=1, q=2,r=3,s=4,\gamma =1,\delta =1,{\sigma }_{1}=1,{\sigma }_{2}=1,l=-10,m=5,n=10\)

Full size image

From the preceding discussion, it is apparent that the IBSEF method and the auxiliary equation approach provide different types of solitons of the dual-core optical fiber equation, including kink, non-topological soliton, symmetrical, bell-shaped soliton, singular kink, compacton, bright soliton, W-shape soliton, irregular periodic soliton, etc. For the sake of simplicity, the other results obtained indicate comparable wave profiles for different values of free parameters and thus not provided here.

5 Conclusion

In this article, the parametric effects on solitary wave propagation and characteristic aspects of long-wave propagation in the dual-core optical fibers have been studied by establishing lots of illustrative, advanced and broad-ranging solitary wave solutions via two significant methods, namely the improved Bernoulli sub-equation function (IBSEF) method and the new auxiliary equation approach. In this study, it has been clearly explained, how the free parameters in the solutions obtained are inextricably associated with the wave profile. We have also discussed the impact of the change of the velocity and wave number in the wave propagation. The physical significance of the solutions attained has been illustrated for the definite values of the included parameters through depicting the 3D profiles. These wave profiles have a wide range of applications in optics and telecommunications. The methods introduced are straightforward, simple, and efficient, and they can be extended to a wide range of nonlinear models in optics and telecommunications.