1 Introduction

Fractional Partial differential equations (FPDEs) are used to represent physical phenomena to better understand their behavior, and they form the foundation of most mathematical and physical simulations of real-world applications. Several real-life situations have been described in terms of fractional derivatives such as optical fiber, porous medium, fluid dynamics, viscoelastic materials, signal processing, ocean waves, plasma physics, electromagnetism, wave propagation, photonic, chaotic systems, nuclear physics, building materials, and many more. A balance of wave dispersion and nonlinearity produces solitons. Temporal solitons are easily generated in optical fiber waveguides and laser resonators in optics, and they have recently been discovered in dielectric micro cavities. The Kerr effect provides nonlinear group velocity dispersion adjustment in each of these circumstances (nonlinear refractive index). Closed-form analytical solutions make a substantial contribution to easily, more correctly, and explicitly expressing these phenomena. Even a simple closed-form solution with no genuine physical implications can be used as a test problem to verify the accuracy and reliability of various numerical, approximate analytical, and asymptotic approaches. In the current era, solitons are the more attractive area of research. The hypothesis of optical solitons is one of the pleasurable themes for the examination of solitons movement through nonlinear optical fibers, extreme laser radiation into plasmas. Within the field of solitary waves, studies of optical solitons have garnered a lot of traction.

Several beneficial strategies have been proposed in recent years in some previous decades, such as the tanh-method (Wazwaz 2005), Darboux transformation (Li et al. 2020), modified Kudryashov’s method (Hosseini et al. 2018), \(\left( {G^{\prime}/G} \right)\)-expansion method (Aniqa and Ahmad 2021; Zhang et al. 2008; Wang et al. 2008), Novel \(\left( {G^{\prime}/G} \right)\)-expansion method (Alam et al. 2013; Shakeel and Mohyud-Din 2015; Hussain et al. 2017), first integral method (Eslami et al. 2017; Rezazadeh et al. 2018), Hirota bilinear technique (Liu et al. 2020), symbolic computational method (Ali et al. 2021), trial equation method (Liu 2019), Auxiliary equation method (Akbulut and Kaplan 2018), Explicit exponential finite difference methods (Inan et al. 2020), a generalized unified method (Osman 2017), Sine-Gordon expansion method (Ali et al. 2020), Genocchi polynomials (Kumar et al. 2021), new extended direct algebraic method (Rehman et al. 2021; Bilal and Ahmad 2021) and so on. Moreover, a new technique called the generalized exponential rational function method was first proposed by Ghanbari and Inc in (2018). This method was fruitfully and effectively employed to a resonance nonlinear Schrödinger equation (Ghanbari and Inc 2018), to a generalized Camassa–Holm–Kadomtsev–Petviashvili equation (Ghanbari and Liu 2020), to a new extension of nonlinear Schrödinger equation (Ghanbari et al. 2020), to conformable Ginzburg–Landau equation with the Kerr law nonlinearity (Ghanbari and Gómez-Aguilar 2019). The nonlinear Schrödinger's (NLS) equation is considered as the most important model related to highlighted research fields (Osman et al. 2020).

The higher-order Schrodinger equation comprising the parameters, which is used to describe cardiac output in optical fibers, is shown to acknowledge the formation of an infinite extension of the four-parameter combination, in addition to the classical NLSE. In the literature, different types of solutions were developed by many authors using different techniques for different types of Schrödinger equations. Recently, several authors have developed a variety of solutions for the MUSE using a variety of methods. The solitary wave solutions and exact solutions were found using the modified extended auxiliary equation mapping approach (Arshad et al. 2017). A rational exponential approach has been used to find the solutions for Schrödinger's unstable equation (Yang et al. 2018). To obtain optical soliton solutions for the unstable Schrödinger equation, an expanded map technique was devised. A simple mathematical method was used to derive the elliptic work solution, dark and bright soliton solutions for MUSE (Jia and Guo 2019). Many authors have looked into multiple ways for solving nonlinear MUSEs (Sinha and Ghosh 2017; Kumar et al. 2015). The Exp-function method was used to find soliton solutions for fractional modified Schrödinger equations (Zulfiqar and Ahmad 2020). The cubic-quartic NLSE and resonant NLSE with parabolic law have optical soliton solutions (Gao et al. 2020). The tanh method and the tanh–coth method have been used to obtain optical solitons from NLSE with quintic nonlinearity identified as the perturbed Gerdjikov–Ivanov equation (Zulfiqar and Ahmad 2021). The nonautonomous complex wave solutions described by the coupled Schrödinger–Boussinesq equation with variable-coefficients (Osman et al. 2018). Optical solutions, traveling wave solutions, and exact solutions for the nonlinear Schrödinger equation with Kerr law nonlinearity have been developed using a variety of methods (Akram and Mahak 2018; Baleanu et al. 2017; Biswas and Konar 2006; Jhangeer et al. 2020).

The pioneer paintings of Malfliet (1992) added the powerful tanh approach for a reliable treatment of the nonlinear wave equations. The beneficial tanh approach is extensively used by many together with Wazwaz. Later, the tanh–coth method, advanced via Wazwaz (2006), is a right away and powerful algebraic approach for coping with nonlinear equations. Many problems have been solved with tanh in the literature, including the Kawahara and modified Kawahara equations (Mohamad-Jawad and Slibi 2012), as well as the combined KdV equation (Jawad et al. 2013). space–time fractional nonlinear Whitham–Broer–Kaup equations, space–time fractional nonlinear coupled Burgers equations, space–time fractional nonlinear coupled mKdV equations (Zayed et al. 2016), and (2 + 1)-some Bogoyavlenskii scheme solved using an extended tanh operation (Leta et al. 2021). In this article, we will study the fractional perturbed Schrödinger equation with Kerr law nonlinearity (p-NSKN) using the conformable derivative. No one has ever read the p-NSKN equation of non-integer orders in the literature, to the author's knowledge. As a result, utilizing the tanh–coth approach to examine the non-integer order p-NSKN equation provides a very plausible way to understand how this model works physically. We will employ the tanh method and the tanh–coth method to obtain new analytical solutions for the fractional p-NSKN equation via conformable derivative in this paper. This conformable derivative definition is based on the fundamental notion of an ingredient limit, which has been effectively applied to a variety of problems like coupled fractional resonant Schrödinger equations arising in quantum mechanics have been resolved in the conformable fractional derivative sense, Fuzzy conformable fractional differential equations, nonlinear conformable time-fractional equation, conformable fractional perturbed Gerdjikov-Ivanov equation (Al-Smadi et al. 2020; Arqub and Al-Smadi 2020; Kaplan 2017; Zulfiqar and Ahmad 2021). The conformable fractional p-NSKN equation is one of the most important dynamic models with several applications in the non-line optical fiber that defines the shortest signal transmission in fiber optics. The exact and approximate solutions of this model have a wide range of applications in telecommunications, engineering, medicine, physics, clinics, and various other areas of science.

Definition

Khalil proposed a thrilling definition of derivative known as conformable spinoff (Khalil 2014) along with a set of properties. This derivative may be considered to be a natural extension of the classical by-product. Moreover, the conformable by-product satisfies all the properties of the same old calculus and is defined by:

$$\left( {D_{\alpha } g} \right)\left( x \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{g\left( {x + \varepsilon x^{1 - \alpha } } \right) - g\left( x \right)}}{\varepsilon },\,{\text{x > 0,}}\;{\upalpha } \in \, \left( {0,1} \right]$$
(1)

2 Method description

Considering the nonlinear equation with the conformable derivative:

$$Q\left( {u,u_{x} ,u_{t} ,D_{t}^{\alpha } ,...} \right) = 0,\,0 < {\upalpha } \le 1.$$
(2)

By means of the transformation

$$u(x,t) = U({\upeta })e^{{i{\uptheta }}} ,{\upeta } = \left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - r\frac{{t^{{\upalpha }} }}{{\upalpha }}} \right),\,{\uptheta } = {\upmu }\frac{{x^{{\upalpha }} }}{{\upalpha }} - s\frac{{t^{{\upalpha }} }}{{\upalpha }}.$$
(3)

Substituting Eq. (3) in Eq. (2) and integrating, one has Eq. (4)

$$R(U,U^{/} ,U^{//} ,U^{///} ,...) = 0.$$
(4)

Introducing a new independent variable

$$y(x,t) = Tanh({\upeta }).$$
(5)

leads to the change of variables

$$\frac{d}{{d{\upeta }}} = (1 - y^{2} )\frac{d}{dy}.$$
$$\frac{{d^{2} }}{{d{\upeta }^{2} }} = - 2y(1 - y^{2} )\frac{d}{dY} + (1 - y^{2} )^{2} \frac{{d^{2} }}{{dy^{2} }}.$$
$$\frac{{d^{3} }}{{d{\upeta }^{3} }} = 2(1 - y^{2} )(3y^{2} - 1)\frac{d}{dy} - 6y(1 - y^{2} )^{2} \frac{{d^{2} }}{{dy^{2} }} + (1 - y^{2} )^{3} \frac{{d^{3} }}{{dy^{3} }}.$$
(6)

For tanh–coth method

$$u(x,t) = U({\upeta }) = \sum\limits_{i = 0}^{m} {a_{i} y^{i} } + \sum\limits_{i = 1}^{m} {b_{j} y^{ - i} } ,$$
(7)

where m is a positive integer, for this method, that will be determined by balancing principle.

Substituting (7) into (5) results is an algebraic system of equations in powers of Y that will lead to the determination of the parameters \(a_{m}\), \(b_{m} .\)

3 Numerical application

The following conformable fractional form p-NSKN equation is considered

$$iD_{t}^{\alpha } u + \,D_{x}^{2\alpha } u + \beta \left| u \right|^{2} \,u\, + i\left[ {f_{1} D_{x}^{3\alpha } u + f_{2} \left| u \right|^{2} \,u + f_{3} D_{x}^{\alpha } \left( {\left| u \right|^{2} } \right)u} \right] = \,0,\,\,0 < \alpha < 1,$$
(8)

where u(x, t) specifies the macroscopic complex-valued wave profile of temporal and spatial independent variables of t and x, respectively, β represents the fiber loss, constants \(f_{1}\) and \(f_{2}\) show the dispersion and nonlinear terms respectively.

Fractional traveling wave transformation is

$$u(x,t) = U({\upeta })e^{{i{\uptheta }}} ,\,{\upeta } = \left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - r\frac{{t^{{\upalpha }} }}{{\upalpha }}} \right),\,{\uptheta } = {\upmu }\frac{{x^{{\upalpha }} }}{{\upalpha }} - s\frac{{t^{{\upalpha }} }}{{\upalpha }},$$
(9)

where \(r\) represents the phase component, \(\mu\) is the wavenumber and s represents the frequency.

Substituting Eq. (9) in  (8) and separating the real and imaginary part, we get

$$f_{1} U^{\prime\prime\prime} + \left( {2{\upmu } - r - 3f_{1} {\upmu }^{2} } \right)U^{\prime} + \left( {f_{2} + 2f_{3} } \right)U^{2} U^{\prime} = 0.$$
(10)
$$\left( {1 - 3f_{1} {\upmu }} \right)U^{\prime\prime} + \left( {s - {\upmu }^{2} + f_{1} {\upmu }^{3} } \right)U + \left( {{\upbeta } - 2f_{2} {\upmu }} \right)U^{3} = 0.$$
(11)

Equations (10) and (11) have the same solutions with the restriction

$${\upmu } = \frac{{f_{2} + 2f_{3} - 3f_{1} {\upbeta }}}{{6f_{1} f_{3} }},s = \frac{{\left( {1 - 3f_{1} {\upmu }} \right)\left( {2{\upmu } - r - 3f_{1} {\upmu }^{2} } \right)}}{{f_{1} }} + {\upmu }^{2} - f_{1} {\upmu }^{3} .$$
(12)

With the restrictions (12), Eqs. (10) and (11) convert into the following single equation:

$$f_{1} U^{\prime\prime} + \left( {2{\upmu } - r - 3f_{1} {\upmu }^{2} } \right)\,U + \left( {f_{2} + 2f_{3} } \right)U^{3} = 0.$$
(13)

Balancing \(U^{\prime\prime}\) with \(U^{3}\), we get \(m = 1\). Equation (13) becomes

$$u\left( {x,t} \right) = a_{0} + a_{1} Y + b_{1} Y^{ - 1} .$$
(14)

By substituting Eq. (14) in  (13) along with Eq. (9), we obtain the system

$$\begin{aligned} y^{6} = & \left( {f_{2} + 2f_{3} } \right)a_{1}^{3} + 6{\upmu }^{2} a_{1} f_{1} = 0, \\ y^{5} = & 6\,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,\,a_{0} a_{1}^{2} = 0, \\ y^{4} = & 6\left( {b_{1} \,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,a_{0}^{2} + \left( { - \frac{{3k^{2} }}{2} - {\upmu }^{2} } \right)\,f_{1} - \frac{c}{2} + k} \right)a_{1} = 0, \\ y^{3} = & 2a_{0} \left( {6b_{1} \,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,a_{1} + \left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,a_{0}^{2} - \frac{{9k^{2} f_{1} }}{2} - \frac{3c}{2} + 3k} \right) = 0, \\ y^{2} = & 6b_{1} \left( {b_{1} \,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,a_{1} + \,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,a_{0}^{2} + \left( { - \frac{{3k^{2} }}{2} - {\upmu }^{2} } \right)\,f_{1} - \frac{c}{2} + k} \right) = 0, \\ y^{1} = & 6\,\left( {f_{3} + \frac{{f_{2} }}{2}} \right)\,\,a_{0} b_{1}^{2} = 0, \\ y^{0} = & \left( {f_{2} + 2f_{3} } \right)b_{1}^{3} + 6{\upmu }^{2} b_{1} f_{1} = 0. \\ \end{aligned}$$
(15)

Solving this system by Maple, we have:

Case 1

$$\begin{aligned} f_{1} = & \frac{c - 2k}{{3k^{2} + 2{\upmu }^{2} }},f_{2} = \frac{{2\left( { - 3k^{2} b_{1}^{2} f_{3} - 2{\upmu }^{2} b_{1}^{2} f_{3} + 3{\upmu }^{2} c - 6{\upmu }^{2} k} \right)}}{{b_{1}^{2} \left( {3k^{2} + 2{\upmu }^{2} } \right)}},k = k,a_{0} = 0, \\ & a_{1} = 0,a_{2} = 0,b_{1} = b_{1} ,f_{3} = f_{3} ,c = c. \\ \end{aligned}$$
(16)
$$u_{1} \left( {x,t} \right) = \frac{{b_{1} \exp \left[ {i\,\left( {\frac{{{\upmu }x^{{\upalpha }} }}{{\upalpha }} - \frac{{st^{{\upalpha }} }}{{\upalpha }}} \right)} \right]}}{{\tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right)}}.$$
(17)

Case 2

$$\begin{aligned} f_{1} = & \frac{c - 2k}{{3k^{2} + 2{\upmu }^{2} }},f_{2} = \frac{{2\left( { - 3k^{2} a_{1}^{2} f_{3} - 2{\upmu }^{2} a_{1}^{2} f_{3} + 3{\upmu }^{2} c - 6{\upmu }^{2} k} \right)}}{{a_{1}^{2} \left( {3k^{2} + 2{\upmu }^{2} } \right)}},k = k,a_{0} = 0, \\ & a_{1} = a_{1} ,b_{1} = 0,f_{3} = f_{3} ,c = c. \\ \end{aligned}$$
(18)
$$u_{2} \left( {x,t} \right) = a_{1} \tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right)\exp \left[ {i\,\left( {\frac{{{\upmu }x^{{\upalpha }} }}{{\upalpha }} - \frac{{st^{{\upalpha }} }}{{\upalpha }}} \right)} \right].$$
(19)

Case 3

$$\begin{aligned} f_{1} = & \frac{c - 2k}{{3k^{2} + 8{\upmu }^{2} }},f_{2} = \frac{{2\left( { - 3k^{2} a_{1}^{2} f_{3} - 8{\upmu }^{2} a_{1}^{2} f_{3} + 3{\upmu }^{2} c - 6{\upmu }^{2} k} \right)}}{{a_{1}^{2} \left( {3k^{2} + 8{\upmu }^{2} } \right)}},k = k,a_{0} = 0, \\ & a_{1} = a_{1} ,b_{1} = a_{1} ,f_{3} = f_{3} ,c = c. \\ \end{aligned}$$
(20)
$$u_{3} \left( {x,t} \right) = \left( {a_{1} \tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right) + \frac{{a_{1} }}{{a_{1} \tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right)}}} \right)\exp \left[ {i\,\left( {\frac{{{\upmu }x^{{\upalpha }} }}{{\upalpha }} - \frac{{st^{{\upalpha }} }}{{\upalpha }}} \right)} \right].$$
(21)

Case 4

$$\begin{aligned} f_{1} = & - \frac{c - 2k}{{3k^{2} - 4{\upmu }^{2} }},f_{2} = \frac{{2\left( { - 3k^{2} a_{1}^{2} f_{3} + 4{\upmu }^{2} a_{1}^{2} f_{3} + 3{\upmu }^{2} c - 6{\upmu }^{2} k} \right)}}{{a_{1}^{2} \left( {3k^{2} - 4{\upmu }^{2} } \right)}},\;k = k,a_{0} = 0, \\ & a_{1} = a_{1} ,b_{1} = a_{1} ,f_{3} = f_{3} ,c = c. \\ \end{aligned}$$
(22)
$$u_{4} \left( {x,t} \right) = \left( {a_{1} \tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right) - \frac{{a_{1} }}{{a_{1} \tanh \left( {{\upmu }\left( {\frac{{x^{{\upalpha }} }}{{\upalpha }} - \frac{{rt^{{\upalpha }} }}{{\upalpha }}} \right)} \right)}}} \right)\exp \left[ {i\,\left( {\frac{{{\upmu }x^{{\upalpha }} }}{{\upalpha }} - \frac{{st^{{\upalpha }} }}{{\upalpha }}} \right)} \right].$$
(23)

Case 5

$$\begin{aligned} f_{1} = & - \frac{c - 2k}{{3k^{2} - 4{\upmu }^{2} }},f_{2} = \frac{{2\left( { - 3k^{2} a_{1}^{2} f_{3} + 4{\upmu }^{2} a_{1}^{2} f_{3} + 3{\upmu }^{2} c - 6{\upmu }^{2} k} \right)}}{{a_{1}^{2} \left( {3k^{2} - 4{\upmu }^{2} } \right)}},k = k,a_{0} = a_{0} , \\ & a_{1} = 0,b_{1} = 0,f_{3} = f_{3} ,c = c. \\ \end{aligned}$$
(24)
$$u_{5} \left( {x,t} \right) = a_{0} \exp \left[ {i\,\left( {\frac{{{\upmu }x^{{\upalpha }} }}{{\upalpha }} - \frac{{st^{{\upalpha }} }}{{\upalpha }}} \right)} \right].$$
(25)

4 Results and discussion

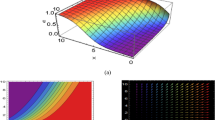
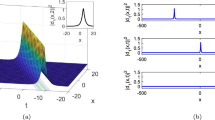
By resolving the fractional p-NSKN problem with the help of conformable fractional derivative, the tanh–coth technique is used to obtain optical soliton solutions in this article. Because of its wide range of applications, the p-NSKN is the most extensively used nonlinear model in applied research. The transmission of optical solitons in Kerr law nonlinearity optical fibers is described by this equation. In the literature, the p-NSKN equation has been resolved to get a different kinds of solutions by the utilization of various techniques such as \(\frac{{G}^{^{\prime}}}{{G}^{2}}\) technique has been applied to get hyperbolic, trigonometric, and rational type solutions (Osman et al. 2018), Riccati–Bernoulli sub-ODE method has been employed to form the new periodic singular, dark singular, dark singular, exact, soliton solutions (Akram and Mahak 2018), the new extended algebraic technique has been developed to derive the singular, bright-dark, and rational type solutions (Biswas and Konar 2006). According to the literature, the proposed model has been solved for integer order. Using the conformable derivative, we resolve the proposed model for both integer and non-integer order in our study. We observed some similarities in the current results for integer order, but we created new and more general conclusions for non-integer order. In addition, the physical appearance of the solitary waves shows the variations in the graphics by fluctuating parametric values. Figures 1, 2, 3, 4, 5 show the graphical behavior of the presented fractional model in 3D, 2D, and contour plots at \({\upalpha } = 0.5,\,\,{\upalpha } = 0.8\) and \(\alpha = 1.\) Figure 1 indicates the solution of \(u_{1} \left( {x,t} \right)\) for \(b_{1} = \frac{1}{4},\,s = 0.1,r = 1.5,\,{\upmu } = 2.\) Figure 2 shows the graphics of \(u_{2} \left( {x,t} \right)\) at \(a_{1} = \frac{1}{2},\,s = 0.1,r = 1,\,{\upmu } = 0.5.\) Figure 3 reveals the solution of \(u_{3} \left( {x,t} \right)\) for \(a_{1} = \frac{1}{2},\,s = 0.1,r = 1,\,{\upmu } = 0.5.\) Figure 4 describes the physical appearance of \(u_{4} \left( {x,t} \right)\) for \(a_{1} = \frac{1}{2},\,s = 0.1,r = 1,\,{\upmu } = 0.5.\) Figure 5 signifies the plot of \(u_{5} \left( {x,t} \right)\) with the parametric values of \(a_{0} = \frac{1}{2},\,s = 0.1,r = 1,\,{\upmu } = 0.5.\)

Fig. 1
figure 1figure 1

Graphics for \(u_{1} \left( {x,t} \right)\), a–c with \(0 \le x \le 5,\,0 \le t \le 10,\) show the 3D plots. d–f with \(- 5 \le x \le 5,\, - 5 \le t \le 5,\)\(- 1 \le x \le 2,\, - 1 \le t \le 2,\) illustrate the contour comparison, and \(- 1 \le x \le 2,\, - 1 \le t \le 2,\) respectively. g Indicates the comparison in the form of 2D plot

Full size image
Fig. 2
figure 2figure 2

Graphics for \(u_{2} \left( {x,t} \right)\), a–c with \(0 \le x \le 20,\,0 \le t \le 10,\) indicate the 3D comparison plots, d–f with \(- 5 \le x \le 5,\, - 5 \le t \le 5\), describe the contour comparison plots. g Indicates the comparison in the form of 2D plot

Full size image
Fig. 3
figure 3figure 3

Graphics for \(u_{3} \left( {x,t} \right)\), a–c with \(0 \le x \le 5,\,0 \le t \le 10,\) indicate the 3D comparison plots, d–f with \(- 1 \le x \le 1,\, - 1 \le t \le 1,\)\(- 5 \le x \le 5,\, - 5 \le t \le 5,\) and \(- 5 \le x \le 5,\, - 5 \le t \le 5,\) depict the contour comparison plots respectively. g Indicates the comparison in the form of 2D plot

Full size image
Fig. 4
figure 4figure 4

Graphics for \(u_{4} \left( {x,t} \right)\), a–c with \(0 \le x \le 10,\,0 \le t \le 5,\) show the 3D comparison plots, d–f with \(- 1 \le x \le 1,\, - 1 \le t \le 1,\)\(- 5 \le x \le 5,\, - 5 \le t \le 5,\) and \(- 5 \le x \le 5,\, - 5 \le t \le 5,\) illustrate the contour comparison plots respectively. g Indicates the comparison in the form of 2D plot

Full size image
Fig. 5
figure 5figure 5

Graphics for \(u_{5} \left( {x,t} \right)\), a–c with \(0 \le x \le 30,\,0 \le t \le 10,\) show the 3D comparison plots, d–f with \(- 5 \le x \le 5,\, - 5 \le t \le 5\) illustrate the contour comparison plots. g Indicates the comparison in the form of 2D plot

Full size image

The presented work shows that the fractional derivative has a very significant part to play in considering the formation of the evolutionary equation and explains the continuous performance of the solution wave all over the process. Comprehensive testing confirms that the method used is reliable, efficient, and very powerful in testing different types of nonlinear FDEs.

5 Conclusion

In this work, we discover and analyze new soliton solutions and dynamic properties in optical nanofibers for fractional perturbed Schrödinger equation and Kerr law nonlinearity. The tanh–coth method with fractional conformable derivative and fractional complex transformation was used to obtain the soliton solutions in closed-form wave structures. Moreover, from the graphical demonstration, we have seen that different boundary values provide different types of solutions by identifying free parameters corresponding to the required limitations to confirm the presence of such optical solitons. The model's solution can be used in a variety of science and engineering domains. As a result, we conclude that the fractional calculus structures model provided in this study is extremely versatile and accurately analyses dynamical global systems. The acquired solutions are more generic, novel, and have not been previously described in the literature. The findings also support the importance and usefulness of the methodologies employed, as well as pique the interest of scholars interested in deciphering the model's intricacy. Using the appropriate fractional operator, we may also extend our work to answer more difficult biological and engineering challenges. The presented analytical method can be applied to the other forms of nonlinear evolution equations arising in engineering, mathematical physics, and biological sciences. The new results of this paper are very encouraging to carry out further studies with the addition of different perturbation and complex nonlinear concepts.