1 Introduction

The phenomena of NLSEs have attracted numerous researchers and scientists of recent era in the field optical fibre communication purposes and nonlinear optics such as, comprising spectroscopy, optical fibers, plasma physics and many more (Seadawy and Lu 2017; Bulut et al. 2018; Seadawy and Cheemaa 2019; Rizvi et al. 2020; Ali et al. 2020). Over the last few decades a renowned scientists have suggested several methods for solving nonlinear evolution equations (NLEEs), such as, the simple equation scheme (Abd El-Hameed 2020; Jawad et al. 2010; Khater et al. 2006; Seadawy and Cheemaa 2019), the exp-function scheme (Zhang 2008; Aslan 2013; Aslan and Marinakis 2011), the sine–cosine method (Wazwaz 2005, 2006), the homogenous balance method (He and Wu 2006; Mingliang 1996), the tanh–sech technique (Malfliet and Hereman 1996), the extended tanh–coth architectonics (Wazwaz 2008), the Kudryashov norm (Arnous and Mirzazadeh 2016), the soliton ansatz method (Fan and Hona 2002; Savescu et al. 2014), the semi-inverse variational principle (Seadawy et al. 2018; Eslami and Mirzazadeh 2016; Malfliet 1992), generalized mapping method Extended and modified direct algebraic method and Seadawy techniques (Seadawy and Cheemaa 2020; Dianchen et al. 2018a, b; Helal et al. 2014; Seadawy et al. 2019; Ozkan 2020). Such equations are extensively used to describe many important phenomena and dynamic processes in physics, chemistry, biology, plasma, optical fibers and other areas of engineering (Ozkan et al. 2020; Malfliet 1991; Arshad et al. 2017; Farah et al. 2020; Ali et al. 2018; Cheemaa et al. 2018, 2019; Iqbal et al. 2020). The NLEEs can be used to explain a wide range of physical phenomena of nature including vibration, heat, electrostatics, electrodynamics, fluid dynamics, elasticity, gravitation, and quantum mechanics (El-Shiekh and Al-Nowehy 2013; Akbulut and Kaplan 2018; Ilie et al. 2018a, b; Hosseini et al. 2020; Li et al. 2011, 2016, 2019).

The main goal of this paper is to search for some novel analytical solutions to the M-fractional paraxial NLSE in Kerr media by employing the modified simple equation MSE technique and the auxiliary equation (AE) method which reads (Atangana et al. 2015; Sirendaoreji and Jiong 2003).

$$\begin{aligned} {iD}^{\alpha ,\beta }_{M,z} u+ \frac{a}{2}D^{2\alpha ,\beta }_{M,t} u +\frac{b}{2}D^{2\alpha ,\beta }_{M,y} u+\gamma |u|^2u=0, \end{aligned}$$
(1)

where \(\mu _1\), \(\mu _2\) and \(\beta\), are the symbols of the dispersion, diffraction, and Kerr non-linearity. The D is a complex-valued function represents soliton profile (Sousa and de Oliveira 2018; Choi and Howell 2014).

This article designed as: in Sect. 2, the MSE technique and the AE scheme are employed to the given Eq. (1), while in Sect. 3 some 3D plots are utilized to demonstrate the structure of various solutions and in the last section some conclusions are illustrated.

2 Mathematical analysis

Consider the transformation

$$\begin{aligned} u(y,z,t)=U(\xi ) e^{i\,\theta }, \end{aligned}$$
(2)

where

$$\begin{aligned} \xi =\frac{\Gamma (\beta +1)}{\alpha }(y+z-ct), \theta =\frac{\Gamma (\beta +1)}{\alpha }\kappa (y+z-ct), \end{aligned}$$
(3)

by using Eq. (2) in Eq. (1) and separating in real and imaginary parts, we obtain,

$$\begin{aligned} -(c^2 a+b)U''+(b \kappa ^2+ a\kappa ^2c^2+2\kappa )U-2\gamma U^3=0, \end{aligned}$$
(4)
$$\begin{aligned} (1+ b\kappa + a\kappa c^2)U'=0, \end{aligned}$$
(5)

As \(U'\) is nonzero so

$$\begin{aligned} b= \frac{-1- a\kappa c^2}{\kappa }, \end{aligned}$$
(6)

putting Eq. (6)into Eq. (4) we get a closed solution,

$$\begin{aligned} U''+ \kappa ^2 U- 2\gamma U^3=0. \end{aligned}$$
(7)

2.1 Applications of the MSEM

To construct the analytical solution to Eq. (7), consider its formal solution by applying the homogenous balance principle

$$\begin{aligned} U = A_0+ A_1\left( \frac{ \psi '(\xi ) }{ \psi (\xi ) }\right) , \end{aligned}$$
(8)

where \(A_0\), \(A_1\) are constant and \(A_1\) not to b zero.

$$\begin{aligned} U' =\frac{A_1 \psi ''(\xi )}{\psi (\xi )}-\frac{A_1 \psi '(\xi )^2}{\psi (\xi )^2}, \end{aligned}$$
(9)
$$\begin{aligned} U''=\frac{A_1 \psi ^{(3)}(\xi )}{\psi (\xi )}+\frac{2 A_1 \psi '(\xi )^3}{\psi (\xi )^3} -\frac{3 A_1 \psi '(\xi ) \psi ''(\xi )}{\psi (\xi )^2}, \end{aligned}$$
(10)

by substituting Eq. (8) with Eq. (9) and Eq. (10)into Eq. (7), we get a system of algebraic equations

$$\begin{aligned} \kappa ^2 A_0-2 A_0^3 \gamma =0, \end{aligned}$$
(11)
$$\begin{aligned} A_1 (\kappa ^2 \psi '+\psi ^{(3)})-6 A_0^2 A_1 \gamma \psi '=0, \end{aligned}$$
(12)
$$\begin{aligned} -6\gamma A_0 A_1^2 \psi '^2-3 A_1 \psi ' \psi ''=0, \end{aligned}$$
(13)
$$\begin{aligned} -2 A_1 ( -1+ \gamma A_1^2 ) \psi '^3=0, \end{aligned}$$
(14)

by solving equation Eqs. (11) and (14), we found a set of following new exact solutions to the Eq. (1)


Case I:

$$\begin{aligned} A_0= \frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, A_1=\frac{1}{\sqrt{\gamma }}, \end{aligned}$$
(15)

by putting Eq. (15) in Eq. (13)

$$\begin{aligned} -\frac{3 \sqrt{2} \kappa \psi '(\xi )^2}{\sqrt{\gamma }} -\frac{3 \psi '(\xi ) \psi ''(\xi )}{\sqrt{\gamma }}=0, \end{aligned}$$
(16)
$$\begin{aligned} \frac{\psi ''(\xi )}{\psi '(\xi )}=-\sqrt{2} \kappa , \end{aligned}$$
(17)

which gives

$$\begin{aligned} \psi = c_1 \exp (-\sqrt{2}\kappa )\xi , \end{aligned}$$
(18)
$$\begin{aligned} \psi = c_1 \exp (-\sqrt{2}\kappa )\xi + c_2, \end{aligned}$$
(19)

hence

$$\begin{aligned} U_1=\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}+\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (-\sqrt{2}\kappa )\xi }{c_1 \exp (-\sqrt{2}\kappa )\xi + c_2}\right) , \end{aligned}$$
(20)

therefore

$$\begin{aligned} u_1(y,z,t)=\left[ \frac{\kappa }{\sqrt{2} \sqrt{\gamma }}+\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (-\sqrt{2}\kappa )\xi }{c_1 \exp (-\sqrt{2}\kappa )\xi + c_2}\right) \right] e^{i\,\theta }. \end{aligned}$$
(21)

Case II:

$$\begin{aligned} A_0= -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, A_1= -\frac{1}{\sqrt{\gamma }}, \end{aligned}$$
(22)

which gives

$$\begin{aligned} U_2 = -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}-\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (-\sqrt{2}\kappa )\xi }{c_1 \exp (-\sqrt{2}\kappa )\xi + c_2}\right) , \end{aligned}$$
(23)

thus

$$\begin{aligned} u_2(y,z,t) =\left[ -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}-\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (-\sqrt{2}\kappa )\xi }{c_1 \exp (-\sqrt{2}\kappa )\xi + c_2}\right) \right] e^{i\,\theta }. \end{aligned}$$
(24)

Case III:

$$\begin{aligned} A_0=\frac{\kappa }{\sqrt{2} \sqrt{\gamma }};\; A_1=-\frac{1}{\sqrt{\gamma }}, \end{aligned}$$
(25)
$$\begin{aligned} U_3 =\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}-\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (\sqrt{2}\kappa )\xi }{c_1 \exp (\sqrt{2}\kappa )\xi + c_2}\right) , \end{aligned}$$
(26)

hence

$$\begin{aligned} u_3 (y,z,t)=\left[ \frac{\kappa }{\sqrt{2} \sqrt{\gamma }}-\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (\sqrt{2}\kappa )\xi }{c_1 \exp (\sqrt{2}\kappa )\xi + c_2}\right) \right] e^{i\,\theta }. \end{aligned}$$
(27)

Case IV:

$$\begin{aligned} A_0=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }};\; A_1=\frac{1}{\sqrt{\gamma }}, \end{aligned}$$
(28)
$$\begin{aligned} U_4 (y,z,t)=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}+\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (\sqrt{2}\kappa )\xi }{c_1 \exp (\sqrt{2}\kappa )\xi + c_2}\right) , \end{aligned}$$
(29)

therefore

$$\begin{aligned} u_4 (y,z,t)=\left[ -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}+\frac{1}{\sqrt{\gamma }} \left( \frac{c_1 \exp (\sqrt{2}\kappa )\xi }{c_1 \exp (\sqrt{2}\kappa )\xi + c_2}\right) \right] e^{i\,\theta }. \end{aligned}$$
(30)

2.2 Applications of the AEM

Consider the solution of Eq. (7) is of the form

$$\begin{aligned} U = A_0+ A_1({\psi (\xi )}), \end{aligned}$$
(31)

where \(\psi (\xi )\) is satisfied the above ODE as:

$$\begin{aligned} \psi '(\xi )^2=c_1 \psi (\xi )^2+c_2 \psi (\xi )^3+c_3 \psi (\xi )^4. \end{aligned}$$
(32)

Substituting Eqs. (31) and (32) into Eq. (7), we get the following system of algebraic equations

$$\begin{aligned} &\kappa ^2 A_0-2\gamma A_0^3 =0,\\ &\kappa ^2 A_1-6\gamma A_0^2 A_1 +A_1 c_1=0,\\ &\frac{3 A_1 c_2}{2}-6\gamma A_0 A_1^2 =0,\\ &2 A_1 c_3-2\gamma A_1^3 =0, \end{aligned}$$

by solving the above system we get the following families of traveling wave solutions


Family I

$$\begin{aligned} \psi (\xi )=\frac{4 c_1 e^{\sqrt{c_1} \xi }}{-2 c_2 e^{\sqrt{c_1} \xi }+e^{2 \sqrt{c_1} \xi }+c_2^2-4 c_1 c_3}. \end{aligned}$$
(33)

Case I:

$$\begin{aligned} c_1=-\kappa ^2, c_2=0, A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=0, c_3=\delta , \end{aligned}$$
(34)

which gives

$$\begin{aligned} U_5=\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (4 \kappa ^2 \delta +e^{2 \sqrt{-\kappa ^2} \xi })}, \end{aligned}$$
(35)

hence

$$\begin{aligned} u_5 (y,z,t)=\left[ \frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (4 \kappa ^2 \delta +e^{2 \sqrt{-\kappa ^2} \xi })}\right] e^{i\,\theta }. \end{aligned}$$
(36)

Case II:

$$\begin{aligned} c_1=-\kappa ^2;c_2=0, A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=0, c_3=\delta , \end{aligned}$$
(37)

result will be:

$$\begin{aligned} U_6=-\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (4\kappa ^2 \delta +e^{2 \sqrt{-\kappa ^2} \xi })}, \end{aligned}$$
(38)

hence

$$\begin{aligned} u_6 (y,z,t)=\left[ -\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (4\kappa ^2 \delta +e^{2 \sqrt{-\kappa ^2} \xi })}\right] e^{i\,\theta }. \end{aligned}$$
(39)

Case III:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }},c_3=\delta , \end{aligned}$$
(40)

third result will be in this form:

$$\begin{aligned} U_7=-\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } (e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi }-4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi })}-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(41)

hence

$$\begin{aligned} u_7 (y,z,t)=\left[ -\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma }(e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi }-4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi })} -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(42)

Case IV:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=-2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, c_3=\delta , \end{aligned}$$
(43)

fourth result will be:

$$\begin{aligned} U_8=\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } (4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }+e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi })}-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(44)

hence

$$\begin{aligned} u_8 (y,z,t)=\left[ \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } (4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }+e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi })} -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(45)

Case V:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=-2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }},A_0=\frac{\kappa }{\sqrt{2} \sqrt{\gamma }},c_3=\delta , \end{aligned}$$
(46)
$$\begin{aligned} U_9=\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma }(4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }+e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi })}-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(47)

hence

$$\begin{aligned} u_9 (y,z,t)=\left[ \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } (4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }+e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi })} -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(48)

Case VI:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=2 \sqrt{2}\kappa \sqrt{c_3},\nonumber \\&A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }},A_0=\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, c_3=\delta , \end{aligned}$$
(49)
$$\begin{aligned} U_{10}=\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi }-4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }\right) }+\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(50)

hence

$$\begin{aligned} u_{10} (y,z,t)=\left[ \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( e^{2 \sqrt{2} \sqrt{\kappa ^2} \xi }-4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }\right) } +\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(51)

Family II


when

$$\begin{aligned} \psi (\xi )=-\frac{4 c_1 e^{\sqrt{c_1} \xi }}{c_2^2 \left( -e^{2 \sqrt{c_1} \xi }\right) +2 c_2 e^{\sqrt{c_1} \xi }+4 c_1 c_3 e^{2 \sqrt{c_1} \xi }-1}. \end{aligned}$$
(52)

Case I:

$$\begin{aligned} c_1=-\kappa ^2, c_2=0, A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=0, c_3=\delta , \end{aligned}$$
(53)
$$\begin{aligned} U_{11}=-\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \kappa ^2 \delta e^{2 \sqrt{-\kappa ^2} \xi }-1\right) }, \end{aligned}$$
(54)

hence

$$\begin{aligned} u_{11} (y,z,t)=\left[ -\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \kappa ^2 \delta e^{2 \sqrt{-\kappa ^2} \xi }-1\right) }\right] e^{i\,\theta }. \end{aligned}$$
(55)

Case II:

$$\begin{aligned} c_1=-\kappa ^2;c_2=0, A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=0, c_3=\delta , \end{aligned}$$
(56)

result will be:

$$\begin{aligned} U_{12}=\frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (-4 \kappa ^2 \delta e^{2 \sqrt{-\kappa ^2} \xi }-1)}, \end{aligned}$$
(57)

hence

$$\begin{aligned} u_{12} (y,z,t)=\left[ \frac{4 \kappa ^2 \sqrt{\delta } e^{\sqrt{-\kappa ^2} \xi }}{\sqrt{\gamma } (-4 \kappa ^2 \delta e^{2 \sqrt{-\kappa ^2} \xi }-1)}\right] e^{i\,\theta }. \end{aligned}$$
(58)

Case III:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }},A_0=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\cdot c_3=\delta , \end{aligned}$$
(59)

result will be in this form:

$$\begin{aligned} U_{13}=\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\beta } \left( 4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1\right) }-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(60)

hence

$$\begin{aligned} u_{13}(y,z,t)=\left[ \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\beta } (4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1)}-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(61)

Case IV:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=-2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }},c_3=\delta , \end{aligned}$$
(62)

result will be:

$$\begin{aligned} U_{14}=-\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1\right) }-\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(63)

hence

$$\begin{aligned} u_{14} (y,z,t)=\left[ -\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1\right) } -\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(64)

Case V:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=-2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=-\frac{\sqrt{c_3}}{\sqrt{\gamma }}, A_0=\frac{\kappa }{\sqrt{2} \sqrt{\gamma }},c_3=\delta , \end{aligned}$$
(65)

result will be:

$$\begin{aligned} U_{15}= \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1\right) }+\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}, \end{aligned}$$
(66)

hence

$$\begin{aligned} u_{15} (y,z,t)=\left[ \frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma } \left( -4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1\right) }+\frac{\kappa }{\sqrt{2} \sqrt{\gamma }}\right] e^{i\,\theta }. \end{aligned}$$
(67)

Case VI:

$$\begin{aligned}&c_1=2 \kappa ^2, c_2=2 \sqrt{2} \kappa \sqrt{c_3},\nonumber \\&A_1=\frac{\sqrt{c_3}}{\sqrt{\gamma }},A_0=\frac{\alpha }{\sqrt{2} \sqrt{\gamma }},c_3=\delta , \end{aligned}$$
(68)

result will be:

$$\begin{aligned} U_{16}= \frac{\kappa }{\sqrt{2} \sqrt{\beta }}-\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma }(4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1)}, \end{aligned}$$
(69)

hence

$$\begin{aligned} u_{16} (y,z,t)=\left[ \frac{\kappa }{\sqrt{2} \sqrt{\beta }}-\frac{8 \kappa ^2 \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }}{\sqrt{\gamma }(4 \sqrt{2} \kappa \sqrt{\delta } e^{\sqrt{2} \sqrt{\kappa ^2} \xi }-1)}\right] e^{i\,\theta }. \end{aligned}$$
(70)

3 Discussion and results

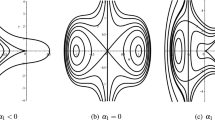
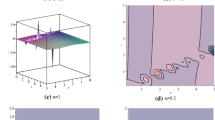
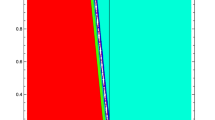
The following figures presents the graphical representation of solitons for various values of the parameters. Mathematica 11.0 is used to carry out simulations and to visualize the behavior of nonlinear waves. In each case Figs. 1, 2, 3, 4, 5, 6 and 7a–c demonstrate the structures for real, imaginary and absolute solutions respectively.

Fig. 1
figure 1

\(u_{1}(y, t)\): \(\alpha ={2}\), \(\beta ={3}\), \(\gamma ={2}\), \(\kappa ={3}\), \(z=0\), \(c_1={3}\), \(c _2={2}\)

Full size image
Fig. 2
figure 2

\(u_{3}(y, t)\): \(\alpha ={4}\), \(\beta ={0.5}\), \(\gamma ={3}\), \(\kappa ={2}\), \(c_1={3}\), \(c_2={2}\), \(z=0\)

Full size image
Fig. 3
figure 3

\(u_{3}(y, t)\): \(\alpha ={0.5}\), \(\beta ={0.5}\), \(\gamma ={2}\), \(\kappa ={1}\), \(c_1={2}\), \(c _2={3}\), \(z=0\)

Full size image
Fig. 4
figure 4

\(u_{5}(y, t)\): \(\alpha ={2}\), \(\beta ={3}\), \(\gamma ={2}\), \(\kappa ={3}\), \(c_1={3}\), \(z=0\), \(c _2={2}\)

Full size image
Fig. 5
figure 5

\(u_{7}(y, t)\): \(\alpha ={1}\), \(\beta ={1.5}\), \(\gamma ={2}\), \(\kappa ={2}\), \(\delta ={1}\), \(z=0\), \(c_1=-\kappa ^2\), \(c _2={0}\), \(c_3=\delta\)

Full size image
Fig. 6
figure 6

\(u_{11}(y, t)\): \(\alpha ={1}\), \(\beta ={1.5}\), \(\gamma ={4}\), \(\kappa ={2}\), \(\delta ={1}\), \(z=0\), \(c _1=-\kappa ^2\), \(c _2={0}\), \(c_3=\delta\)

Full size image
Fig. 7
figure 7

\(u_{14}(y, t)\): \(\alpha ={1}\), \(\beta ={1.5}\), \(\gamma ={4}\), \(\kappa ={2}\), \(\delta ={1}\), \(z=0\), \(c _1=-\kappa ^2\), \(c_2=-2\sqrt{2}\kappa \sqrt{c_3}\), \(c_3=\delta\)

Full size image

4 Concluding remarks

In this article, a set integration tools, namely the MSE technique and the AE methods are employed to find some novel exact traveling wave solutions to the M-Fractional paraxial NLSE with Kerr media. The proposed techniques are very powerful and may be effective to deal with many other nonlinear models arising in the recent era of the theory of optics. The geometrical structures of some selected solutions are also illustrated with the help of Mathematica 11.0.