1 Introduction

In real-world, nonlinear evolution equations (NLEEs) play significant roles because every natural phenomenon is modelled by these types of equations. Their solutions help us to better understand and analyse our Universe. Therefore, finding analytical solutions of NLEEs increase is important nowadays. Scientists have proposed many methods, such as the generalised exponential rational function method [1], the Lie symmetry analysis [2], the extended trial equation method [3], the auto-Bäcklund transformation method [4, 5], the Hirota bilinear method [6,7,8,9], the sine-Gordon expansion method [10, 11], modified \(\exp (-\Omega \left( \xi \right) )\)-expansion function method [12, 13] etc. to get exact solutions.

In this work, we study the newly developed method, that is the rational sine-Gordon expansion method (RSGEM), which is the generalised form of the well-known sine-Gordon expansion method, to obtain new types of soliton solutions of the governing equations. Solitons, also known as solitary waves, are important in theoretical physics. Solitons can be seen everywhere in natural life: in neuroscience, plasma physics, quantum field theory, optical fibres, fluid dynamics, magnetic field etc. In literature, many different types of solitons can be seen. For example, chirped, conoidal, lumps, M-shaped, tunable solitons, rogue waves, Bell waves, double breather waves [14,15,16].

Chiral solitons arise in quantum mechanics, especially in the quantum Hall effect field. The CNLSE has both bright and dark solitons which have significant applications in the quantum Hall effect. In literature, bright soliton (known as Bell-shaped soliton or non-topological soliton) solutions symbolise the singular travelling wave properties and the dark solitons (known as topological soliton or simply topological defect) arise during calculations of magnetic moment and rapidity of special relativity.

Quantum Hall effect is a general quantum mechanical statement of the classical Hall effect observed in two-dimensional structures at very low temperatures. The chiral nonlinear Schrödinger equation (CNLSE) describes the edge states of the fractional quantum Hall effect [17,18,19,20]. In 1998, Nishino et al found progressive wave solutions, bright soliton and dark soliton, of the (1\(+\)1)-dimensional nonlinear chiral Schrödinger equation [21]. The CNLSE with Bohm potential has been studied in [22,23,24,25,26,27] using various methods. The simplified extended sinh-Gordon equation expansion method is used to obtain various soliton solutions of (2\(+\)1)-dimensional CNLSE such as singular solitons and combined dark–bright solitons [28]. The sine-Gordon expansion method is proposed to get soliton solutions of the (1\(+\)1) and (2\(+\)1)-dimensional CNLSE in [29]. Both the extended direct algebraic method and extended trial equation method were used to get exact solutions of the (2\(+\)1)-dimensional CNLSE [30]. These studies have proposed different kinds of solutions including Jacobi elliptic function solutions, optical soliton solutions, dark-bright soliton solutions, hyperbolic function solutions to science.

The (1\(+\)1)-dimensional nonlinear chiral Schrödinger equation is given as [26]

$$\begin{aligned}&i{{q}_{t}}+\alpha {{q}_{xx}}+i\beta ( qq_{x}^{*}-{{q}^{*}}{{q}_{x}} )q=0, \end{aligned}$$
(1)

where q is the complex function which depends on \(x\text { and }t\), superscript \(*\) represents complex conjugate, \(\alpha \) is the coefficient of dispersion terms and \(\beta \) is the nonlinear coupling constant.

The (2\(+\)1)-dimensional CNLSE is given as [23]

$$\begin{aligned}&i{{q}_{t}}+\alpha \left( {{q}_{xx}}+{{q}_{yy}} \right) +i\big ( {{\beta }_{1}}\left( qq_{x}^{*}-{{q}^{*}}{{q}_{x}} \right) \nonumber \\&\quad +{{\beta }_{2}}( qq_{y}^{*}-{{q}^{*}}{{q}_{y}} ) \big )q=0, \end{aligned}$$
(2)

where q is the complex function which depends on \(x\text { and }t\), superscript \(*\) represents complex conjugate, \(i=\sqrt{-1}\) , \(\alpha \) is the coefficient of the dispersion terms, \({{\beta }_{1}},{{\beta }_{2}}\) are the nonlinear coupling constants. Both eqs (1) and (2) are nonlinear equations and this nonlinearity is known as the current density. We consider the (1\(+\)1)- and (2\(+\)1)-dimensional CNLSE with the sense of the conformable derivative by using the RSGEM in this framework. The conformable fractional derivative was developed by Khalil et al [31]. In recent years, the conformable fractional derivative has been more preferred to other fractional derivative definitions such as Riemann–Liouville, Caputo–Fabrizio, Caputo [32,33,34]. The paper is organised as follows: we give definition and some properties of conformable derivative in §2, description of the proposed method, the rational sine-Gordon expansion method (RSGEM) is given in §3, application of the given method to the (1\(+\)1)- and (2\(+\)1)-dimensional CNLSE is demonstrated in §4 and in §5, some conclusions are given.

2 Preliminaries on conformable derivative

DEFINITION

Suppose that \(f:\left[ 0,\infty \right) \rightarrow {\mathbb {R}}\). The conformable fractional derivative of f of order \(\alpha \) is defined as

$$\begin{aligned} T_{\alpha }\left( f \right) \left( t \right) =\underset{\varepsilon \rightarrow 0}{ \lim }\,\frac{f\left( t+\varepsilon {{t}^{1-\alpha }} \right) -f\left( t \right) }{\varepsilon }, \end{aligned}$$

for all \(t>0\), \(\alpha \in \left( 0,1 \right] \) [31].

Theorem

Let \({{T}_{\alpha }}\) be a fractional derivative operator with order \(\alpha \) and \(\alpha \in \left( 0,1 \right] \), f, g be \(\alpha \)-differentiable at point \(t>0.\) Then [31,32,33,34,35]

  • \({{T}_{\alpha }}\left( af+bg \right) =a{{T}_{\alpha }}\left( f \right) +b{{T}_{\alpha }}\left( g \right) ,\forall a,b\in {\mathbb {R}}.\)

  • \({{T}_{\alpha }}\left( {{t}^{p}} \right) =p{{t}^{p-\alpha }},\forall p\in {\mathbb {R}}.\)

  • \({{T}_{\alpha }}\left( fg \right) =f{{T}_{\alpha }}\left( g \right) +g{{T}_{\alpha }}\left( f \right) .\)

  • \({{T}_{\alpha }}\left( \frac{f}{g} \right) =\frac{g{{T}_{\alpha }}\left( f \right) -f{{T}_{\alpha }} \left( g \right) }{{{g}^{2}}}.\)

  • \({{T}_{\alpha }}\left( \lambda \right) =0,\) for all constant functions \(f\left( t \right) =\lambda .\)

  • If f is differentiable then \({{T}_{\alpha }}\left( f \right) \left( t \right) ={{t}^{1-\alpha }}\frac{\mathrm {d}f}{\mathrm {d}t}\left( t \right) .\)

Theorem (chain rule). Let \(h,g:\left( a,\infty \right) \rightarrow R\) be \(\alpha \)-differentiable functions, where \(0<\alpha \le 1\). Let \(k\left( t \right) =h\left( g\left( t \right) \right) \). Then \(k\left( t \right) \) is \(\alpha \)-differentiable and for all t with \(t\ne a\) and \(g\left( t \right) \ne 0\), we have [36]

$$\begin{aligned} \left( L_{\alpha }^{a}k \right) \left( t \right) =\left( L_{\alpha }^{a}h \right) \left( g\left( t \right) \right) \cdot \left( L_{\alpha }^{a}g \right) \left( t \right) g{{\left( t \right) }^{\alpha -1}}. \end{aligned}$$

If \(t=a\), we have

$$\begin{aligned} \left( L_{\alpha }^{a}k \right) \left( t \right) =\underset{t\rightarrow {{a}^{+}}}{\mathop {\lim }}\,\left( L_{\alpha }^{a}h \right) \left( g\left( t \right) \right) \cdot \left( L_{\alpha }^{a}g \right) \left( t \right) g{{\left( t \right) }^{\alpha -1}}. \end{aligned}$$

3 Fundamental properties of the rational sine-Gordon expansion method

In this section, we explain the rational sine-Gordon expansion method (SGEM). Firstly, we give the general facts of the well-known SGEM. Let suppose the sine-Gordon equation

$$\begin{aligned} {{\varphi }_{xx}}-{{\varphi }_{tt}}={{m}^{2}}\sin (\varphi ), \end{aligned}$$
(3)

where \(\varphi =\varphi (x,t)\) and m is a real constant. Considering the wave transform \(\varphi =\varphi (x,t)=\Phi (\xi ),\) \(\xi =\mu \left( x-ct \right) \) to eq. (2), it yields the nonlinear ordinary differential equation

$$\begin{aligned} {\Phi }''=\frac{{{m}^{2}}}{{{\mu }^{2}}\left( 1-{{c}^{2}} \right) }\sin (\Phi ), \end{aligned}$$
(4)

where \(\Phi =\Phi (\xi ), \xi \) is the amplitude and c is the velocity of the travelling wave. After complete simplification, we find eq. (4) as follows:

$$\begin{aligned} {{\left[ {{\left( \frac{\Phi }{2} \right) }^{\prime }} \right] }^{2}}=\frac{{{m}^{2}}}{{{\mu }^{2}}\left( 1-{{c}^{2}} \right) }{{\sin }^{2}}\left( \frac{\Phi }{2} \right) +C, \end{aligned}$$
(5)

where C is the constant of integration. Substituting \(C=0,\varpi \left( \xi \right) ={\Phi }/{2}\) and \({{a}^{2}}={{{m}^{2}}}/({{{\mu }^{2}}\left( 1-{{c}^{2}}) \right) }\) in eq. (5), we get

$$\begin{aligned} {\varpi }'=a\sin \left( \varpi \right) . \end{aligned}$$
(6)

Setting \(a=1\) in eq. (6), we get

$$\begin{aligned} {\varpi }'=\sin \left( \varpi \right) . \end{aligned}$$
(7)

Solving eq. (7) by the variables separable method, we get two important properties of trigonometric functions as follows:

$$\begin{aligned} \sin (\varpi )= & {} \sin \left( \varpi \left( \xi \right) \right) \nonumber \\= & {} {{\left. \frac{2p{{\mathrm {e}}^{\xi }}}{{{p}^{2}}{{\mathrm {e}}^{2\xi }}+1} \right| }_{p=1}}=\quad \mathrm {sech}(\xi ),\end{aligned}$$
(8)
$$\begin{aligned} \cos (\varpi )= & {} \cos \left( \varpi \left( \xi \right) \right) \nonumber \\= & {} {{\left. \frac{{{p}^{2}}{{\mathrm {e}}^{2\xi }}-1}{{{p}^{2}}{{\mathrm {e}}^{2\xi }}+1} \right| }_{p=1}}=\mathrm {tanh}(\xi ), \end{aligned}$$
(9)

where p is the non-zero integral constant. Let us consider the nonlinear partial differential equation of the following form which searches the solution;

$$\begin{aligned} P\left( \varphi ,{{\varphi }_{x}},{{\varphi }_{t}},{{\varphi }_{xx}},{{\varphi }_{tt}},{{\varphi }_{xt}},{{\varphi }_{xxx}},{{\varphi }_{xxt}},... \right) =0, \end{aligned}$$
(10)
$$\begin{aligned} N\left( \Phi ,\frac{\mathrm {d}\Phi }{\mathrm {d}\xi },\frac{{{\mathrm {d}}^{2}}\Phi }{\mathrm {d}{{\xi }^{2}}},\ldots \right) =0, \end{aligned}$$

where N is a nonlinear ordinary equation (NODE) whose partial derivatives of \(\Phi \) depends on \(\xi \). In the SGEM, the solution of eq. (10) is considered in the following form:

$$\begin{aligned} \Phi \left( \xi \right) =\sum \limits _{i=1}^{n}{{{\tanh }^{i-1}}\left( \xi \right) \left[ {{B}_{i}}\,\mathrm {sech}\!\left( \xi \right) +{{A}_{i}}\tanh \! \left( \xi \right) \right] }+{{A}_{0}}. \end{aligned}$$
(11)

Equation (11) can be rearranged by considering eqs (8) and (9) as follows:

$$\begin{aligned} \Phi \left( \varpi \right)&=\sum \limits _{i=1}^{n}{{\cos }^{i-1}}\left( \varpi \right) \left[ {{B}_{i}}\sin \left( \varpi \right) \right. \nonumber \\&\quad \left. +{{A}_{i}}\cos \left( \varpi \right) \right] +{{A}_{0}}. \end{aligned}$$
(12)

We know that rational functions are more general than polynomial functions. If we consider the solution function as a rational function, we can find considerably better wave solutions than the above form. Contrary to other works in the literature, our solution functions have two auxiliary functions, viz.\({\text {sech}}\!\left( \xi \right) ,\tanh \!\left( \xi \right) \). We consider the following solution form [37]:

$$\begin{aligned}&\Phi \left( \xi \right) \nonumber \\&\quad =\frac{\sum _{i=1}^{M}{{{\tanh }^{i-1}}\left( \xi \right) \left[ {{A}_{i}}\mathrm {sech}\!\!\,\left( \xi \right) +{{C}_{i}}\tanh \!\!\,\left( \xi \right) \right] }+{{A}_{0}}}{\sum _{i=1}^{M}{{{\tanh }^{i-1}}\left( \xi \right) \left[ {{B}_{i}}\mathrm {sech}\!\!\,\left( \xi \right) +{{D}_{i}}\tanh \!\!\,\left( \xi \right) \right] }+{{B}_{0}}}\nonumber \\ \end{aligned}$$
(13)

which is also written as

$$\begin{aligned}&\Phi \left( \varpi \right) \nonumber \\&{=}\frac{\sum _{i=1}^{M}{{{\cos }^{i-1}}\left( \varpi \right) \left[ {{A}_{i}}\sin \left( \varpi \right) +{{C}_{i}}\cos \left( \varpi \right) \right] }+{{A}_{0}}}{\sum _{i=1}^{M}{{{\cos }^{i-1}}\left( \varpi \right) \left[ {{B}_{i}}\sin \left( \varpi \right) +{{D}_{i}}\cos \left( \varpi \right) \right] }+{{B}_{0}}}.\nonumber \\ \end{aligned}$$
(14)

\({{A}_{i}},{{B}_{i}},{{C}_{i}},{{D}_{i}},{{A}_{0}},{{B}_{0}}\) are constants to be determined later. The values of \({{A}_{i}},{{B}_{i}},{{C}_{i}},{{D}_{i}}\) are not zero at the same time. Applying the balance principle between the highest power nonlinear term and highest derivative in NODE, the value of M is identified. Reducing the expression that corresponds to the same denominator and taking the coefficients of \({{\sin }^{i}}\left( \varpi \right) {{\cos }^{j}}\left( \varpi \right) \) to zero, we get a set of algebraic equation \({{A}_{i}},{{B}_{i}},{{C}_{i}},{{D}_{i}},{{A}_{0}},\) \({{B}_{0}},\mu \text { and }c\), the values of which are found by solving the set of algebraic equations by relevant software. In the end, we substitute these values into eq. (13) and get new travelling wave solutions to eq. (10).

4 Applications of the RSGEM

4.1 Solutions of the conformable (1\(+\)1)-dimensional CNLSE

The conformable (1\(+\)1)-dimensional chiral nonlinear Schrödinger’s equation is given as

$$\begin{aligned} iq_{t}^{\mu }+\alpha {{q}_{xx}}+i\beta \left( qq_{x}^{*}-{{q}^{*}}{{q}_{x}} \right) q=0, \end{aligned}$$
(15)

where \(0<\mu \le 1\) is conformable derivative order, \(\alpha ,\beta \) are real constants. We shall take \(\alpha =1\) in this paper.

Let us consider the wave transform given as follows:

$$\begin{aligned}&q\left( x,t \right) =u\left( \zeta \right) {{\mathrm {e}}^{i\theta }},\quad \zeta =p\left( x+v\frac{{{t}^{\mu }}}{\mu } \right) ,\nonumber \\&\theta =kx+w\frac{{{t}^{\mu }}}{\mu }+\phi , \end{aligned}$$
(16)

where p represents the soliton shape, v is the velocity, k is the soliton frequency, w is the wave number and \(\phi \) is the phase constant. Using the conformable derivative operator, we put eq. (16) into eq. (15), and we obtain imaginary and real parts of the following nonlinear ordinary differential equation:

$$\begin{aligned}&{{p}^{2}}{u}''+2k\beta {{u}^{3}}-( w+{{k}^{2}} )u=0, \end{aligned}$$
(17)
$$\begin{aligned}&\left( 2k+v \right) p{u}'=0. \end{aligned}$$
(18)

Homogen balance principle gives \(M=1\) in eq. (17). For \(M=1\), eq. (14) turns to

$$\begin{aligned} u\left( \zeta \right) =\frac{{{A}_{1}}\sin \!\left( \zeta \right) +{{C}_{1}}\cos \!\left( \zeta \right) +{{A}_{0}}}{{{B}_{1}}\sin \!\left( \zeta \right) +{{D}_{1}}\cos \!\left( \zeta \right) +{{B}_{0}}}. \end{aligned}$$
(19)

Putting eq. (19) and its second-order derivative into eq. (17), we get a polynomial in powers of \({{\sin }^{i}}\!\!\left( \varpi \right) \,{{{\cos }^{j}}\!\!\left( \varpi \right) }\) functions. Collecting the coefficients of \({{\sin }^{i}}\left( \varpi \right) {{\cos }^{j}}\left( \varpi \right) \) of similar power and equating each sum to zero, gives an algebraic equation system. Inserting the system of algebraic equations produces the values of \({{A}_{1}},{{B}_{1}},{{C}_{1}},{{D}_{1}}\), \({{A}_{0}},{{B}_{0}}\) and other parameters. By substituting the values of the parameters for eq. (13), we obtain some new rational travelling wave results for eq. (1).

Case 1: When the coefficients are as follows:

$$\begin{aligned}&\text { }{{A}_{1}}=\frac{p}{2}\sqrt{\frac{B_{0}^{2}-D_{1}^{2}}{k\beta }},\quad {{A}_{0}}=\frac{ip{{D}_{1}}}{2\sqrt{k\beta }},\nonumber \\&{{C}_{1}}=\frac{ip{{B}_{0}}}{2\sqrt{k\beta }},\quad W =-{{k}^{2}}-\frac{{{p}^{2}}}{2},\quad {{B}_{1}}=0, \end{aligned}$$
(20)

we get

$$\begin{aligned} {{q}_{1}}\left( x,t \right) =\frac{{{\mathrm {e}}^{i( kx+\frac{( -{{k}^{2}}-\frac{{{p}^{2}}}{2} ){{t}^{\mu }}}{\mu }+\phi )}}p{\text {sech}}( p( x+\frac{v{{t}^{\mu }}}{\mu } ) )\sqrt{B_{0}^{2}-D_{1}^{2}}+ip( {{D}_{1}}+{{B}_{0}}\tanh ( p( x+\frac{v{{t}^{\mu }}}{\mu } ) ) )}{2\sqrt{k\beta }( {{B}_{0}}+{{D}_{1}}\tanh ( p( x+\frac{v{{t}^{\mu }}}{\mu } ) ) )}. \end{aligned}$$
(21)

Case 2: For the coefficients

$$\begin{aligned}&{{A}_{1}}=-\frac{p}{2}\sqrt{\frac{B_{0}^{2}-D_{1}^{2}}{k\beta }},{{C}_{1}}=\frac{ip{{B}_{0}}}{2\sqrt{k\beta }},\nonumber \\&w=-{{k}^{2}}-\frac{{{p}^{2}}}{2},\quad {{A}_{0}}={{D}_{1}}=0, \end{aligned}$$
(22)

we get the following wave solution:

$$\begin{aligned} {{q}_{2}}\left( x,t \right) =-\frac{{{\mathrm {e}}^{i( kx+\frac{( -{{k}^{2}}-\frac{{{p}^{2}}}{2} ){{t}^{\mu }}}{\mu }+\phi )}}p( -i\sinh ( p( x+\frac{v{{t}^{\mu }}}{\mu } ) ){{B}_{0}}+\sqrt{B_{0}^{2}-D_{1}^{2}} )}{2\sqrt{k\beta }( \cosh ( p( x+\frac{v{{t}^{\mu }}}{\mu } ) ){{B}_{0}}+{{B}_{1}} )}. \end{aligned}$$
(23)

Case 3: For the values

$$\begin{aligned}&{{C}_{1}}=-\frac{ip{{B}_{0}}}{\sqrt{k\beta }},\quad {{A}_{0}}=-\frac{ip{{D}_{1}}}{\sqrt{k\beta }},\nonumber \\&w=-{{k}^{2}}-2{{p}^{2}},\quad {{A}_{1}}={{B}_{1}}=0, \end{aligned}$$
(24)

we get

$$\begin{aligned}&{{q}_{3}}\left( x,t \right) =-i\frac{{{\mathrm {e}}^{i( kx+\frac{( -{{k}^{2}}-2{{p}^{2}} ){{t}^{^{\mu }}}}{^{\mu }}+\phi )}}p( {{D}_{1}}+{{B}_{0}}\tanh ( p( x+\frac{v{{t}^{^{\mu }}}}{\mu } ) ) )}{\sqrt{k\beta }( {{B}_{0}}+{{D}_{1}}\tanh ( p( x+\frac{v{{t}^{^{\mu }}}}{\mu } ) ) )}. \end{aligned}$$
(25)

Case 4: When

$$\begin{aligned}&{{A}_{1}}=\frac{\sqrt{\left( -B_{0}^{2}+D_{1}^{2} \right) C_{1}^{2}}}{{{B}_{0}}},\quad k=-\sqrt{-\frac{{{p}^{2}}}{2}-w},\nonumber \\&\beta =\frac{{{p}^{2}}B_{0}^{2}}{2\sqrt{2}\sqrt{-{{p}^{2}}-2w}C_{1}^{2}},\quad {{A}_{0}}={{D}_{1}}=0, \end{aligned}$$
(26)

we have

$$\begin{aligned} {{q}_{4}}\left( x,t \right) =\frac{{{\mathrm {e}}^{i( -\sqrt{-\frac{{{p}^{2}}}{2}-w}x+\frac{w{{t}^{^{\mu }}}}{\mu }+\phi )}}\left( \frac{{\text {sech}}( p( x+\frac{v{{t}^{^{\mu }}}}{\mu } ) )\sqrt{( -B_{0}^{2}+D_{1}^{2} )C_{1}^{2}}}{{{B}_{0}}}+{{C}_{1}}\tanh ( p( x+\frac{v{{t}^{^{\mu }}}}{\mu } ) )\right) }{{{B}_{0}}+{\text {sech}}( p( x+\frac{v{{t}^{^{\mu }}}}{\mu } ) ){{B}_{1}}}. \end{aligned}$$
(27)

Case 5: For the selected coefficients

$$\begin{aligned}&{{A}_{1}}=-\frac{p\sqrt{B_{0}^{2}-B_{1}^{2}-D_{1}^{2}}}{2\sqrt{k\beta }},\quad {{A}_{0}}=-\frac{ip{{D}_{1}}}{2\sqrt{k\beta }},\nonumber \\&{{C}_{1}}=-\frac{ip{{B}_{0}}}{2\sqrt{k\beta }},\quad w=-{{k}^{2}}-\frac{{{p}^{2}}}{2}, \end{aligned}$$
(28)

we have

$$\begin{aligned} {{q}_{5}}\left( x,t \right) =-\frac{{{\mathrm {e}}^{i( kx+\frac{( -{{k}^{2}}-\frac{{{p}^{2}}}{2} ){{t}^{\mu }}}{\mu }+\phi )}}p( i\sinh ( p( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{B}_{0}}+i\cosh ( p( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{D}_{1}}+\sqrt{B_{0}^{2}-B_{1}^{2}-D_{1}^{2}} )}{2\sqrt{k\beta }( \cosh ( p( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{B}_{0}}+{{B}_{1}}+\sinh ( p( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{D}_{1}} )}. \end{aligned}$$
(29)

Case 6: If the coefficients are selected as

$$\begin{aligned}&{{A}_{0}}=\frac{{{A}_{1}}{{D}_{1}}}{\sqrt{B_{1}^{2}+D_{1}^{2}}},\quad p=\sqrt{2\left( -{{k}^{2}}-w \right) },\nonumber \\&\beta =\frac{\left( {{k}^{2}}+w \right) \left( B_{1}^{2}+D_{1}^{2} \right) }{2kA_{1}^{2}},\quad {{C}_{1}}={{B}_{0}}=0, \end{aligned}$$
(30)

we get

$$\begin{aligned}&{{q}_{6}}( x,t)\nonumber \\&=\frac{{{\mathrm {e}}^{i( kx+\frac{w{{t}^{\mu }}}{\mu }+\phi )}}{{A}_{1}}\left( 1\,{+}\,\frac{\cosh ( \sqrt{2( -{{k}^{2}}-w )}( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{D}_{1}}}{\sqrt{B_{1}^{2}+D_{1}^{2}}} \right) }{{{B}_{1}}+\sinh ( \sqrt{2( -{{k}^{2}}-w )}( x-\frac{2k{{t}^{\mu }}}{\mu } ) ){{D}_{1}}}.\nonumber \\ \end{aligned}$$
(31)

Case 7: For

$$\begin{aligned}&p=\sqrt{\frac{-{{k}^{2}}-w}{2}},\quad \beta =\frac{\left( {{k}^{2}}+w \right) B_{0}^{2}}{2kC_{1}^{2}},\nonumber \\&{{A}_{0}}=\frac{{{C}_{1}}{{D}_{1}}}{{{B}_{0}}},\quad {{A}_{1}}={{B}_{1}}=0, \end{aligned}$$
(32)

we have

$$\begin{aligned}&{{q}_{7}}( x,t )=\nonumber \\&\frac{{{\mathrm {e}}^{i( kx+\frac{w{{t}^{\mu }}}{\mu }+\phi )}}{{C}_{1}}\left( {{D}_{1}}+{{B}_{0}}\tanh \left( \frac{\sqrt{-{{k}^{2}}-w}( x-\frac{2k{{t}^{\mu }}}{\mu } )}{\sqrt{2}} \right) \right) }{{{B}_{0}}\left( {{B}_{0}}+{{D}_{1}}\tanh ( \frac{\sqrt{-{{k}^{2}}-w}( x-\frac{2k{{t}^{\mu }}}{\mu } )}{\sqrt{2}} ) \right) }.\nonumber \\ \end{aligned}$$
(33)

Case 8: When

$$\begin{aligned}&{{A}_{1}}=\frac{{{C}_{1}}\sqrt{-B_{0}^{2}+D_{1}^{2}}}{{{B}_{0}}},\quad {{A}_{0}}=\frac{{{C}_{1}}{{D}_{1}}}{{{B}_{0}}},\nonumber \\&\beta =\frac{\left( {{k}^{2}}+w \right) B_{0}^{2}}{2kC_{1}^{2}},\quad p=-\sqrt{2\left( -{{k}^{2}}-w \right) },\quad {{B}_{1}}=0, \nonumber \\ \end{aligned}$$
(34)

the following solution is obtained:

$$\begin{aligned} {{q}_{8}}\left( x,t \right) =\frac{{{\mathrm {e}}^{i( kx+\frac{w{{t}^{\mu }}}{\mu }+\phi )}}{{C}_{1}}( {{D}_{1}}+{\text {sech}}( p( -x+\frac{2k{{t}^{\mu }}}{\mu } ) )\sqrt{-B_{0}^{2}+D_{1}^{2}}-{{B}_{0}}\tanh ( p( -x+\frac{2k{{t}^{\mu }}}{\mu } ) ) )}{{{B}_{0}}( {{B}_{0}}-{{D}_{1}}\tanh ( p( -x+\frac{2k{{t}^{\mu }}}{\mu } ) ) )}. \end{aligned}$$
(35)

4.2 Solutions of the conformable (2\(+\)1)-dimensional CNLSE

The conformable (2\(+\)1)-dimensional chiral nonlinear Schrödinger’s equation is given by

$$\begin{aligned}&iq_{t}^{\mu }+\alpha \left( {{q}_{xx}}+{{q}_{yy}} \right) \nonumber \\&\quad +i( {{\beta }_{1}}(qq_{x}^{*}-{{q}^{*}}{{q}_{x}})+{{\beta }_{2}}( qq_{y}^{*}-{{q}^{*}}{{q}_{y}}))q=0, \nonumber \\ \end{aligned}$$
(36)

where \(0<\mu \le 1\) is the conformable derivative order, \(\alpha , {{\beta }_{1}}, {{\beta }_{2}}\) are real constants. Let us consider the wave transform as follows:

$$\begin{aligned}&q\left( x,y,t \right) =u\left( \zeta \right) {{\mathrm {e}}^{i\theta }},\quad \zeta =ax+by-v\frac{{{t}^{\mu }}}{\mu },\nonumber \\&\theta =rx+sy+w\frac{{{t}^{\mu }}}{\mu }+\phi , \end{aligned}$$
(37)

where v is the velocity, r is the soliton frequency, w is the wave number, \(\phi \) is the phase constant, a, b, r, s are real constants. Using conformable derivative, we put eq. (37) into eq. (36) and we obtain the imaginary and the real parts of the nonlinear differential equation as follows:

$$\begin{aligned}&\alpha \left( {{a}^{2}}+{{b}^{2}} \right) {u}''-\left( \alpha \left( {{r}^{2}}+{{s}^{2}} \right) +w \right) u\nonumber \\&\quad +2\left( r{{\beta }_{1}}+s{{\beta }_{2}} \right) {{u}^{3}}=0, \end{aligned}$$
(38)
$$\begin{aligned}&\left( 2\alpha \left( ar+bs \right) -v \right) {u}'=0. \end{aligned}$$
(39)

Homogen balance principle gives \(M=1\) in eq. (38). For \(M=1\), eq. (14) turns to

$$\begin{aligned} u\left( \zeta \right) =\frac{{{A}_{1}}\sin \!\left( \zeta \right) +{{C}_{1}}\cos \!\left( \zeta \right) +{{A}_{0}}}{{{B}_{1}}\sin \!\left( \zeta \right) +{{D}_{1}}\cos \!\left( \zeta \right) +{{B}_{0}}}. \end{aligned}$$
(40)

Putting eq. (40) and its second-order derivative into eq. (38), yields a polynomial in powers of \({{\sin }^{i}}\!\!\left( \varpi \right) {{\cos }^{j}}\!\!\left( \varpi \right) \) functions. Collecting the coefficients of \({{\sin }^{i}}\!\!\left( \varpi \right) {{\cos }^{j}}\left( \varpi \right) \) of similar power and equating each sum to zero, gives an algebraic equation system. Inserting the system of algebraic equations produces the values of \({{A}_{1}},{{B}_{1}},{{C}_{1}},{{D}_{1}}\), \({{A}_{0}},{{B}_{0}}\) and other parameters. By substituting the values of the parameters for eq. (13), we obtain some new rational travelling wave results for eq. (1).

Case 1: When

$$\begin{aligned}&w=-\frac{\alpha ( {{\alpha }^{2}}{{\left( {{a}^{2}}+{{b}^{2}} \right) }^{2}}B_{1}^{4}+8\alpha s\left( {{a}^{2}}+{{b}^{2}} \right) B_{1}^{2}C_{1}^{2}{{\beta }_{2}}+8C_{1}^{4}\left( \left( 2{{s}^{2}}+{{a}^{2}}+{{b}^{2}} \right) \beta _{1}^{2}+2{{s}^{2}}\beta _{2}^{2} \right) )}{16C_{1}^{4}\beta _{1}^{2}}, \nonumber \\&r=-\frac{\alpha \left( {{a}^{2}}+{{b}^{2}} \right) B_{1}^{2}+4s{{\beta }_{2}}C_{1}^{2}}{4{{\beta }_{1}}C_{1}^{2}},\quad {{B}_{0}}={{B}_{1}},\quad {{A}_{0}}={{A}_{1}}={{D}_{1}}=0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \; \end{aligned}$$
(41)

we get the following solution:

$$\begin{aligned} {{q}_{1}}\left( x,y,t \right) =\frac{{{\mathrm {e}}^{i\left( -\frac{\alpha ( {{a}^{2}}+{{b}^{2}} )B_{1}^{2}+4s{{\beta }_{2}}C_{1}^{2}}{4{{\beta }_{1}}C_{1}^{2}}x+sy+w\frac{{{t}^{\mu }}}{\mu }+\phi \right) }}{{C}_{1}}\tanh ( \frac{1}{2}( ax+by-\frac{2\alpha ( sb+r ){{t}^{\mu }}}{\mu } ) )}{{{B}_{1}}}. \end{aligned}$$
(42)

Case 2: If

$$\begin{aligned}&{{\beta }_{1}}=-\frac{\alpha \left( {{a}^{2}}+{{b}^{2}} \right) B_{1}^{2}+4s{{\beta }_{2}}\left( A_{1}^{2}+C_{1}^{2} \right) }{4r\left( A_{1}^{2}+C_{1}^{2} \right) },\nonumber \\&w=-\frac{1}{2}\alpha \left( 2{{r}^{2}}+2{{s}^{2}}+{{a}^{2}}+{{b}^{2}} \right) ,\nonumber \\&{{B}_{0}}=\frac{{{B}_{1}}{{C}_{1}}}{\sqrt{A_{1}^{2}+C_{1}^{2}}},\quad {{A}_{0}}={{D}_{1}}=0, \end{aligned}$$
(43)

we have

$$\begin{aligned} {{q}_{2}}\left( x,y,t \right) =\frac{{{\mathrm {e}}^{i( rx+sy+\frac{w{{t}^{\mu }}}{\mu }+\phi )}}{\text {sech}}( ax+by-\frac{2\alpha ( ra+sb ){{t}^{\mu }}}{\mu } )( {{A}_{1}}+\sinh a( ax+by-\frac{2\alpha ( ra+sb ){{t}^{\mu }}}{\mu } ){{C}_{1}} )}{{{B}_{1}}\left( {\text {sech}}( ax+by-\frac{2\alpha ( ra+sb ){{t}^{\mu }}}{\mu } )+\frac{{{C}_{1}}}{\sqrt{A_{1}^{2}+C_{1}^{2}}} \right) }.\qquad \qquad \quad \end{aligned}$$
(44)

Case 3: When

$$\begin{aligned}&\beta =-\frac{\sqrt{-{{\alpha }^{2}}{{a}^{2}}B_{1}^{4}-4{{\alpha }^{2}}rB_{1}^{2}C_{1}^{2}{{\beta }_{1}}-4C_{1}^{2}{{\beta }_{2}}( C_{1}^{2}{{\beta }_{2}}+\sqrt{-\alpha \left( \alpha {{r}^{2}}+w \right) B_{1}^{4}+2\alpha rB_{1}^{2}C_{1}^{2}{{\beta }_{1}}+C_{1}^{4}\beta _{2}^{2}} )}}{\alpha B_{1}^{2}}, \nonumber \\&s=\frac{C_{1}^{2}{{\beta }_{2}}+\sqrt{-\alpha \left( \alpha {{r}^{2}}+w \right) B_{1}^{4}+2\alpha rB_{1}^{2}C_{1}^{2}{{\beta }_{1}}+C_{1}^{4}\beta _{2}^{2}}}{\alpha B_{1}^{2}},{{B}_{0}}=-{{B}_{1}},\quad {{A}_{0}}={{A}_{1}}={{D}_{1}}=0, \end{aligned}$$
(45)

we get

$$\begin{aligned} {{q}_{3}}\left( x,y,t \right) =\frac{{{\mathrm {e}}^{i\left( rx+\frac{C_{1}^{2}{{\beta }_{2}}+\sqrt{-\alpha \left( \alpha {{r}^{2}}+w \right) B_{1}^{4}+2\alpha rB_{1}^{2}C_{1}^{2}{{\beta }_{1}}+C_{1}^{4}\beta _{2}^{2}}}{\alpha B_{1}^{2}}y+\frac{w{{t}^{\mu }}}{\mu }+\phi \right) }}}{{{B}_{1}}} \coth \left( \frac{1}{2}\left( ax+by-2abs\frac{{{t}^{\mu }}}{\mu } \right) \right) {{C}_{1}}. \end{aligned}$$
(46)

Case 4: If the coefficients are selected as

$$\begin{aligned}&{{\beta }_{1}}=\frac{\alpha \left( {{a}^{2}}+{{b}^{2}} \right) \left( B_{0}^{2}-D_{1}^{2} \right) -s{{\beta }_{2}}A_{1}^{2}}{rA_{1}^{2}},\nonumber \\&w=\alpha \left( -{{r}^{2}}-{{s}^{2}}+{{a}^{2}}+{{b}^{2}} \right) ,\quad {{A}_{0}}={{B}_{1}}={{C}_{1}}=0, \nonumber \\ \end{aligned}$$
(47)

we have

Fig. 1
figure 1

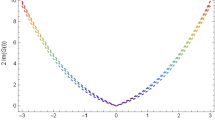
The 3D, 2D and contour simulations of the absolute value of eq. (23).

Full size image
Fig. 2
figure 2

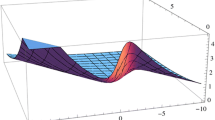
The 3D, 2D and contour simulations of the absolute value of eq. (31).

Full size image
Fig. 3
figure 3

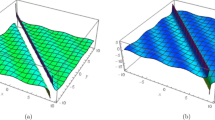
The 3D, 2D and contour simulations of the absolute value of eq. (42).

Full size image
Fig. 4
figure 4

The 3D, 2D and contour simulations of the absolute value of eq. (44).

Full size image
Fig. 5
figure 5

The 3D, 2D and contour simulations of the absolute value of eq. (46).

Full size image
Fig. 6
figure 6

The 3D, 2D and contour simulations of the absolute value of eq. (48).

Full size image
$$\begin{aligned} {{q}_{4}}\left( x,y,t \right) =\frac{{{\mathrm {e}}^{i\left( rx+sy+\frac{\alpha \left( -{{r}^{2}}-{{s}^{2}}+{{a}^{2}}+{{b}^{2}} \right) {{t}^{\mu }}}{\mu }+\phi \right) }}{\text {sech}}\left( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } \right) {{A}_{1}}}{{{B}_{0}}+{{D}_{1}}\tanh \left( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } \right) }. \end{aligned}$$
(48)

Case 5: If

$$\begin{aligned}&s=-\frac{\alpha \left( {{a}^{2}}+{{b}^{2}} \right) D_{1}^{2}+4r{{\beta }_{1}}}{4{{\beta }_{2}}},\nonumber \\&w=\frac{\alpha }{16}\Big ( -8\left( 2{{r}^{2}}+{{a}^{2}}+{{b}^{2}} \right) \nonumber \\&\qquad \qquad -\frac{{{\left( \alpha \left( {{a}^{2}}+{{b}^{2}} \right) D_{1}^{2}+4r{{\beta }_{1}} \right) }^{2}}}{\beta _{2}^{2}} \Big ), \nonumber \\&{{A}_{1}}=-\frac{\sqrt{B_{1}^{2}+D_{1}^{2}}}{{{D}_{1}}},{{A}_{0}}=1,{{C}_{1}}={{B}_{0}}=0, \end{aligned}$$
(49)

we have

$$\begin{aligned} {{q}_{5}}( x,y,t )=\frac{{{\mathrm {e}}^{i( rx+sy+\frac{w{{t}^{\mu }}}{\mu }+\phi )}}\left( \cosh ( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } )-\frac{\sqrt{B_{1}^{2}+D_{1}^{2}}}{{{D}_{1}}} \right) }{{{B}_{1}}+\sinh ( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } ){{D}_{1}}}. \end{aligned}$$
(50)

Case 6: If

$$\begin{aligned}&{{\beta }_{2}}=\frac{\left( \alpha \left( {{r}^{2}}+{{s}^{2}} \right) +w \right) D_{1}^{2}-2r{{\beta }_{1}}}{2s},\nonumber \\&{{A}_{1}}=-\frac{\sqrt{B_{1}^{2}-B_{0}^{2}+D_{1}^{2}}}{{{D}_{1}}},\quad {{C}_{1}}=\frac{{{B}_{0}}}{{{D}_{1}}}, \nonumber \\&b=-\sqrt{\frac{-2w-\left( \alpha \left( {{r}^{2}}+{{s}^{2}} \right) +{{a}^{2}} \right) }{\alpha }},\quad {{A}_{0}}=1, \end{aligned}$$
(51)

we have

$$\begin{aligned} {{q}_{6}}\left( x,y,t \right)= & {} {{\mathrm {e}}^{i\left( rx+sy+\frac{w{{t}^{\mu }}}{\mu }+\phi \right) }}\nonumber \\&\times \frac{\left( {{D}_{1}}-{\text {sech}}\left( ax+by-\frac{2\alpha ( sb+ra ) {{t}^{\mu }}}{\mu }\right) \sqrt{-B_{0}^{2}+B_{1}^{2}+D_{1}^{2}}+{{B}_{0}}\tanh \left( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } \right) \right) }{{{D}_{1}}( {{B}_{0}}+{\text {sech}}( ax+by-\frac{2\alpha ( sb+ra ){{t}^{\mu }}}{\mu } ){{B}_{1}}+{{D}_{1}}\tanh ( ax+by-\frac{2a( sb+ra ){{t}^{\mu }}}{\mu } ) )}.\nonumber \\ \end{aligned}$$
(52)

5 Conclusion

In this framework, we proposed a newly developed analytical method which is the rational sine-Gordon expansion method (RSGEM). The main advantage of this method is that it provides more general solutions that include solutions that are obtained by different methods. This method is effective in finding new solutions to governing models with powerful nonlinearity. Using the new method, we constructed new exact travelling wave solutions to the conformable (1\(+\)1)- and (2\(+\)1)-dimensional chiral nonlinear Schrödinger’s equation which describe the edge states of the fractional quantum Hall effect. We acquired explicit soliton solutions including bright, dark, singular, combined dark-bright soliton solutions of the conformable (1\(+\)1)- and (2\(+\)1)-dimensional CNLSE by using RSGEM. These types of soliton solutions (solitary waves) often have been used for understanding stable or unstable nonlinear dynamic models such as fluid dynamics, quantum physics, nuclear physics, electromagnetism etc. Chiral solitons play a vital role in the field of quantum Hall effect, where chiral excitations are known to appear. In future, it can be extended to other perturbation terms of the mentioned models by using the proposed method. The solutions to be obtained for different order values of the CNLS equation can provide novelties in the quantum Hall effect field where chiral excitations appear. Consequently, we estimate that the results found in this paper may be used to explain phenomena, especially in nuclear physics and quantum mechanics.