Novel optical soliton solutions for time-fractional resonant nonlinear Schrödinger equation in optical fiber

Abstract

The time-fractional resonant nonlinear Schrödinger equation is studied in this paper using the modified auxiliary equation approach. This effort yields several innovative optical soliton solutions to the investigated problem. An equivalent nonlinear ordinary differential equation with integer-order has been obtained from the time-fractional RNLSE using the modified Riemann–Liouville derivative along with fractional complex transform, and then the emerged equations are solved using the most impressive direct method, the modified auxiliary equation method. As a consequence, novel optical soliton solutions have been successfully developed, with several 3-D graphs demonstrating their behaviour.

1 Introduction

The fractional differential equation (Saha Ray 2020a; Sabatier et al. 2007; Li et al. 2011) has been occurring gradationally in several study fields over the past two decades. Numerous critical phenomena in bioengineering, viscoelasticity, pollution control, cosmology, biomathematics, signal analysis, traffic flow, biomedicine, electrochemistry, financial systems, and many others may be better understood using this fractional differential equation. The fractional calculus is a non-integer order extension of classical differentiation and integration (Saha Ray 2015). This is one of the indispensable subjects not only by mathematicians but also by engineers, physicists, and many others. One of the foremost significant nonlinear evolution equations in nonlinear optics (Boyd 2020) is the nonlinear Schrödinger equation (NLSE) (Fibich 2015), and many optical soliton (Liu et al. 2022; Ma et al. 2021a, b; Wang and Liu 2020; Yan and Liu 2021; Wang et al. 2021a, b) solutions can be obtained by using the various approach. A significant aspect of this NLSE in a nonlinear dispersive medium (Bélanger et al. 1989) is that it interprets wave propagation. The NLSE is widely used in a variety of domains, including plasma physics, semiconductor materials, fluids, and many more. For the discovery of exact solutions of NLSE, different schemes are employed, such as the $\tan \left( {\phi (\xi )/2} \right)$-expansion method (Verma and Kaur 2019), the elliptic function expansion and He’s semi-inverse techniques (Abdelrahman et al. 2020), the Jacobi elliptic ansatz method (Aslan and Inc 2019), the Fourier transform (Fitio et al. 2015), the extended $\left( {G^{\prime}/G^{2} } \right)$-expansion method and the first integral method (Akram and Mahak 2018), the Hirota method (Dai et al. 2016), the extended auxiliary equation method (Saha Ray 2020b), the trial equation method (Biswas et al. 2018), the extended trial equation method (Ekici et al. 2017), the Riemann–Hilbert method (Peng et al. 2019), the new extended auxiliary equation method (Zayed and Alurrfi 2016), the Fokas method (Tian 2016), the fractional Riccati method and fractional dual-function method (Wang et al. 2020), the auxiliary equation of the direct algebraic method (Seadawy 2017), etc. In Serkin and Hasegawa (2000), the methodology created allows for the systematic way to find and study an infinite number of the new solitary waves with changing dispersion, nonlinearity, gain, or absorption for the NLSE has been presented. Also, the general solutions of traveling diminishment for higher-order NLSE have been shown in Kudryashov (2021). In Yang et al. (2018), on the basis of nonlocal NLSE, the investigation of the propagation of sinh-Gaussian beams in highly nonlocal nonlinear media has been presented.

In this paper, consider time-fractional resonant nonlinear Schrödinger equation (RNLSE) (Seadawy et al. 2021) as follows

$$iD_{t}^{\alpha } u + \alpha_{1} u_{xx} + \alpha_{2} F(\,\left| u \right|^{2} )u + \alpha_{3} \left\{ {\frac{{\left| u \right|_{xx} }}{\left| u \right|}} \right\}u = 0,$$

(1)

where the complex wave profile is defined as $u = u(x,t)$, and for $\alpha \in (0,1]$, the fractional derivative is alluded to as the operator $D^{\alpha }$ of order $\alpha$. The coefficients of group-velocity dispersion are denoted by $\alpha_{1}$, and non-Kerr nonlinearity is represented by $\alpha_{2}$, whereas the coefficient of resonant nonlinearity is characterized by $\alpha_{3}$. In the case of nonlinear fiber optics, the aforementioned type of nonlinearity occurs naturally.

In this paper, to devise the exact solutions of NLSE, the modified auxiliary equation (MAE) method (Khater et al. 2019a, b) has been engaged to the time-fractional RNLSE along Kerr law nonlinearity. To attain a nonlinear ordinary differential equation (ODE), fractional complex transform (FCT) (Li and He 2010; He et al. 2012) and modified Riemann–Liouville (mRL) derivative (Guner et al. 2017; Jumarie 2006) has been employed to the Eq. (1).

In Seadawy et al. (2021), diverse kinds of optical soliton solutions of time-fractional resonant nonlinear Schrödinger equation with conformable derivative in the optical fiber have been obtained by applying extended rational sine–cosine/sinh-cosh and advance expansion schemes. But in this paper, many more novel optical soliton solutions of the time-fractional resonant nonlinear Schrödinger equation with mRL derivative in optical fiber have been obtained by applying the MAE approach.

The following is a basic explanation of how this paper is organized: a brief summary of the MAE approach is given in Sect. 2. The implementation of the MAE technique for the time-fractional RNLSE is discussed in Sect. 3. In Sect. 4, certain 3-D graphs have been presented to demonstrate the behaviour of the obtained solutions, and in Sect. 5, the conclusion of the paper is presented.

2 Fundamental steps of the MAE method

The suggested MAE method’s main steps are summarized below:

Step I Assume the following form for a nonlinear partial differential equation (NLPDE) for the function $u = u(x,t)$:

$$\wp (u,\,u_{x} ,\,u_{t} ,\,u_{xx} ,u_{tt} ,\,u_{xt} , \ldots ,\,D_{t}^{\alpha } u, \ldots ) = 0,$$

(2)

where $D_{t}^{\alpha } u$ is mRL derivative of $u$, polynomial of $u$ is $\wp$, and unknown function is $u$.

Using the wave transformation

$$u(x,t) = U(\xi ),\;\xi = kx + ct$$

Equation (2) can be transformed into a nonlinear ODE

$$\Theta (U,kU^{\prime},\,cU^{\prime},k^{2} U^{\prime\prime},c^{2} U^{\prime\prime}, \ldots ) = 0,$$

(3)

where the prime stands for $\partial /\partial \xi$ and the constants $k$ and $c$ will be determined afterward.

Step II The solution of Eq. (3) is assumed as follows:

$$U(\xi ) = r_{0} + \sum\limits_{j = 1}^{M} {r_{j} K^{jf(\xi )} } + \sum\limits_{j = 1}^{M} {w_{j} K^{ - jf(\xi )} } ,$$

(4)

in which $r_{0} ,\,r_{j} (1 \le j \le M),\,K$ are arbitrary constants to be obtained afterward and $f(\xi )$ satisfies the following ODE

$$f^{\prime}(\xi ) = \frac{{\beta + \eta K^{ - f(\xi )} + \sigma K^{f(\xi )} }}{\ln (K)},$$

(5)

wherein $\beta ,\,\eta$ and $\sigma$ are parameters to be obtained afterward and $K > 0,\,K \ne 1$.

Step III To determine $M$, whenever $M$ become a positive integer, it can be determined by the aid of homogeneous balancing principle between the highest order derivative and nonlinear terms in Eq. (3). A transformation formula can be used to get rid of the difficulty whenever $M$ is not an integer.

Step IV In Eq. (3), substituting Eq. (4) along with Eq. (5) and collecting together all of the terms of the equal power $K^{if(\xi )}$ where $(i = - M, \ldots ,\,M)$ and equating all of them to zero, yielding a set of the over-determined equation for $r_{i} ,\,w_{i}$ and $(\beta ,\,\eta ,\,\sigma )$.

Step V Solving the obtained algebraic equations in Step IV and putting all these values and all the solutions of Eq. (5) into the Eq. (4), the exact solutions of Eq. (1) can be determined.

The following are the instances in which the solution of Eq. (5) is valid:

If $\eta \sigma > 0\,$ where $(\eta \ne 0,\,\beta = 0)$, then

$$K^{f(\xi )} = \frac{{\eta \tan (\sqrt {\eta \sigma } \xi )}}{{\sqrt {\eta \sigma } }},$$

$$K^{f(\xi )} = - \frac{{\eta \cot (\sqrt {\eta \sigma } \xi )}}{{\sqrt {\eta \sigma } }}.$$

If $\eta \sigma < 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$K^{f(\xi )} = \frac{\sqrt \eta \tan (\sqrt \eta \sqrt \sigma \xi )}{{\sqrt \sigma }},$$

$$K^{f(\xi )} = \frac{{\eta \coth (\sqrt { - \eta \sigma } \xi )}}{{\sqrt { - \eta \sigma } }}.$$

If $\beta = 0$ and $\eta = - \sigma$, then

$$K^{f(\xi )} = \coth (\eta \xi ).$$

If $\beta = 0$ and $\eta = \sigma$, then

$$K^{f(\xi )} = \tan (\eta \xi ).$$

If $\beta^{2} - 4\eta \sigma < 0$ and $\sigma \ne 0$, then

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt {4\eta \sigma - \beta^{2} } \tan \left( {\frac{1}{2}\sqrt {4\eta \sigma - \beta^{2} } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt {4\eta \sigma - \beta^{2} } \cot \left( {\frac{1}{2}\sqrt {4\eta \sigma - \beta^{2} } \xi } \right)}}{2\sigma }.$$

If $\beta^{2} - 4\eta \sigma > 0$ and $\sigma \ne 0$, then

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {\beta^{2} - 4\eta \sigma } \tanh \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\eta \sigma } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {\beta^{2} - 4\eta \sigma } \coth \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\eta \sigma } \xi } \right)}}{2\sigma }.$$

If $\beta^{2} + 4\eta^{2} < 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt { - 4\eta^{2} - \beta^{2} } \tan \left( {\frac{1}{2}\sqrt { - 4\eta^{2} - \beta^{2} } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt { - 4\eta^{2} - \beta^{2} } \cot \left( {\frac{1}{2}\sqrt { - 4\eta^{2} - \beta^{2} } \xi } \right)}}{2\sigma }.$$

If $\beta^{2} + 4\eta^{2} > 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {4\eta^{2} + \beta^{2} } \tanh \left( {\frac{1}{2}\sqrt {4\eta^{2} + \beta^{2} } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {4\eta^{2} + \beta^{2} } \coth \left( {\frac{1}{2}\sqrt {4\eta^{2} + \beta^{2} } \xi } \right)}}{2\sigma }.$$

If $\beta^{2} - 4\eta^{2} < 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt {4\eta^{2} - \beta^{2} } \tan \left( {\frac{1}{2}\sqrt {4\eta^{2} - \beta^{2} } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta + \sqrt {4\eta^{2} - \beta^{2} } \cot \left( {\frac{1}{2}\sqrt {4\eta^{2} - \beta^{2} } \xi } \right)}}{2\sigma }.$$

If $\beta^{2} - 4\eta^{2} > 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {\beta^{2} - 4\eta^{2} } \tanh \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\eta^{2} } \xi } \right)}}{2\sigma },$$

$$K^{f(\xi )} = \frac{{ - \beta - \sqrt {\beta^{2} - 4\eta^{2} } \coth \left( {\frac{1}{2}\sqrt {\beta^{2} - 4\eta^{2} } \xi } \right)}}{2\sigma }.$$

If $\eta = 0$, then

$$K^{f(\xi )} = \frac{{ - \beta \left( {\frac{2}{\sigma \exp (\beta \xi ) - 2} + 1} \right)}}{\sigma }.$$

If $\beta = 0$ and $\eta = \sigma$, then

$$K^{f(\xi )} = \frac{\eta \tan (\eta \xi )}{\sigma }.$$

3 Application of MAE method for time-fractional RNLSE

For Kerr law nonlinearity in Eq. (1), yields

$$iD_{t}^{\alpha } u + \alpha_{1} u_{xx} + \alpha_{2} \,\left| u \right|^{2} u + \alpha_{3} \left\{ {\frac{{\left| u \right|_{xx} }}{\left| u \right|}} \right\}u = 0.$$

(6)

Assume the wave transformation as follows

$$u(x,t:\alpha ) = U(\xi )\exp (i\theta ),\quad \xi = kx + \frac{{ct^{\alpha } }}{\Gamma (1 + \alpha )},\quad \theta = lx + \frac{{mt^{\alpha } }}{\Gamma (1 + \alpha )}.$$

(7)

Applying Eq. (7) into Eq. (6), the following nonlinear ODE is derived as

$$k^{2} (\alpha_{1} + \alpha_{3} )U^{\prime\prime} - (m + \alpha_{1} l^{2} )U + \alpha_{2} U^{3} = 0,$$

(8)

taken from the real component and the relation $c = - 2lk\alpha_{1}$ taken from the imaginary component.

Balancing $U^{\prime\prime}$ and $U^{3}$ by the use of homogeneous balance principle yields

$$M = 1.$$

Therefore, the traveling wave solution is given as follows

$$U(\xi ) = r_{0} + r_{1} K^{f(\xi )} + w_{1} K^{ - f(\xi )} .$$

(9)

Substituting Eq. (9) along with Eq. (5) into Eq. (8) and collecting all the coefficients of the equal powers of $K^{f(\xi )}$ and equating them to zero, generates the system of following nonlinear algebraic equations:

$$K^{{f(\xi )^{0} }} :\; - mr_{0} - l^{2} r_{0} \alpha_{1} + r_{0}^{3} \alpha_{2} + k^{2} r_{1} \alpha_{1} \beta \eta + k^{2} r_{1} \alpha_{3} \beta \eta + 6r_{0} r_{1} \alpha_{2} w_{1} + k^{2} \alpha_{1} \beta \sigma w_{1} + k^{2} \alpha_{3} \beta \sigma w_{1} = 0,$$

$$K^{{f(\xi )^{1} }} :\; - mr_{1} - l^{2} r_{1} \alpha_{1} + 3r_{0}^{2} r_{1} \alpha_{2} + k^{2} r_{1} \alpha_{1} \beta^{2} + k^{2} r_{1} \alpha_{3} \beta^{2} + 2k^{2} r_{1} \alpha_{1} \eta \sigma + 2k^{2} r_{1} \alpha_{3} \eta \sigma + 3r_{1}^{2} \alpha_{2} w_{1} = 0,$$

$$K^{{f(\xi )^{2} }} :\;3r_{0} r_{1}^{2} \alpha_{2} + 3k^{2} r_{1} \alpha_{1} \beta \sigma + 3k^{2} r_{1} \alpha_{3} \beta \sigma = 0,$$

$$K^{{f(\xi )^{3} }} :\;r_{1}^{3} \alpha_{2} + 2k^{2} r_{1} \alpha_{1} \sigma^{2} + 2k^{2} r_{1} \alpha_{3} \sigma^{2} = 0,$$

$$K^{{f(\xi )^{ - 1} }} :\; - mw_{1} - l^{2} \alpha_{1} w_{1} + 3r_{0}^{2} \alpha_{2} w_{1} + k^{2} \alpha_{1} \beta^{2} w_{1} + k^{2} \alpha_{3} \beta^{2} w_{1} + 2k^{2} \alpha_{1} \eta \sigma w_{1} + 2k^{2} \alpha_{3} \eta \sigma w_{1} + 3r_{1} \alpha_{2} w_{1}^{2} = 0,$$

$$K^{{f(\xi )^{ - 2} }} :\;3k^{2} \alpha_{1} \beta \eta w_{1} + 3k^{2} \alpha_{3} \beta \eta w_{1} + 3r_{0} \alpha_{2} w_{1}^{2} = 0,$$

$$K^{{f(\xi )^{ - 3} }} :\;2k^{2} \alpha_{1} \eta^{2} w_{1} + 2k^{2} \alpha_{3} \eta^{2} w_{1} + \alpha_{2} w_{1}^{3} = 0.$$

The following findings are acquired by solving the preceding system of algebraic equations:

Family I

$$r_{0} = - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }},\quad r_{1} = - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma }}{{\sqrt {\alpha_{2} } }},\quad w_{1} = 0,\quad m = \frac{1}{2}\left( { - 2l^{2} \alpha_{1} - k^{2} \alpha_{1} \beta^{2} - k^{2} \alpha_{3} \beta^{2} + 4k^{2} \alpha_{1} \eta \sigma + 4k^{2} \alpha_{3} \eta \sigma } \right).$$

(10)

If $\eta \sigma > 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{1}^{I} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \tan (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(11)

$$u_{2}^{I} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \cot (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(12)

If $\eta \sigma < 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{3}^{I} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt \eta \sqrt \sigma \tan (\sqrt \eta \xi \sqrt \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(13)

$$u_{4}^{I} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \eta \sigma } \coth (\xi \sqrt { - \eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(14)

If $\beta = 0$ and $\eta = - \sigma$, then

$$u_{5}^{I} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \coth (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(15)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{6}^{I} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tan (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(16)

If $\beta^{2} - 4\eta \sigma < 0$ and $\sigma \ne 0$, then

$$u_{7}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\eta \sigma } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(17)

$$u_{8}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\eta \sigma } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(18)

If $\beta^{2} - 4\eta \sigma > 0$ and $\sigma \ne 0$, then

$$u_{9}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\eta \sigma } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(19)

$$u_{10}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\eta \sigma } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(20)

If $\beta^{2} + 4\eta^{2} < 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{11}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} - 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(21)

$$u_{12}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} - 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(22)

If $\beta^{2} + 4\eta^{2} > 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{13}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} + 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(23)

$$u_{14}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} + 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(24)

If $\beta^{2} - 4\eta^{2} < 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{15}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(25)

$$u_{16}^{I} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(26)

If $\beta^{2} - 4\eta^{2} > 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{17}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(27)

$$u_{18}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(28)

If $\eta = 0$, then

$$u_{19}^{I} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta (2 + \exp (\beta \xi )\sigma )}}{{\sqrt 2 \sqrt {\alpha_{2} } ( - 2 + \exp (\beta \xi )\sigma )}}} \right)\exp (i\theta ).$$

(29)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{20}^{I} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tan (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(30)

Family II

$$r_{0} = - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }},\quad r_{1} = 0,\quad w_{1} = - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \eta }}{{\sqrt {\alpha_{2} } }},\quad m = \frac{1}{2}\left( { - 2l^{2} \alpha_{1} - k^{2} \alpha_{1} \beta^{2} - k^{2} \alpha_{3} \beta^{2} + 4k^{2} \alpha_{1} \eta \sigma + 4k^{2} \alpha_{3} \eta \sigma } \right).$$

(31)

If $\eta \sigma > 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{1}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \cot (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(32)

$$u_{2}^{II} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \tan (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(33)

If $\eta \sigma < 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{3}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt \eta \sqrt \sigma \cot (\sqrt \eta \xi \sqrt \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(34)

$$u_{4}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \eta \sigma } \tanh (\xi \sqrt { - \eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(35)

If $\beta = 0$ and $\eta = - \sigma$, then

$$u_{5}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tanh (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(36)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{6}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \cot (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(37)

If $\beta^{2} - 4\eta \sigma < 0$ and $\sigma \ne 0$, then

$$u_{7}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta - \sqrt { - \beta^{2} + 4\eta \sigma } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(38)

$$u_{8}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta - \sqrt { - \beta^{2} + 4\eta \sigma } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(39)

If $\beta^{2} - 4\eta \sigma > 0$ and $\sigma \ne 0$, then

$$u_{9}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta + \sqrt {\beta^{2} - 4\eta \sigma } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(40)

$$u_{10}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta + \sqrt {\beta^{2} - 4\eta \sigma } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(41)

If $\beta^{2} + 4\eta^{2} < 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{11}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} - 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(42)

$$u_{12}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} - 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(43)

If $\beta^{2} + 4\eta^{2} > 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{13}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} + 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(44)

$$u_{14}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} + 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(45)

If $\beta^{2} - 4\eta^{2} < 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{15}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} + 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(46)

$$u_{16}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} + 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(47)

If $\beta^{2} - 4\eta^{2} > 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{17}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} - 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(48)

$$u_{18}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} - 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(49)

If $\eta = 0$, then

$$u_{19}^{II} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(50)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{20}^{II} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \cot (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta )$$

(51)

Family III

$$r_{0} = \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }},\quad r_{1} = \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma }}{{\sqrt {\alpha_{2} } }},\quad w_{1} = 0,\quad m = \frac{1}{2}\left( { - 2l^{2} \alpha_{1} - k^{2} \alpha_{1} \beta^{2} - k^{2} \alpha_{3} \beta^{2} + 4k^{2} \alpha_{1} \eta \sigma + 4k^{2} \alpha_{3} \eta \sigma } \right).$$

(52)

If $\eta \sigma > 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{1}^{III} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \tan (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(53)

$$u_{2}^{III} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \cot (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(54)

If $\eta \sigma < 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{3}^{III} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt \eta \sqrt \sigma \tan (\sqrt \eta \xi \sqrt \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(55)

$$u_{4}^{III} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \eta \sigma } \coth (\xi \sqrt { - \eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(56)

If $\beta = 0$ and $\eta = - \sigma$, then

$$u_{5}^{III} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \coth (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(57)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{6}^{III} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tan (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(58)

If $\beta^{2} - 4\eta \sigma < 0$ and $\sigma \ne 0$, then

$$u_{7}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\eta \sigma } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(59)

$$u_{8}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\eta \sigma } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(60)

If $\beta^{2} - 4\eta \sigma > 0$ and $\sigma \ne 0$, then

$$u_{9}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\eta \sigma } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(61)

$$u_{10}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\eta \sigma } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(62)

If $\beta^{2} + 4\eta^{2} < 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{11}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} - 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(63)

$$u_{12}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} - 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(64)

If $\beta^{2} + 4\eta^{2} > 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{13}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} + 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(65)

$$u_{14}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} + 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(66)

If $\beta^{2} - 4\eta^{2} < 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{15}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(67)

$$u_{16}^{III} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \beta^{2} + 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(68)

If $\beta^{2} - 4\eta^{2} > 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{17}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(69)

$$u_{18}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\beta^{2} - 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(70)

If $\eta = 0$, then

$$u_{19}^{III} (x,t) = \left( { - \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta (2 + \exp (\beta \xi )\sigma )}}{{\sqrt 2 \sqrt {\alpha_{2} } ( - 2 + \exp (\beta \xi )\sigma )}}} \right)\exp (i\theta ).$$

(71)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{20}^{III} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tan (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(72)

Family IV

$$r_{0} = \frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }},\quad r_{1} = 0,\quad w_{1} = \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \eta }}{{\sqrt {\alpha_{2} } }},\quad m = \frac{1}{2}\left( { - 2l^{2} \alpha_{1} - k^{2} \alpha_{1} \beta^{2} - k^{2} \alpha_{3} \beta^{2} + 4k^{2} \alpha_{1} \eta \sigma + 4k^{2} \alpha_{3} \eta \sigma } \right).$$

(73)

If $\eta \sigma > 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{1}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \cot (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(74)

$$u_{2}^{IV} (x,t) = \left( { - \frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt {\eta \sigma } \tan (\xi \sqrt {\eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta )$$

(75)

If $\eta \sigma < 0$ where $(\eta \ne 0,\,\beta = 0)$, then

$$u_{3}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt \eta \sqrt \sigma \cot (\sqrt \eta \xi \sqrt \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(76)

$$u_{4}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sqrt { - \eta \sigma } \tanh (\xi \sqrt { - \eta \sigma } )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(77)

If $\beta = 0$ and $\eta = - \sigma$, then

$$u_{5}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \tanh (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(78)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{6}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \cot (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(79)

If $\beta^{2} - 4\eta \sigma < 0$ and $\sigma \ne 0$, then

$$u_{7}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta - \sqrt { - \beta^{2} + 4\eta \sigma } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(80)

$$u_{8}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta - \sqrt { - \beta^{2} + 4\eta \sigma } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(81)

If $\beta^{2} - 4\eta \sigma > 0$ and $\sigma \ne 0$, then

$$u_{9}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta + \sqrt {\beta^{2} - 4\eta \sigma } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(82)

$$u_{10}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{4\eta \sigma }{{\beta + \sqrt {\beta^{2} - 4\eta \sigma } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\eta \sigma } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(83)

If $\beta^{2} + 4\eta^{2} < 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{11}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} - 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(84)

$$u_{12}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} - 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(85)

If $\beta^{2} + 4\eta^{2} > 0$ and $\eta = - \sigma \,(\sigma \ne 0)$, then

$$u_{13}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} + 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(86)

$$u_{14}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta + \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} + 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(87)

If $\beta^{2} - 4\eta^{2} < 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{15}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} + 4\sigma^{2} } \tan \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(88)

$$u_{16}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta - \sqrt { - \beta^{2} + 4\sigma^{2} } \cot \left( {\frac{1}{2}\xi \sqrt { - \beta^{2} + 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(89)

If $\beta^{2} - 4\eta^{2} > 0$ and $\eta = \sigma \,(\eta \ne 0)$, then

$$u_{17}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} - 4\sigma^{2} } \tanh \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ),$$

(90)

$$u_{18}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \left( {\beta - \frac{{4\sigma^{2} }}{{\beta + \sqrt {\beta^{2} - 4\sigma^{2} } \coth \left( {\frac{1}{2}\xi \sqrt {\beta^{2} - 4\sigma^{2} } } \right)}}} \right)}}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(91)

If $\eta = 0$, then

$$u_{19}^{IV} (x,t) = \left( {\frac{{ik\sqrt {\alpha_{1} + \alpha_{3} } \beta }}{{\sqrt 2 \sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(92)

If $\beta = 0$ and $\eta = \sigma$, then

$$u_{20}^{IV} (x,t) = \left( {\frac{{i\sqrt 2 k\sqrt {\alpha_{1} + \alpha_{3} } \sigma \cot (\xi \sigma )}}{{\sqrt {\alpha_{2} } }}} \right)\exp (i\theta ).$$

(93)

4 Numeral simulation and physical interpretation

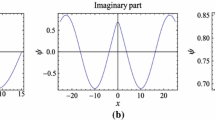
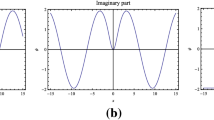
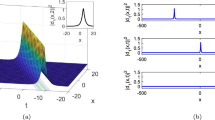
For the time-fractional RNLSE, the present numerical simulation revealed the graphs of 3-D surface solutions. In addition, the discussion has been presented here to explore the physical behaviours of the solutions.

For changing the magnitude of the value of fractional order $\alpha$ and for suitable parameters values, physical behaviors of different types of soliton solution become changes, and that has been shown from Figs. 1, 2, 3, 4, 5, 6 and 7. Figure 1 shows the 3-D complex soliton solution of $\left| {u_{1}^{I} (x,t)} \right|$ with fractional order $\alpha = 0.75$ and for parameter values $\beta = 0\,,\;\alpha_{1} = 0.76\,,\;\alpha_{2} = 0.11\,,\;\alpha_{3} = 2.66\,,\;\sigma = 0.45\,,\;k = - 0.86\,,\;l = - 0.52\,,\;\eta = 0.04$. Figure 2 displays the 3-D solitary wave solution of $\left| {u_{3}^{I} (x,t)} \right|$ with fractional order $\alpha = 0.25$ along with for parameter values $\beta = 0\,,\,\alpha_{1} = 0.775\,,\,\alpha_{2} = 0.325,\;\alpha_{3} = 0.516,\;\sigma = 0.636,\;k = - 0.896,\;l = - 0.996,\;\eta = 0.289$. Also, Fig. 3 demonstrate the 3-D solitary wave solution of $\left| {u_{6}^{I} (x,t)} \right|$ with fractional order $\alpha = 0.75$ and $\beta = 0,\;\alpha_{1} = 0.363,\;\alpha_{2} = 0.365,\;\alpha_{3} = 0.744,\;\eta = \,\sigma = 0.714,\;k = - 0.597,\;l = - 0.795$ for all parameter values. Similarly, Fig. 4 exhibits the 3-D complex solitary wave solution of $\left| {u_{7}^{II} (x,t)} \right|$ with fractional order $\alpha = 0.85$ and $\beta = 0.51,\;\alpha_{1} = 0.95,\;\alpha_{2} = 0.56,\;\,\alpha_{3} = 0.58,\;\sigma = 0.57,\;k = - 0.89,\;l = - 0.14,\;\eta = 0.29$ for all parameter values. For fractional order $\alpha = 0.99$ and for all parameter values $\beta = 0.17,\;\alpha_{1} = 0.56,\;\alpha_{2} = 0.32,\;\alpha_{3} = 0.79,\;\eta = \sigma = 0.55,\;k = - 0.68,\;l = - 0.94$, the 3-D solitary wave solution surface of $\left| {u_{17}^{II} (x,t)} \right|$ has been presented in Fig. 5. Also, Fig. 6 depicts the 3-D solitary wave solution surface of $\left| {u_{2}^{III} (x,t)} \right|$, for fractional order $\alpha = 0.75$ and for all parameter values $\beta = 0,\;\alpha_{1} = 0.345,\;\alpha_{2} = 0.067,\;\alpha_{3} = 0.559,\;\sigma = 0.658,\;k = - 0.576,\;l = - 0.554,\;\eta = 0.505$. Lastly, Fig. 7 displays the 3-D bell-shape solution surface of $\left| {u_{6}^{IV} (x,t)} \right|$, for fractional order $\alpha = 0.85$ and $\beta = 0,\;\alpha_{1} = 0.35,\;\alpha_{2} = 0.47,\;\alpha_{3} = 0.69,\;\eta = \sigma = 0.14,\;k = - 0.58,\;l = - 0.87$ for all parameter values.

Fig. 1

The 3-D soliton solution surface of $\left| {u_{1}^{I} (x,t)} \right|$ appearing in Family I, when $\alpha = 0.75$, $\beta = 0\,,\;\alpha_{1} = 0.76\,,\;\alpha_{2} = 0.11\,,\;\alpha_{3} = 2.66\,,\;\sigma = 0.45\,,\;k = - 0.86\,,\;l = - 0.52\,,\;\eta = 0.04$

Fig. 2

The 3-D solitary wave solution surface of $\left| {u_{3}^{I} (x,t)} \right|$ appearing in Family I, when $\alpha = 0.25$, $\beta = 0\,,\,\alpha_{1} = 0.775\,,\,\alpha_{2} = 0.325,\;\alpha_{3} = 0.516,\;\sigma = 0.636,\;k = - 0.896,\;l = - 0.996,\;\eta = 0.289$

Fig. 3

The 3-D solitary wave solution surface of $\left| {u_{6}^{I} (x,t)} \right|$ appearing in Family I, when $\alpha = 0.75$,$\beta = 0,\;\alpha_{1} = 0.363,\;\alpha_{2} = 0.365,\;\alpha_{3} = 0.744,\;\eta = \,\sigma = 0.714,\;k = - 0.597,\;l = - 0.795$

Fig. 4

The 3-D solitary wave solution surface of $\left| {u_{7}^{II} (x,t)} \right|$ appearing in Family II, when $\alpha = 0.85$, $\beta = 0.51,\;\alpha_{1} = 0.95,\;\alpha_{2} = 0.56,\;\,\alpha_{3} = 0.58,\;\sigma = 0.57,\;k = - 0.89,\;l = - 0.14,\;\eta = 0.29$

Fig. 5

The 3-D solitary wave solution surface of $\left| {u_{17}^{II} (x,t)} \right|$ appearing in Family II, when $\alpha = 0.99$, $\beta = 0.17,\;\alpha_{1} = 0.56,\;\alpha_{2} = 0.32,\;\alpha_{3} = 0.79,\;\eta = \sigma = 0.55,\;k = - 0.68,\;l = - 0.94$

Fig. 6

The 3-D solitary wave solution surface of $\left| {u_{2}^{III} (x,t)} \right|$ appearing in Family III, when $\alpha = 0.75$, $\beta = 0,\;\alpha_{1} = 0.345,\;\alpha_{2} = 0.067,\;\alpha_{3} = 0.559,\;\sigma = 0.658,\;k = - 0.576,\;l = - 0.554,\;\eta = 0.505$

Fig. 7

The 3-D bell-shape solution surface of $\left| {u_{6}^{IV} (x,t)} \right|$ appearing in Family IV, when $\alpha = 0.85$, $\beta = 0,\;\alpha_{1} = 0.35,\;\alpha_{2} = 0.47,\;\alpha_{3} = 0.69,\;\eta = \sigma = 0.14,\;k = - 0.58,\;l = - 0.87$

5 Conclusion

In this article, the MAE method was effectively used in the time-fractional RNLSE to explore the novel type of analytical solutions. Diverse kinds of straightforward optical soliton solutions have been revealed in this paper. All the obtained novel solutions give further information and explications of this equation. Using the mRL derivative and FCT, the time-fractional RNLSE has been transformed to the nonlinear ODE, and then the MAE method has been exerted to the emerged equation. In comparison to other methods, the MAE approach gives many more novel exact solutions than any other method, and this approach is one of the foremost modern techniques determined in this area. Some 3-D soliton solution surface, solitary wave solution surface, and bell-shape solution surface of obtained solutions have been presented herein Figs. 1–7 to exhibit their behaviors. The obtained results well establish that the MAE method is one of the most prominent, competent, and efficient techniques in this field. This approach may be prudent to utilize for solving a variety of NLPDEs.