Applications of the Resonanat nonlinear Schrödinger equation with self steeping phenomena for chirped periodic waves

Abstract

In this paper, we investigate resonanat nonlinear Schrödinger equation (RNLSE) with self steeping phenomena to obtain some chirped periodic (CP) and soliton waves. A chirp is a signal in which the frequency increases (up chirp) or decreases (down-chirp) with time. It is commonly used in sonar, radar and laser systems and in other applications, such as in spread-spectrum communications. We obtain chirped periodic waves (CPW) with some Jacobi elliptic functions (JEF). We also obtain some solitary waves (SW) like dark, bright, singular waves of type I and II, hyperbolic, periodic and other solutions. The dynamical behaviour for these waves will also be presented.

1 Introduction

The soliton phenomena has got a lot of attention because of its physical and commercial applications in various fields of sciences like optical fiber, optical metamaterial, fluid mechanics, plasma physics, biology, chemistry and so on. Solitons appear as a balance between nonlinearity and dispersion. Solitons solution comes from family of NLSEs which shows the light propagation of waves in many fields of sciences such as nonlinear optics, optical fiber and telecommunications (Xu et al. 2020a, b; Rizvi et al. 2021; Younas et al. 2021; Lan and Guo 2020; Zhao 2021; Lan 2020; Özkan et al. 2021; Rizvi et al. 2020; Younas et al. 2020). Several sophisticated tools have been designed to evaluate NLS models and determine their precise solutions. Optical solitons are one of the most intriguing and fascinating topics in modern communications, aroused by its prospective uses in optical fiber transmission. The study of soliton pulse solutions with nonlinear chirping has shown to be an interesting field of research. The reason behind this is that chirped pulses can be useful in a variety of technological applications, like optic fiber amplifier design, optical pulse compressor design and SW based communications link design (Seadawy et al. 2019; Mecozzi et al. 2012; Dianchen et al. 2018; Ozkan et al. 2020).

The generalised resonant dispersive NLSE (GRD-NLSE) is a mathematical physical model used in nonlinear sciences, such as nonlinear optics, fluid mechanics and condensed matter physics. Recently, many authors have studied the GRD-NLSE to examine the behaviour of solutions (El-Dessoky and Islam 2019; Wang et al. 2007; Al-Ghafri 2019; Seadawy et al. 2019). To construct exact solutions several integration schemes have been implemented, such as ansatz approach (Raza Rizvi et al. 2020; Aly and Cheemaa 2019a), semi-inverse variational principle (Aly and Cheemaa 2019b), simplest equation scheme (Ali et al. 2020), first integral approach (Rizvi et al. 2020a), functional variable scheme (Akram et al. 2021), sine-cosine function approach (Younas et al. 2020a), $G'/G$-expansion scheme, trial solution method and generalized extended tanh scheme (Younas et al. 2020b; 2021). In GRD-NLSE, the parameter n represents the generalized evolution and generalized group velocity dispersion (GVD).

$$\begin{aligned} i(\mid \Xi \mid ^{n-1} \Xi )_t+\alpha (\mid \Xi \mid ^{n-1} \Xi _{xx}+b({\mid \Xi \mid }^n) \Xi +c{\frac{({\mid \Xi \mid }^n_){xx}}{\mid \Xi \mid }}\Xi =0, \end{aligned}$$

(1)

When $n=1$, the GRD-NLSE reduces to the RNLSE (Aly and Cheemaa 2020; Ilie et al. 2018; Raza Rizvi et al. 2020; Aly and Cheemaa 2019a, b; Ali et al. 2020; Rizvi et al. 2020a; Akram et al. 2021; Younas et al. 2020a; El-Dessoky and Islam 2019). A special type of NLSE that is used to describe the Madelung fluids and the dynamic of solitons in various nonlinear systems is the RNLSE. The dimensionless form of the RNLSE is given by:

$$\begin{aligned} i\Xi _t+\alpha \Xi _{xx}+b{\mid \Xi \mid }^2 \Xi +b{\mid \Xi \mid }^4 \Xi +b{\mid \Xi \mid }^6 \Xi +c{\frac{{\mid \Xi \mid }_{xx}}{\mid \Xi \mid }}\Xi =0, ~~ \end{aligned}$$

(2)

where $\alpha$ is the coefficient of group-velocity dispersion, b is the coefficient of non-Kerr nonlinearity and c presents the coefficient of resonant nonlinearity. In an optical fiber medium with Kerr dispersion and quintic nonlinearity, we investigate the propagation characteristics of nonlinear PW (Rizvi et al. 2019, 2021; Chow et al. 2003, 2008; Triki and Wazwaz 2016; Palacios 2003). In such a system, the quintic derivative nonlinear NLSE is used to simulate the development of femtosecond light waves. Our findings demonstrate that Kerr dispersion is critical in producing a nonlinear chirp for PW and SW. In this paper, we will obtain chirped soliton solutions for RNLSE and also present SW solutions.

The paper is organised as follows: In Sect. 3, we will get CPW for RNLSE. In Sect. 4, we present various SW solutions. In Sect. 5, our results and profile of our solutions will be discussed. In Sect. 6, we will provide conclusion of our results.

2 Mathematical analysis

We assume the following transformation:

$$\begin{aligned} \Xi (x,t)=h(\iota )\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(3)

where $\iota =x-\vartheta t$ and $h(\iota )$ and $Y(\iota )$ are real functions of $\iota$, while p is the wave number constant $(p>0)$. The chirping that is associated with this as shown below:

$$\begin{aligned} \delta \Xi =-\frac{\partial }{\partial x}[Y(\iota )-\Omega t]=Y'(\iota ), \end{aligned}$$

(4)

Now putting Eq. (3) into Eq. (2). Then, we get the real and imaginary parts that are shown below:

$$\begin{aligned} \alpha h''+ch'' +hY'\vartheta +h\Omega -\alpha hY'^2+bh^3+bh^5+bh^7=0, \end{aligned}$$

(5)

and

$$\begin{aligned} \alpha hY'' +2\alpha h'Y'-\vartheta h'=0, \end{aligned}$$

(6)

Now multiply Eq. (5) with $h(\iota )$ and integration yield,

$$\begin{aligned} Y'=\frac{N}{\alpha h^2}+\frac{\vartheta }{2\alpha }, \end{aligned}$$

(7)

where N is the constant of integration. Hence, the resultant chirping take the form:

$$\begin{aligned} \delta \Xi (X,t)=-\frac{N}{\alpha h^2}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(8)

Put the expression Eq. (7) into Eq. (5), hence the required differential equation is:

$$\begin{aligned} (\alpha +c)h''+\left( \frac{\vartheta ^2+4\alpha \Omega }{4\alpha }\right) h+bh^3 +bh^5 +bh^7 -\frac{N^2}{\alpha h^3}=0, \end{aligned}$$

(9)

Divide by $\alpha (\alpha +c)$ on both side of the Eq. (9), Since

$$\begin{aligned} h''+\left( \frac{\vartheta ^2+4\alpha \Omega }{4\alpha (\alpha +c)}\right) h+\left( \frac{b}{\alpha +c}\right) h^3 +\left( \frac{b}{\alpha +c}\right) h^5 +\frac{b}{\alpha +c}h^7 -\frac{N^2}{\alpha (\alpha +c)h^3}=0, \end{aligned}$$

(10)

Multiply the Eq. (10) by $2h'd\iota$ and integration;

$$\begin{aligned}&(h')^2+\left( \frac{\vartheta ^2 +4\alpha \Omega }{4\alpha (\alpha +c)}\right) h^2 +\left( \frac{b}{2(\alpha +c)}\right) h^4 +\left( \frac{b}{3(\alpha +c)}\right) h^6\nonumber \\&\quad +\left( \frac{b}{4(\alpha +c)}\right) h^8 -\frac{N}{\alpha (\alpha +c)h^2}+2R=0, \end{aligned}$$

(11)

Where R is a constant. Now after substituting $\Upsilon =h^2$ into Eq. (11) we get the equation:

$$\begin{aligned} (\Upsilon ')^2+V(\Upsilon )=0, \end{aligned}$$

(12)

where $V(\Upsilon )$ is expressed as:

$$\begin{aligned} V(\Upsilon )=\gamma \Upsilon ^5+\nu \Upsilon ^4+\lambda \Upsilon ^3 +\epsilon \Upsilon ^2+\sigma \Upsilon +G, \end{aligned}$$

(13)

with the coefficients:

$$\begin{aligned} \gamma =\frac{b}{\alpha +c},~~~~~ \nu =\frac{4b}{3(\alpha +c)},~~~~ \lambda =\frac{2b}{\alpha +c},~~~~ \epsilon =\frac{\vartheta ^2+4\alpha \Omega }{\alpha (\alpha +c)},~~~~~ \sigma =8R,~~~~ G=\frac{4N^2}{\alpha (\alpha +c)}, \end{aligned}$$

(14)

Equation (12) shows the dynamics of partial with energy and potentials. The general wave solution of Eq. (2) is:

$$\begin{aligned} \Xi (x,t)=\sqrt{\Upsilon (\iota )}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(15)

where $\Upsilon (\iota )$ satisfies the Eq. (12) and $Y(\xi )$ can be obtained with the help of Eq. (7). Now using these relations into Eq. (8) we can obtained chirping function $\delta u(x,t)$ as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Upsilon (\iota )}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(16)

The structure of above equation is nontrivial. The first term in Eq. (16) are intensity dependent term and the last one is linear. Now it is clear from the Eq. (16) that the first term is inversely proportional to the intensity and the last term shows the linear chirp. Our aim is to obtain the chirped solutions for Eq. (16) with the condition that $\Upsilon (\iota )\ne 0$ along with $N\ne 0$ and under some constrained conditions.

3 CPW solution

The exact periodic wave (PW) solutions of Eq. (2) are obtained by applying the transformation Eq. (14) to various types of elliptic ordinary differential Eq. (12).

3.1 CPW of the cn-type

We use the following transformation for cn-type PW:

$$\begin{aligned} \Upsilon (\iota )=A\{1\pm Wcn[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(17)

where $\iota _o$ is the constant and cn(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we find the equations that are as follows:

$$\begin{aligned}&G+A^5\gamma + A^2 \epsilon + A^3 \lambda + A\sigma + A^4 \nu =0, \end{aligned}$$

(18)

$$\begin{aligned}&5A^5W\gamma +2A^2 W\epsilon + 3A^3 W\lambda + AW\sigma +4A^4 W\nu =0, \end{aligned}$$

(19)

$$\begin{aligned}&10A^5W^2\gamma +A^2 W^2 \epsilon + 3A^3 W^2 \lambda + 6A^4 W^2 \nu =0, \end{aligned}$$

(20)

$$\begin{aligned}&10A^5W^3\gamma +A^3 W^3 \lambda + 4A^4 W^3 \nu =0, \end{aligned}$$

(21)

$$\begin{aligned}&5A^5W^4\gamma +A^4W^4\nu =0, \end{aligned}$$

(22)

The values of W and A in the solutions are obtained as:

$$\begin{aligned} W=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ A=-\frac{\nu }{5\gamma }, \end{aligned}$$

(23)

After solving the above equation we also obtained the following values:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(24)

By the substitution of the Eqs. (18, 19, 20, 21, 22) along with Eq. (23) into Eq. (15), we get a following periodic solutions for the Eq. (1) as:

$$\begin{aligned} \Xi (x,t)=\{A[1\pm Wcn(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(25)

where $\zeta =x-\vartheta t-\iota _o$. We can find the integration constant N and R by equating the Eq. (14) and Eq. (24) that are:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(26)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(27)

The chirping that corresponds to this PW can be easily obtained as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha A[1\pm Wcn(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(28)

3.2 CPW of the cd-type

We use the following transformation for cd-type PW:

$$\begin{aligned} \Upsilon (\iota )=j\{1\pm Lcd[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(29)

where $\iota _o$ is the constant and cd(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we find the equations that are as follows:

$$\begin{aligned} G+j^5\gamma + j^2 \epsilon + j^3 \lambda + j\sigma + j^4 \nu =0, \end{aligned}$$

(30)

$$\begin{aligned} 5j^5L\gamma +2j^2 L\epsilon + 3j^3 L\lambda + jL\sigma +4j^4 L\nu =0, \end{aligned}$$

(31)

$$\begin{aligned} 10j^5L^2\gamma +j^2 L^2 \epsilon + 3j^3 L^2 \lambda + 6j^4 L^2 \nu =0, \end{aligned}$$

(32)

$$\begin{aligned} 10j^5L^3\gamma +j^3 L^3 \lambda + 4j^4 L^3 \nu =0, \end{aligned}$$

(33)

$$\begin{aligned} 5j^5L^4\gamma +j^4L^4\nu =0, \end{aligned}$$

(34)

The values of j and L in the solutions are obtained as:

$$\begin{aligned} L=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ j=-\frac{\nu }{5\gamma }, \end{aligned}$$

(35)

After solving the above equation we also obtained the following values:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(36)

By substituting the Eqs. (30, 31, 32, 33, 34) with Eq. (35) into Eq. (15), we get a periodic solutions of cd-type for the Eq. (2) as:

$$\begin{aligned} \Xi (x,t)=\{j[1\pm Lcd(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(37)

where $\zeta =x-\vartheta t-\iota _o$. We can find the integration constant N and R by equating the Eqs. (14) and (36) that are:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(38)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(39)

The chirping that corresponds to this PW can be easily obtained as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha j[1\pm Lcd(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(40)

3.3 CPW of the cs-type

We use the following transformation for cs-type PW.

$$\begin{aligned} \Upsilon (\iota )=\Theta \{1\pm \Gamma cs[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(41)

where $\iota _o$ is the constant and cs(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we find the equations that are as follows:

$$\begin{aligned}&G+\Theta ^5\gamma + \Theta ^2 \epsilon + \Theta ^3 \lambda + \Theta \sigma + \Theta ^4 \nu =0, \end{aligned}$$

(42)

$$\begin{aligned}&5\Theta ^5\Gamma \gamma +2\Theta ^2 \Gamma \epsilon + 3\Theta ^3 \Gamma \lambda + \Theta \Gamma \sigma +4\Theta ^4 \Gamma \nu =0, \end{aligned}$$

(43)

$$\begin{aligned}&10\Theta ^5\Gamma ^2\gamma +\Theta ^2 \Gamma ^2 \epsilon + 3\Theta ^3 \Gamma ^2 \lambda + 6\Theta ^4 \Gamma ^2 \nu =0, \end{aligned}$$

(44)

$$\begin{aligned}&10\Theta ^5\Gamma ^3\gamma +\Theta ^3 \Gamma ^3 \lambda + 4\Theta ^4 \Gamma ^3 \nu =0, \end{aligned}$$

(45)

$$\begin{aligned}&5\Theta ^5\Gamma ^4\gamma +\Theta ^4\Gamma ^4\nu =0, \end{aligned}$$

(46)

The values of $\Theta$ and $\Gamma$ in the solutions are obtained as:

$$\begin{aligned} \Gamma =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Theta =-\frac{\nu }{5\gamma }, \end{aligned}$$

(47)

After solving the above equation we also obtained the following values:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(48)

By substitution of the Eqs. (42, 43, 44, 45, 46) with Eq. (47) into Eq. (15), we get a solutions of cs-type for the Eq. (2) as:

$$\begin{aligned} \Xi (x,t)=\{j[1\pm Lcd(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(49)

where $\zeta =x-\vartheta t-\iota _o$. We can find the integration constant N and R by equating the Eqs. (14) and (48) that are:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(50)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(51)

The chirping that corresponds to this PW can be easily obtained as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Theta [1\pm \Gamma cd(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(52)

3.4 CPW of the dn-type

The PW solution of dn-type of Eq. (12) are given by:

$$\begin{aligned} \Upsilon (\iota )=e\{1\pm Fdn[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(53)

where dn(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we get the some equations that are:

$$\begin{aligned} G+e^5\gamma +e^2 \epsilon +e^3 \lambda +e\sigma +e^4 \nu =0, \end{aligned}$$

(54)

$$\begin{aligned} 5e^5F\gamma +2e^2 F\epsilon + 3e^3 F\lambda + eF\sigma +4e^4F\nu =0, \end{aligned}$$

(55)

$$\begin{aligned} 10e^5F^2\gamma +e^2 F^2 \epsilon + 3e^3 F^2 \lambda + 6e^4 F^2 \nu =0, \end{aligned}$$

(56)

$$\begin{aligned} 10e^5F^3\gamma +e^3 F^3 \lambda + 4e^4 F^3 \nu =0, \end{aligned}$$

(57)

$$\begin{aligned} 5e^5F^4\gamma +e^4F^4\nu =0, \end{aligned}$$

(58)

In this solution, the parameters e and F are defined as:

$$\begin{aligned} F=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ e=-\frac{\nu }{5\gamma }, \end{aligned}$$

(59)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(60)

The dn-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{e[1\pm Fdn(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(61)

where $\zeta =x-\vartheta t-\iota _o$.By Equating Eqs. (14) and (60), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(62)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(63)

The following chirping is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha e[1\pm Fdn(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(64)

3.5 CPW of the dc-type

The PW solution of dc-type of Eq. (12) are given by:

$$\begin{aligned} \Upsilon (\iota )=n\{1\pm m dc[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(65)

where dc(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the equations that are given below:

$$\begin{aligned} G+n^5\gamma +n^2 \epsilon +n^3 \lambda +n\sigma +n^4 \nu =0, \end{aligned}$$

(66)

$$\begin{aligned} 5n^5m\gamma +2n^2 m\epsilon + 3n^3 m\lambda + nm\sigma +4n^4m\nu =0, \end{aligned}$$

(67)

$$\begin{aligned} 10n^5m^2\gamma +n^2 m^2 \epsilon + 3n^3 m^2 \lambda + 6n^4 m^2 \nu =0, \end{aligned}$$

(68)

$$\begin{aligned} 10n^5m^3\gamma +n^3 m^3 \lambda + 4n^4 m^3 \nu =0, \end{aligned}$$

(69)

$$\begin{aligned} 5n^5m^4\gamma +e^4m^4\nu =0, \end{aligned}$$

(70)

In this solution, the parameters m and n are defined as:

$$\begin{aligned} m=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ n=-\frac{\nu }{5\gamma }, \end{aligned}$$

(71)

We also find the value of $\sigma$ and G by the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(72)

The dc-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{n[1\pm mdc(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(73)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (72), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(74)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(75)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha n[1\pm mdc(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(76)

3.6 CPW of the ds-type

The PW solution of ds-type of Eq. (12) are given by:

$$\begin{aligned} \Upsilon (\iota )=J\{1\pm \varsigma ds[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(77)

where ds(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+J^5\gamma +J^2 \epsilon +J^3 \lambda +J\sigma +J^4 \nu =0, \end{aligned}$$

(78)

$$\begin{aligned} 5J^5\varsigma \gamma +2J^2 \varsigma \epsilon + 3J^3 \varsigma \lambda + J\varsigma \sigma +4J^4\varsigma \nu =0, \end{aligned}$$

(79)

$$\begin{aligned} 10J^5\varsigma ^2\gamma +J^2 \varsigma ^2 \epsilon + 3J^3 \varsigma ^2 \lambda + 6J^4 \varsigma ^2 \nu =0, \end{aligned}$$

(80)

$$\begin{aligned} 10J^5\varsigma ^3\gamma +J^3 \varsigma ^3 \lambda + 4J^4 \varsigma ^3 \nu =0, \end{aligned}$$

(81)

$$\begin{aligned} 5J^5\varsigma ^4\gamma +J^4\varsigma ^4\nu =0, \end{aligned}$$

(82)

In this solution, the parameters J and $\varsigma$ are defined as:

$$\begin{aligned} \varsigma =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ J=-\frac{\nu }{5\gamma }, \end{aligned}$$

(83)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(84)

The ds-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{J[1\pm \varsigma ds(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(85)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (84), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(86)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(87)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha J[1\pm \varsigma ds(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(88)

3.7 CPW of the sn-type

Equation (12) provides the sn-type PW solution as:

$$\begin{aligned} \Upsilon (\iota )=B\{1\pm Xsn[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(89)

where sn(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+B^5\gamma +B^2 \epsilon +B^3 \lambda +B\sigma +B^4 \nu =0, \end{aligned}$$

(90)

$$\begin{aligned} 5B^5X\gamma +2B^2 X\epsilon + 3B^3 X\lambda + BX\sigma +4B^4X\nu =0, \end{aligned}$$

(91)

$$\begin{aligned} 10B^5X^2\gamma +B^2 X^2 \epsilon + 3B^3 X^2 \lambda + 6B^4 X^2 \nu =0, \end{aligned}$$

(92)

$$\begin{aligned} 10B^5X^3\gamma +B^3 X^3 \lambda + 4B^4 X^3 \nu =0, \end{aligned}$$

(93)

$$\begin{aligned} 5B^5X^4\gamma +B^4X^4\nu =0, \end{aligned}$$

(94)

In this solution, the parameters B and X are defined as:

$$\begin{aligned} X=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ B=-\frac{\nu }{5\gamma }, \end{aligned}$$

(95)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(96)

The sn-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{B[1\pm Xsn(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(97)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (96), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(98)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(99)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha B[1\pm Xsn(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(100)

3.8 CPW of the sc-type

Equation (12) provides the sc-type PW solution as:

$$\begin{aligned} \Upsilon (\iota )=\Lambda \{1\pm dsc[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(101)

where sc(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+\Lambda ^5\gamma +\Lambda ^2 \epsilon +\Lambda ^3 \lambda +\Lambda \sigma +\Lambda ^4 \nu =0, \end{aligned}$$

(102)

$$\begin{aligned} 5\Lambda ^5d\gamma +2\Lambda ^2 d\epsilon + 3\Lambda ^3 d\lambda + \Lambda d\sigma +4\Lambda ^4d\nu =0, \end{aligned}$$

(103)

$$\begin{aligned} 10\Lambda ^5d^2\gamma +\Lambda ^2 d^2 \epsilon + 3\Lambda ^3 d^2 \lambda + 6\Lambda ^4 d^2 \nu =0, \end{aligned}$$

(104)

$$\begin{aligned} 10\Lambda ^5d^3\gamma +\Lambda ^3 d^3 \lambda + 4\Lambda ^4 d^3 \nu =0, \end{aligned}$$

(105)

$$\begin{aligned} 5\Lambda ^5d^4\gamma +\Lambda ^4d^4\nu =0, \end{aligned}$$

(106)

In this solution, the parameters $\Lambda$ and d are defined as:

$$\begin{aligned} d=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Lambda =-\frac{\nu }{5\gamma }, \end{aligned}$$

(107)

We obtain the values of $\sigma$ and G in contrast of the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(108)

The sc-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{\Lambda [1\pm d sc(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(109)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (108), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2=\frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(110)

$$\begin{aligned} R=\frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(111)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Lambda [1\pm d sc(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(112)

3.9 CPW of the sd-type

Equation (12) provides the sd-type PW solution as:

$$\begin{aligned} \Upsilon (\iota )=q\{1\pm \varpi sd[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(113)

where sd(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+q^5\gamma +q^2 \epsilon +q^3 \lambda +q\sigma +q^4 \nu =0, \end{aligned}$$

(114)

$$\begin{aligned} 5q^5\varpi \gamma +2q^2 \varpi \epsilon + 3q^3 \varpi \lambda + q\varpi \sigma +4q^4\varpi \nu =0, \end{aligned}$$

(115)

$$\begin{aligned} 10q^5\varpi ^2\gamma +q^2 \varpi ^2 \epsilon + 3q^3 \varpi ^2 \lambda + 6q^4 \varpi ^2 \nu =0, \end{aligned}$$

(116)

$$\begin{aligned} 10q^5\varpi ^3\gamma +q^3 \varpi ^3 \lambda + 4q^4 \varpi ^3 \nu =0, \end{aligned}$$

(117)

$$\begin{aligned} 5q^5\varpi ^4\gamma +q^4\varpi ^4\nu =0, \end{aligned}$$

(118)

In this solution, the parameters q and $\varpi$ are defined as:

$$\begin{aligned} \varpi =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ q=-\frac{\nu }{5\gamma }, \end{aligned}$$

(119)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(120)

The sd-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{q[1\pm \varpi sd(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(121)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (120), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(122)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(123)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha q[1\pm \varpi sd(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(124)

3.10 CPW of the nc-type

The PW solution of nc-type of Eq. (12) are given by:

$$\begin{aligned} \Upsilon (\iota )=M\{1\pm O nc[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(125)

where nc(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned}&G+M^5\gamma +M^2 \epsilon +M^3 \lambda +M\sigma +M^4 \nu =0, \end{aligned}$$

(126)

$$\begin{aligned}&5M^5O\gamma +2M^2 O\epsilon + 3M^3 O\lambda + MO\sigma +4M^4O\nu =0, \end{aligned}$$

(127)

$$\begin{aligned}&10M^5O^2\gamma +M^2 O^2 \epsilon + 3M^3 O^2 \lambda + 6M^4 O^2 \nu =0, \end{aligned}$$

(128)

$$\begin{aligned}&10M^5O^3\gamma +M^3 O^3 \lambda + 4M^4 O^3 \nu =0, \end{aligned}$$

(129)

$$\begin{aligned}&5M^5O^4\gamma +M^4O^4\nu =0, \end{aligned}$$

(130)

In this solution, the parameters M and O are defined as:

$$\begin{aligned} O=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ M=-\frac{\nu }{5\gamma }, \end{aligned}$$

(131)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(132)

The nc-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{M[1\pm O nc(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(133)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (132), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(134)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(135)

The chirping that accompanies is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha M[1\pm Onc(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(136)

3.11 CPW of the ns-type

The PW solution of ns-type of Eq. (12) are given by:

$$\begin{aligned} \Upsilon (\iota )=k\{1\pm T ns[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(137)

where ns(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+k^5\gamma +k^2 \epsilon +k^3 \lambda +k\sigma +k^4 \nu =0, \end{aligned}$$

(138)

$$\begin{aligned} 5k^5T\gamma +2k^2 T\epsilon + 3k^3 T\lambda + kT\sigma +4k^4T\nu =0, \end{aligned}$$

(139)

$$\begin{aligned} 10k^5T^2\gamma +k^2 T^2 \epsilon + 3k^3 T^2 \lambda + 6k^4 T^2 \nu =0, \end{aligned}$$

(140)

$$\begin{aligned} 10k^5T^3\gamma +k^3 T^3 \lambda + 4k^4 T^3 \nu =0, \end{aligned}$$

(141)

$$\begin{aligned} 5k^5T^4\gamma +k^4T^4\nu =0, \end{aligned}$$

(142)

In this solution, the parameters k and T are defined as:

$$\begin{aligned} T=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ k=-\frac{\nu }{5\gamma }, \end{aligned}$$

(143)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(144)

The ns-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{k[1\pm T ns(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(145)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and Eq. (144), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(146)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(147)

The following chirping is provided by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha k[1\pm T ns(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(148)

3.12 CPW of the nd-type

The PW solution of nd-type of Eq. (12) are given by :

$$\begin{aligned} \Upsilon (\iota )=z\{1\pm r nd[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(149)

where nd(x, p) is JEF with modulus p taking values $0<p<1$. By solving this, we obtain the some equations that are given below:

$$\begin{aligned} G+z^5\gamma +z^2 \epsilon +z^3 \lambda +z\sigma +z^4 \nu =0, \end{aligned}$$

(150)

$$\begin{aligned} 5z^5r\gamma +2z^2 r\epsilon + 3z^3 r\lambda + zr\sigma +4z^4r\nu =0, \end{aligned}$$

(151)

$$\begin{aligned} 10z^5r^2\gamma +z^2 r^2 \epsilon + 3z^3 r^2 \lambda + 6z^4 r^2 \nu =0, \end{aligned}$$

(152)

$$\begin{aligned} 10z^5r^3\gamma +z^3 r^3 \lambda + 4z^4 r^3 \nu =0, \end{aligned}$$

(153)

$$\begin{aligned} 5z^5r^4\gamma +z^4r^4\nu =0, \end{aligned}$$

(154)

In this solution, the parameters z and r are defined as:

$$\begin{aligned} r=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ z=-\frac{\nu }{5\gamma }, \end{aligned}$$

(155)

We also find the value of $\sigma$ and G in contrast to the above relations:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(156)

The nd-type periodic solutions to Eq. (2) can be written as:

$$\begin{aligned} \Xi (x,t)=\{z[1\pm r nd(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(157)

where $\zeta =x-\vartheta t-\iota _o$. By Equating Eqs. (14) and (156), we can get the integration constant N and R for this case are given by:

$$\begin{aligned} N^2=\frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(158)

$$\begin{aligned} R=\frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(159)

The chirping that accompanies with it is given by:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha z[1\pm r nd(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(160)

3.13 CPW of the $nc+sc$-type

Equation (12) admits the $nc+sc$-types of the PW solution of the form:

$$\begin{aligned} \Upsilon (\iota )=S\{1\pm \eta (nc+sc)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(161)

where $nc+sc(x,p)$ is JEF of modulus p taking values $0<p<1$. we found some equation by the solution of periodic solutions in this type:

$$\begin{aligned} G+S^5\gamma +S^2 \epsilon +S^3 \lambda +S\sigma +S^4 \nu =0, \end{aligned}$$

(162)

$$\begin{aligned} 5S^5\eta \gamma +2S^2 \eta \epsilon + 3S^3 \eta \lambda + S\eta \sigma +4S^4\eta \nu =0, \end{aligned}$$

(163)

$$\begin{aligned} 10S^5\eta ^2\gamma +S^2 \eta ^2 \epsilon + 3S^3 \eta ^2 \lambda + 6S^4 \eta ^2 \nu =0, \end{aligned}$$

(164)

$$\begin{aligned} 10S^5\eta ^3\gamma +S^3 \eta ^3 \lambda + 4S^4 \eta ^3 \nu =0, \end{aligned}$$

(165)

$$\begin{aligned} 5S^5\eta ^4\gamma +S^4\eta ^4\nu =0, \end{aligned}$$

(166)

The parameters are S and $\eta$ in the solutions are shown in this expressions:

$$\begin{aligned} \eta =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ S=-\frac{\nu }{5\gamma },, \end{aligned}$$

(167)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(168)

the $nc+sc$-type periodic solutions for the Eq. (2) is given below:

$$\begin{aligned} \Xi (x,t)=\{S[1\pm \eta (nc+sc)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(169)

where $\zeta =x-\vartheta t-\iota _o$. By equating Eqs. (14) and (168), integration constant N and R can be obtained as:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(170)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(171)

The chirped PW may be written as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha S[1\pm \eta (nc+sc)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(172)

3.14 CPW of the $ns+cs$-type

Equation (12) admits the $ns+cs$-form of the PW solution of the form:

$$\begin{aligned} \Upsilon (\iota )=D\{1\pm \varphi (ns+cs)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(173)

where $ns+cs(x,p)$ is JEF of modulus p taking values $0<p<1$. By solving periodic solutions in this type, we found certain equations.:

$$\begin{aligned} G+D^5\gamma +D^2 \epsilon +D^3 \lambda +D\sigma +D^4 \nu =0, \end{aligned}$$

(174)

$$\begin{aligned} 5D^5\varphi \gamma +2D^2 \varphi \epsilon + 3D^3 \varphi \lambda + D\varphi \sigma +4D^4\varphi \nu =0, \end{aligned}$$

(175)

$$\begin{aligned} 10D^5\varphi ^2\gamma +D^2 \varphi ^2 \epsilon + 3D^3 \varphi ^2 \lambda + 6D^4 \varphi ^2 \nu =0, \end{aligned}$$

(176)

$$\begin{aligned} 10D^5\varphi ^3\gamma +D^3 \varphi ^3 \lambda + 4D^4 \varphi ^3 \nu =0, \end{aligned}$$

(177)

$$\begin{aligned} 5D^5\varphi ^4\gamma +D^4\varphi ^4\nu =0, \end{aligned}$$

(178)

The parameters are D and $\varphi$ in the solutions are shown in this expressions:

$$\begin{aligned} \varphi =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ D=-\frac{\nu }{5\gamma },, \end{aligned}$$

(179)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(180)

the $ns+cs$-type periodic solutions for the Eq. (2) is given below:

$$\begin{aligned} \Xi (x,t)=\{D[1\pm \varphi (ns+cs)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(181)

where $\zeta =x-\vartheta t-\iota _o$. By equating Eqs. (14) and (180), integration constant N and R can be obtained as:

$$\begin{aligned} N^2=\frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(182)

$$\begin{aligned} R=\frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(183)

The PW’s chirping can be found as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha D[1\pm \varphi (ns+cs)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(184)

3.15 CPW of the $ns+ds$-type

Equation (12) provides $ns+ds$-type of the PW solution:

$$\begin{aligned} \Upsilon (\iota )=Q\{1\pm \tau (ns+ds)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(185)

where $ns+ds(x,p)$ is JEF of modulus p taking values $0<p<1$. We obtained some equations in this type by solving periodic solutions.:

$$\begin{aligned} G+Q^5\gamma +Q^2 \epsilon +Q^3 \lambda +Q\sigma +Q^4 \nu =0, \end{aligned}$$

(186)

$$\begin{aligned} 5Q^5\tau \gamma +2Q^2 \tau \epsilon + 3Q^3 \tau \lambda + Q\tau \sigma +4D^4\tau \nu =0, \end{aligned}$$

(187)

$$\begin{aligned} 10Q^5\tau ^2\gamma +Q^2 \tau ^2 \epsilon + 3Q^3 \tau ^2 \lambda + 6Q^4 \tau ^2 \nu =0, \end{aligned}$$

(188)

$$\begin{aligned} 10Q^5\tau ^3\gamma +Q^3 \tau ^3 \lambda + 4Q^4 \tau ^3 \nu =0, \end{aligned}$$

(189)

$$\begin{aligned} 5Q^5\tau ^4\gamma +Q^4\tau ^4\nu =0, \end{aligned}$$

(190)

The parameters are Q and $\tau$ in the solutions are shown in this expressions:

$$\begin{aligned} \tau =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ Q=-\frac{\nu }{5\gamma },, \end{aligned}$$

(191)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(192)

the $ns+ds$-type periodic solutions for the Eq. (2) is given below:

$$\begin{aligned} \Xi (x,t)=\{Q[1\pm \tau (ns+ds)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(193)

where $\zeta =x-\vartheta t-\iota _o$. By equating Eqs. (14) and (192), integration constant N and R can be obtained as:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(194)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(195)

The chirping associated with this PW is as shown below:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha Q[1\pm \tau (ns+ds)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(196)

3.16 CPW of the $sn+icn$-type

Equation (12) has the following constrained periodic solutions:

$$\begin{aligned} \Upsilon (\iota )=H\{1\pm \varrho (sn+icn)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(197)

where $sn+icn(x,p)$ is JEF of modulus p taking values $0<p<1$. By the solution of periodic solutions in this type we fond some equations:

$$\begin{aligned} G+H^5\gamma +H^2 \epsilon +H^3 \lambda +H\sigma +H^4 \nu =0, \end{aligned}$$

(198)

$$\begin{aligned} 5H^5\varrho \gamma +2H^2 \varrho \epsilon + 3H^3 \varrho \lambda + H\varrho \sigma +4H^4\varrho \nu =0, \end{aligned}$$

(199)

$$\begin{aligned} 10H^5\varrho ^2\gamma +H^2 \varrho ^2 \epsilon + 3H^3 \varrho ^2 \lambda + 6H^4 \varrho ^2 \nu =0, \end{aligned}$$

(200)

$$\begin{aligned} 10H^5\varrho ^3\gamma +H^3 \varrho ^3 \lambda + 4H^4 \varrho ^3 \nu =0, \end{aligned}$$

(201)

$$\begin{aligned} 5H^5\varrho 4\gamma +H^4\varrho ^4\nu =0, \end{aligned}$$

(202)

The parameters H and $\varrho$ are:

$$\begin{aligned} \varrho =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ H=-\frac{\nu }{5\gamma },, \end{aligned}$$

(203)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(204)

The periodic solutions for Eq. (2) in $sn+icn$-type are shown below:

$$\begin{aligned} \Xi (x,t)=\{H[1\pm \varrho (sn+icn)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(205)

where $\zeta =x-\vartheta t-\iota _o$. By equating Eqs. (14) and (204), integration constant N and R can be obtained as:

$$\begin{aligned} N^2=\frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(206)

$$\begin{aligned} R=\frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(207)

The nonlinearity chirped PW’s chirping has the following form:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha H[1\pm \varrho (sn+icn)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(208)

3.17 CPW of the $\sqrt{1-m^2} sd+cd$-type

Equation (12) may be get for $\sqrt{1-m^2} sd+cd$-type of the PW solution:

$$\begin{aligned} \Upsilon (\iota )=\omega \{1\pm \Delta (\sqrt{1-m^2} sd+cd)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(209)

where $\sqrt{1-m^2} sd+cd(x,p)$ is JEF of modulus p taking values $0<p<1$. we get some equation by the solution of periodic solutions in this type:

$$\begin{aligned}&G+\omega ^5\gamma +\omega ^2 \epsilon +\omega ^3 \lambda +\omega \sigma +\omega ^4 \nu =0, \end{aligned}$$

(210)

$$\begin{aligned}&5\omega ^5\Delta \gamma +2\omega ^2 \Delta \epsilon + 3\omega ^3 \Delta \lambda + \omega \Delta \sigma +4\omega ^4\Delta \nu =0, \end{aligned}$$

(211)

$$\begin{aligned}&10\omega ^5\Delta ^2\gamma +\omega ^2 \Delta ^2 \epsilon + 3\omega ^3 \Delta ^2 \lambda + 6\omega ^4 \Delta ^2 \nu =0, \end{aligned}$$

(212)

$$\begin{aligned}&10\omega ^5\Delta ^3\gamma +\omega ^3 \Delta ^3 \lambda + 4\omega ^4 \Delta ^3 \nu =0, \end{aligned}$$

(213)

$$\begin{aligned}&5\omega ^5\Delta ^4\gamma +\omega ^4\Delta ^4\nu =0, \end{aligned}$$

(214)

The parameters are $\omega$ and $\Delta$ in the solutions are given as:

$$\begin{aligned} \Delta =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \omega =-\frac{\nu }{5\gamma },, \end{aligned}$$

(215)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(216)

the $\sqrt{1-m^2} sd+cd$-type periodic solutions for the Eq. (2) is given below:

$$\begin{aligned} \Xi (x,t)=\{\omega [1\pm \Delta (\sqrt{1-m^2} sd+cd)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(217)

where $\zeta =x-\vartheta t-\iota _o$. By equating Eqs. (14) and (216), integration constant N and R can be obtained as:

$$\begin{aligned}&N^2=\frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(218)

$$\begin{aligned} R=\frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(219)

As a result, Eq. (2)’s CP solution is given as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \omega [1\pm \Delta (\sqrt{1-m^2} sd+cd)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(220)

3.18 CPW of the $mcd+i\sqrt{1-m^2} nd$-type

Equation (12) admits the $mcd+i\sqrt{1-m^2} nd$-type of the PW solution of the form:

$$\begin{aligned} \Upsilon (\iota )=\beta \{1\pm \Sigma (mcd+i\sqrt{1-m^2} nd)[\mu (\iota -\iota _o),p]\}, \end{aligned}$$

(221)

where $mcd+i\sqrt{1-m^2} nd(x,p)$ is JEF of modulus p taking values $0<p<1$. we found some equation by the solution of periodic solutions in this type:

$$\begin{aligned}&G+\beta ^5\gamma +\beta ^2 \epsilon +\beta ^3 \lambda +\beta \sigma +\beta ^4 \nu =0, \end{aligned}$$

(222)

$$\begin{aligned}&5\beta ^5\Sigma \gamma +2\beta ^2 \Sigma \epsilon + 3\beta ^3 \Sigma \lambda + \beta \Sigma \sigma +4\beta ^4\Sigma \nu =0, \end{aligned}$$

(223)

$$\begin{aligned}&10\beta ^5\Sigma ^2\gamma +\beta ^2 \Sigma ^2 \epsilon + 3\beta ^3 \Sigma ^2 \lambda + 6\beta ^4 \Sigma ^2 \nu =0, \end{aligned}$$

(224)

$$\begin{aligned}&10\beta ^5\Sigma ^3\gamma +\beta ^3 \Sigma ^3 \lambda + 4\beta ^4 \Sigma ^3 \nu =0, \end{aligned}$$

(225)

$$\begin{aligned}&5\beta ^5\Sigma ^4\gamma +\beta ^4\Sigma ^4\nu =0, \end{aligned}$$

(226)

The parameters are $\Sigma$ and $\beta$ in the solutions are shown in this expressions:

$$\begin{aligned} \Sigma =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \beta =-\frac{\nu }{5\gamma },, \end{aligned}$$

(227)

the value of $\sigma$ and G are:

$$\begin{aligned} \sigma =\frac{\nu (100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{125\gamma ^3},~~~~~~ G= \frac{\nu ^2(11\nu ^3+375\gamma ^2\epsilon )}{3124\gamma ^4}, \end{aligned}$$

(228)

the $\sqrt{1-m^2} sd+cd$-type periodic solution for the Eq. (2) is:

$$\begin{aligned} \Xi (x,t)=\{\beta [1\pm \Sigma (mcd+i\sqrt{1-m^2} nd)(\mu \zeta ,p)]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(229)

where $\zeta =x-\vartheta t-\iota _o$.By equating Eqs. (14) and (228), integration constant N and R can be get as:

$$\begin{aligned} N^2= & {} \frac{\nu ^2\alpha (\alpha +c)(11\nu ^3+375\gamma ^2\epsilon )}{12500\gamma ^4}, \end{aligned}$$

(230)

$$\begin{aligned} R= & {} \frac{\nu ^2(100\gamma ^2\epsilon +3\nu (\nu ^2-5\lambda \gamma ))}{1000\gamma ^3}, \end{aligned}$$

(231)

The resultant chirping can be given as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \beta [1\pm \Sigma (mcd+i\sqrt{1-m^2} nd)(\mu \zeta ,p)]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(232)

4 The SW limit

It’s quite interesting to look for alternative explicit and exact local pulse solutions that propagate in a fiber optic system. We can appreciate the physical phenomena and dynamic process described by the NLS model very well with the assistance of these closed form solutions on their existence. We can find the precise chirped SW solutions of Eq. (2). In the long-wave limit, the JEF degenerate into hyperbolic functions, which correspond to prightarrow0 and prightarrow1 respectively. Each of these optical pulses has a nonlinear chirp, which is calculated as well.

4.1 Chirped bright SW

In the limiting case $p\rightarrow 1$, the function $cn(\zeta ,p)\rightarrow {{\,\mathrm{sech}\,}}(\zeta )$ and Eq. (25) yields the following SW solution of Eq. (2):

$$\begin{aligned} \Xi (x,t)=\{A[1\pm W {{\,\mathrm{sech}\,}}[\mu _o(x-\vartheta t- \iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(233)

The values of A and W in the solution are expressed as:

$$\begin{aligned} W=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ A=-\frac{\nu }{5\gamma }, \end{aligned}$$

(234)

The chirping that relates to the nonlinearly chirped SW can be easily achieved as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha A[1\pm W{{\,\mathrm{sech}\,}}[\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(235)

4.2 Chirped periodic-I SW

In the limiting case $p\rightarrow 0$, the function $cn(\zeta ,p)\rightarrow \cos (\zeta )$ and Eq. (25) yields the following SW solution of Eq. (2):

$$\begin{aligned} \Xi (x,t)=\{A[1\pm W \cos [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(236)

The values of A and W in the solution are expressed as:

$$\begin{aligned} W=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ A=-\frac{\nu }{5\gamma }, \end{aligned}$$

(237)

The chirping that relates to the nonlinearly chirped SW can be obtained as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha A[1\pm W\cos [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(238)

4.3 Chirped periodic-II SW

In the limiting case $p\rightarrow 0$, the function $cs(\zeta ,p)\rightarrow \cot (\zeta )$ and Eq. (49) yields the following SW solution of Eq. (2):

$$\begin{aligned} \Xi (x,t)=\{\Theta [1\pm \Gamma \cot [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(239)

where the parameters are given:

$$\begin{aligned} \Gamma =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Theta =-\frac{\nu }{5\gamma }, \end{aligned}$$

(240)

The chirping that corresponds to the nonlinearly chirped SW may be obtained as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Theta [1\pm \Gamma \cot [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(241)

4.4 Chirped periodic-III SW

In the limiting case $p\rightarrow 0$, the function $sn(\zeta ,p)\rightarrow \sin (\zeta )$ and Eq. (97) gives the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{B[1\pm X \sin [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(242)

where the variables are expressed as:

$$\begin{aligned} X=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ B=-\frac{\nu }{5\gamma }, \end{aligned}$$

(243)

The nonlinear chirped SW’s chirping may be represented as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha B[1\pm X\sin [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(244)

4.5 Chirped periodic-IV SW

In the limiting case $p\rightarrow 0$, the function $ns(\zeta ,p)\rightarrow \csc (\zeta )$ and Eq. (145) shows the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{k[1\pm T \csc [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(245)

where the variables are expressed as:

$$\begin{aligned} T=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ k=-\frac{\nu }{5\gamma }, \end{aligned}$$

(246)

The chirping of a nonlinear chirped SW can be expressed in the form::

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha k[1\pm T\csc [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(247)

4.6 Chirped dark SW

In the limiting case $p\rightarrow 1$, the function $sn(\zeta ,p)\rightarrow \tanh (\zeta )$ and Eq. (97) expressed the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{B[1\pm X \tanh [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(248)

where the variables are given as:

$$\begin{aligned} X=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ B=-\frac{\nu }{5\gamma }, \end{aligned}$$

(249)

The nonlinearly chirped SW’s chirping may be written as

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha B[1\pm X\tanh [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(250)

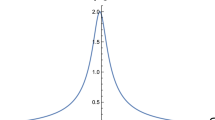
4.7 Chirped singular-I SW

In the limiting case $p\rightarrow 1$, the function $ns(\zeta ,p)\rightarrow \coth (\zeta )$ and Eq. (145) represents the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{k[1\pm T \coth [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(251)

where the variables are shown as:

$$\begin{aligned} T=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ k=-\frac{\nu }{5\gamma }, \end{aligned}$$

(252)

The chirping that belongs to the nonlinearly chirped SW may be shown as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha k[1\pm T\coth [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(253)

4.8 Chirped singular-II SW

In the limiting case $p\rightarrow 1$, the function $cs(\zeta ,p)\rightarrow {{\,\mathrm{csch}\,}}(\zeta )$ and Eq. (49) yields the following SW solution of Eq. (2):

$$\begin{aligned} \Xi (x,t)=\{\Theta [1\pm \Gamma {{\,\mathrm{csch}\,}}[\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(254)

where the parameters are given:

$$\begin{aligned} \Gamma =\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Theta =-\frac{\nu }{5\gamma }, \end{aligned}$$

(255)

obtain the chirping that corresponds to the nonlinearly chirped SW as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Theta [1\pm \Gamma {{\,\mathrm{csch}\,}}[\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(256)

4.9 Chirped hyperbolic-I SW

In the limiting case $p\rightarrow 1$, the function $sc(\zeta ,p)\rightarrow \sinh (\zeta )$ and Eq. (109) shows the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{\Lambda [1\pm d \sinh [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(257)

where the variables are expressed as:

$$\begin{aligned} d=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Lambda =-\frac{\nu }{5\gamma }, \end{aligned}$$

(258)

The chirping that belongs to the nonlinearly chirped SW may be expressed as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Lambda [1\pm d\sinh [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(259)

4.10 Chirped hyperbolic-II SW

In the limiting case $p\rightarrow 1$, the function $nc(\zeta ,p)\rightarrow \cosh (\zeta )$ and Eq. (133) gives the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{M[1\pm O \cosh [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(260)

where the variables are given as:

$$\begin{aligned} O=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ M=-\frac{\nu }{5\gamma }, \end{aligned}$$

(261)

The chirping that belongs to the nonlinearly chirped SW may be expressed as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha M[1\pm O\cosh [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(262)

4.11 Chirped bell SW

In the limiting case $p\rightarrow 0$, the function $nc(\zeta ,p)\rightarrow \sec (\zeta )$ and Eq. (133) gives the SW solution of Eq. (2) as follows:

$$\begin{aligned} \Xi (x,t)=\{M[1\pm O \sec [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(263)

where the variables are expressed as:

$$\begin{aligned} O=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ M=-\frac{\nu }{5\gamma }, \end{aligned}$$

(264)

The chirping that belongs to the nonlinearly chirped SW may be represent as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha M[1\pm O\sec [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(265)

4.12 Chirped kink SW

In the limiting case $p\rightarrow 0$, the function $sc(\zeta ,p)\rightarrow \tan (\zeta )$ and Eq. (109) gives the SW solution of Eq. (1) as follows:

$$\begin{aligned} \Xi (x,t)=\{\Lambda [1\pm d \tan [\mu _o(x-\vartheta t-\iota _o)]]\}^\frac{1}{2}\exp [i(Y(\iota )-\Omega t)], \end{aligned}$$

(266)

where the variables are expressed as:

$$\begin{aligned} d=\frac{4p\mu \sqrt{\gamma }}{\nu },~~~~~ \Lambda =-\frac{\nu }{5\gamma }, \end{aligned}$$

(267)

The chirping that belongs to the nonlinearly chirped SW may be expressed as:

$$\begin{aligned} \delta \Xi (x,t)=-\frac{N}{\alpha \Lambda [1\pm d\tan [\mu _o(x-\vartheta t-\iota _o)]]}-\frac{\vartheta }{2\alpha }, \end{aligned}$$

(268)

5 Results and discussion

In this section, we will discuss our results. El-Dessoky and Islam (2019) studied the chirped solitons of the GRD-NLSE equation. Ekiki et al. studied the extended JEF expansion technique to obtain traveling wave solutions of RNLSE. Akram et al. (2021) discussed the soliton solutions of the RNLSE in fibre optics with time dependent co-coefficients obtained by using $G'/G$-expansion approach. over and above, many researchers studied the RNLSE model to obtain different types of solutions solutions like bright soliton, singular soliton, peaked soliton, compacton solutions, solitary pattern solutions, rational solution, Weierstrass elliptic doubly periodic type solution, explicit bright solitons, singular periodic solutions, rogue wave solutions and many other solitons solutions (Ilie et al. 2018; Raza Rizvi et al. 2020; Aly and Cheemaa 2019a, b; Ali et al. 2020; Rizvi et al. 2020a; Younas et al. 2020a; El-Dessoky and Islam 2019).

In this manuscript, we obtained the several forms of CP and optical solitons. Equation (25) illustrating a cn-type periodic solution that degenerates into a bright soliton when $p\rightarrow 1$ and periodic-I solitons when $p\rightarrow 0$. Equation (49) depicts a periodic cs-type solution that degenerates into solitary-II solitons when $p\rightarrow 1$ and periodic-II solitons when $p\rightarrow 0$. Equation (97) displays the sn-type PW solution, which degenerates to dark solitons when $p\rightarrow 1$ and to periodic-III solitons when $p\rightarrow 0$. Equation (109) displays the sc-type PW solution, which degenerates to hyperbolic-I solitons when $p\rightarrow 1$ and to kink solitons when $p\rightarrow 0$. Equation (133) shows a periodic nc-type solution that degenerates into hyperbolic-II solitons when $p\rightarrow 1$ and Bell type solitons when $p\rightarrow 0$. Equation (145) shows a periodic ns-type solution that degenerates into solitary-I solitons when $p\rightarrow 1$ and periodic-IV solitons when $p\rightarrow 0$ (Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 and 24).

Fig. 1

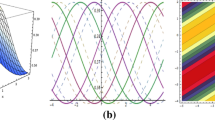
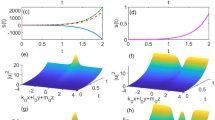
The dynamical behaviour of the $\Xi (x,t)$ in Eq. (25) at $\alpha =0.6$, $b=0.15, c=0.7$, $\mu =1.02$, $\vartheta =0.5$, $p=0.5$, $\delta =1$

Fig. 2

The graphical representation of the $\Xi (x,t)$ in Eq. (37) at $\alpha =0.98$, $b=0.56, c=0.78$, $\mu =1.25$, $\vartheta =0.82$, $p=0.57$, $\delta =1$

Fig. 3

The graphical representation of the $\Xi (x,t)$ in Eq. (49) at $\alpha =0.88$, $b=0.6, c=0.66$, $\mu =1.05$, $\vartheta =0.6$, $p=0.5$, $\delta =1$

Fig. 4

The graphical description of $\Xi (x,t)$ in Eq. (61) at $\alpha =0.5$, $b=0.7, c=1.2, p=1.09$, $\mu =1.04$, $\vartheta =0.9$, $\delta =1$

Fig. 5

The graphical description of $\Xi (x,t)$ in Eq. (73) at $\alpha =0.7$, $b=0.75, c=1.02, p=1.09$, $\delta =1$, $\mu =1.32$, $\vartheta =0.85$

Fig. 6

The graph of $\Xi (x,t)$ in Eq. (85) at $\alpha =0.78$, $b=0.75, c=1.05, p=1.09$, $\delta =1$, $\mu =1.35$, $\vartheta =0.95$

Fig. 7

The dynamical behaviour of $\Xi (x,t)$ in Eq. (97) at $\alpha =0.9$, $b=1, c=1.5, p=1.5$, $\delta =1.5$, $\mu =1.06$, $\vartheta =0.7$

Fig. 8

The dynamical behaviour of $\Xi (x,t)$ in Eq. (109) at $\alpha =0.86$, $b=0.73, c=1.4, p=1.35$, $\delta =1$, $\mu =1.43$, $\vartheta =0.35$

Fig. 9

The graphical description of $\Xi (x,t)$ in Eq. (133) at $\alpha =0.956$, $b=0.725, c=1.53, p=0.98$, $\delta =1$, $\mu =1.523$, $\vartheta =0.525$

Fig. 10

The graphical description of $\Xi (x,t)$ in Eq. (145) at $\alpha =0.956$, $b=0.515, c=1.753, p=0.28$, $\delta =1$, $\mu =1.523$, $\vartheta =0.525$

Fig. 11

The graphical description of $\Xi (x,t)$ in Eq. (157) at $\alpha =0.856$, $b=0.815, c=1.653, p=0.88$, $\delta =1$, $\mu =1.653$, $\vartheta =0.725$

Fig. 12

The shape profile of $\Xi (x,t)$ in Eq. (169) at $\alpha =0.96$, $b=0.72, c=1.43, p=1.6$ , $\delta =1.25$, $\mu =1.423$, $\vartheta =0.55$, $\Omega =1.5$

Fig. 13

The shape profile of $\Xi (x,t)$ in Eq. (181) at $\alpha =1.2$, $b=0.92, c=1.3, p=1.1$, $\delta =1.25$, $\mu =1.623$, $\vartheta =0.75$, $\Omega =1.5$

Fig. 14

The shape profile of $\Xi (x,t)$ in Eq. (205) at $\alpha =0.87$, $b=1.02, c=1.3$, p=1.65, $\delta =1.25$, $\mu =1.8$, $\vartheta =0.57$, $\Omega =1.5$, $i=\sqrt{-1}$

Fig. 15

The graphical representation of $\Xi (x,t)$ in Eq. (229) at $\alpha =0.87$, $b=1.02, c=1.3$, p=1.2, $\delta =1.25$, $\mu =1.8$, $\vartheta =0.7$, $\Omega =1.5$, m=0.5, $i=\sqrt{-1}$

Fig. 16

The graphical description of $\Xi (x,t)$ in Eq. (233) at $\alpha =0.6$, $b=0.15 , c=0.7$, $\mu =1$, $\vartheta =1$, $\Omega =1$, $\delta =1$

Fig. 17

The graph of $\Xi (x,t)$ in Eq. (236) at $\alpha =0.6$, $b=0.15, c=0.7$, $\mu =1$, $\vartheta =1$, $\Omega =1$, $\delta =1$

Fig. 18

The graphical description of $\Xi (x,t)$ in Eq. (239) at $\alpha =0.9$, $b=1, c=1.5$, $\Omega =1.5$, $\delta =1.5$, $\mu =1$, $\vartheta =0.8$

Fig. 19

Graph of $\Xi (x,t)$ in Eq. (242) at $\alpha =0.88$, $b=0.6, c=0.66$, $\mu =1$, $\vartheta =0.6$, $\Omega =1.5$, $\delta =1$

Fig. 20

The graphical description of $\Xi (x,t)$ in Eq. (245) at $\alpha =0.956$, $b=0.515, c=1.753$, $\Omega =1.28$, $\delta =1$, $\mu =1.2$, $\vartheta =0.525$

Fig. 21

The graphical description of $\Xi (x,t)$ in Eq. (248) at $\alpha =0.9$, $b=1, c=1.5$, $\Omega =1.5$, $\delta =1.5$, $\mu =1$, $\vartheta =0.8$

Fig. 22

Graph of $\Xi (x,t)$ in Eq. (251) at $\alpha =0.956$, $b=0.515$, c=1.753, $\Omega =1.28$, $\delta =1$, $\mu =1.2$, $\vartheta =0.525$

Fig. 23

The figure of $\Xi (x,t)$ in Eq. (263) at $\alpha =0.956$, $b=0.515, c=1.753$, $\Omega =1.9$, $\delta =1.25$, $\mu =1.5$, $\vartheta =0.7$

Fig. 24

The figure of $\Xi (x,t)$ in Eq. (266) at $\alpha =0.86$, $b=0.73, c=1.4$, $\Omega =1.35$, $\delta =1$, $\mu =1.3$, $\vartheta =0.35$

6 Conclusion

In this paper, we have studied RNLSE for chirped waves with JEF functions. As a consequence, several chirped soliton solutions such as bright, dark, singular, periodic, hyperbolic, and other solitons have been studied. For each of these optical solitons, the corresponding chirp is also produced. By selecting appropriate parameter values, graphical representations for certain obtained chirped solitons are also displayed.