1 Introduction

Fractional calculus was firstly proposed by Leibniz in 1695 (see [1, 2] and references therein). As a natural generalization of the classical calculus, the subject of fractional calculus has attracted much interest and attention from a lot of scholars and researchers. Because the fractional-order operators have the nonlocal feature and weakly singular kernels, the fractional-order models can provide a powerful tool to characterize the hereditary and memory properties of various phenomena and processes such as viscoelastic materials [3], market dynamics [4], physics [5], diffusion [6], control systems [7] and biological systems [8] and so on.

As we all know, the stability problem is a very important performance measure for any dynamical system. Recently, the various kinds of stability problems for fractional-order differential systems including Mittag-Leffler stability [9], asymptotic stability [10] and uniform stability [11] have been widely discussed. For example, Li et al. [9] investigated the Mittag-Leffler stability and generalized Mittag-Leffler stability of nonlinear fractional-order dynamic systems based on Lyapunov direct method and Mittag-Leffler function. Li et al. [12] discussed the global Mittag-Leffler stability of coupled system of fractional-order differential equations on network by using graph theory and the Lyapunov method. Wu et al. [13] proposed linear state feedback control law and partial state feedback control law to Mittag-Leffler stabilize the fractional-order BAM neural networks based on Lyapunov approach. On the other hand, time delay phenomenon is almost an inevitable problem in the practical systems, which often has an important on the dynamics of systems [14]. Liu et al. [15] investigated the Mittag-Leffler stability of nonlinear fractional neutral singular systems under Caputo and Riemann–Liouville derivatives.

In the past few decades, the neural networks were extensively applied to solve some signal processing, image processing and optimal control problems including cellular neural networks [16], Hopfield neural networks [17], recurrent neural networks [18, 19], Cohen-Grossberg neural networks [20], bidirectional associative memory (BAM) neural networks [21], and complex-valued neural networks [19, 22,23,24] and so on. In 1987, Kosko first introduced the double layers BAM neural network models (see [25]). The remarkable feature of BAM neural networks contains the close relation of the neurons between the U-layer and V-layer. That is, the neurons in one layer are fully interconnected to the one in the other layer, but there are not any interconnection among neurons in the same layer. Recently, we note that the fractional-order operators have been introduced to neural networks to establish the fractional-order neural networks by many researchers in [26,27,28,29,30,31,32]. Compared with the integer-order neural network models, the fractional-order ones could better describe the dynamical behaviors of the neurons. Many important results have been presented with regard to the various classes of stability analysis of fractional-order neural networks such as uniform stability [26, 29], delay-independent stability [27], finite-time stability [28], asymptotic stability [30, 31] and Mittag-Leffler stability [32].

The synchronization of dynamical systems mainly refers to a dynamical process wherein many chaotic systems modify a given property of their motion to a common behaviour due to a coupling or to a forcing. In [33,34,35,36,37,38,39,40,41], the authors discussed the various synchronization schemes for the integer-order network systems such as exponential synchronization [33, 34], adaptive synchronization [35], finite-time synchronization [36, 37], fixed-time synchronization [38], cluster synchronization [39], pinning-controlled synchronization [40] and impulsive synchronization [41]. It is worth mentioning that many researchers have been devoted to investigating the synchronization problems for fractional-order neural networks [42,43,44] and fractional-order delayed neural networks [32, 45,46,47,48,49,50]. The various effective control approaches have been applied to deal with synchronization problems concerning the integer-order or fractional-order neural networks such as distributed control [39], impulsive control [40], linear feedback control [42, 45], sliding model control [43, 44], adaptive feedback control [46, 47], adaptive pinning control [48] and linear delay feedback control [49]. Many real systems in physics, engineering, chemistry, biology, and information science, may experience abrupt changes as certain instants. This kind of impulsive behaviors can be modelled by impulsive systems [21, 22, 30, 32, 51]. For instance, Stamova [32] studied the global Mittag-Leffler synchronization of impulsive fractional-order neural networks with time-varying delays, while the interconnection effects of the neurons between U-layer and V-layer were not involved in the network model. Chen et al. [42] discussed the global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks, in which the impulsive effects and delay factor are not been considered. Rajivganthi et al. [47] discussed the adaptive synchronization and finite-time synchronization of Caputo fractional-order memristor-based BAM delayed neural networks, yet the impulsive effects are not been taken into account.

Compared with the advances of the integer-order delayed neural networks [16,17,18,19,20,21,22,23,24, 33,34,35,36,37,38,39,40,41], the research on the dynamical behaviours of fractional-order delayed neural networks is still at the stage of developing and exploiting [32, 45,46,47,48,49,50]. To the best of our knowledge, there are few results on the fractional-order BAM neural networks with multiple time-varying delays and impulsive effects. Motivated by the above discussions, this paper will consider the global Mittag-Leffler synchronization for Caputo fractional-order neural networks with multiple time-varying delays and impulsive effects. The main challenges and contributions of this paper are summarized as follows:

  • The differentiability of the neuron activation functions and time-varying delay functions in the addressed system are not necessarily required. The presented results are less conservative and more general.

  • The considered BAM network includes impulsive effects, multiple time-varying delays, fractional-order derivative and the interconnection effects of the neurons between U-layer and V-layer and so on. We sufficiently take into account the impact of these factors on the synchronization schemes of the network systems.

  • The delayed-feedback control strategy and Lyapunov functional approach are applied to derive global Mittag-Leffler synchronization conditions between fractional master system and slave system. The control gain constants can be searched in a wider range following the Mittag-Leffler synchronization conditions.

  • The global Mittag-Leffler synchronization conditions are described as the algebraic inequalities, which are concise and easy to test. The numerical simulations of an illustrative example are presented to show the validity and feasibility of the theoretical results based on the modified predictor–corrector algorithm [52].

2 Preliminaries and Model Description

In this section, we recall some definitions and related properties of fractional calculus. Moreover, a class of Caputo type fractional-order bidirectional associative memory (BAM) neural network models with multiple time-varying delays and impulsive effects is presented.

Definition 2.1

[2] The Riemann–Liouville fractional integral of order q for a function f is defined as:

$$\begin{aligned} {}_{t_0}D_{t}^{-q}f(t)=\frac{1}{\Gamma (q)}\int _{t_0}^{ t}(t-s)^{q-1}f(s)ds, \end{aligned}$$

where \(q>0, t\geqslant t_0\). The Gamma function \(\Gamma (q)\) is defined by the integral

$$\begin{aligned} \Gamma (z)=\int _0^{+\infty }s^{z-1}e^{-s}ds,\quad ({{\mathfrak {R}}}{\mathfrak {e}}(z)>0). \end{aligned}$$

The composition property with Riemann–Liouville fractional integral can be described by

$$\begin{aligned} _{\ t_0} D_{t}^{-p}{{}_{t_0}}D_{t}^{-q}f(t)={{}_{\ t_0} D}_{t}^{-(p+q)}f(t),\quad p,\ q>0. \end{aligned}$$

The Caputo fractional operator often plays a key role in the dynamics analysis of fractional-order systems, and the expression form of the initial value problems is similar to integer-order systems. Therefore, we deal with fractional-order BAM delayed neural networks with Caputo derivative in this paper , whose definition and properties are given below.

Definition 2.2

[2] The Caputo fractional derivative of order q for a function f is defined as

$$\begin{aligned} _{t_0}^{C}D_{t}^{q}f(t)=\frac{1}{\Gamma (m-q)} \int _{t_0}^{t}(t-s)^{m-q-1}f^{(m)}(s)ds, \end{aligned}$$

where \(0\leqslant m-1<q<m, m\in {\mathbb {Z}}^{+}\). Particularly, for \(0<\alpha <1\) case, one can get

$$\begin{aligned} _{t_0}^{C}D_{t}^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )} \int _{t_0}^{t}(t-s)^{-\alpha }f'(s)ds. \end{aligned}$$

According to Definition 2.2, for any constants \(L_1\in {\mathbb {R}}\) and \(L_2\in {\mathbb {R}}\), the linearity of Caputo’s fractional derivative is described by

$$\begin{aligned} _{t_0}^{C}D_{t}^{q}\Big (L_1f(t)+L_2g(t)\Big )=L_1 {{}_{t_0}^{C}D_{t}^{q}}f(t)+L_2{{}_{t_0}^{C}D_{t}^{q}}g(t). \end{aligned}$$

In this paper, we are devoted to discussing a class of Caputo type fractional-order BAM neural networks with multiple time-varying delays and impulsive effects described by the states equations

$$\begin{aligned} \left\{ \begin{aligned}&{}_{0}^{C}D_{t}^{\alpha } x_i(t)=-a_{i}x_i(t)+\sum \limits _{j=1}^{m}b_{ij}g_j\big (y_j(t)\big ) +\sum \limits _{j=1}^{m}c_{ ij}g_j\Big (y_j\big (t-\tau _{ij}(t)\big )\Big )+I_i,\quad t\ne t_k, \\&\Delta x_i(t)=\gamma _{k}^{(1)}\Big (x_i(t)\Big ),\quad t=t_k,\quad i=1,2, \ldots , n;\quad k=1,2, \ldots ,\\&{}_{0}^{C}D_{t}^{\alpha } y_j(t)=-{\overline{a}}_{j}y_j(t)+\sum \limits _{i=1}^{n}{\overline{b}}_{ji}f_i\big (x_i(t)\big )+\sum \limits _{i=1}^{n}{\overline{c}}_{ji }f_i\Big (x_i\big (t-\sigma _{ji}(t)\big )\Big )+{\overline{I}}_j,\quad t\ne t_k,\\&\Delta y_j(t)=\gamma _{k}^{(2)}\Big (y_j(t)\Big ),\quad t=t_k,\quad j=1,2, \ldots , m;\quad k=1,2, \ldots . \end{aligned}\right. \end{aligned}$$
(1)

There are two layers \(U=\{x_1, x_2, \ldots , x_n\}\) and \(V=\{y_1, y_2, \ldots , y_m\}\) in the fractional network system (1); \(x_i(t)\) and \(y_j(t)\) denote the membrane voltages of i-th neuron in the U-layer and the membrane voltages of j-th neuron in the V-layer, respectively; \(_{0}^{C}D_{t}^{\alpha } x_i(\cdot )\) denotes the order \(\alpha \) Caputo type fractional derivatives of \(x_i(\cdot )\) with \(0<\alpha <1\); \(a_i>0\) and \({\overline{a}}_j>0\) mean the decay coefficients of signals from neurons \(x_i\) to \(y_j\); \(f_i(\cdot )\) and \(g_j(\cdot )\) are the activation functions for neurons; \(b_{ij}, c_{ij}, {\overline{b}}_{ji}\) and \({\overline{c}}_{ji}\) represent the weight coefficients of the neurons; \(I_i\) and \({\overline{I}}_j\) denote external input of U-layer and V-layer, respectively; \(\tau _{ij}(t)\) and \(\sigma _{ji}(t)\) are the transmission time-varying delays at time t from neuron to another; Moreover, the impulsive moments \(\big \{t_k|k=1,2,\ldots \big \}\) satisfy \(0=t_0<t_1<t_2<\cdots<t_k<\cdots ,\ t_k\rightarrow +\infty \) as \(k\rightarrow +\infty \), and

$$\begin{aligned} \left\{ \begin{aligned}&\Delta x_i(t_k)=x_i(t_k^+)-x_i(t_k^-),\quad x_i(t_k^+)=\lim _{\varepsilon \rightarrow 0^+}x_i(t_k+\varepsilon ),\quad x_i(t_k^-)=x_i(t_k),\\&\Delta y_j(t_k)=y_j(t_k^+)-y_j(t_k^-),\quad y_j(t_k^+)=\lim _{\varepsilon \rightarrow 0^+}y_j(t_k+\varepsilon ),\quad y_j(t_k^-)=y_j(t_k),\\ \end{aligned}\right. \end{aligned}$$
(2)

\(x_i(t_k^+)\) and \(x_i(t_k^-)\) represent the right and left limits of \(x_i(t)\) at \(t=t_k\), respectively; \(x_i(t_k^-)=x_i(t_k)\) and \(y_j(t_k^-)=y_j(t_k)\) imply that \(x_i(t)\) and \(y_j(t)\) are both left continuous at \(t=t_k\). Correspondingly, the state vector of fractional-order network system can be denoted by

$$\begin{aligned} \Big (x(t),y(t)\Big )=\Big (x_1(t), x_2(t),\ldots , x_n(t), y_1(t), y_2(t),\ldots , y_m(t)\Big )^T\in {\mathbb {R}}^{n+m}. \end{aligned}$$

Throughout this paper, we make the following assumption conditions.

H1 The neuron activation functions \(f_i(\cdot )\) and \(g_j(\cdot )\) are Lipschitz continuous. That is, there exist positive constants \(L_i^f, L_j^g\in {\mathbb {R}}^+\) such that

$$\begin{aligned} \begin{aligned}&\big |f_i(x_1)-f_i(x_2)\big |\leqslant L_i^f\big |x_1-x_2\big |,\quad i=1,2,\ldots ,n,\quad \forall x_1, x_2\in {\mathbb {R}}\\&\big |g_j(y_1)-g_j(y_2)\big |\leqslant L_j^g\big |y_1-y_2\big |, \quad j=1,2,\ldots ,m, \quad \forall y_1, y_2\in {\mathbb {R}}, \end{aligned} \end{aligned}$$
(3)

where \(L_i^f, L_j^g\in {\mathbb {R}}^+\) are Lipschitz constants.

H2 The impulsive operators \(\gamma _{k}^{(1)}(\cdot )\) and \(\gamma _{k}^{(2)}(\cdot )\) satisfy

$$\begin{aligned} \left\{ \begin{aligned}&\gamma _{k}^{(1)}\Big (e_i(t_k)\Big )=-\lambda _{ik}^{(1)} e_i(t_k) ,\quad i=1,2,\ldots , n;\quad k=1,2,\ldots ,\\&\gamma _{k}^{(2)}\Big ({\overline{e}}_j(t_k)\Big )=-\lambda _{jk}^{(2)} {\overline{e}}_j(t_k) ,\quad j=1,2,\ldots , m;\quad k=1,2,\ldots ,\\ \end{aligned}\right. \end{aligned}$$
(4)

where \(\lambda _{ik}^{(1)}\in (0,2)\ (i=1,2,\ldots , n;\ k=1,2,\ldots ),\) and \(\lambda _{jk}^{(2)}\in (0,2)\ (j=1,2,\ldots , m;\ k=1,2,\ldots )\).

H3 The variable delay functions \(\tau _{ij}(\cdot )\) and \(\sigma _{ji}(\cdot )\) are continuous and bounded on the interval \([0,+\infty )\). That is, there exists a positive constant \(\tau {>}0\) such that \( \tau _{ij}(t), \sigma _{ji}(t)\in [0,\tau ].\)

The main advantage of Caputo derivative is that the initial conditions for Caputo fractional-order differential equations take on the same expression form as the integer-order differential equations (see [1, 2]). Therefore, the initial conditions associated with Caputo type fractional-order BAM network system (1) can be expressed as:

$$\begin{aligned} \begin{aligned} x_i(t)=\varphi _i(t), \quad y_j(t)=\phi _j(t),\quad t\in [-\tau ,0], \end{aligned} \end{aligned}$$
(5)

where \(\varphi _i(t),\ \phi _j(t)\) denote the real-valued piecewise continuous functions defined on \([-\tau ,0]\) with the norm given by

$$\begin{aligned} \Vert \varphi \Vert =\sum \limits _{i=1}^n{\sup \limits _{\theta \in [-\tau ,0]}}\bigg \{\Big |\varphi _i(\theta )\Big |\bigg \},\quad \Vert \phi \Vert =\sum \limits _{j=1}^m\sup \limits _{\theta \in [-\tau ,0]}\bigg \{\Big |\phi _j(\theta )\Big |\bigg \}. \end{aligned}$$

In order to realize the global Mittag-Leffler synchronization between fractional-order master neural network and slave neural network, we refer to fractional-order network system (1) as the master system, and fractional-order slave system is described as the following form:

$$\begin{aligned} \left\{ \begin{aligned}&{}_{0}^{C}D_{t}^{\alpha } {\overline{x}}_i(t)=-a_{i}{\overline{x}}_i(t)+\sum \limits _{j=1}^{m}b_{ij}g_j\big ({\overline{y}}_j(t)\big ) +\sum \limits _{j=1}^{m}c_{ ij}g_j\big ({\overline{y}}_j(t-\tau _{ij}(t))\big )+u_i(t)+I_i, \\&\triangle e_i(t_k)=\gamma _{k}^{(1)}\Big (e_i(t_k)\Big ),\quad i=1,2,\ldots ,n;\quad k=1,2,\ldots ,\\&{}_{0}^{C}D_{t}^{\beta } {\overline{y}}_j(t)=-{\overline{a}}_{j}{\overline{y}}_j(t)+\sum \limits _{i=1}^{n}{\overline{b}}_{ji}f_i\big ({\overline{x}}_i(t)\big )+\sum \limits _{i=1}^{n}{\overline{c}}_{ji }f_i\big ({\overline{x}}_i(t-\sigma _{ji}(t))\big )+v_j(t)+{\overline{I}}_j,\\&\triangle {\overline{e}}_j(t_k)=\gamma _{k}^{(2)}\Big ({\overline{e}}_j(t_k)\Big ),\quad j=1,2,\ldots ,m; \quad k=1,2,\ldots , \end{aligned}\right. \end{aligned}$$
(6)

with the initial conditions \({\overline{x}}_i(t)={\overline{\varphi }}_i(t), \ {\overline{y}}_j(t)={\overline{\phi }}_j(t),\ t\in [-\tau ,0].\)

Let \(e_i(t)={\overline{x}}_i(t)-x_i(t),\ {\overline{e}}_j(t)={\overline{y}}_j(t)-y_j(t)\ (i=1,2,\ldots ,n;\ j=1,2,\ldots ,m)\) be the synchronization errors. From fractional master system (1) and fractional slave system (6), we can obtain fractional error system

$$\begin{aligned} \left\{ \begin{aligned}&{{}_{0}^{C}D_{t}^{\alpha }} \Big \{e_i(t)\Big \}=-a_{i}e_i(t)+\sum \limits _{j=1}^{m}b_{ij}g_j\big ({\overline{e}}_j(t)\big )+\sum \limits _{j=1}^{m}c_{ ij}g_j\big ({\overline{e}}_j(t-\tau _{ij}(t))\big )+u_i(t) , \\&\triangle e_i(t_k)=\gamma _{k}^{(1)}\Big (e_i(t_k)\Big ),\quad i=1,2,\ldots ,n;\quad k=1,2,\ldots ,\\&{{}_{0}^{C}D_{t}^{\beta }}\Big \{{\overline{e}}_j(t)\Big \}=-{\overline{a}}_j{\overline{e}}_j(t)+\sum \limits _{i=1}^{n}{\overline{b}}_{ji}f_i\big (e_i(t)\big )+\sum \limits _{i=1}^{n}{\overline{c}}_{ji }f_i\big (e_i(t-\sigma _{ji}(t))\big )+v_j(t)\\&\triangle {\overline{e}}_j(t_k)=\gamma _{k}^{(2)}\Big ({\overline{e}}_j(t_k)\Big ),\quad j=1,2,\ldots ,m;\quad k=1,2,\ldots , \end{aligned}\right. \end{aligned}$$
(7)

where \(g_j\big ({\overline{e}}_j(t)\big )=g_j\big ({\overline{y}}_j(t)\big )-g_j\big (y_j(t)\big ),\ f_i\big (e_i(t)\big )=f_i\big (x_i(t)\big )-f_i\big (x_i(t)\big )\).

Similar to the discussions of the equilibrium solution to integer-order differential systems, noting that Caputo fractional-order derivative of a nonzero constant is equal to zero, then we can define the equilibrium solution of system (1) as follows:

Definition 2.3

A constant vector \(({x^*}^T,{y^*}^T)^T=(x_1^*, x_2^*,\ldots , x_n^*, y_1^*, y_2^*, \ldots , y_m^* )^T\in {\mathbb {R}}^{n+m}\) is an equilibrium solution of system (1) if and only if \(x^*=(x_1^*, x_2^*,\ldots , x_n^*)^T\) and \(y^*=(y_1^*, y_2^*,\ldots , y_m^*)^T\) satisfy the following equations:

$$\begin{aligned} \left\{ \begin{aligned}&- a_{i} x_i^*+\sum \limits _{j=1}^{m}b_{ij}g_j\big (y_j^*\big )+\sum \limits _{j=1}^{m}c_{ ij}g_j\big (y_j^*\big )+I_i=0,\quad i=1,2,\ldots ,n,\\&- {\overline{a}}_{j}y_j^*+\sum \limits _{i=1}^{n}{\overline{b}}_{ji}f_i\big (x_i^*\big )+\sum \limits _{i=1}^{n}{\overline{c}}_{j i}f_i\big (x_i^*\big )+{\overline{J}}_j=0,\quad j=1,2,\ldots ,m, \end{aligned}\right. \end{aligned}$$

and the impulsive jumps \(\gamma _{k}^{(1)}\Big (x_i(t_k)\Big )\) and \(\gamma _{k}^{(2)}\Big (y_j(t_k)\Big )\) satisfy

$$\begin{aligned} \gamma _{k}^{(1)}\big (x_i^*\big )=0,\quad \gamma _{k}^{(2)}\big (y_j^*\big )=0,\quad i=1,2,\ldots ,n;\quad j=1,2,\ldots , m;\quad k=1,2,\ldots . \end{aligned}$$

In what follows, we introduce the definition of global Mittag-Leffler synchronization and a basic lemma, which will be used to the proof of the main results.

Definition 2.4

Fractional master system (1) achieves global Mittag-Leffler synchronization with fractional slave system (6) under the control inputs \(u_i(t)\) and \(v_j(t)\), if and only if there exist two positive constants \(\lambda >0\) and \(M\geqslant 1\) such that fractional error system (7) satisfies the following inequality

$$\begin{aligned} \begin{aligned} \big \Vert e(t)\big \Vert +\big \Vert {\overline{e}}(t)\big \Vert \leqslant M\bigg \{\big \Vert \varphi -{\overline{\varphi }}\big \Vert + \big \Vert \phi -{\overline{\phi }}\big \Vert \bigg \}E_{\alpha }(-\lambda t^\alpha ),\quad 0<\alpha <1, \end{aligned} \end{aligned}$$
(8)

where \((\varphi ,\phi )\) and \(({\overline{\varphi }}, {\overline{\phi }})\) are different initial values of master system (1) and slave system (6), respectively.

Lemma 2.1

[42] Let V(t) be a continuous function on \([0,+\infty )\) and satisfies

$$\begin{aligned} \begin{aligned} {}_{0}^{C}D_{t}^{\alpha }V(t)\leqslant -\lambda V(t),\quad t>0, \end{aligned} \end{aligned}$$

where \(0<\alpha <1\) and \(\lambda \) is a constant. Then

$$\begin{aligned} V(t)\leqslant V(0)E_{\alpha }\big (-\lambda t^\alpha \big ),\quad t\in [0,+\infty ). \end{aligned}$$

Remark 2.1

The main purpose of this paper is devoted to investigating the global Mittag-Leffler synchronization problem for Caputo type fractional-order BAM delayed neural networks. It should be pointed out that the differentiability of the neuron activation functions \(f_i(\cdot ), g_j(\cdot )\) and time-varying delay functions \(\tau _{ij}(\cdot ), \sigma _{ji}(\cdot )\) in system (1) are not necessarily required.

Remark 2.2

The remarkable feature of BAM neural networks includes the complex relations of the neurons between the U-layer and V-layer. Several factors such as the multiple time-varying delays, impulsive effects and fractional order derivative \(\alpha \in (0,1)\) bring the significant challenge to the analysis of dynamical behaviours. In this paper, a delayed-feedback control strategy will be designed to overcome these difficulties to achieve global Mittag-Leffler synchronization between fractional master system (1) and fractional slave system (6).

3 Global Mittag-Leffler Synchronization Schemes

In this section, we discuss the global Mittag-Leffler synchronization schemes for fractional-order BAM neural networks with multiple variable delays and impulsive effects. By designing a set of delayed feedback controllers, the global Mittag-Leffler synchronization between fractional master system (1) and fractional slave system (6) is achieved based on fractional calculus theory and Lyapunov functional approach.

Choosing the delay-feedback control strategy for fractional slave system (6) by the following forms:

$$\begin{aligned} \begin{aligned}&u_i(t)=-\eta _ie_i(t)-\beta \text {sgn}\big (e_i(t)\big )\big |e_i(t-\tau )\big |,\quad i=1,2,\ldots ,n,\\&v_j(t)=-{\overline{\eta }}_j{\overline{e}}_j(t)-\beta \text {sgn}\big ({\overline{e}}_j(t)\big )\big |{\overline{e}}_j(t-\tau )\big |, \quad j=1,2,\ldots ,m, \end{aligned} \end{aligned}$$
(9)

where \( \eta _i>0, \ {\overline{\eta }}_j>0,\ \beta >0\) are all control gains to be determined, and \(\text {sgn}(\cdot )\) denotes the sign function.

Combining fractional error system (7) with the linear feedback controllers (9) and condition (H2) yields the following fractional error system

(10)

where \(g_j\big ({\overline{e}}_j(t)\big )=g_j\big ({\overline{y}}_j(t)\big )-g_j\big (y_j(t)\big ),\ f_i\big (e_i(t)\big )=f_i\big ({\overline{x}}_i(t)\big )-f_i\big (x_i(t)\big )\), \(\lambda _{ik}^{(1)}\in (0,2),\ \lambda _{jk}^{(2)}\in (0,2).\)

According to Definition 2.3, we immediately know that \((e_i^{\ *},{\overline{e}}_j^{\ *})^T=(0,0,\ldots ,0)^T\in {\mathbb {R}}^{n+m}\) is an equilibrium solution of error system (10). The impulsive operators also satisfy

$$\begin{aligned} \gamma _{k}^{(1)}\big (e_i^{\ *}\big )=0,\quad \gamma _{k}^{(2)}\big ({\overline{e}}_j^{\ *}\big )=0,\quad i=1,2,\ldots ,n;\quad j=1,2,\ldots , m;\quad k=1,2,\ldots . \end{aligned}$$

In what follows, the global Mittag-Leffler synchronization results are derived between fractional master system (1) and fractional slave system (6) based on the delayed feedback controllers (9).

Theorem 3.1

Suppose that the conditions (H1)–(H3) hold, then fractional master system (1) can achieve Mittag-Leffler synchronization with fractional slave system (4) under the delayed feedback controllers (9), if there exist two positive constants \(\omega _1, \omega _2\) such that \(\omega _2>\omega _1>0\), where

$$\begin{aligned} \begin{aligned}&\omega _1=\max \Bigg \{\max _{1\leqslant j\leqslant m}\sum \limits _{i=1}^{n}\big |{\overline{c}}_{ji}\big |L_i^f-\beta ,\ \max _{1\leqslant i\leqslant n}\sum \limits _{j=1}^{m}\big |c_{ij}\big |L_j^g-\beta \Bigg \}>0,\\&\omega _2=\min \Bigg \{\min _{1\leqslant i\leqslant n} \Big [a_{i}+\eta _{i}-L_i^f\sum \limits _{j=1}^{m} \big |{\overline{b}}_{ji}\big |\Big ],\ \min _{1\leqslant j\leqslant m}\Big [{\overline{a}}_{j}+{\overline{\eta }}_j-L_j^g\sum \limits _{i=1}^{n} \big |b_{ij}\big |\Big ] \Bigg \}>\omega _1. \end{aligned} \end{aligned}$$
(11)

Proof

Suppose \(\big (x^T(t),y^T(t)\big )^T=\big (x_1(t),\ldots ,x_n(t),y_1(t),\ldots ,y_m(t)\big )^T\) is a solution of fractional master system (1) with the initial value \(\big (\varphi ^T(0),\phi ^T(0)\big )^T=\big (\varphi _1(0),\ldots ,\varphi _n(0),\phi _1(0),\ldots ,\phi _m(0)\big )^T\). Corresponding, let \(\big ({\overline{x}}^T(t),{\overline{y}}^T(t)\big )^T=\big ({\overline{x}}_1(t),\ldots ,{\overline{x}}_n(t),{\overline{y}}_1(t),\ldots ,{\overline{y}}_m(t)\big )^T\) be a solution of slave system (4) with the initial value \(\big ({\overline{\varphi }}^T(0),{\overline{\phi }}^T(0)\big )^T=\big ({\overline{\varphi }}_1(0),\ldots ,{\overline{\varphi }}_n(0),{\overline{\phi }}_1(0),\ldots ,{\overline{\phi }}_m(0)\big )^T\) satisfying \(e_i(0)\ne 0,\ {\overline{e}}_j(0)\ne 0 \) for \(i=1,2,\ldots ,n; \ j=1,2,\ldots ,m.\)

Obviously, \((e_i^{\ *},{\overline{e}}_j^{\ *})^T=(0,0,\ldots ,0)^T\in {\mathbb {R}}^{n+m}\) is an equilibrium solution of fractional error system (10). Choosing a piecewise continuous Lyapunov functional by the following forms

$$\begin{aligned} \begin{aligned} V\big (t,e,{\overline{e}}\big )=\sum \limits _{i=1}^{n}\big |e_i(t)\big |+\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t)\big |. \end{aligned} \end{aligned}$$
(12)

By carrying out the following discussions of two cases, we can obtain the time fractional derivative of \(V\big (t,e,{\overline{e}}\big )\) along the trajectories of fractional error system (10):

Case 1 For \(t=t_k\), from (2) and (H2), one has

$$\begin{aligned} \begin{aligned} V\Big (t_k^{+},e(t_k^{+}),{\overline{e}}(t_k^{+})\Big )=&\sum \limits _{i=1}^{n}\Big |e_i(t_k)+\gamma _{k}^{(1)}\big (e_i(t_k)\big )\Big | +\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t_k)+\gamma _{k}^{(2)}\big ({\overline{e}}_j(t_k)\big )\Big |\\ \leqslant&\sum \limits _{i=1}^{n}\Big |e_i(t_k)-\lambda _{ik}^{(1)}e_i(t_k)\Big | +\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t_k)-\lambda _{jk}^{(2)}{\overline{e}}_j(t_k)\Big |. \end{aligned} \end{aligned}$$

Note that \(\lambda _{ik}^{(1)}\in (0,2),\ \lambda _{jk}^{(2)}\in (0,2)\ (i=1,2,\ldots ,n;\ j=1,2,\ldots , m;\ k=1,2,\ldots )\), then

$$\begin{aligned} \big |1-\lambda _{ik}^{(1)}\big |<1,\quad \big |1-\lambda _{jk}^{(2)}\big |<1,\quad i=1,2,\ldots ,n;\ j=1,2,\ldots ,m. \end{aligned}$$

Therefore

$$\begin{aligned} V\Big (t_k^{+},e(t_k^{+}),{\overline{e}}(t_k^{+})\Big )\leqslant & {} \sum \limits _{i=1}^{n}\Big |1-\lambda _{ik}^{(1)}\Big |\big |e_i(t_k^{-})\big |+\sum \limits _{j=1}^{m}\Big |1-\lambda _{jk}^{(2)}\Big |\big |{\overline{e}}_j(t_k^{-})\big |\end{aligned}$$
(13)
$$\begin{aligned}\leqslant & {} \sum \limits _{i=1}^{n} \big |e_i(t_k^{-})\big |+\sum \limits _{j=1}^{m} \big |{\overline{e}}_j(t_k^{-})\big |\end{aligned}$$
(14)
$$\begin{aligned}= & {} V\Big (t_k,e(t_k),{\overline{e}}(t_k)\Big ),\quad k=1,2,\ldots . \end{aligned}$$
(15)

Case 2 For \(t\ne t_k\), that is, \(t\in [t_{k-1},t_k)\), similar to the discussions of the single layer fractional neural networks in [32], from (12) we obtain the upper right Caputo fractional derivative

$$\begin{aligned} \begin{aligned} {}_{0}^{C}D_{t}^{\alpha }V\Big (t, e(t), {\overline{e}}(t)\Big )=\&{{}_{0}^{C}D}_{t}^{\alpha }\left[ \sum \limits _{i=1}^{n}\big |e_i(t)\big |\right] +{{}_{0}^{C}D}_{t}^{\alpha }\left[ \sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t)\big |\right] \end{aligned} \end{aligned}$$
(16)

The applications of Definition 2.2 yield that the following inequalities

$$\begin{aligned} {{}_{ 0}^{C}D}_{t}^{\alpha }\Big |e_i(t)\Big |=\text {sgn}\big (e_i(t)\big )\cdot \bigg ({{}_{ 0}^{C}D}_{t}^{\alpha }e_i(t)\bigg ),\quad {{}_{ 0}^{C}D}_{t}^{\alpha }\Big |{\overline{e}}_j(t)\Big |=\text {sgn}\big ({\overline{e}}_j(t)\big )\cdot \bigg ({{}_{ 0}^{C}D}_{t}^{\alpha }{\overline{e}}_j(t)\bigg ), \end{aligned}$$

where \(\text {sgn}\big (\cdot )\) denotes the sign function. Then, we can obtain the fractional-order derivatives along the solutions of first equation and third equation of system (10),

$$\begin{aligned} \left\{ \begin{aligned}&_{0}^{C}D_{t}^{\alpha }\big |e_i(t)\big |\leqslant -(a_{i}+\eta _i)\big |e_i(t)\big |+\sum \limits _{j=1}^{m}|b_{ij}| \big |g_j\big ({\overline{e}}_j(t)\big )\big |\\&\qquad +\sum \limits _{j=1}^{m}|c_{ij}| \big |g_j\big ({\overline{e}}_j(t-\tau _{ij}(t))\big )\big |-\beta \big |e_i(t-\tau )\big |,\\&{}_{0}^{C}D_{t}^{\alpha } \big |{\overline{e}}_j(t)\big |\leqslant -({\overline{a}}_{j}+{\overline{\eta }}_j)\big |{\overline{e}}_j(t)\big |+\sum \limits _{i=1}^{n}|{\overline{b}}_{ji}| \big |f_i\big (e_i(t)\big )\big |\\&\qquad +\sum \limits _{i=1}^{n}|{\overline{c}}_{ji}| \big |f_i\big (e_i(t-\sigma _{ji}(t))\big )\big |-\beta \big |{\overline{e}}_j(t-\tau )\big |. \end{aligned}\right. \end{aligned}$$
(17)

It follows from (H1) that

(18)

where \(i=1,2,\ldots ,n;\ j=1,2,\ldots ,m.\) Combining (16) with (18) yields that

$$\begin{aligned} {}_{0}^{C}D_{t}^{\alpha }\Big \{V\big (t, e(t), {\overline{e}}(t)\big )\Big \}&\leqslant -\sum \limits _{i=1}^{n}\Bigg [a_{i}+\eta _i-L_i^f \sum \limits _{j=1}^{m}\big |{\overline{b}}_{ji}\big |\Bigg ]\big |e_i(t)\big |\nonumber \\&-\sum \limits _{j=1}^{m}\Bigg [{\bar{a}}_{j}+{\overline{\eta }}_j-L_j^g \sum \limits _{i=1}^{n}\big |b_{ij}\big |\Bigg ]\big |{\overline{e}}_j(t)\big |\nonumber \\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{m}\big |c_{ij}\big | L_j^g\big |{\overline{e}}_j(t-\tau _{ij}(t))\big |\nonumber \\&+\sum \limits _{j=1}^{m}\sum \limits _{i=1}^{n}\big |{\overline{c}}_{ji}\big | L_i^f\big |e_i(t-\sigma _{ji}(t))\big |\nonumber \\&-\beta \sum \limits _{i=1}^{n}\big |e_i(t-\tau )\big |-\beta \sum \limits _{j=1}^{m} \big |{\overline{e}}_j(t-\tau )\big |. \end{aligned}$$
(19)

By computations, from (19) one can get

$$\begin{aligned} \begin{aligned} {}_{0}^{C}D_{t}^{\alpha }\Big \{V\big (t, e(t), {\overline{e}}(t)\big )\Big \} \leqslant&-\min _{1\leqslant i\leqslant n} \Bigg \{a_{i}+\eta _{i}-L_i^f\sum \limits _{j=1}^{m} \big |{\overline{b}}_{ji}\big |\Bigg \}\sum \limits _{i=1}^{n} \big |e_i(t)\big |\\&-\min _{1\leqslant j\leqslant m}\Bigg \{{\overline{a}}_{j}+{\overline{\eta }}_j-L_j^g\sum \limits _{i=1}^{n} \big |b_{ij}\big |\Bigg \}\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t)\big |\\&+\max _{1\leqslant j\leqslant m}\sum \limits _{i=1}^{n}\big |{\overline{c}}_{ji}\big |L_i^f\sum \limits _{i=1}^{n}\big |e_i(t-\sigma _{ji}(t))\big |-\beta \sum \limits _{i=1}^{n}\big |e_i(t-\tau )\big |\\&+\max _{1\leqslant i\leqslant n}\sum \limits _{j=1}^{m}\big |c_{ij}\big |L_j^g\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t-\tau _{ij}(t))\big |-\beta \sum \limits _{j=1}^{m} \big |{\overline{e}}_j(t-\tau )\big |\\ \leqslant&-\omega _2V\big (t, e(t), {\overline{e}}(t)\big )+\omega _1\sup \limits _{t-\tau \leqslant s\leqslant t} V\big (s, e(s), {\overline{e}}(s)\big ), \end{aligned} \end{aligned}$$
(20)

where \(\tau _{ij}(t), \sigma _{ji}(t)\in [0,\tau ]\) in (H3), and \(\omega _1, \omega _2\) are defined in (11) as follows:

$$\begin{aligned}&\omega _1=\max \Bigg \{\max _{1\leqslant j\leqslant m}\sum \limits _{i=1}^{n}\big |{\overline{c}}_{ji}\big |L_i^f-\beta ,\ \max _{1\leqslant i\leqslant n}\sum \limits _{j=1}^{m}\big |c_{ij}\big |L_j^g-\beta \Bigg \}>0,\\&\omega _2=\min \Bigg \{\min _{1\leqslant i\leqslant n} \Big [a_{i}+\eta _{i}-L_i^f\sum \limits _{j=1}^{m} \big |{\overline{b}}_{ji}\big |\Big ],\ \min _{1\leqslant j\leqslant m}\Big [{\overline{a}}_{j}+{\overline{\eta }}_j-L_j^g\sum \limits _{i=1}^{n} \big |b_{ij}\big |\Big ] \Bigg \}>\omega _1. \end{aligned}$$

According to the above estimate, we know that any solution \((e^T(t),{\overline{e}}^T(t))^T\) of fractional error system (10) satisfies the following Razumikhin condition (see [51])

$$\begin{aligned} V\Big (s,e(s),{\overline{e}}(s)\Big )\leqslant V\Big (t,e(t),{\overline{e}}(t)\Big ),\quad t-\tau \leqslant s \leqslant t. \end{aligned}$$

Note that \(\omega _2>\omega _1>0\), then there exists a real positive number \(\lambda \) such that \(0<\lambda \leqslant \omega _2-\omega _1\). Thus, we have

$$\begin{aligned} \begin{aligned} _{0}^{C}D_{t}^{\alpha }\Big \{V\big (t,e(t),{\overline{e}}(t)\big )\Big \}\leqslant -\lambda V\Big (t,e(t),{\overline{e}}(t)\Big ),\quad t>0,\quad t\ne t_k. \end{aligned} \end{aligned}$$
(21)

Combining (131415) and (21), it follows from Lemma 2.1 that

$$\begin{aligned} V\big (t,e(t),{\overline{e}}(t)\big )\leqslant V\Big (0,e(0),{\overline{e}}(0)\Big )E_{\alpha }\big (-\lambda t^\alpha \big ),\quad \forall t\in [0,+\infty ). \end{aligned}$$

Hence

$$\begin{aligned} \big \Vert e(t)\big \Vert +\big \Vert {\overline{e}}(t)\big \Vert&= \sum \limits _{i=1}^{n}\big |e_i(t)\big |+\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(t)\big |\nonumber \\&\leqslant E_{\alpha }(-\lambda t^\alpha )\left\{ \sum \limits _{i=1}^{n}\big |e_i(0)\big |+\sum \limits _{j=1}^{m}\big |{\overline{e}}_j(0)\big |\right\} \nonumber \\&= E_{\alpha }(-\lambda t^\alpha )\left\{ \sum \limits _{i=1}^{n}\big |\varphi _i(0)-{\overline{\varphi }}_i(0)\big |+\sum \limits _{j=1}^{m}\big |\phi _j(0)-{\overline{\phi }}_j(0)\big |\right\} \nonumber \\&\leqslant E_{\alpha }(-\lambda t^\alpha )\Bigg \{\big \Vert \varphi -{\overline{\varphi }}\big \Vert + \big \Vert \phi -{\overline{\phi }}\big \Vert \Bigg \}, \quad t>0. \end{aligned}$$
(22)

According to Definition 2.4, fractional master system (1) achieves global Mittag-Leffler synchronization with fractional slave system (6) under the delayed feedback controllers \(u_i(t)\) and \(v_j(t)\) in (9). This completes the proof of Theorem 3.1.\(\square \)

Note that global Mittag-Leffler stability implies globally asymptotic stability (see [9]), then we can get global asymptotical complete synchronization result between fractional master system (1) and fractional slave system (6). Similar to the proof of Theorem 3.1, we have the following result.

Theorem 3.2

Suppose that the conditions (H1)–(H3) hold, then fractional master system (1) can achieve global asymptotic synchronization with fractional slave system (6) based on the delayed feedback controllers (9), if there exist two positive constants \(\omega _1, \omega _2\) such that \(\omega _2>\omega _1>0\), where

$$\begin{aligned} \begin{aligned}&\omega _1=\max \Bigg \{\max _{1\leqslant j\leqslant m}\sum \limits _{i=1}^{n}\big |{\overline{c}}_{ji}\big |L_i^f-\beta ,\ \max _{1\leqslant i\leqslant n}\sum \limits _{j=1}^{m}\big |c_{ij}\big |L_j^g-\beta \Bigg \}>0,\\&\omega _2=\min \Bigg \{\min _{1\leqslant i\leqslant n} \Big [a_{i}+\eta _{i}-L_i^f\sum \limits _{j=1}^{m} \big |{\overline{b}}_{ji}\big |\Big ],\ \min _{1\leqslant j\leqslant m}\Big [{\overline{a}}_{j}+{\overline{\eta }}_j-L_j^g\sum \limits _{i=1}^{n} \big |b_{ij}\big |\Big ] \Bigg \}>0. \end{aligned} \end{aligned}$$
(23)

Remark 3.1

Theorem 3.1 presents the global Mittag-Leffler synchronization conditions between master system (1) and fractional slave system (6) under the delayed feedback controllers (9), which reveals the close relations between the network coefficients, neuron activation functions and delayed-feedback control gain constants. The global Mittag-Leffler synchronization conditions are described as the algebraic inequalities, which are easy to achieve global Mittag-Leffler synchronization by choosing the appropriate control gain constants \(\eta _i, {\overline{\eta }}_j\) and \(\beta \).

Remark 3.2

In [33,34,35,36,37,38,39,40,41], the authors focused on discussing the various synchronization schemes for integer-order neural networks including exponential synchronization [33, 34], adaptive synchronization [35], finite-time synchronization [36, 37], fixed-time synchronization [38], cluster synchronization [39], pinning-controlled synchronization [40] and impulsive synchronization [41]. As a generalization of exponential synchronization with the integer-order derivative, this paper is devoted to investigating global Mittag-Leffler synchronization scheme with the fractional-order derivative.

Remark 3.3

The various effective control approaches have been applied to deal with synchronization problems concerning the integer-order or fractional-order neural networks such as distributed control [39], impulsive control [40], linear feedback control [42, 45], sliding model control [43, 44], adaptive feedback control [46, 47], adaptive pinning control [48] and linear delay feedback control [49]. In this paper, the delayed feedback controllers (9) are designed to achieve global Mittag-Leffler synchronization between fractional master system (1) and fractional slave system (6). The main advantage of the proposed strategy is that the control gain parameters \(\eta _i, {\overline{\eta }}_j\) and \(\beta \) can be searched in a wider range following the Mittag-Leffler synchronization conditions (11).

Remark 3.4

In the past few decades, the bidirectional associative memory (BAM) neural networks were extensively studied in [20, 21, 30, 47]. For instance, Rajivganthi et al. [47] have discussed the adaptive synchronization and finite-time synchronization of Caputo fractional-order memristor-based BAM delayed neural networks, yet the impulsive effects are not been taken into account. It should be pointed out that finite-time stability and global Mittag-Leffler stability are mutually independent concepts, because finite-time stability does not contain Mittag-Leffler synchronization, and vise versa (see [9, 28]). Stamova [32] studied the global Mittag-Leffler synchronization of impulsive fractional-order neural networks with time-varying delays, while the interconnection effects of the neurons between U-layer and V-layer were not involved in the network model. Chen et al. [42] discussed the global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks, in which the impulsive effects and delay factor are not been considered. In addition, the global Mittag-Leffler stability implies global asymptotic stability, but global asymptotic stability does not contain global Mittag-Leffler stability. Therefore, under the conditions of Theorem 3.1, fractional master system (1) and fractional slave system (6) can achieve globally asymptotic synchronization.

4 An Numerical Example

In this section, a numerical example for Caputo type fractional-order BAM neural networks with multiple time-varying delays and impulsive effects is given to illustrate the effectiveness and feasibility of the theoretical results. The MATLAB toolbox and modified predictor–corrector algorithm (see [52]) will be applied to deal with the numerical simulations.

Example 4.1

Consider the four-state Caputo fractional-order BAM neural network model with multiple time-varying delays and impulsive effects described by the following state equations

$$\begin{aligned} \left\{ \begin{aligned}&{}_{0}^{C}D_{t}^{\alpha } x_i(t)=-a_{i}x_i(t)+\sum \limits _{j=1}^{2}b_{ij}g_j\big (y_j(t)\big )+\sum \limits _{j=1}^{2}c_{ij}g_j\Big (y_j(t-\tau _{ij}(t))\Big )+I_i,\quad t\ne t_k,\\&\Delta x_i(t_k)=-0.3\Big (x_i(t_k)\Big ),\quad i=1,2;\quad k\in {\mathbb {N}}^+,\\&{}_{0}^{C}D_{t}^{\alpha } y_j(t)=-{\overline{a}}_{j}y_j(t)+\sum \limits _{i=1}^{2}{\overline{b}}_{ji}f_i\big (x_i(t)\big )+\sum \limits _{i=1}^{2}{\overline{c}}_{ji }f_i\Big (x_i(t-\sigma _{ji}(t))\Big )+{\overline{I}}_j,\quad t\ne t_k,\\&\Delta y_j(t_k)=-0.5\Big (y_j(t_k)\Big ),\quad j=1,2;\quad k\in {\mathbb {N}}^+,\\ \end{aligned}\right. \end{aligned}$$
(24)

where \(\alpha \in (0,1)\) and

$$\begin{aligned} \left[ \begin{array}{cc} a_1&{} 0\\ 0&{} a_2\\ \end{array} \right]= & {} \left[ \begin{array}{cc} 2&{} 0\\ 0&{} 3\\ \end{array} \right] ,\quad \left[ \begin{array}{cc} b_{11}&{} b_{12}\\ b_{21}&{} b_{22}\\ \end{array} \right] = \left[ \begin{array}{cc} 1&{} 0.5\\ 1&{} 0.5\\ \end{array} \right] ,\quad \left[ \begin{array}{cc} c_{11}&{} c_{12}\\ c_{21}&{} c_{22}\\ \end{array} \right] = \left[ \begin{array}{cc} 0.45&{} 0.15\\ -0.35&{} 0.25\\ \end{array} \right] \\ \left[ \begin{array}{cc} \tau _{11}(t)&{} \tau _{12}(t)\\ \tau _{21}(t)&{} \tau _{22}(t)\\ \end{array} \right]= & {} \left[ \begin{array}{cc} |\sin t|&{} 0.5(1+\cos t)\\ 1+\sin t&{} |\cos t|\\ \end{array} \right] ,\quad \left[ \begin{array}{cc} \sigma _{11}(t)&{} \sigma _{12}(t)\\ \sigma _{21}(t)&{} \sigma _{22}(t)\\ \end{array} \right] = \left[ \begin{array}{cc} |\cos t|&{} 2\sin t\\ \sin t&{} |\cos t|\\ \end{array} \right] .\\ \left[ \begin{array}{cc} {\overline{a}}_1&{} 0\\ 0&{} {\overline{a}}_2\\ \end{array} \right]= & {} \left[ \begin{array}{cc} 5&{} 0\\ 0&{} 4\\ \end{array} \right] ,\quad \left[ \begin{array}{cc} {\overline{b}}_{11}&{} {\overline{b}}_{12}\\ {\overline{b}}_{21}&{} {\overline{b}}_{22}\\ \end{array} \right] = \left[ \begin{array}{cc} 0.5&{} 0.5\\ 0.5&{} -1\\ \end{array} \right] ,\quad \left[ \begin{array}{cc} {\overline{c}}_{11}&{} {\overline{c}}_{12}\\ {\overline{c}}_{21}&{} {\overline{c}}_{22}\\ \end{array} \right] = \left[ \begin{array}{cc} 0.15&{} -0.25\\ 0.35&{} 0.45\\ \end{array} \right] ,\\ f_i(x_i)= & {} \frac{1}{2}\Big (\big |x_i+1\big |-\big |x_i-1\big |\Big ),\quad i=1,2,\quad g_j(y_j)=\frac{1}{2}\Big (\big |y_j+1\big |-\big |y_j-1\big |\Big ),\\ j= & {} 1,2. \end{aligned}$$

From above parameters, we know that \(\tau =2\), \(\lambda _{ik}^{(1)}=0.3\in (0,2)\ (i=1,2),\ \lambda _{jk}^{(2)}=0.5\in (0,2)\ (j=1,2),\) and

$$\begin{aligned} \begin{aligned} L_1^f=L_2^f=L_1^g=L_2^g=1, \quad (\tau _{ij})_{2\times 2}= \left[ \begin{array}{cc} 1&{} 1\\ 2&{} 1\\ \end{array} \right] ,\quad (\sigma _{ji})_{2\times 2}= \left[ \begin{array}{cc} 1&{} 2\\ 1&{} 1\\ \end{array} \right] . \end{aligned} \end{aligned}$$

Choosing (24) as fractional master system, the corresponding slave system can be written as

$$\begin{aligned} \left\{ \begin{aligned}&{}_{0}^{C}D_{t}^{\alpha } x_i(t)=-a_{i}x_i(t)+\sum \limits _{j=1}^{2}b_{ij}g_j\big (y_j(t)\big )+\sum \limits _{j=1}^{2}c_{ij}g_j\Big (y_j(t-\tau _{ij}(t))\Big )+u_i(t)+I_i,\\&\qquad \qquad t\ne t_k,\\&\Delta x_i(t_k)=-0.3\Big (x_i(t_k)\Big ),\quad i=1,2;\quad k\in {\mathbb {N}}^+,\\&{}_{0}^{C}D_{t}^{\alpha } y_j(t)=-{\overline{a}}_{j}y_j(t)+\sum \limits _{i=1}^{2}{\overline{b}}_{ji}f_i\big (x_i(t)\big )+\sum \limits _{i=1}^{2}{\overline{c}}_{ji }f_i\Big (x_i(t-\sigma _{ji}(t))\Big )+v_j(t)+{\overline{I}}_j,\\&\qquad \qquad t\ne t_k,\\&\Delta y_j(t_k)=-0.5\Big (y_j(t_k)\Big ),\quad j=1,2;\quad k\in {\mathbb {N}}^+,\\ \end{aligned}\right. \end{aligned}$$
(25)

In what follows, we will apply Theorems 3.1 and 3.2 to design the suitable delayed-feedback controllers (9), such that fractional master system (24) and fractional slave system (25) can achieve global Mittag-Leffler synchronization and globally asymptotic synchronization.

In fact, we can choose the delayed-feedback controllers as follows:

$$\begin{aligned} \begin{aligned}&u_1(t)=-0.1e_1(t)-0.3 \text {sgn}\big (e_1(t)\big )\big |e_1(t-2)\big |,\\&u_2(t)=-0.2e_2(t)-0.3 \text {sgn}\big (e_2(t)\big )\big |e_2(t-2)\big |,\\&v_1(t)=-0.4{\overline{e}}_1(t)-0.3 \text {sgn}\big ({\overline{e}}_1(t)\big )\big |{\overline{e}}_1(t-2)\big |,\\&v_2(t)=-0.3{\overline{e}}_2(t)-0.3 \text {sgn}\big ({\overline{e}}_2(t)\big )\big |{\overline{e}}_2(t-2)\big |. \end{aligned} \end{aligned}$$
(26)

Then, we can obtain the following fractional error system with the delayed-feedback controllers (26)

(27)

By computations, we get

$$\begin{aligned}&\varepsilon _1=\max _{1\leqslant j\leqslant 2}\sum \limits _{i=1}^{2}\big |{\overline{c}}_{ji}\big |L_i^f-\beta =0.5,\quad \varepsilon _2=\max _{1\leqslant i\leqslant 2}\sum \limits _{j=1}^{2}\big |c_{ij}\big |L_j^g-\beta =0.3,\\&\xi _1=\min _{1\leqslant i\leqslant 2} \left[ a_{i}+\eta _{i}-L_i^f\sum \limits _{j=1}^{2} \big |{\overline{b}}_{ji}\big |\right] =1.1, \xi _2=\min _{1\leqslant j\leqslant 2}\left[ {\overline{a}}_{j}+{\overline{\eta }}_j-L_j^g\sum \limits _{i=1}^{2} \big |b_{ij}\big |\right] =3.3,\\&\omega _1=\max \Big \{\varepsilon _1, \varepsilon _2 \Big \}=0.5,\quad \omega _2=\min \Big \{\xi _1, \xi _2\Big \}=1.1. \end{aligned}$$

Thus, the conditions \(\omega _2>\omega _1>0\) and (H1)–(H3) in Theorems 3.1 and 3.2 are satisfied.

Fig. 1
figure 1

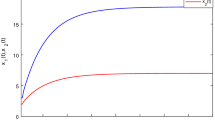
Trajectories of state norm for system (27) with different fractional order. a\(\alpha =0.4\). b\(\alpha =0.8\)

Full size image
Fig. 2
figure 2

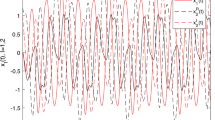
State trajectories of error system (27) with different fractional order. a\(\alpha =0.4\). b\(\alpha =0.8\)

Full size image

For numerical simulations, the trajectories of state norm for fractional error system (27) are depicted with different order \(\alpha =0.4\) and \(\alpha =0.8\) in Fig. 1, which shows that the state norm \(\Vert e(t)\Vert +\Vert {\overline{e}}(t)\Vert \) asymptotically converges to zero. At the same time, we find an interesting phenomenon that the convergence speed of the state norm \(\Vert e(t)\Vert +\Vert {\overline{e}}(t)\Vert \) is faster and faster with the increasing of the order \(\alpha \in (0,1)\) with regard to Caputo fractional derivative. Furthermore, the asymptotic behaviors of system (27) are presented by the state trajectories with different fractional order \(\alpha =0.4\) and \(\alpha =0.8\) in Fig. 2. It can be directly observed that fractional master system (24) can achieve global Mittag-Leffler synchronization and globally asymptotic synchronization with fractional slave system (25) under the delayed-feedback controllers (26). Therefore, Theorems 3.1 and 3.2 are verified by means of the numerical simulations in Figs. 1 and 2.

Remark 4.1

By choosing the suitable delayed-feedback controllers (25), we have achieved global Mittag-Leffler synchronization and globally asymptotic synchronization between master system (24) and slave system (26). The control gain parameters can be flexibly chosen in terms of (11). The modified predictor–corrector algorithm (see [52]) has been applied to deal with the numerical simulations by the MATLAB toolbox. The numerical simulations in Example 4.1 further confirm the feasibility and effectiveness of the theoretical results.

5 Conclusions

In this paper, the global Mittag-Leffler synchronization and globally asymptotic synchronization for a class of Caputo fractional BAM with multiple time-varying delays and impulsive effects are investigated. The sufficient conditions are derived to ensure the global Mittag-Leffler synchronization and globally asymptotic synchronization based on delayed-feedback control strategy and Lyapunov functional approach, which are described as the algebraic inequalities in terms of network parameters. The control gain constants can be searched in a wider range following the proposed synchronization conditions. The differentiability of the neuron activation functions and time-varying delay functions in the addressed fractional network system are not necessarily required. Therefore, the proposed results are more general and less conservative than the ones in the existing literature. A numerical example is also presented to illustrate the feasibility and effectiveness of the theoretical results.