1 Introduction

Fractional calculus mainly deals with derivatives and integrals of arbitrary non-integer order. As an extension of integer-order differentiation and integration, the subject of fractional calculus has drawn much attention from many researchers. Since fractional-order derivatives are nonlocal and have weakly singular kernels [1], fractional-order models own better description of memory and hereditary properties of various processes than integer-order ones. In recent decades, fractional differential equations [2, 3] have been proved to be an excellent tool in the modelling of many phenomena in various fields of electrochemistry [4], diffusion [5], viscoelastic materials [6], control systems [7, 8], biological systems [9] and so on.

As we all know, stability is one of the most concerned problems for any dynamic system. Recently, various kinds of stability of fractional-order dynamic systems including Mittag-Leffler stability [10, 11], Ulam stability [12], uniform stability [13] and asymptotic stability [14] have been extensively investigated. At the same time, time delay is one of the inevitable problems in dynamic systems, which usually has an important effect on the stability and performance of systems. For example, finite-time stability problems for fractional-order delayed differential equations are discussed based on Gronwall’s inequality approach [15], in which finite-time stability conditions are dependent on the size of time delays.

Note that various classes of neural networks such as Hopfield neural networks [16, 17], recurrent neural networks [18,19,20], cellular neural networks [21, 22], Cohen–Grossberg neural networks [23] and bidirectional associative memory neural networks [24, 25] have been widely used in solving some signal processing, image processing and optimal control problems [26]. A reference model approach and nonlinear measure approach to stability analysis of real-valued and complex-valued neural networks were proposed [27, 28], respectively. The stability properties of the equilibrium for various classes of neural networks at the presence of time delays have received a great deal of attention in the recent literatures [17,18,19,20,21,22,23,24,25,26]. In [29,30,31], the authors have sufficiently taken into account the influence of time delay factors on the dynamical behaviors of the network systems. In the classical neural network models, the time delays are usually in the states of the neural system. However, since the time derivatives of the states are the functions of time, in order to completely determine the stability properties of equilibrium point, some delay parameters must be introduced into the time derivatives of states of the system. The neural network model having time delays in the time derivatives of states is called delayed neutral-type systems [23, 25, 32,33,34,35,36,37,38]. This class of integer-order neutral systems has been extensively applied in many fields such as population ecology [32], distributed networks with lossless transmission lines [32], propagation and diffusion models [33] and VLSI systems [33].

Recently, some researchers have introduced fractional-order operators to neural networks to form fractional-order neural models [39,40,41], which could better describe the dynamical behavior of the neurons. It is worth mentioning that notable contributions have been made to various kinds of stability analysis of fractional-order neural networks [42,43,44,45,46]. For instance, the multi-stability problems of fractional-order neural networks without delay have been investigated by the characteristic roots analysis [39]. The uniform stability of the fractional-order neural networks has been presented in fixed time-intervals by analysis technique [40]. Mittag-Leffler stability of impulsive Caputo fractional-order delayed neural networks has been investigated by applying fractional Razumikhin approach [42]. The uniform stability and global stability of Riemann–Liouville fractional-order delayed neural networks have been considered based on fractional Lyapunov functional method and a Leibniz rule for fractional differentiation [44]. The Finite-time stability of Caputo fractional-order delayed neural networks has been studied by applying Gronwall’s inequality approach [45, 46].

There is no doubt that Lyapunov functional method provides a very effective approach to analyze stability of integer-order nonlinear systems. Compared with integer-order systems, it is more difficult to choose Lyapunov functionals for fractional order cases, which results in many difficulties in investigating the asymptotic behavior of such systems. For example, the well-known Leibniz rule does not hold for fractional derivative, and a counterexample (see [47]) was given to show that some incorrect uses of the Leibniz rule for fractional derivatives in the existing literature. In fact, it is very difficult to calculate fractional-order derivative of the Lyapunov functionals. This is the main reason that there are very few practical algebraic criteria on stability of fractional-order neural networks. To the best of our knowledge, the study of neutral-type neural networks mainly focused on neural networks with only first derivative of the states and delayed states [23, 25, 32,33,34,35,36,37,38]. There are few results on the asymptotic stability of fractional-order neutral-type delayed neural networks. Thus, it is necessary and challenging to take fractional-order derivative account into neutral type delayed neural networks.

Motivated by the above discussions, this paper will consider the delay-independent stability of Riemann–Liouville fractional-order neutral-type delayed neural networks. Compared to integer-order neural networks with or without time delays, the research on the stability of fractional-order neutral-type delayed neural networks is still at the stage of exploiting and developing. The main challenges and contributions of this paper are the following aspects:

  1. (i)

    It is difficult to calculate fractional-order derivatives of Lyapunov functionals. In order to overcome the difficulty, we construct a suitable functional including fractional integral and fractional derivative terms, and calculate its first-order derivative to derive the delay-independent stability conditions;

  2. (ii)

    The considered system includes state time delays, fractional-order derivatives of the states and time delays in fraction-order derivatives of states. We take into account the impact of these factors on the stability of network system simultaneously. The presented results contribute to the control and design of Riemann–Liouville fractional-order neutral-type delayed network systems. Moreover, we realize the analogue simulation of two examples to show the effectiveness of the theoretical results;

  3. (iii)

    The neuron activation functions discussed in Riemann–Liouville fractional neutral type neutral network model are not necessarily required to be differential. Compared to the existing results concerning integer-order neutral type neural networks [34, 35], the ones of this paper are more general and less conservative.

This paper is organized as follows. In Sect. 2, we recall some definitions concerning fractional calculus and describe the Riemann–Liouville fractional-order neutral-type neural network model. In Sect. 3, some sufficient conditions for the asymptotic stability of Riemann–Liouville fractional-order neutral-type neural networks are derived, which are described as the matrix inequalities or algebraic inequalities in terms of the networks parameters only. Two numerical examples are given to show the effectiveness and applicability of the proposed results in Sect. 4. Finally, some concluding remarks are drawn in Sect. 5.

Notations

Throughout the paper, \(\mathbb {R}^n\) denotes an n-dimensional Euclidean space, \(\mathbb {R}^{n\times m}\) is the set of all \(n\times m\) real matrices, I stands for the identity matrix with appropriate dimension, \(U^T\) means the transpose of a real matrix or vector U, \(V>0\) denotes the symmetric matrix V is positive definite. The matrix norm is defined by \(\Vert P\Vert _2=[\lambda _{M}(P^TP)]^{\frac{1}{2}}\), where \(\lambda _{M}(\cdot )\) denotes the maximun eigenvalue of the matrix \((\cdot )\).

2 Preliminaries and Model Description

In this section, we recall definitions of fractional calculus and several lemmas which will be used later. Moreover, the problem formulation on fractional-order neutral-type delayed neural networks is presented.

Definition 2.1

[3] The Riemann–Liouville fractional integral of order q for a function f is defined as:

$$\begin{aligned} _{t_0}D_{t}^{-q}f(t)=\frac{1}{\Gamma (q)}\int _{t_0}^{ t}(t-s)^{q-1}f(s)ds, \end{aligned}$$

where \(q>0, t\geqslant t_0\). The Gamma function \(\Gamma (q)\) is defined by the integral

$$\begin{aligned} \Gamma (z)=\int _0^{+\infty }s^{z-1}e^{-s}ds,\quad (\mathfrak {Re}(z)>0). \end{aligned}$$

Currently, there exist several definitions with regard to the fractional derivative of order \(q>0\) including Gr\(\ddot{u}\)nwald–Letnikov (GL) definition, Riemann–Liouville (RL) definition and Caputo definition. Among these definitions, Riemann–Liouville fractional operator often plays an important role in the stability analysis of fractional-order systems. Our consideration in this paper is the fractional-order neutral-type delayed neural networks with Riemann–Liouville derivative, whose definition and properties are given below (see [2, 3]).

Definition 2.2

The Riemann–Liouville fractional derivative of order q for a function f is defined as

$$\begin{aligned} _{\ t_0}^{RL}D_{t}^{q}f(t)=\frac{1}{\Gamma (m-q)}\frac{d^m}{dt^m} \int _{t_0}^{t}(t-s)^{m-q-1}f(s)ds, \end{aligned}$$

where \(0\leqslant m-1\leqslant q<m, m\in \mathbb {Z}^{+}\).

Property 2.1

\(_{\ t_0}^{RL}D_{t}^{q}C=\frac{C(t-t_0)^{-q}}{\Gamma (1-q)}\) holds, where C is any constant.

Property 2.2

For any constants \(k_1\in \mathbb {R}\) and \(k_2\in \mathbb {R}\), the linearity of Riemann–Liouville’s fractional derivative is described by

$$\begin{aligned} _{\ t_0}^{RL}D_{t}^{q}\Big (k_1f(t)+k_2g(t)\Big )=k_1 {_{\ t_0}^{RL}D_{t}^{q}}f(t)+k_2{_{\ t_0}^{RL}D_{t}^{q}}g(t). \end{aligned}$$

Property 2.3

If \(p>q>0\), then the following equaility

$$\begin{aligned} _{\ t_0}^{RL}D_{t}^{p}{_{t_0}}D_{t}^{-q}f(t)={_{\ t_0}^{RL}D}_{t}^{p-q}f(t) \end{aligned}$$

holds for sufficiently good functions f(t). In particular, this relation holds if f(t) is integrable.

The following two lemmas will be used in the proof of our main results.

Lemma 2.1

[14] Let \(x(t): \mathbb {R}^n\rightarrow \mathbb {R}^n\) be a vector of differentiable function. Then, for any time instant \(t\geqslant t_0\), the following relationship holds

$$\begin{aligned} _{\ t_0}^{RL}D_{t}^{q}\Big (x^T(t)Px(t)\Big )\leqslant 2x(t)P\Big ( {_{\ t_0}^{RL}D}_{t}^{q}x(t)\Big ),\quad q\in (0,1), \end{aligned}$$

where \(P\in \mathbb {R}^{n\times n}\) is a constant, square, symmetric and positive definite matrix.

Lemma 2.2

[21] Let G, H and P be real matrices of appropriate dimensions with \(P>0\). Then, for any vectors x, y with appropriate dimensions, the following inequality holds:

$$\begin{aligned} 2x^T{\textit{GHy}}\leqslant x^T{\textit{GPG}}^Tx+y^TH^TP^{-1}{\textit{Hy}}. \end{aligned}$$

In this paper, we consider the delay-independent stability of a class of Riemann–Liouville fractional-order neutral-type delayed neural networks with the state equations:

$$\begin{aligned} \begin{aligned} _{ \ 0}^{RL}D_{t}^{\alpha } x_i(t)=&-a_{i}x_i(t)+\sum \limits _{j=1}^{n}b_{ij}f_j\big (x_j(t)\big ) +\sum \limits _{j=1}^{n}c_{ij}f_j\big (x_j(t-\tau )\big )\\&+\sum \limits _{j=1}^{n} e_{ij}\Bigg ({_{0}^{RL}D_{t}^{\alpha } x_i(t-\tau )\Bigg )},\ t\geqslant 0, \end{aligned} \end{aligned}$$
(1)

or in the matrix-vector notation

$$\begin{aligned} _{ \ 0}^{RL}D_{t}^{\alpha }x(t)=-Ax(t)+Bf(x(t))+Cf(x(t-\tau ))+E \Big ( {_{ \ 0}^{RL}D}_{t}^{\alpha }x(t-\tau )\Big ),\ t\geqslant 0, \end{aligned}$$
(2)

where \(_{ \ 0}^{RL}D_{t}^{\alpha } x(\cdot )\) denotes an \(\alpha \) order Riemann–Liouville fractional derivative of \(x(\cdot )\), the positive constant \(\alpha \) satisfies \(0<\alpha <1\), n is the number of neurons in the indicated neural network, \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\) is the state vector of the network at time t, the functions \(f_i(\cdot )\) denote the neurons activations with \(f_i(0)=0\), \(A=\) diag \((a_1,a_2,\ldots ,a_n)\) is a diagonal matrix with \(a_i>0\) for \(i=1,2,\ldots ,n\), \(B=(b_{ij})_{n\times n},\ C=({c_{ij}})_{n\times n}, E=({e_{ij}})_{n\times n}\) are the constant matrices, \(\tau >0\) denotes the maximum possible transmission delay from neuron to another.

The initial condition associated with Riemann–Liouville fractional system (1) can be written as [2, 3]

$$\begin{aligned} {{_0}D}_{t}^{-(1-\alpha )}x(t)=\varphi (t),\quad t\in [-\tau ,0],\quad \alpha \in (0,1), \end{aligned}$$

where \(\varphi (t)\in \mathbf {C}([-\tau ,0],\mathbb {R}^n)\) is the initial state function, and \(\mathbf {C}([-\tau ,0],\mathbb {R}^n)\) denotes the space of all continuous functions mapping the interval \([-\tau ,0]\) into \(\mathbb {R}^n\).

Throughout this paper, we assume that the activation functions \(f_i(\cdot )\) are Lipschitz continuous. Note that \(f_i(0)=0\), then there exist positive constants \(k_i>0\ (i=1,2,\ldots ,n)\) such that

$$\begin{aligned} \big |f_i(x_i(t))\big |\leqslant k_i\big |x_i(t)\big |, \quad i=1,2,\cdots ,n. \end{aligned}$$
(3)

According to Definition 2.2 and \(f_i(0)=0\) , we immediately know that the origin \(x^*=0\) is an equilibrium point of system (1).

Remark 2.1

The purpose of this paper is to investigate the delay-independent stability conditions of the equilibrium point for Riemann–Liouville fractional neutral-type delayed neural networks (1). In the stability of neural-networks, it is usually assumed that the neuron activation functions are bounded and monotonic [24], differential [43, 44]. However, in this paper, we adopt the assumption on the neuron activation functions in which the differentiability is not required.

3 Delay-Independent Stability Criteria

In this section, by constructing a suitable Lyapunov functional including fractional integral and fractional derivative terms, several sufficient conditions are presented to ensure that the origin of system (1) is asymptotically stable. These stability criteria are independent on the size of the delays, and described as the matrix inequalities or algebraic inequalities in terms of the network systems parameters only.

Theorem 3.1

The origin of system (1) is asymptotically stable, if there exist a positive diagonal matrix M and positive definite matrices P, Q and R such that the following matrix inequalities hold:

$$\begin{aligned} \Omega _{1}= & {} -\left( A^2-M^2\right) K^{-2}+B^{T}\left( I+P^{-1}+Q^{-1}\right) B<0, \end{aligned}$$
(4)
$$\begin{aligned} \Omega _{2}= & {} -M^2K^{-2}+C^{T}\left( I+P+R^{-1}\right) C<0, \end{aligned}$$
(5)
$$\begin{aligned} \Omega _{3}= & {} E^T(I+Q+R)E-I<0, \end{aligned}$$
(6)

where \(K=diag \{k_1, k_2, \ldots , k_n\}>0\) and I is the identity matrix with dimension \(n\times n\).

Proof

Construct a Lyapunov functional including fractional integral and fractional derivative terms:

$$\begin{aligned} V(x_t)= {{_0}D}_{t}^{-(1-\alpha )}\left( x^T(t)Ax(t)\right) +\int _{t-\tau }^{t}x^{T} (s)M^2x(s)ds+\int _{t-\tau }^{t}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(s)\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(s)\right) ds, \end{aligned}$$
(7)

where \(\alpha \in (0,1)\), \(A=\) diag\(\{a_i\}\ (a_i>0)\) and \(M=\) diag\(\{m_i\}\ (m_i>0)\) are both positive definite diagonal matrices.

From Definitions 2.1 and 2.2, we know that \(V(x_t)\) is a positive definite functional. According to Property 2.3, the time derivative of \(V(x_t)\) along the trajectories of system (1) is obtained as follows:

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)=\,\,&\,{_{ \ 0}^{RL}}D_{t}^{\alpha }\left( x^T(t)Ax(t)\right) +x^{T}(t)M^2x(t)-x^{T}(t-\tau )M^2x(t-\tau )\\&+\,\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t)\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t)\right) -\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) . \end{aligned} \end{aligned}$$
(8)

An application of Lemma 2.1 yields that

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant \,\,&\, 2x^T(t)A\left( {_{ \ 0}^{RL}}D_{t}^{\alpha }x(t)\right) +x^{T}(t)M^2x(t)-x^{T}(t-\tau )M^2x(t-\tau )\\&+\,\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t)\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t)\right) -\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) \\ =&\left( {_{ \ 0}^{RL}}D_{t}^{\alpha }x(t)\right) ^{T}\left[ 2Ax(t)+{_{ \ 0}^{RL}}D_{t}^{\alpha }x(t)\right] +x^T(t)M^2x(t)-x^{T}(t-\tau )M^2x(t-\tau )\\&-\,\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) ^{T}\left( {_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\right) . \end{aligned} \end{aligned}$$
(9)

Substituting (1) into (9), one can get that

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&\Big [-Ax(t)+Bf(x(t))+Cf(x(t-\tau ))+E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\Big ]^{T}\\&\times \,\Big [Ax(t)+Bf(x(t))+Cf(x(t-\tau ))+E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\Big ]\\&+\,x^T(t)M^2x(t)-x^{T}(t-\tau )M^2x(t-\tau )\\&-\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ). \end{aligned} \end{aligned}$$

By computations, we get

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&\ -x^T(t)A^2x(t)-x^T(t)A^TBf(x(t))-x^T(t)A^TCf(x(t-\tau ))\\&-\,x^T(t)A^TE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )+f^{T}(x(t))B^{T}Ax(t)+f^{T}(x(t))B^{T}Bf(x(t))\\&+\,f^{T}(x(t))B^{T}Cf(x(t-\tau ))+f^{T}(x(t))B^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\\&+\,f^{T}(x(t-\tau ))C^{T}Ax(t)+f^{T}(x(t-\tau ))C^{T}Bf(x(t))\\&+\,f^{T}(x(t-\tau ))C^{T}Cf(x(t-\tau ))\\&+\,f^{T}(x(t-\tau ))C^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )+\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TAx(t)\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TBf(x(t))+\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TCf(x(t-\tau ))\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )+x^T(t)M^2x(t)\\&-\,x^{T}(t-\tau )M^2x(t-\tau )-\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ). \end{aligned} \end{aligned}$$
(10)

Note that the following equalities hold:

$$\begin{aligned} x^T(t)A^TBf(x(t))= & {} f^{T}(x(t))B^{T}Ax(t),\\ x^T(t)A^TCf(x(t-\tau ))= & {} f^{T}(x(t-\tau ))C^{T}Ax(t),\\ x^T(t)A^TE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )= & {} \Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TAx(t),\\ f^{T}(x(t))B^{T}Cf(x(t-\tau ))= & {} f^{T}(x(t-\tau ))C^{T}Bf(x(t)),\\ f^{T}(x(t))B^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )= & {} \Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TBf(x(t)),\\ f^{T}(x(t-\tau ))C^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )= & {} \Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TCf(x(t-\tau )). \end{aligned}$$

Combining the above equalities with (10) yields that

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&-x^T(t)A^2x(t)+f^{T}(x(t))B^{T}Bf(x(t))+2f^{T}(x(t))B^{T}Cf(x(t-\tau ))\\&+2f^{T}(x(t))B^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )+f^{T}(x(t-\tau ))C^{T}Cf(x(t-\tau ))\\&+2f^{T}(x(t-\tau ))C^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )+\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}E^TE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\\&+x^T(t)M^2x(t)-x^{T}(t-\tau )M^2x(t-\tau )-\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ). \end{aligned} \end{aligned}$$
(11)

From Lemma 2.2, we get the following inequalities

$$\begin{aligned} 2f^{T}(x(t))B^{T}Cf(x(t-\tau ))\leqslant & {} f^{T}(x(t))B^TP^{-1}Bf(x(t))\nonumber \\&+\,x(t-\tau )^TC^TPCx(t-\tau ), \end{aligned}$$
(12)
$$\begin{aligned} 2f^{T}(x(t))B^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\leqslant & {} f^{T}(x(t))B^{T}Q^{-1}Bf(x(t))\nonumber \\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^TE^TQE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ), \end{aligned}$$
(13)
$$\begin{aligned} 2f^{T}(x(t-\tau ))C^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\leqslant & {} f^{T}(x(t-\tau ))C^{T}R^{-1}Cf^{T}(x(t-\tau ))\nonumber \\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^TE^TRE\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ), \end{aligned}$$
(14)

Substituting (12)–(14) into (11), we have

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&-x^T(t)(A^2-M^2)x(t)+f^{T}(x(t))\Big (B^{T}B+B^TP^{-1}B+B^{T}Q^{-1}B\Big )f(x(t)\\&+\,f^{T}(x(t-\tau ))\Big (C^{T}C+C^TPC+C^{T}R^{-1}C\Big ) f(x(t-\tau ))\\&-\,x^{T}(t-\tau )M^2x(t-\tau )\\&+\,\Big ({_{0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big (E^TE+E^TQE+E^TRE-I\Big )\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ).\\ \end{aligned} \end{aligned}$$
(15)

From the assumption on the activation functions given by (3), we can get

$$\begin{aligned}&\begin{aligned} -x^T(t)(A^2-M^2)x(t)&=-\sum _{i=1}^{n}(a_i^2-m_i^2)x_i^2(t)\\&\leqslant -\sum _{i=1}^{n}\frac{a_i^2-m_i^2}{k_i^2}x_i^2(t)f_i^2(x_i(t))\\&=-f^T(x(t))(A^2-M^2)K^{-2}f(x(t)), \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned}&\begin{aligned}&-x^{T}(t-\tau )M^2x(t-\tau )\leqslant -f^T(x(t-\tau ))M^2K^{-2}f(x(t-\tau )). \end{aligned} \end{aligned}$$
(17)

Using (16) (17) in (15) yields that

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&\ f^{T}(x(t))\Big [-(A^2-M^2)K^{-2}+B^{T}B+B^TP^{-1}B+B^{T}Q^{-1}B\Big ]f(x(t)\\&+\,f^{T}(x(t-\tau ))\Big [-M^2K^{-2}+C^{T}C+C^TPC+C^{T}R^{-1}C\Big ]f(x(t-\tau ))\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big (E^TE+E^TQE+E^TRE-I\Big )\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\\ =&\ f^{T}(x(t))\Omega _1f(x(t)+f^{T}(x(t-\tau ))\Omega _2f(x(t-\tau ))\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Omega _3\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ), \end{aligned} \end{aligned}$$
(18)

where \(\Omega _1<0, \Omega _2<0, \Omega _3<0\), then we have \(\dot{V}(x_t)<0\). Thus, it can be concluded from the standard Lyapunov theorem [48] that the origin of system (1) is asymptotically stable.

Remark 3.1

In the proof of Theorem 3.1, a suitable Lyapunov functional including fractional integral and fractional derivative terms is constructed. It should be to point out that the positive definiteness of constructed Lyapunov functional is guaranteed by the definitions of Riemann–Liouville fractional-order differentiation and integration.

Remark 3.2

Recently, the various approaches were applied to discuss the stability problems of fractional-order neural networks including analysis technique [40], fractional Razumikhin approach [42], fractional Lyapunov functional method and a Leibniz rule for fractional differentiation [44], Gronwall’s inequality approach [45, 46] and so on. Different from the above mentioned approaches, we only need to calculate first-order derivative of Lyapunov functional to derive the delay-independent stability conditions based on the standard Lyapunov theorem. Thus, we can avoid computing fractional-order derivative of Lyapunov functional. In fact, it is often very difficult to calculate fractional-order derivatives of a Lyapunov functional.

The following algebraic criteria are the direct results of Theorem 3.1.

Corollary 3.1

The origin of system (1) is asymptotically stable, if there exist positive constants m, p, q and r such that the following conditions hold:

$$\begin{aligned} \Omega _{1}^*= & {} -(1-m)A^2 K^{-2}+\left( 1+\frac{1}{p}+\frac{1}{q}\right) B^{T}B<0,\\ \Omega _{2}^*= & {} -mA^2K^{-2}+\left( 1+\frac{1}{p}+\frac{1}{r}\right) C^{T}C<0,\\ \Omega _{3}^*= & {} (1+q+r)\Vert E\Vert _2^2-1<0, \end{aligned}$$

where \(K=diag\{k_1, k_2, \ldots , k_n\}>0\).

Corollary 3.2

The origin of system (1) is asymptotically stable, if there exist positive constants m, p, q and r such that the following conditions hold:

$$\begin{aligned} \delta _1= & {} -(1-m)\lambda ^2+\left( 1+\frac{1}{p}+\frac{1}{q}\right) \Vert B\Vert _2^2<0,\\ \delta _2= & {} -m\lambda ^2+\left( 1+\frac{1}{p}+\frac{1}{r}\right) \Vert C\Vert _2^2<0,\\ \delta _3= & {} (1+q+r)\Vert E\Vert _2^2-1<0, \end{aligned}$$

where \(\lambda =\min \nolimits _{1\leqslant i\leqslant n}\Big \{\frac{a_i}{k_i}\Big \}\).

Theorem 3.2

The origin of system (1) is asymptotically stable, if there exist a positive diagonal matrix M and positive constants \(\beta \) and \(\gamma \) such that the following conditions hold:

$$\begin{aligned} \Theta _{1}= & {} -(A^2-M^2)K^{-2}+2B^{T}B+\frac{1}{\beta }B^{T}EE^TB<0,\\ \Theta _{2}= & {} -M^2K^{-2}+2C^{T}C+\frac{1}{\gamma }C^{T}EE^TC<0,\\ \Theta _{3}= & {} E^TE+(\beta +\gamma -1)I<0, \end{aligned}$$

where \(K=diag \{k_1, k_2, \ldots , k_n\}>0\) and I is the identity matrix of dimension of \(n\times n\).

Proof

We note that the following inequalities hold in the proof of Theorem 3.1:

$$\begin{aligned} 2f^{T}(x(t))B^{T}Cf(x(t{-}\tau ))\leqslant&f^{T}(x(t))B^TBf(x(t)){+}x(t-\tau )^TC^TCx(t-\tau ), \end{aligned}$$
(19)
$$\begin{aligned} 2f^{T}(x(t))B^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\leqslant&\frac{1}{\beta } f^{T}(x(t))B^{T}E E^TBf(x(t))\nonumber \\&+\,\beta \Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^T\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ), \end{aligned}$$
(20)
$$\begin{aligned} 2f^{T}(x(t-\tau ))C^{T}E\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\leqslant&\ \frac{1}{\gamma }f^{T}(x(t-\tau ))C^{T}E E^TCf^{T}(x(t-\tau ))\nonumber \\&+\,\gamma \Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^T\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ),\qquad \end{aligned}$$
(21)

Substituting (19)–(21) into (11), we have

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&-x^T(t)(A^2-M^2)x(t)+f^{T}(x(t))\Big (2B^{T}B+\frac{1}{\beta } B^{T}E E^TB\Big )f(x(t)\\&+\,f^{T}(x(t-\tau ))\Big (2C^{T}C+\frac{1}{\gamma }C^{T}E E^TC\Big )f(x(t-\tau ))-x^{T}(t-\tau )M^2x(t-\tau )\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big (E^TE+\beta I+\gamma I-I\Big )\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ).\qquad \\ \end{aligned} \end{aligned}$$
(22)

Using (16) (17) in (22) yields that

$$\begin{aligned} \begin{aligned} \dot{V}(x_t)\leqslant&f^{T}(x(t))\Big [-(A^2-M^2)K^{-2}+2B^{T}B+\frac{1}{\beta } B^{T}E E^TB\Big ]f(x(t)\\&+\,f^{T}(x(t-\tau ))\Big [-M^2K^{-2}+2C^{T}C+\frac{1}{\gamma }C^{T}E E^TC\Big ]f(x(t-\tau ))\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Big (E^TE+\beta I+\gamma I-I\Big )\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )\\ =&f^{T}(x(t))\Theta _1f(x(t)+f^{T}(x(t-\tau ))\Theta _2f(x(t-\tau ))\\&+\,\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big )^{T}\Theta _3\Big ({_{\ 0}^{RL}}D_{t}^{\alpha }x(t-\tau )\Big ), \end{aligned} \end{aligned}$$
(23)

where \(\Theta _1<0, \Theta _2<0, \Theta _3<0\), then we have \(\dot{V}(x_t)<0\). Thus, it can be concluded from the standard Lyapunov Theorems [40] that the origin of system (1) is asymptotically stable. \(\square \)

The following corollary is the direct result of Theorem 3.2.

Corollary 3.3

The origin of system (1) is asymptotically stable, if there exist a positive diagonal matrix M and positive constants \(\beta \) and \(\gamma \) such that the following conditions hold:

$$\begin{aligned} \omega _{1}= & {} -(1-m)\lambda ^{2}+2\Vert B\Vert _2^2+\frac{1}{\beta }\Vert B\Vert _2^2 \Vert E\Vert _2^2<0,\\ \omega _{2}= & {} -m\lambda ^{2}+2\Vert C\Vert _2^2+\frac{1}{\gamma }\Vert C\Vert _2^2 \Vert E\Vert _2^2<0,\\ \omega _{3}= & {} \Vert E\Vert _2^2+\beta +\gamma -1<0, \end{aligned}$$

where \(\lambda =\min \nolimits _{1\leqslant i\leqslant n}\Big \{\frac{a_i}{k_i}\Big \}\).

Remark 3.3

In [45, 46], the authors focused on studying the finite time stability of fractional-order delayed neural networks. However, it should be pointed out that the finite-time stability and Lyapunov asymptotic stability are mutually independent concepts, because finite-time stability does not contain Lyapunov asymptotic stability, and vise versa. Here, the asymptotic stability of fractional-order neutral-type delayed neural networks is discussed firstly.

Remark 3.4

Several sufficient conditions to ensure the asymptotic stability of system (1) are derived in this paper, which are concise and described as the matrix inequalities or the algebraic inequalities. According to the different network system parameters, we can flexibly choose an appropriate criterion to check the stability.

Remark 3.5

Note that the Remiann-Liouville derivative is a continuous operator of the order \(\alpha \) (see [2, 3]). Therefore, we can obtain the delay-independent stability criteria for integer-order neutral-type delayed neural networks from the results of this paper. In the past few decades, the integer-order neutral-type delayed neural networks were extensively discussed in [23, 25, 32,33,34,35,36,37,38]. For example, delay-dependent stability criteria for integer-order neutral-type neural networks with time-varying delays was obtained in terms of linear matrix inequalities (LMIs) [38]. General speaking, the LMI approach to the stability problem of neutral-type neural networks involves some difficulties with determining the constraint conditions on the network parameters as it requires to test positive definiteness of high dimensional matrices.

4 Illustrative Examples

In this section, two examples for Riemann–Liouville fractional-order neutral-type delayed neural networks are given to illustrate the effectiveness and feasibility of the theoretical results.

Example 4.1

Consider the two-state Riemann–Liouville fractional-order neutral-type neural network model (1), where

$$\begin{aligned} A= & {} \left[ \begin{array}{cc} 1.5&{} 0 \\ 0&{} 1.5 \end{array} \right] ,\quad B=\left[ \begin{array}{cc} -0.25&{} 0.25\\ -0.25&{} -0.25 \end{array} \right] ,\quad C=\left[ \begin{array}{cc} -0.25&{} 0.25\\ -0.25&{} -0.25 \end{array} \right] ,\quad E=\left[ \begin{array}{cc} 0.5&{} 0\\ 0&{} 0.5 \end{array} \right] ,\\ M= & {} \left[ \begin{array}{cc} 1&{} 0\\ 0&{} 1 \end{array} \right] , \quad K=\left[ \begin{array}{cc} 0.2&{} 0\\ 0&{} 0.2 \end{array} \right] , \quad \tau =0.4. \end{aligned}$$

The positive matrices P, Q and R in the conditions of Theorem 3.1 are chosen as follows:

$$\begin{aligned} P=\left[ \begin{array}{cc} \frac{1}{5} &{} 0 \\ 0 &{} \frac{1}{5} \end{array} \right] ,\quad Q=\left[ \begin{array}{cc} \frac{1}{5} &{} 0 \\ 0 &{} \frac{1}{5} \end{array} \right] ,\quad R=\left[ \begin{array}{cc} \frac{1}{10}&{} 0\\ 0&{} \frac{1}{10} \end{array} \right] . \end{aligned}$$

Then we obtain

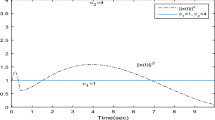
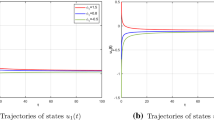
$$\begin{aligned} \begin{aligned}&\Omega _{1}=-(A^2-M^2)K^{-2}+B^{T}B+B^TP^{-1}B+B^{T}Q^{-1}B=\left[ \begin{array}{cc} -17.5&{} 0\\ 0&{} -17.5\\ \end{array} \right]<0,\\&\Omega _{2}=-M^2K^{-2}+C^{T}C+C^TPC+C^{T}R^{-1}C=\left[ \begin{array}{cc} -11&{} 0\\ 0&{} -11\\ \end{array} \right]<0,\\&\Omega _{3}=E^TE+E^TQE+E^TRE-I=\left[ \begin{array}{cc} -0.675&{} 0\\ 0&{} -0.675\\ \end{array} \right] <0. \end{aligned} \end{aligned}$$

Thus, the conditions of Theorem 3.1 are satisfied. The dynamical responses of state trajectories of neural network system are depicted in Figs. 1 and 2, which shows that the state variable \((x_1(t), \ x_2(t))^T\) converges to the equilibrium point \((0,0)^T\). Therefore, the results of Theorem 3.1 are verified by means of this simulation.

Fig. 1
figure 1

State trajectories of neural network model (1) with \(\alpha =0.8, \ \tau =0.4\) under different initial values

Full size image
Fig. 2
figure 2

State trajectories of neural network model (1) with different fractional order \(\alpha =0.6,\ 0.8, \ 1\)

Full size image
Fig. 3
figure 3

State trajectories of neural network model (1) with \(\alpha =0.8, \ \tau =0.4\) under different initial values

Full size image

Example 4.2

Consider the four-state Riemann–Liouville fractional-order neutral-type neural network model (1), where

$$\begin{aligned} A=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }} 1&{}\,0&{}\, 0&{}\, 0\\ 0&{}\,1&{}\, 0&{}\, 0\\ 0&{}\,0&{}\, 1&{}\, 0\\ 0&{}\,0&{}\, 0&{}\, 1 \end{array} \right] ,\quad B=C=\frac{1}{8} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1&{}\,1&{}\, 1&{}\, 1\\ -1&{}\,-1&{}\, 1&{}\, 1\\ 1&{}\, -1&{}\, 1&{}\, -1\\ -1&{}\, 1&{}\, 1&{}\, -1 \end{array} \right] ,\quad \tau =0.4. \end{aligned}$$

We assume that \(\Vert E\Vert _2=\frac{1}{2}\) and \(k_1=k_2=k_3=k_4=1\). By computation, we have \(\Vert B\Vert _2=\Vert C\Vert _2=\frac{1}{4}, \ \lambda =1\). Here, we choose \(m=\frac{1}{2}, \beta =\gamma =\frac{1}{10}\). Then one has

$$\begin{aligned} \omega _{1}= & {} -(1-m)\lambda ^{2}+2\Vert B\Vert _2^2+\frac{1}{\beta }\Vert B\Vert _2^2 \Vert E\Vert _2^2=-\frac{7}{32}<0,\\ \omega _{2}= & {} -m\lambda ^{2}+2\Vert C\Vert _2^2+\frac{1}{\gamma }\Vert C\Vert _2^2 \Vert E\Vert _2^2=-\frac{7}{32}<0,\\ \omega _{3}= & {} \Vert E\Vert _2^2+\beta +\gamma -1=-\frac{11}{20}<0. \end{aligned}$$

Thus, the conditions of Corollary 3.3 are satisfied. For numerical simulations, the state trajectories are depicted in Figs. 3 and 4 under different initial conditions and different fractional-order derivatives, respectively. It can be directly observed that the numeric conclusions affirm Corollary 3.3.

Remark 4.1

In particular, if fractional-order \(\alpha =1\), then system (1) will be reduced to an integer-order neutral-type delayed neural networks [23, 25, 32,33,34,35,36,37,38]. From the proof of Theorems 3.1 and 3.2, it is obvious that the results of this paper still hold for \(\alpha =1\) case.

For integer-order case, in order to compare with the existing results in the literature, we carry out the following analysis and discussion.

Fig. 4
figure 4

State trajectories of neural network model (1) with different fractional order \(\alpha =0.4,\ 0.6, \ 1\)

Full size image

In fact, for \(\alpha =1\) case, similar to [36], we consider the network parameters as follows:

$$\begin{aligned} A=\left[ \begin{array}{llll} 1&{}\, 0&{}\, 0&{}\, 0\\ 0&{}\, 1&{}\, 0&{}\, 0\\ 0&{}\, 0&{}\, 1&{}\, 0\\ 0&{}\, 0&{}\, 0&{}\, 1 \end{array} \right] ,\quad B=C= \left[ \begin{array}{llll} \eta &{}\, \eta &{}\, \eta &{}\, \eta \\ -\eta &{}\, -\eta &{}\, \eta &{}\, \eta \\ \eta &{}\, -\eta &{}\, \eta &{}\, \eta \\ -\eta &{}\, \eta &{}\, \eta &{}\, -\eta \end{array} \right] ,\quad \alpha =1,\quad \tau =0.6. \end{aligned}$$

We assume that \(\Vert E\Vert _2=\frac{1}{2}\) and \(k_1=k_2=k_3=k_4=1\). By computations, we have \(\Vert B\Vert _2=\Vert C\Vert _2=\frac{1}{4}, \ \lambda =1\). Here, we choose \(m=\frac{1}{2}, \beta =\gamma =\frac{1}{10}\). We first check the conditions of Corollary 3.3. In this case,

$$\begin{aligned} \omega _{1}=\frac{1}{2}-18\eta ^2>0, \quad \omega _{2}=\frac{1}{2}-18\eta ^2>0, \quad \omega _{3}=\frac{4}{5}-\Vert E\Vert _2^2>0, \end{aligned}$$

hence, the conditions of Corollary 3.3 are satisfied if \(\eta <\frac{1}{6}\). When \(\frac{1}{12}\leqslant \eta <\frac{1}{6}\), the conditions of Corollary 3.3 are satisfied but the condition in [34] does not hold. Furthermore, the condition holds in [35] if \(\eta \leqslant \frac{\sqrt{3}}{24}\), which is more restrictive when compared with \(\eta <\frac{1}{6}\) imposed by the conditions of Corollary 3.3.

Remark 4.2

The asymptotic stability criteria for integer-order neutral-type delayed neural networks were derived [34, 35], in which the authors imposed the strict constraint conditions on network parameters. Compared with the stability conditions [34, 35], the results of this paper are more general and less conservative, and can be more easily verified. The above numerical simulations further confirm the theoretical results.

5 Conclusions

In this paper, we construct an appropriate functional including fractional integral and fractional derivative terms, and calculate its first-order derivative to derive delay-independent stability conditions. Several criteria on the delay-independent stability of Riemann–Liouville fractional neutral-type delayed neural networks are obtained. The proposed method avoids computing fractional-order derivative of Lyapunov functional. Furthermore, the presented results are described as matrix or algebra inequalities, which are valid and feasible to check stability. The presented results contribute to the control and design of Riemann–Liouville fractional-order neutral-type delayed network systems. The future work will focus on the investigation of the dynamical behaviors of Riemann–Liouville and Caputo fractional-order neutral type neural networks with both leakage and time-varying delays.