Nonlinear Measure Approach for the Stability Analysis of Complex-Valued Neural Networks

Abstract

Based on the nonlinear measure method and the matrix inequality techniques, this paper addresses the global asymptotic stability for the complex-valued neural networks with delay. Furthermore, robust stability of the addressed neural network with norm-bounded parameter uncertainties is also tackled. By constructing an appropriate Lyapunov functional candidate, several sufficient criteria are obtained to ascertain the existence, uniqueness and global stability of the equilibrium point of the addressed complex-valued neural networks, which are easy to be verified and implemented in practice. Finally, one example is given to illustrate the effectiveness of the obtained results.

1 Introduction

In the past decades, there has been increasing attention payed to investigate the dynamical behaviors of the neural networks due to their extensive applications in associative memory, classification of pattern recognition, engineering optimization, image processing, signal processing and so on, see Refs. [1–6] and the references cited therein. In practical applications, complex signals often appear, which stimulate the introducing and investigating of complex-valued neural networks [7]. Generally speaking, there are many differences between the real-valued neural networks and the complex-valued ones. Compared with the real-valued neural networks, the states, connection weights and activation functions of the latter are all complex-valued. Actually, the complex-valued networks have much more complicated properties than the real-valued ones in many aspects, which makes it possible to solve lots of problems that can not be solved with the real-valued counterparts. For example, both the XOR problem and the detection of symmetry problem can not be solved with a single real-valued neuron, which, however, can be done with a single complex-valued neuron with orthogonal decision boundaries [8]. Therefore, it is necessary to investigate the dynamics of the complex-valued neural networks, especially the stability of the network.

Up till now, there have been increasing research interests in the dynamical analysis for the complex-valued networks, see Refs. [9–14] for example. In [15], by utilizing the method of local inhibition and energy minimization, several criteria have been obtained to guarantee the complete stability and boundedness of the continuous-time complex-valued neural networks with delay. In [16], the activation dynamics of the complex-valued neural network on a general time scale have been investigated. In addition, the global exponential stability of the considered networks has been also discussed. In [17], a class of discrete-time neural networks with complex-valued linear threshold neurons have been discussed, and some conditions have been derived to ascertain the global attractivity, boundedness and complete stability of such networks. For more works on the stability analysis, one could refer to Refs. [18, 19].

In practical life, time delay often appears for the reason of the finite switching speed of the amplifiers, and it also occurs in the electronic implementation of the neural networks when processing the signal transmission, which may greatly influence the dynamical behaviors of the networks in the form of instability, bifurcation and oscillation [20, 21]. Hence, it is very important to study the dynamics of the delayed complex-valued neural networks. During the past several years, a large amount of results associated with this area have been obtained by researchers [22]. For example, in [23], the delayed complex-valued recurrent neural network under two classes of complex-valued activation functions has been investigated, and several sufficient criteria have been presented to assure the existence, uniqueness, global asymptotic/exponential stability of the equilibrium point for the network. On another front, the activation functions also play a remarkable role in the dynamics of neural systems. According to the Liouville’s theorem [24] in the complex domain, every bounded entire function must be a constant function. Therefore, if the activation functions of the complex-valued neural networks are chosen to be the smooth and bounded ones as done for the real-valued neural networks, it will not be appropriate to investigate the dynamics of the complex-valued networks. Hence, it is a big challenge for choosing appropriate activation functions for the complex-valued networks [25]. It should be noted that in Refs. [23, 26], the restrictions on the activation functions are too strong, which motivates the first attempt for the formation of the present paper.

Normally, the parameters of neural networks, including the release rates of neurons and connection weights, may be subject to some deviations because of the tolerance of electronic components employed in the design of neural networks or in the electronic implementation of neural networks. What is more, the stability of neural networks might often be destroyed due to the existence of modeling errors, parameter fluctuation or external disturbance. Hence, it is important and necessary to study the robust stability of neural networks. For the real-valued neural networks, lots of significant results have been developed in the literatures [27–29]. When referring to the complex-valued network, to the best knowledge of the authors, there are only a few results [9], which motivates us to further consider the global robust stability of the complex-valued neural networks.

There are different kinds of approaches for investigating the dynamics of neural networks, such as the Lyapunov function method, the energy function method, the matrix measure method and so on. In [30], by constructing an appropriate Lyapunov function, the global asymptotic stability of the complex-valued neural networks has been studied. In [31], the properties of the activation functions have been discussed so as to find complex functions with good properties by using the energy function method. There are also some results on the stability of neural networks by utilizing the matrix measure method [32, 33]. However, few results have been concerned by using the nonlinear measure method on the global stability of the complex-valued networks with delay, which forms another motivation for developing the presented research.

Inspired by the above discussions, under one general class of activation functions, several sufficient conditions are derived ensuring the global asymptotic stability of the addressed complex-valued network with/without parameter uncertainties by utilizing the nonlinear measure method and the matrix inequality techniques. Compared with the previous related works on the complex-valued systems, the main contribution of the present paper could be summarized as follows. (1) The restrictions on the activation functions are reduced, i.e., both the real and the imaginary parts of the activation functions are no longer required to be derivable. (2) Global asymptotic stability is investigated for the complex-valued neural networks with deterministic/norm-bounded uncertain parameters. And (3) a novel nonlinear measure approach is developed to investigate the stability of the neural system, which is easy to ascertain the existence and uniqueness of the equilibrium point for the networks. The remaining part of the paper is organized as follows. In Sect. 2, the complex-valued model is presented , and some preliminaries are briefly outlined. In Sect. 3, a novel nonlinear measure approach is employed, and by constructing appropriate Lyapunov functional candidate, several criteria are proposed to ascertain the global stability of the complex-valued networks with/without parameter uncertainties. In Sect. 4, one numerical example is given to show the effectiveness of the obtained conditions. Finally, conclusions are drawn in Sect. 5.

Notations The notation used throughout this paper is fairly standard. ${{\mathbb {C}}}^n, {{\mathbb {C}}}^{m\times n}$ and ${\mathbb R}^{m\times n}$ denote the set of n-dimensional complex vectors, $m\times n$ complex matrices and $m\times n$ real matrices, respectively. Let i be the imaginary unit, i.e. $i=\sqrt{ - 1}$. The superscript ‘T’ represents the matrix transposition. $X \ge Y$ (respectively, $X > Y$) means that $X-Y$ is real, symmetric and positive semi-definite (respectively, positive definite). $P^R$ and $P^I$ refer to, respectively, the real and the imaginary parts of matrix $P\in \mathbb {C}^{m\times n}$. $\otimes$ and $<\cdot ,\cdot >$ means, respectively, the Kronecker product and the inner product of vectors.

2 Problem Formulation and some Preliminaries

Consider the complex-valued neural networks described by the following nonlinear delay differential equations:

(1)

where $u(t) = (u_1(t),u_2(t), \ldots ,u_n(t) )^T \in {{\mathbb {C}}}^n$ is the state vector of the neural networks with n neurons at time $t, C = \mathrm{diag}\{ c_1 ,c_2 , \cdots ,c_n \} \in {\mathbb R}^{n\times n}$ with $c_k>0$ ($k=1,2,\ldots ,n$) is the self-feedback connection weight matrix, $A = (a_{kj} )_{n \times n} \in {\mathbb C}^{n\times n}$ and $B = (b_{kj} )_{n \times n} \in {\mathbb C}^{n\times n}$ are, respectively, the connection weight matrix and the delayed connection weight matrix. $L=(l_1,l_2,\ldots ,l_n)^T \in {{\mathbb {C}}}^n$ is the external input vector. $f(u(t)) = (f_1(u_1(t)),f_2(u_2(t)), \ldots ,f_n(u_n(t)) )^T : {{\mathbb {C}}}^n \rightarrow {{\mathbb {C}}}^n$  and  $g(u(t-\tau )) = (g_1(u_1(t-\tau )),g_2(u_2(t-\tau )), \ldots ,g_n(u_n(t-\tau )) )^T : {{\mathbb {C}}}^n \rightarrow {{\mathbb {C}}}^n$ denote, respectively, the vector-valued activation functions without and with time delays in which $\tau$ is the transmission delay, and the nonlinear activation functions are assumed to satisfy the conditions given below:

Assumption 1

For $u=x+iy\in \mathbb {C}$ with $x, y\in \mathbb {R}, f_k(u)$ and $g_k(u)$ are expressed as

$$\begin{aligned} f_k(u)=f_{k}^R(x,y)+if_{k}^I(x,y),~g_k(u)=g_{k}^R(x,y)+ig_{k}^I(x,y); \end{aligned}$$

where $k=1, 2, \cdots , n$. There exist positive constants $\lambda _{k}^{RR},\lambda _{k}^{RI},\lambda _{k}^{IR},\lambda _{k}^{II}$ and $\xi _k^{RR},\xi _k^{RI},\xi _k^{IR},\xi _k^{II}$ such that the following inequalities

$$\begin{aligned}&\mid f_{k}^R(x_1,y_1)-f_{k}^R(x_2,y_2)\mid \le \lambda _{k}^{RR}\mid x_1-x_2 \mid + \lambda _{k}^{RI}\mid y_1-y_2\mid ,\\&\mid f_{k}^I(x_1,y_1)-f_{k}^I(x_2,y_2)\mid \le \lambda _{k}^{IR}\mid x_1-x_2 \mid + \lambda _{k}^{II}\mid y_1-y_2\mid ;\\&\mid g_{k}^R(x_1,y_1)-g_{k}^R(x_2,y_2)\mid \le \xi _{k}^{RR}\mid x_1-x_2 \mid + \xi _{k}^{RI}\mid y_1-y_2\mid ,\\&\mid g_{k}^I(x_1,y_1)-g_{k}^I(x_2,y_2)\mid \le \xi _{k}^{IR}\mid x_1-x_2 \mid + \xi _{k}^{II}\mid y_1-y_2\mid \end{aligned}$$

for any $x_1, x_2, y_1, y_2 \in \mathbb {R}$.

Remark 1

In Assumption 1 of Refs. [23] and [26], where the global stability of complex-valued neural networks with time-varying delays has been studied, the activation functions are supposed to be in the same forms as above with additional restrictions that the partial derivatives of $f_j^R(\cdot ,\cdot )$ and $f_j^I(\cdot ,\cdot )$ exist and are continuous. However, in our paper, both the real and the imaginary parts of the activation functions are no longer assumed to be derivable.

Denote $u(t)=x(t)+iy(t)$ with $x(t), y(t)\in \mathbb {R}^n$, then the complex-valued neural network (1) can be rewritten as follows:

$$\begin{aligned} \mathop {\alpha }\limits ^\centerdot \centerdot (t)=-C_1\alpha (t)+A_1\overline{f_1}(\alpha (t)) +A_2\overline{f_2}(\alpha (t))+B_1\overline{g_1}(\alpha (t-\tau )) +B_2\overline{g_2}(\alpha (t-\tau ))+\zeta , \nonumber \\ \end{aligned}$$

(2)

where

$$\begin{aligned}&\alpha (t)=\left( \begin{array}{c@{\quad }c} x(t) \\ y(t) \end{array} \right) ,~~~ C_1=\left( \begin{array}{c@{\quad }c} C &{} 0 \\ 0 &{} C \end{array} \right) ,~~~ \zeta =\left( \begin{array}{c@{\quad }c} L^R \\ L^I \end{array} \right) , ~~~ A_1=\left( \begin{array}{c@{\quad }c} A^R &{} 0 \\ 0 &{} A^I \end{array} \right) ,\\&A_2=\left( \begin{array}{c@{\quad }c} -A^I &{} 0 \\ 0 &{} A^R \end{array} \right) , ~~~B_1=\left( \begin{array}{c@{\quad }c} B^R &{} 0 \\ 0 &{} B^I \end{array} \right) ,~~~ B_2=\left( \begin{array}{c@{\quad }c} -B^I &{} 0 \\ 0 &{} B^R \end{array} \right) , \end{aligned}$$

$$\begin{aligned} \overline{f_1}(\alpha (t))&=((f^R(x(t),y(t)))^T,(f^R(x(t),y(t)))^T)^T,\\ \overline{f_2}(\alpha (t))&=((f^I(x(t),y(t)))^T,(f^I(x(t),y(t)))^T)^T,\\ \overline{g_1}(\alpha (t))&=((g^R(x(t),y(t)))^T,(g^R(x(t),y(t)))^T)^T,\\ \overline{g_2}(\alpha (t))&=((g^I(x(t),y(t)))^T,(g^I(x(t),y(t)))^T)^T. \end{aligned}$$

The aim of this paper is to find some conditions, under which system (2) [or equivalently, system (1)] is globally asymptotically stable, where the conditions are to be presented by the nonlinear measure method.

First, the definition of the nonlinear measure is introduced. It should be noted that such a definition has been firstly introduced in Ref. [34] to investigate the global/local stability of Hopfield-type networks, and then extended in Ref. [35] to study the dynamics of static neural networks.

Definition 1

[35] Suppose that $\Omega$ is an open set of $\mathbb {R}^n$, and $G: \Omega \rightarrow \mathbb {R}^n$ is an operator. The constant

$$\begin{aligned} m_{\Omega }(G)&\triangleq \sup _{x,y\in \Omega , x\ne y}\frac{<G(x)-G(y),x-y>}{\Vert x-y\Vert _2^2}\\&=\sup _{x,y\in \Omega , x\ne y}\frac{(x-y)^T(G(x)-G(y))}{\Vert x-y\Vert _2^2} \end{aligned}$$

is called the nonlinear measure of G on $\Omega$ with the Euclidean norm $\Vert \cdot \Vert _2$.

Before deriving our main results, some useful lemmas are introduced as follows.

Lemma 1

[36] For any vectors $X, Y\in \mathbb {R}^n$, matrix $0<W\in \mathbb {R}^{n\times n}$ and a positive real constant $\gamma$, we have

$$\begin{aligned} X^TWY+Y^TWX\le \gamma X^TWX+\frac{1}{\gamma }Y^TWY. \end{aligned}$$

Lemma 2

[37] Given constant matrices P, Q and R with $P=P^T$ and $~Q=Q^T$, then

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} P&{}R\\ R^T&{}Q \end{array} \right] <0 \end{aligned}$$

is equivalent to one of the following conditions:

(1):

$Q<0, P-RQ^{-1}R^T<0$.

(2):

$P<0, Q-R^TP^{-1}R<0$.

Lemma 3

[35] If $m_{\Omega }(G)< 0$, then G is an injective mapping on $\Omega$. In addition, if $\Omega =\mathbb {R}^n$, then G is a homeomorphism of $\mathbb {R}^n$.

Remark 2

From Lemma 3, it is easy to obtain that if $m_{\Omega }(G)< 0$ and $\Omega =\mathbb {R}^n$, then $G(w)=0~(\forall w\in \mathbb {R}^n)$ will have one unique solution. Combining the nonlinear measure with the Euclidean norm $\Vert \cdot \Vert _2$ and some matrix inequality techniques, in this paper, some sufficient conditions are to be given assuring the stability of the addressed neural networks.

3 Main Results

In this section, based on the nonlinear measure method and by constructing appropriate Lyapunov functional candidate, some criteria are presented to ascertain the global asymptotical stability of the complex-valued neural network (1) with constant time delay. The main results are stated one by one as follows.

Theorem 1

Suppose that the Assumption 1 holds, the complex-valued neural network (1) has one unique equilibrium which is globally asymptotically stable if there exist a matrix $P>0$, positive diagonal matrices $Q_k$ and $S_k=\mathrm{diag}\{s_k^1,s_k^2,\ldots ,s_k^n\}~(k=1,2,3,4)$ such that

$$\begin{aligned} \Xi =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Psi &{}PA_1&{}PA_2&{}PB_1&{}PB_2\\ A_1^TP&{}-I_2\otimes S_1&{}0&{}0&{}0 \\ A_2^TP&{}0&{}-I_2\otimes S_2&{}0&{}0 \\ B_1^TP&{}0&{}0&{}-I_2\otimes S_3&{}0 \\ B_2^TP&{}0&{}0&{}0&{}-I_2\otimes S_4 \\ \end{array} \right] <0, \end{aligned}$$

(3)

$$\begin{aligned} \Pi _1\le Q_1,~~ \Pi _2\le Q_2,~~ \Pi _3\le Q_3,~~ \Pi _4\le Q_4;~~ \end{aligned}$$

(4)

where $\Psi =-PC_1-C_1P+2Q_1+2Q_2+2Q_3+2Q_4, I_2$ is the unitary matrix in $\mathbb {R}^{2\times 2}$,

$$\begin{aligned}&\Pi _1=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} S_1(\Lambda _1^{RR})^2&{}S_1\Lambda _1^{RR}\Lambda _1^{RI}\\ S_1\Lambda _1^{RR}\Lambda _1^{RI}&{}S_1(\Lambda _1^{RI})^2 \end{array} \right) ,~~&\Pi _2=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} S_2(\Lambda _1^{IR})^2&{}S_2\Lambda _1^{IR}\Lambda _1^{II}\\ S_2\Lambda _1^{IR}\Lambda _1^{II}&{}S_2(\Lambda _1^{II})^2 \end{array} \right) ,\\&\Pi _3=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} S_3(\Lambda _2^{RR})^2&{}S_3\Lambda _2^{RR}\Lambda _2^{RI}\\ S_3\Lambda _2^{RR}\Lambda _2^{RI}&{}S_3(\Lambda _2^{RI})^2 \end{array} \right) ,~~&\Pi _4=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} S_4(\Lambda _2^{IR})^2&{}S_4\Lambda _2^{IR}\Lambda _2^{II}\\ S_4\Lambda _2^{IR}\Lambda _2^{II}&{}S_4(\Lambda _2^{II})^2 \end{array} \right) \end{aligned}$$

with $\Lambda _1^{RR}=\mathrm{diag}\{\lambda _1^{RR},\lambda _2^{RR},\ldots ,\lambda _n^{RR}\}, \Lambda _1^{RI}=\mathrm{diag}\{\lambda _1^{RI},\lambda _2^{RI},\ldots ,\lambda _n^{RI}\}, \Lambda _{1}^{IR}=\mathrm{diag}\{\lambda _1^{IR},\lambda _2^{IR},\ldots ,\lambda _n^{IR}\}, \Lambda _1^{II}=\mathrm{diag}\{\lambda _1^{II},\lambda _2^{II},\ldots ,\lambda _n^{II}\}, \Lambda _2^{RR}=\mathrm{diag}\{\xi _{1}^{RR},\xi _2^{RR},\ldots ,\xi _{n}^{RR}\}, \Lambda _2^{RI}=\mathrm{diag}\{\xi _1^{RI},\xi _2^{RI},\ldots ,\xi _n^{RI}\}, \Lambda _2^{IR}=\mathrm{diag}\{\xi _1^{IR},\xi _2^{IR},\ldots ,\xi _n^{IR}\}, \Lambda _2^{II}=\mathrm{diag}\{\xi _1^{II},\xi _2^{II},\ldots ,\xi _n^{II}\}$.

Proof

The result will be proved in two steps. First, the equilibrium point of system (2) will be proved to exist and be unique. Second, the unique equilibrium point of system (2) will be shown to be globally asymptotically stable.

Step 1 Define an operator $H: \mathbb {R}^{2n}\rightarrow \mathbb {R}^{2n}$ as follows:

$$\begin{aligned} H(\alpha )=-C_1\alpha +A_1\overline{f_1}(\alpha )+A_2\overline{f_2}(\alpha )+B_1\overline{g_1}(\alpha )+B_2\overline{g_2}(\alpha )+\zeta ,~ \alpha \in \mathbb {R}^{2n}. \end{aligned}$$

And construct a differential system given below:

$$\begin{aligned} \mathop \beta \limits ^\centerdot \centerdot (t)=PH(\beta (t)). \end{aligned}$$

(5)

Since the matrix P is invertible, it is easy to obtain that the equilibrium points sets of system (2) and system (5) are the same to each other. In the following, we will prove that $m_{\mathbb {R}^{2n}}(PH)<0$.

For $\alpha =((x^{\alpha })^T,(y^{\alpha })^T)^T, \beta =((x^{\beta })^T,(y^{\beta })^T)^T \in \mathbb {R}^{2n}$ with $\alpha \ne \beta$ and $x^{\alpha }, x^{\beta }, y^{\alpha }, y^{\beta }\in \mathbb {R}^n$, one has that

$$\begin{aligned}&(\alpha -\beta )^TP(H(\alpha )-H(\beta ))\nonumber \\&\le \frac{1}{2}\left\{ (\alpha -\beta )^T(-PC_1-C_1P)(\alpha -\beta )+(\alpha -\beta )^TPA_1(I_2\otimes S_1^{-1})A_1^TP(\alpha -\beta )\right. \nonumber \\&\,\quad +(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))^T(I_2\otimes S_1)(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))+(\alpha -\beta )^TPA_2(I_2\otimes S_2^{-1})A_2^TP(\alpha -\beta )\nonumber \\&\,\quad +(\overline{f_2}(\alpha )-\overline{f_2}(\beta ))^T(I_2\otimes S_2)(\overline{f_2}(\alpha )-\overline{f_2}(\beta ))+(\alpha -\beta )^TPB_1(I_2\otimes S_3^{-1})B_1^TP(\alpha -\beta )\nonumber \\&\,\quad +(\overline{g_1}(\alpha )-\overline{g_1}(\beta ))^T(I_2\otimes S_3)(\overline{g_1}(\alpha )-\overline{g_1}(\beta ))+(\alpha -\beta )^TPB_2(I_2\otimes S_4^{-1})B_2^TP(\alpha -\beta )\nonumber \\&\,\quad +\left. (\overline{g_2}(\alpha )-\overline{g_2}(\beta ))^T(I_2\otimes S_4)(\overline{g_2}(\alpha )-\overline{g_2}(\beta ))\right\} , \end{aligned}$$

(6)

in which Lemma 1 has been utilized in the second step when deriving (6), and $S_k~(k=1,2,3,4)$ are positive diagonal matrices solution of inequality conditions (3)–(4). By utilizing Assumption 1, one gets that

$$\begin{aligned}&(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))^T(I_2\otimes S_1)(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))\nonumber \\&\quad =2\sum _{k=1}^ns_1^k\left( f_k^R(x_k^\alpha ,y_k^\alpha )-f_k^R(x_k^\beta ,y_k^\beta )\right) ^2\nonumber \\&\quad \le 2\sum _{k=1}^n \left( \begin{array}{c@{\quad }c} |x_k^\alpha -x_k^\beta | \\ |y_k^\alpha -y_k^\beta | \end{array} \right) ^T \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} s_1^k(\lambda _k^{RR})^2&{}s_1^k\lambda _k^{RR}\lambda _k^{RI}\\ s_1^k\lambda _k^{RR}\lambda _k^{RI}&{}s_1^k(\lambda _k^{RI})^2 \end{array} \right) \left( \begin{array}{c@{\quad }c} |x_k^\alpha -x_k^\beta | \\ |y_k^\alpha -y_k^\beta | \end{array} \right) \nonumber \\&\quad =2 \left( \begin{array}{c@{\quad }c} |x^\alpha -x^\beta | \\ |y^\alpha -y^\beta | \end{array} \right) ^T \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} S_1(\Lambda _1^{RR})^2&{}S_1\Lambda _1^{RR}\Lambda _1^{RI}\\ S_1\Lambda _1^{RR}\Lambda _1^{RI}&{}S_1(\Lambda _1^{RI})^2 \end{array} \right) \left( \begin{array}{c@{\quad }c} |x^\alpha -x^\beta | \\ |y^\alpha -y^\beta | \end{array} \right) \nonumber \\&\quad \le 2|\alpha -\beta |^TQ_1|\alpha -\beta |\nonumber \\&\quad =2(\alpha -\beta )^TQ_1(\alpha -\beta ), \end{aligned}$$

(7)

where condition (4) has been resorted to in the fifth step, $x^\alpha =(x_1^\alpha ,x_2^\alpha ,\ldots ,x_n^\alpha )^T$ and $y^\alpha , x^\beta , y^\beta$ are similarly defined. Similarly, one also has that

$$\begin{aligned} \overline{(f_2}(\alpha )-\overline{f_2}(\beta ))^T(I_2\otimes S_2)(\overline{f_2}(\alpha )-\overline{f_2}(\beta ))\le 2(\alpha -\beta )^TQ_2(\alpha -\beta ), \end{aligned}$$

(8)

$$\begin{aligned} (\overline{g_1}(\alpha )-\overline{g_1}(\beta ))^T(I_2\otimes S_3)(\overline{g_1}(\alpha )-\overline{g_1}(\beta ))\le 2(\alpha -\beta )^TQ_3(\alpha -\beta ),\end{aligned}$$

(9)

$$\begin{aligned} (\overline{g_2}(\alpha )-\overline{g_2}(\beta ))^T(I_2\otimes S_4)(\overline{g_2}(\alpha )-\overline{g_2}(\beta ))\le 2(\alpha -\beta )^TQ_4(\alpha -\beta ). \end{aligned}$$

(10)

Substituting (7)–(10) into (6) yields that

$$\begin{aligned}&(\alpha -\beta )^TP(H(\alpha )-H(\beta ))\nonumber \\ \le&\frac{1}{2}(\alpha -\beta )^T\left( -PC_1-C_1P+2Q_1+2Q_2+2Q_3+2Q_4+PA_1(I_2\otimes S_1^{-1})A_1^TP\right. \nonumber \\&\left. +PA_2(I_2\otimes S_2^{-1})A_2^TP+PB_1(I_2\otimes S_3^{-1})B_1^TP+PB_2(I_2\otimes S_4^{-1})B_2^TP \right) (\alpha -\beta ). \end{aligned}$$

(11)

Utilizing Lemma 2, it follows from condition (3) that $\Psi +PA_1(I_2\otimes S_1^{-1})A_1^TP+PA_2(I_2\otimes S_2^{-1})A_2^TP+PB_1(I_2\otimes S_3^{-1})B_1^TP+PB_2(I_2\otimes S_4^{-1})B_2^TP<0$, which combining (11) and the fact that $\alpha \ne \beta$ infers that

$$\begin{aligned}&(\alpha -\beta )^TP(H(\alpha )-H(\beta ))<0. \end{aligned}$$

(12)

From (12), according to Definition 1, one gets that $m_{\mathbb {R}^{2n}}(PH)<0$. Therefore, it follows from Lemma 3 that system (5) has a unique equilibrium point, which implies that system (2) also has a unique equilibrium point.

Step 2 Suppose that $\alpha ^*=((x^*)^T,(y^*)^T)^T$ is an equilibrium point of (2), i.e., $-C_1\alpha ^*+A_1\overline{f_1}(\alpha ^*)+ A_2\overline{f_2}(\alpha ^*)+B_1\overline{g_1}(\alpha ^*) +B_2\overline{g_2}(\alpha ^*)+\zeta =0$. For simplicity, let $e(t)=\alpha (t)-\alpha ^*$, then system (2) could be transformed into the following form:

$$\begin{aligned} \mathop {e}\limits ^\centerdot \centerdot (t)\!=\!-C_1e(t)+A_1 \widetilde{f}_1(e(t))\!+\!A_2\widetilde{f}_2(e(t))+B_1 \widetilde{g}_1(e(t-\tau )) +B_2\widetilde{g}_2(e(t-\tau )), \end{aligned}$$

(13)

where

$$\begin{aligned} \widetilde{f}_1(e(t))&=\overline{f_1}(e(t)+\alpha ^*)- \overline{f_1}(\alpha ^*),\\ \widetilde{g}_1(e(t-\tau ))&=\overline{g_1}(e(t-\tau ) +\alpha ^*)-\overline{g_1}(\alpha ^*),\\ \widetilde{f}_2(e(t))&=\overline{f_2}(e(t)+\alpha ^*)- \overline{f_2}(\alpha ^*),\\ \widetilde{g}_2(e(t-\tau ))&=\overline{g_2}(e(t-\tau ) +\alpha ^*)-\overline{g_2}(\alpha ^*). \end{aligned}$$

Consider the following Lyapunov functional candidate:

$$\begin{aligned} V(t,e_t)= & {} e(t)^TPe(t)+\int _{t-\tau }^t{\widetilde{g}_1(e(s))^T(I_2\otimes S_3)\widetilde{g}_1(e(s))ds}\\&+\int _{t-\tau }^t{\widetilde{g}_2(e(s))^T(I_2\otimes S_4)\widetilde{g}_2(e(s))ds}, \end{aligned}$$

where $e_t(\theta )\triangleq e(t+\theta )$ for $\theta \in [-\tau ,0]$. Calculate the derivative of $V(t,e_t)$ along the trajectory of system (13), one obtains that

$$\begin{aligned} \mathop V\limits ^\centerdot \centerdot (t,e_t) =\,&2e(t)^TP\left( -C_1e(t)+A_1\widetilde{f}_1(e(t))+A_2\widetilde{f}_2(e(t))\right. \nonumber \\&\left. +B_1\widetilde{g}_1(e(t-\tau ))+B_2\widetilde{g}_2(e(t-\tau ))\right) \nonumber \\&+\widetilde{g}_1(e(t))^T(I_2\otimes S_3)\widetilde{g}_1(e(t)) -\widetilde{g}_1(e(t-\tau ))^T(I_2\otimes S_3)\widetilde{g}_1(e(t-\tau ))\nonumber \\&+\widetilde{g}_2(e(t))^T(I_2\otimes S_4)\widetilde{g}_2(e(t))-\widetilde{g}_2(e(t-\tau ))^T(I_2\otimes S_4)\widetilde{g}_2(e(t-\tau ))\nonumber \\ \le \,&e(t)^T(-PC_1-C_1P)e(t)+e(t)^TPA_1(I_2\otimes S_1^{-1})A_1^TPe(t)\nonumber \\&+\widetilde{f}_1(e(t))^T(I_2\otimes S_1)\widetilde{f}_1(e(t))\nonumber \\&+e(t)^TPA_2(I_2\otimes S_2^{-1})A_2^TPe(t)+\widetilde{f}_2(e(t))^T(I_2\otimes S_2)\widetilde{f}_2(e(t))\nonumber \\&+e(t)^TPB_1(I_2\otimes S_3^{-1})B_1^TPe(t)+\widetilde{g}_1(e(t))^T(I_2\otimes S_3)\widetilde{g}_1(e(t))\nonumber \\&+e(t)^TPB_2(I_2\otimes S_4^{-1})B_2^TPe(t)+\widetilde{g}_2(e(t))^T(I_2\otimes S_4)\widetilde{g}_2(e(t)). \end{aligned}$$

(14)

By the similar way as shown in (7)–(10), it is easy to obtain that

$$\begin{aligned}&\widetilde{f}_1(e(t))^T(I_2\otimes S_1)\widetilde{f}_1(e(t))\le 2e(t)^TQ_1e(t),\nonumber \\&\widetilde{f}_2(e(t))^T(I_2\otimes S_2)\widetilde{f}_2(e(t))\le 2e(t)^TQ_2e(t); \end{aligned}$$

(15)

$$\begin{aligned}&\widetilde{g}_1(e(t))^T(I_2\otimes S_3)\widetilde{g}_1(e(t))\le 2e(t)^TQ_3e(t),\nonumber \\&\widetilde{g}_2(e(t))^T(I_2\otimes S_4)\widetilde{g}_2(e(t))\le 2e(t)^TQ_4e(t). \end{aligned}$$

(16)

Substituting (15)–(16) into (14) yields that

$$\begin{aligned} \mathop V\limits ^\centerdot \centerdot (t,e_t) \le&e(t)^T\left( -PC_1-C_1P+2Q_1+2Q_2+2Q_3+2Q_4+PA_1(I_2\otimes S_1^{-1})A_1^TP\right. \nonumber \\&\left. +PA_2(I_2\otimes S_2^{-1})A_2^TP +PB_1(I_2\otimes S_3^{-1})B_1^TP+PB_2(I_2\otimes S_4^{-1})B_2^TP \right) e(t). \end{aligned}$$

It follows from Lemma 2 and condition (3) that $\mathop V\limits ^\centerdot \centerdot (t,e_t)<0$ for all $e(t)\ne 0$, which implies that the equilibrium point of system (13) (and consequently, system (1)) is globally asymptotically stable. The proof is complete.

Corollary 1

Suppose that the Assumption 1 holds, the complex-valued neural network (1) has one equilibrium which is globally asymptotically stable if there exist a matrix $P>0$, positive diagonal matrices $S_k~(k=1,2,3,4)$ such that

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \widetilde{\Psi }&{}PA_1&{}PA_2&{}PB_1&{}PB_2\\ A_1^TP&{}-I_2\otimes S_1&{}0&{}0&{}0 \\ A_2^TP&{}0&{}-I_2\otimes S_2&{}0&{}0 \\ B_1^TP&{}0&{}0&{}-I_2\otimes S_3&{}0 \\ B_2^TP&{}0&{}0&{}0&{}-I_2\otimes S_4 \\ \end{array} \right] <0, \end{aligned}$$

(17)

where $\widetilde{\Psi }=-PC_1-C_1P+4I_2\otimes (S_1\Gamma _1^T\Gamma _1) +4I_2\otimes (S_2\Gamma _2^T\Gamma _2)+4 {I}_2\otimes (S_3\Gamma _3^T\Gamma _3)+4I_2\otimes (S_4\Gamma _4^T\Gamma _4), \Gamma _1=\mathrm{diag}\{\lambda _1^M,\lambda _2^M,\ldots ,\lambda _n^M\}, \Gamma _2=\mathrm{diag}\{\lambda _1^N,\lambda _2^N,\ldots ,\lambda _n^N\}, \Gamma _3=\mathrm{diag}\{\xi _1^M,\xi _2^M,\ldots ,\xi _n^M\}, \Gamma _4=\mathrm{diag}\{\xi _1^N,\xi _2^N,\ldots ,\xi _n^N\}$, and $\lambda _k^M=\max \{\lambda _k^{RR},\lambda _k^{RI}\}, \lambda _k^N=\max \{\lambda _k^{IR},\lambda _k^{II}\}, \xi _k^M=\max \{\xi _k^{RR},\xi _k^{RI}\}, \xi _k^N=\max \{\xi _k^{IR},\xi _k^{II}\}, k=1,2,\dots ,n$.

Proof

Along the similar proof lines of Theorem 1, by utilizing Assumption 1, one gets that

$$\begin{aligned}&(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))^T(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))\\&\quad =\left( \begin{array}{cc} f^R(x^\alpha ,y^\alpha )-f^R(x^\beta ,y^\beta ) \\ f^R(x^\alpha ,y^\alpha )-f^R(x^\beta ,y^\beta ) \end{array} \right) ^T \left( \begin{array}{cc} f^R(x^\alpha ,y^\alpha )-f^R(x^\beta ,y^\beta ) \\ f^R(x^\alpha ,y^\alpha )-f^R(x^\beta ,y^\beta ) \end{array} \right) \\&\quad =2\sum _{k=1}^n\left( f_k^R(x_k^\alpha ,y_k^\alpha )-f_k^R(x_k^\beta ,y_k^\beta )\right) ^2\\&\quad \le 4\sum _{k=1}^n(\lambda _k^M)^2\left( (x_k^\alpha -x_k^\beta )^2+ (y_k^\alpha -y_k^\beta )^2\right) \\&\quad =4(\alpha -\beta )^T(I_2\otimes (\Gamma _1^T\Gamma _1))(\alpha -\beta ), \end{aligned}$$

which immediately infers that for positive diagonal matrix $S_1$, the following inequality holds:

$$\begin{aligned} (\overline{f_1}(\alpha )-\overline{f_1}(\beta ))^T(I_2\otimes S_1)(\overline{f_1}(\alpha )-\overline{f_1}(\beta ))\le 4(\alpha -\beta )^T(I_2\otimes (S_1\Gamma _1^T\Gamma _1))(\alpha -\beta ). \end{aligned}$$

Similarly, one gets

$$\begin{aligned}&(\overline{f_2}(\alpha )-\overline{f_2}(\beta ))^T(I_2\otimes S_2)(\overline{f_2}(\alpha )-\overline{f_2}(\beta ))\le 4(\alpha -\beta )^T(I_2\otimes (S_2\Gamma _2^T\Gamma _2))(\alpha -\beta ),\\&(\overline{g_1}(\alpha )-\overline{g_1}(\beta ))^T(I_2\otimes S_3)(\overline{g_1}(\alpha )-\overline{g_1}(\beta ))\le 4(\alpha -\beta )^T(I_2\otimes (S_3\Gamma _3^T\Gamma _3))(\alpha -\beta ),\\&(\overline{g_2}(\alpha )-\overline{g_2}(\beta ))^T(I_2\otimes S_4)(\overline{g_2}(\alpha )-\overline{g_2}(\beta ))\le 4(\alpha -\beta )^T(I_2\otimes (S_4\Gamma _4^T\Gamma _4))(\alpha -\beta ). \end{aligned}$$

Along the similar proof lines of Theorem 1, one could obtain the result here. The proof is completed.

It is well known to us that the parameters of the system are often affected by external disturbance. In this paper, it is assumed that the parameter uncertainties appear in system (13) with the following form:

$$\begin{aligned} \mathop e\limits ^\centerdot \centerdot (t)=&-(C_1+\Delta C_1(t))e(t)+(A_1+\Delta A_1(t))\widetilde{f}_1(e(t))+(A_2+\Delta A_2(t))\widetilde{f}_2(e(t))\nonumber \\&+(B_1+\Delta B_1(t))\widetilde{g}_1(e(t-\tau ))+(B_2+\Delta B_2(t))\widetilde{g}_2(e(t-\tau )), \end{aligned}$$

(18)

where the matrices $\Delta C_1(t),\Delta A_1(t),\Delta A_2(t),\Delta B_1(t)$ and $\Delta B_2(t)$ are the uncertainties having the following norm-bounded form:

$$\begin{aligned}{}[\Delta C_1(t),\Delta A_1(t),\Delta A_2(t),\Delta B_1(t),\Delta B_2(t)]=DF(t)[E_{C_1},E_{A_1},E_{A_2},E_{B_1},E_{B_2}], \end{aligned}$$

(19)

in which $D,E_{C_1},E_{A_1},E_{A_2},E_{B_1}$ and $E_{B_2}$ are known constant real matrices with appropriate dimensions, and F(t) is an unknown matrix function with Lebesgue-measurable elements bounded by

$$\begin{aligned} F(t)^TF(t)\le I. \end{aligned}$$

(20)

Lemma 4

[36] Given symmetric matrix $\Xi , D$ and E of appropriate dimensions, then

$$\begin{aligned} \Xi +DF(t)E+E^TF(t)^TD^T<0 \end{aligned}$$

holds for all F(t) satisfying $F(t)^TF(t)\le I$ if and only if there exists $\varepsilon >0$ such that

$$\begin{aligned} \Xi +\varepsilon DD^T+\varepsilon ^{-1}E^TE<0. \end{aligned}$$

Now, we are ready to investigate the global asymptotic robust stability of the system (18).

Theorem 2

Suppose that the Assumption 1 holds, the system (18) with parameter uncertainties (19)-(20) is globally robustly asymptotically stable if there exist a matrix $P>0$, positive diagonal matrices $Q_k$ and $S_k~(k=1,2,3,4)$ and a scalar $\varepsilon >0$ such that inequality (4) and the following inequality

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Psi +\varepsilon E_{C_1}^TE_{C_1} &{}PA_1 -\varepsilon E_{C_1}^TE_{A_1}&{}PA_2-\varepsilon E_{C_1}^TE_{A_2}&{}PB_1-\varepsilon E_{C_1}^TE_{B_1} &{}PB_2 -\varepsilon E_{C_1}^TE_{B_2}&{}PD\\ A_1^TP -\varepsilon E_{A_1}^TE_{C_1} &{}-(I_2\otimes S_1) +\varepsilon E_{A_1}^TE_{A_1} &{} \varepsilon E_{A_1}^TE_{A_2}&{} \varepsilon E_{A_1}^TE_{B_1}&{} \varepsilon E_{A_1}^TE_{B_2}&{}0 \\ A_2^TP-\varepsilon E_{A_2}^TE_{C_1} &{} \varepsilon E_{A_2}^TE_{A_1}&{}-(I_2\otimes S_2) +\varepsilon E_{A_2}^TE_{A_2}&{} \varepsilon E_{A_2}^TE_{B_1}&{} \varepsilon E_{A_2}^TE_{B_2}&{}0\\ B_1^TP-\varepsilon E_{B_1}^TE_{C_1} &{} \varepsilon E_{B_1}^TE_{A_1} &{} \varepsilon E_{B_1}^TE_{A_2}&{}-(I_2\otimes S_3) +\varepsilon E_{B_1}^TE_{B_1}&{} \varepsilon E_{B_1}^TE_{B_2}&{}0 \\ B_2^TP-\varepsilon E_{B_2}^TE_{C_1} &{} \varepsilon E_{B_2}^TE_{A_1} &{} \varepsilon E_{B_2}^TE_{A_2}&{} \varepsilon E_{B_2}^TE_{B_1}&{}-(I_2\otimes S_4) + \varepsilon E_{B_2}^TE_{B_2}&{}0 \\ D^TP &{} 0 &{} 0&{} 0&{} 0&{}-\varepsilon I\\ \end{array} \right] <0 \end{aligned}$$

(21)

hold, where the matrix $\Psi$ is the same as defined in Theorem 1.

Proof

Let $\Upsilon _D=[D^TP, 0, 0, 0, 0]^T, \Upsilon _E=[-E_{C_1},E_{A_1},E_{A_2},E_{B_1},E_{B_2}]$. By resorting to Lemma 2 and condition (3), it is easy to obtain that inequality (21) is equivalent to

$$\begin{aligned} \Xi +\varepsilon ^{-1}\Upsilon _D\Upsilon _D^T+ \varepsilon \Upsilon _E^T\Upsilon _E<0. \end{aligned}$$

(22)

It follows from Lemma 4 that (22) holds if and only if

$$\begin{aligned} \Xi +\Upsilon _DF(t)\Upsilon _E+\Upsilon _E^TF(t)^T\Upsilon _D^T<0 \end{aligned}$$

(23)

holds for all F(t) satisfying $F(t)^TF(t)\le I$, which implies that

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Psi &{}P(A_1+\Delta A_1(t))&{}P(A_2+\Delta A_2(t))&{}P(B_1+\Delta B_1(t))&{}P(B_2+\Delta B_2(t))\\ (A_1+\Delta A_1(t))^TP&{}-(I_2\otimes S_1)&{}0&{}0&{}0 \\ (A_2+\Delta A_2(t))^TP&{}0&{}-(I_2\otimes S_2)&{}0&{}0 \\ (B_1+\Delta B_1(t))^TP&{}0&{}0&{}-(I_2\otimes S_3)&{}0 \\ (B_2+\Delta B_2(t))^TP&{}0&{}0&{}0&{}-(I_2\otimes S_4) \\ \end{array} \right] <0. \end{aligned}$$

(24)

Utilizing Theorem 1 and (24), one gets the conclusion that the system (18) is globally robustly asymptotically stable. The proof is complete.

Corollary 2

Suppose that the Assumption 1 holds, the system (18) with parameter uncertainties (19)–(20) is globally robustly asymptotically stable if there exist a matrix $P>0$, positive diagonal matrices $S_k~(k=1,2,3,4)$ and a scalar $\varepsilon >0$ such that

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \widetilde{\Psi }+\varepsilon E_{C_1}^TE_{C_1} &{}PA_1 -\varepsilon E_{C_1}^TE_{A_1}&{}PA_2-\varepsilon E_{C_1}^TE_{A_2}&{}PB_1-\varepsilon E_{C_1}^TE_{B_1} &{}PB_2 -\varepsilon E_{C_1}^TE_{B_2}&{}PD\\ A_1^TP -\varepsilon E_{A_1}^TE_{C_1} &{}-(I_2\otimes S_1) +\varepsilon E_{A_1}^TE_{A_1} &{} \varepsilon E_{A_1}^TE_{A_2}&{} \varepsilon E_{A_1}^TE_{B_1}&{} \varepsilon E_{A_1}^TE_{B_2}&{}0 \\ A_2^TP-\varepsilon E_{A_2}^TE_{C_1} &{} \varepsilon E_{A_2}^TE_{A_1}&{}-(I_2\otimes S_2) +\varepsilon E_{A_2}^TE_{A_2}&{} \varepsilon E_{A_2}^TE_{B_1}&{} \varepsilon E_{A_2}^TE_{B_2}&{}0\\ B_1^TP-\varepsilon E_{B_1}^TE_{C_1} &{} \varepsilon E_{B_1}^TE_{A_1} &{} \varepsilon E_{B_1}^TE_{A_2}&{}-(I_2\otimes S_3) +\varepsilon E_{B_1}^TE_{B_1}&{} \varepsilon E_{B_1}^TE_{B_2}&{}0 \\ B_2^TP-\varepsilon E_{B_2}^TE_{C_1} &{} \varepsilon E_{B_2}^TE_{A_1} &{} \varepsilon E_{B_2}^TE_{A_2}&{} \varepsilon E_{B_2}^TE_{B_1}&{}-(I_2\otimes S_4) + \varepsilon E_{B_2}^TE_{B_2}&{}0 \\ D^TP &{} 0 &{} 0&{} 0&{} 0&{}-\varepsilon I\\ \end{array} \right] <0, \end{aligned}$$

(25)

where $\widetilde{\Psi }$ is the same as defined in Corollary 1.

Remark 3

In [22], the global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales has been studied, whereas the global attractiveness is not taken into account. In this paper, both the global stability and the global attractiveness have been simultaneously considered. From this view point, the criteria here are more general than the results in Ref. [22].

Remark 4

The global $\mu$-stability of the complex-valued neural networks with unbounded time-varying delays has been investigated under the assumption that the equilibrium point of the network should exist in Ref. [38]. It is well known to us that the equilibrium points of the complex-valued system may not exist, which implies that the results in Ref. [38] could not be utilized under the situation that the equilibrium points of the complex-valued system don’t exist. However, based on the nonlinear measure method, it is easy to ascertain the existence and uniqueness of the equilibrium point for the complex-valued neural networks.

Remark 5

Recently, global exponential periodicity and stability have been investigated in Refs. [39, 40], respectively, for the complex-valued neural networks in continuous-time and discrete-time forms. If the parameters of the network are disturbed from the external environments, the results there would not verify whether the complex-valued system is stable or not. Whereas in this paper, besides the global asymptotic stability, the robust stability of the complex-valued network with norm-bounded parameter uncertainties has also been considered.

4 Numerical Examples

In this section, we will give one numerical example to illustrate the effectiveness of the obtained results.

Example 1

Consider a two-neuron complex-valued neural network with constant delay described in (1) with $C=\mathrm{diag}\{8,6\}, \tau =0.8, L=(1-i,3+2i)^T$,

$$\begin{aligned} A= & {} \left[ \begin{array}{c@{\quad }c} 0.8957 + 0.7913i &{} 0.9979 + 0.5437i\\ 0.2741 + 0.6566i &{} 0.8344 + 0.3867i\\ \end{array} \right] ,~~\\ B= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.8222 + 0.7883i &{} 0.7816 + 0.4856i\\ 0.5953 + 0.8529i &{} 0.9877 + 0.8738i\\ \end{array} \right] . \end{aligned}$$

For $u_k=x_k+iy_k$ with $x_k, y_k\in \mathbb {R}, k=1,2$, the activation functions are taken as the same ones given in Ref. [14] as follows:

$$\begin{aligned} f_k(u_k)=\frac{1-\exp (-x_k)}{1+\exp (-x_k)}+i\frac{1}{1+\exp (-y_k)},\\ g_k(u_k)=\frac{1}{1+\exp (-x_k)}+i\frac{1-\exp (-y_k)}{1+\exp (-y_k)}. \end{aligned}$$

And, it is easy to calculate that $\lambda _k^{RR}=0.5, \lambda _k^{RI}=0, \lambda _k^{IR}=0, \lambda _k^{II}=0.25$ and $\xi _k^{RR}=0.25, \xi _k^{RI}=0, \xi _k^{IR}=0, \xi _k^{II}=0.5$.

It can be checked that there does not exist a positive Hermite matrix satisfying the conditions given in Theorem 1 in Ref. [14], which implies that the criteria in Ref. [14] could not guarantee whether the complex-valued neural network (1) is globally asymptotically stable or not. However, it is easy to find feasible solutions to (3) and (4) in Theorem 1 of our paper by utilizing the Matlab Toolbox. Here, only part of it is listed for space consideration: $Q_1=\mathrm{diag}\{0.9146, 0.8224, 0.7407, 0.6438\}, S_2=\mathrm{diag}\{ 1.2238, 1.2597\}, Q_3=\mathrm{diag}\{0.7829, 0.6874, 0.7407, 0.6438\}, S_4=\mathrm{diag}\{ 1.2467, 1.2627\}$ and

$$\begin{aligned} P =\left[ \begin{array}{cccccc} 0.5315 &{}\quad 0.0798 &{}\quad 0 &{}\quad 0\\ 0.0798 &{}\quad 0.6657 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0.5328 &{}\quad 0.0801\\ 0 &{}\quad 0 &{}\quad 0.0801 &{}\quad 0.6676\\ \end{array} \right] . \end{aligned}$$

Therefore, our result is less conservative than that of Theorem 1 in Ref. [14].

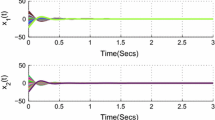
Figures 1 and 2 illustrate the time responses of the states for the complex-valued neural network (1) with the following six kinds of initial conditions, which further illustrates the effectiveness of the obtained results. Case 1 with the initial state $u_1(t)=-6.7+0.3i, u_2(t)=2.3-3.7i$ for $t\in [-0.8,0]$. Case 2 with the initial state $u_1(t)=-0.7-1.7i, u_2(t)=-5.7-0.2i$ for $t\in [-0.8,0]$. Case 3 with the initial state $u_1(t)=0.3-7.7, u_2(t)=3.3+0.3i$ for $t\in [-0.8,0]$. Case 4 with the initial state $u_1(t)=-4.7-6.7i, u_2(t)=-9.7+1.3i$ for $t\in [-0.8,0]$. Case 5 with the initial state $u_1(t)=-1.7+1.3i, u_2(t)=-7.7-4.2i$ for $t\in [-0.8,0]$. Case 6 with the initial state $u_1(t)=1.8-4.7i, u_2(t)=1.8-8.7i$ for $t\in [-0.8,0]$.

Fig. 1

Trajectories of the real parts x(t) of the states u(t) for neural network (1)

Fig. 2

Trajectories of the imaginary parts y(t) of the states u(t) for neural network (1)

Next, we consider the system (18) with parameter uncertainties satisfying (19)–(20) with

$$\begin{aligned} D= \left[ \begin{array}{cccc} 0.3435 &{}\quad 0.0242 &{}\quad 0.8814 &{}\quad 0.0800\\ 0.0093 &{}\quad 0.5500 &{}\quad 0.0247 &{}\quad 0.0794\\ 0.1924 &{}\quad 0.2762 &{}\quad 0.3412 &{}\quad 0.0724\\ 0.5074 &{}\quad 0.6962 &{}\quad 0.4214 &{}\quad 0.9003\\ \end{array} \right] ,~~ E_{C_1}= \left[ \begin{array}{cccc} 0.9693 &{}\quad 0.7920 &{}\quad 0.0064 &{}\quad 0.7115\\ 0.3913 &{}\quad 0.7983 &{}\quad 0.9199 &{}\quad 0.5384\\ 0.3136 &{}\quad 0.8633 &{}\quad 0.0180 &{}\quad 0.5246\\ 0.5533 &{}\quad 0.7980 &{}\quad 0.0294 &{}\quad 0.5022\\ \end{array} \right] ,\\ E_{A_1}= \left[ \begin{array}{cccc} 0.0657 &{}\quad 0.0705 &{}\quad 0.1285 &{}\quad 0.2690\\ 0.2300 &{}\quad 0.0600 &{}\quad 0.6371 &{}\quad 0.4340\\ 0.1170 &{}\quad 0.6616 &{}\quad 0.7465 &{}\quad 0.4018\\ 0.9898 &{}\quad 0.3441 &{}\quad 0.8053 &{}\quad 0.6081\\ \end{array} \right] ,~~ E_{A_2}= \left[ \begin{array}{cccc} 0.7701 &{}\quad 0.3783 &{}\quad 0.2375 &{}\quad 0.6382\\ 0.9411 &{}\quad 0.9937 &{}\quad 0.2200 &{}\quad 0.5041\\ 0.1315 &{}\quad 0.3410 &{}\quad 0.9911 &{}\quad 0.3581\\ 0.2557 &{}\quad 0.8996 &{}\quad 0.9511 &{}\quad 0.7685\\ \end{array} \right] ,\\ E_{B_1}= \left[ \begin{array}{cccc} 0.7844 &{}\quad 0.7997 &{}\quad 0.6167 &{}\quad 0.5907\\ 0.0289 &{}\quad 0.6302 &{}\quad 0.3087 &{}\quad 0.3031\\ 0.0524 &{}\quad 0.9828 &{}\quad 0.0851 &{}\quad 0.1681\\ 0.3234 &{}\quad 0.1582 &{}\quad 0.8768 &{}\quad 0.3399\\ \end{array} \right] ,~~ E_{B_2}= \left[ \begin{array}{cccc} 0.0674 &{}\quad 0.2990 &{}\quad 0.1866 &{}\quad 0.0499\\ 0.6535 &{}\quad 0.4188 &{}\quad 0.2709 &{}\quad 0.1013\\ 0.2443 &{}\quad 0.0558 &{}\quad 0.0662 &{}\quad 0.0719\\ 0.7579 &{}\quad 0.0309 &{}\quad 0.3335 &{}\quad 0.9045\\ \end{array} \right] , \end{aligned}$$

and the other parameters are the same as given above. One could obtain feasible solution to (4) and (21) in Theorem 2, part of which is given as follows:

$$\begin{aligned} P= \left[ \begin{array}{cccc} 159.2878 &{}\quad 48.9322 &{}\quad 7.8929 &{}\quad 23.7156\\ 48.9322 &{}\quad 253.7204 &{}\quad 14.3785 &{}\quad 48.6977\\ 7.8929 &{}\quad 14.3785 &{}\quad 294.2601 &{}\quad 30.8278\\ 23.7156 &{}\quad 48.6977 &{}\quad 30.8278&{}\quad 156.2125\\ \end{array} \right] , \end{aligned}$$

$S_1=\mathrm{diag}\{ 1072.3, 867.1\}, S_4=\mathrm{diag}\{ 2604.6, 660.3\}, Q_2=\mathrm{diag}\{ 56.5595, 58.5228, 353.4201, 140.5313\}, Q_3=\mathrm{diag}\{113.2508, 125.0990, 178.1286, 15.2007\}$ and $\varepsilon = 88.3343$. Therefore, it follows from Theorem 2 that the system (18) is globally robustly asymptotically stable.

By taking $F(t)=I$ for simulation, Fig. 3 illustrates the time responses of the states for the system (18) with the same initial conditions given earlier, which further verifies the validity and effectiveness of the criteria obtained.

Fig. 3

Trajectories of the states e(t) for the system (18)

5 Conclusions

In this paper, the global stability of the complex-valued neural networks with and without parameter uncertainties has been investigated, respectively. Based on the nonlinear measure method and by constructing appropriate Lyapunov functional candidate, several sufficient criteria have been obtained to ascertain the global robust stability of the addressed network under one general class of activation functions. Finally, one example has been illustrated in the end of the paper to show the effectiveness of our main results.

In the future, investigations such as multistability will be carried out further for the complex-valued neural systems with real-imaginary-type activation functions and distributed delays. Moreover, motivated from the works in Refs. [41, 42], other research topics will also be included such as the state estimation of the complex-valued systems with incomplete information.