1 Introduction

Generally speaking, neural networks (NNs) are comprised of a great deal of interconnected neural units that are present in natural and artificial systems, including power grid, financial system and biological network [1,2,3], etc. In recent decades, NNs have become an irreplaceable tool to dissect practical issues in diverse disciplines, such as digital communication, industrial manufacture, image recognition and engineering fields [4,5,6,7,8]. Kosko [9] in 1987 proposed bidirectional associative memory NNs (BAMNNs), which make up two layers of hetero associative neurons. Each layer is connected to each others by neurons, and one layer is connected to another, there is no direct interconnection between the same layer elements. Unlike the ecumenic NNs with only the one layer, it is the fact that BAMNNs with two layers that can implement more effectively and quickly handle some practical problems. For example, BAMNNs can be highly accurate simulation the human brain thanks to forming excellent performance in parallel processing aspect. More scholars have concentrated on the theme of BAMNNs and some remarkable papers have been published in [10,11,12,13,14] owing to the potential applications in pattern recognition, chemical processes, associative memory, optimization problems and electrical engineering [15,16,17,18], etc. In addition, in the electronic NNs, it is noted that the time delay will inescapably engender owing to the limited exchanging speeds of data processing and amplifier circuitry [19], the influence of delay has also been taken into account for BAMNNs.

It is well known that the fractional-order (FO) calculus, as an extension of the integer order (IO) calculus, has been brought into focus due to wide range of applications in image encryption, viscoelastic systems, mathematical biology and science engineering [20,21,22]. These days, FO calculus becomes a kinetic research motif because FO calculus can describe precisely dynamic behavior, which opens up entirely possibilities for science development. It is worth emphasizing that the ascendency from the fact that FO calculus offers an exceptional facility for depicting the memory and heritability of diverse materials and processes compared with the conventional IO calculus. Furthermore, the introduction of the FO calculus into the controlled system produces degrees of freedom, which can ameliorate the elasticity of controller design. Recently, serval dynamics analysis results for fractional-order neural networks (FONNs) have been obtained in [23,24,25,26,27,28] and references therein. Among which, the synchronization analysis of FONNs has captured gigantic attention.

It is the fact remarkably that massive applications of FONNs rest with their essential properties, expressly synchronization. Synchronization, which represents interesting collective dynamics and delineates the state of two or more systems, tends to be concordant. Synchronization phenomenon, as the most essential performance quota, has become a hot subject due to stupendous potential applications in distrinct realms, such as in secure communication, pattern recognition, information science and industrial automation [29,30,31]. From the complex view of the system structure, fractional-order BAMNNs (FOBAMNNs) can display prosperous dynamical behaviors. Nowadays, the multitudinous synchronization problems for FOBAMNNs containing Mittag-Leffler synchronization [32], fixed-time synchronization [33], quasi-synchronization [34] and so on have been divulged by the various control strategies. However, to our best knowledge, the novel and effectual measures for the synchronization analysis of delayed FOBAMNNs (DFOBAMNNs) are still lacking, which has evoked our research enthusiasms.

There is no doubt that the precise value of parameter cannot be procured because of the disturbances in the measurement errors and the added perturbations, which bring about system parameter uncertainties. One should note that parameter uncertainties should be noticed in the research of dynamical behaviors because they can destroy the synchronization and some other excellent properties. Most previous works on the thesis that the system parameters are affirmatory in advance have been obtainable. However, there are very few efforts about the synchronization issues for uncertain DFOBAMNNs, this research gap has bestirred us to explore the challenging tasks of synchronization for uncertain DFOBAMNNs. To address this problem, the following questions are naturally raised: whether uncertain DFOBAMNNs can reach the finite-time synchronization and Mittag-Leffler synchronization based on pertinent state feedback control strategies and parameters update laws? If we can get synchronization conditions, how to devise the fitting controllers and to dispose of the delay terms.

Vigorously provoked by the above discussions, we attempt to delve the problems of synchronization analysis and parameters identification for uncertain DFOBAMNNs. The main novelty of this paper is reflected in the following aspects. (1) The copious existing synchronization problems for BAMNNs neglect the element of parameter uncertainties, uncertain DFOBAMNN model is established in this paper. (2) In this paper, we not only ponder the influences of parameter uncertainties in BAMNNs, but also consider the time delay effects in BAMNNs, i.e., the parameter uncertainties and time delay are brought into FOBAMNNs. (3) The novel controllers and parameters updated laws are designed. (4) The synchronization and parameters identification issues of uncertain DFOBAMNNs are firstly investigated, some sufficient criteria are procured to guarantee the synchronization and to actualize parameters identification for uncertain DFOBAMNNs.

The remainder of the paper is organized in brief as follows. In Sect. 2, system description and preliminary knowledge are given. In Sect. 3, the synchronization and parameters identification for uncertain DFOBAMNNs are addressed through designing two novel controllers. In Sect. 4, two examples are provided to illustrate the effectiveness of the results. Finally, conclusion is clarified in Sect. 5.

2 Preliminaries and model description

Notations: \(\mathbb {R}\) denotes the set of real numbers, \(\mathbb {N}^+=\{1,2,3,\cdots \}\) is the set of the positive integer, \(\Vert h\Vert _1=\sum \nolimits _{\varrho =1}^n|h_\varrho |\) represents the 1-norm of h, \(\mathcal {A}=\{1,2,\cdots ,n\}\), \(\mathcal {B}=\{1,2,\cdots ,m\}\), \(\mathrm {sign}(\cdot )\) shows the standard symbolic function.

2.1 Preliminaries

In order to derive our main results of this paper, some useful definitions and lemmas are proposed, which will smoothly promote the proof of the results in the sequel.

Definition 1

[35] The fractional integral of order \(\eta\) for function h(t) is defined as

$$\begin{aligned} _{t_0}D_{t}^{-\eta }h(t)= \frac{1}{\Gamma ({\eta })}\int _{t_0}^{t}(t-{\rho })^{{\eta }-1}h({\rho })\mathrm{d}{\rho }, \quad \eta >0, \end{aligned}$$

where \(\Gamma (\cdot )\) is the Gamma function, and \(\Gamma (\eta )=\int _0^{+\infty }{\rho }^{\eta -1}e^{-\rho }d{\rho }.\)

Definition 2

[35] Caputo fractional derivative of order \(\eta\) for function h(t) is described by

$$\begin{aligned} _{t_0}^{c}D_{t}^{\eta }h(t)= \frac{1}{\Gamma (1-{\eta })}\int _{t_0}^{t}\frac{h^{'}(\rho )}{(t-{\rho })^{\eta }}\mathrm{d}{\rho }. \end{aligned}$$

Definition 3

[35] The Mittag-Leffler function with a parameter \(\eta >0\) is denoted by

$$\begin{aligned} E_{\eta }(h)=\sum _{\varrho =0}^{\infty }\frac{h^\varrho }{\Gamma ({\eta }\varrho +1)}. \end{aligned}$$

Lemma 1

[35] Let \(t \ge t_0,\) then \(E_\eta (\rho (t-t_0)^\eta )\) is monotonically non-increasing and \(0 \le E_\eta (\rho (t- t_0)^\eta )\le 1\) for \(\rho \le 0.\)

Lemma 2

[36] If \(h(t)\in C([t_0,+\infty ],\mathbb {R})\) describes a continuously differentiable function, for any \(0<\eta <1\), then the following inequality holds

$$_{{t_{0} }}^{c} D_{t}^{\eta } |h(t)| \le {\text{sign}}(h(t))_{{t_{0} }}^{c} D_{t}^{\eta } h(t).$$

Lemma 3

[28] Let u(t), v(t) be two nonnegative continuous functions and satisfy

$$\begin{aligned} _{t_0}^{c}D_{t}^{\eta }{\Big (u(t)+v(t)\Big )}\le {-\Upsilon }u(t)+\hbar , \end{aligned}$$

where \(0<\eta <1,\Upsilon >0\) and \(\hbar >0,\) then

$$\begin{aligned} u(t)\le \Big (u(t_0)+v(t_0)-\frac{\hbar }{\Upsilon }\Big )E_\eta \Big ({-\Upsilon }(t-t_0)^{\eta }\Big )+\frac{\hbar }{\Upsilon },\quad t\ge t_0+\big (\frac{\Gamma (\eta )}{\Upsilon }\big )^\frac{1}{1-{\eta }}. \end{aligned}$$

In particular, when the constant term \(\hbar =0\), the following corollary will be yielded based on the Lemma 3.

Corollary 1

Let u(t), v(t) be two nonnegative continuous functions and satisfy

$$\begin{aligned} _{t_0}^{c}D_{t}^{\eta }{\Big (u(t)+v(t)\Big )}\le {-\Upsilon }u(t), \end{aligned}$$
(1)

where \(0<\eta <1,\Upsilon >0\), then

$$\begin{aligned} u(t)\le \Big (u(t_0)+v(t_0)\Big )E_\eta \Big ({-\Upsilon }(t-t_0)^{\eta }\Big ),\quad t\ge t_0+\big (\frac{\Gamma (\eta )}{\Upsilon }\big )^\frac{1}{1-{\eta }}. \end{aligned}$$
(2)

Proof

It follows from (1) that there exists a nonnegative function \(\Phi (t)\) satisfying

$$\begin{aligned} _{t_0}^{c}D_{t}^{\eta }{\Big (u(t)+v(t)\Big )}+ \Phi (t)={-\Upsilon }u(t), \end{aligned}$$

it is obvious that the inequality (1) above is a simple modification based on Lemma 5 in [28], then the rest testify is similar to Lemma 5 in [28], here is omitted.

Lemma 4

[38]. Let h(t) be a continuous function on \(t\in [t_0,+\infty )\), which satisfies

$$\begin{aligned} {}_{t_0}^{c}D_{t}^{\eta }h(t)\le \imath h(t), \end{aligned}$$

where \(0<\eta <1\), \(\imath \in \mathbb {R}\), then

$$\begin{aligned} h(t)\le h(t_0)E_\eta [\imath (t-t_0)^\eta ]. \end{aligned}$$

2.2 Model description

In the real world, the system parameter may not be precisely known. Hence, it is necessary to identify the uncertain parameter. Next, we consider a uncertain DFOBAMNN, which is proposed by

$$ \left\{ \begin{aligned} _{{t_{0} }}^{c} D_{t}^{\eta } x_{h} (t) = & - a_{h} x_{h} (t) + \sum\limits_{{j = 1}}^{n} {c_{{jh}} } f_{j} (y_{j} (t)) + \sum\limits_{{j = 1}}^{n} {d_{{jh}} } f_{j} (y_{j} (t - \kappa )) \\ & + \Theta _{h} (t),h \in {\mathcal{A}}, \\ _{{t_{0} }}^{c} D_{t}^{\eta } y_{j} (t) = & - \alpha _{j} y_{j} (t) + \sum\limits_{{h = 1}}^{m} {\beta _{{hj}} } g_{h} (x_{h} (t)) + \sum\limits_{{h = 1}}^{m} {b_{{hj}} } g_{h} (x_{h} (t - \kappa )) \\ & + \Theta _{j} (t),j \in {\mathcal{B}}, \\ \end{aligned} \right. $$
(3)

where \(\eta \in (0,1)\), \(t\ge 0\), \(h=1, 2,\cdots , m\) and \(j = 1, 2,\cdots , n\), \(\begin{gathered} x(t) = (x_{1} (t),x_{2} (t), \cdots ,x_{n} (t))^{T} \hfill \\ y(t) = (y_{1} (t),y_{2} (t), \cdots ,y_{m} (t))^{T} \hfill \\ \end{gathered}\), \(x_h(t)\), \(y_j(t)\) denote the state vectors of the hth neuron in the x-layer and jth neuron in the y-layer at time t, \(a_h, \alpha _j >0\) represent decay rate coefficients of neuron, \(c_{jh}, d_{jh}\) and \(\beta _{hj}, b_{hj}\) indicate the synaptic connection parameters of unknown or uncertain between the neurons in the two layers at time t and \(t-\kappa\), respectively, \(f_j, g_h\) are the activation functions of the neurons at time t and \(t-\kappa\), \(\Theta _h(t), \Theta _j(t)\) stand for the external inputs, \(\kappa \ge 0\) is the constant time delay. The initial conditions associated with (3) are

$$ \left\{ \begin{aligned} x_{h} (s) & = \psi _{h} (s),\quad s \in [t_{0} - \kappa ,t_{0} ],\quad h \in {\mathcal{A}}, \\ y_{j} (s) & = \phi _{j} (s),\quad s \in [t_{0} - \kappa ,t_{0} ],\quad j \in {\mathcal{B}}, \\ \end{aligned} \right. $$
(4)

where \(h\in \mathcal {A}, j\in \mathcal {B}\), \(\psi _h(s), \phi _j(s)\in C([t_0-\kappa ,t_0],\mathbb {R})\).

Hypothesis 1

For any \(\Re _1, \Re _2 \in \mathbb {R}\), there exist \(F_j>0\) and \(G_h>0\) such that

$$\begin{aligned}&|f_j(\Re _1)-f_j(\Re _2)|\le F_j|\Re _1-\Re _2|, \\&|g_h(\Re _1)-g_h(\Re _2)|\le G_h|\Re _1-\Re _2|, \end{aligned}$$

where \(h\in \mathcal {A}, j\in \mathcal {B}\).

Hypothesis 2

For any \(h\in \mathcal {A}, j\in \mathcal {B}\), there exist positive constants F, G such that \(|f_j(\cdot )|\le F\), \(|g_h(\cdot )|\le G\).

Remark 1

The Lipschitz conditions in Hypothesis 1, which were widely used in much of the existing literature works in [39, 40], are essential in studying the synchronization and stability issues of uncertain networks, including traditional activation functions, piecewise linear function and the sigmoid function and so on.

In this paper, we will reach the derive-response synchronization, for convenience, we regard the uncertain DFOBAMNN (3) as the drive system, and the controlled response system can be denoted by

$$\left\{ \begin{aligned} _{{t_{0} }}^{c} D_{t}^{\eta } \tilde{x}_{h} (t) = & - a_{h} \tilde{x}_{h} (t) + \sum\limits_{{j = 1}}^{n} {\mathop c\limits^{} _{{jh}} } f_{j} (\tilde{y}_{j} (t)) + \sum\limits_{{j = 1}}^{n} {\mathop d\limits^{} _{{jh}} } f_{j} (\tilde{y}_{j} (t - \kappa )) + \Theta _{h} (t) \\ & + U_{h} (t),\quad h \in {\mathcal{A}}, \\ _{{t_{0} }}^{c} D_{t}^{\eta } \tilde{y}_{j} (t) = & - \alpha _{j} \tilde{y}_{j} (t) + \sum\limits_{{h = 1}}^{m} {\mathop \beta \limits^{} _{{hj}} } g_{h} (\tilde{x}_{h} (t)) + \sum\limits_{{h = 1}}^{m} {\mathop b\limits^{} _{{hj}} } g_{h} (\tilde{x}_{h} (t - \kappa )) + \Theta _{j} (t) \\ & + U_{j} (t),\quad j \in {\mathcal{B}}, \\ \end{aligned} \right.$$
(5)

where we assume that \(\check{c}_{jh}, \check{d}_{jh}\) and \(\check{\beta }_{hj}\), \(\check{b}_{hj}\) are the estimated values of the unknown parameters \(c_{jh}, d_{jh}\) and \(\beta _{hj}, b_{hj}\), respectively, other parameters are the same as those shown in uncertain DFOBAMNN (3), \(U_h(t), U_j(t)\) denote the devised controllers that will realize the synchronization of uncertain DFOBAMNNs (3) and (5). The initial conditions of (5) can be depicted as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \tilde{x}_h(s)=\tilde{\psi }_h(s), \quad \quad \quad s\in [t_0-\kappa ,t_0], \quad h\in \mathcal {A},\\ \displaystyle \tilde{y}_j(s)=\tilde{\phi }_j(s), \quad \quad \quad s\in [t_0-\kappa ,t_0], \quad j\in \mathcal {B},\\ \end{array}\right. \end{aligned}$$
(6)

where \(h\in \mathcal {A}, j\in \mathcal {B}\), \(\tilde{\psi }_h(s), \tilde{\phi }_j(s)\in C([t_0-\kappa ,t_0],\mathbb {R})\).

Definition 4

Uncertain DFOBAMNNs (3) and (5) are said to achieve finite-time synchronization together with designing proper controller, if there exists a constant \(0<\tilde{t} <+\infty\) such that \( \lim _{{t \to \tilde{t}}} \Vert \tilde{x}_h(t)-x_h(t)\Vert +\Vert \tilde{y}_j(t)-y_j(t)\Vert =0\) and \(\Vert \tilde{x}_h(t)-x_h(t)\Vert +\Vert \tilde{y}_j(t)-y_j(t)\Vert \equiv 0\) for all \(t>\tilde{t}\).

Definition 5

For any solutions \(x_1(t), x_2(t)\) and \(y_1(t), y_2(t)\) of uncertain DFOBAMNNs (3) and (5) with different initial values denoted by \(x_{10}, x_{20}\) and \(y_{10}, y_{20}\) if there exist two positive constants P and \(m_0\) such that

$$\begin{aligned} \Vert x_1(t)-x_2(t)\Vert +\Vert y_1(t)-y_2(t)\Vert \le P(\Vert x_{10}-x_{20}\Vert +\Vert y_{10}-y_{20}\Vert )E_\eta (-m_0t^\eta ), \end{aligned}$$

then uncertain DFOBAMNNs (3) and (5) can achieve Mittag-Leffler synchronization.

Define synchronization error signals \(z_h(t)\) and \(e_j(t)\), where \(z_h(t)=\tilde{x}_h(t)-x_h(t), e_j(t)=\tilde{y}_j(t)-y_j(t)\), from (3) and (5), the dynamics of synchronization errors \(z_h(t), e_j(t)\) can be expressed by

$$\left\{ \begin{aligned} _{{t_{0} }}^{c} D_{t}^{\eta } z_{h} (t) = & - a_{h} z_{h} (t) + \sum\limits_{{j = 1}}^{n} {c_{{jh}} } (f_{j} (\tilde{y}_{j} (t)) - f_{j} (y_{j} (t))) + \sum\limits_{{j = 1}}^{n} {d_{{jh}} } \\ & (f_{j} (\tilde{y}_{j} (t - \kappa )) - f_{j} (y_{j} (t - \kappa ))) + \sum\limits_{{j = 1}}^{n} {(\mathop c\limits^{} _{{jh}} - c_{{jh}} )} f_{j} (\tilde{y}_{j} (t)) \\ & + \sum\limits_{{j = 1}}^{n} {(\mathop d\limits^{} _{{jh}} - d_{{jh}} )} f_{j} (\tilde{y}_{j} (t - \kappa )) + U_{h} (t),\quad h \in {\mathcal{A}}, \\ _{{t_{0} }}^{c} D_{t}^{\eta } e_{j} (t) = & - \alpha _{j} e_{j} (t) + \sum\limits_{{h = 1}}^{m} {\beta _{{hj}} } (g_{h} (\tilde{x}_{h} (t)) - g_{h} (x_{h} (t))) + \sum\limits_{{h = 1}}^{m} {b_{{hj}} } \\ & (g_{h} (\tilde{x}_{h} (t - \kappa )) - g_{h} (x_{h} (t - \kappa ))) + \sum\limits_{{h = 1}}^{m} {(\mathop \beta \limits^{} _{{hj}} - \beta _{{hj}} )g_{h} (\tilde{x}_{h} (t))} \\ & + \sum\limits_{{h = 1}}^{m} {(\mathop b\limits^{} _{{hj}} - b_{{hj}} )} g_{h} (\tilde{x}_{h} (t - \kappa )) + U_{j} (t),\quad j \in {\mathcal{B}}. \\ \end{aligned} \right.$$
(7)

3 Main results

In this section, by taking advantage of the constructed properly Lyapunov functions and devising state feedback controllers, several sufficient criteria are derived to reach Mittag-Leffler synchronization and finite-time synchronization for uncertain DFOBAMNNs (3) and (5).

To study the synchronization behaviors and parameters identification for uncertain DFOBAMNNs (3) and (5), distinct state feedback controls are proposed to synchronize uncertain DFOBAMNNs (3) and (5) with different initial conditions. Based on diverse control strategies, some theoretical results are developed for uncertain DFOBAMNNs (3) and (5). Next, in order to realize Mittag-Leffler synchronization, we design the following state feedback control protocol

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle U_h(t)=-k_hz_h(t)-l_hz_h(t-\kappa ),\\ \displaystyle U_j(t)=-\sigma _je_j(t)-\epsilon _je_j(t-\kappa ),\\ \end{array}\right. \end{aligned}$$
(8)

where \(k_h, l_h\) and \(\sigma _j, \epsilon _j\) are the positive control gains and updated laws of the parameters \(\check{c}_{jh}, \check{d}_{jh}\) and \(\check{\beta }_{hj}, \check{b}_{hj}\) are taken as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{c}_{jh}=-\xi _{h}(\check{c}_{jh}-c_{jh}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{d}_{jh}=-\xi _{h}(\check{d}_{jh}-d_{jh}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{\beta }_{hj}=-\mu _{j}(\check{\beta }_{hj}-\beta _{hj}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{b}_{hj}=-\mu _{j}(\check{b}_{hj}-b_{hj}),\\ \end{array}\right. \end{aligned}$$
(9)

where \(\xi _{h}, \mu _{j}\) are arbitrary tunable constants.

3.1 Mittag-Leffler synchronization control

In this subsection, based on Hypotheses 1 and 2 as well as the idea that the parameters are uncertain, state feedback controller is provided to achieve Mittag-Leffler synchronization.

Theorem 1

Let Hypotheses 1 and 2 hold, then uncertain DFOBAMNNs (3) and (5) can realize Mittag-Leffler synchronization based on state feedback controller (8) and adaptive law (9), control gains \(k_{h}, l_{h}, \sigma _j, \epsilon _j\) are constants, which satisfy the following conditions:

$$\begin{aligned} {\Xi }_1= & {} \min _{h\in \mathcal {A}}\left\{a_h+k_h-\sum \limits _{j=1}^n\beta _{hj}G_h\right\}&>0, \end{aligned}$$
(10)
$$\begin{aligned} {\Xi }_2= & {} \min _{j\in \mathcal {B}}\left\{\alpha _j+\sigma _j-\sum \limits _{h=1}^mc_{jh}F_j\right\}>0, \end{aligned}$$
(11)
$$\begin{aligned}&l_h>\sum \limits _{j=1}^nb_{hj}G_h, \end{aligned}$$
(12)
$$\begin{aligned}&\epsilon _j>\sum \limits _{h=1}^md_{jh}F_j. \end{aligned}$$
(13)

Proof

Introducing the following Lyapunov function

$$\begin{aligned} V(t)=V_1(t)+V_2(t), \end{aligned}$$
(14)

where

$$ V_{1} (t) = \sum\limits_{{h = 1}}^{m} | z_{h} (t)| + \sum\limits_{{j = 1}}^{m} | e_{j} (t)|, $$
(15)
$$ V_{2} (t) = \sum\limits_{{h = 1}}^{m} {\sum\limits_{{j = 1}}^{n} {\left( {|\mathop c\limits^{} _{{jh}} - c_{{jh}} | + |\mathop d\limits^{} _{{jh}} - d_{{jh}} | + |\mathop \beta \limits^{} _{{hj}} - \beta _{{hj}} | + |\mathop b\limits^{} _{{hj}} - b_{{hj}} |} \right).} } $$
(16)

By applying Lemma 2 and Hypotheses 1 and 2, the Caputo derivative of V(t) along the trajectory of (7) with state feedback controller (8) and parameters updated laws (9) can be derived as

$$\begin{aligned} \begin{array}{ccl}\displaystyle {} _{t_{0}}^{c}D_{t}^{\eta }V(t) &{}=&{}\sum \limits _{h=1}^{m}{}_{t_0}^{c}D_{t}^{\eta }|z_{h}(t)|+\sum \limits _{j=1}^{n}{}_{t_0}^{c}D_{t}^{\eta }|e_{j}(t)| +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{}_{t_0}^{c}D_{t}^{\eta }\big (|\check{c}_{jh}-c_{jh}|\\ &{}&{}\displaystyle +|\check{d}_{jh}-d_{jh}|+|\check{\beta }_{hj}-\beta _{hj}|+|\check{b}_{hj}-b_{hj}|\big )\\ &{}\le &{}\sum \limits _{h=1}^{m}{} \mathrm {sign}(z_{h}(t)){}_{t_0}^{c}D_{t}^{\eta }z_{h}(t) +\sum \limits _{j=1}^{n}{} { \mathrm {sign}}(e_{j}(t)){}_{t_0}^{c}D_{t}^{\eta }e_{j}(t)\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{c}_{jh}-c_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{c}_{jh}-c_{jh})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{d}_{jh}-d_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{d}_{jh}-d_{jh})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{\beta }_{hj} -\beta _{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{\beta }_{hj}-\beta _{hj})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{b}_{hj}-b_{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{b}_{hj}-b_{hj})\\ \end{array}\nonumber \\ \begin{array}{ccl}\displaystyle {} \displaystyle {} &{}=&{}\sum \limits _{h=1}^{m}{} { \mathrm {sign}}(z_{h}(t))\Big [-a_hz_h(t) +\sum \limits _{j=1}^nc_{jh}\Big (f_j(\tilde{y}_j(t))-f_j(y_j(t))\Big )+\sum \limits _{j=1}^nd_{jh}\\ &{}&{}\displaystyle \Big (f_j(\tilde{y}_j(t-\kappa ))-f_j(y_j(t-\kappa ))\Big ) +\sum \limits _{j=1}^n(\check{c}_{jh}-c_{jh})f_j(\tilde{y}_j(t))\\ &{}&{}\displaystyle +\sum \limits _{j=1}^n(\check{d}_{jh}-d_{jh})f_j(\tilde{y}_j(t-\kappa ))-k_hz_h(t)-l_hz_h(t-\kappa )\Big ]\\ &{}&{}+\sum \limits _{j=1}^{n}{} { \mathrm {sign}}(e_{j}(t))\Big [-\alpha _je_j(t) +\sum \limits _{h=1}^m\beta _{hj}\Big (g_h(\tilde{x}_h(t))-g_h(x_h(t))\Big )+\sum \limits _{h=1}^mb_{hj}\\ &{}&{}\displaystyle \Big (g_h(\tilde{x}_h(t-\kappa ))-g_h(x_h(t-\kappa ))\Big ) +\sum \limits _{h=1}^m(\check{\beta }_{hj}-\beta _{hj})g_h(\tilde{x}_h(t))\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m(\check{b}_{hj}-b_{hj})g_h(\tilde{x}_h(t-\kappa ))-\sigma _je_j(t)-\epsilon _je_j(t-\kappa )\Big ]\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{c}_{jh}-c_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{c}_{jh}-c_{jh})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{d}_{jh}-d_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{d}_{jh}-d_{jh})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{\beta }_{hj} -\beta _{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{\beta }_{hj}-\beta _{hj})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{b}_{hj}-b_{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{b}_{hj}-b_{hj})\\ &{}\le &{}\displaystyle \sum \limits _{h=1}^m\Big [-a_h|z_h(t)|+\sum \limits _{j=1}^nc_{jh}F_j|e_j(t)|+\sum \limits _{j=1}^nd_{jh}F_j|e_j(t-\kappa )|\\ &{}&{}\displaystyle +\sum \limits _{j=1}^nF|\check{c}_{jh}-c_{jh}| +\sum \limits _{j=1}^nF|\check{d}_{jh}-d_{jh}|-l_h|z_h(t)|-l_h|z_h(t-\kappa )|\Big ]\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\Big [-\alpha _j|e_j(t)|+\sum \limits _{h=1}^m\beta _{hj}G_h|z_h(t)| +\sum \limits _{h=1}^mb_{hj}G_h|z_h(t-\kappa )|\\ &{}&{}\displaystyle +\sum \limits _{j=1}^nG|\check{\beta }_{hj}-\beta _{hj}| +\sum \limits _{j=1}^nG|\check{b}_{hj}-b_{hj}|-\sigma _j|e_j(t)|-\epsilon _j|e_j(t-\kappa )|\Big ]\\ &{}&{}\displaystyle -\sum \limits _{h=1}^m\sum \limits _{j=1}^n\xi _h|\check{c}_{jh}-c_{jh}| -\sum \limits _{h=1}^m\sum \limits _{j=1}^n\xi _h|\check{d}_{jh}-d_{jh}|\\ &{}&{}\displaystyle -\sum \limits _{h=1}^m\sum \limits _{j=1}^n\mu _j|\check{\beta }_{hj}-\beta _{hj}| -\sum \limits _{h=1}^m\sum \limits _{j=1}^n\mu _j|\check{b}_{hj}-b_{hj}|\\ \displaystyle {} &{}\le &{}\displaystyle \sum \limits _{h=1}^m\big (-a_h-k_h+\sum \limits _{j=1}^n\beta _{hj}G_h\big )|z_h(t)| +\sum \limits _{h=1}^m(\sum \limits _{j=1}^nb_{hj}G_h-l_h)|z_h(t-\kappa )|\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\big (-\alpha _j-\sigma _j+\sum \limits _{h=1}^mc_{jh}F_j\big )|e_jt)| +\sum \limits _{j=1}^n(\sum \limits _{h=1}^md_{jh}F_j-\epsilon _j)|e_j(t-\kappa )|\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n(F-\xi _h)|\check{c}_{jh}-c_{jh}| +\sum \limits _{h=1}^m\sum \limits _{j=1}^n(F-\xi _h)|\check{d}_{jh}-d_{jh}|\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m\sum \limits _{j=1}^n(G-\mu _j)|\check{\beta }_{jh}-\beta _{jh}| +\sum \limits _{h=1}^m\sum \limits _{j=1}^n(G-\mu _j)|\check{b}_{jh}-b_{jh}|.\\ \end{array} \end{aligned}$$
(17)

Correctly choosing \(l_h, \epsilon _j, \xi _h\) and \(\mu _j\) such that \(l_h>\sum \nolimits _{j=1}^nb_{hj}G_h\), \(\epsilon _j>\sum \nolimits _{h=1}^md_{jh}F_j\), \(\xi _h>F\), \(\mu _j>G\). Applying those to (17) yields

$$\begin{aligned} _{{t_{0} }}^{c} D_{t}^{\eta } V(t) & \le - \sum\limits_{{h = 1}}^{n} {\Xi _{1} } |z_{h} (t)| - \sum\limits_{{j = 1}}^{m} {\Xi _{2} } |e_{j} (t)| \\ & \le - \Xi V_{1} (t), \\ \end{aligned}$$
(18)

where \(\Xi = \min \{\Xi _1,\Xi _2 \}\), \({\Xi }_1=\min \limits _{h\in \mathcal {A}}\Big \{a_h+k_h- \sum\nolimits_{{j = 1}}^{n} {\beta _{{hj}} } G_{h} \Big \}>0\), \({\Xi }_2=\min \limits _{j\in \mathcal {B}}\Big \{\alpha _j+\sigma _j-\ \sum\nolimits_{{h = 1}}^{m} {c_{{jh}} } F_{j} \Big \}>0\), it can be concluded from the inequality (18) and Corollary 1 that

$$V_{1} (t) \le \left( {V_{1} (t_{0} } \right) + V_{2} (t_{0} ))E_{\eta } ( - \Xi (t - t_{0} )^{\eta } ),$$
(19)

which implies that

$$\begin{aligned} \Vert z(t)\Vert _1+\Vert e(t)\Vert _1\le (V_1(t_0)+V_2(t_0))E_{\eta }\big (-\Xi (t-t_0)^{\eta }\big ), \end{aligned}$$
(20)

where \(V_1(t_0)=\sum \nolimits _{h=1}^m|z_h(t_0)|+\sum\nolimits _{j=1}^n|e_j(t_0)|\), \(V_2(t_0)= \sum \nolimits _{h=1}^m\sum\nolimits _{j=1}^n\big (|\check{c}_{jh}-c_{jh}|+|\check{d}_{jh}-d_{jh}|+|\check{\beta }_{hj}-\beta _{hj}|+|\check{b}_{hj}-b_{hj}|\big )\). Thus, uncertain DFOBAMNNs (3) and (5) can realize Mittag-Leffler synchronization and the unknown parameters \(c_{jh}, d_{jh}\) and \(\beta _{hj}, b_{hj}\) can be triumphantly identified by \(\check{c}_{jh}, \check{d}_{jh}\) and \(\check{\beta }_{hj}, \check{b}_{hj}\) based on the controller (8) and adaptive law (9), the proof is completed.

3.2 Finite-time synchronization control

In the following subsection, it is the aim to derive some sufficient criteria studying finite-time synchronization problem for uncertain DFOBAMNNs (3) and (5) via proposed delayed state feedback control. In order to achieve the finite-time synchronization, the delayed state feedback controller is described by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle U_h(t)=-p_hz_h(t)-\sum \limits _{j=1}^nd_{jh}F_j|e_j(t-\kappa )|-\lambda _h{ \mathrm {sign}}(z_h(t)),\\ \displaystyle U_j(t)=-q_je_j(t)-\sum \limits _{h=1}^mb_{hj}G_h|z_h(t-\kappa )|-\omega _j{ \mathrm {sign}}(e_j(t)),\\ \end{array}\right. \end{aligned}$$
(21)

where \(p_h,q_j\) are the control gains, \(\lambda _h, \omega _j\) depict the tunable positive constants. The parameters are adapted according to the following rules:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{c}_{jh}=-\sum \limits _{j=1}^n|f_j(\tilde{y}_j(t))|(\check{c}_{jh}-c_{jh}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{d}_{jh}=-\sum \limits _{j=1}^n|f_j(\tilde{y}_j(t-\kappa ))|(\check{d}_{jh}-d_{jh}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{\beta }_{hj}=-\sum \limits _{h=1}^m|g_h(\tilde{x}_h(t))|(\check{\beta }_{hj}-\beta _{hj}),\\ \displaystyle _{t_{0}}^{c}D_{t}^{\eta }\check{b}_{hj}=-\sum \limits _{h=1}^m|g_h(\tilde{x}_h(t-\kappa ))|(\check{b}_{hj}-b_{hj}).\\ \end{array}\right. \end{aligned}$$
(22)

Remark 2

On the one hand, it is worth mentioning that the third terms about symbolic function the above controller (21) are based on the finite-time control protocol, that is to say, by adding the third terms to the control law (21), we can reach finite-time synchronization. Otherwise, the synchronization time is infinite, which is commonly called asymptotic synchronization. On the other hand, it should be noticed that the global Mittag-Leffler synchronization suggests the global asymptotical synchronization.

Theorem 2

Under Hypothesis 1, uncertain DFOBAMNNs (3) can reach finite-timely synchronized onto (5) under the control law (21) and the adaptive law (22) if the control parameters satisfy

$$\begin{aligned} H_1=\min \limits _{h\in \mathcal {A}}\Big (a_h+p_h-\sum \limits _{j=1}^n|\beta _{hj}|G_h\Big )>0, \end{aligned}$$
(23)

and

$$\begin{aligned} H_2=\min \limits _{j\in \mathcal {B}}\Big (\alpha _j+q_j-\sum \limits _{h=1}^m|c_{jh}|F_j\Big )>0. \end{aligned}$$
(24)

In addition, the settling time \(\tilde{t}\) of finite-time synchronization is given by

$$\begin{aligned} \tilde{t}=t_0+\Big (\frac{\Gamma ({\eta +1})V(t_0)}{\lambda +\omega }\Big )^{\frac{1}{\eta }}, \end{aligned}$$
(25)

where \(\lambda =\min \limits _{i\in \mathcal {A}}{\lambda _h}\), \(\omega =\min \limits _{j\in \mathcal {B}}{\omega _j}\).

Proof

We construct the following function

$$\begin{aligned} W(t)=W_1(t)+W_2(t), \end{aligned}$$
(26)

where

$$\begin{aligned}&\begin{array}{ccl} \displaystyle W_1(t) &=&\sum \limits _{h=1}^m(|z_h(t)|+|\check{c}_{jh}-c_{jh}|+|\check{d}_{jh}-d_{jh}|),\\ \end{array} \end{aligned}$$
(27)
$$\begin{aligned}&\begin{array}{ccl} \displaystyle W_2(t) &=&\sum \limits _{j=1}^n(|e_j(t)|+|\check{\beta }_{hj}-\beta _{hj}|+|\check{b}_{hj}-b_{hj}|).\\ \end{array} \end{aligned}$$
(28)

According to the Lemma 2 and Hypothesis 1, the Caputo derivative of W(t) along the trajectory of (7) with state feedback controller (21) and parameters updated laws (22) can be evaluated

$$\begin{aligned} \begin{array}{ccl}\displaystyle {} _{t_{0}}^{c}D_{t}^{\eta }W(t) &{}=&{}\sum \limits _{h=1}^{m}{}_{t_0}^{c}D_{t}^{\eta }|z_{h}(t)| +\sum \limits _{h=1}^{m}{}_{t_0}^{c}D_{t}^{\eta }|\check{c}_{jh}-c_{jh}| +\sum \limits _{h=1}^{m}{}_{t_0}^{c}D_{t}^{\eta }|\check{d}_{jh}-d_{jh}|\\ &{}&{}\displaystyle +\sum \limits _{j=1}^{n}{}_{t_0}^{c}D_{t}^{\eta }|e_{j}(t)| +\sum \limits _{j=1}^{n}{}_{t_0}^{c}D_{t}^{\eta }|\check{\beta }_{hj}-\beta _{hj}| +\sum \limits _{j=1}^{n}{}_{t_0}^{c}D_{t}^{\eta }|\check{b}_{hj}-b_{hj}|\\ &{}\le &{}\sum \limits _{h=1}^{m}{} { \mathrm {sign}}(z_{h}(t)){}_{t_0}^{c}D_{t}^{\eta }z_{h}(t) +\sum \limits _{h=1}^{m}{} { \mathrm {sign}}(\check{c}_{jh}-c_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{c}_{jh}-c_{jh})\\ &{}&{}\displaystyle +\sum \limits _{h=1}^{m}{} { \mathrm {sign}}(\check{d}_{jh}-d_{jh}){}_{t_0}^{c}D_{t}^{\eta }(\check{d}_{jh}-d_{jh})\\ &{}&{}\displaystyle +\sum \limits _{j=1}^{n}{} { \mathrm {sign}}(e_{j}(t)){}_{t_0}^{c}D_{t}^{\eta }e_{j}(t) +\sum \limits _{j=1}^{n}{} { \mathrm {sign}}(\check{\beta }_{hj}-\beta _{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{\beta }_{hj}-\beta _{hj})\\ &{}&{}\displaystyle +\sum \limits _{j=1}^{n}{} { \mathrm {sign}}(\check{b}_{hj}-b_{hj}){}_{t_0}^{c}D_{t}^{\eta }(\check{b}_{hj}-b_{hj})\\ &=&\sum \limits _{h=1}^m{ \mathrm {sign}}(z_{h}(t))\big [-a_hz_h(t) +\sum \limits _{j=1}^nc_{jh}\big (f_j(\tilde{y}_j(t))-f_j(y_j(t))\big )\\ &{}&{}\displaystyle +\sum \limits _{j=1}^nd_{jh}\big (f_j(\tilde{y}_j(t-\kappa ))-f_j(y_j(t-\kappa ))\big ) +\sum \limits _{j=1}^n(\check{c}_{jh}-c_{jh})f_j(\tilde{y}_j(t))\\ &{}&{}\displaystyle +\sum \limits _{j=1}^n(\check{d}_{jh}-d_{jh})f_j(\tilde{y}_j(t-\kappa ))-p_hz_h(t) -\sum \limits _{j=1}^nd_{jh}F_j|e_{j}(t-\kappa )|\\ &{}&{}\displaystyle -\lambda _h{ \mathrm {sign}}(z_h(t))\big ]-\sum \limits _{h=1}^{m}\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{c}_{jh} -c_{jh})|f_j(\tilde{y}_j(t))|(\check{c}_{jh}-c_{jh})\\ &{}&{}\displaystyle -\sum \limits _{h=1}^m\sum \limits _{j=1}^n{ \mathrm {sign}}(\check{d}_{jh}-d_{jh})f_j(\tilde{y}_j(t-\kappa ))|\check{d}_{jh}-d_{jh}|\\ &{}&{}\displaystyle +\sum \limits _{j=1}^n{ \mathrm {sign}}(e_{j}(t))\big [-\alpha _je_j(t) +\sum \limits _{h=1}^m\beta _{hj}\big (g_h(\tilde{x}_h(t))-g_h(x_h(t))\big )\\ &{}&{}\displaystyle +\sum \limits _{h=1}^mb_{hj}\big (g_h(\tilde{x}_h(t-\kappa ))-g_h(x_h(t-\kappa ))\big ) +\sum \limits _{h=1}^m(\check{\beta }_{hj}-\beta _{hj})g_h(\tilde{x}_h(t))\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m(\check{b}_{hj}-b_{hj})g_h(\tilde{x}_h(t-\kappa ))-q_j e_j(t)-\sum \limits _{h=1}^mb_{hj}G_h|z_{h}(t-\kappa )|\\ &{}&{}-\omega _j{ \mathrm {sign}}(e_j(t))\big ]\displaystyle -\sum \limits _{j=1}^{n}\sum \limits _{h=1}^m{ \mathrm {sign}}(\check{\beta }_{hj} -\beta _{hj})|g_h(\tilde{x}_h(t))|(\check{\beta }_{hj}-\beta _{hj})\\ &{}&{}\displaystyle -\sum \limits _{j=1}^n\sum \limits _{h=1}^m{ \mathrm {sign}}(\check{b}_{hj}-b_{hj})|g_h(\tilde{x}_h(t-\kappa ))|\check{b}_{hj}-b_{hj}|\\ &{}\le &{}\displaystyle \sum \limits _{h=1}^m\big [-a_h|z_h(t)|+\sum \limits _{j=1}^n|c_{jh}||f_j(\tilde{y}_j(t))-f_j(y_j(t))|+ \sum \limits _{j=1}^n|d_{jh}|\\ &{}&{}\displaystyle |f_j(\tilde{y}_j(t-\kappa ))-f_j(y_j(t-\kappa ))|+\sum \limits _{j=1}^n|\check{c}_{jh}-c_{jh}||f_j(\tilde{y}_j(t))|\\ \displaystyle {} \end{array}\nonumber \\ \begin{array}{ccl} &{}&{}\displaystyle +\sum \limits _{j=1}^n|\check{d}_{jh}-d_{jh}||f_j(\tilde{y}_j(t-\kappa ))|-p_h|z_h(t)| -\sum \limits _{j=1}^n|d_{jh}|F_j|e_j(t-\kappa )|\\ &{}&{}\displaystyle -\lambda _h\big ]-\sum \limits _{h=1}^m\sum \limits _{j=1}^n|f_j(\tilde{y}_j(t))||\check{c}_{jh}-c_{jh}| -\sum \limits _{h=1}^m\sum \limits _{j=1}^n|f_j(\tilde{y}_j(t-\kappa ))||\check{d}_{jh}-d_{jh}|\\ &{}&{}\displaystyle +\sum \limits _{j=1}^n\big [-\alpha _j|e_j(t)|+\sum \limits _{h=1}^m|\beta _{hj}||g_h(\tilde{x}_h(t))-g_h(x_h(t))|+ \sum \limits _{h=1}^m|b_{hj}|\\ &{}&{}\displaystyle |g_h(\tilde{x}_h(t-\kappa ))-g_h(x_h(t-\kappa ))|+\sum \limits _{h=1}^m|\check{\beta }_{hj}-\beta _{hj}||g_h(\tilde{x}_h(t))|\\ &{}&{}\displaystyle +\sum \limits _{h=1}^m|\check{b}_{hj}-b_{hj}||g_h(\tilde{x}_h(t-\kappa ))|-q_j|e_j(t)| -\sum \limits _{h=1}^m|b_{hj}|G_h|z_h(t-\kappa )|\\ &{}&{}\displaystyle -\omega _j\big ]-\sum \limits _{h=1}^m\sum \limits _{j=1}^n|g_h(\tilde{x}_h(t))||\check{\beta }_{hj}-\beta _{hj}| -\sum \limits _{h=1}^m\sum \limits _{j=1}^n|g_h(\tilde{x}_h(t-\kappa ))||\check{b}_{hj}-b_{hj}|\\ &{}\le &{}\displaystyle \sum \limits _{h=1}^m\big (-a_h|z_h(t)|+\sum \limits _{j=1}^n|c_{jh}|F_j|e_j(t)| +\sum \limits _{j=1}^n|d_{jh}|F_j|e_j(t-\kappa )|\\ &{}&{}\displaystyle -p_h|z_h(t)|-\sum \limits _{j=1}^n|d_{jh}|F_j|e_j(t-\kappa )|-\lambda _h\big )\\ &{}&{}\displaystyle +\sum \limits _{j=1}^n\big (-\alpha _j|e_j(t)|+\sum \limits _{h=1}^m|\beta _{hj}|G_h|z_h(t)| +\sum \limits _{h=1}^m|b_{hj}|G_h|z_h(t-\kappa )|\\ &{}&{}\displaystyle -q_j|e_j(t)|-\sum \limits _{h=1}^m|b_{hj}|G_h|z_h(t-\kappa )|-\omega _j\big )\\ &=&\sum \limits _{h=1}^m-(a_h+p_h-\sum \limits _{j=1}^n|\beta _{hj}|G_h)|z_h(t)|-\sum \limits _{h=1}^m\lambda _h\\ &{}&{}\displaystyle -\sum \limits _{j=1}^n(\alpha _j+q_j-\sum \limits _{h=1}^m|c_{jh}|F_j)|e_j(t)|-\sum \limits _{j=1}^n\omega _j.\\ \end{array} \end{aligned}$$
(29)

We choose \(H_1=\min \limits _{h\in \mathcal {A}}\Big (a_h+p_h- \left( {a_{h} + p_{h} - \sum\nolimits_{{j = 1}}^{n} {|\beta _{{hj}} |G_{h} } } \right) \Big ) { > } 0\), \(H_2=\min \limits _{j\in \mathcal {B}}\Big (\alpha _j+q_j- \sum\nolimits_{{h = 1}}^{m} {|c_{{jh}} |F_{j} } \Big ){ > }0\) leading to

$$\begin{aligned} _{{t_{0} }}^{c} D_{t}^{\eta } W(t) & = - \sum\nolimits_{{h = 1}}^{m} {\lambda _{h} } - \sum\nolimits_{{j = 1}}^{n} {\omega _{j} } \\ & \le - (\lambda + \omega ), \\ \end{aligned}$$
(30)

where \(\lambda =\min \limits _{i\in \mathcal {A}}{\lambda _h}\), \(\omega =\min \limits _{j\in \mathcal {B}}{\omega _j}\). For (30), there exists a nonnegative function \(\daleth (t)\) satisfying

$$\begin{aligned} _{t_0}^cD_{t}^{\eta }W(t)+\daleth (t)=-(\lambda +\omega ), \end{aligned}$$
(31)

it follows from Definition 1 and (31) that

$$\begin{aligned} W(t) & = W(t_{0} )-_{t_0}D_{t}^{-\eta }\daleth (t)-_{t_0}D_{t}^{-\eta }(\lambda +\omega )\\ & = W(t_{0} ) - \frac{1}{\Gamma ({\eta })}\int _{t_0}^{t}(t-{\rho })^{{\eta }-1}\daleth ({\rho })\mathrm{d}{\rho }-\frac{\lambda +\omega }{\Gamma ({\eta })}\int _{t_0}^{t}(t-{\rho })^{{\eta }-1}\mathrm{d}{\rho }. \\\end{aligned}$$
(32)

Using \({\Gamma ({\eta })}>0\), \((t-{\rho })^{{\eta }-1}\daleth ({\rho })>0\), for any \(\rho \in (t_0,t)\), lead to \(_{t_0}D_{t}^{-\eta }\daleth (t)\ge 0\), then

$$ \begin{aligned} W(t) & \le W(t_{0} ) - _{{t_{0} }} D_{t}^{{ - \eta }} (\lambda + \omega ) \\ & = W(t_{0} ) - \frac{{(\lambda + \omega )(t - t_{0} )^{\eta } }}{{\Gamma (\eta + 1)}}. \\ \end{aligned} $$
(33)

Denote \(S(t)=W(t_0)-\frac{(\lambda +\omega )(t-t_0)^\eta }{\Gamma ({\eta +1})}\), it is the fact that S(t) is the strictly increasing function, thus \(S(t)=0\) if and only if

$$\begin{aligned} \tilde{t}=t_0+\big (\frac{\Gamma ({\eta +1})W(t_0)}{(\lambda +\omega )}\big )^{\frac{1}{\eta }}. \end{aligned}$$
(34)

\(S(t)\le 0\) for any \(t\ge \tilde{t}\), thus \(W(t)\le S(t)\le 0\) for any \(t\ge \tilde{t}\), and W(t) is a nonnegative function, thus \(W(t)\equiv 0\) for any \(t\ge \tilde{t}\). Therefore, \(\sum\nolimits_{{h = 1}}^{n} {z(t)| + } \sum\nolimits_{{j = 1}}^{m} | e(t)| \equiv 0\) for \(t\ge \tilde{t}\), through Definition 5, uncertain DFOBAMNNs (3) and (5) can achieve synchronization in a finite time under delayed state feedback controller (21) and adaptive rule (22).

Remark 3

The theoretical results obtained in Theorems 1 and 2 show that the controllers (8) and (21) can solve Mittag-Leffler synchronization and finite-time synchronization as well as parameters identification problems with the help of adapted laws (9) and (22), respectively, if the parameters meet conditions (10)–(13), (23)–(24). In other words, our main purposes can also be achieved despite the system synaptic connection parameters \(c_{jh}, d_{jh}\) and \(\beta _{hj}, b_{hj}\) cannot be known in advance.

Expressly, if \(\lambda _h=0, \omega _j=0\) in state feedback controller (21), then controller (21) is degenerated into the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle U_h(t)=-p_hz_h(t)-\sum \limits _{j=1}^nd_{jh}F_j|e_j(t-\kappa )|,\\ \displaystyle U_j(t)=-q_je_j(t)-\sum \limits _{h=1}^mb_{hj}G_h|z_h(t-\kappa )|.\\ \end{array}\right. \end{aligned}$$
(35)

For the case, we can further get the following corollary.

Corollary 2

Under hypothesis 1, uncertain DFOBAMNNs (3) can reach asymptotically synchronized onto (5) under the control law (35) and the adaptive law (22) if the control parameters satisfy

$$\begin{aligned} H_1=\min \limits _{h\in \mathcal {A}}\Big (a_h+p_h-\sum \limits _{j=1}^n|\beta _{hj}|G_h\Big )>0, \end{aligned}$$
(36)

and

$$\begin{aligned} H_2=\min \limits _{j\in \mathcal {B}}\Big (\alpha _j+q_j-\sum \limits _{h=1}^m|c_{jh}|F_j\Big )>0. \end{aligned}$$
(37)

Proof

Considering the following Lyapunov function

$$\begin{aligned} W(t)=W_1(t)+W_2(t), \end{aligned}$$
(38)

where

$$W_{1} (t) = \sum\limits_{{h = 1}}^{m} {(|z_{h} (} t) \check{c}_{jh}-c_{jh}|+|\check{d}_{jh}-d_{jh}|),$$
(39)
$$W_{2} (t) = \sum\limits_{{j = 1}}^{n} {(|e_{j} (} t)| + \check{\beta }_{hj}-\beta _{hj}|+|\check{b}_{hj}-b_{hj}|),$$
(40)

the rest testify is similar to Theorem 2, here is omitted.

Remark 4

It is the fact that the integer calculus is a special case of the fractional calculus, and the exponential function can be regarded as the form of the integer order of the Mittag-Leffler function. Thus, when \(\eta =1\), the theoretical results of this paper also hold, then the synchronization and parameters identification for uncertain DFOBAMNNs are discussed in the framework of integer order. It is worth emphasizing that time delay term is added to the controller adopted in this paper, which makes our theoretical results get very smoothly. If otherwise, it is impossible. This suggests that time delay plays an important role in studying dynamics behavior for uncertain DFOBAMNNs.

Remark 5

For the sake of identifying the uncertain parameters, the conditions in the Theorems 1 and 2 must be met. When synchronization is implemented, i.e., \(\tilde{x}_h(t)-x_h(t)=z_h(t)\rightarrow 0\) and \(\tilde{y}_j(t)-y_j(t)=e_j(t)\rightarrow 0\), as \(t\rightarrow \infty\), the dynamics of error system (7) can be briefed in the following form:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {}_{t_0}^{c}D_{t}^{\eta }z_h(t)= \sum \limits _{j=1}^n(\check{c}_{jh}-c_{jh})f_j(\tilde{y}_j(t)) +\sum \limits _{j=1}^n(\check{d}_{jh}-d_{jh})f_j(\tilde{y}_j(t-\kappa )), \quad i\in \mathcal {A},\\ \displaystyle {}_{t_0}^{c}D_{t}^{\eta }e_j(t)= \sum \limits _{h=1}^m(\check{\beta }_{hj}-\beta _{hj})g_h(\tilde{x}_h(t)) +\sum \limits _{h=1}^m(\check{b}_{hj}-b_{hj})g_h(\tilde{x}_h(t-\kappa )), \quad i\in \mathcal {B}.\\ \end{array}\right. \end{aligned}$$
(41)

Based on the linearly independence in the Advanced Algebra, accurate identification of the unknown parameters \(\check{c}_{jh}, \check{d}_{jh}\) and \(\check{\beta }_{hj}, \check{b}_{hj}\), which is equivalent to the function elements \({f_j(\tilde{y}_j(t)), f_j(\tilde{y}_j(t-\kappa ))}\) and \({g_h(\tilde{x}_h(t)), g_h(\tilde{x}_h(t-\kappa ))},\) is linearly independent, respectively.

Remark 6

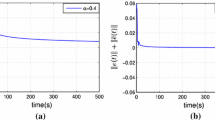
On the whole, the conclusion we can get from Fig. 9 is that the convergence rate of \(\Vert e(t)\Vert +\Vert z(t)\Vert\) reduces as the order \(\eta\) enlarges.

4 Numerical simulation

In this section, two examples are presented to demonstrate our Theorems 1, 2, respectively.

Example 1

Consider two-dimensional uncertain DFOBAMNN as follows:

$$\left\{ \begin{aligned} _{0}^{c} D_{t}^{\eta } x_{h} (t) = & - a_{h} x_{h} (t) + \sum\limits_{{j = 1}}^{2} {c_{{jh}} } f_{j} (y_{j} (t)) + \sum\limits_{{j = 1}}^{2} {d_{{jh}} } f_{j} (y_{j} (t - \kappa )) \\ & + \Theta _{h} (t),\quad h = 1,2, \\ _{0}^{c} D_{t}^{\eta } y_{j} (t) & = - \alpha _{j} y_{j} (t) + \sum\limits_{{h = 1}}^{2} {\beta _{{hj}} } g_{h} (x_{h} (t)) + \sum\limits_{{h = 1}}^{2} {b_{{hj}} } g_{h} (x_{h} (t - \kappa )) \\ & + \Theta _{j} (t),\quad j = 1,2, \\ \end{aligned} \right.$$
(42)

where \(\eta =0.98\), functions \(f(s)=g(s)=\tan h(s)\), intercalating the parameters as \(a_1 = a_2=0.5, \alpha _1 = \alpha _2=0.5, x=(x_1, x_2)^T, y=(y_1, y_2)^T, \Theta =(0,0)^T, G=G_h=F_j=F=1, \kappa =0.2\), the initial values are taken as \(x(s)=[3,2]^T\) and \(y(s)=[2,4]^T\) for all \(s\in [-0.2, 0]\). The connective weights are defined as

$$\begin{array}{*{20}c} \begin{gathered} {\mathbf{C}} = \left( {\begin{array}{*{20}c} {3\quad } & {0.3} \\ {1.3\quad } & {1.2} \\ \end{array} } \right),{\mathbf{D}} = \left( {\begin{array}{*{20}c} {4.3\quad } & {1.3} \\ { - 1.2\quad } & {2.2} \\ \end{array} } \right), \hfill \\ \beta = \left( {\begin{array}{*{20}c} {2.5\quad } & {0.1} \\ { - 0.3\quad } & {7.3} \\ \end{array} } \right),{\mathbf{B}} = \left( {\begin{array}{*{20}c} {5\quad } & {0.3} \\ {1.3\quad } & {1.6} \\ \end{array} } \right). \hfill \\ \end{gathered} \\ \end{array}$$

Figs. 1 and 2 exhibit the time evolution of the state trajectories of uncertain DFOBAMNN (42).

Fig. 1
figure 1

Time responses of \(x_1(t)\) and \(x_2(t)\) with \(\omega\)=0.98

Full size image
Fig. 2
figure 2

Time responses of \(y_1(t)\) and \(y_2(t)\) with \(\omega\)=0.98

Full size image

The corresponding response system is denoted by

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle _{0}^{c}D_{t}^{\eta }\tilde{x}_h(t)=&{}-a_h\tilde{x}_h(t)+\sum \limits _{j=1}^2\check{c}_{jh}f_j(\tilde{y}_j(t))+\sum \limits _{j=1}^2\check{d}_{jh}f_j(\tilde{y}_j(t-\kappa ))+\Theta _h(t)\\ &{}+U_h(t),\quad h=1,2,\\ \displaystyle _{0}^{c}D_{t}^{\eta }\tilde{y}_j(t)=&{}-\alpha _j\tilde{y}_j(t)+\sum \limits _{h=1}^2\check{\beta }_{hj}g_h(\tilde{x}_h(t))+\sum \limits _{h=1}^2\check{b}_{hj}g_h(\tilde{x}_h(t-\kappa ))+\Theta _j(t)\\ &{}+U_j(t), \quad j=1,2, \\ \end{array}\right. \end{aligned}$$
(43)

with

$$\begin{aligned} \begin{array}{cccc} {\textbf {C}}=\left( {\begin{array}{ll} \check{c}_{11}\quad &{}0.3\\ 1.3\quad &{}\check{c}_{22}\\ \end{array}}\right) , {\textbf {D}}=\left( {\begin{array}{ll} \check{d}_{11}\quad &{}1.3\\ -1.2&{}\quad \check{d}_{22}\\ \end{array}}\right) , {{\beta }}=\left( {\begin{array}{ll} \check{\beta }_{11}\quad &{}0.1\\ -0.3\quad &{} \check{\beta }_{22}\\ \end{array}}\right) , {\textbf {B}}=\left( {\begin{array}{ll} \check{b}_{11}\quad &{}0.3\\ 1.3\quad &{}\check{b}_{22}\\ \end{array}}\right) . \end{array} \end{aligned}$$

where \(\check{c}_{jh}, \check{d}_{jh}, \check{\beta }_{hj}\) and \(\check{b}_{hj}\) are the estimations of parameters \(c_{jh}, d_{jh}, \beta _{hj}, b_{hj}\), respectively.

In the following, the control strategies (8)–(9) can be applied to identify the uncertain parameters, we choose \(\xi _1=\xi _2=5, \mu _1=\mu _1=5\), \(k_h=\sigma _j=1.6\), \(l_h=\epsilon _j=8\) for \(h,j=1,2\). For convenience, we presume only the eight parameters\(c_{11}=3, c_{22}=1.2, d_{11}=4.3, d_{22}=2.2, \beta _{11}=2.5, \beta _{22}=7.3, b_{11}=5, b_{22}=1.6\) will be identified, we take the initial conditions as \([\check{c}_{11}(0), \check{c}_{22}(0), \check{d}_{11}(0), \check{d}_{22}(0)]^T=[1,1,1.2,1.2]\), \([\check{\beta }_{11}(0), \check{\beta }_{22}(0), \check{b}_{11}(0), \check{b}_{22}(0)]^T=[0.8,0.8,0.8,0.8]\). By calculation, the conditions of Theorem 1 are satisfied. Fig. 3 depicts that the synchronization errors converge to zero. Fig. 4 displays the identification trajectory of unknown parameters, which all the unknown parameters can be triumphantly identified, the evaluation of unknown parameters can converge to certain constants. Figs. 1, 2, 3 and 4 prove our theoretical result of Theorem 1.

Fig. 3
figure 3

Time responses of synchronization errors \(e_1\), \(e_2\) and \(z_1\), \(z_2\) under controller (8)

Full size image
Fig. 4
figure 4

Identification for unknown parameters \(\check{c}_{jh}\), \(\check{d}_{jh}\), \(\check{\beta }_{hj}\) and \(\check{b}_{hj}\) under controller (8)

Full size image

Example 2

The two-dimensional uncertain DFOBAMNN is described by

$$\left\{ \begin{aligned} _{0}^{c} D_{t}^{\eta } x_{h} (t) = & - a_{h} x_{h} (t) + \sum\limits_{{j = 1}}^{2} {c_{{jh}} } f_{j} (y_{j} (t)) + \sum\limits_{{j = 1}}^{2} {d_{{jh}} } f_{j} (y_{j} (t - \kappa )) \\ & + \Theta _{h} (t),\quad h = 1,2, \\ _{0}^{c} D_{t}^{\eta } y_{j} (t) = & - \alpha _{j} y_{j} (t) + \sum\limits_{{h = 1}}^{2} {\beta _{{hj}} } g_{h} (x_{h} (t)) + \sum\limits_{{h = 1}}^{2} {b_{{hj}} } g_{h} (x_{h} (t - \kappa )) \\ & + \Theta _{j} (t),\quad j = 1,2, \\ \end{aligned} \right.$$
(44)

where \(\eta =0.97\), functions \(f(s)=g(s)=\tan h(s)\), we take the parameters as \(a_1 = a_2=1, \alpha _1 = \alpha _2=2, x=(x_1, x_2)^T, y=(y_1, y_2)^T, \Theta =(0,0)^T, G=G_h=F_j=F=1, \kappa =0.2\), the initial values are selected as \(x(s)=[-0.2,-0.3]^T\) and \(y(s)=[-0.1,-0.4]^T\) for all \(s\in [-0.2, 0]\). The connective weights are presented by

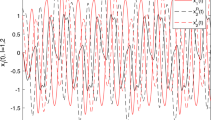
$$\begin{aligned} \begin{array}{cccc} {\textbf {C}}=\left( {\begin{matrix} 2.8\quad &{}1.3\\ 1.3\quad &{}4\\ \end{matrix}}\right) , {\textbf {D}}=\left( {\begin{matrix} 4.6\quad &{}1.3\\ -1.2\quad &{}3.9\\ \end{matrix}}\right) , {{\beta }}=\left( {\begin{matrix} 3\quad &{}1.5\\ -1.3\quad &{} 1\\ \end{matrix}}\right) , {\textbf {B}}=\left( {\begin{matrix} 1.5\quad &{}2.3\\ 1.3\quad &{}2.3\\ \end{matrix}}\right) . \end{array} \end{aligned}$$

Figs. 5 and 6 display the time evolution of the state trajectories of uncertain DFOBAMNN (44).

Fig. 5
figure 5

Time responses of \(x_1(t)\) and \(x_2(t)\) with \(\omega\)=0.97

Full size image
Fig. 6
figure 6

Time responses of \(y_1(t)\) and \(y_2(t)\) with \(\omega\)=0.97

Full size image

In order to substantiate the validity of Theorem 2, we suppose that parameters \(c_{jh}, d_{jh}, \beta _{hj}, b_{hj}\) are unknown, then the corresponding controlled system is denoted by

$$ \left\{ \begin{aligned} _{0}^{c} D_{t}^{\eta } \tilde{x}_{h} (t) = & - a_{h} \tilde{x}_{h} (t) + \sum\limits_{{j = 1}}^{2} {\mathop c\limits^{} _{{jh}} } f_{j} (\tilde{y}_{j} (t)) + \sum\limits_{{j = 1}}^{2} {\mathop d\limits^{} _{{jh}} } f_{j} (\tilde{y}_{j} (t - \kappa )) + \Theta _{h} (t) \\ & + U_{h} (t),\quad h = 1,2, \\ _{0}^{c} D_{t}^{\eta } \tilde{y}_{j} (t) = & - \alpha _{j} \tilde{y}_{j} (t) + \sum\limits_{{h = 1}}^{2} {\mathop \beta \limits^{} _{{hj}} } g_{h} (\tilde{x}_{h} (t)) + \sum\limits_{{h = 1}}^{2} {\mathop b\limits^{} _{{hj}} } g_{h} (\tilde{x}_{h} (t - \kappa )) + \Theta _{j} (t) \\ & + U_{j} (t),\quad j = 1,2, \\ \end{aligned} \right. $$
(45)

with

$${{\mathbf{C}} = \left( {\begin{array}{*{20}c} {\mathop c\limits^{} _{{11}} } & {1.3} \\ {1.3} & {\mathop c\limits^{} _{{22}} } \\ \end{array} } \right),{\mathbf{D}} = \left( {\begin{array}{*{20}c} {\mathop d\limits^{} _{{11}} } & {1.3} \\ { - 1.2} & {\mathop d\limits^{} _{{22}} } \\ \end{array} } \right),\beta = \left( {\begin{array}{*{20}c} {\mathop \beta \limits^{} _{{11}} } & {1.5} \\ { - 1.3} & {\mathop \beta \limits^{} _{{22}} } \\ \end{array} } \right),{\mathbf{B}} = \left( {\begin{array}{*{20}c} {\mathop b\limits^{} _{{11}} } & {2.3} \\ {1.3} & {\mathop b\limits^{} _{{22}} } \\ \end{array} } \right).}$$

where \(\check{c}_{jh}, \check{d}_{jh}, \check{\beta }_{hj}\) and \(\check{b}_{hj}\) are the estimations of parameters \(c_{jh}, d_{jh}, \beta _{hj}, b_{hj}\), respectively.

In addition, the controller (21) is taken as \(p_h=q_j=5\), \(\lambda _h=\omega _j=0.5\) for \(h,j=1,2\). For simplicity, we presume only the eight parameters \(c_{11}=2.8, c_{22}=4, d_{11}=4.6, d_{22}=3.9, \beta _{11}=3, \beta _{22}=1, b_{11}=1.5, b_{22}=2.3\) need to be identified, we choose the initial conditions as \([\check{c}_{11}(0), \check{c}_{22}(0), \check{d}_{11}(0), \check{d}_{22}(0)]^T=[1.2,1.2,1.4,1.4]\),\([\check{\beta }_{11}(0), \check{\beta }_{22}(0), \check{b}_{11}(0), \check{b}_{22}(0)]^T=[0.6,0.6,0.8,0.8]\) Fig. 7 exhibits that the synchronization errors converge to zero in a finite time, thus, we can conclude that the uncertain DFOBAMNNs (44) and (45) can be synchronized in finite time through state feedback control (21) and parameter updated law (22). From Fig. 8, it can be clearly seen that all the unknown system parameters \(\check{c}_{jh}, \check{d}_{jh}, \check{\beta }_{hj}\) and \(\check{b}_{hj}\) are successfully identified, respectively. From Figs. 5, 6, 7 and 8, we can conclude the validity of the result of Theorem 2 via designing method.

Fig. 7
figure 7

Time responses of synchronization errors \(e_1\), \(e_2\) and \(z_1\), \(z_2\) under controller (21)

Full size image
Fig. 8
figure 8

Identification for unknown parameters \(\check{c}_{jh}\), \(\check{d}_{jh}\), \(\check{\beta }_{hj}\) and \(\check{b}_{hj}\) under controller (21)

Full size image
Fig. 9
figure 9

The evolutions of \(\Vert e(t)\Vert +\Vert z(t)\Vert\) with \(\eta = 0.98,\eta = 0.68,\eta = 0.38\)

Full size image

5 Conclusion

In this paper, the synchronization for uncertain DFOBAMNNs has been discussed and the unknown parameters have been identified triumphantly. By applying Lyapunov function and inequality technique, some sufficient conditions on uncertain DFOBAMNNs are derived to ensure the finite-time synchronization and the Mittag-Leffler synchronization as well as parameters identification. Moreover, the settling time of the finite-time synchronization is estimated. Our results improve existing results about the synchronization in FO Lyapunov framework as special cases without considering unknown parameters. In addition, the measures in this paper can also be extended to investigate the synchronization for other NNs with parameters uncertainties and time delays. Finally, the feasibilities of the theoretical results are showed by proposing numerical examples. How to apply the results in practices, such as the associative memory, machine learning and so on, synchronization problem for memristor-based NNs with parameters uncertainties and time delays, will be our future research topics.