1 Introduction

Fractional-order calculus, that is, the theory of derivatives and integrals of non-integer order, is firstly considered by Leibniz in 1695 [1]. Then it is applied and theoretical studied by Abel, Liouville, and other mathematicians since the first half of the nineteenth century. Unlike the classical integer derivative operator, fractional derivative operator is non-local in nature, which means that the future state relies on the present state as well as all the history of its previous states. From this point of view, fractional-order models can provide a powerful tool to delicately depict the memory and hereditary properties of various materials and processes and are thus receiving extensive applications in a variety of field such as medical imaging, electronic circuit, system control, economics, biology and so on [2,3,4,5,6]. In [7], Arena et al. firstly introduce fractional-order derivatives into a cellular neural networks. Subsequently the fractional-order neural networks were proposed and designed for more precisely modelling the real world owing to its high effective information processing and the independent transformation of the oscillation frequency of neurons [8]. Recently, some important and interesting results on fractional-order neural networks have been obtained and various issues have been investigated by many authors, such as the chaotic behavior [9], stability [10], bifurcations [11, 12] and limit cycles  [13] for fractional-order neural networks.

Due to the development and further application of neural networks, the complex-valued neural networks (CVNNs), namely the input/output signals, connection weights, and activation functions are all taken from the complex field, come into being and have attracted much interest among researchers and practitioners [14,15,16]. CVNNs have advantaged superiority in simpler network structure, shorter training time and more powerful learning ability during complex signal processing compared to real valued neural networks (RVNNs). For instance, both the well-known Exclusive-OR (XOR) problem and the detection of symmetry problem can be realized by only a single complex-valued neuron with the orthogonal decision boundaries, whereas neither of them could be accomplished by RVNNs with such a simple network structure [17]. Furthermore, in RVNNs, we usually employ bounded and smooth functions as activation function such as the Sigmoid type functions, however, activation functions with such properties in CVNNs are impermissible, since on the basis of Liouvilles theorem [18], the function which is both bounded and analytic over complex number field must be a constant. As a result, choosing appropriate activation function is an important and difficult task for CVNNs. According to the above discussion, despite being an extension of RVNNs, CVNNs are very different and more complicated compared to RVNNs. Hence, it is necessary to analyze the dynamic behavior of CVNNs, and considerable efforts have been devoted to study the stability and synchronization of CVNNs [19,20,21,22]. However, there is a little literature to consider the dynamic behavior of fractional-order CVNNs. Until recently, the stability and uniformly stability of this networks are investigated in [23, 24], and the synchronization of a class of fractional-order CVNNs is discussed in [15].

As we all know, stability is one of the most concerned problems for any dynamic system. It is worth noting that most of the existing results focus on the stability of system in the sense of Lyapunov, including asymptotic stability, uniform stability and exponential stability, etc, which are all recognized as infinite-time behavior of such systems. Nevertheless, in some practical situations we may be more interested in the finite-time stability, which sustains the trajectories do not exceed a certain threshold during a fixed short time under a given bound on the initial conditions, since most actual networks only act over finite time. The initial concept of finite-time stability is given in [25] for a class of integer order differential system, and then has been extensively studied [26,27,28,29,30]. Very recently, finite-time stability of fractional order systems are considered and lots of useful results about finite-time stability of fractional-order neural networks are put forward [31,32,33,34], while, up to now, the results on finite-time stability of fractional-order CVNNs are not considered in the existing literatures.

Motivated by the above discussion, the target of this paper is to establish the finite-time stability criterion for fractional-order CVNNs with time delays. By means of Gronwall inequality, Cauchy-Schiwartz inequality and inequality scaling techniques, some sufficient conditions are given to admit the finite-time stability of the system. The reminder of the paper is organized as follows. In Sect. 2, some definitions about fractional calculus and necessary lemmas are recalled, as well as the model of network are described; Then, two sufficient conditions admitting the finite-time stability of fractional-order CVNNs respectively with order \(0<\alpha <1/2\) and \(1/2\le \alpha <1\) are proposed in Sect. 3; The effectiveness of the theoretical results is shown by two numerical simulation examples in Sects. 4 and 5 is the conclusion of this paper.

Notations

Throughout the paper, \({\mathbb {R}}^{n}\) denotes the n dimensional real space. \({\mathbb {R}}^{n\times m}\) is a set of \(n\times m\) real matrices. The superscript “T” represents the transpose. \({\mathbb {C}}, {\mathbb {C}}^n, {\mathbb {C}}^{n\times m}\) respectively denote the set of all complex number, the set of all n-dimensional complex-valued vectors and the set of all \(n\times m\) complex-valued matrices. \(\mathrm {i}\) shows the imaginary unit, i.e. \(\mathrm {i}=\sqrt{-1}\). For any complex number \(z=x+\mathrm {i}y\in {\mathbb {C}}\), the notation |z| stands for the module of z, namely \(|z|=\sqrt{x^2+y^2}\). Given vector \(z \in {\mathbb {C}}^n\), \(\Vert z\Vert \) denotes the 2-norm of z, i.e. \(\Vert z\Vert =(\sum _{j=1}^n |z_j|^2)^{\frac{1}{2}}\). \(C^n(M, N)\) denotes the space consisting of n-order continuous differentiable functions from M into N, and \(C(M)\triangleq C^0(M, {\mathbb {R}})\). For function \(\phi (t): [t_0-\tau , \tau ]\rightarrow {\mathbb {C}}^n\), define the norm \(\Vert \phi \Vert _C=\sup _{s\in [t_0-\tau , t_0]}\Vert \phi (s)\Vert \).

2 Preliminaries

In this section, some basic definitions and results relating to fractional calculus are firstly recalled.

2.1 Fractional Calculus and Preliminary Lemmas

Definition 2.1

[35] The fractional integral with non-integer order \(\alpha >0\) of function f(x) is defined as follows:

$$\begin{aligned} D^{-\alpha }_{t{_0},\,\,t}f(t)=\frac{1}{\Gamma (\alpha )}\int _{t_{_0}}^t (t-\tau )^{\alpha -1}f(\tau )\,\mathrm {d}\tau , \end{aligned}$$

where \(\Gamma (\cdot )\) is the Gamma function \(\Gamma (\alpha )=\int _0^\infty t^{\alpha -1}e^{-t}\,\mathrm {d}t\).

Currently there exist several definitions referring to the fractional derivative of order \(\alpha >0\), including the Grünwald–Letnikov (GL) definition, the Riemann–Liouville (RL) definition and the Caputo definition  [35]. Among these definitions, the Caputo derivative has the unique advantage in that it only claims initial conditions provided as the integer-order derivative of \(f(\cdot )\) and the function itself, which is conducive to express some well-understood features of physical situations, making it more applicable to the real world. Therefore, our consideration in this paper is the fractional-order neural networks with Caputo derivative, whose definition is given below.

Definition 2.2

[35] The Caputo derivative of fractional order \(\alpha \) of function f(x) is defined as follows:

$$\begin{aligned} {}^C_{t_{_0}}D^{\alpha }_t f(t)=D^{-(n-\alpha )}_{t_{_0},\,\,t}f^{(n)}(t) =\frac{1}{\Gamma (n-\alpha )}\int _{t_{_0}}^t (t-\tau )^{n-\alpha -1}f^{(n)}(\tau )\,\mathrm {d}\tau , \end{aligned}$$

where \(n-1<\alpha <n\in \mathbb {Z}^+\).

For simplicity \(D^{-\alpha }_{0,t}\) and \({}^C_{_0}D^{\alpha }_{t}\) are respectively rewritten by \(D^{-\alpha }\) and \(D^{\alpha }\), and some properties on these two operator are introduced.

Lemma 2.1

 [36] If \(f(t)\in \mathrm {C}^n[0,\,\infty )\), and \(n-1<\alpha <n\in \mathbb {Z}^+\), then

  1. (1)

    \(D^{-\alpha }D^{-\beta }f(t)=D^{-(\alpha +\beta )}f(t),\quad \alpha ,\beta >0\);

  2. (2)

    \(D^{\alpha }D^{-\alpha }f(t)=f(t),\quad \alpha \ge 0\);

  3. (3)

    \(D^{-\alpha }D^{\alpha }f(t)=f(t)-\sum _{j=0}^{n-1}( t^j/j\,!)f^{(j)}(0),\quad \alpha \ge 0\).

Now some well-known inequalities will be introduced for the proofs of main results in this paper.

Lemma 2.2

(H\(\ddot{\mathrm {o}}\)lder inequality [37]) Assume that \(q,p>1\), and \(\frac{1}{p}+\frac{1}{q}=1\), if \(|f(\cdot )|^p,|g(\cdot )|^q\in L^1(\Omega )\), then \(f(\cdot )g(\cdot )\in L^1(\Omega )\) and

$$\begin{aligned} \int _{\Omega }|f(x)g(x)|\mathrm {d}x \le \left( \int _{\Omega }|f(x)|^p\mathrm {d}x\right) ^{1/p}\cdot \left( \int _{\Omega }|g(x)|^q\mathrm {d}x\right) ^{1/q}, \end{aligned}$$
(1)

where \(L^1(\Omega )\) is the Banach space of all Lebesgue measurable functions \(f:\Omega \rightarrow {\mathbb {R}}\) with \(\int _{\Omega }|f(x)|\mathrm {d}x<\infty \).

Especially, let \(p,q=2\), it reduces to the Cauchy-Schwartz inequality:

$$\begin{aligned} \left( \int _{\Omega }|f(x)g(x)|\mathrm {d}x\right) ^2 \le \int _{\Omega }|f(x)|^2\mathrm {d}x\cdot \int _{\Omega }|g(x)|^2\mathrm {d}x. \end{aligned}$$
(2)

Lemma 2.3

 [38] Let \(n\in \mathbb {N},\,\,\omega >1\), and \(x_i\in \mathbb {R^+}, i=1,\ldots n\), then

$$\begin{aligned} \left( \sum _{i=1}^{n}x_i\right) ^{\omega }\le n^{\omega -1}\sum _{i=1}^{n}x_i^{\omega }. \end{aligned}$$

Lemma 2.4

(Gronwall inequality [39]) If

$$\begin{aligned} x(t)\le h(t)+\int _{t_{_0}}^t k(s)x(s)\mathrm {d}s,\quad t\in [t_0,\,T), \end{aligned}$$

where all the functions involved are continuous on \([t_0,\,T), T\le \infty \), and \(k(t)\ge 0\), then x(t) satisfies

$$\begin{aligned} x(t)\le h(t)+\int _{t_{_0}}^t k(s)h(s)\mathrm {exp}\Big (\int _s^t k(u)\mathrm {d}u\Big )\mathrm {d}s,\quad t\in [t_{_0},\,T). \end{aligned}$$
(3)

If, in addition, h(t) is nondecreasing, then

$$\begin{aligned} x(t)\le h(t)\mathrm {exp}\Big (\int _s^t k(u)\mathrm {d}u\Big ),\quad t\in [t_{_0},\,T). \end{aligned}$$

2.2 Model Description

In this paper, we consider the following fractional-order CVNNs with time delays:

$$\begin{aligned} \left\{ \begin{aligned}&D^{\alpha }z_j(t)=-c_jz_j(t)+\sum _{k=1}^n a_{jk}f_k(z_k(t))+\sum _{k=1}^n b_{jk}g_k(z_k(t-\tau ))+U_j,\\&z_i(t)=\phi _i(t),\quad t\in [t_0-\tau ,\,t_0], \end{aligned} \right. \end{aligned}$$
(4)

where \(j=1,2,\ldots ,n\), or in the vector form

$$\begin{aligned} \left\{ \begin{aligned}&D^{\alpha }z(t)=-Cz(t)+AF(z(t))+BG(z(t-\tau ))+U,\\&z(t)=\phi (t),\quad t\in [t_0-\tau ,\,t_0], \end{aligned} \right. \end{aligned}$$
(5)

where \(0<\alpha <1\), n is the number of neurons, \(z(t)=(z_1(t),z_2(t),\ldots , z_n(t))^T\in {\mathbb {C}}^n\) is the state vector, \(F(z(t))=(f_1(z_1(t)),\ldots , f_n(z_n(t)))^T\), \(G(z(t))=(g_1(z_1(t)),\ldots ,g_n(z_n(t)))^T\), and \(f_j(\cdot ),g_j(\cdot ):{\mathbb {C}}^n\rightarrow {\mathbb {C}}\) denote the activation functions of the jth neuron without and with time delays; \(A=(a_{jk})_{n\times n}, B=(b_{jk})_{n\times n}\in {\mathbb {C}}^{n\times n}\) are, respectively, the connection weight matrix without and with time delays; \(C=diag\{c_1, c_2, \ldots ,c_n\}\in {\mathbb {R}}^{n\times n}\) with \(c_j>0\) is the self-feedback connection weight matrix, \(U=(U_1,U_2,\ldots ,U_n)^T\in {\mathbb {C}}^n\) is the external input vector; \(t_0\) is the initial time for observation of the system, \(\phi (t)=(\phi _1(t),\tau _2(t),\ldots ,\phi _n(t))^T\in C([t_0-\tau , t_0], {\mathbb {C}}^n)\) is the initial function.

Definition 2.3

 [28] Set a time \(T>0\), given positive numbers \(\delta ,\epsilon \) with \(\delta <\epsilon \), a solution \(z(t,t_0, \phi )\) of system (5) is said to be finite-time stable with respect to \((t_0, J, \delta , \epsilon )\), if for any solution \(z'(t,t_0, \phi ')\) of (5), \(\Vert \phi '-\phi \Vert _C<\delta \) implies \(\Vert z'(t,t_0,\phi ')-z(t,t_0, \phi )\Vert <\epsilon , \, \forall t\in J=[t_0, t_0+T]\), where \(\phi (t), \phi '(t)\) for \(t\in [t_0-\tau , t_0]\) is initial functions.

System (5) is said to be finite-time stable with respect to \((t_0, J, \delta ,\epsilon )\) if any solution z(t) of (5) is finite-time stability with respect to \((t_0, J, \delta , \epsilon ).\)

Remark 2.1

The finite-time stability, also called short-time stability, is initial introduced in [25]. Inspired by LaSalle and Lefschet’s “brief discussion” on practical stability in [40], the stability defined constant set trajectory bounds over finite time interval is proposed by Weiss and Infante [25] for continuous-time systems, and further development on such theory is explored by Lam and Weiss in [41]. Then, a more vivid concept called “practical stability with settling time” is in consideration in [42, 43] by Grujić. Essentially, these definitions all consist of maintaining the system response within a certain threshold over a short time interval, based on the preset range of initial value change, which is as described by Definition 2.3.

Remark 2.2

It should be pointed out that the finite-time stability and the stability in the sense of Lyapunov are different concepts, because Lyapunov stability or asymptotic stability does not contain finite-time stability, and vise versa [28]. Besides, the finite-time stability considered here is also quite different from the fixed-time stability or finite-time stability in [44] and [45] , which requires the trajectory of system both finite-time attractive and Lyapunov stable, noting that the latter is a special case of Lyapunov stability. Sometimes a system can be stable or asymptotically stable but yet no use at all due to its undesirable transient performances. Consequently, it may be helpful to study its stability within a certain subset of the state space which are defined a priori over a finite time interval. That is the prime task of this paper.

To facilitate in establishing our main results, the following assumptions are utilized.

Assumption 1

Let \(z=x+\mathrm {i}y\), F(z(t)) and \(G(z(t-\tau ))\) are analytic and can be expressed by separating their real and imaginary parts as

$$\begin{aligned} F(z(t))= & {} F^R(x(t),y(t))+\mathrm {i}F^I(x(t),y(t)),\\ G(z(t-\tau ))= & {} G^R(x(t-\tau ),y(t-\tau ))+\mathrm {i}G^I(x(t-\tau ),y(t-\tau )), \end{aligned}$$

where \(F^k(x,y)=(f^k_1(x_1,y_1),\ldots ,f^k_n(x_n,y_n))^T\), \(G^k(x,y)=(g^k_1(x_1,y_1),\ldots ,g^k_n(x_n,y_n))^T\), and \(f^k_j(x,y)\), \(g^k_j(x,y):{\mathbb {R}}^2\rightarrow {\mathbb {R}}\) are real differentiable, \(j=1,2,\ldots ,n;\,k=R,I.\)

Similarly, the complex matrices A and B can be separated by \(A=A^R+\mathrm {i}A^I\), \(B=B^R+\mathrm {i}B^I\), and let \(\bar{A}=\Vert A^R\Vert , \tilde{A}=\Vert A^I\Vert , \bar{B}=\Vert B^R\Vert , \tilde{B}=\Vert B^I\Vert \).

Assumption 2

\(f^k_j(\cdot ,\cdot ), g^k_j(\cdot ,\cdot )\,(k=R,I;j=1,2,\ldots ,n)\) satisfy the Lipschitz conditions in \({\mathbb {R}}^2\), that is, for any \((u, v), (u',v')\in {\mathbb {R}}^2\), there exist positive constants \(F^k_j,G^k_j\), such that

$$\begin{aligned} |f^k_j(u',v')-f^k_j(u,v)|&\le F^k_j\sqrt{(u'-u)^2+(v'-v)^2},\\ |g^k_j(u',v')-g^k_j(u,v)|&\le G^k_j\sqrt{(u'-u)^2+(v'-v)^2},\quad k=R,I;j=1,2,\ldots ,n. \end{aligned}$$

Remark 2.3

Noting that for any \(z, z' \in {\mathbb {C}}^n\), let \(z=x+\mathrm {i}y, z'=x'+\mathrm {i}y'\), then \((x,y), (x',y')\in {\mathbb {R}}^{\,n\times 2}\), and we have

$$\begin{aligned} \Vert z'-z\Vert =\left( \sum _{j=1}^n |z'_j-z_j|^2\right) ^{1/2} =\left( \sum _{j=1}^n (|x'_j-x_j|^2+|y'_j-y_j|^2)\right) ^{1/2}. \end{aligned}$$

Letting \(\bar{F}=\max \nolimits _{1\le j\le n}\{F^R_j\}\) and using Assumption 2, one can easily obtain

$$\begin{aligned} \Vert F^R(x',y')-F^R(x,y)\Vert =\left( \sum _{j=1}^n|f_j^R(x'_j,y'_j)-f_j^R(x_j,y_j)|^2\right) ^{1/2}\le \bar{F}\Vert z'-z\Vert . \end{aligned}$$
(6)

Similarly, it could be derived

$$\begin{aligned} \Vert F^I(x',y')-F^I(x,y)\Vert\le & {} \tilde{F}\Vert z'-z\Vert , \end{aligned}$$
(7)
$$\begin{aligned} \Vert G^R(x',y')-G^R(x,y)\Vert\le & {} \bar{G}\Vert z'-z\Vert ,\quad \Vert G^I(x',y')-G^I(x,y)\Vert \le \tilde{G}\Vert z'-z\Vert , \end{aligned}$$
(8)

where \(\tilde{F}=\max \nolimits _{1\le j\le n}\{F^I_j\},\, \bar{G}=\max \nolimits _{1\le j\le n}\{G^R_j\}, \,\) and \(\tilde{G}=\max \nolimits _{1\le j\le n} \{G^I_j\}\).

For convenience, we set \(t_0=0\) throughout this paper and then our initial interval is \([-\tau , 0].\) Assuming that z(t) and \(z'(t)\) are two solution of (5) with different initial functions \(\phi (t)\) and \(\phi '(t)\) for \(t\in [-\tau ,0]\), let \(e(t)=z'(t)-z(t),\, \theta (t)=\phi '(t)-\phi (t)\), one has the error system

$$\begin{aligned} \left\{ \begin{aligned}&D^{\alpha }e(t)=-Ce(t)+A[F(z'(t))-F(z(t))]+B[G(z'(t-\tau ))-G(z(t-\tau ))],\\&e(t)=\theta (t),\quad t\in [-\tau ,\,0], \end{aligned} \right. \end{aligned}$$
(9)

From Definition 2.3, the finite-time stability for system (5) is equivalent to the finite time stability of trivial solution for the error system (9). Thus we just consider system (9) hereafter.

3 Main Results

In this section, we derive the sufficient conditions for finite-time stability of a class of fractional-order complex-valued neural networks with time delays, which are discussed into two cases: \(\frac{1}{2}\le \alpha <1\) and \(0<\alpha <\frac{1}{2}\). For simplification, the following notations are employed:

$$\begin{aligned} z(t)= & {} x(t)+\mathrm {i}y(t),\quad t\ge 0; \quad \Phi (t)=\phi (t)+\mathrm {i}\varphi (t),\quad t\in [-\tau ,0]; \end{aligned}$$
(10)
$$\begin{aligned} z'(t)= & {} x'(t)+\mathrm {i}y'(t),\quad t\ge 0; \quad \Phi '(t)=\phi '(t)+\mathrm {i}\varphi '(t),\quad t\in [-\tau ,0]; \end{aligned}$$
(11)
$$\begin{aligned} \bar{e}(t)= & {} x'(t)-x(t),\quad \tilde{e}(t)=y'(t)-y(t),\quad x_{\tau }(\cdot )=x(\cdot -\tau ). \end{aligned}$$
(12)

Then from (12), \(e(t)=\bar{e}(t)+\mathrm {i}\tilde{e}(t)\), and by means of (10), (11) and (9), we have

$$\begin{aligned} D^{\alpha }\bar{e}(t)= & {} -C\bar{e}(t)+A^R\left[ F^R(x',y')-F^R(x,y)\right] -A^I\left[ F^I(x',y')-F^I(x,y)\right] \nonumber \\&+B^R\left[ G^R(x'_{\tau },y'_{\tau })-G^R(x_{\tau },y_{\tau })\right] -B^I\left[ G^I(x'_{\tau },y'_{\tau })-G^I(x_{\tau },y_{\tau })\right] , \end{aligned}$$
(13)
$$\begin{aligned} D^{\alpha }\tilde{e}(t)= & {} -C\tilde{e}(t)+A^R[F^I(x',y')-F^I(x,y)]+A^I[F^R(x',y')-F^R(x,y)]\nonumber \\&+B^R\left[ G^I(x'_{\tau },y'_{\tau })-G^I(x_{\tau },y_{\tau })\right] +B^I\left[ G^R(x'_{\tau },y'_{\tau })-G^R(x_{\tau },y_{\tau })\right] . \end{aligned}$$
(14)

Theorem 3.1

When \(\frac{1}{2}\le \alpha <1\), if Assumptions 1 and 2 holds and

$$\begin{aligned} \sqrt{\frac{8+(4N+MN+2M)e^{(2+N)t}}{2+N}}<\frac{\epsilon }{\delta }, \end{aligned}$$
(15)

for all \(t\in J=[0,T]\), then system (9) is finite time stable with respect to \([t_0, J, \delta , \epsilon ]\), where

$$\begin{aligned} M&=\frac{4\Gamma (2\alpha -1)\big [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^2+(\bar{B}\tilde{G}+ \tilde{B}\bar{G})^2\big ](1-e^{-2\tau })}{4^\alpha \Gamma ^2(\alpha )},\nonumber \\ N&=\frac{8\Gamma (2\alpha -1)\big [\Vert C\Vert ^2+(\bar{A}\bar{F}+\tilde{A}\tilde{F})^2+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^2+ [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^2+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^2]e^{-2\tau }\big ]}{4^\alpha \Gamma ^2(\alpha )}. \end{aligned}$$
(16)

Proof

Based on Lemma 2.1, the system (13) can be expressed by

$$\begin{aligned} \bar{e}(t)= & {} \bar{e}(0)+D^{-\alpha }\left\{ -C\bar{e}(t)+A^R[F^R(x',y')-F^R(x,y)]-A^I[F^I(x',y')-F^I(x,y)]\right. \\&+\left. B^R[G^R(x'_{\tau },y'_{\tau })-G^R(x_{\tau },y_{\tau })]-B^I[G^I(x'_{\tau },y'_{\tau })-G^I(x_{\tau },y_{\tau })]\right\} \\= & {} \bar{e}(0)+\frac{1}{\Gamma {(\alpha )}}\int _0^t(t-s)^{\alpha -1}\left\{ -C\bar{e}(s)+A^R[F^R(x'(s),y'(s))-F^R(x(s),y(s))]\right. \\&-\,A^I[F^I(x'(s),y'(s))-F^I(x(s),y(s))]+B^R[G^R(x'_{\tau }(s),y'_{\tau }(s))\\&-\,G^R(x_{\tau }(s),y_{\tau }(s))]-B^I\left. [G^I(x'_{\tau }(s),y'_{\tau }(s))-G^I(x_{\tau }(s),y_{\tau }(s))]\right\} \mathrm {d}s. \end{aligned}$$

From Assumption 2 and Eqs. (6)–(8), it yields

$$\begin{aligned} \Vert \bar{e}(t)\Vert&\le \Vert \bar{e}(0)\Vert +\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1} \left\{ \Vert C\Vert \Vert \bar{e}(s)\Vert +\bar{A}\bar{F}\Vert e(s)\Vert +\tilde{A}\tilde{F}\Vert e(s)\Vert \right. \nonumber \\&\quad \left. +\bar{B}\bar{G}\Vert e_{\tau }(s)\Vert +\tilde{B}\tilde{G}\Vert e_{\tau }(s)\Vert \right\} \mathrm {d}s=\Vert \bar{e}(0)\Vert \nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}\Vert C\Vert \Vert \bar{e}(s)\Vert \mathrm {d}s+ \frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}[\bar{A}\bar{F}+\tilde{A}\tilde{F}]\Vert e(s)\Vert \mathrm {d}s\nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}[\bar{B}\bar{G}+\tilde{B}\tilde{G}]\Vert e_{\tau }(s)\Vert \mathrm {d}s. \end{aligned}$$
(17)

By using the Cauchy-Schwartz inequality (2), one has

$$\begin{aligned} \int _0^t(t-s)^{\alpha -1}\Vert C\Vert \Vert \bar{e}(s)\Vert \mathrm {d}s&=\Vert C\Vert \int _0^t(t-s)^{\alpha -1}e^se^{-s}\Vert \bar{e}(s)\Vert \mathrm {d}s\nonumber \\&\le \left( \int _0^t(t-s)^{2\alpha -2}e^{2s}\mathrm {d}s\right) ^{\frac{1}{2}}\cdot \Vert C\Vert \left( \int _0^te^{-2s}\Vert \bar{e}(s)\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}}. \end{aligned}$$
(18)

Similarly, we have

$$\begin{aligned}&\int _0^t(t-s)^{\alpha -1}[\bar{A}\bar{F}+\tilde{A}\tilde{F}]\Vert e(s)\Vert \mathrm {d}s\nonumber \\&\quad \le \left( \int _0^t(t-s)^{2\alpha -2}e^{2s}\mathrm {d}s\right) ^{\frac{1}{2}}\cdot (\bar{A}\bar{F}+\tilde{A}\tilde{F})\left( \int _0^te^{-2s}\Vert e(s)\Vert ^2 \mathrm {d}s\right) ^{\frac{1}{2}}, \end{aligned}$$
(19)
$$\begin{aligned}&\quad \int _0^t(t-s)^{\alpha -1}[\bar{B}\bar{G}+\tilde{B}\tilde{G}]\Vert e_{\tau }(s)\Vert \mathrm {d}s\nonumber \\&\quad \le \left( \int _0^t(t-s)^{2\alpha -2}e^{2s}\mathrm {d}s\right) ^{\frac{1}{2}}\cdot (\bar{B}\bar{G}+\tilde{B}\tilde{G})\left( \int _0^te^{-2s}\Vert e_{\tau }(s)\Vert ^2 \mathrm {d}s\right) ^{\frac{1}{2}}. \end{aligned}$$
(20)

Noting that the expression of Gama function \(\Gamma (\alpha )=\int _0^{\infty }t^{\alpha -1}e^{-t}\mathrm {d}t\), we obtain

$$\begin{aligned} \int _0^t(t-s)^{2\alpha -2}e^{2s}\mathrm {d}s&=\int _0^tv^{2\alpha -2}e^{2t-2v}\mathrm {d}v =e^{2t}\int _0^tv^{2\alpha -2}e^{-2v}\mathrm {d}v\nonumber \\&=\frac{e^{2t}}{2^{2\alpha -1}}\int _0^{2t}u^{2\alpha -2}e^{-u}\mathrm {d}u \le \frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1). \end{aligned}$$
(21)

Substituting (18)–(21) into (17), it could be derived

$$\begin{aligned} \Vert \bar{e}(t)\Vert&\le \Vert \bar{e}(0)\Vert +\frac{\Vert C\Vert }{\Gamma (\alpha )} \left( \frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1)\right) ^{\frac{1}{2}} \left( \int _0^te^{-2s}\Vert \bar{e}(s)\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}} \nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\left( \frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1) \right) ^{\frac{1}{2}} \cdot \left\{ (\bar{A}\bar{F}+\tilde{A}\tilde{F})\left( \int _0^te^{-2s}\Vert e(s)\Vert ^2 \mathrm {d}s\right) ^{\frac{1}{2}}\right. \nonumber \\&\quad \left. +\,(\bar{B}\bar{G}+\tilde{B}\tilde{G})\left( \int _0^te^{-2s}\Vert e_{\tau }(s)\Vert ^2 \mathrm {d}s\right) ^{\frac{1}{2}} \right\} . \end{aligned}$$
(22)

From Lemma 2.3, and let \(n=4\), \(\omega =2\), it follows from (22) that

$$\begin{aligned} \Vert \bar{e}(t)\Vert ^2&\le 4\Vert \bar{e}(0)\Vert ^2+\frac{4\Vert C\Vert ^2}{\Gamma ^2(\alpha )}\frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1) \int _0^te^{-2s}\Vert \bar{e}(s)\Vert ^2\mathrm {d}s+ \frac{4}{\Gamma ^2(\alpha )}\frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1)\nonumber \\&\quad \cdot \left\{ (\bar{A}\bar{F}+\tilde{A}\tilde{F})^2\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s+ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2\int _0^te^{-2s}\Vert e_{\tau }(s)\Vert ^2\mathrm {d}s\right\} . \end{aligned}$$
(23)

From the initial condition of system (9), we can get

$$\begin{aligned} \int _0^te^{-2s}\Vert e_{\tau }(s)\Vert ^2\mathrm {d}s&=\int _0^te^{-2s}\Vert e(s-\tau )\Vert ^2\mathrm {d}s =\int _{-\tau }^{t-\tau }e^{-2(u+\tau )}\Vert e(u)\Vert ^2\mathrm {d}u\nonumber \\&<e^{-2\tau }\int _{-\tau }^0e^{-2u}\Vert e(u)\Vert ^2\mathrm {d}u+e^{-2\tau }\int _0^te^{-2u}\Vert e(u)\Vert ^2\mathrm {d}u\nonumber \\&=e^{-2\tau }\int _{-\tau }^0e^{-2s}\Vert \theta (s)\Vert ^2\mathrm {d}s+e^{-2\tau }\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\nonumber \\&\le \Vert \theta \Vert ^2e^{-2\tau }\int _{-\tau }^0e^{-2s}\mathrm {d}s+e^{-2\tau }\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\nonumber \\&=\frac{\Vert \theta \Vert ^2}{2}\left( 1-e^{-2\tau }\right) +e^{-2\tau }\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s. \end{aligned}$$
(24)

Thus (23) can be written by

$$\begin{aligned} \Vert \bar{e}(t)\Vert ^2&\le 4\Vert \bar{e}(0)\Vert ^2+\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }\Vert C\Vert ^2 \int _0^te^{-2s}\Vert \bar{e}(s)\Vert ^2\mathrm {d}s\nonumber \\&\quad + \frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha } (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2\frac{\Vert \theta \Vert _C^2}{2}\left( 1-e^{-2\tau }\right) \nonumber \\&\quad +\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }[(\bar{A}\bar{F}+\tilde{A}\tilde{F})^2+ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2e^{-2\tau }]\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s. \end{aligned}$$
(25)

Applying the similar techniques, we can obtain the estimation of imaginary part for the solution of system (9) as follow

$$\begin{aligned} \Vert \tilde{e}(t)\Vert ^2&\le 4\Vert \tilde{e}(0)\Vert ^2+\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }\Vert C\Vert ^2 \int _0^te^{-2s}\Vert \tilde{e}(s)\Vert ^2\mathrm {d}s\nonumber \\&\quad + \frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha } (\bar{B}\tilde{G}+\tilde{B}\bar{G})^2\frac{\Vert \theta \Vert _C^2}{2}\left( 1-e^{-2\tau }\right) \nonumber \\&\quad +\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }[(\bar{A}\tilde{F}+\tilde{A}\bar{F})^2+ (\bar{B}\tilde{G}+\tilde{B}\bar{G})^2e^{-2\tau }]\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s. \end{aligned}$$
(26)

Note that \(\Vert e(s)\Vert ^2=\Vert \bar{e}(s)\Vert ^2+\Vert \tilde{e}(s)\Vert ^2\), for \(s\in [0,t]\), the combination of (25) and (26) induces

$$\begin{aligned} \Vert e(t)\Vert ^2&\le 4\Vert e(0)\Vert ^2+\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }\Vert C\Vert ^2 \int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\\&\quad +\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }\left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2 +(\bar{B}\tilde{G}+\bar{B}\tilde{G})^2\right] \left( 1-e^{-2\tau }\right) \frac{\Vert \theta \Vert _C^2}{2} +\frac{8e^{2t}\Gamma (2\alpha -1)}{\Gamma ^2(\alpha )4^\alpha }\\&\quad \cdot \left\{ (\bar{A}\bar{F}+\tilde{A}\tilde{F})^2+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^2+ \left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2+(\bar{B}\tilde{G}+\bar{B}\tilde{G})^2\right] e^{-2\tau }\right\} \\&\quad \int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \quad \Vert e(t)\Vert ^2e^{-2t}&\le \left\{ 4e^{-2t}+\frac{4(1-e^{-2\tau })\Gamma (2\alpha -1)}{4^\alpha \Gamma ^2(\alpha )}\left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2+ (\bar{B}\tilde{G}+\tilde{B}\bar{G})^2\right] \right\} \Vert \theta \Vert _C^2\nonumber \\&\quad +\frac{8\Gamma (2\alpha -1)}{4^\alpha \Gamma ^2(\alpha )}\cdot \left\{ \Vert C\Vert ^2+(\bar{A}\bar{F}+\tilde{A}\tilde{F})^2+ (\bar{A}\tilde{F}+\tilde{A}\bar{F})^2+\left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^2\right. \right. \nonumber \\&\quad \left. \left. + (\bar{B}\tilde{G}+\tilde{B}\bar{G})^2\right] e^{-2\tau }\right\} \int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\nonumber \\&\quad \mathop {=}\limits ^{\triangle }[4e^{-2t}+M]\Vert \theta \Vert _C^2+N\int _0^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s, \end{aligned}$$
(27)

where M, N is the form of (16). From the Gronwall inequality (3), one has

$$\begin{aligned} \Vert e(t)\Vert ^2e^{-2t}&\le [4e^{-2t}+M]\Vert \theta \Vert _C^2+\int _0^t N[4e^{-2s}+M]\Vert \theta \Vert _C^2e^{\int _s^tN\mathrm {d}s_1}\mathrm {d}s\\&=\frac{8e^{-2t}+(4N+MN+2M)e^{Nt}}{2+N}\Vert \theta \Vert _C^2. \end{aligned}$$

Thus

$$\begin{aligned} \Vert e(t)\Vert ^2\le \frac{8+(4N+MN+2M)e^{(2+N)t}}{2+N}\Vert \theta \Vert _C^2. \end{aligned}$$
(28)

It follows that when \(\Vert \theta \Vert _C<\delta \) and if (15) is satisfied for all \(t\in J\), then \(\Vert e(t)\Vert <\epsilon \), from Definition 2.3, system (5) is finite-time stable with respect to \((t_0, J, \delta , \epsilon )\).

Theorem 3.2

When \(0<\alpha <1/2\), if assumption 1 and 2 are satisfied, and

$$\begin{aligned} \root {}^{{}^q} \of {\frac{2^{\frac{5q-6}{2}}q+\left( 2^{\frac{5q-6}{2}}+\tilde{M}\tilde{N}+ q\tilde{M}\right) e^{(\tilde{N}+q)t}}{q+\tilde{N}}}<\frac{\epsilon }{\delta }, \end{aligned}$$
(29)

for all \(t\in J=[0,T]\), then system (5) is finite time stable with respect to \((t_0, J, \delta , \epsilon )\), where \(p=1+\alpha , q=1+1/\alpha \), and

$$\begin{aligned} \tilde{M}&=2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p(\alpha -1)+1)}{\Gamma ^{^p}(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot \left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q\right] \frac{1-e^{-q\tau }}{q},\nonumber \\ \tilde{N}&=2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p(\alpha -1)+1)}{\Gamma ^{^p}(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot \left\{ \Vert C\Vert ^q+(\bar{A}\bar{F}+\tilde{A}\tilde{F})^q+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^q\right. \nonumber \\&\quad \left. +\left[ (\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q\right] e^{-q\tau }\right\} . \end{aligned}$$
(30)

Proof

As the same in Theorem 3.1, we have the following estimation for the real part of solution of system (9).

$$\begin{aligned} \Vert \bar{e}(t)\Vert&\le \Vert \bar{e}(0)\Vert +\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}\Vert C \Vert \Vert \bar{e}(s)\Vert \mathrm {d}s+ \frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}[\bar{A}\bar{F}\nonumber \\&\quad +\;\tilde{A}\tilde{F}] \Vert e(s)\Vert \mathrm {d}s+\;\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}[\bar{B}\bar{G}+\tilde{B} \tilde{G}]\Vert e_{\tau }(s)\Vert \mathrm {d}s. \end{aligned}$$
(31)

As \(p=1+\alpha , q=1+1/\alpha \), obviously \(p, q>1\) and \(1/p+1/q=1\). By using the Hölder inequality (1), one has

$$\begin{aligned} \quad \int _0^t(t-s)^{\alpha -1}\Vert C\Vert \Vert \bar{e}(s)\Vert \mathrm {d}s&=\int _0^t(t-s)^{\alpha -1}e^s\Vert C\Vert e^{-s}\Vert \bar{e}(s)\Vert \mathrm {d}s\nonumber \\&\le \left( \int _0^t(t-s)^{p(\alpha -1)}e^{ps}\mathrm {d}s\right) ^{\frac{1}{p}}\cdot \Vert C\Vert \left( \int _0^te^{-qs}\Vert \bar{e}(s)\Vert ^q\mathrm {d}s\right) ^{\frac{1}{q}}. \end{aligned}$$
(32)

Similarly, we have

$$\begin{aligned}&\int _0^t(t-s)^{\alpha -1}[\bar{A}\bar{F}+\tilde{A}\tilde{F}]\Vert e(s)\Vert \mathrm {d}s\nonumber \\&\quad \le \left( \int _0^t(t-s)^{p(\alpha -1)}e^{ps}\mathrm {d}s\right) ^{\frac{1}{p}}\cdot [\bar{A}\bar{F}+\tilde{A}\tilde{F}]\left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s \right) ^{\frac{1}{q}}, \end{aligned}$$
(33)
$$\begin{aligned}&\quad \int _0^t(t-s)^{\alpha -1}[\bar{B}\bar{G}+\tilde{B}\tilde{G}]\Vert e_{\tau }(s)\Vert \mathrm {d}s\nonumber \\&\quad \le \left( \int _0^t(t-s)^{p(\alpha -1)}e^{ps}\mathrm {d}s\right) ^{\frac{1}{p}}\cdot [\bar{B}\bar{G}+\tilde{B}\tilde{G}]\left( \int _0^te^{-qs}\Vert e_{\tau }(s)\Vert ^q\mathrm {d}s \right) ^{\frac{1}{q}}. \end{aligned}$$
(34)

Noting that the expression of function \(\Gamma (\cdot )\), we derive

$$\begin{aligned} \quad \int _0^t(t-s)^{p(\alpha -1)}e^{ps}\mathrm {d}s&=e^{p\,t}\int _0^tv^{p\alpha -p}e^{-pv}\mathrm {d}v\nonumber \\&=\frac{e^{p\,t}}{p^{p(\alpha -1)+1}}\int _0^{p\,t}u^{p\alpha -p}e^{-u}\mathrm {d}u \le \frac{e^{p\,t}}{p^{p(\alpha -1)+1}}\Gamma (p\alpha -p+1). \end{aligned}$$
(35)

Substituting (32)–(35) into (31), one obtains

$$\begin{aligned} \Vert \bar{e}(t)\Vert&\le \Vert \bar{e}(0)\Vert +\frac{\Vert C\Vert }{\Gamma (\alpha )}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{p^{p(\alpha -1)+1}}\right] ^{\frac{1}{p}}\cdot \left[ \int _0^te^{-qs}\Vert \bar{e}(s)\Vert ^q\mathrm {d}s\right] ^{\frac{1}{q}}\nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{p^{p(\alpha -1)+1}} \right] ^\frac{1}{p}\cdot \left\{ [\bar{A}\bar{F}+\tilde{A}\tilde{F}]\left( \int _0^te^{-qs}\Vert e(s)\Vert ^q \mathrm {d}s\right) ^{\frac{1}{q}}\right. \nonumber \\&\quad \left. +\,[\bar{B}\bar{G}+\tilde{B}\tilde{G}]\left( \int _0^te^{-qs}\Vert e_{\tau }(s)\Vert ^q \mathrm {d}s\right) ^{\frac{1}{q}} \right\} . \end{aligned}$$
(36)

From Lemma 2.3, and let \(n=4\), \(\omega =q\), it follows from (36) that

$$\begin{aligned} \Vert \bar{e}(t)\Vert ^q&\le 4^{q-1}\Vert \bar{e}(0)\Vert ^q +4^{q-1}\Vert C\Vert ^q\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot \int _0^te^{-qs}\Vert \bar{e}(s)\Vert ^q\mathrm {d}s\nonumber \\&\quad +4^{q-1}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\cdot \left\{ [\bar{A}\bar{F}+\tilde{A}\tilde{F}]^q\right. \nonumber \\&\quad \left. \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s+ [\bar{B}\bar{G}+\tilde{B}\tilde{G}]^q\int _0^te^{-qs}\Vert e_{\tau }(s)\Vert ^q\mathrm {d}s \right\} . \end{aligned}$$
(37)

From the initial condition of system (9), we can get

$$\begin{aligned} \int _0^te^{-qs}\Vert e_{\tau }(s)\Vert ^q\mathrm {d}s&=\int _0^te^{-qs}\Vert e(s-\tau )\Vert ^q\mathrm {d}s =\int _{-\tau }^{t-\tau }e^{-q(u+\tau )}\Vert e(u)\Vert ^q\mathrm {d}u\nonumber \\&<e^{-q\tau }\int _{-\tau }^0e^{-qu}\Vert e(u)\Vert ^q\mathrm {d}u+e^{-q\tau }\int _0^te^{-qu}\Vert e(u)\Vert ^q\mathrm {d}u\nonumber \\&=e^{-q\tau }\int _{-\tau }^0e^{-qs}\Vert \theta (s)\Vert ^q\mathrm {d}s+e^{-q\tau }\int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\nonumber \\&\le \Vert \theta \Vert ^qe^{-q\tau }\int _{-\tau }^0e^{-qs}\mathrm {d}s+e^{-q\tau }\int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\nonumber \\&=\frac{\Vert \theta \Vert ^q}{q}(1-e^{-q\tau })+e^{-q\tau }\int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s. \end{aligned}$$
(38)

Thus (37) can be estimated by

$$\begin{aligned} \Vert \bar{e}(t)\Vert ^q&\le 4^{q-1}\Vert \bar{e}(0)\Vert ^q +4^{q-1}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot [\bar{B}\bar{G}+\tilde{B}\tilde{G}]^q\frac{\Vert \theta \Vert _C^q}{q}(1-e^{-q\tau })\nonumber \\&\quad +4^{q-1}\Vert C\Vert ^q\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot \int _0^te^{-qs}\Vert \bar{e}(s)\Vert ^q\mathrm {d}s\nonumber \\&\quad +4^{q-1}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\cdot \left\{ [\bar{A}\bar{F}+\tilde{A}\tilde{F}]^q+ [\bar{B}\bar{G}+\tilde{B}\tilde{G}]^qe^{-q\tau }\right\} \nonumber \\&\quad \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s. \end{aligned}$$
(39)

Applying the similar strategies, we can obtain

$$\begin{aligned} \Vert \tilde{e}(t)\Vert ^q&\le 4^{q-1}\Vert \tilde{e}(0)\Vert ^q +4^{q-1}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}}\cdot [\bar{B}\tilde{G}+\tilde{B}\bar{G}]^q\frac{\Vert \theta \Vert _C^q}{q}(1-e^{-q\tau })\nonumber \\&\quad +4^{q-1}\Vert C\Vert ^q\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}} \cdot \int _0^te^{-qs}\Vert \tilde{e}(s)\Vert ^q\mathrm {d}s\nonumber \\&\quad +4^{q-1}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\cdot \left\{ [\bar{A}\tilde{F}+\tilde{A}\bar{F}]^q+ [\bar{B}\tilde{G}+\tilde{B}\bar{G}]^qe^{-q\tau }\right\} \nonumber \\&\quad \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s. \end{aligned}$$
(40)

Since \(0<\alpha <1/2\), \(q/2=(1+1/\alpha )/2>3/2\), then applying Lemma 2.3, and let \(n=2\), \(\omega =q/2\), it follows from (39) and (38) that

$$\begin{aligned} \Vert e(t)\Vert ^q&=(\Vert e(t)\Vert ^2)^{\frac{q}{2}}=(\Vert \bar{e}(t)\Vert ^2+\Vert \tilde{e}(t)\Vert ^2)^{\frac{q}{2}} \le 2^{\frac{q}{2}-1}\left( \Vert \bar{e}(t)\Vert ^q+\Vert \tilde{e}(t)\Vert ^q\right) \nonumber \\&\le 2^{\frac{5q-6}{2}}[\Vert \bar{e}(0)\Vert ^q+\Vert \tilde{e}(0)\Vert ^q] +2^{\frac{5q-6}{2}}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}} \frac{(1-e^{-q\tau })}{q}\nonumber \\&\quad \cdot [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]\Vert \theta \Vert _C^q+2^{\frac{5q-6}{2}}\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\nonumber \\&\quad \cdot \left\{ (\bar{A}\bar{F}+\tilde{A}\tilde{F})^q+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^q+ [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]e^{-q\tau }\right\} \nonumber \\&\quad \cdot \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s +2^{\frac{5q-6}{2}}\Vert C\Vert ^q\left[ \frac{e^{p\,t}\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\cdot \nonumber \\&\quad \int _0^te^{-qs}(\Vert \bar{e}(s)|^q+\Vert \tilde{e}(s)\Vert ^q)\mathrm {d}s. \end{aligned}$$
(41)

Noting that \(a^{\omega }+b^{\omega }\le (a+b)^{\omega }\), for \(a,b>0\) and \(\omega >1\), hence

$$\begin{aligned} \Vert \bar{e}(s)\Vert ^q+\Vert \tilde{e}(s)\Vert ^q&=(\Vert \bar{e}(s)\Vert ^2)^{\frac{q}{2}}+(\Vert \tilde{e}(s)\Vert ^2)^{\frac{q}{2}}\nonumber \\&\le (\Vert \bar{e}(s)\Vert ^2+\Vert \tilde{e}(s)\Vert ^2)^{\frac{q}{2}}=\Vert e(s)\Vert ^q,\quad s\in [0,t]. \end{aligned}$$
(42)

Applying (42) to (41), and multiplying by \(e^{-qt}\) on both sides of (41), we have

$$\begin{aligned} \Vert e(t)\Vert ^qe^{-qt}&\le 2^{\frac{5q-6}{2}}\Vert e(0)\Vert ^qe^{-qt} +2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}} \frac{(1-e^{-q\tau })}{q}\nonumber \\&\quad \cdot [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]\Vert \theta \Vert _C^q\quad +2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\nonumber \\&\quad \cdot \left\{ (\bar{A}\bar{F}+\tilde{A}\tilde{F})^q+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^q+ [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]e^{-q\tau }\right\} \nonumber \\&\quad \cdot \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s +2^{\frac{5q-6}{2}}\Vert C\Vert ^q\left[ \frac{\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\cdot \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\nonumber \\&\le \left\{ 2^{\frac{5q-6}{2}}e^{-qt}+2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^{\frac{q}{p}} \frac{(1-e^{-q\tau })}{q}\cdot [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q\right. \nonumber \\&\quad \left. +(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]\right\} \Vert \theta \Vert _C^q+2^{\frac{5q-6}{2}}\left[ \frac{\Gamma (p\alpha -p+1)}{\Gamma ^p(\alpha )p^{p(\alpha -1)+1}}\right] ^\frac{q}{p}\nonumber \\&\quad \cdot \left\{ \Vert C\Vert ^q+(\bar{A}\bar{F}+\tilde{A}\tilde{F})^q+(\bar{A}\tilde{F}+\tilde{A}\bar{F})^q\right. \nonumber \\&\quad +\left. [(\bar{B}\bar{G}+\tilde{B}\tilde{G})^q+(\bar{B}\tilde{G}+\tilde{B}\bar{G})^q]e^{-q\tau }\right\} \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\end{aligned}$$
(43)
$$\begin{aligned}&\mathop {=}\limits ^{\triangle }(2^{\frac{5q-6}{2}}e^{-qt}+\tilde{M})\Vert \theta \Vert ^q+\tilde{N}\int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s, \end{aligned}$$
(44)

where \(\tilde{M}, \tilde{N}\) is the form of (30). From the Gronwall inequality (3), one has

$$\begin{aligned} \Vert e(t)\Vert ^qe^{-qt}&\le (2^{\frac{5q-6}{2}}e^{-qt}+\tilde{M})\Vert \theta \Vert _C^q+\Vert \theta \Vert _C^q \int _0^t(2^{\frac{5q-6}{2}}e^{-qs}+\tilde{M})\tilde{N}e^{\int _s^t\tilde{N}\mathrm {d}s_1}\mathrm {d}s\nonumber \\&=\frac{2^{\frac{5q-6}{2}}qe^{-qt}+(2^{\frac{5q-6}{2}}\tilde{N}+\tilde{M}\tilde{N}+ q\tilde{M})e^{\tilde{Nt}}}{q+\tilde{N}}\Vert \theta \Vert _C^q, \end{aligned}$$
(45)

which is equivalent to

$$\begin{aligned} \Vert e(t)\Vert \le \root q \of {\frac{2^{\frac{5q-6}{2}}q+(2^{\frac{5q-6}{2}}\tilde{N}+\tilde{M}\tilde{N}+ q\tilde{M})e^{(\tilde{N}+q)t}}{q+\tilde{N}}}\Vert \theta \Vert _C. \end{aligned}$$

It follows that when \(\Vert \theta \Vert _C<\delta \) and if (29) is satisfied, then \(\Vert e(t)\Vert <\epsilon \) for all \(t\in J\), from Definition 2.3, system (5) is finite-time stable with respect to \((t_0, J, \delta , \epsilon )\).

Remark 3.1

Reference [24] investigated the uniform stability of system (4), but the conditions are so tedious and complicate that it is hard to meet in reality. References [33, 34] considered the finite-time stability only for linear time invariant RVNNs. References [31, 32] proposed some criterions for the finite-time stability of nonlinear fractional-order neural networks, just confined to real number field. Here, a popular fractional-order nonlinear delayed CVNNs are discussed. It is worth mentioning that if the parameters, states, and activation functions in system (5) are all specially selected from real number field, resulting a fractional-order real-valued system, our results are still valid. As long as set the parameters associated with the imaginary parts in Theorem 1 and Theorem 2 as zero, we can get conclusions similar to [32], which means, to some extent, our results include those of [32].

Remark 3.2

In practice, the selection for the setting time T largely relies on the parameters such as \(\alpha , \tau , \delta \) and \(\varepsilon \). By the aid of values for the above parameters and (15) [or (29)], we could obtain an approximation namely \(T_e\) for the setting time T, which called “estimate time”, then given a time T being no more than \(T_e\), the system is finite-time stability.

4 Numerical Examples

In this section, to demonstrate the effectiveness of our proposed theoretical results, two numerical simulations for fractional-order CVNNs models will be carried out. Dealing with fractional delayed models, the frequently used numerical method is the modified predictor-corrector algorithm, see [46, 47] and references therein.

Example 1

Consider a two-neuron fractional-order Hopfield neural networks described as

$$\begin{aligned} D^{\alpha }z(t)=-Cz(t)+AF(z(t))+BG(z(t-\tau ))+U, \end{aligned}$$
(46)

where

$$\begin{aligned} C&= \begin{pmatrix} 0.3 &{} 0\\ 0 &{} 0.45 \end{pmatrix}, A= \begin{pmatrix} 0.1-0.2\mathrm {i} &{} 0.2-0.3\mathrm {i}\\ 0.2+0.3\mathrm {i} &{} -0.1-0.2\mathrm {i} \end{pmatrix}, \\ B&= \begin{pmatrix} -0.1+0.5\mathrm {i} &{} 0.3-0.4\mathrm {i}\\ 0.3+0.4\mathrm {i}&{} -0.2+0.5\mathrm {i} \end{pmatrix}, U= \begin{pmatrix} 0.45+0.4\mathrm {i} \\ 0.75+0.5\mathrm {i} \end{pmatrix}; \end{aligned}$$

\(F(z)=(f_1(z_1), f_2(z_2))^T\), \(G(z)=(g_1(z_1), g_2(z_2))^T\), and for \(j=1,2\)

$$\begin{aligned} f_j(z_j)= & {} \frac{1-\mathrm {exp}(-2x_j-y_j)}{1+\mathrm {exp}(-2x_j-y_j)}+ \mathrm {i}\frac{1}{1+\mathrm {exp}(-x_j+2y_j)},\\ g_j(z_j)= & {} \frac{1}{1+\mathrm {exp}(-x_j+2y_j)}+ \mathrm {i}\frac{1-\mathrm {exp}(-2x_j-y_j)}{1+\mathrm {exp}(-2x_j-y_j)}. \end{aligned}$$

So \(\Vert C\Vert =0.45\), \(\bar{A}=0.3, \tilde{A}=0.3606, \bar{B}=0.4541, \tilde{B}=0.6403\). Obviously, the system satisfies Assumptions 1 and 2 with \(\bar{F}=\sqrt{5}/2, \tilde{F}=\sqrt{5}/4, \bar{G}=\sqrt{5}/4, \tilde{G}=\sqrt{5}/2\). Then we aim to check the finite-time stability with respect to \((t_0=0, J=[0,T],\delta =0.1,\epsilon =1)\). When \(\alpha =0.88, \tau =0.1\), it could be calculated that \(M\approx 0.3723, N\approx 5.3470\), from the condition (15) of Theorem 1, it immediately follows

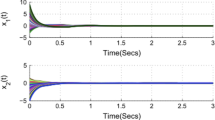
$$\begin{aligned} \sqrt{\frac{8+24.1233\,\mathrm {exp}\,(7.3470t)}{7.3470}}<\frac{1}{0.1}, \end{aligned}$$

then the estimated time of finite-time stability is \(T_e\approx 0.4635\), this means for given T which less than 0.4653, the considered system is finite-time stability. For simulations, the following five different initial states are considered respectively:

$$\begin{aligned} \phi ^1(t)&= \begin{pmatrix} 0.1+\mathrm {i} \\ -1.52+2.3\mathrm {i} \end{pmatrix}, \phi ^2(t)= \begin{pmatrix} 0.05+1.0\mathrm {i}i \\ -1.58+2.4\mathrm {i} \end{pmatrix}, \phi ^3(t)= \begin{pmatrix} 0.08+1.05\mathrm {i} \\ -1.55+2.35\mathrm {i} \end{pmatrix},\\ \phi ^4(t)&= \begin{pmatrix} 0.03+1.08\mathrm {i} \\ -0.6+2.4\mathrm {i} \end{pmatrix}, \phi ^5(t)= \begin{pmatrix} 0.09+1.07\mathrm {i} \\ -1.63+2.38\mathrm {i} \end{pmatrix}, \quad t\in [-\tau ,0]. \end{aligned}$$

Also, trajectories corresponding to these initial values are depicted in Fig. 1. Especially, the error between the solutions under initial values \(\phi ^5\) and \(\phi ^3\) and its norm are respectively illustrated in Figs. 2, 3. As shown in Fig. 1, the difference, between any two trajectories of the system with initial error no more than \(\delta \), does not exceed \(\epsilon \) over interval time [0, T], and Figs. 2, 3 more accurately confirm this point. Thus, the results of Theorem 1 are verified by means of this simulation.

Fig. 1
figure 1

Trajectories of the neural networks with \(\alpha =0.88\), \(\tau =0.1\) under different initial values. a The real part of \(z_1(t)\). b The imaginary part of \(z_1(t)\). c The real part of \(z_2(t)\). d The imaginary part of \(z_2(t)\)

Full size image
Fig. 2
figure 2

The time evolution of error for solutions of the system with \(\alpha =0.88,\tau =0.1\)

Full size image
Fig. 3
figure 3

The time evolution of error norm of solutions \(\alpha =0.88,\tau =0.1\)

Full size image

Example 2

Consider a CVNNs as described in (46), where

$$\begin{aligned} C&= \begin{pmatrix} 0.5 &{} 0\\ 0 &{} 0.6 \end{pmatrix}, A= \begin{pmatrix} -0.3+0.2\mathrm {i} &{} 0.2-0.1\mathrm {i}\\ 0.1+0.2\mathrm {i} &{} 0.2+0.3\mathrm {i} \end{pmatrix}, \\ B&= \begin{pmatrix} 0.1-0.5\mathrm {i} &{} 0.3+0.4\mathrm {i}\\ 0.4-0.3\mathrm {i} &{} -0.2+0.1\mathrm {i} \end{pmatrix}, U= \begin{pmatrix} 0.2-0.1\mathrm {i} \\ 0.3+0.4\mathrm {i} \end{pmatrix}.\\ f_j(z_j)&=\frac{1-\mathrm {exp}(-x_j)}{1+\mathrm {exp}(-x_j)}+ \mathrm {i}\frac{1}{1+\mathrm {exp}(-y_j)},\quad g_j(z_j)=\frac{1-\mathrm {exp}(-y_j)}{1+\mathrm {exp}(-y_j)}+ \mathrm {i}\frac{1}{1+\mathrm {exp}(-x_j)},\\&\quad j=1,2. \end{aligned}$$
Fig. 4
figure 4

Trajectories of the neural networks with \(\alpha =0.48\), \(\tau =0.3\) under different initial values. a The real part of \(z_1(t)\). b The imaginary part of \(z_1(t)\). c The real part of \(z_2(t)\). d The imaginary part of \(z_2(t)\)

Full size image
Fig. 5
figure 5

The time evolution of error for solutions of the system with \(\alpha =0.48,\tau =0.3\)

Full size image
Fig. 6
figure 6

The time evolution of error norm for solutions with \(\alpha =0.48,\tau =0.3\)

Full size image

Then \(\Vert C\Vert =0.6\), \(\bar{A}=0.3623, \tilde{A}=0.3623, \bar{B}=0.4515, \tilde{B}=0.7073\). Clearly, the system satisfies Assumptions 1 and 2 with \(\bar{F}=0.5, \tilde{F}=0.25, \bar{G}=0.5, \tilde{G}=0.25\). Next there is the task to test the finite-time stability with respect to \((t_0=0; J=[0,T],\delta =0.1, \epsilon =1)\). When \(\alpha =0.48, \tau =0.3\), according to (30), it could be derived that \(p=1+\alpha =1.48\), \(q=1+1/\alpha =3.0833\), \(\tilde{M}\approx 1.7492, \tilde{N}\approx 17.4862\) and from the condition (29) of Theorem 2, we have

$$\begin{aligned} \root 3.0833 \of {\frac{80.6046+62.1222\,\mathrm {exp}\, (20.5695t)}{20.5695}}<\frac{1}{0.1}, \end{aligned}$$

then it could be obtained that the estimated time of finite-time stability is \(T_e\approx 0.2913\). For numerical simulations, the following five initial states are considered respectively:

$$\begin{aligned}&\phi ^1(t)= \begin{pmatrix} 0.7+0.56\mathrm {i} \\ 0.25+1.41\mathrm {i} \end{pmatrix}, \phi ^2(t)= \begin{pmatrix} 0.75+0.5\mathrm {i} \\ 0.27+1.39\mathrm {i} \end{pmatrix}, \phi ^3(t)= \begin{pmatrix} 0.73+0.51\mathrm {i} \\ 0.23+1.42\mathrm {i} \end{pmatrix},\\&\phi ^4(t)= \begin{pmatrix} 0.69+0.53\mathrm {i} \\ 0.24+1.45\mathrm {i} \end{pmatrix}, \phi ^5(t)= \begin{pmatrix} 0.72+0.54\mathrm {i} \\ 0.28+1.44\mathrm {i} \end{pmatrix}, \quad t\in [-\tau ,0]. \end{aligned}$$

Trajectories corresponding to these initial values are showed in Fig. 4. Take the solutions referring to initial values \(\phi ^4\) and \(\phi ^1\) into extra consideration, the error between them and its norm are respectively described in Figs. 5, 6. From Figs. 4, 5, 6, it can be directly observed that the numeric conclusions affirm Theorem 2.

5 Conclusions

In this paper, the non-Lyapunov point of view (finite-time stability) of fractional-order CVNNs with time delays have been studied. Not as in integer-order systems, it is hard to search Lyapunov functionals for fractional order cases, causing more difficulties in consideration of infinite-time behavior for such systems. Most important, sometimes it is more critical to study its stability within a certain subset of the state space which are defined a priori over a finite time interval. As a result, the finite-time stability is reasonable and practical. Refer to methods and theoretical foundations, Gronwall inequality, Cauchy–Schiwartz inequality and some inequality scaling techniques are all employed to analysis our model. Some sufficient conditions are obtained for admitting the finite-time stability of the system. Finally, the effectiveness of the theoretical results is showed with the help of two numerical examples. It is worth mentioning that for an exploration of fractional-order CVNNs, our results may be somewhat conservative, which require to be relaxed in the future.