1 Introduction

In the past decades, neural networks as a special kind of nonlinear systems have received considerable attention due to their wide applications in a variety of areas including such as pattern recognition, associative memory and combinational optimization. Dynamical behaviors such as the stability, the attractivity and the periodic solution of the neural networks are known to be crucial in applications. For instance, if a neural network is employed to solve some optimization problems, it is highly desirable for the neural network to have a unique globally stable equilibrium. Therefore, stability analysis of neural networks has received much attention, and a great number of results have been available in the literature [1–6].

As one of the most popular and typical neural networks models, Cohen–Grossberg neural network (CGNN) has been proposed by Cohen and Grossberg [7]. Since it includes a number of models from neurobiology, population biology and evolution theory, as well as the Hopfield neural networks, CGNN has attracted considerable attention in recent years. By combining Cohen–Grossberg neural networks with an arbitrary switching rule, the mathematical model of a class of switched Cohen–Grossberg neural networks with mixed time-varying delays is established in [8]. This paper [9] is concerned with the problem of exponential stability for a class of Markovian jump impulsive stochastic Cohen–Grossberg neural networks with mixed time delays and known or unknown parameters. The existence and uniqueness of the solution of interval fuzzy CGNNs with piecewise constant argument are discussed in [10]. It is shown in [11] that finite-time synchronization is discussed for a class of delayed neural networks with Cohen–Grossberg type. In [12], the authors discussed the following Cohen–Grossberg BAM neural networks with neutral-type delays

$$ \left\{ \begin{array}{lll} x^{\prime }_i(t)+\sum \limits _{j=1}^me_{ij}x^{\prime }_j(t-h) =-a_i(x_i(t))\left\{ b_i(x_i(t))-\sum \limits _{j=1}^ms_{ij} f_j\left( x_j\left( t-\sigma _{ij}\right) ,y_j\left( t-\tau _{ij}\right) \right) +I_i\right\} ,\\ y^{\prime }_j(t)+\sum \limits _{i=1}^mv_{ji}y^{\prime }_i(t-d) =-c_j(y_j(t))\left\{ d_j\left( y_j(t)\right) -\sum \limits _{i=1}^mt_{ji} g_i\left( x_i\left( t-\delta _{ji}\right) ,y_i\left( t-\eta _{ji}\right) \right) +J_j\right\} , \end{array}\right. $$
(1)

where m is an integer, \(i, j=1,2,\ldots ,m\), \(x_i\in R\) and \(y_j\in R\) denote the state variables of the ith neuron and the jth neuron, respectively. \(a_i(x_i(\cdot ))>0,~c_j(y_j(\cdot ))>0\) represent amplification functions. \(b_i(x_i(\cdot ))\) and \(d_j(y_j(\cdot ))\) represent appropriately behaved functions. And \(f_j,~g_i\) are the activation functions. Moreover, \(s_{ij},~t_{ji},~e_{ij},~v_{ji}\) are the connection weights, which denote the strengths of connectivity between the ith and jth neurons. \(I_i,~J_j\) are the exogenous inputs of the ith neuron and the jth neuron, respectively. \(\sigma _{ij}\ge 0,~\delta _{ji}\ge 0,~\tau _{ij}\ge 0, ~\eta _{ji}\ge 0\) denote the transmission delays, which are related to the jth and ith neurons. \(d\ge 0,~h\ge 0\) are neutral-type time delays.

In the above-mentioned literature, most of CGNNs are considered to be one dimensional. However, two-dimensional system model represents a wide range of practical systems, such as image data processing and transmission, thermal processes, gas absorption and water stream heating. The research on two-dimensional systems has mainly been inspired by the practical needs to represent continuous- and discrete-time nonlinear dynamic systems by using the Volterra series. Hence, the two-dimensional systems, where the information propagation occurs in two independent directions, have received considerable research attention in the past few decades [13–20]. The authors in [21] investigate the fault detection for 2-D Markovian jump systems with partly unknown transition probabilities and missing measurements. It is shown in [22] that the problem of robust synchronization is discussed for a class of 2-D coupled uncertain dynamical networks. In [23], the state estimation is addressed for two-dimensional complex networks with randomly occurring nonlinearities and randomly varying sensor delays.

To the best of authors’ knowledge, there are few dynamical discussions for the two-dimensional neutral-type Cohen–Grossberg BAM neural networks. Hence, in this paper, our purpose is to extend model (1) to be two dimensional and neutral type and derive sufficient conditions ensuring the global asymptotic stability problem for the two-dimensional neutral-type Cohen–Grossberg BAM neural networks based on inequality technique and Lyapunov functional. The main contribution of this paper is twofold: (1) A two-dimensional neutral-type Cohen–Grossberg BAM neural network model will be proposed to illustrate the two-dimensional structure and the neutral-type delays in Cohen–Grossberg BAM neural networks. (2) Sufficient conditions will be proposed to achieve the global asymptotic stability of two-dimensional neutral-type Cohen–Grossberg BAM neural networks.

Notation: Throughout this study, for any matrix \(A,~A^{{\text {T}}}\) stands for the transpose of A and \(A^{-1}\) denotes the inverse of A, tr(A) is the trace of the A that is the sum of the diagonal elements of A. For a symmetric matrix A, \(A>0~ (A\ge 0)\) means that A is positive definite (positive semi-definite). Similarly, \(A<0 ~(A\le 0)\) means that A is negative definite (negative semi-definite). \(\lambda _M(A),~\lambda _m(A)\) denote the maximum and minimum eigenvalue of a square matrix A, respectively. \(\Vert A\Vert \) denotes the spectral norm defined by \(\Vert A\Vert =(\lambda _M(A^{{\text {T}}}A))^{\frac{1}{2}}\). For \(x=(x_1, ~x_2,~\ldots ,~x_m)^{{\text {T}}} \in R^m\), the norm is the Euclidean vector norm, i.e., \(\Vert x\Vert=(\sum\nolimits _{i=1}^{m}x_i^2)^{\frac{1}{2}}\). Moreover, \(|A|=(|a_{ij}|),~|x|=(|x_1|,\ldots ,|x_m|)^{{\text {T}}}\).

2 Preliminaries

Motivated by [12, 22, 24], we are concerned with the following two-dimensional neutral-type Cohen–Grossberg BAM neural networks:

$$\left\{ \begin{array}{lllll} \frac{\partial x_i\left( t_1,t_2\right)} {\partial t_1} + \sum \limits _{j=1}^{m}e_{ij} \frac{\partial x_j\left( t_1-h,t_2\right)} {\partial t_1} & = -a_i\left( x_i\left( t_1,t_2\right) \right)\left\{ b_i\left( x_i\left( t_1,t_2\right) \right)\right. \\ & \quad \left. -\sum \limits _{j=1}^{m}s_{ij}f_j\left( x_j\left( t_1-\sigma ,t_2\right) ,y_j\left( t_1,t_2-\tau \right) \right) +I_i\right\} ,\quad i=1,2,\ldots ,m,\\ \frac{\partial y_j(t_1,t_2)}{\partial t_2}+\sum \limits _{i=1}^{m}v_{ji}\frac{\partial y_i(t_1,t_2-d)}{\partial t_2}&= -c_j\left( y_j\left( t_1,t_2\right) \right) \left\{ d_j\left( y_j\left( t_1,t_2\right) \right) \right. \\ &\quad\left. -\sum \limits _{i=1}^{m}t_{ji}g_i\left( x_i\left( t_1-\delta ,t_2\right) ,y_i\left( t_1,t_2-\eta \right) \right) +J_j\right\} ,\quad j=1,2,\ldots ,m, \end{array}\right. $$
(2)

with initial value conditions:

$$ x_i(\theta ,t_2)=\phi _i(\theta ,t_2),\quad y_j(t_1,\theta ) =\varphi _j(t_1,\theta ),\quad \theta \in [-r,0], $$
(3)

where \(r={\text {max}}\{d,h,\sigma ,\delta ,\tau ,\eta \}\), and all the signs have the same definitions with model (1). Here, \(\sigma ,~\tau ,~\delta ,~\eta \) are all time delays in system (2).

Remark 1

The two-dimensional neutral-type neural network model (2) has its practical significance. On the one hand, for example, in [25], much effort has been devoted to the study of two dimensional in vivo neural networks, in which neural activity can be measured by means of a two-dimensional array of microelectrodes, and network morphology is visualized by light microscopy. Also, a novel flow sensor with two-dimensional \(360^\circ \) direction sensitivity has been proposed in [26]. On the other hand, time delays cannot be avoided in the hardware implementation of neural networks due to the finite switching speed of amplifiers in electronic neural networks or the finite signal propagation time in biological networks.

Remark 2

The existence and uniqueness of the equilibrium point in system (2) can be obtained by using the similar methods in [12]. The detailed process is omitted here to simplify our paper.

Remark 3

Compared with model (1) in [12], the contribution of this paper is that we extend model (1) to be two dimensional, which is more reasonable since two-dimensional dynamical systems have to be considered in many practical applications, such as image data processing and transmission, thermal processes, gas absorption and water stream heating. Moreover, as mentioned in Remark 1, some issues such as in vivo neural networks and flow sensors have been considered to be two dimensional.

Rewrite system (2) in the matrix form

$$ \left\{ \begin{array}{lll} \frac{\partial x\left( t_1,t_2\right) }{\partial t_1}+E\frac{\partial x\left( t_1-h,t_2\right) }{\partial t_1}= -A\left( x\left( t_1,t_2\right) \right) \left\{ B\left( x\left( t_1,t_2\right) \right) -Sf\left( x\left( t_1-\sigma ,t_2\right) ,y\left( t_1,t_2-\tau \right) \right) +I\right\} ,\\ \frac{\partial y\left( t_1,t_2\right) }{\partial t_2}+V \frac{\partial y\left( t_1,t_2-d\right) }{\partial t_2}= -C\left( y\left( t_1,t_2\right) \right) \left\{ D\left( y\left( t_1,t_2\right) \right) -Tg\left( x\left( t_1-\delta ,t_2\right) ,y\left( t_1,t_2-\eta \right) \right) +J\right\} , \end{array}\right. $$
(4)

where \(x=(x_1,x_2,\ldots , x_m)^{{\text {T}}}\), \(y=(y_1,y_2,\ldots , y_m)^{{\text {T}}}\), \(f(x(t_1,t_2),y(t_1,t_2))=(f_1(x_1(t_1,t_2),y_1(t_1,t_2))\), \(\ldots \), \(f_m(x_m(t_1,t_2)\), \(y_m(t_1,t_2)))^{{\text {T}}}\in R^{m}\), \(g(x(t_1,t_2),y(t_1,t_2))=(g_1(x_1(t_1,t_2),y_1(t_1,t_2)),\ldots ,g_m(x_m(t_1,t_2)\) \(,y_m(t_1,t_2)))^{{\text {T}}}\in R^{m}\). \(A(x(t_1,t_2))={\text {diag}}(a_{1}(x_1(t_1,t_2)), a_{2}(x_2(t_1,t_2)), \ldots ,a_{m}(x_m(t_1,t_2)))\in R^{m\times m}\), \(B(x(t_1,t_2)) =(b_{1}(x_1(t_1,t_2))\), \(b_{2}(x_2(t_1,t_2))\), \(\ldots \), \(b_{m}(x_m(t_1,t_2)))^{{\text {T}}}\in R^{m}\), \(C(y(t_1,t_2))\) \(={\text {diag}}(c_{1}(y_1(t_1,t_2)),c_{2}(y_2(t_1,t_2)),\ldots ,c_{m}(y_m(t_1,t_2)))\in R^{m\times m}\), \(D(y(t_1,t_2))=(d_{1}(y_1(t_1,t_2))\), \(d_{2}(y_2(t_1,t_2)),\ldots ,d_{m}(y_m(t_1,t_2)))^{{\text {T}}}\in R^{m}\), \(S=(s_{ij})_{m\times m}\), \(T=(t_{ji})_{m\times m}\), \(E=(e_{ij})_{m\times m}\), \(V=(v_{ji})_{m\times m}\), \(I= (I_1,I_2, \ldots ,I_m)\in R^m\), \(J= (J_1,J_2, \ldots ,J_m)\in R^m.\)

Throughout the whole paper, we give the following assumptions.

Assumption 1

There exist positive constants \(\alpha _j,~\beta _j,~\xi _i,~\eta _i\) such that for \(\forall ~ x,~y,~u,~v\in R,~i,~j=1,2,\ldots ,m\), \(|f_j(x,y)-f_j(u,v)|\le \alpha _j|x-u|+\beta _j|y-v|\), \(~~|g_i(x,y)-g_i(u,v)|\le \xi _i|x-u|+\eta _i|y-v|\).

Assumption 2

\(b_i(x)\) and \(d_j(y)\) are differentiable and there exist positive constants \(B_i,~D_j~(i,~j=1,~2,\ldots ,~m)\), such that \(~b_i^{\prime }(x)>B_i>0,~~d_j^{\prime }(y)>D_j>0,~\forall ~ x,~y\in R\). By applying the mean value theorem, one can get that \(b_i(x)-b_i(y)=b_i^{\prime }(\xi _i)(x-y),~d_j(x)-d_j(y)=d_j^{\prime }(\eta _j)(x-y)\), where \(\forall ~x,~y\in R,~\xi _i,~\eta _j\) are two scalars between x and y.

Assumption 3

There exist positive constants \(a_i,~c_i\) \((i=1,2)\) such that \(0<a_1<a_i(x_i)<a_2\), \(0<c_1<c_j(y_j)<c_2\), for \(\forall ~x_i\in R\), \(\forall ~y_j\in R\).

3 Main results

In this section, we will discuss the global asymptotic stability of system (2) according to the inequality technique, linear matrix inequalities and Lyapunov functional.

Definition 1

A point \((x^*,~y^*)^T \in R^m\times R^m\) is said to be an equilibrium point of system (2) if

$$ \left\{ \begin{array}{lll} a_i\left( x_i^*\right) \left\{ b_i\left( x_i^*\right) -\sum \limits _{j=1}^{m}s_{ij} f_j\left( x_j^*,y_j^*\right) +I_i\right\} =0,\quad i=1,~2,\ldots ,m,\\ c_j\left( y_j^*\right) \left\{ d_j(y_j^*)-\sum \limits _{i=1}^{m}t_{ji} g_i\left( x_i^*,y_i^*\right) +J_j\right\} =0,\quad j=1,~2,\ldots ,m, \end{array}\right. $$
(5)

where \(x^*=(x_1^*,~x_2^*,\ldots ,x_m^*,)^T,~~~y^*=(y_1^*,~y_2^*,\ldots ,y_m^*)^T\).

According to Remark 2, we define \((x^*,~y^*)^T\) to be the unique equilibrium of systems (4). For the sake of convenience, some other notations are given: for all \(x\in R^m\), \(\overline{x} \in R^m\) \(y\in R^m\), \(\overline{y} \in R^m\) (\(x\ne \overline{x}\) , \(y \ne \overline{y}\)), define that \(E(x-\overline{x})=(u_1,~\ldots ,u_m)^T, \) \( V(y-\overline{y})=(v_1,\ldots ,v_m)^T,\) and \(u(t_1,~t_2)=x(t_1,~t_2)+Ex(t_1-h,~t_2)\), \(z(t_1,~t_2)=y(t_1,~t_2)+Vy(t_1,~t_2-d)\). Moreover, \(E(x-x^*)=(\overline{u}_1,\ldots ,\overline{u}_m)^T,~ V(y-y^*)=(\overline{v}_1,\ldots ,\overline{v}_m)^T,\) \(~u^*=x^*+Ex^*,\) \(~z^*=y^*+Vy^*\).

Lemma 1

[27] If \(a>0,~b>0,~p>1,~q>1,~\frac{1}{p}+\frac{1}{q}=1\), then \(ab\le \frac{a^p}{p}+\frac{b^q}{q}\).

According to the Lemma 1 and [12], one has the following lemma.

Lemma 2

Assume Assumptions 1–3 hold, there exists a positive integer \(r\ge 1\) and two positive definite diagonal matrices \(P=[p_i]_{m\times m},~Q=[q_i]_{m\times m}\) such that

$$\begin{aligned}&2\sum _{i=1}^{m}\sum _{j=1}^{m}r\left| x_i(t_1,t_2)-\overline{x_i}\right| ^{2r-1}p_ia_2 \times |s_{ij}|\left| f_j\left( x_j\left( t_1,t_2\right) ,y_j\left( t_1,t_2\right) \right) -f_j\left( \overline{x_j},\overline{y_j}\right) \right| \\&\qquad \le \,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\alpha _j\left[ (2r-1) \left( x_i\left( t_1,t_2\right) -\overline{x_i}\right) ^{2r}+\left( x_j\left( t_1,t_2\right) -\overline{x_j}\right) ^{2r}\right] \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\beta _j\left[ (2r-1)\left( x_i\left( t_1,t_2\right) -\overline{x_i}\right) ^{2r} +\left( y_j\left( t_1,t_2\right) -\overline{y_j}\right) ^{2r}\right] , \end{aligned}$$
(6)
$$\begin{aligned}&2r\sum _{i=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left| x_i\left( t_1,t_2\right) -\overline{x_i}\right| ^k \left| u_{i}\left( t_1,t_2\right) \right| ^{2r-1-k}p_ia_2B_i\left| x_i\left( t_1,t_2\right) -\overline{x_i}\right| \\&\qquad \le \,\frac{1}{2r-1}\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2}B_{i}\left\{ 2rk \left( x_{i}\left( t_1,t_2\right) -\overline{x_i}\right) ^{2r}\right. \\&\qquad \left. +\,(2r-1-k)\left[ (2r-1) \left( \left| u_i\left( t_1,t_2\right) \right| ^{2r}\right) +\left( x_i\left( t_1,t_2\right) -\overline{x_i}\right) ^{2r}\right] \right\} , \end{aligned}$$
(7)
$$\begin{aligned}&2r\sum _{i=1}^{m}\sum _{j=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}|x_i(t_1,t_2)-\overline{x_i}|^k |u_{i}(t_1,t_2)|^{2r-1-k}p_ia_2|s_{ij}| \\&\qquad \times \,\left| f_j\left( x_j\left( t_1,t_2\right) ,y_j\left( t_1,t_2\right) \right) -f_j\left( \overline{x_j},\overline{y_j}\right) \right| \\&\qquad \le \,\frac{1}{2r-1}\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2} |s_{ij}|\left\{ k\alpha _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-\overline{x_i}\right) ^{2r}\right. \right. \\&\left. \left. \qquad \quad+\,\left( x_j(t_1,t_2)-\overline{x_j}\right) ^{2r}\right] +(2r-1-k)\alpha _j\left[ (2r-1)\left( {u}_i(t_1,t_2)\right) ^{2r}\right. \right. \\&\qquad \quad\left. \left. +\,\left( x_j(t_1,t_2)-\overline{x_j}\right) ^{2r}\right] +k\beta _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-\overline{x_i}\right) ^{2r} \right. \right. \\&\qquad \quad\left. \left. +\,\left( y_j(t_1,t_2)-\overline{y_j}\right) ^{2r}\right] +(2r-1-k)\beta _j\left[ (2r-1) \left( u_i(t_1,t_2)\right) ^{2r}+\left( y_j(t_1,t_2)-\overline{y_j}\right) ^{2r}\right] \right\} , \end{aligned}$$
(8)
$$\begin{aligned}&2\sum _{i=1}^{m}\sum _{j=1}^{m}r|y_j(t_1,t_2)-\overline{y_j}|^{2r-1}q_jc_2 \times |t_{ji}||g_i(x_i(t_1,t_2),y_i(t_1,t_2))-g_i(\overline{x_i},\overline{y_i})| \\&\qquad \le \,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\xi _i\left[ (2r-1) \left( y_j(t_1,t_2)-\overline{y_j}\right) ^{2r}+\left( x_i(t_1,t_2)-\overline{x_i}\right) ^{2r}\right] \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\eta _i\left[ (2r-1)\left( y_j(t_1,t_2)-\overline{y_j}\right) ^{2r} +\,\left( y_i(t_1,t_2)-\overline{y_i}\right) ^{2r}\right] ,\end{aligned}$$
(9)
$$\begin{aligned}&2r\sum _{i=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}|y_i(t_1,t_2)-\overline{y_i}|^k |{v}_{i}(t_1,t_2)|^{2r-1-k}q_ic_2D_i|y_i(t_1,t_2)-\overline{y_i}| \\&\qquad \le \,\frac{1}{2r-1}\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_{i}c_{2}D_{i}\left\{ 2rk \left( y_{i}(t_1,t_2)-\overline{y_i}\right) ^{2r}\right. \\&\left. \qquad +\,(2r-1-k)\left[ (2r-1) {v}_i(t_1,t_2)^{2r}+\left( y_i(t_1,t_2)-\overline{y_i}\right) ^{2r}\right] \right\} ,\end{aligned}$$
(10)
$$\begin{aligned}&2r\sum _{i=1}^{m}\sum _{j=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}|y_j(t_1,t_2)-\overline{y_j}|^k |{v}_{j}(t_1,t_2)|^{2r-1-k}q_jc_2|t_{ji}| \\&\qquad \times \,|g_i\left( x_i(t_1,t_2),y_i(t_1,t_2)\right) -g_i\left( \overline{x_i},\overline{y_i}\right) | \\&\qquad \le \,\frac{1}{2r-1}\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_{j}c_{2} |t_{ji}|\left\{ k\xi _{i}\left[ (2r-1)\left( y_{j}(t_1,t_2)-\overline{y_j}\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_i(t_1,t_2)-\overline{x_i}\right) ^{2r}\right] +(2r-1-k)\xi _i\left[ (2r-1) {v}_j(t_1,t_2)^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_i(t_1,t_2)-\overline{x_i}\right) ^{2r}\right] +k\eta _{i}\left[ (2r-1)\left( y_{j}(t_1,t_2)-\overline{y_j}\right) ^{2r}\right. \right. \\&\left. \left. \qquad +\,\left( y_i(t_1,t_2)-\overline{y_i}\right) ^{2r}\right] +(2r-1-k)\eta _i\left[ (2r-1) {v}_j(t_1,t_2) ^{2r}+\left( y_i(t_1,t_2)-\overline{y_i}\right) ^{2r}\right] \right\} . \end{aligned}$$
(11)

Lemma 3

Assume Assumptions 1–3 hold, with the same P and Q, one has from Lemma 2

$$\begin{aligned}&\frac{\partial \left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^\text{{T}}P\left( u(t_1,t_2)-u^*\right) ^r}{\partial t_1} \le -2\sum _{i=1}^mrp_iB_ia_1\left( x_i-x_i^*\right) ^{2r} \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\alpha _j\left[ (2r-1) \left( x_i(t_1,t_2)-x_i^*\right) ^{2r}+\left( x_j\left( t_1-\sigma ,t_2\right) -x_j^*\right) ^{2r}\right] \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\beta _j\left[ (2r-1)\left( x_i(t_1,t_2)-x_i^*\right) ^{2r}+\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2}B_{i}\left\{ 2rk \left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r}\right. \\&\left. \qquad +\,(2r-1-k)\left[ (2r-1) \overline{u}_i(t_1-h,t_2)^{2r}+\left( x_i(t_1,t_2)-x_i^*\right) ^{2r}\right] \right\} \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2} |s_{ij}|\left\{ k\alpha _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_j(t_1-\sigma ,t_2)-x_j^*\right) ^{2r}\right] +(2r-1-k)\alpha _j\left[ (2r-1)\overline{u}_i(t_1-h,t_2)^{2r}\right. \right. \\&\left. \left. \qquad +\,\left( x_j(t_1-\sigma ,t_2)-x_j^*\right) ^{2r}\right] +k\beta _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r} \right. \right. \\&\qquad \left. \left. +\,\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] +(2r-1-k)\beta _j\left[ (2r-1) \overline{u}_i(t_1-h,t_2)^{2r}\right. \right. \\&\left. \left. \qquad +\,\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] \right\} , \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial \left[ \left( z(t_1,t_2)-z^*\right) ^r\right] ^\text{{T}}Q\left( z(t_1,t_2)-z^*\right) ^r}{\partial t_2} \le -2\sum _{i=1}^mrq_iD_ic_1\left( y_i-y_i^*\right) ^{2r} \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\xi _i\left[ (2r-1) \left( y_j(t_1,t_2)-y_j^*\right) ^{2r}+\left( x_i(t_1-\delta ,t_2)-x_i^*\right) ^{2r}\right] \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\eta _i\left[ (2r-1) \left( y_j(t_1,t_2)-y_j^*\right) ^{2r}+\left( y_i(t_1,t_2-\eta )-y_i^*\right) ^{2r}\right] \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_{i}c_{2}D_{i}\left\{ 2rk \left( y_{i}(t_1,t_2)-y_i^*\right) ^{2r}\right. \\&\qquad \left. +(2r-1-k)\left[ (2r-1) \overline{v}_i(t_1,t_2-d)^{2r}+\left( y_i(t_1,t_2)-y_i^*\right) ^{2r}\right] \right\} \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_{j}c_{2} |t_{ji}|\left\{ k\xi _{i}\left[ (2r-1)\left( y_{j}(t_1,t_2)-y_j^*\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_i(t_1-\delta ,t_2)-x_i^*\right) ^{2r}\right] +(2r-1-k)\xi _i\left[ (2r-1)\overline{v}_j(t_1,t_2-d)^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_i(t_1-\delta ,t_2)-x_i^*\right) ^{2r}\right] +k\eta _{i}\left[ (2r-1)\left( y_{j}(t_1,t_2)-y_j^*\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( y_i(t_1,t_2-\eta )-y_i^*\right) ^{2r}\right] +(2r-1-k)\eta _i\left[ (2r-1)\overline{v}_j(t_1,t_2-d)^{2r}\right. \right. \\&\left. \left. \qquad +\,\left( y_i(t_1,t_2-\eta )-y_i^*\right) ^{2r}\right] \right\} . \end{aligned}$$
(13)

Proof

We first prove the inequality (12). Under Assumptions 2–3, one has

$$\begin{aligned}&\frac{\partial \left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^\text{{T}}P\left( u(t_1,t_2)-u^*\right) ^r}{\partial t_1} \\= \,& 2r\left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^\text{{T}}P\left( u(t_1,t_2)-u^*\right) ^{r-1}\left\{ -A\left( x(t_1,t_2)\right) \left[ B\left( x(t_1,t_2)\right) -B(x^*)\right] \right. \\&\quad \left. +\,A\left( x(t_1,t_2)\right) S\left[ f\left( x(t_1-\sigma ,t_2),y(t_1,t_2-\tau )\right) -f(x^*,y^*)\right] \right\} \\= & -2\sum _{i=1}^{m}r\left( x_i(t_1,t_2)-x_i^*\right) ^{2r-1}p_ia_i\left( x_i(t_1,t_2)\right) \left[ b_i\left( x_i(t_1,t_2)\right) -b_i(x_i^*)\right] \\&-\,2r\sum _{i=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left( x_i(t_1,t_2)-x_i^*\right) ^k \overline{u}_{i}(t_1-h,t_2)^{2r-1-k}p_ia_i\left( x_i(t_1,t_2)\right) \left[ b_i\left( x_i(t_1,t_2)\right) -b_i(x_i^*)\right] \\&+\,2r\sum _{i=1}^{m}\sum _{j=1}^{m}\left( x_i(t_1,t_2)-x_i^*\right) ^{2r-1}p_is_{ij}a_i\left( x_i(t_1,t_2)\right) \left[ f_j\left( x_j(t_1-\sigma ,t_2),y_j(t_1,t_2-\tau )\right) -f_j\left( x_j^*,y_j^*\right) \right] \\&+\,2r\sum _{i=1}^{m}\sum _{k=0}^{2r-2}\sum _{j=1}^{m}C_{2r-1}^{k}a_i\left( x_i(t_1,t_2)\right) \left( x_i(t_1,t_2)-x_i^*\right) ^k\overline{u}_{i}(t_1-h,t_2)^{2r-1-k}p_is_{ij} \\&\qquad \quad \left[ f_j\left( x_j(t_1-\sigma ,t_2),y_j(t_1,t_2-\tau )\right) -f_j\left( x_j^*,y_j^*\right) \right] \\\le & -2\sum _{i=1}^{m}rp_iB_ia_1\left( x_i(t_1,t_2)-x_i^*\right) ^{2r} +2\sum _{i=1}^{m}\sum _{j=1}^{m}r|x_i(t_1,t_2)-x_i^*|^{2r-1}p_ia_2 \\&\times |s_{ij}|\left| f_j\left( x_j(t_1-\sigma ,t_2),y_j(t_1,t_2-\tau )\right) -f_j\left( x_j^*,y_j^*\right) \right| \\&+\,2r\sum _{i=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left| x_i\left( t_1,t_2\right) -x_i^*\right| ^k \left| \overline{u}_{i}\left( t_1-h,t_2\right) \right| ^{2r-1-k}p_ia_2B_i\left| x_i(t_1,t_2)-x_i^*\right| \\&+\,2r\sum _{i=1}^{m}\sum _{j=1}^{m}\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left| x_i(t_1,t_2)-x_i^*\right| ^k \left| \overline{u}_{i}\left( t_1-h,t_2\right) \right| ^{2r-1-k}p_ia_2|s_{ij}| \\&\times \,\left| f_j\left( x_j\left( t_1-\sigma ,t_2\right) ,y_j\left( t_1,t_2-\tau \right) \right) -f_j\left( x_j^*,y_j^*\right) \right| . \end{aligned}$$
(14)

Using Lemma 2 and inequalities (6)–(8), one can obtain

$$\begin{aligned}&\frac{\partial \left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^TP\left( u(t_1,t_2)-u^*\right) ^r}{\partial t_1} \le -2\sum _{i=1}^mrp_iB_ia_1\left( x_i-x_i^*\right) ^{2r} \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\alpha _j\left[ (2r-1) \left( x_i(t_1,t_2)-x_i^*\right) ^{2r}+\left( x_j(t_1-\sigma ,t_2)-x_j^*\right) ^{2r}\right] \\&\qquad +\,\sum _{i=1}^m\sum _{j=1}^mp_ia_2|s_{ij}|\beta _j\left[ (2r-1)\left( x_i(t_1,t_2)-x_i^*\right) ^{2r} +\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2}B_{i}\left\{ 2rk \left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r}\right. \\&\qquad \left. +\,(2r-1-k)\left[ (2r-1) \overline{u}_i(t_1-h,t_2)^{2r}+\left( x_i(t_1,t_2)-x_i^*\right) ^{2r}\right] \right\} \\&\qquad +\,\frac{1}{2r-1}\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_{i}a_{2} \left| s_{ij}\right| \left\{ k\alpha _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_j(t_1-\sigma ,t_2)-x_j^*\right) ^{2r}\right] +(2r-1-k)\alpha _j\left[ (2r-1)\overline{u}_i(t_1-h,t_2)^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( x_j (t_1-\sigma ,t_2)-x_j^*\right) ^{2r}\right] +k\beta _{j}\left[ (2r-1)\left( x_{i}(t_1,t_2)-x_i^*\right) ^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] +(2r-1-k)\beta _j\left[ (2r-1) \overline{u}_i(t_1-h,t_2)^{2r}\right. \right. \\&\qquad \left. \left. +\,\left( y_j(t_1,t_2-\tau )-y_j^*\right) ^{2r}\right] \right\} . \end{aligned}$$
(15)

Using the above similar method, one can obtain the inequality (13).

Theorem 1

Consider system (2). Assume Assumptions 1–3 hold. There exists a positive integer \(r\ge 1\) and two positive definite diagonal matrices \(P_{m\times m},~Q_{m\times m}\), such that

$$ -2ra_1PB+M+\Vert E\Vert ^{2r}\Vert W\Vert I<0,\quad -2rc_1QD+N+\Vert V\Vert ^{2r}\Vert L\Vert I<0, $$
(16)

where \(B={\text {diag}}(B_1,\ldots ,B_m),\) \(~D={\text {diag}}(D_1,\ldots ,D_m),\) \(P={\text {diag}}(p_1,~p_2,\ldots ,p_m),\) \(~E=(e_{ij})_{m \times m}\),\(~Q=\) \({\text {diag}}(q_1,~q_2,\ldots ,q_m)\), \(M={\text {diag}}(m_1,~m_2,\ldots ,m_m)\),\(~W={\text {diag}}(w_1,~w_2,\ldots ,w_m)\), \(~V=(v_{ji})_{m \times m}\), \(N={\text {diag}}(n_1,~n_2,\ldots ,n_m)\), \(~L={\text {diag}}(l_1,~l_2,\ldots ,l_m)\), with \(m_{i}=\sum \nolimits _{j=1}^m(p_ia_2|s_{ij}|(\alpha _j+\beta _j)(2r-1) +p_ja_2|s_{ji}|\alpha _i+q_jc_2|t_{ji}|\xi _i +\sum \nolimits _{k=0}^{2r-2}C_{2r-1}^{k}(p_ia_2|s_{ij}|k(\alpha _j+\beta _j) +p_ja_2|s_{ji}| \alpha _i+q_jc_2|t_{ji}|\xi _i)) +\frac{1}{2r-1}\sum \nolimits _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2B_i (2rk+2r-1-k),~ w_{i}=\sum \nolimits _{k=0}^{2r-2}\{C_{2r-1}^{k}p_ia_2B_i(2r-1-k) +\sum \nolimits _{j=1}^mC_{2r-1}^{k}p_ia_2|s_{ij}|(2r-1-k)(\alpha _j+\beta _j)\}, ~n_{i}=\sum\nolimits _{j=1}^m(q_ic_2|t_{ij}|(\xi _j+\eta _j)(2r-1) +q_jc_2|t_{ji}|\eta _i+p_ja_2|s_{ji}|\beta _i +\sum\nolimits _{k=0}^{2r-2}C_{2r-1}^{k}(q_ic_2|t_{ij}|k(\xi _j+\eta _j)\) \(+q_jc_2|t_{ji}| \eta _i+p_ja_2|s_{ji}|\beta _i)) +\frac{1}{2r-1}\sum \nolimits _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2D_i(2rk+2r-1-k), ~l_{i}=\sum \nolimits _{k=0}^{2r-2}\{C_{2r-1}^{k}q_ic_2D_i(2r-1-k) +\sum \nolimits _{j=1}^mC_{2r-1}^{k}q_ic_2|t_{ij}|(2r-1-k)(\xi _j+\eta _j)\},~i=1,~2,\ldots ,m.\) Then, the equilibrium point of system (2) is globally asymptotically stable.

Proof

Based on (2), we define the following Lyapunov functional

$$ V=V_1+V_2, $$
(17)

with

$$\begin{aligned} V_1= & \left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^{\text {T}}P\left( u(t_1,t_2)-u^*\right) ^r \\&+\,\sum _{i=1}^m\sum _{j=1}^mp_ja_2|s_{ji}|\alpha _i\int _{t_1-\sigma }^{t_1}\left[ x_i(s,t_2)- x_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2B_i(2r-1-k)\int _{t_1-h}^{t_1} \overline{u}_i(s,t_2)^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ja_2|s_{ji}| \alpha _i\int _{t_1-\sigma }^{t_1}\left[ x_i(s,t_2)-x_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2|s_{ij}|(2r-1-k) \left( \alpha _j+\beta _{j}\right) \int _{t_1-h}^{t_1}\overline{u}_i(s,t_2)^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\xi _i\int _{t_1-\delta }^{t_1}\left[ x_i(s,t_2)-x_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_jc_2|t_{ji} |\xi _{i}\int _{t_1-\delta }^{t_1}\left[ x_i(s,t_2)-x_i^*\right] ^{2r}{\text {d}}s, \end{aligned}$$
(18)
$$\begin{aligned} V_2= & \left[ \left( z(t_1,t_2)-z^*\right) ^r\right] ^\text{{T}}Q\left( z(t_1,t_2)-z^*\right) ^r \\&+\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\eta _i\int _{t_2-\eta }^{t_2}\left[ y_i(t_1,s)- y_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2D_i(2r-1-k)\int _{t_2-d}^{t_2} \overline{v}_i(t_1,s)^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_jc_2|t_{ji}|\eta _i \int _{t_2-\eta }^{t_2}\left[ y_i(t_1,s)-y_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2|t_{ij}|(2r-1-k) \left( \eta _j+\xi _{j}\right) \int _{t_2-d}^{t_2}\overline{v}_i(t_1,s)^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^mp_ja_2|s_{ji}|\beta _i\int _{t_2-\tau }^{t_2}\left[ y_i(t_1,s)-y_i^*\right] ^{2r}{\text {d}}s \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ja_2|s_{ji}|\beta _i \int _{t_2-\tau }^{t_2}\left[ y_i(t_1,s)-y_i^*\right] ^{2r}{\text {d}}s . \end{aligned}$$
(19)

The derivative of \(V(x(t_1,t_2),y(t_1,t_2))\) along \(\zeta (t_1,t_2)=\left( \begin{array}{ll} \frac{\partial x(t_1,t_2)}{\partial t_1},~~~ \frac{\partial y(t_1,t_2)}{\partial t_2} \end{array} \right) ^\text{{T}} \) is given by

$$\begin{aligned} \nabla _{\zeta }V\left( \left[ x(t_1,t_2),y(t_1,t_2)\right] ^\text{{T}}\right)= & (\nabla V)^\text{{{T}}} \zeta (t_1,t_2) \\= & \left[ \frac{\partial V}{\partial x}~~\frac{\partial V}{\partial y}\right] \zeta (t_1,t_2) \\= & \frac{\partial V_1(t_1,t_2)}{\partial x(t_1,t_2)}\frac{\partial x(t_1,t_2)}{\partial t_1}+ \frac{\partial V_2(t_1,t_2)}{\partial y(t_1,t_2)}\frac{\partial y(t_1,t_2)}{\partial t_2} \\= & \frac{\partial V_1(t_1,t_2)}{\partial t_1}+\frac{\partial V_2(t_1,t_2)}{\partial t_2}. \end{aligned}$$
(20)

Then, one has

$$\begin{aligned} \nabla _{\zeta }V= & \frac{\partial V_1(t_1,t_2)}{\partial t_1}+\frac{\partial V_2(t_1,t_2)}{\partial t_2}\\\le & \frac{\partial \left[ \left( u(t_1,t_2)-u^*\right) ^r\right] ^\text{{T}}P\left( u(t_1,t_2)-u^*\right) ^r}{\partial t_1}\\&+\,\sum _{i=1}^m\sum _{j=1}^mp_ja_2|s_{ji}|\alpha _i\left\{ \left[ x_i(t_1,t_2)- x_i^*\right] ^{2r}-\left[ x_i(t_1-\sigma ,t_2)-x_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2B_i(2r-1-k)\left\{ \overline{u}_i(t_1,t_2)^{2r}-\overline{u}_i(t_1-h,t_2)^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ja_2|s_{ji}| \alpha _i\left\{ \left[ x_i(t_1,t_2)-x_i^*\right] ^{2r}-\left[ x_i\left( t_1-\sigma ,t_2\right) -x_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2|s_{ij}|(2r-1-k) \left( \alpha _j+\beta _{j}\right) \left\{ \overline{u}_i(t_1,t_2)^{2r}-\overline{u}_i(t_1-h,t_2)^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\xi _i\left\{ \left[ x_i(t_1,t_2)-x_i^*\right] ^{2r}-\left[ x_i(t_1-\delta ,t_2)-x_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_jc_2|t_{ji} |\xi _{i}\left\{ \left[ x_i(t_1,t_2)-x_i^*\right] ^{2r}-\left[ x_i\left( t_1-\delta ,t_2\right) -x_i^*\right] ^{2r}\right\} \\&+\,\frac{\partial \left[ \left( z(t_1,t_2)-z^*\right) ^r\right] ^\text{{T}}Q\left( z(t_1,t_2)-z^*\right) ^r}{\partial t_2}\\&+\,\sum _{i=1}^m\sum _{j=1}^mq_jc_2|t_{ji}|\eta _i\left\{ \left[ y_i\left( t_1,t_2\right) -y_i^*\right] ^{2r} -\left[ y_i\left( t_1,t_2-\eta \right) -y_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2D_i(2r-1-k)\left\{ \overline{v}_i(t_1,t_2)^{2r}-\overline{v}_i(t_1,t_2-d)^{2r}\right\} \\&\left. +\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_jc_2|t_{ji}|\eta _i \left[ y_i(t_1,t_2)-y_i^*\right] ^{2r}-\left[ y_i\left( t_1,t_2-\eta \right) -y_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2|t_{ij}|(2r-1-k) (\eta _j+\xi _{j})\left\{ \overline{v}_i(t_1,t_2)^{2r}-\overline{v}_i(t_1,t_2-d)^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^mp_ja_2|s_{ji}|\beta _i\left\{ \left[ y_i(t_1,t_2)-y_i^*\right] ^{2r}- \left[ y_i(t_1,t_2-\tau )-y_i^*\right] ^{2r}\right\} \\&+\,\sum _{i=1}^m\sum _{j=1}^m\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ja_2|s_{ji}|\beta _i\left\{ \left[ y_i(t_1,t_2)-y_i^*\right] ^{2r}-\left[ y_i(t_1,t_2-\tau )-y_i^*\right] ^{2r}\right\} . \end{aligned}$$

According to Lemma 3, one gets

$$\begin{aligned} \nabla _{\zeta }V\le & \sum _{i=1}^m\left\{ -2rp_iB_ia_1+\sum _{j=1}^m[p_ia_2|s_{ij} \left| \left( \alpha _j+\beta _j\right) (2r-1) +p_ja_2\right| s_{ji}|\alpha _i+q_jc_2|t_{ji}|\xi _i\right. \\&\left. +\,\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left[ p_ia_2|s_{ij}|k\left( \alpha _j+\beta _j\right) +p_ja_2|s_{ji}| \alpha _i+q_jc_2|t_{ji}|\xi _i\right] \right. \\&\left. +\,\frac{1}{2r-1}\sum _{k=0}^{2r-2}C_{2r-1}^{k}p_ia_2B_i \left( 2rk+2r-1-k\right) \right\} \left( x_i-x_i^*\right) ^{2r} \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}\left\{ C_{2r-1}^{k}p_ia_2B_i(2r-1-k)\right. \\&\left. +\,\sum _{j=1}^mC_{2r-1}^{k}p_ia_2|s_{ij}|(2r-1-k)\left( \alpha _j+\beta _j\right) \right\} \left[ \overline{u}_i\right] ^{2r} \\&+\,\sum _{i=1}^m\left\{ -2rq_iD_ic_1+\sum _{j=1}^m\left[ q_ic_2|t_{ij}|\left( \xi _j+\eta _j\right) (2r-1)+q_jc_2|t_{ji}|\eta _i+p_ja_2|s_{ji}|\beta _i\right. \right. \\&\left. \left. +\,\sum _{k=0}^{2r-2}C_{2r-1}^{k}\left[ q_ic_2|t_{ij}|k\left( \xi _j+\eta _j\right) +q_jc_2|t_{ji}| \eta _i+p_ja_2|s_{ji}|\beta _i\right] \right] \right. \\&\left. +\,\frac{1}{2r-1}\sum _{k=0}^{2r-2}C_{2r-1}^{k}q_ic_2D_i \left( 2rk+2r-1-k\right) \right\} \left( y_i-y_i^*\right) ^{2r} \\&+\,\sum _{i=1}^m\sum _{k=0}^{2r-2}\left\{ C_{2r-1}^{k}q_ic_2D_i(2r-1-k)\right. \\&\left. +\,\sum _{j=1}^mC_{2r-1}^{k}q_ic_2|t_{ij}|(2r-1-k)(\xi _j+\eta _j)\right\} [\overline{v}_i]^{2r} \\=\, & \left[ \left( x(t_1,t_2)-x^*\right) ^{r}\right] ^\text{{T}}\left( -2rPBa_1+M\right) \left( x(t_1,t_2)-x^*\right) ^{r} \\&+\,\left[ \left( y(t_1,t_2)-y^*\right) ^{r}\right] ^\text{{T}}(-2rQDc_1+N)\left( y(t_1,t_2)-y^*\right) ^{r} \\&+\,\left[ (E\left( x(t_1,t_2)-x^*)\right) ^{r}\right] ^\text{{T}}W\left( E\left( x(t_1,t_2)-x^*\right) \right) ^{r} \\&+\,\left[ \left( V\left( y(t_1,t_2)-y^*\right) \right) ^{r}\right] ^\text{{T}}L\left( V\left( y(t_1,t_2)-y^*\right) \right) ^{r} \\\le & \left[ \left( x(t_1,t_2)-x^*\right) ^{r}\right] ^\text{{T}}(-2rPBa_1+M)\left( x(t_1,t_2)-x^*\right) ^{r} \\&+\,\left[ \left( y(t_1,t_2)-y^*\right) ^{r}\right] ^\text{{T}}(-2rQDc_1+N)\left( y(t_1,t_2)-y^*\right) ^{r} \\&+\,\Vert E\Vert \Vert x(t_1,t_2)-x^*\Vert \cdots \cdots \Vert E\Vert \Vert x(t_1,t_2)-x^*\Vert \\&\Vert W\Vert \Vert E\Vert \Vert x(t_1,t_2)-x^*\Vert \cdots \cdots \Vert E\Vert \Vert x(t_1,t_2)-x^*\Vert \\&+\,\Vert V\Vert \Vert y(t_1,t_2)-y^*\Vert \cdots \cdots \Vert V\Vert \Vert y(t_1,t_2)-y^*\Vert \\&\Vert L\Vert |V\Vert \Vert y(t_1,t_2)-y^*\Vert \cdots \cdots \Vert V\Vert \Vert y(t_1,t_2)-y^*\Vert \\= & \left[ \left( x(t_1,t_2)-x^*\right) ^{r}\right] ^\text{{T}}(-2ra_1PB+M+\Vert E\Vert ^{2r}\Vert W\Vert I)\left( x(t_1,t_2)-x^*\right) ^{r} \\&+\,\left[ \left( y(t_1,t_2)-y^*\right) ^{r}\right] ^\text{{T}}(-2rc_1QD+N+\Vert V\Vert ^{2r}\Vert L\Vert I)(y(t_1,t_2)-y^*)^{r}. \end{aligned}$$
(21)

Then, according to (16), it concludes that the equilibrium point of system (2) is globally asymptotically stable. This completes the proof.

Remark 4

The problem of positive real control for two-dimensional (2-D) discrete delayed systems has been considered in [16]. Compared with model (1) in [16], our model (2) is more general since it considers the interaction between two neural networks and it is a neutral neural network. Moreover, the LMI conditions (12) and (22) in [16] are more difficult to be checked than condition (16) of this paper when the dimension of the states of the discussed model is not small.

Remark 5

Two-dimensional (2-D) complex networks with randomly occurring nonlinearities have been proposed in [22, 23]. Compared with [22, 23], our contribution of this paper is twofold: (1) In this paper , the Cohen–Grossberg BAM neural network model (2) considers the interaction between two neural networks and is neutral. (2) Condition (16) of this paper is simpler to be obtained in the application than conditions (8) and (16) in [22] and conditions (17) and (18) in [23], which are more complicated when the dimension of the states of the discussed model is large.

In system (2), define \(a_i(x_i(\cdot ))=1,~c_j(y_j(\cdot ))=1\), we consider the following simple model

$$ \left\{ \begin{array}{lllll} \frac{\partial x_i(t_1,t_2)}{\partial t_1}+\sum \limits _{j=1}^{m}e_{ij}\frac{\partial x_j(t_1-h,t_2)}{\partial t_1}=-\left\{ b_i(x_i(t_1,t_2)) -\sum \limits _{j=1}^{m}s_{ij}f_j(x_j(t_1-\sigma ,t_2),y_j(t_1,t_2-\tau )) +I_i\right\} ,\\ \frac{\partial y_j(t_1,t_2)}{\partial t_2}+\sum \limits _{i=1}^{m}v_{ji}\frac{\partial y_i(t_1,t_2-d)}{\partial t_2}=-\left\{ d_j(y_j(t_1,t_2)) -\sum \limits _{i=1}^{m}t_{ji}g_i(x_i(t_1-\delta ,t_2),y_i(t_1,t_2-\eta )) +J_j\right\} , \end{array}\right. $$
(22)

where \(i,j=1,2,\ldots ,m\). Then, one has the following result according to Theorem 1.

Corollary 1

Assume Assumptions 1 and 2 hold, if one can choose appropriate diagonal matrices \(P_{m\times m},~Q_{m\times m}\) such that

$$ -2PB+M+\Vert E\Vert ^{2}\Vert W\Vert I<0,~~~ -2QD+N+\Vert V\Vert ^{2}\Vert L\Vert I<0, $$
(23)

where \(B=\text{{diag}}(B_1,\ldots ,B_m),\) \(D=\text{{diag}}(D_1,\ldots ,D_m),\) \(P=\text{{diag}}(p_1,p_2,\ldots ,p_m),\) \(E=(e_{ij})_{m \times m}\), \(Q=\) \(\text{{diag}}(q_1,q_2,\ldots ,q_m)\), \(M=\text{{diag}}(m_1,m_2,\ldots ,m_m)\), \(W=\text{{diag}}(w_1,w_2,\ldots ,w_m)\), \( V=(v_{ji})_{m \times m}\), \(N=\text{{diag}}(n_1,n_2,\ldots ,n_m)\), \( L=\text{{diag}}(l_1,l_2,\ldots ,l_m)\), \(s=\max \limits _{i,j}(|s_{ij}|)\), \(\alpha =\max \limits _{j}(\alpha _{j})\), \(\beta =\max \limits _{j}(\beta _{j})\), \(t=\max \limits _{i,j}(|t_{ji}|)\), \(\xi =\max \limits _{i}(\xi _{i})\), \(\eta =\max \limits _{i}(\eta _{i})\) with \(m_i=mp_is(\alpha +\beta )+2s\alpha tr(P)+2t\xi tr(Q)+p_iB_i\), \(w_i=p_iB_i+mp_is(\alpha +\beta )\), \(n_i=mq_it(\xi +\eta )+2t\eta tr(Q)+2s\beta tr(P)+q_iD_i\), \(l_i=q_iD_i+mq_it(\xi +\eta )\), the equilibrium point of system (22) is globally asymptotically stable.

To date, there are few literatures on the event-triggered stability of neutral-type Cohen–Grossberg BAM neural networks. However, the on-board resources are always limited and the event-triggered strategy is a good choice to deal with the limitations [28, 29]. Hence, we introduce the event-triggered strategy in our model. For simplification, in Eq. (22), we let \(e_{ij}=0,~v_{ji}=0,~\sigma =0,~\tau =0,~\delta =0,~ \eta =0\) and \(b_i(0)=0,~d_j(0)=0\). Moreover, we consider the event-triggered strategy in the activation functions \(f_j\) and \(g_i\). Then, we have the following model.

$$ \left\{ \begin{array}{lllll} \frac{\partial x_i(t_1,t_2)}{\partial t_1}=-\left\{ b_i(x_i(t_1,t_2)) -\sum \limits _{j=1}^{m}s_{ij}f_j\left( x_j\left( t_1^k,t_2^k\right) ,y_j\left( t_1^k,t_2^k\right) \right) +I_i\right\} ,\\ \frac{\partial y_j(t_1,t_2)}{\partial t_2}=-\left\{ d_j(y_j(t_1,t_2)) -\sum \limits _{i=1}^{m}t_{ji}g_i\left( x_i\left( t_1^k,t_2^k\right) ,y_i\left( t_1^k,t_2^k\right) \right) +J_j\right\} , \end{array}\right. $$
(24)

where \(i,j=1,2,\ldots ,m\). \({t_1^k},~{t_2^k}\), \(k=0,1,2,\ldots \) are the information broadcasting time sequences of the ith neuron. For \(t_1\in [t_1^k,t_1^{k+1}),~t_2\in [t_2^k,~t_2^{k+1})\), we define the state measurement errors are

$$ e_{xi}(t_1,t_2)=x_i\left( t_1^k,t_2^k\right) -x_i(t_1,t_2), \quad e_{yi}(t_1,t_2)=y_i\left( t_1^k,t_2^k\right) -y_i(t_1,t_2). $$
(25)

The event-triggering conditions for neuron i are designed as

$$ |e_{xi}(t_1,t_2)|=\kappa _1|{x_i\left( t_1^k,t_2^k\right) }-x_i^*|,~~ |e_{yi}(t_1,t_2)|=\kappa _2|{y_i\left( t_1^k,t_2^k\right) }-y_i^*|, $$
(26)

where \(\kappa _1>0\) and \(\kappa _2>0\) are constants. With the inequality method, it is easy to see that \(|e_{xi}(t_1,t_2)|=\kappa _1|x_i(t_1^k,t_2^k)-x_i^*| =\kappa _1|e_{xi}(t_1,t_2)+x_i(t_1,t_2)-x_i^*| \le \kappa _1|e_{xi}(t_1,t_2)|+\kappa _1|x_i(t_1,t_2)-x_i^*|\), then

$$ |e_{xi}(t_1,t_2)|\le \frac{\kappa _1}{1-\kappa _1}|x_i(t_1,t_2)-x_i^*|, $$
(27)

where \(\kappa _1\in (0,1)\). Also, one can get

$$ |e_{yi}(t_1,t_2)|\le \frac{\kappa _2}{1-\kappa _2}|y_i(t_1,t_2)-y_i^*|, $$
(28)

where \(\kappa _2\in (0,1)\).

Corollary 2

Under the event-triggering condition (26), Assumptions 1 and 2 hold, and \(b_i'(x_i)<B_i^1,~d_j'(y_j)<D_j^1\), \(B_i^1\) and \(D_j^1\) are constant. Choosing appropriate \(\kappa _1\in (0,1)\), \(\kappa _2\in (0,1)\), diagonal matrices \(P_{m\times m},~Q_{m\times m}\) to satisfy inequality (23) (here, \(\alpha _j\), \(\beta _j\), \(\xi _i\) and \(\eta _i\) are changed to be \(\frac{\alpha _j}{1-\kappa _1}\), \(\frac{\beta _j}{1-\kappa _2}\), \(\frac{\xi _i}{1-\kappa _1}\) and \(\frac{\eta _i}{1-\kappa _2}\), respectively), one has that the equilibrium point of system (24) is globally asymptotically stable.

Proof

According to Assumption 1, it is easy to see that \(|f_j(x_j(t_1^k,t_2^k),y_j(t_1^k,t_2^k))-f_j(\overline{x_j}, \overline{y_j})|= |f_j(e_{xj}+x_j,e_{yj}+y_j)-f_j(\overline{x_j},\overline{y_j})|\le \alpha _j|e_{xj}|+\alpha _j|x_j-\overline{x_j}|+\beta _j|e_{yj}|+ \alpha _j|y_j-\overline{y_j}|\). Using (27) and (28), one can obtain \(|f_j(x_j(t_1^k,t_2^k),y_j(t_1^k,t_2^k)) -f_j(\overline{x_j},\overline{y_j})|\le \frac{\alpha _j}{1-\kappa _1}|x_j-\overline{x_j}| +\frac{\beta _j}{1-\kappa _2}|y_j-\overline{y_j}|\). Similarly, \(|g_i(x_i(t_1^k,t_2^k),y_i(t_1^k,t_2^k))-g_i (\overline{x_i},\overline{y_i})|\le \frac{\xi _i}{1-\kappa _1}|x_i-\overline{x_i}|+ \frac{\eta _i}{1-\kappa _2}|y_i-\overline{y_i}|\). As a result, Lemma 2 is still satisfied. Hence, the equilibrium point of system (24) is globally asymptotically stable.

Next, we will show that the event-triggering time instants for each neuron are strictly positive, i.e., \(t_1^{k+1}-t_1^{k}>0\) and \(t_2^{k+1}-t_2^{k}>0\) for all \(k\in Z\). Between the two events, the evolutions of the \(e_{xi},~e_{yj}\) over \(t_1\in [t_1^k,t_1^{k+1}),~t_2\in [t_2^k,t_2^{k+1})\) are given by

$$ \left\{ \begin{array}{lllll} \frac{\partial e_{xi}(t_1,t_2)}{\partial t_1}=-\frac{\partial x_i(t_1,t_2)}{\partial t_1}=\left\{ b_i(x_i(t_1,t_2)) -\sum \limits _{j=1}^{m}s_{ij}f_j\left( x_j\left( t_1^k,t_2^k\right) ,y_j\left( t_1^k,t_2^k\right) \right) +I_i\right\} ,\\ \frac{\partial e_{yj}(t_1,t_2)}{\partial t_2}=-\frac{\partial y_j(t_1,t_2)}{\partial t_2}=\left\{ d_j(y_j(t_1,t_2)) -\sum \limits _{i=1}^{m}t_{ji}g_i\left( x_i\left( t_1^k,t_2^k\right) ,y_i\left( t_1^k,t_2^k\right) \right) +J_j\right\} , \end{array}\right. $$
(29)

Due to \(b_i(0)=0,~d_j(0)=0\) and \(b_i'(x_i)<B_i^1,~d_j'(y_j)<D_j^1\), one can get

$$ \left\{ \begin{array}{lllll} \frac{\partial |e_{xi}(t_1,t_2)|}{\partial t_1}\le |\frac{\partial |e_{xi}(t_1,t_2)|}{\partial t_1}|\le B_i^1|x_i\left( t_1^k,t_2^k\right) |+B_i^1|e_{xi}(t_1,t_2)| +\sum \limits _{j=1}^{m}|s_{ij}|\cdot |f_j\left( x_j\left( t_1^k,t_2^k\right) ,y_j\left( t_1^k,t_2^k\right) \right) | +I_i,\\ |\frac{\partial e_{yj}(t_1,t_2)}{\partial t_2}|\le \frac{\partial |e_{yj}(t_1,t_2)|}{\partial t_2}\le D_j^1|y_j\left( t_1^k,t_2^k\right) |+D_j^1|e_{yj}(t_1,t_2)| +\sum \limits _{i=1}^{m}|t_{ji}|\cdot |g_i\left( x_i\left( t_1^k,t_2^k\right) ,y_i\left( t_1^k,t_2^k\right) \right) | +J_j. \end{array}\right. $$
(30)

Let \(\widetilde{f}_i=B_i^1\left| x_i\left( t_1^k,t_2^k\right) \right| + \sum \nolimits _{j=1}^{m}|s_{ij}|\cdot \left| f_j\left( x_j\left( t_1^k,t_2^k\right) ,y_j\left( t_1^k,t_2^k\right) \right) \right| +I_i\) and \(\widetilde{g}_j=D_j^1\left| y_j\left( t_1^k,t_2^k\right) \right| + \sum \nolimits _{i=1}^{m}|t_{ji}|\cdot \left| g_i\left( x_i\left( t_1^k,t_2^k\right) ,y_i\left( t_1^k,t_2^k\right) \right) \right| +J_j\), it is easy to get that \(t_1^{k+1}-t_1^{k}>\frac{1}{B_i^1}ln(\frac{B_i^1\kappa _1}{\widetilde{f}_i}|x_i(t_1^k,t_2^k)-x_i^*|+1)\) and \(t_2^{k+1}-t_2^{k}>\frac{1}{D_j^1}ln(\frac{D_j^1\kappa _2}{\widetilde{g}_j}|y_j(t_1^k,t_2^k)-y_j^*|+1),\) for all \(k\in Z\). The proof is completed.

4 Illustrative examples

In this section, numerical examples are presented to demonstrate the effectiveness of our results.

Example 1

Consider the following two-dimensional neutral-type Cohen–Grossberg BAM neural networks:

$$ \left\{ \begin{array}{ll} \frac{\partial x_i(t_1,t_2)}{\partial t_1}+\sum \limits _{j=1}^{2}e_{ij}\frac{\partial x_j(t_1-0.2,t_2)}{\partial t_1}=-a_i(x_i(t_1,t_2))\left\{ b_i(x_i(t_1,t_2))\right. \\ \qquad\qquad\qquad \left. -\,\sum \limits _{j=1}^{2}s_{ij}f_j(x_j(t_1-0.1,t_2),y_j(t_1,t_2-0.2)) +I_i\right\} ,\quad i=1,2 \\ \frac{\partial y_j(t_1,t_2)}{\partial t_2}+\sum \limits _{i=1}^{2}v_{ji}\frac{\partial y_i(t_1,t_2-0.3)}{\partial t_2}=-c_j(y_j(t_1,t_2))\left\{ d_j(y_j(t_1,t_2))\right. \\ \qquad\qquad\qquad \left. -\,\sum \limits _{i=1}^{2}t_{ji}g_i(x_i(t_1-0.1,t_2),y_i(t_1,t_2-0.2)) +J_j\right\} ,~~~j=1,2 \end{array}\right. $$
(31)

where \(a_i(x_i(t_1,t_2))=5+{\text{cos}}(x_i),~\) \(f_j(x,y)=0.1|x|+0.1|y|,~\) \(b_i(x_i)=2.1x_i,\) \(~I_i=1,~\) \(c_j(y_j(t_1,t_2))=4+{\text{sin}}(y_j),~\) \(g_i(x,y)=0.1|x|+0.1|y|,~\) \(d_j(y_j)=3.1y_j,\) \(~J_j=2,~i,~j=1,~2.\) The initial value conditions given by \(x_1=\frac{40}{3} \theta +2+t_2~\), \(x_2=10 \theta +t_2~\), \(y_1=\frac{20}{3}\theta +1+t_1~\) \(y_2=\frac{40}{3} \theta +2-t_1~\), \(\theta \in [-0.3,0]\). Let \(r=1\),\(~B_i=2,~D_j=3\),\(~c_1=3,~c_2=5,~a_1=4,~a_2=6\),\(~s_{11}=0.1,~s_{12}=0.1,~s_{21}=0.4, ~s_{22}=0.4,~t_{11}=0.1,~t_{12}=0.1,~t_{21}=0.4, ~t_{22}=0.4,~i,j=1,2,\) \(p_i=2,~q_j=2,~\alpha _i=0.1,~\beta _i=0.1,~\xi _j=0.1,~\eta _j=0.1,~t_{ij}=0.1,~ v_{ji}=0.1,~i,j=1,2.\) With a simple calculation, one has \(m_i=29.44,~w_i=25.92,~n_i=35.12,~l_i=31.6,\) and \( -2ra_1PB+M+\Vert E\Vert ^{2r}\Vert W\Vert I=\left( \begin{array}{ll} -2.5185 &0\\ 0&-2.5185\\ \end{array} \right) <0,\) and \( -2rc_1QD+N+\Vert V\Vert ^{2r}\Vert L\Vert I=\left( \begin{array}{ll} -0.8294 &0\\ 0& -0.8294\\ \end{array} \right) <0.\) It is easy to verify that all conditions are satisfied. According to Theorem 1, one has that the equilibrium point \((x^*,y^*)\) (here, \(x^*=(x_1^*,x_2^*)^T=(0.0037,0.0201)^T,~y^* =(y_1^*,y_2^*)^T=(0.0066,0.0265)^T\)) of system (31) is existent and asymptotically stable. It can be seen from Figs. 1, 2, 3, 4, 5 and 6 that the equilibrium point \((x^*,y^*)\) of system (31) is indeed asymptotically stable under the above conditions.

Fig. 1
figure 1

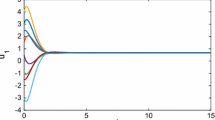
The numeric simulation of \(x_1(t_1,t_2)\) in system (31)

Full size image
Fig. 2
figure 2

The numeric simulation of \(x_2(t_1,t_2)\) in system (31)

Full size image
Fig. 3
figure 3

The numeric simulation of \(y_1(t_1,t_2)\) in system (31)

Full size image
Fig. 4
figure 4

The numeric simulation of \(y_2(t_1,t_2)\) in system (31)

Full size image
Fig. 5
figure 5

The numeric simulation of \(x_i\), \(y_j\) about \(t_1\) in system (31)

Full size image
Fig. 6
figure 6

The numeric simulation of \(x_i\), \(y_j\) about \(t_2\) in system (31)

Full size image

Example 2

For system (22), we define

$$ \left\{ \begin{array}{lll} \frac{\partial x_1(t_1,t_2)}{\partial t_1}+0.1\frac{\partial x_1(t_1-0.1,t_2)}{\partial t_1}=-(b_1(x_1(t_1,t_2)) -0.1f_1(x_1(t_1,t_2),y_1(t_1,t_2)) +I_1), \\ \frac{\partial y_1(t_1,t_2)}{\partial t_2}+0.1\frac{\partial y_1(t_1,t_2-0.1)}{\partial t_2}=-(d_1(y_1(t_1,t_2)) -0.1g_1(x_1(t_1,t_2),y_1(t_1,t_2)) +J_1), \end{array}\right. $$
(32)

where \(f_1(x,y)=2{\text{sin}}(x)+2{\text{sin}}(y), \) \(b_1(x_1)=1.5x_1,\) \(I_1=4,\) \(g_1(x,y)=2cos(x)+2cos(y)\), \(d_1(y_1)=1.5y_1, \) \(J_1=3,~\sigma =0,~\tau =0,~\delta =0,~\eta =0\). The initial value conditions given by \(x_1=\frac{40}{3} \theta +0.5+t_2~\), \(y_1=2\theta t_1~\), \(\theta \in [-0.1,0]\). One can calculate the equilibrium point. \(1.5x_1-0.1(2sin(x_1)+2sin(y_1))+4=0\) and \(1.5y_1-0.1(2cos(x_1)+2cos(y_1))+3=0\). Get \((x_1^*,y_1^*)=(-2.8166,-2.2054)\). Using the result, one can get \(B=1.4,~D=1.4,~e=0.1,~v=0.1,~s=0.1,~t=0.1,~m=1\), \(\alpha =2,~\beta =2,~\xi =2,~\eta =2\), \(P=p=4,~Q=q=3.\) With a simple calculation, one has \(m_1=mps(\alpha +\beta )+2sp\alpha +2tq\xi +pB=10,\) \(~w_1=pB+mps(\alpha +\beta )=7.2\), \(~n_1=mqt(\xi +\eta )+2tq\eta +2sp\beta +qD=8.2\), \(~l_1=qD+mqt(\xi +\eta )=5.4\). And \(-2PB+m_1+e^{2}w_1=-1.2\) and \(-2QD+n_1+v_1^{2}l_1=-0.2\). It is easy to verify that all conditions are satisfied. According to Corollary 1, one has that the equilibrium point \((x_1^*,y_1^*)=(-2.8166,-2.2054)\) of system (32) is existent and asymptotically stable. It can be seen from Figs. 7, 8, 9 and 10 that the equilibrium point \((x_1^*,y_1^*)\) of system (32) is indeed asymptotically stable under the above conditions.

Fig. 7
figure 7

The numeric simulation of \(x_1(t_1,t_2)\) in system (32)

Full size image
Fig. 8
figure 8

The numeric simulation of \(y_1(t_1,t_2)\) in system (32)

Full size image
Fig. 9
figure 9

The numeric simulation of \(x_1\), \(y_1\) about \(t_1\) in system (32)

Full size image
Fig. 10
figure 10

The numeric simulation of \(x_1\), \(y_1\) about \(t_2\) in system (32)

Full size image

Remark 6

In Figs. 1, 2, 3 and 4, the state variables tend to constants when \(t_1\) and \(t_2\) tend to infinity. That is, the state variables are asymptotically stable when \(t_1\) and \(t_2\) tend to infinity. Figures 5 and 6 show the numeric simulation of state variables in system (31) about \(t_1\) and \(t_2\), respectively. Similarly, Figs. 7, 8, 9 and 10 show the numerical solution of model (32). one can also see that the state variables tend to the constants when \(t_1\) and \(t_2\) tend to infinity.

Example 3

The dynamical process in gas absorption, water stream and air drying can be described by the following equation

$$ \frac{\partial ^2 s(x,t)}{\partial x\partial t}=a_0s(x,t)+a_1\frac{\partial s(x,t)}{\partial t}+a_2\frac{\partial s(x,t)}{\partial x}+bf(x,t). $$
(33)

where s(x, t) is an unknown function of x and t; \(a_0, a_1, a_2\) and b are real coefficients, f(x, t) is the input function. Considering the time delay, we change (33) to the following equation with \(t\in [-h, \infty )\)

$$ \frac{\partial ^2 s(x,t)}{\partial x\partial t}=-a_3\frac{\partial ^2 s(x,t-h)}{\partial x\partial t}+a_0s(x,t)+a_1\frac{\partial s(x,t)}{\partial t}+a_1\frac{\partial s(x,t-h)}{\partial t}+a_2\frac{\partial s(x,t)}{\partial x}+bf(x,t), $$
(34)

with the initial and boundary condition \(s(0,t)=\phi (0,t),~s(x,\theta )=\varphi (t,\theta ),~ \theta \in [-h,0]\). Define \(X(x,t)=s(x,t)-C\) and \(Y(x,t)=\frac{\partial s(x,t)}{\partial x}-a_1s(x,t)\), where C is a constant, the following 2-D system can be obtained:

$$ \left\{ \begin{array}{l} \frac{\partial X(x,t)}{\partial x}=a_1X+a_1C+Y, \\ \frac{\partial Y(x,t)}{\partial t}+a_3\frac{\partial Y(x,t-h)}{\partial t}=(a_1a_2+a_0)X+a_2Y+(a_1a_2+a_0)C+bf(x,t), \end{array}\right. $$
(35)

with the initial and boundary condition \(X(0,t)=s(0,t)-C=\phi (0,t)-C,~Y(x,\theta )=\frac{\partial s(x,\theta )}{\partial x}-a_1s(x,\theta ),~ \theta \in [-h,0]\). It is worth nothing that \(t_1=x\) is the space variable and \(t_2=t\) is the time variable.

Let \(a_0=1.25,~a_1=-1.5,~a_2=-1.5,~a_3=0.1,~b=1,~C=2,~f(x,t)=0.1*{\text{sin}}(X) +0.05*{\text{cos}}(Y)\,-\,(a_1a_2+a_0)X\) and \(s(0,t)=2*t,~s(x,\theta )=x^2+\theta ^2\), the system can be given by

$$\left\{ \begin{array}{l} \frac{\partial X(x,t)}{\partial x}=-1.5X+Y-3, \\ \frac{\partial Y(x,t)}{\partial t}+0.1\frac{\partial Y(x,t-h)}{\partial t}=-1.5Y+0.1*{\text{sin}}(X)+0.05*{\text{cos}}(Y)-2, \end{array}\right. $$

where initial and boundary conditions are \(X(0,t)=2*t-2,~Y(x,\theta )=2x+\theta ^2-a1(x^2+\theta ^2)\). For \(~h=0.2\), one can have \(P=1,~Q=2\), \(m_1=3.6,~w_1=3,~n_1=5.502,~l_1=3.102,\) and \(-2PB+m_1+e^{2}w_1=-0.2\) and \(-2QD+n_1+v_1^{2}l_1=-0.067\). It is easy to verify that all assumptions are satisfied. By using the MATLAB tool, one has that the equilibrium point is \((X^*,Y^*)=(1.1522,4.7283)\) in system (35), which is asymptotically stable. It can be seen in Figs. 11, 12, 13 and 14 that the equilibrium point \((X^*,Y^*)\) of system (35) is indeed asymptotically stable under the above conditions.

Fig. 11
figure 11

The numeric simulation of \(X(x,t)\) in system (35)

Full size image
Fig. 12
figure 12

The numeric simulation of \(Y(x,t)\) in system (35)

Full size image
Fig. 13
figure 13

The numeric simulation of \(X,~Y\) about x in system (35)

Full size image
Fig. 14
figure 14

The numeric simulation of \(X,~Y\) about t in system (35)

Full size image

5 Conclusions

The asymptotical stability problem of two-dimensional neutral-type Cohen–Grossberg BAM neural networks has been discussed in this paper. Mathematical models have first been designed to show two-dimensional structure and the neutral-type delays of Cohen–Grossberg BAM neural networks. Based on some inequality technique, a sufficient condition has been given to achieve the stability of two-dimensional neutral-type continuous Cohen–Grossberg BAM neural networks. Finally, numerical examples with the simulations have been provided to illustrate the usefulness of the obtained criterion.