1 Introduction

In recent years, interest has increased in the studies of laser beam propagating through atmospheric turbulence due to many applications (Andrews and Philips 1998; Baykal 2004; Eyyuboglu 2005; Cai and He 2006; Appl 2006; Noriega-Manez and Gutiérrez-Vega 2007; Korotkova and Gbur 2007; Lukin et al. 2012; Wang et al. 2015). In particular, new types of laser excitations have been introduced and investigated to promote their applications in free space optical communication (FSO), optical microscopy, wireless communications and optical micromanipulation (Allen et al. 1992; Kuga et al. 1997; Paterson et al. 2001; Ponomarenko 2001; Cai et al. 2003; Bishop et al. 2004; Wang et al. 2004,2012; Zhu et al. 2016). The so-called vortex hollow dark beams (vHDBs) have been extensively studied over the last few years due to their interesting properties (Dai et al. 2011; Ni and Zhou 2013; Zhou et al. 2013; Mei et al. 2015; Zhou and Zhou 2014; Guo et al. 2014; Kotlyar et al. 2015; Liu et al. 2015; Rubinsztein-Dunlop et al. 2017; Boufalah et al. 2018; Yaalou et al. 2019; Hricha et al. 2020a). The beams have zero intensity at the center surrounded by an annular spot (or an array bright spots) due to the embedded vortex charge. Furthermore, the beams possess a spirally wave-front phase, which makes them enable to carry the orbital angular momentum. In practical applications, the vortex charge of the beam can be used as optical traps for micro-particles as well as beam spanner (Gao et al. 2000; Simpson et al. 1997). The hollow vortex Gaussian beam represents the simplest and typical model for the hollow vortex beams which has been widely investigated in many laser papers. The propagation characteristics of the hollow vortex Gaussian beam in various optical systems including turbulent media have been researched (Zhou et al. 2013; Mei et al. 2015; Zhou and Zhou 2014). Recently, an extended form of the hollow vortex Gaussian beam, named as vortex cosine-hyperbolic Gaussian beam, has been introduced and its propagation in the turbulent atmosphere has been examined by our research group (Hricha et al. 2020b,2021a). Moreover, a generalized beam expression for the hollow vortex Gaussian field has been proposed in Hricha et al. 2021b, the obtained beam is called vortex-Hermite-cosh-Gaussian beam (vHChG). The vHChGB possesses three key parameters namely the beam orders, the decentered parameter b and the vortex charge number M. The beam is hollow dark array-like and can be reduced by choosing the appropriate values of the beam parameters to well-known laser beams including the vortex-Gaussian beam (Zhou et al. 2013), vortex Hermite-Gaussian beam (Kotlyar et al. 2015) and vortex-cosine-hyperbolic Gaussian beam (vChGB) (Hricha et al. 2020b). The intensity distribution pattern, the spot size and the central dark width of the vHChGB can be controlled by the appropriate choice of the beam parameters. The high degree of freedom in control of beam parameters offers a prospective technic for manipulating the pattern of the beam without the use of special optical media or potentials. With the embedded vortex charge, the vHCHGBs can be used in optical application as micro-particle traps; they may be able to trap both high- and low-index micro-particles as well as to set them into rotation by use of the OAM of light.

The evolution of intensity distribution of the vHChGB upon propagating in free space has been widely investigated in Ref. (Hricha et al. 2021b). The present paper is the extension of this previous work, and therefore is aimed at investigating the propagation properties of a vHChGB propagating in a turbulent atmosphere. The theoretical analysis is based on the extended Huygens–Fresnel integral and Rytov method. The evolution of a vHChGB propagating in the turbulent atmosphere, and the influence of the turbulence strength on the beam intensity distribution under different beam parameters conditions are investigated with numerical examples. The remainder of the manuscript is structured as follows: in the coming Section, we present the theoretical formulation for the propagation of a vHChGB in atmospheric turbulence, and derive a propagation equation for the average intensity distribution of the beam. In the third Section, the propagation properties of vHChGB through the turbulent atmosphere are illustrated numerically and discussed versus the turbulence strength under the change of the beam parameters. The main results are outlined in the conclusion part.

2 Propagation properties of a vHChG through turbulent atmosphere

In the rectangular coordinates system, the field of a vHChGB propagating along the z-axis is defined at the original plane of z = 0 as follows (Hricha et al. 2021b)

$$E\left( {x_{0} ,y_{0} ,z = 0} \right) = H_{p} \left( {\frac{\sqrt 2 }{{\omega_{0} }}x_{0} } \right)H_{q} \left( {\frac{\sqrt 2 }{{\omega_{0} }}y_{0} } \right)\cosh \left( {b\frac{{x_{0} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega_{0} }}} \right)e^{{ - \left( {\frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)}} \left( {x_{0} + iy_{0} } \right)^{M} ,$$
(1)

where \(\left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)\) are the transverse Cartesian coordinates in the source plane and \(\omega_{0}\) is the waist radius of the Gaussian part. b is the decentered beam parameter (or the parameter b for short) associated to the cosh part. M is an integer which denotes the topological charge of the vortex, and (p, q) are the mode indexes associated with the Hermite polynomials \(H_{p} \left( . \right)\) and \(H_{q} \left( . \right)\) in the x- and y-directions.

When b = 0, Eq. (1) reduces to the hollow vortex Hermite-Gaussian beam (Kotlyar et al. 2015). In the case M = 0, i.e., in the absence of the vortex, Eq. (1) will describe the well-known Hermite-cosh-Gaussian beam (Casperson and Tovar 1998; Tovar and Casperson 1998; Belafhal and Ibnchaikh 2000; Ibnchaikh et al. 2001; Hricha and Belafhal 2005). For convenience and without loss generality, we will consider in the following a vHCHGB with p = q, i.e., with x–y symmetry. The profile of the intensity of this beam at the initial plane z = 0 has been presented in Ref. (Hricha et al. 2021b), from which it was found that the intensity profile of a vHChGB is array-like with a dark central region surrounded by a multi-spot structure. The beam shape is mirror symmetric and can have two pattern configurations depending strongly on the value of the parameter b. Indeed, for small values of b (b < 1), the beam exhibits 4p lobes, including four main lobes which are located at the vertices of the squared beam spot. While for large values of b (saying b > 2) the beam is four-petal like.

Within the frame of the paraxial approximation, the propagation of a light beam through the turbulent atmosphere along the z-axis can be formulated by the extended Huygens–Fresnel diffraction integral (Andrews and Philips 1998)

$$E\left( {\vec{r},z} \right) = \frac{ik}{{2\pi z}}\exp \left( { - ikz} \right)\,\iint {E\left( {\vec{r}_{0} ,0} \right)\exp \left[ { - \frac{ik}{{2z}}\left( {\vec{r}_{0} - \vec{r}} \right)^{2} + \psi \left( {\vec{r}_{0} ,\vec{r},z} \right)} \right]d\vec{r}_{0} },$$
(2)

where \(\vec{r}_{0} = (x_{0} ,y_{0} )\) and \(\vec{r} = (x,y)\) are the transverse coordinates in the initial plane and receiver plane, respectively. z is the distance between the initial plane z = 0 and the receiver plane.\(\psi \left( {\vec{r}_{0} ,\vec{r},z} \right)\) denotes the random part for the complex phase of a spherical wave spreading from the source plane to the output plane, \(k = \frac{2\pi }{\lambda }\) is the wavenumber and \(\lambda\) is the wavelength of radiation in vacuum. Here, the integration is performed over the whole space for the unapertured light beam.

The average intensity of the vHChGB propagating through turbulent atmosphere is expressed as

$$\begin{gathered} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \iiint {\int {} }{\kern 1pt} E_{0} \left( {x_{01} ,y_{01} ,0} \right)E_{0} *\left( {x_{02} ,y_{02} ,0} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left[ { - \frac{ik}{{2z}}\left\{ {\left( {x_{01} - x} \right)^{2} + \left( {y_{01} - y} \right)^{2} - \left( {x_{02} - x} \right)^{2} - \left( {y_{02} - y} \right)^{2} } \right\}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\exp \left[ {\psi \left( {\vec{r}_{01} ,\vec{r}} \right) + \psi *\left( {\vec{r}_{02} ,\vec{r}} \right)} \right]} \right\rangle d\vec{r}_{01} d\vec{r}_{02} \,\,, \hfill \\ \end{gathered}$$
(3)

where * and 〈〉 denote the complex conjugation and the ensemble average over the medium statistics, respectively.

Within the framework of Rytov method and under weak atmosphere turbulence conditions, the ensemble average term in Eq. (3) is given as (Andrews and Philips 1998)

$$\left\langle {\exp \left[ {\psi \left( {x_{01} ,y_{01} ,x,y} \right) + \psi *\left( {x_{02} ,y_{02} ,x,y} \right)} \right]} \right\rangle {\kern 1pt} = \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left\{ {\left( {x_{01} - x_{02} } \right)^{2} + \left( {y_{01} - y_{02} } \right)^{2} } \right\}} \right],$$
(4)

where \(\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}}\) is the coherence length of a spherical wave propagating in the turbulent medium, with \(C_{n}^{2}\) is the refractive index structure constant of the medium.

Substituting from Eqs. (1) and (4) into Eq. (3), and recalling the binomial formula (Gradshteyn and Ryzhik 1994)

$$\left( {x + {\kern 1pt} iy{\kern 1pt} } \right)^{M} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{M} {a_{l}^{M} } x^{l} \left( {iy} \right)^{M - l} ,$$
(5a)

where

$$a_{l}^{M} = \frac{M!}{{l!\left( {M - l} \right){\kern 1pt} !}},$$
(5b)

the result can be written as:

$$\left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = 0}^{M} {\sum\limits_{n = 0}^{M} {a_{l}^{M} a_{n}^{M} } } \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {F_{n} \left( {x,y,x_{02} ,y_{02} } \right)G_{l} \left( {x,y,x_{02} ,y_{02} } \right)} } dx_{02} dy_{02} ,$$
(6a)

where

$$\begin{aligned} F_{n} \left( {x,y,x_{{02}} ,y_{{02}} } \right) = & x_{{02}}^{n} \left( { - iy_{{02}} } \right)^{{M - n}} H_{p} \left( {\frac{{\sqrt 2 }}{{\omega _{0} }}x_{{02}} } \right)H_{p} \left( {\frac{{\sqrt 2 }}{{\omega _{0} }}y_{{02}} } \right)\cosh \left( {b\frac{{x_{{02}} }}{{\omega _{0} }}} \right)\cosh \left( {b\frac{{y_{{02}} }}{{\omega _{0} }}} \right) \\ \times & \exp \left( { - \delta *x_{{02}}^{2} - \frac{{ikx}}{z}x_{{02}} } \right)\exp \left( { - \delta *y_{{02}}^{2} - \frac{{iky}}{z}y_{{02}} } \right), \\ \end{aligned}$$
(6b)

and

$$G_{l} \left( {x,y,x_{02} ,y_{02} } \right) = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {g_{l} \left( {x,y,x_{01} ,y_{01} ,x_{02} ,y_{02} } \right)dx_{01} dy_{01} } } ,$$
(6c)

with

$$\begin{aligned} g_{l} \left( {x,y,x_{{01}} ,y_{{01}} ,x_{{02}} ,y_{{02}} } \right) = & x_{{01}}^{l} \left( {iy_{{01}} } \right)^{{M - l}} H_{p} \left( {\frac{{\sqrt 2 }}{{\omega _{0} }}x_{{01}} } \right)\cosh \left( {b\frac{{x_{{01}} }}{{\omega _{0} }}} \right)\exp \left[ { - \delta x_{{01}}^{2} + \left( {\frac{{ikx}}{z} + \frac{{2x_{{02}} }}{{\rho _{0}^{2} }}} \right)x_{{01}} } \right] \\ \times & H_{p} \left( {\frac{{\sqrt 2 }}{{\omega _{0} }}y_{{01}} } \right)\cosh \left( {b\frac{{y_{{01}} }}{{\omega _{0} }}} \right)\exp \left[ { - \delta y_{{01}}^{2} + \left( {\frac{{iky}}{z} + \frac{{2y_{{02}} }}{{\rho _{0}^{2} }}} \right)y_{{01}} } \right]{\kern 1pt} {\kern 1pt} , \\ \end{aligned}$$
(6d)

δ is the auxiliary parameter defined by

$$\delta = \frac{ik}{{2z}} + \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }}.$$
(6e)

Using the explicit form of cosh (.) and the variable separation technique to perform the double integral in Eq. (6c), we can obtain

$$G_{l} \left( {x,y,x_{02} ,y_{02} } \right) = \left( i \right)^{M - l} \hat{g}_{{_{l} }} \left( {x,x_{02} } \right)\hat{g}_{{_{l} }} \left( {y,y_{02} } \right),$$
(7a)

with

$$\hat{g}_{l} \left( {v,v_{02} } \right) = \frac{1}{2}\left[ {\hat{g}_{l}^{ + } \left( {v,v_{02} } \right) + \hat{g}_{l}^{ - } \left( {v,v_{02} } \right)} \right]{\kern 1pt} ,$$
(7b)

and where

$$\hat{g}_{l}^{ \pm } \left( {v,v_{02} } \right){\kern 1pt} = \int\limits_{ - \infty }^{ + \infty } {u^{l} H_{p} \left( {\frac{\sqrt 2 }{{\omega_{0} }}u} \right)\exp \left( { - \delta u^{2} } \right)\exp \left[ {\left( {\frac{ikv}{z} + \frac{{2v_{02} }}{{\rho_{0}^{2} }} \pm \frac{b}{{\omega_{0} }}} \right)u} \right]} du.$$
(7c)

in which v represents either x or y.

Now, by recalling the following integral formula (Belafhal et al. 2020)

$$\int\limits_{ - \infty }^{ + \infty } {x^{l} H_{m} \left( {\alpha x} \right)e^{{ - px^{2} + 2qx}} } dx = \frac{1}{{2^{l} }}e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \sum\limits_{k = 0}^{\left[\frac{m}{2}\right]}{\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} \left( {\frac{\alpha }{i\sqrt p }} \right)^{m + l - 2k} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right),{\text{ with Re}}p> 0$$
(8)

Equation (7c) can be expressed as:

$$g_{l}^{ \pm } \left( {v,v_{02} } \right) = \frac{1}{{2^{l} }}e^{{\frac{{q_{ \pm }^{2} \left( {v,v_{02} } \right)}}{\delta }}} \sqrt {\frac{\pi }{\delta }} \sum\limits_{s = 0}^{\left[\frac{p}{2}\right]} {\frac{{\left( { - 1} \right)^{s} p!}}{{s!\left( {p - 2s} \right)!}}} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{p + l - 2s} H_{p + l - 2s} \left( {\frac{{iq_{ \pm } \left( {v,v_{02} } \right)}}{\sqrt \delta }} \right),$$
(9a)

with

$$q_{ \pm } \left( {v,v_{02} } \right) = \frac{ikv}{{2z}} + \frac{{v_{02} }}{{\rho_{0}^{2} }} \pm \frac{b}{{2\omega_{0} }},$$
(9b)

Substituting Eqs. 9(a) and (7a) into Eq. (6a), we obtain

$$\begin{aligned} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = & \frac{1}{{2^{M + 2} }}\frac{\pi }{\delta }\left( {\frac{k}{2\pi z}} \right)^{2} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{M} \sum\limits_{l = 0}^{M} {\sum\limits_{n = 0}^{M} {a_{l}^{M} \left( i \right)^{M - l} a_{n}^{M} } } \left( { - i} \right)^{M - n} \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {dx_{02} dy_{02} {\kern 1pt} F_{n} \left( {x,y,x_{02} ,y_{02} } \right)} } \\ \times & \sum\limits_{s = 0}^{\left[\frac{p}{2}\right]} {\frac{{\left( { - 1} \right)^{s} p!}}{{s!\left( {p - 2s} \right)!}}} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{p - 2s} \sum\limits_{t = 0}^{\left[\frac{p}{2}\right]} {\frac{{\left( { - 1} \right)^{t} p!}}{{t!\left( {p - 2t} \right)!}}} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{p - 2t} \\ \times & \left[ {\exp \left( {\frac{{q_{ + }^{2} \left( {x,x_{02} } \right)}}{\delta }} \right)H_{p + l - 2s} \left( {\frac{{iq_{ + } \left( {x,x_{02} } \right)}}{\sqrt \delta }} \right) + \exp \left( {\frac{{q_{ - }^{2} \left( {x,x_{02} } \right)}}{\delta }} \right)H_{p + l - 2s} \left( {\frac{{iq_{ - } \left( {x,x_{02} } \right)}}{\sqrt \delta }} \right)} \right] \\ \times & \left[ {\exp \left( {\frac{{q_{ + }^{2} \left( {y,y_{02} } \right)}}{\delta }} \right)H_{p + M - l - 2t} \left( {\frac{{iq_{ + } \left( {y,y_{02} } \right)}}{\sqrt \delta }} \right) + \exp \left( {\frac{{q_{ - }^{2} \left( {y,y_{02} } \right)}}{\delta }} \right)H_{p + M - l - 2t} \left( {\frac{{iq_{ - } \left( {y,y_{02} } \right)}}{\sqrt \delta }} \right)} \right]{\kern 1pt} . \\ \end{aligned}$$
(10)

The integral expression on the right–hand of Eq. (10) can be performed directly by using the separation of variable method. So, by recalling the expanding form of Hermite polynomial (Gradshteyn and Ryzhik 1994)

$$H_{m} \left( x \right) = \sum\limits_{j = 0}^{\left[\frac{m}{2}\right]} {\frac{{( - 1)^{j} m!}}{{j!\left( {m - 2j} \right)!}}\left( {2x} \right)^{m - 2j} } ,$$
(11)

rand with the help again of Eq. (8), and after lengthy algebraic calculations, the average intensity of the vHChGB propagating through turbulent atmosphere can be expressed as

$$\begin{aligned} I\left( {x,y,z} \right) = & \frac{1}{{2^{M + 4} }}\frac{1}{\delta \eta }\left( \frac{k}{2z} \right)^{2} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{M} \sum\limits_{l = 0}^{M} {a_{l}^{M} \left( i \right)^{M - l} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \left( { - i} \right)^{M - n} \\ \times & \left[ {Q_{l,n}^{ + } \left( x \right) + Q_{l,n}^{ - } \left( x \right)} \right]\left[ {K_{M - l,M - n}^{ + } \left( y \right) + K_{M - l,M - n}^{ - } \left( y \right)} \right], \\ \end{aligned}$$
(12)

where \(Q_{l,n}^{ \pm } \left( x \right)\) is given by

$$\begin{aligned} Q_{l,n}^{ \pm } \left( x \right) = & \sum\limits_{s = 0}^{{\left[ {{\raise0.7ex\hbox{$p$} \!\mathord{\left/ {\vphantom {p 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right]}} {\frac{{\left( { - 1} \right)^{s} p!}}{{s!\left( {p - 2s} \right)!}}} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \delta }}} \right)^{p - 2s} \sum\limits_{j = 0}^{{\left[ {\frac{\mu }{2}} \right]}} {\frac{{\left( { - 1} \right)^{j} \mu !}}{{j!\left( {\mu - 2j} \right)!}}} \sum\limits_{{j_{1} = 0}}^{\mu - 2j} {a_{{j{}_{1}}}^{\mu - 2j} \left( {\frac{2i}{{\rho_{0}^{2} \sqrt \delta }}} \right)^{{\mu - 2j - j_{1} }} \left( {\frac{2i}{{\sqrt \delta }}} \right)^{{j_{1} }} \frac{1}{{2^{N} }}} \\ \times & \left\{ {\sum\limits_{{j_{2} = 0}}^{{\left[ \frac{p}{2} \right]}} {\frac{{\left( { - 1} \right)^{{j_{2} }} p!}}{{j_{2} !\left( {p - 2j_{2} } \right)!}}} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \eta }}} \right)^{{N + p - 2j_{2} }} \left\{ \begin{gathered} \left( {\frac{ikx}{{2z}} + \frac{b}{{2\omega_{0} }}} \right)^{{j_{1} }} \exp \left( {Ax^{2} + B^{ \pm } x + C^{ \pm } } \right)H_{{N + p - 2j{}_{2}}} \left( {\frac{i\alpha }{{\sqrt \eta }}x + \frac{{i\beta^{ \pm } }}{\sqrt \eta }} \right) \hfill \\ + \left( {\frac{ikx}{{2z}} - \frac{b}{{2\omega_{0} }}} \right)^{{j_{1} }} \exp \left( {Ax^{2} - B^{ \mp } x + C^{ \mp } } \right)H_{{N + p - 2j{}_{2}}} \left( {\frac{i\alpha }{{\sqrt \eta }}x - \frac{{i\beta^{ \mp } }}{\sqrt \eta }} \right) \hfill \\ \end{gathered} \right\}} \right\}, \\ \end{aligned}$$
(13a)

and

$$K_{M - l,M - n}^{ \pm } \left( y \right)$$
(13b)

is expressed as Eq. (13b) with

$$\mu = p + l - 2s,$$
(13c)
$$d = p + M - l - 2t,$$
(13d)
$$N = \mu + n - 2j - j_{1} ,$$
(13e)
$$N_{1} = d + M - n - 2h - t_{1} ,$$
(13f)
$$\eta = \delta * - \frac{1}{{\delta \rho_{0}^{4} }},$$
(13g)
$$\alpha = \frac{ik}{{2z}}\left( {\frac{1}{{\delta \rho_{0}^{2} }} - 1} \right),$$
(13h)
$$\beta^{ \pm } = \frac{b}{{2\omega_{0} }}\left( {\frac{1}{{\delta \rho_{0}^{2} }} \pm 1} \right),$$
(13i)
$$A = \frac{{\alpha^{2} }}{\eta } - \frac{{k^{2} }}{{4z^{2} \delta }},$$
(13j)
$$B^{ \pm } = \frac{ikb}{{2z\omega_{0} \delta }} + \frac{{2\alpha \beta^{ \pm } }}{\eta },$$
(13k)

and

$$C^{ \pm } = \frac{{b^{2} }}{{4\omega_{0}^{2} \delta }} + \frac{{\left( {\beta^{ \pm } } \right)^{2} }}{\eta }\,.$$

Equation (12) is the main analytical result of this paper, which provides us with a convenient way to investigate the propagation properties of the vHChGB in turbulent atmosphere. In the particular case when p = 0, Eq. (12) will give the propagation equation for the vChGB, and the result will be consistent with the corresponding expression given in Ref. (Hricha et al. 2021a).

3 Numerical examples and analysis

In the present section, based on the numerical calculation of Eq. (12), the propagation properties of a vHChGB through atmospheric turbulence are illustrated graphically as function of the turbulence strength and under different beam parameters conditions. As it is known, the incident vHChGB can have one of the two beam profile configurations depending on the value of the parameter b. Therefore, in the following, the behaviors of the beam in both configurations are examined separately. The calculation parameters are set as \(\omega_{0} = 2\,cm\), \(\lambda = 1060\,nm\) and \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\) (otherwise, it is indicated). For the sake of clarity the numerical results related to the free space propagation case are also shown for comparison.

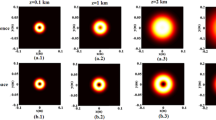
Figures 1 and 2 illustrate the normalized average intensity of a vHChGB (for the small and large b cases, respectively) in turbulent atmosphere at different propagation distances (z = 0.1 km, 1 km, 2 km and 5 km) with M = 1 and for three beam orders (p = 1, 2 and 3). The corresponding intensity evolution in free space (i.e., in the absence of turbulence) is also shown for the sake of comparison. From the plots, one can easily see that the perturbed vHChGB widens gradually and its initial hollow profile persists within a small distance range in the near field, and with the propagation distance increasing the beam lobes overlap and the central hole-intensity is filled at a certain propagation distance. With more increasing the propagation distance the beam evolves into Gaussian–like beam, and the central peak intensity reaches a maximum value (see the columns on the right in Figs. 2 and 3). After that, the peak intensity decreases gradually with the propagation distance. It can also be seen that the beam evolution is affected strongly by the turbulent atmosphere in the far field; the perturbed beam becomes Gaussian-like beam, while in free space the beam evolves into a dark hollow beam around by petals (see the rows b, d and f). Furthermore, one can note the apparition of some secondary weak lobes at central region for the beam with small b configuration and higher beam orders (p = 2 and 3) within the intermediate propagation distance range: 1 km < z < 2 km. From the rows (a, c, e) of Fig. 1, one can also notice that for a vHChGB with small parameter b, the deformation (i.e., the rotation effect) of the main lobes, as well as the intensity of secondary lobes, is weaker as the beam order p is larger. Such an evolution of the beam is caused physically by the dynamics of the random homogeneities of the turbulent medium. The average beam energy tends to concentrate near the axis, and the structure deformation of the initial beam takes place mainly at the intermediate distance of propagation. When the propagation distance is significant, the perturbed beam structure evolves into a pure Gaussian averaged beam, and the point of null intensity of the initial beam center is filled completely in the far field.

Fig. 1
figure 1

The normalized average intensity distribution of a vHChGB in a turbulent atmosphere at different propagation distances z, and for b = 0.1 and different values of p, with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 1060\,\,nm\), \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\), rows a-b for p = 1, c-d for p = 2 and e–f for p = 3

Full size image
Fig. 2
figure 2

The same as Fig. 1, except b = 4

Full size image
Fig. 3
figure 3

The average intensity distribution of a vHChGB in a turbulent atmosphere for different values M, with \(\lambda = 1060\,\,nm\), \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) \(\omega_{0} = 0.02\,m,\) p = 1, a,b: M = 2 and c,d: M = 4

Full size image

From more detailed numerical simulations, we found that the propagation distance zo at which the lobes begin to overlap is strongly dependent on the beam parameters conditions. For the parameters calculation used in Fig. 1, the numerical values of zo for both configurations of the vHChGB (i.e., b = 0.1 and b = 4) are summarized in Table 1. One can see that the distance of overlapping increases with the increase of the beam order and/or the parameter b.

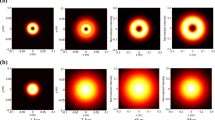
Table 1 Numerical values of zo for the vHChGBs in turbulent atmosphere
Full size table

The effect of the topological charge M on the vHChGBs with p = 1 and 2 propagating in turbulent atmosphere is demonstrated in Figs. 3 and 4. One can see that the beam lobes are slightly wider and the lobes interspace is larger when M increases from 2 to 4. One can also notice that the main lobes are more deformed for the beam with small b configuration (b = 0.1) when M is increased. While for beam of large b configuration case, the effect of M is less observable. In addition, one can clearly see from Fig. 2 that the rising speed of the central peak intensity becomes slower as M or p is larger.

Fig. 4
figure 4

The same as Fig. 3 except p = 2

Full size image

The influence of the atmospheric turbulence strength on the vHChGB spreading is demonstrated in Fig. 5, in which we have illustrated the normalized axial intensity upon propagation for three values of the turbulence strength \(C_{n}^{2} = 10^{ - 15} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\)\(,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 10^{ - 14} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} \,\,\) and \({\kern 1pt} {\kern 1pt} \,5.10^{ - 14} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\). The plots show that when \(C_{n}^{2}\) increases the rising speed of the central peak intensity becomes faster. In addition, one can note that if M is increased the rising speed of the central peak will be slower, which confirms the result shown in Figs. 3 and 4.

Fig. 5
figure 5

The normalized axial intensity versus propagation distance z of a vHChGB in a turbulent atmosphere for a different values of the refractive index structure \(C_{n}^{2}\) with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 1060\,\,\,nm\) and p = 1

Full size image

Figures 6 and 7 illustrate, the effects of the waist radius \(\omega_{0}\) on the transverse intensity distribution (in the x-direction) and on the axial intensity, respectively of the vHChGB in turbulent atmosphere at different propagation distance for M = 1 and p = 1. It can be clearly seen that when ω0 is larger the beam lobes becomes wider and the central hole-intensity filling is slower.

Fig. 6
figure 6

The normalized intensity in x-direction of a vHChGB in a turbulent atmosphere at different propagation distance z as follow: M = 1, p = 1, \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} ,\)\(\lambda = 632.8\,\,nm,\) (a.1–2): b = 0.1, (b.1–2): b = 4, and different values of the waist \(\omega_{0}\)

Full size image
Fig. 7
figure 7

The normalized axial intensity versus propagation distance z of a vHChGB in a turbulent atmosphere for a different values of the waist \(\omega_{0}\) with M = 1, p = 1, \(\lambda = 1060\,\,\,nm\) and \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\).a: b = 0.1, b, b = 4

Full size image

In order to investigate the influence of the wavelength λ on the beam propagation, Fig. 8 gives the evolution of normalized average intensity in the x-direction of a vHChGB upon propagating through turbulent atmosphere. It can be seen that the beam in the small b configuration widens faster with the propagation distance when λ is larger, whereas the effect of λ is less visible for the large b configuration. Furthermore, it is found from Fig. 9 that for a vHChGB with small b configuration the profile change (from “fan blade” shape to a Gaussian beam–like) is more in advance when the wavelength is lowered, i.e., the rising speed of the central peak is slower when λ is larger. While for the beam with large b configuration, the four lobes widen and overlap faster as λ is increased. This means that the propagating beam may lose its dark dip center faster when the wavelength is larger.

Fig. 8
figure 8

The normalized intensity in x-direction of a vHChGB in a turbulent atmosphere at different propagation distance as follow: M = 1, p = 1,\(\omega_{0} = 0.02\,m,\)\(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\), (a.1–2-3): b = 0.1, (b.1–2-3): b = 4 and different values of the wavelength \(\lambda\)

Full size image
Fig. 9
figure 9

The normalized intensity of a vHChGB turbulent atmosphere for different values of the wavelength \(\lambda\) with M = 1, p = 1, z = 2 km, \(\omega_{0} = 0.02\,\,m\) and \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\). Colums (a.1–b.1) \(\rm\lambda = 632.8\,nm\rm\), (a.2–b.2) \(\rm\lambda = 1060\,\,\,nm\rm\), (a.3–b.3) \(\rm\lambda = 1550\,\,\,nm\rm\) and (a.4–b.4) \(\rm\lambda = 2000\,nm\rm\).

Full size image

4 Conclusion

In summary, based on the extended Huygens–Fresnel diffraction integral and the Rytov method, the propagation formula of a vHChGB in turbulent atmosphere is derived in detail. It is shown from numerical calculations that the propagation properties of the perturbed vHChGB are altered by the turbulence strength and the change of the beam parameters. The profile of the beam will change during propagation in the turbulent media from hollow array–distribution to the Gaussian-like. When the turbulence strength is larger or the beam order, vortex charge and Gaussian waist width are smaller, the speed of profile change will be faster. For a vHChGB with a small parameter b, the profile change is faster as λ is larger, whereas the reverse behavior is obtained when b is large. It is expected that this study will be useful for the applications of vHChGB in free space communication optics and improving information transmission in atmospheric turbulence.