Propagation characteristics of dark and antidark Gaussian beams in turbulent atmosphere

Abstract

In this work, we investigated theoretically the propagation characteristics of dark and antidark Gaussian beams (DADGBs) in turbulent atmosphere. Based on the Huygens–Fresnel diffraction integral and by mean of the expansion form of a hard aperture function into a finite sum of Gaussian functions we derived analytically the on-axis intensity distribution of an apertured DADGB propagating in turbulent atmosphere. The dependence of the axial intensity distribution on the turbulent strength and on the parameters of the beam is illustrated with numerical examples. The results show that the axial intensity decreases rapidly when the turbulent strength parameter is large, and the propagation distance is shorter for large wavelengths and for small beam waist width.

1 Introduction

Over the last decade, several papers have been devoted to studying the propagation properties of laser beams in turbulent atmosphere. In particular, the Hollow laser beams have attracted much interest due to their potential applications in optical communications, imaging system and remote sensing (Andrews and Philips 1998; Noriega-Manez and Gutiérrez-Vega 2007; Korotkova and Gbur 2007; Cang and Zhang 2010; Cai and He 2006). Especially, the analytical expression for the average intensity of Dark hollow beams propagating in turbulent atmosphere has been derived by Cai and He (2006). Recently, Khannous et al. (2016) have investigated in detail the propagation of Hollow Gaussian beams within the regime of weak fluctuations by using the paraxial approximation and the Rytov theory. More recently, Saad et al. (2017) and Boufalah et al. (2018) have studied, respectively, the propagation characteristics of Generalized spiraling Bessel and Generalized Laguerre–Gaussian beams in turbulent atmosphere.

On the other hand, a novel class of partially coherent diffraction free modes called Dark and Antidark beams (DADBs) were introduced theoretically by Ponomarenko et al. (2007). These beams have intensity profiles with dips or peaks on a cw background. The authors noted the similitude of their basic features with those of Dark and Antidark solitons. The DADBs have been freshly realized experimentally from, in one hand, the uncorrelated superposition of Bessel modes generated by holographic technic and by the aid of a spatial light modulator (SLM), and in the second hand by using the genuine cross-spectral density function criterion (Zhu et al. 2019; Hyde and Avramov-Zumarovic 2019). In the present work, we consider a new family of paraxial coherent beams whose amplitude at the z = 0 plane is of the form of Dark (or Antidark) mode multiplied by a Gaussian profile. These modes that will be termed as Dark and Antidark Gaussian beams (DADGBs) may carry finite energy and can then be generated experimentally. We point out that this class of beams has been introduced firstly by Saad and Belafhal (2018) where they investigated the characteristics of the conical diffraction for these beams in a biaxial crystal.

Up to now, and to the best of our knowledge, the propagation characteristics of such beams through a turbulent atmosphere haven’t been examined elsewhere. The current work is aimed to such a subject. The propagation characteristics of DADGB in turbulent atmosphere are obtained in Rytov theory by mean of the extended Huygens-Fresnel integral diffraction and by considering the fact that a hard edged aperture can be expanded into a finite sum of Gaussian functions.

The rest of the paper is structured as follows; in the coming Section, we present the intensity profiles of DADGBs at the source plane. In the third Section, we investigate analytically the average axial intensity of the considered beams when propagating in an atmospheric turbulent medium. In Sect. 4, some numerical calculations are presented to illustrate the effects of refractive index structure of the medium and the beam parameters on the axial intensity upon the propagation. A summary of our results is presented in the conclusion.

2 Principle of the propagation of truncated DADGB in turbulent atmosphere

Let us consider a Dark and Antidark Gaussian beam (DADGB) whose amplitude field in the source plane z = 0 is given by (Saad and Belafhal 2018)

$$E\left( {r,z = 0} \right) = E_{0} \left( {1 + \alpha J_{0} \left( {2\beta r} \right)} \right)\exp \left( {\frac{{ - r^{2} }}{{w_{0}^{2} }}} \right),$$

(1)

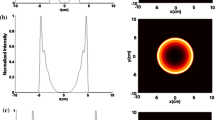
where $J_{0} (.)$ is the zero-order Bessel function and r is the transversal distance from the propagation axis $z$. $E_{0}$ is a normalization factor, for the sake of simplification chosen equal to unity. $\beta$ is the transverse number of $J_{0}$ Bessel mode, $\alpha$ is a constant which takes values $\left| \alpha \right| \le 1$, and $w_{0}$ is the waist size of the Gaussian envelope at the source plane. The mode of Eq. (1) has a finite energy and may correspond to the paraxial form expression of the ideal dark (antidark) diffraction free beam investigated by Ponomarenko et al. (2007). It is worthy nothing that the considered beams can be regarded as an incoherent superposition of a Gaussian and Bessel–Gauss modes. The incoherent superposition of these modes can be realized in laboratory by adding up a Gaussian and Bessel–Gauss beams generated from two independent sources or by using the holographic technic as in Ponomarenko et al. (2007) with employing only two phase patterns sequence with the SLM. In the case α = 0, Eq. (1) may reduces directly to fundamental Gaussian field. The intensity distribution of DADGB which is given as the square modulus of the expression of Eq. (1) may describe qualitatively a Dark beam when $- 1 \le \alpha < 0$ and an Antidark beam for $0 \le \alpha \le 1$. In Fig. 1, the intensity distributions are presented for the two values $\alpha = - 1$ and $\alpha = 1$ with the simulation parameters $\omega_{0} = 2\,{\text{cm}}$ and $\beta = 1\,mm^{ - 1}$. It is seen from the plots that the value $\alpha = - 1$ leads to a doughnut beam with a dark notch in the center (see Fig. 1a) whereas for $\alpha = 1$, one obtains a bright beam with a peak central spot (Fig. 1b).

Fig. 1

Intensity distribution of the DADGB at z = 0 plane a $\alpha$ = − 1 and b $\alpha$ = 1

The propagation of a laser beam in turbulent atmosphere can be formulated via the Huygens–Fresnel integral (Andrews and Philips 1998; Born and Wolf 1999)

$$E\left( {\vec{\rho },z,t} \right) = - \frac{ik}{2\pi z}\exp (i\,k\,z)\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {E\left( {\vec{r},0} \right)} } \exp \left[ {\frac{ik}{2z}\left( {\vec{r} - \vec{\rho }} \right)^{2} + \psi \left( {\vec{r},\vec{\rho }} \right) - 2i\pi ft} \right]d\vec{r},$$

(2)

where $E\left( {\vec{r},0} \right)$ is the field at a point $\vec{r} = \left( {r,\theta } \right)$ in the source plane and $E\left( {\vec{\rho },0} \right)$ is the one in the receiver plane at point $\vec{\rho } = \left( {\rho ,\phi } \right)$. z is the distance between the source plane and the receiver plane. $\psi \left( {\vec{r}_{{}} ,\vec{\rho }} \right)$ is the solution to the Rytov method that represents the random part of the complex phase of a spherical wave spreading from the source plane to the output plane, f is the frequency, t denotes the time, $\lambda$ is the wavelength and $k = \frac{2\pi }{\lambda }$ is the wave number. The parameter a denotes the radius of the circular aperture. A schematic illustration of a turbulent atmospheric optical system is presented in Fig. 2.

Fig. 2

Schematic system of the propagation of the DADGB in turbulent atmosphere

The average intensity at the receiver plane is given by

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle & = \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {E\left( {\vec{r}_{1} ,0} \right)E*\left( {\vec{r}_{2} ,0} \right)} } } } \\ & \quad \exp \left[ {\frac{ik}{2z}\left\{ {\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} - \left( {\vec{r}_{2} - \vec{\rho }} \right)^{2} } \right\}} \right]\left\langle {\exp \left[ {\psi \left( {\vec{r}_{1} ,\vec{\rho }} \right) + \psi *\left( {\vec{r}_{2} ,\vec{\rho }} \right)} \right]} \right\rangle d\vec{r}_{1} d\vec{r}_{2} . \\ \end{aligned}$$

(3)

where the asterisk and angular brackets denote the complex conjugate and the ensemble average over the medium statistics, respectively.

The ensemble average term in the right side of Eq. (3) can be expressed as (Andrews and Philips 1998)

$$\left\langle {exp\left[ {\psi \left( {\vec{r}_{1} ,\vec{\rho }} \right) + \psi *\left( {\vec{r}_{2} ,\vec{\rho }} \right)} \right]} \right\rangle = exp\left[ { - 0.5D_{\psi } \left( {\vec{r}_{1} - \vec{r}_{2} } \right)} \right],$$

(4a)

where $D_{\psi } \left( {\vec{r}_{1} - \vec{r}_{2} } \right)$ is the phase structure function in Rytov’s representation given by

$$D_{\psi } \left( {\vec{r}_{1} - \vec{r}_{2} } \right) = \frac{2}{{\rho_{0}^{2} }}\left( {\vec{r}_{1} - \vec{r}_{2} } \right)^{2}$$

(4b)

with

$$\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{ - 3/5}$$

is the spherical-wave lateral coherence length and $C_{n}^{2}$ is the refractive index structure constant.

By substituting from Eqs. (1), (4a) and (4b) into Eq. (3), and after doing some algebraic manipulations, one obtains the following form

$$\begin{aligned} \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle & = \frac{1}{{\lambda^{2} z^{2} }}\int\limits_{0}^{a} {\int\limits_{0}^{a} {} } \int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left( {1 + \alpha J_{0} \left( {2\beta r_{1} } \right)} \right)} } \left( {1 + \alpha J_{0} \left( {2\beta r_{2} } \right)} \right)exp\left( { - \frac{{r_{1}^{2} + r_{2}^{2} }}{{w_{0}^{2} }}} \right) \\ & \quad exp\left[ {\frac{ik}{2z}\left( {r_{1}^{2} - r_{2}^{2} } \right)} \right]exp\left\{ {\frac{ik}{z}\left[ {r_{1} \rho cos\left( {\theta_{1} - \psi } \right) - r_{2} \rho cos\left( {\theta_{2} - \psi } \right)} \right]} \right\} \\ & \quad exp\left( { - \frac{{r_{1}^{2} + r_{2}^{2} }}{{\rho_{0}^{2} }}} \right)exp\left[ {\frac{{2r_{1} r_{2} cos\left( {\theta_{1} - \theta_{2} } \right)}}{{\rho_{0}^{2} }}} \right]r_{1} r_{2} dr_{1} dr_{2} d\theta_{1} d\theta_{2} . \\ \end{aligned}$$

(5)

In the following, we will focus on the axial intensity characteristics the DADGB passing through a turbulent atmosphere medium.

3 Axial intensity distribution of a truncated DADGB in turbulent atmosphere

To calculate the on-axis average intensity of the truncated beam we use the expansion form of the hard aperture function into a finite sum of complex Gaussian functions given as (Wen and Breazeale 1988)

$$H\left( r \right) = \sum\limits_{k = 1}^{N} {A_{k} \exp \left( { - \frac{{B_{k} }}{{a^{2} }}r^{2} } \right)} ,$$

(6)

where $A_{k}$ and $B_{k}$ denote the expansion and the Gaussian coefficients, respectively, which can be obtained by numerical optimization (Wen and Breazeale 1988). By inserting the aperture function of Eq. (6) into Eq. (5) and by limiting our consideration to the on axis intensity $\left\langle {I(0,z)} \right\rangle$, we get

$$\begin{aligned} \left\langle {I\left( {0,z} \right)} \right\rangle & = \frac{1}{{\lambda^{2} z^{2} }}\sum\limits_{k = 1}^{N} {A_{k} } \sum\limits_{p = 1}^{N} {A_{p} } \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {} } \int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left( {1 + \alpha J_{0} \left( {2\beta r_{1} } \right)} \right)\left( {1 + \alpha J_{0} \left( {2\beta r_{2} } \right)} \right)} } \\ & \quad exp\left( {\left[ {\frac{ik}{2z} - \frac{1}{{w_{0}^{2} }} - \frac{1}{{\rho_{0}^{2} }} - \frac{{B_{k} }}{{a^{2} }}} \right]r_{1}^{2} } \right)exp\left( {\left[ { - \frac{ik}{2z} - \frac{1}{{w_{0}^{2} }} - \frac{1}{{\rho_{0}^{2} }} - \frac{{B_{p} }}{{a^{2} }}} \right]r_{2}^{2} } \right) \\ & \quad exp\left[ {\frac{2}{{\rho_{0}^{2} }}r_{1} r_{2} cos\left( {\theta_{1} - \theta_{2} } \right)} \right]r_{1} r_{2} dr_{1} dr_{2} d\theta_{1} d\theta_{2} . \\ \end{aligned}$$

(7)

To perform the integrations in last equation with respect to the angles $\theta_{1}$ and $\theta_{2}$ we use the following integral formula and the property of Bessel function (Abramowitz and Stegun 1964).

$$\int_{0}^{2\pi } {\exp \left\{ { - in\theta + z\cos \left( {\theta - \phi } \right)} \right\}} d\theta = 2\pi \exp \left( { - in\phi } \right)I_{n} \left( z \right),$$

(8a)

and

$$I{}_{n}\left( z \right) = \left( i \right)^{ - n} J{}_{n}\left( {iz} \right){\kern 1pt} .$$

(8b)

Doing that and after tedious algebra, Eq. (7) yields

$$\begin{aligned} \left\langle {I\left( {0,z} \right)} \right\rangle & = \frac{{4\pi^{2} }}{{\lambda^{2} z^{2} }}\sum\limits_{k = 1}^{N} {A_{k} } \sum\limits_{p = 1}^{N} {A_{p} } \int\limits_{0}^{\infty } {r_{1} exp\left( { - \delta_{1}^{k} r_{1}^{2} } \right)\left( {1 + \alpha J_{0} \left( {2\beta r_{1} } \right)} \right)} \\ & \quad \left\{ {\int\limits_{0}^{\infty } {r_{2} exp\left( { - \delta_{2}^{k} r_{2}^{2} } \right)\left( {1 + \alpha J_{0} \left( {2\beta r_{2} } \right)} \right)} J_{0} \left( {\frac{{2r_{1} r_{2} }}{{\rho_{0}^{2} }}} \right)dr_{2} } \right\}dr_{1} , \\ \end{aligned}$$

(9a)

where

$$\delta_{1}^{k} = - \frac{ik}{2z} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{k} }}{{a^{2} }},$$

(9b)

and

$$\delta_{2}^{k} = \frac{ik}{2z} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{p} }}{{a^{2} }}.$$

(9c)

Recalling the following integral formulae (Gradshteyn and Ryzhik 1994)

$$\begin{aligned} \int_{0}^{\infty } {x^{\mu } e^{{ - \alpha \,x^{2} }} J_{\nu } \left( {\beta x} \right)dx} & = \frac{{\beta^{\nu } \varGamma \left( {\frac{1}{2}v + \frac{1}{2}\mu + \frac{1}{2}} \right)}}{{2^{v + 1} \alpha^{{\frac{1}{2}\left( {v + \mu + 1} \right)}} \varGamma \left( {v + 1} \right)}}{}_{1}F_{1} \left( {\frac{1}{2}\left( {v + \mu + 1} \right);v + 1; - \frac{{\beta^{2} }}{4\alpha }} \right), \\ & \quad \left[ {\text{Re} \alpha > 0,\text{Re} \left( {\nu + \mu } \right) > - 1} \right] \\ \end{aligned}$$

(10a)

$$\begin{aligned} \int_{0}^{\infty } {xe^{{ - \alpha \,x^{2} }} I_{\nu } \left( {\beta x} \right)J_{\nu } \left( {\gamma x} \right)dx} & = \frac{1}{2\alpha }\exp \left( {\frac{{\beta^{2} - \gamma^{2} }}{4\alpha }} \right)J_{\upsilon } \left( {\frac{\beta \gamma }{2\alpha }} \right), \\ & \quad \left[ {\text{Re} \left( \alpha \right) > 0,\text{Re} \left( \nu \right) > - 1} \right] \\ \end{aligned}$$

(10b)

and

$$\begin{aligned} \int_{0}^{\infty } {xe^{{ - \alpha \,x^{2} }} J_{\nu } \left( {\beta \,x} \right)J_{\nu } \left( {\gamma \,x} \right)dx} = \frac{1}{2\alpha }\exp \,\left( { - \frac{{\beta^{2} + \gamma^{2} }}{4\alpha }} \right)I_{\upsilon } \left( {\frac{\beta \gamma }{2\alpha }} \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {\,\text{Re} \left( \nu \right) > - 1,\left| {\arg \left( \alpha \right)} \right| \prec \frac{\pi }{4},\beta > 0,\gamma > 0\,} \right], \hfill \\ \end{aligned}$$

(10c)

and after doing some algebra, Eq. (9a) reduces to

$$\left\langle {I\left( {0,z} \right)} \right\rangle = \frac{{4\pi^{2} }}{{\lambda^{2} z^{2} }}\sum\limits_{k = 1}^{N} {A_{k} } \sum\limits_{p = 1}^{N} {A_{p} } \left( {\frac{1}{{4\delta_{2}^{k} \delta_{3}^{k} }}} \right)\left( {1 + \alpha e^{{\frac{{ - \beta^{2} }}{{\delta_{3}^{k} }}}} + \alpha \exp \left[ { - \frac{{\beta^{2} }}{{\delta_{2}^{k} }}\left( {1 + \frac{1}{{\delta_{2}^{k} \delta_{3}^{k} \rho_{0}^{4} }}} \right)} \right]\left( {1 + \alpha .e^{{\frac{{ - \beta^{2} }}{{\delta_{3}^{k} }}}} I_{0} \left( {\frac{{2\beta^{2} }}{{\delta_{2}^{k} \delta_{3}^{k} \rho_{0}^{2} }}} \right)} \right)} \right),$$

(11)

with

$$\delta_{3}^{k} = \delta_{1}^{k} - \frac{1}{{\delta_{2}^{k} \rho_{0}^{4} }}.$$

(12)

Equation (11) is the main result of this work. It expresses an approximate on-axis average intensity of a truncated DADGB propagating in turbulent atmosphere in terms of the characteristics of the medium and the parameters of the incident beam.

Setting $\alpha = 0$ in Eq. (11), we obtain

$$\left\langle {I\left( {0,z} \right)} \right\rangle = \frac{{4\pi^{2} }}{{\lambda^{2} z^{2} }}\sum\limits_{k = 1}^{N} {\sum\limits_{p = 1}^{N} {A_{k} A_{p} } } \left( {\frac{1}{{4\delta_{2}^{k} \delta_{3}^{k} }}} \right).$$

(13)

Equation (13) is the axial intensity for the apertured fundamental Gaussian beam. One can easily check that this equation is consistent with the findings of Cang and Zhang (2010).

For the unapertured case, we take $\alpha \to \infty$ in Eq. (11), this yields

$$\left\langle {I\left( {0,z} \right)} \right\rangle = \frac{{4\pi^{2} }}{{\lambda^{2} z^{2} }}\left( {\frac{1}{{4\delta_{2}^{\infty } {\kern 1pt} \delta_{3}^{\infty } }}} \right)\left( {1 + \alpha .e^{{\frac{{ - \beta^{2} }}{{\delta_{3}^{\infty } }}}} + \alpha exp\left[ { - \frac{{\beta^{2} }}{{\delta_{2}^{\infty } }}\left( {1 + \frac{1}{{\delta_{2}^{\infty } \delta_{3}^{\infty } \rho_{0}^{4} }}} \right)} \right]\left( {1 + \alpha .e^{{\frac{{ - \beta^{2} }}{{\delta_{3}^{\infty } }}}} I_{0} \left( {\frac{{2\beta^{2} }}{{\delta_{2}^{\infty } \delta_{3}^{\infty } \rho_{0}^{2} }}} \right)} \right)} \right),$$

(14)

with

$$\delta_{1}^{\infty } = - \frac{ik}{2z} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }}\,,$$

(14a)

$$\delta_{2}^{\infty } = \frac{ik}{2z} + \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }}\,,$$

(14b)

and

$$\delta_{3}^{\infty } = \delta_{1}^{\infty } - \frac{1}{{\delta_{2}^{\infty } \rho_{0}^{4} }}.$$

(14c)

We point out that Eq. (14) can be obtained directly from Eq. (2), without considering the approximation of Eq. (6).

4 Numerical simulations and discussion

To examine the effect of the turbulent atmosphere on the axial intensity of the DADGB, we present some numerical calculations based on Eq. (11). Figure 3 shows the on-axis intensity for different turbulent strengths constant $C_{n}^{2}$. The calculation parameters are taken as $\omega_{0} = 0.05\,{\text{m}}$, ${\text{a}} = 0.05\,{\text{m}}$, $\beta = 10\,{\text{mm}}^{ - 1}$ and $\lambda = 632.8\,{\text{nm}}$. Plots of Fig. 3a show that the axial intensity increases with the propagation distance z until it reaches a threshold maximum value for Z_max and then it decreases gradually and falls off for large values of z. As can be seen from the plots, the beam is focused when z < z_max and becomes defocused when z > z_max. We infer that the propagating beam presents two different comportments, one for the near field and the second one for the far filed. We can note also that the axial intensity decreases rapidly and the propagation is shorter when the turbulent strength parameter $C_{n}^{2}$ is larger. This means that in the far field, the beam is hardly influenced by the turbulent media. From the plots of Fig. 3b that correspond to the dark Bessel–Gauss beam ($\alpha = - 1$) it is seen that the axial intensity keeps approximately weak values within the first hundred meters in the near field (z < 500 m), afterwards it increases significantly upon propagation until it reaches a threshold value for z_max and then it decreases monotonically and vanishes in the far field. Further, one can observe the decreasing of the length z_max when the turbulent strength increases.

Fig. 3

Plots of the on-axis average intensity versus propagation distance z of the DADGB with $\lambda = 632.8\,{\text{nm}}$ and for different values of $C_{n}^{2}$ for a $\alpha = + 1$ and b $\alpha = - 1$

Figure 4 shows the effect of the wavelength $\lambda$ on the axial intensity of the DADGB propagating in turbulent atmosphere. The other parameters in the numerical simulations are $C_{n}^{2} = 10^{ - 14} {\text{m}}^{ - 2/3} ,$$\omega_{ 0} { = 0} . 0 5\,{\text{m}}$, ${\text{a}} = 0.05\,{\text{m}}$ and $\beta = 10\,{\text{mm}}^{ - 1}$. From these plots, it can be seen that the value of z_max increases with increasing values of the wavelength $\lambda$ for the dark and antidark Gaussian beams.

Fig. 4

Plots of the on-axis average intensity versus propagation distance z of the DADGB with $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$ and for different values of $\lambda$ at a $\alpha = + 1$ and b $\alpha = - 1$

Figure 5 presents the on-axis average intensity of the DADGB for various values of the waist width $w_{0}$ = 3, 5, 6 and 8 cm, where the parameters in the numerical simulations are taken: $C_{n}^{2} = 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} ,$ $\lambda = 1060\,\,{\text{nm}},$ ${\text{a}} = 0.05\,\,{\text{m}}$ and $\beta = 10\,{\text{mm}}^{ - 1}$. From the curves, one can note that the upon propagation the axial average intensity increases when beam waist width increases, and the z_max smaller when the beam waist is narrower.

Fig. 5

Plot of the on-axis average intensity versus propagation distance z of the DADGB with $C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$ and for different values of w₀ at a $\alpha = + 1$ and b $\alpha = - 1$

5 Conclusion

In summary, we have studied the propagation properties Dark and antidark beams (DADGBs) through a turbulent atmosphere medium. Based on the extended Huygens-Fresnel integral formula and by means of the Rytov theory and with the help of the Gaussian expansion form of a hard aperture function. The approximate analytical expression of the on-axis average intensity of DADGB has been derived. It is shown that the on-axis average intensity the propagating beam is affected by the change of the turbulent strengths, the wavelength and the waist size of the Gaussian part. The numerical results show that the propagation of the DADGB becomes very shorter when the turbulent strength constant, and when the wavelength is larger and the waist spot is smaller. The results of this work could be exploited into some applications of atmospheric optics such as remote sensing, free space optical communications and combination technology of laser beams.