1 Introduction

In recent years, the propagation of laser beams in atmosphere have received a great attention from the laser researchers due to many applications such as the remote sensing, imaging, optics communications and so on (Andrews and Philips 1998; Wang et al. 2015). The propagation characteristics of laser beams with various excitations in the atmospheric turbulence have been examined (Baykal 2004; Cai and He 2006; Cai 2006; Noriega-Manez and Gutiérrez-Vega 2007; Chu et al. 2007; Cang and Zhang 2010; Wang et al. 2010; Khannous et al. 2016; Boufalah et al. 2018; Saad et al. 2018; Yaalou et al. 2019; Hricha et al. 2020a), and also new beam models have been discovered and studied for their applications in free space optical communication systems. Among them, one can cite the hollow vortex Gaussian beam which is a fundamental Gaussian beam including a topological vortex charge (Zhou et al. 2013). The said beam belongs to the wide family of hollow vortex beams, i.e. the beams which can carry the orbital angular momentum. During the last few years, a great deal of attention has been paid to the propagation proprieties of hollow vortex beams in various optics medium owing to promote their applications in optical microscopy, wireless communications, micromanipulation, etc. (Allen et al. 1992; Kuga et al. 1997; Paterson et al. 2001; Ponomarenko 2001; Cai et al. 2003; Bishop et al. 2004; Wang et al. 2004,2012; Lukin et al. 2012; Zhu et al. 2016; Rubinsztein-Dunlop 2017). In particular, the propagation characteristics of the hollow vortex Gaussian beams in free space and in turbulent atmosphere have been investigated in details in Refs. Zhou et al. (2013) and Mei et al. (2015). The extended form of the hollow vortex Gaussian beam which is called the vortex cosine-hyperbolic Gaussian beam (vChGB) has been introduced very recently in Ref. Hricha et al. (2020b). In latter paper, it is reported that if the appropriate values of beam parameters, mainly the decentered parameter b, the vChGB can reduce either to the vortex Gaussian beam or may resemble the four-petal Gaussian vortex beam. The spatial characteristics of the vChGB upon propagating in free space, through a FrFT system and in strongly nonlocal nonlinear media have been examined in detail (Hricha et al. 2020b,2021).

The present work is aimed at investigating the propagation properties of the vChGB in the turbulent atmosphere. The formulation is based on the extended Huygens–Fresnel integral diffraction and the Rytov method. The evolution of the diffracted vChGB in turbulent atmosphere, and the influences of the beam parameters and the turbulence strength on the behavior of the beam intensity distribution are investigated in detail. The remainder of the manuscript is organized as follow: in the Second section, we present the theoretical analysis for the propagation of vChGB in turbulent atmosphere, and we derive the propagation equation of the average intensity distribution. In Sect. 3, numerical examples are presented to discuss the evolution of intensity of vChGB in the turbulent atmosphere as a function of the involved parameters. A conclusion is outlined in the end of the paper.

2 Propagation characteristics of a vChGB in turbulent atmosphere

In the rectangular coordinates system, a vChGB propagating along the z-axis in the source plane z = 0 can be expressed as (Hricha et al. 2020b).

$$E\left( {x_{0} ,y_{0} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0} }}{{\omega _{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega _{0} }}} \right)e^{{ - \left( {\frac{{x_{0} ^{2} + y_{0} ^{2} }}{{\omega _{0}^{2} }}} \right)}} \left( {x_{0} + iy_{0} } \right)^{M} ,$$
(1)

where \(\left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)\) are the Cartesian coordinates at arbitrary point in the source plane and ω0 is the waist radius of the Gaussian part. b being a real valued parameter associated to the cosh part, it is named as the decentered parameter b. M being a positive integer which denotes the topological charge of the vortex.

The field of Eq. (1) can be generated in practice by passing a collimated cosine-hyperbolic Gaussian beam (ChGB) through a spiral phase plate.

When b = 0, Eq. (1) reduces to the hollow vortex Gaussian beam (Zhou et al. 2013), while for M = 0 (i.e., in the absence of the vortex case), one obtains the conventional ChGB (Casperson and Tovar 1998; Tovar and Casperson 1998; Lu and Zhang 1999; Belafhal and Ibnchaikh 2000; Hricha and Belafhal 2005).

From the paper (Hricha et al. 2020b), it found that the vChGB pattern depends crucially on the parameter b. Indeed, the beam can exhibit two kinds of profiles depending on the magnitude of the decentered parameter b: when b is small (say \(b < 1.5\)), the beam has a central dark spot surrounded by a bright ring spot, whereas for large b (\(b \ge 4\)), the beam possesses four symmetrical bright lobes.

Within the frame of the paraxial approximation, a light beam propagating through the turbulent atmosphere along the z-axis can be formulated by the extended Huygens–Fresnel diffraction integral (Born and Wolf 1999)

$$E\left( {\vec{r},z} \right) = - \frac{{ik}}{{2\pi z}}\exp \left( { - i\,k\,z} \right)\,\int_{{ - \infty }}^{{ + \infty }} {\int_{{ - \infty }}^{{ + \infty }} {E\left( {\vec{r}_{0} ,0} \right)\exp \left[ { - \frac{{ik}}{{2z}}\left( {\vec{r}_{0} - \vec{r}} \right)^{2} + \psi \left( {\vec{r}_{0} ,\vec{r},z} \right)} \right]} } d\vec{r}_{0} ,$$
(2)

where \(\vec{r}_{0} = (x_{0} ,y_{0} )\) and \(\vec{r} = (x,y)\) are the transverse coordinates in the source and the receiver planes, respectively. z is the distance between the initial plane z = 0 and the receiver plane.\(\psi \left( {\vec{r}_{0} ,\vec{r},z} \right)\) denotes the random part for the complex phase of a spherical wave spreading from the source plane to the output plane, \(k = \frac{{2\pi }}{\lambda }\) is the wavenumber, and \(\lambda\) is the wavelength of the source radiation in vacuum.

The average intensity of the vChGB through turbulent atmosphere is given as

$$\begin{aligned} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle & = \frac{{k^{2} }}{{4\pi ^{2} z^{2} }}\int\limits_{{ - \infty }}^{{ + \infty }} {\,\int\limits_{{ - \infty }}^{{ + \infty }} {} } \int\limits_{{ - \infty }}^{{ + \infty }} {\,\int\limits_{{ - \infty }}^{{ + \infty }} {} } E_{0} \left( {x_{{01}} ,y_{{01}} ,0} \right)E_{0} *\left( {x_{{02}} ,y_{{02}} ,0} \right) \\ & \quad \times \exp \left[ { - \frac{{ik}}{{2z}}\left\{ {\left( {x_{{01}} - x} \right)^{2} + \left( {y_{{01}} - y} \right)^{2} - \left( {x_{{02}} - x} \right)^{2} - \left( {y_{{02}} - y} \right)^{2} } \right\}} \right] \\ & \quad \times \left\langle {\exp \left[ {\psi \left( {\vec{r}_{{01}} ,\vec{r}} \right) + \psi *\left( {\vec{r}_{{02}} ,\vec{r}} \right)} \right]} \right\rangle d\vec{r}_{{01}} d\vec{r}_{{02}} , \\ \end{aligned}$$
(3)

where * and 〈 〉 denote the complex conjugation and the ensemble average over the medium statistics, respectively. Within the Rytov theory, the ensemble average in Eq. (3) is given by Andrews and Philips (1998)

$$\left\langle {\exp \left[ {\psi \left( {x_{{01}} ,y_{{01}} ,x,y} \right) + \psi *\left( {x_{{02}} ,y_{{02}} ,x,y} \right)} \right]} \right\rangle {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \exp \left[ { - \frac{1}{{\rho _{0}^{2} }}\left\{ {\left( {x_{{01}} - x_{{02}} } \right)^{2} + \left( {y_{{01}} - y_{{02}} } \right)^{2} } \right\}} \right],$$
(4)

where \(\rho _{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}}\) is the coherence length of a spherical wave propagating in the turbulent medium with \(C_{n}^{2}\) is the refractive index structure constant.

Substituting Eqs. (1) and (4) into Eq. (3), and recalling the binomial formula (Abramowitz and Stegun 1964)

$$\left( {u{\kern 1pt} + {\kern 1pt} v{\kern 1pt} } \right)^{m} {\kern 1pt} = {\kern 1pt} \sum\limits_{{l = 0}}^{m} {C_{l}^{m} } u^{l} v^{{_{{m - l}} }} ,$$
(5a)

where

$$C_{l}^{m} = {\kern 1pt} \frac{{m!}}{{l!\left( {m - l} \right)!}},$$
(5b)

leads to

$$\left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{{2\pi z}}} \right)^{2} \sum\limits_{{m_{1} = 0}}^{M} {C_{{m_{1} }}^{M} \sum\limits_{{m_{2} = 0}}^{M} {C_{{m_{2} }}^{M} } } \,\int\limits_{{ - \infty }}^{{ + \infty }} {\,\int\limits_{{ - \infty }}^{{ + \infty }} {f\left( {x_{{02}} ,y_{{02}} } \right)\,J\left( {x_{{02}} ,y_{{02}} } \right)} } dx_{{02}} dy_{{02}} ,$$
(6a)

where

$$\begin{aligned} f_{{xy}} \left( {x_{{02}} ,y_{{02}} } \right){\kern 1pt} & = x_{{02}}^{{m_{2} }} \,\left( { - iy_{{02}}^{{_{{}} }} } \right)^{{M - m_{2} }} \cosh \left( {b\frac{{x_{{02}} }}{{\omega _{0} }}} \right)\cosh \left( {b\frac{{y_{{02}} }}{{\omega _{0} }}} \right) \\ & \quad \times \exp \left( { - \delta *x_{{02}}^{2} - \frac{{ikx}}{z}x_{{02}} } \right)\exp \left( { - \delta *y_{{02}}^{2} - \frac{{iky}}{z}y_{{02}} } \right), \\ \end{aligned}$$
(6b)

and

$$J_{{xy}} \left( {x_{{02}} ,y_{{02}} } \right) = \int\limits_{{ - \infty }}^{{ + \infty }} {\,\int\limits_{{ - \infty }}^{{ + \infty }} {F\left( {x_{{01}} ,y_{{01}} ,x_{{02}} ,y_{{02}} } \right)dx_{{01}} \,dy_{{01}} } } ,$$
(6c)

with

$$\begin{aligned} F_{{xy}} \left( {x_{{01}} ,y_{{01}} ,x_{{02}} ,y_{{02}} } \right){\kern 1pt} {\kern 1pt} & = x_{{01}}^{{m_{1} }} \,\left( {iy_{{01}}^{{_{{}} }} } \right)^{{M - m_{1} }} \cosh \left( {b\frac{{x_{{01}} }}{{\omega _{0} }}} \right)\exp \left[ { - \delta x_{{01}}^{2} + \left( {\frac{{ikx}}{z} + \frac{{2x_{{02}} }}{{\rho _{0}^{2} }}} \right)x_{{01}} } \right] \\ & \quad \times \cosh \left( {b\frac{{y_{{01}} }}{{\omega _{0} }}} \right)\exp \left[ { - \delta y_{{01}}^{2} + \left( {\frac{{iky}}{z} + \frac{{2y_{{02}} }}{{\rho _{0}^{2} }}} \right)y_{{01}} } \right]{\kern 1pt} , \\ \end{aligned}$$
(6d)

and δ is the auxiliary parameter defined by

$$\delta = \frac{{ik}}{{2z}} + \frac{1}{{\omega _{0} ^{2} }} + \frac{1}{{\rho _{0}^{2} }}.$$
(6e)

Using the definition of cosh function and the separation of variable method to perform the double integration in Eq. (6c), one gets

$$J_{{xy}} \left( {x_{{02}} ,y_{{02}} } \right){\kern 1pt} {\kern 1pt} = \left( i \right)^{{M - m_{1} }} F_{m} \left( {x_{{02}} ,x} \right){\kern 1pt} {\kern 1pt} F_{m} \left( {y_{{02}} ,y} \right),$$
(7a)

with

$$F_{m} \left( {s_{{02}} ,s} \right){\kern 1pt} = \frac{1}{2}\left( {F_{m}^{ + } \left( {s_{{02}} ,s} \right) + F_{m}^{ - } \left( {s_{{02}} ,s} \right)} \right),\quad s = x{\kern 1pt} {\kern 1pt} {\text{or}}{\kern 1pt} y$$
(7b)

where

$$F_{m}^{ \pm } \left( {s_{{02}} ,s} \right){\kern 1pt} = \int\limits_{{ - \infty }}^{{ + \infty }} {u^{m} \,\exp \left( { - \delta _{1} u^{2} } \right)\exp \left[ {\left( {\frac{{iks}}{z} + \frac{{2s_{{02}} }}{{\rho _{0}^{2} }} \pm \frac{b}{{\omega _{0} }}} \right)u} \right]} du,$$
(7c)

Now, by using the integral formula (Belafhal et al. 2020; Gradshteyn and Ryzhik 1994)

$$\int\limits_{{ - \infty }}^{{ + \infty }} {x^{n} e^{{ - px^{2} + 2qx}} } dx = e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \left( {\frac{1}{{2i\sqrt p }}} \right)^{n} H_{n} \left( {\frac{{iq}}{{\sqrt p }}} \right),$$
(8)

where \(H_{n} \left( {.{\kern 1pt} {\kern 1pt} } \right)\) is the Hermite polynomial of nth-order, Eq. 7(c) reads

$$F_{m}^{ \pm } \left( {s_{{02}} ,x} \right){\kern 1pt} = e^{{\frac{{q_{ \pm } \left( {s_{{02}} ,s} \right)^{2} }}{{\delta _{1} }}}} \sqrt {\frac{\pi }{{\delta _{1} }}{\kern 1pt} {\kern 1pt} } \left( {\frac{1}{{2i\sqrt {\delta _{1} } }}} \right)^{{m_{1} }} H_{{m_{1} }} \left( {\frac{{iq_{ \pm } \left( {s_{{02}} ,s} \right)}}{{\sqrt {\delta _{1} } }}} \right),$$
(9a)

where

$$q_{ \pm } \left( {s_{{02}} ,s} \right) = \frac{{iks}}{{2z}} + \frac{{s_{{02}} }}{{\rho _{0}^{2} }} \pm \frac{b}{{2\omega _{0} }},$$
(9b)

in which s represents either x or y.

The substitution of Eqs. 9(a–b) and (7a) into Eq. (6a) leads to

$$\begin{aligned} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle & = \frac{1}{4}\frac{\pi }{\delta }\left( {\frac{k}{{2\pi z}}} \right)^{2} \left( {\frac{1}{{2i\sqrt \delta }}} \right)^{M} \sum\limits_{{m_{1} = 0}}^{M} {C_{{m_{1} }}^{M} \left( i \right)^{{M - m_{1} }} \sum\limits_{{m_{2} = 0}}^{M} {C_{{m_{2} }}^{M} } } \int\limits_{{ - \infty }}^{{ + \infty }} {\int\limits_{{ - \infty }}^{{ + \infty }} {f\left( {x_{{02}} ,y_{{02}} ,x,y} \right)} } \\ & \quad \times \left\{ \begin{gathered} \left[ {\exp \left( {\frac{{q_{ + } \left( {x_{{02}} ,x} \right)^{2} }}{{\delta _{1} }}} \right)H_{{m_{1} }} \left( {\frac{{iq_{ + } \left( {x_{{02}} ,x} \right)}}{{\sqrt \delta }}} \right) + \exp \left( {\frac{{q_{ - } \left( {x_{{02}} ,x} \right)^{2} }}{\delta }} \right)H_{{m_{1} }} \left( {\frac{{iq_{ - } \left( {x_{{02}} ,x} \right)}}{{\sqrt \delta }}} \right)} \right] \hfill \\ + \left[ {\exp \left( {\frac{{q_{ + } \left( {y_{{02}} ,y} \right)^{2} }}{\delta }} \right)H_{{M - m_{1} }} \left( {\frac{{iq_{ + } \left( {y_{{02}} ,y} \right)}}{{\sqrt \delta }}} \right) + \exp \left( {\frac{{q_{ - } \left( {y_{{02}} ,y} \right)^{2} }}{\delta }} \right)H_{{M - m_{1} }} \left( {\frac{{iq_{ - } \left( {y_{{02}} ,y} \right)}}{{\sqrt \delta }}} \right)} \right] \hfill \\ \end{gathered} \right\}dx_{{02}} dy_{{02}} . \\ \end{aligned}$$
(10)

The integral expression on the right–hand of the last equation can be performed straightforwardly as following: By using the separation of variable method, and the expanding form of Hermite polynomial (Gradshteyn and Ryzhik 1994),

$$H_{m} \left( x \right) = \sum\limits_{{j = 0}}^{{\left[ {{\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right]}} {\frac{{( - 1)^{j} m!}}{{j!\left( {m - 2j} \right)!}}\left( {2x} \right)^{{m - 2j}} } ,$$
(11)

and with the help a second time of Eq. (8), and after lengthy algebraic calculations, the average intensity of the diffracted vChGB in the turbuence atmosphere is expressed as

$$\begin{aligned} I\left( {x,y,z} \right) & = \left( {\frac{k}{{2z}}} \right)^{2} \frac{1}{{16\delta _{1} \eta }}\left( {\frac{1}{{2i\sqrt {\delta _{1} } }}} \right)^{M} \,\sum\limits_{{m_{1} = 0}}^{M} {C_{{m_{1} }}^{M} \left( i \right)^{{M - m1}} \sum\limits_{{m_{2} = 0}}^{M} {C_{{m_{2} }}^{M} } } \left( { - i} \right)^{{M - m_{2} }} \\ & \quad \times \left[ {G_{{m_{1} m_{2} }}^{ + } \left( {x,z} \right) + G_{{m_{1} m_{2} }}^{ - } \left( {x,z} \right)} \right]\,\left[ {H_{{m_{1} m_{2} }}^{ + } \left( {y,z} \right) + H_{{m_{1} m_{2} }}^{ - } \left( {y,z} \right)} \right], \\ \end{aligned}$$
(12)

where

$$\begin{aligned} G_{{m_{1} m_{2} }}^{ \pm } \left( {x,z} \right) & = \sum\limits_{{s{}_{1} = 0}}^{{\left[ {\frac{{m_{1} }}{2}} \right]}} {\frac{{\left( { - 1} \right)^{{s_{1} \,}} \,m_{1} \,!}}{{s_{1} !\,\left( {m_{1} - 2s_{1} } \right)\,!}}} \,\left( {\frac{{2i}}{{\sqrt \delta }}} \right)^{{m_{1} - 2s_{1} }} \sum\limits_{{j_{1} = 0}}^{{m_{1} - 2s_{1} }} {C_{{j{}_{1}}}^{{m_{1} - 2s_{1} }} \,\left( {\frac{1}{{2i\sqrt \eta }}} \right)^{{m_{2} + j_{1} }} \left( {\frac{1}{{\rho _{0}^{2} }}} \right)^{{j_{1} }} } \\ & \times \left\{ {\,\left\{ \begin{gathered} \left( {\left( {\frac{{ikx}}{{2z}} + \frac{b}{{2\omega _{0} }}} \right)} \right)^{{m_{1} - 2s_{1} - j_{1} }} \exp \left( {A\,x^{2} + B_{1}^{ \pm } x\, + C_{1}^{ \pm } } \right)H_{{m_{2} + j{}_{2}}} \left( {\frac{{i\alpha }}{{\sqrt \eta }}\,x + \frac{{i\beta ^{ \pm } }}{{\sqrt \eta }}} \right) \hfill \\ + \,\left( {\left( {\frac{{ikx}}{{2z}} - \frac{b}{{2\omega _{0} }}} \right)} \right)^{{m_{1} - 2s_{1} - j_{1} }} \exp \left( {A\,x^{2} + B_{2}^{ \mp } \,x\, + C_{2}^{ \mp } } \right)H_{{m_{2} + j{}_{2}}} \left( {\frac{{i\alpha }}{{\sqrt \eta }}\,x - \frac{{i\beta ^{ \mp } }}{{\sqrt \eta }}} \right) \hfill \\ \end{gathered} \right\}} \right\}, \\ \end{aligned}$$
(13a)
$$\begin{aligned} H_{{m_{1} m_{2} }}^{ \pm } \left( {y,z} \right) & = \sum\limits_{{s_{2} = 0}}^{{\left[ {\frac{{M - m_{1} }}{2}} \right]}} {\frac{{\left( { - 1} \right)^{{s_{2} \,}} \,\left( {M - m_{1} } \right)!}}{{s_{2} !\,\left( {M - m_{1} - 2s_{2} } \right)!}}} \left( {\frac{{2i}}{{\sqrt \delta }}} \right)^{{M - m_{1} - 2s_{2} }} \sum\limits_{{j_{2} = 0}}^{{M - m_{1} - 2s_{2} }} {C_{{j{}_{2}}}^{{M - m_{1} - 2s_{2} }} \left( {\frac{1}{{2i\sqrt \eta }}} \right)^{{M - m_{2} + j_{2} }} \left( {\frac{1}{{\rho _{0}^{2} }}} \right)^{{j_{2} }} } \\ & \quad \times \left\{ {\,\left\{ \begin{gathered} \left( {\left( {\frac{{iky}}{{2z}} + \frac{b}{{2\omega _{0} }}} \right)} \right)^{{M - m_{1} - 2s_{2} - j_{2} }} \exp \left( {Ay^{2} + B_{1}^{ \pm } y + C_{1}^{ \pm } } \right)H_{{M - m_{2} + j_{2} }} \left( {\frac{{i\alpha }}{{\sqrt \eta }}\,y + \frac{{i\beta ^{ \pm } }}{{\sqrt \eta }}} \right) \hfill \\ + \left( {\left( {\frac{{iky}}{{2z}} - \frac{b}{{2\omega _{0} }}} \right)} \right)^{{M - m_{1} - 2s_{2} - j_{2} }} \exp \left( {Ay^{2} + B_{2}^{ \mp } y + C_{2}^{ \mp } } \right)H_{{M - m_{2} + j_{2} }} \left( {\frac{{i\alpha }}{{\sqrt \eta }}\,y - \frac{{i\beta ^{ \mp } }}{{\sqrt \eta }}} \right) \hfill \\ \end{gathered} \right\}} \right\}, \\ \end{aligned}$$
(13b)

with

$$\eta = \delta * - \frac{1}{{\delta \rho _{0} ^{4} }},{\text{and}}\,d*\,{\text{denotes}}\,{\text{the}}\,{\text{complex}}\,{\text{conjugate}}\,{\text{of}}\,d,$$
(13c)
$$\alpha = \frac{{ik}}{{2z}}\left( {\frac{1}{{\delta \rho _{0} ^{2} }} - 1} \right),$$
(13d)
$$\beta ^{ \pm } = \frac{b}{{2\omega _{0} }}\left( {\frac{1}{{\delta \rho _{0} ^{2} }} \pm 1} \right),$$
(13e)
$$A = \frac{{\alpha ^{2} }}{\eta } - \frac{{k^{2} }}{{4z^{2} \delta }},$$
(13f)
$$B_{1}^{ \pm } = \frac{{ikb}}{{2z\omega _{0} \delta }} + \frac{{2\alpha \beta ^{ \pm } }}{\eta },$$
(13g)
$$B_{2}^{ \mp } = - \left( {\frac{{ikb}}{{2z\omega _{0} \delta }} + \frac{{2\alpha \beta ^{ \mp } }}{\eta }} \right){\kern 1pt} {\kern 1pt} ,$$
(13h)
$$C_{1}^{ \pm } = \frac{{b^{2} }}{{4\omega _{0} ^{2} \delta }} + \frac{{\left( {\beta ^{ \pm } } \right)^{2} }}{\eta },$$
(13i)

and

$$C_{2}^{ \mp } = \frac{{b^{2} }}{{4\omega _{0} ^{2} \delta }} + \frac{{\left( {\beta ^{ \mp } } \right)^{2} }}{\eta }{\kern 1pt} .$$
(13j)

Equation (12) is the main analytical result of this work, and it will be convenient for analyzing the evolution of the intensity of vChGB propagating through turbulent atmosphere.

In the limit case \(C_{n}^{2} = 0\), i.e., in the absence of the atmospheric turbulence, Eq. (12) reduces to the propagation equation of vChGB in free-space, the obtained result is consistent with Eq. (8a) of Ref. Hricha et al. (2020b).

The on-axis intensity can be deduced by putting x = y = 0 in Eq. (12), so we get

$$\begin{aligned} I\left( {0,0,z} \right) & = \left( {\frac{k}{{2z}}} \right)^{2} \frac{1}{{16\delta \eta }}\left( {\frac{1}{{2i\sqrt \delta }}} \right)^{M} \,\sum\limits_{{m_{1} = 0}}^{M} {C_{{m_{1} }}^{M} \left( i \right)^{{M - m1}} \sum\limits_{{m_{2} = 0}}^{M} {C_{{m_{2} }}^{M} } } \left( { - i} \right)^{{M - m_{2} }} \\ & \quad \times \left[ {G_{{m1m2}}^{ + } \left( {0,z} \right) + G_{{m1m2}}^{ - } \left( {0,z} \right)} \right]\,\left[ {H_{{m1m3}}^{ + } \left( {0,z} \right) + H_{{m1m2}}^{ - } \left( {0,z} \right)} \right], \\ \end{aligned}$$
(14a)

where

$$\begin{aligned} G_{{m1m2}}^{ \pm } \left( {0,z} \right) & = \sum\limits_{{s{}_{1} = 0}}^{{\left[ {\frac{{m_{1} }}{2}} \right]}} {\frac{{\left( { - 1} \right)^{{s_{1} \,}} \,m_{1} \,!}}{{s_{1} !\,\left( {m_{1} - 2s_{1} } \right)\,!}}} \,\left( {\frac{{2i}}{{\sqrt \delta }}} \right)^{{m_{1} - 2s_{1} }} \sum\limits_{{j_{1} = 0}}^{{m_{1} - 2s_{1} }} {C_{{j{}_{1}}}^{{m_{1} - 2s_{1} }} \,\left( {\frac{1}{{2i\sqrt \eta }}} \right)^{{m_{2} + j_{1} }} \left( {\frac{1}{{\rho _{0}^{2} }}} \right)^{{j_{1} }} } \\ & \quad \times \left\{ {\,\left\{ {\left( {\frac{b}{{2\omega _{0} }}} \right)^{{m_{1} - 2s_{1} - j_{1} }} \exp \left( {C_{1} } \right)H_{{m_{2} + j{}_{2}}} \left( {\frac{{i\beta ^{ \pm } }}{{\sqrt \eta }}} \right) + \,\left( {\frac{b}{{2\omega _{0} }}} \right)^{{m_{1} - 2s_{1} - j_{1} }} \exp \left( {C_{2} } \right)H_{{m_{2} + j{}_{2}}} \left( { - \frac{{i\beta ^{ \mp } }}{{\sqrt \eta }}} \right)} \right\}} \right\}, \\ \end{aligned}$$
(14b)
$$\begin{aligned} H_{{m1m2}}^{ \pm } \left( {0,z} \right) & = \sum\limits_{{s_{2} = 0}}^{{\left[ {\frac{{M - m_{1} }}{2}} \right]}} {\frac{{\left( { - 1} \right)^{{s_{2} {\kern 1pt} }} \left( {M - m_{1} } \right)!}}{{s_{2} !\left( {M - m_{1} - 2s_{2} } \right)!}}} \left( {\frac{{2i}}{{\sqrt \delta }}} \right)^{{M - m_{1} - 2s_{2} }} \sum\limits_{{j_{2} = 0}}^{{M - m_{1} - 2s_{2} }} {C_{{j_{2} }}^{{M - m_{1} - 2s_{2} }} {\mkern 1mu} \left( {\frac{1}{{2i\sqrt \eta }}} \right)^{{M - m_{2} + j_{2} }} \left( {\frac{1}{{\rho _{0}^{2} }}} \right)^{{j_{2} }} } \\ & \quad \times \left\{ {{\mkern 1mu} \left\{ {\left( {\frac{b}{{2\omega _{0} }}} \right)^{{M - m_{1} - 2s_{2} - j_{2} }} \exp \left( {C_{1} } \right)H_{{M - m_{2} + j_{2} }} \left( {\frac{{i\beta ^{ \pm } }}{{\sqrt \eta }}} \right) + \left( {\frac{b}{{2\omega _{0} }}} \right)^{{M - m_{1} - 2s_{2} - j_{2} }} {\mkern 1mu} \exp \left( {C_{2} } \right)H_{{M - m_{2} + j_{2} }} \left( { - \frac{{i\beta ^{ \mp } }}{{\sqrt \eta }}} \right)} \right\}} \right\}. \\ \end{aligned}$$
(14c)

It is worth noting that in the two limiting cases b = 0 and M = 0, the above formulation gives the propagation equation and the intensity distribution for the vortex Gaussian and ChGB beams (respectively) in turbulent atmosphere (Chu et al. 2007).

3 Numerical results and analyses

The propagation characteristics of vChGB propagating in atmospheric turbulence are numerically investigated based on the main formula given by Eq. (12). Since the initial shape of the vChGB is dependent on the value of the decentered parameter b, therefore, in the following, the two configurations of the beam, i.e., the beam with small and large values of b will be separately examined.

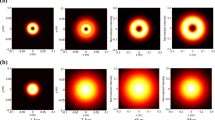
In Figs. 1 and 2, we illustrated the normalized intensity distribution of vChGB in turbulent atmosphere at different propagation distance z (z  = 0.1 km, 1 km, 2 km and 5 km). The calculation parameters are set as ω0  =  cm, M =1 , λ  =  1060 nm and \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\). In addition, the same characteristics of the beam in free-space are presented for the sake of comparison. From the illustrated plots, it is seen that the vChGB keeps its initial profile, i.e., a ringed pattern with hole-intensity at the center, until a certain propagation distance, and then the beam gradually changes profile and the central hole-intensity is filled upon propagation at large propagation distance (see Figs. 1-a3 and 2-a4). From the plots (b1–b4), it can be seen that the evolution of vChGB in atmospheric turbulence is different from that in free-space; in free-space the hole-intensity persists even in far-field. Furthermore, one can note that the widening of the beam in turbulent atmosphere is stronger compared to the free-space case.

Fig. 1
figure 1

The normalized intensity of a vChGB in a turbulent atmosphere for different values of the propagation distance z with \(\omega _{0} = 0.02\,{\text{m}}\), topological charge M  = 1, b  = 0.1 \(\lambda = 1060\,{\text{nm}}\) and \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\)

Full size image
Fig. 2
figure 2

The normalized intensity of a vChGB in a turbulent atmosphere for different values of the propagation distance z with \(\omega _{0} = 0.02\,{\text{m}}\), topological charge M  = 1, b   = 4, \(\lambda = 1060\,{\text{nm}}\) and \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\)

Full size image
Fig. 3
figure 3

a The average intensity of a vChGB in a turbulent atmosphere for different values of the topological charge with \(\lambda = 1060\,{\text{nm}}\), \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\) and \(\omega _{0} = 0.02\,{\text{m}}\). b The normalized axial intensity of a vChGB in a turbulent atmosphere versus propagation distance versus the topological charge M, for b = 0.1 and b = 4, with \(\lambda = 1060\,{\text{nm}}\), \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\) and \(\omega _{0} = 0.02\,{\text{m}}\)

Full size image
Fig. 4
figure 4

The normalized intensity of a vChGB in a turbulent atmosphere for a different values of the refractive index structure \(C_{n}^{2}\) with \(\omega _{0} = 0.02\,{\text{m}}\), z = 2 km and \(\lambda = 1060\,{\text{nm}}\)

Full size image

Figure 3a, b display the intensity distribution pattern and the on-axis intensity (respectively) of vChGB in turbulent atmosphere for different values of the topological charge M (M = 0, 1, 2 and 3). It is clearly seen that the rising speed of peak intensity at the center (for both beam configurations) is faster as M increases.

In order to analysis the effect of the turbulence strength on the beam propagation, we have illustrated in Fig. 4 the normalized intensity distribution for different values of turbulence strength \(C_{n}^{2}\) \(\,\left( {C_{n}^{2} = 10^{{ - 16}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 10^{{ - 15}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \,{\text{and}}\,5.10^{{ - 15}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \,} \right)\). The plots show that the rising speed of the central peak is faster when the turbulence strength is stronger for both beam configurations. In addition, one can note the increase of the beam widening with increasing the turbulence strength.\(C_{n}^{2}\).

Figure 5 presents the effect of the waist size \(\omega _{0}\) on the evolution of the intensity distribution of vChGB in turbulent atmosphere at the propagation distance z = 2 km, for M = 1. From the illustrations in Fig. 5, one can clearly see that the beam widens faster and the rising speed of the central peak is slower when ω0 increases.

Fig. 5
figure 5

The normalized intensity of a vChGB in a turbulent atmosphere for different values of the waist \(\omega _{0}\) with M = 1, z = 2 km, \(\lambda = 1060\,{\text{nm}}\) and \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\). (a.1, b.1) \(\omega _{0} = 0.02\,{\text{m}}\), (a.2, b.2) \(\omega _{0} = 0.05\,{\text{m}}\), (a.3, b.3) \(\omega _{0} = 0.1\,{\text{m}}\) and (a.4, b.4) \(\omega _{0} = 0.2\,{\text{m}}\)

Full size image

The influence of the wavelength λon the evolution intensity distribution is depicted in Fig. 6, from which it is readily seen that the perturbed beam widens gradually as λ increases. Furthermore, the central hole-intensity is filled faster when λ is smaller in the small b case, whereas the opposite evolution occurs with large b case.

Fig. 6
figure 6

The normalized intensity of a vChGB in a turbulent atmosphere for different values of the wavelength \(\lambda\) with M  = 1, z   = 2 km, \(\omega _{0} = 0.02\,{\text{m}}\) and \(C_{n}^{2} = 10^{{ - 14}} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\). (a.1, b.1) \(\lambda = 632.8\,{\text{nm}}\), (a.2, b.2) \(\lambda = 1060\,{\text{nm}}\), (a.3, b.3) \(\lambda = 1550\,{\text{nm}}\) and (a.4,b.4) \(\lambda = 2000\,{\text{nm}}\)

Full size image

4 Conclusion

The propagation characteristics of a vChGB propagating in turbulent atmosphere are investigated in detail. The analytical expression of the average intensity of the diffracted vChGB in turbulent atmosphere is derived within the framework of the Huygens–Fresnel diffraction and the Rytov method. Numerical examples illustrating the effects of the turbulence strength, the beam parameters and the wavelength on the beam propagation are performed. It is found that the incident vChGB keeps its initial profile within a certain propagation distance, and then loses gradually its central hole-intensity and transformed into a Gaussian–like beam. The rising speed of central peak is faster for larger strength turbulence, higher vortex charge and smaller Gaussian waist size. The obtained results can be beneficial for applications of vChG in free space optical communication systems.