1 Introduction

During the last few years, there has been growing interest for the study of dark hollow vortex beams due to their potential applications in various fields, such as optical trapping, optical microscopy, wireless communications and optical micromanipulations (Ito et al. 1996; Kuga et al. 1997; Paterson et al. 2001; Cai et al. 2003; Bishop et al. 2004; Torok and Munro 2004; Cai and Ge 2006; Wang et al. 2012; Rubinsztein-Dunlop, et al. 2017). Several vortex beams which were introduced for the cylindrical symmetry are separable in the polar coordinates, as examples, we cite the well-known Laguerre-Gaussian (Allen et al. 1992; Kennedy et al. 2002; Vallone 2015), Bessel-Gaussian (Arlt and Dholakia 2000; McGloin and Dholakia 2005; Kotlyar et al. 2006; Vaity and Rusch 2015), hypergeometric-Gaussian (Kotlyar et al. 2007; Karimi et al. 2007; Skidanov et al. 2013) and flat-topped Gaussian beams (Liu et al. 2015). While, the well–known rectangular laser beams which are separable in the orthogonal direction, such as Hermite sinusoidal-Gaussian (Casperson and Tovar 1998; Tovar and Casperson 1998), four-petal Gaussian (Duan and Lü 2006), Lorentz-Gaussian (Zhou 2010) and Finite Airy beams (Siviloglou et al. 2007; Siviloglou and Christodoulides 2007) are not originally vortex modes but they can be embedded by vortex phase amplitude. The resulting vortex beams can then carry the orbital angular momentum and have specific shape patterns. Some of the beams considered above were generated experimentally by means of laser resonators or diffractive optical elements (Guo et al. 2014; Wang et al. 2019; Kotlyar et al. 2015; Monin and Ustinov 2018; Dai et al. 2010; Zhou and Ru 2013). A kind of hollow vortex-beam, named as hollow vortex-Gaussian beams, has been discovered by Zhou et al. (Zhou et al. 2013, 2018). These beams show a high propagation stability in free space and thus may have potential application in optical micromanipulations. More recently, a vortex cosh-Gaussian beam (vChGB), which is a cosh-Gaussian field embedded with a vortex phase has been proposed to describe a more general type of hollow vortex beams in the rectangular symmetry (Hricha et al. 2020). The proposed model beam has one additional control parameter more than to the simple vortex Gaussian beam. The propagation properties of this beam in free-space and in FrFT system have been investigated in details (Hricha et al. (2020)). In the source plane, the vChGB may resembles to the vortex-Gaussian field for small values of b, whereas it splits into a four-lobes structure resembling to the four-petal Gaussian beam when b is large. To extend further our research on rectangular beams carrying vortex phase structure, we propose in this paper a Hermite-cosh-Gaussian beam embedded with a vortex phase, which we will refer to as vortex Hermite-cosh-Gaussian beam (vHChGB). In the source plane, the vHChGB has three key parameters, namely the beam orders (p, q), the decentered parameter b and the vortex charge number M. The high number of the parameter permits to produce a broad variety of beam patterns, and the well-known vortex-Gaussian, vortex Hermite-Gaussian and vortex-cosh-Gaussian beams can be regarded as limiting cases of the vHChGB. The present paper is aimed at investigating the propagation characteristics of the vHChGB passing through a paraxial optical system. The closed-form expression of the propagated vHChGB in a paraxial optical medium is derived based on the Collins formula. The spatial characteristics of the beam are analyzed numerically with illustrated examples. The reminder of the manuscript is organized as follows: in Sect. 2, the vHChGB pattern is illustrated, in the source plane, as a function of the beam parameters. Then in Sect. 3, the propagation formula of the vHChGB through a paraxial ABCD optical system is derived by means of the Huygens-Fresnel diffraction integral. In Sect. 4, the spatial characteristics of the vHChGB in free space are discussed numerically with illustrated examples. The main results are outlined in the conclusion part.

2 Characteristics of the vHChGB pattern at the source plane

In the Cartesian coordinates system, the z-axis is taken to be as the propagation direction. A vHChGB can be for instance generated by using a Hermite-cosine hyperbolic-Gaussian beam (HChGB) (Belafhal and Ibnchaikh 2000; Ibnchaikh et al. 2001; Hricha and Belafhal 2005a, 2005b) in passage through a spiral phase plate (SPP) (Oemrawsingh et al. 2004; Kotlyar et al. 2005). The SPP may modulate the wave-front phase of the field so that the resulting beam may acquire the orbital angular momentum, which is associated with a vortex charge M at the beam’s center.

The general vHChGB in the source plane z = 0 takes the form

$$E_{pq} \left( {x_{0} ,y_{0} ,\,z = 0} \right) = E_{p} \left( {x_{0} ,z = 0} \right){\kern 1pt} E_{q} \left( {y_{0} ,z = 0} \right)\left( {x_{0} + iy_{0} } \right)^{M}$$
(1a)

where

$$E_{j} \left( {u,z = 0} \right) = H_{j} \left( {\frac{\sqrt 2 u}{{\omega_{0} }}} \right)\cosh \left( {\frac{b}{{\omega_{0} }}u} \right)\exp \left( { - \frac{{u^{2} }}{{\omega_{0}^{2} }}} \right)\,,$$
(1b)

with \(j = p{\kern 1pt} {\kern 1pt} {\kern 1pt} or{\kern 1pt} {\kern 1pt} \,q\), and \(u = x_{0} {\kern 1pt} {\kern 1pt} {\kern 1pt} or{\kern 1pt} {\kern 1pt} \,y_{0}\). \(\left( {x_{0,} y_{0} } \right)\) being the Cartesian coordinates at the source plane, and (p, q) are the mode indexes associated with the Hermite polynomials \(H_{p} \left( . \right)\) and \(H_{q} \left( . \right)\) in the x- and y-directions, respectively. \(\cosh \left( . \right)\) denotes the hyperbolic-cosine function, ω0 is the waist size of the Gaussian part, b is the decentered parameter associated with the cosh part, and the integer parameter M denotes the topological charge of the spiral phase plate.

From Eq. (1a) one can deduce that the profile of a vHChGB at the source plane is determined by five parameters, i.e., p, q, b, M and ω0. By setting particular values of the beam parameters, Eq. (1a) may describe a set of well-known beams, such as the Gaussian beam when \(p = q = M{\kern 1pt} = b = 0\), hollow vortex-Gaussian beam for \(p = q = b = 0\) (Zhou et al. 2013), vortex-cosh-Gauss beam (vChGB) when \(p = q = 0\) (Hricha et al. 2020), vortex Hermite–Gaussian beam (vHGB) (Kotlyar et al. 2015; Monin and Ustinov 2018) for b = 0 and HChG beam for M = 0 (Belafhal and Ibnchaikh 2000; Ibnchaikh et al. 2001; Hricha and Belafhal 2005a). With the embedded vortex charge, the vCHGBs can be used as optical traps; they may be able to trap both high- and low-index microparticles as well as to set them into rotation by use of the orbital angular momentum of light.

Equation (1a) can also be rewritten as

$$\begin{gathered} E_{p\,q} \left( {x_{0} ,y_{0} {\kern 1pt} ,z = 0} \right) = \frac{1}{4}\exp \left( {\frac{{b^{2} }}{4}} \right)H_{p} \left( {\frac{{\sqrt 2 x_{0} }}{{\omega_{0} }}} \right)H_{q} \left( {\frac{{\sqrt 2 y_{0} }}{{\omega_{0} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\{ {\exp \left[ { - \left( {\frac{{x_{0} }}{{\omega_{0} }} - \frac{b}{2}} \right)^{2} } \right] + \exp \left[ { - \left( {\frac{{x_{0} }}{{\omega_{0} }} + \frac{b}{2}} \right)^{2} } \right]} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\{ {\exp \left[ { - \left( {\frac{{y_{0} }}{{\omega_{0} }} - \frac{b}{2}} \right)^{2} } \right] + \exp \left[ { - \left( {\frac{{y_{0} }}{{\omega_{0} }} + \frac{b}{2}} \right)^{2} } \right]} \right\}\left( {x_{0} + iy_{0} } \right)^{M} {\kern 1pt} , \hfill \\ \end{gathered}$$
(2)

this suggests that the vHChG beam can be obtained by a superposition of four Hermite-decentered Gaussian modes embedded with the same vortex phase.

As a preliminarily illustration of vHChG field at the source plane, we depicted in Figs. (1, 2), the intensity distributions of the beam versus the parameters (p, q), b and M. For convenience, the waist width is fixed to be ω0 = 1 mm in all calculations.

Fig. 1
figure 1

The normalized intensity distribution of a vHChG beam at the source plane with ω0 = 1 mm and M = 1 for different values of (p,q) and b. The top, middle and bottom rows denote respectively p = q = 1, p = q = 2 and p = q = 3:(a.1–3) b = 0, (b.1–3) b = 1, (c.1–3) b = 1.5 and (d.1–3) b = 4

Full size image
Fig. 2
figure 2

The normalized intensity distribution of vHChG beam at the source plane with \(\omega_{0} = 1\,\,mm\) and p = q = 3 for different b. The first, second, third and fourth rows denote respectively M = 1, M = 2, 4 and M = 6: (a.1–4) b = 0, (b.1–4) b = 1.5 and (c.1–4) b = 4

Full size image

From the plots of these figures, it is shown that a vHChG field has a multi-petal structure with a dark central region. The shape pattern is mirror symmetric and depends crucially on the value of b parameter, that is, for small b (b < 1), the beam exhibits 2(p + q) petals (see Fig. 1). The main lobes are located at the vertices of the four-squared beam pattern. While for large b, the secondary lobes disappear and only the main lobes remain visible (see Fig. 1, columns (c–d)); the beam profile resembles closely to the four-petal beam (Duan and Lü 2006). One can also see a slight increasing of the inter-lobes space, and a narrowing of the lobes width when the beam orders (p, q) are increased (see the intensity distribution in the x-direction in the right side of Fig. 1).

Figure 2 illustrates the influence of the topological charge M on the vHChGB pattern. As can be seen, the main four petals slightly widen and elongate into an elliptical form under the effect of increasing the topological charge. In addition, one can note also an increasing of the inter-lobes space; this is clearly illustrated in Fig. 3 which presents the normalized intensity distribution in the x-direction.

Fig. 3
figure 3

The normalized intensity distribution of vHChG beam at the source plane with ω0 = 1 mm, b = 4 and p = 2 for different topological charge values M

Full size image

3 Theoretical model

Within the framework of the paraxial approximation, the propagation of a laser beam through a paraxial ABCD optical system obeys the Collins formula (Collins 1970):

$$E\left( {x,y,z} \right) = \frac{ik}{{2\pi B}}e^{ - ikz} \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{0} \left( {x_{0} ,{\kern 1pt} y_{0} ,{\kern 1pt} {\kern 1pt} 0} \right)\exp \left\{ { - \frac{ik}{{2B}}\left[ {A\left( {x_{0}^{2} {\kern 1pt} {\kern 1pt} + {\kern 1pt} y_{0}^{2} {\kern 1pt} } \right) - 2\left( {xx_{0} {\kern 1pt} {\kern 1pt} + {\kern 1pt} yy_{0} } \right) + D\left( {x^{2} + y^{2} {\kern 1pt} } \right)} \right]} \right\}dx_{0} y_{0} } } {\kern 1pt} {\kern 1pt} ,$$
(3)

where \(E_{0} \left( {x_{0} ,{\kern 1pt} y_{0} ,{\kern 1pt} {\kern 1pt} 0} \right)\) and \(E\left( {x,y,z} \right)\) are the fields at the source (z = 0) and the receiver planes, respectively. z is the propagation distance, A, B, and D are the matrix elements of the optical system, \(k = \frac{2\pi }{\lambda }\) is the wave number and · is the wavelength of radiation in vacuum.

Substituting from Eq. (1a) into Eq. (3), and recalling the binomial expansion (Gradshteyn and Ryzhik 1994)

$$\left( {x_{0} {\kern 1pt} {\kern 1pt} + {\kern 1pt} iy_{0} {\kern 1pt} } \right)^{M} {\kern 1pt} = {\kern 1pt} \sum\limits_{m = 0}^{M} {C_{m}^{M} } x_{0}^{m} \left( {iy_{0} } \right)^{{_{M - m} }}$$
(4a)

where

$$C_{m}^{M} = {\kern 1pt} \frac{M!}{{m!\left( {M - m} \right)\,!}}$$
(4b)

we obtain

$$E\left( {x,y,z} \right) = \frac{ik}{{2\pi B}}e^{ - ikz} {\kern 1pt} e^{{ - \frac{ikD}{{2B}}\left( {x^{2} + y^{2} } \right)}} \sum\limits_{m = 0}^{M} {C_{m}^{M} } \left( i \right)^{{_{M - m} }} I_{m} \left( x \right)I_{M - m} \left( y \right){\kern 1pt} ,$$
(5a)

where

$$I_{n} \left( u \right){\kern 1pt} {\kern 1pt} = \int\limits_{ - \infty }^{ + \infty } {u_{0}^{r} \cosh \left( {b\frac{{u_{0} }}{{\omega_{0} }}} \right)e^{{ - \alpha u_{0}^{2} + \frac{ik}{B}uu_{0} }} H_{j} \left( {\frac{{\sqrt 2 u_{0} }}{{\omega_{0} }}} \right)} du_{0}$$
(5b)

with \(u = x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} or\,\,y\), r is an integer, \(j = p{\kern 1pt} {\kern 1pt} {\kern 1pt} or{\kern 1pt} {\kern 1pt} \,q\) and α is the auxialiary parameter defined as

$$\alpha {\kern 1pt} = {\kern 1pt} \frac{ikA}{{2B}} + \frac{1}{{\omega_{0}^{2} }}.$$
(5c)

Using the expansion form of the Hermite function \(H_{j} \left( {{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} } \right)\) (Gradshteyn and Ryzhik 1994),

$$H_{j} \left( x \right) = \sum\limits_{p = 0}^{{\left[ {j/2} \right]}} {\frac{{( - 1)^{p} j!}}{{p!\left( {j - 2p} \right)\,!}}\left( {2x} \right)^{j - 2p} }$$
(6)

and recalling the following integral formula (Prudnikov et al. 1986; Belafhal et al. 2020)

$$\int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} } dx = e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right)$$
(7)

then carrying on some tedious calculations, Eq. (5) turns out to be

$$\begin{aligned} E\left( {x,y,z} \right) & = \,e^{{ - ikz}} \frac{{ik}}{{8\alpha B}}\left( {\frac{1}{{2i\sqrt \alpha }}} \right)^{M} \left( {\frac{{\sqrt 2 }}{{i\omega _{0} \sqrt \alpha }}} \right)^{{\left( {p + q} \right)}} e^{{\frac{{b^{2} }}{{2\alpha \omega _{0} ^{2} }}}} e^{{ - \left( {\frac{{ikD}}{{2B}} + \frac{{k^{2} }}{{4\alpha B^{2} }}} \right)\left( {x^{2} + y^{2} } \right)}} \\ & \times \sum\limits_{{m = 0}}^{M} {C_{m}^{M} } \left( i \right)^{{_{{M - m}} }} \left[ {f_{{p,m}}^{ + } \left( x \right) + f_{{p,m}}^{ - } \left( x \right)} \right]{\kern 1pt} {\kern 1pt} \left[ {f_{{q,M - m}}^{ + } \left( y \right) + f_{{q,M - m}}^{ - } \left( y \right)} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned}$$
(8)

where

$$f_{p,m}^{ \pm } \left( x \right) = {\kern 1pt} \sum\limits_{s = 0}^{{\left[ \frac{p}{2} \right]}} {\frac{p!}{{s!\left( {p - 2s} \right)\,!}}} {\kern 1pt} \left( {\frac{{\alpha \omega_{0}^{2} }}{2}} \right)^{s} e^{{ \pm \frac{ikbx}{{2\alpha B\omega_{0} }}}} H_{p + m - 2s} \left( {\frac{ik}{{2B\sqrt \alpha }}x \pm \frac{ib}{{2\omega_{0} \sqrt \alpha }}} \right){\kern 1pt}$$
(9a)

and

$$f_{q,M - m}^{ \pm } \left( y \right) = {\kern 1pt} \sum\limits_{h = 0}^{{\left[ \frac{q}{2} \right]}} {\frac{q!}{{h!\left( {q - 2h} \right)\,!}}} {\kern 1pt} \left( {\frac{{\alpha \omega_{0}^{2} }}{2}} \right)^{h} e^{{ \pm \frac{ikby}{{2\alpha B\omega_{0} }}}} H_{q + M - m - 2h} \left( {\frac{ik}{{2B\sqrt \alpha }}y \pm \frac{ib}{{2\omega_{0} \sqrt \alpha }}} \right){\kern 1pt}$$
(9b)

Equation (8) is the propagation formula of a vHChGB passing through a paraxial optical system.

This formula can be reduced in the following cases:

  1. (1)

    When b = 0, Eq. (8) will give the diffracted vortex Hermite–Gaussian beam which can be expressed as

    $$E\left( {x,y,z} \right) = \frac{ik}{{2\alpha B}}\left( {\frac{1}{2i\sqrt \alpha }} \right)^{M} \left( {\frac{\sqrt 2 }{{i\omega_{0} \sqrt \alpha }}} \right)^{p + q} e^{ - ikz} \,e^{{ - \left( {\frac{ikD}{{2B}} + \frac{{k^{2} }}{{4\alpha B^{2} }}} \right)\left( {x^{2} + y^{2} } \right)}} \sum\limits_{m = 0}^{M} {C_{m}^{M} } \left( i \right)^{{_{M - m} }} f_{p,m}^{{}} \left( x \right){\kern 1pt} f_{q,M - m}^{{}} \left( y \right){\kern 1pt} {\kern 1pt} ,$$
    (10a)

    where

    $$f_{p,m}^{{}} \left( u \right) = {\kern 1pt} \sum\limits_{s = 0}^{{\left[ \frac{p}{2} \right]}} {\frac{p!}{{s!\left( {p - 2s} \right)!}}} {\kern 1pt} \left( {\frac{{\alpha \omega_{0}^{2} }}{2}} \right)^{s} H_{p + m - 2s} \left( {\frac{ik}{{2B\sqrt \alpha }}u} \right){\kern 1pt} \quad {\text{with }}u = x\,{\text{or}}\,y$$
    (10b)

    Equation (10a) is consistent with the result of Ref. (Kotlyar et al. 2015).

  2. (2)

    In the case \(p = q = 0\), Eq. (8) will give the propagation formula of the vChGB, which can be expressed as

    $$\begin{aligned} E\left( {x,y,z} \right) = & \frac{{ik}}{{8\alpha B}}\left( {\frac{1}{{2i\sqrt \alpha }}} \right)^{M} e^{{ - ikz}} \sum\limits_{{m = 0}}^{M} {C_{m}^{M} } \left( i \right)^{{M - m}} e^{{\frac{{b^{2} }}{{2\alpha \omega _{0}^{2} }}}} e^{{ - \left( {\frac{{ikD}}{{2B}} + \frac{{k^{2} }}{{4\alpha B^{2} }}} \right)\left( {x^{2} + y^{2} } \right)}} \\ & \times \left[ {f_{m}^{ + } \left( x \right) + f_{m}^{ - } \left( x \right)} \right]\left[ {f_{{M - m}}^{ + } \left( y \right) + f_{{M - m}}^{ - } \left( y \right)} \right] \\ \end{aligned}$$
    (11a)

    where

    $$f_{n}^{ \pm } \left( u \right) = {\kern 1pt} e^{{ \pm \frac{ikbu}{{2\alpha B\omega_{0} }}}} H_{n} \left( {\frac{ik}{{2B\sqrt \alpha }}u \pm \frac{ib}{{2\omega_{0} \sqrt \alpha }}} \right){\kern 1pt} \quad {\text{with }}u = x\,{\text{or}}\,y\,{\text{and}}\,n = m\,{\text{or}}\,M - m$$
    (11b)

    The obtained equation is consistent with the result of Hricha et al. (2020).

    Equation (10a) is consistent with the result of (Kotlyar et al. 2015).

  3. (3)

    When \(p = q = b = 0\), Eq. (8) will reduce to the hollow vortex Gaussian beam propagating trough ABCD optical system (Zhou and Ru 2013), which can be written as

    $$E\left( {x,y,z} \right) = \frac{ik}{{2\alpha B}}\left( {\frac{1}{2i\sqrt \alpha }} \right)^{M} e^{ - ikz} e^{{ - \left( {\frac{ikD}{{2B}} + \frac{{k^{2} }}{{4\alpha B^{2} }}} \right)\left( {x^{2} + y^{2} } \right)}} \sum\limits_{m = 0}^{M} {C_{m}^{M} } \left( i \right)^{{_{M - m} }} \left[ {{\kern 1pt} H_{m} \left( {\frac{ik}{{2B\sqrt \alpha }}x} \right){\kern 1pt} H_{M - m} \left( {\frac{ik}{{2B\sqrt \alpha }}y} \right){\kern 1pt} } \right]{\kern 1pt} {\kern 1pt} .$$
    (12)

    It is worth noting that the Eq. (12) is equivalent to Eq. (8) of Zhou et al. (2013) (if we take n = m/2 in Zhou et al. (2013)) even if they are different in form.

    Equation (10a) is consistent with the result of Kotlyar et al. (2015).

4 Numerical results and discussions

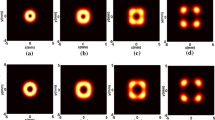
Here, we investigate the evolution behavior of the vHChGB propagating in free space by calculating Eq. (8). The calculation parameters are taken as λ = 632.8 nm, ω0 = 1 mm and \(z{}_{R} = \frac{{k\omega_{0}^{2} }}{2}\) denotes the Gaussian Rayleigh length, which is used as the unit scale for the propagation distance. Figure (4) presents the typical intensity distributions of a vHChGB beam with M = 1 at the initial plane (z = 0), near field (z = zR) and far field (z = 15zR), respectively, for different values of b and for p = q = 1 and p = q = 2. From the plots of Fig. 4, it is shown that in near field, the main lobes widen gradually and the secondary lobes disappear completely (see plots (a.4)–(a.5); the field evolves into a four petal-like beam. In far-field, the size of the beam spot widens and the lobes bond. When b is large, the beam morphs into a “fan blades” structure whose pattern depends crucially on beam orders (p,q) (see the plots (d.3)-(d. 6)).

Fig. 4
figure 4

Normalized intensity distribution of the vHChG beam with ω0 = 1 mm, \(\lambda = 632.8\,\,nm\) and M = 1 for different propagation distance and different parameter values of b. the first three rows and the second ones denote respectively p = q = 1 and p = q = 2. The first (z = 0), the second (z = zR) and the third row (z = 15zR): (a.1–6) b = 0, (b.1–6) b = 0.1, (c.1–6) b = 1.5 and (d.1–6) b = 4

Full size image

The effects of the beam orders (p, q) and the topological charge M on the vHChG beam shape in far field are illustrated in Figs. (5) and (6). It is seen that for small b, the beam keeps the four-petal shape and the inter-lobes space increases with the increase of the beam orders (p, q). Whereas for large b and with M = 1, the four lobes overlap and morphs into fan blades-like pattern with a dark spot at the center for all the beam orders (p,q) (see Fig. 5(d.1–d.3). For M = 2 and large values of b (see Fig. 6), the beam shape and the intensity at its center depend on the parity of p and q; when (p,q) are odd the beam shape evolves into nine petals of mirror symmetry with a bright central core (see Fig. 6.(a4–c4)), whereas when (p,q) are even, the beam has four symmetrical wide spots with a dark central core (see Fig. 6. (b4–d4)).

Fig. 5
figure 5

Normalized intensity distribution of the vHChG beam with ω0 = 1 mm, \(\lambda = 632.8\,\,nm\) and M = 1 at z = 15zR for different parameter values of b. The top, middle and bottom rows denote respectively p = q = 1, p = q = 2 and p = q = 3: (a.1–3) b = 0, (b.1–3) b = 1, (c.1–3) b = 1.5 and (d.1–3) b = 4

Full size image
Fig. 6
figure 6

Normalized intensity distribution of the vHChG beam with ω0 = 1 mm, \(\lambda = 632.8\,\,nm\) and M = 2 at z = 15zR for different values of p and q. The first, second, third and the fourth rows denote respectively b = 0.1, b = 1, 1.5 and b = 4: (a.1–4) p = q = 1, (b.1–4) p = q = 2, (c.1–4) p = q = 3 and (d.1–4) p = q = 4

Full size image

Figure 7 illustrates the same characteristics as in Fig. 6 but with taking M = 3. From the obtained plots, one can note the absence of the bright central core for all the orders presented; this is in accordance with the result obtained with M = 1 (see Fig. 5). This means that the parity of M is crucial for controlling the intensity at the beam’s center.

Fig. 7
figure 7

The same as Fig. 6 except M = 3

Full size image

Figure 8 shows the effect of the topological charge M (M = 5, 6 and 8) on the beam shape in far field. One can clearly see that the main lobes elongate into elliptic form and separate with increasing the value of M. It follows from the above analysis that when the b parameter is large, the beam shape and the central area intensity of the diffracted vHChGB in far field depend significantly on the values and the parities of M, p and q.

Fig. 8
figure 8

Normalized intensity distribution of the vHChG beam with ω0 = 1 mm and \(\lambda = 632.8\,\,nm\) at z = 15zR for different values of M. The first and the second rows denote respectively b = 2 and p = q = 2, b = 4 and p = q = 4. (a.1–2) M = 5, (b.1–2) M = 6 and (c.1–2) M = 8

Full size image

5 Conclusion

In summary, a vHChG beam is introduced. Based on the Collins diffraction integral, the propagation formula of the vHChGB through a paraxial ABCD optical system is derived. It emerges from illustrated examples that the beam parameters influence crucial the intensity pattern of the propagated vHChGB in free space. The shape of the vHChGB gradually changes upon propagating in near field, then morphs drastically in far-field. The size, the structure of the petals and the intensity of the central area of the beam can be controlled by adjusting the beam parameters. Our results may be useful in many applications where special intensity pattern of beam is privileged such as micro-optics, beam splitting techniques and optical communications.