1 Introduction

In the last few years, extensive investigations on the propagation properties of laser beams through turbulent atmosphere have been conducted due to their potential applications in free-space optical communications, remote sensing, laser radar systems, etc. (Andrews and Philips 1998; Wang et al. 2015). With the rapid development in laser optics, various models of coherent laser beams have been introduced and their propagation characteristics in the turbulent atmosphere have been investigated, e.g., the Hermite-sinusoidal-Gaussian beams (Baykal 2004; Eyyuboğlu and Baykal 2005; Eyyuboğlu 2005), dark hollow beams (Cai and He 2006), flat-topped beams (Appl 2006; Kinani et al. 2011), Helmholtz-Gauss beams (Noriega-Manez and Gutiérrez-Vega 2007), hollow Gaussian beams (Khannous et al. 2016), Bessel–Gaussian beams (Zhu et al. 2008; Belafhal et al. 2011), generalized Bessel-Laguerre-Gaussian beams (Boufalah et al. 2018), generalized spiraling Bessel beams (Saad et al. 2018), Dark and Antidark Gaussian beams (Yaalou et al. 2019), double–half inverse Gaussian hollow beams (Hricha et al. 2020a), vortex cosine-hyperbolic-Gaussian beams (vChGB) (Hricha et al. 2021a), vortex Hermite-cosine-hyperbolic-Gaussian beams (vHChGB) (Hricha et al. 2021b), Lommel-Gaussian beams (Ez-zariy et al. 2016) and Pearcey-Gaussian beams (Boufalah et al. 2016). Almost all of the cited researchers have been extended from fully coherent beams to partially coherent beams. The advantages of partially coherent beams over fully coherent beams include the resistance to the alteration effects of the turbulence, beam truncation, aberrations, the reduction of speckle, and the effects of dust particles, (Liu et al. 2017; Zeng et al. 2019).

On the other hand, the hollow vortex beams have received much interest due to their novel features brought by the twisted wave-front phase and orbital angular momentum (OAM). The OAM provides a new tool for encoding data in free-space optical systems, and the vortex beams can greatly improve the transmission rate (Wang et al. 2012; Huang et al. 2014; Zhu et al. 2016). The topological charge and phase singularity of vortex beams can be exploited in optical trapping, micro-manipulation, and light spanners (Zeng et al. 2019; Allen et al. 1992; Kuga et al. 1997; Paterson et al. 2001; Bishop et al. 2004; Wang et al. 2004). During the last years, the evolution properties of various types of partially coherent beams, including the average intensity distribution and coherence characteristics in the turbulent atmosphere, have been reported, such as those of partially coherent multiple Gaussian beams (Baykal et al. 2009), partially coherent standard, and elegant Laguerre-Gaussian beams (Wang et al. 2010), radially polarized partially coherent beams (Wang et al. 2011), elliptical Gaussian-Schell beams (Chu 2011), partially coherent dark hollow beams (Taherabadi et al. 2012), partially coherent flat-topped beams (Cheng and Cai 2011), and partially coherent four-petal Gaussian vortex beams (Liu et al. 2016). Furthermore, we have recently investigated the propagation properties of the so-called partially coherent vortex cosine-hyperbolic-Gaussian beam (PCvChGB) in a paraxial ABCD optical system (Hricha et al. 2020b). The influences of both the initial beam parameters and the degree of spectral coherence on the average intensity distribution for a PCvChGB propagating in free space have been and through an FRFT optical system have been demonstrated in detail. However, as far as we know, the propagation of such beams through the turbulent atmosphere has not been reported. Therefore, the present paper is aimed at investigating the evolution and transformation properties of a PCvChGB in weak atmospheric turbulence conditions. The theoretical model of this study is based on the extended Huygens–Fresnel principle and the Rytov method. The remainder of the manuscript is organized as follows. In Sect. 2, we will present the theoretical analysis for the paraxial propagation of a PCvChGB through the turbulent atmosphere and derive in detail the analytical expression of the average intensity distribution of the output beam. In Sect. 3, many numerical examples are presented to illustrate the effects of the turbulent atmosphere and the initial beam parameters on the propagated PCvChGB. Finally, the main results obtained in this study are summarized in the conclusion part.

2 Theory model

In the Cartesian coordinate system, taking the z-axis as the propagation direction, the cross-spectral density function of a PCvChGB in the source plane (z = 0) can be written as (Hricha et al. 2020b; Lazrek et al. 2021)

$$W\left( {\vec{r}_{01} ,\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right) = E\left( {\vec{r}_{01} ,{\kern 1pt} {\kern 1pt} 0} \right)\,E*\left( {\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \right)\,g\left( {\vec{r}_{01} - \vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right)$$
(1)

where \(E\left( {r_{0i} ,z = 0} \right)\) (i = 1 or 2) is the electric field associated with a fully coherent vChGB (Hricha et al. 2020b), which is given as

$$E\left( {\vec{r}_{0i} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0i} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0i} }}{{\omega_{0} }}} \right)\exp \left( { - \frac{{x_{0i}^{2} + y_{0i}^{2} }}{{\omega_{0}^{2} }}} \right)\left( {x_{0i} + iy_{0i} } \right)^{M}$$
(2a)

\(g\left( {\vec{r}_{01} - \vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right)\) is the degree of coherence of a Schell model source

$$g\left( {\vec{r}_{01} - \vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right) = \exp \left( { - \frac{{\left( {\vec{r}_{01} - \vec{r}_{02} } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right)$$
(2b)

where the asterisk symbol * means the complex conjugation, \(\vec{r}_{0i} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \left( {x_{0i} ,{\kern 1pt} y_{0i} } \right)\) is the position vector at the initial plane z = 0, and \(\omega_{0}\) is the Gaussian beam waist radius. b is the decentered parameter associated with the cosh part. M denotes the topological charge of the beam and σ0 is the spatial coherence length at the source plane.

The field of Eq. (1), which can be deemed as the extension form of a partially coherent hollow Gaussian beam, may describe a dark hollow beam with an arbitrary spatial coherence and a variable central dark region. Obviously, in the limit case when σ0 tends to be infinite, Eq. (1) will reduce to the fully coherent vChGB (Hricha et al. 2021a, 2021c, 2021d; Lazrek et al. 2022).

Based on the extended Huygens–Fresnel principle, the average intensity of a PCvChGB traveling in a turbulent atmosphere at the plane z can be expressed as (Andrews and Philips 1998)

$$\begin{gathered} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {W\left( {\vec{r}_{01} ,\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right)} } } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left[ { - \frac{ik}{{2z}}\left\{ {\left( {x_{01} - x} \right)^{2} + \left( {y_{01} - y} \right)^{2} - \left( {x_{02} - x} \right)^{2} - \left( {y_{02} - y} \right)^{2} } \right\}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\exp \left[ {\psi \left( {\vec{r}_{01} ,\vec{r}} \right) + \psi *\left( {\vec{r}_{02} ,\vec{r}} \right)} \right]} \right\rangle d\vec{r}_{01} d\vec{r}_{02} \,\,, \hfill \\ \end{gathered}$$
(3)

where \(\vec{r}{\kern 1pt} = {\kern 1pt} {\kern 1pt} \left( {x,{\kern 1pt} y} \right)\), and x and y are the transverse coordinates at the output plane z. \(\psi \left( {\vec{r}_{0i} ,\vec{r}} \right)\) denotes the random part for the complex phase of a spherical wave spreading from the source plane to the output plane, \(k = \frac{2\pi }{\lambda }\) is the wavenumber with λ is the wavelength. The angle brackets denote the ensemble average over the medium statistics covering the log-amplitude and phase fluctuation due to the turbulence. \(d\vec{r}_{0i} {\kern 1pt} = dx_{0i} dy_{0i}\) is an elementary area in the source plane.

According to the Rytov theory, the ensemble average in Eq. (3) is given as (Andrews and Philips 1998; Wang et al. 2015)

$$\left\langle {\exp \left[ {\psi \left( {\overrightarrow {r}_{01} ,\overrightarrow {r} } \right) + \psi *\left( {\overrightarrow {r}_{02} ,\overrightarrow {r} } \right)} \right]} \right\rangle {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {\vec{r}_{01} - \vec{r}_{02} } \right)^{2} } \right]$$
(4)

where \(\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}}\) is the lateral coherence length of a spherical wave propagating in the turbulent medium. \(C_{n}^{2}\) is the refractive index structure constant, and represents the strength of the turbulence.

By substituting from Eqs. (1) and (4) into Eq. (3), and recalling the binomial formula (MAbramowitzIAStegun1964Handbook of Mathematical FunctionsNat. Bureau of Standards WashingtonDCM. Abramowitz, I.A. Stegun (Eds.), “Handbook of Mathematical Functions”. Nat. Bureau of Standards Washington, DC (1964). 1964)

$$\left( {u{\kern 1pt} + {\kern 1pt} v{\kern 1pt} } \right)^{m} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{m} {C_{l}^{m} } u^{l} v^{{_{m - l} }}$$
(5a)

with

$$C_{l}^{m} = {\kern 1pt} \frac{m!}{{l!\left( {m - l} \right)!}}$$
(5b)

the result can be written as

$$\left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = 0}^{M} {C_{l}^{M} \left( i \right)^{M - l} } \sum\limits_{n = 0}^{M} {C_{n}^{M} \left( { - i} \right)^{M - n} } \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {F_{xy} \left( {x_{01} ,y_{01} } \right)\,G_{xy} \left( {x_{01} ,y_{01} } \right)} } dx_{01} \,dy_{01} {\kern 1pt} ,$$
(6a)

where

$$\begin{gathered} F_{xy} \left( {x_{01} ,y_{01} } \right){\kern 1pt} {\kern 1pt} = x_{01}^{l} \,\left( {y_{01}^{{_{{}} }} } \right)^{M - l} \cosh \left( {b\frac{{x_{01} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{01} }}{{\omega_{0} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - \delta \,x_{01}^{2} + \frac{ikx}{z}x_{01} } \right)\exp \left( { - \delta \,y_{01}^{2} + \frac{iky}{z}y_{01} } \right), \hfill \\ \end{gathered}$$
(6b)

and

$$G_{xy} \left( {x_{01} ,y_{01} } \right) = \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {\left\{ \begin{gathered} x_{02}^{n} \,\cosh \left( {b\frac{{x_{02} }}{{\omega_{0} }}} \right)\exp \left[ { - \delta^{ * } x_{02}^{2} + \left( {\frac{ikx}{z} + \frac{{2x_{01} }}{{\rho_{0}^{2} }} + \frac{{x_{01} }}{{2\sigma_{0}^{2} }}} \right)x_{02} } \right] \hfill \\ \times \left( {y_{02}^{{_{{}} }} } \right)^{M - n} \cosh \left( {b\frac{{y_{02} }}{{\omega_{0} }}} \right)\exp \left[ { - \delta^{ * } y_{02}^{2} + \left( {\frac{iky}{z} + \frac{{2y_{01} }}{{\rho_{0}^{2} }} + \frac{{x_{01} }}{{2\sigma_{0}^{2} }}} \right)y_{02} } \right] \hfill \\ \end{gathered} \right\}dx_{02} \,dy_{02} } }$$
(6c)

with δ is the auxiliary parameter defined by

$$\delta = \frac{ik}{{2z}} + \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}$$
(6d)

By using the separation of variable technic to perform the double integral in Eq. (6c), one can obtain

$$G_{xy} \left( {x_{01} ,y_{01} } \right){\kern 1pt} {\kern 1pt} = \frac{1}{4}\left( {F_{n}^{ + } \left( {s_{01} ,s} \right) + F_{n}^{ - } \left( {s_{01} ,s} \right)} \right){\kern 1pt} \left( {F_{M - n}^{ + } \left( {s_{01} ,s} \right) + F_{M - n}^{ - } \left( {s_{01} ,s} \right)} \right){\kern 1pt} {\kern 1pt}$$
(7a)

where

$$F_{n}^{ \pm } \left( {s_{01} ,s} \right){\kern 1pt} = \int\limits_{ - \infty }^{ + \infty } {u^{n} \,\exp \left( { - \delta^{ * } \,u^{2} } \right)\exp \left[ {\left( {\frac{iks}{z} + \frac{{2s_{01} }}{{\rho_{0}^{2} }} + \frac{{s_{01} }}{{2\sigma_{0}^{2} }} \pm \frac{b}{{\omega_{0} }}} \right)u} \right]} du$$
(7b)

in which s represents either x or y,

Now, by recalling the following integral formula (Belafhal et al. 2020)

$$\int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} } dx = e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),Re\left( p \right) > 0$$
(8)

where \(H_{n} \left( {.{\kern 1pt} {\kern 1pt} } \right)\) is the Hermite polynomial of nth-order (Gradshteyn and Ryzhik 1994), and which is given as

$$H_{m} \left( x \right) = \sum\limits_{j = 0}^{{\left[ {{\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right]}} {\frac{{( - 1)^{j} m!}}{{j!\left( {m - 2j} \right)!}}\left( {2x} \right)^{m - 2j} }$$
(9)

and after carrying out the tedious algebraic calculations, one obtains the following expression of the average intensity

$$\begin{gathered} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \frac{1}{16}\frac{\pi }{{\delta^{ * } \eta }}\left( \frac{k}{2z} \right)^{2} \left( {\frac{1}{{2i\sqrt {\delta^{ * } } }}} \right)^{M} \,\sum\limits_{l = 0}^{M} {C_{l}^{M} \left( i \right)^{M - l} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \left( { - i} \right)^{M - n} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left[ {Q_{l,n}^{ + } \left( x \right) + Q_{l,n}^{ - } \left( x \right)} \right]\,\left[ {Q_{M - l,n - l}^{ + } \left( y \right) + Q_{M - l,M - n}^{ - } \left( y \right)} \right] \hfill \\ \end{gathered}$$
(10)

where

$$\begin{gathered} Q_{l,n}^{ \pm } \left( s \right) = \exp \left\{ {\frac{1}{{\delta^{ * } }}\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{s = 0}^{n} {C_{s}^{n} } \left( {\frac{i}{{\sqrt {\delta^{ * } } }}\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)} \right)^{s} H_{n - s} \left( {\frac{i}{{\sqrt {\delta^{ * } } }}\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left( {\frac{1}{2i\sqrt \eta }} \right)^{l + s} \left\{ {\exp \left\{ {\frac{{\left( {q^{ \pm } \left( s \right)} \right)^{2} }}{\eta }} \right\}H_{l + s} \left( {\frac{{iq^{ \pm } \left( s \right)}}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {v^{ \pm } \left( s \right)} \right)^{2} }}{\eta }} \right\}H_{l + s} \left( {\frac{{iv^{ \pm } \left( s \right)}}{\sqrt \eta }} \right)\,} \right\}\, \hfill \\ \end{gathered}$$
(11a)

with

$$\eta = \delta - \frac{1}{\delta *}\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)^{2}$$
(11b)
$$q^{ \pm } \left( s \right) = \frac{1}{\delta *}\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{iks}{{2z}} + \frac{b}{{2\omega_{0} }}} \right)$$
(11c)

and

$$v^{ \pm } \left( s \right) = \frac{1}{\delta *}\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{iks}{{2z}} - \frac{b}{{2\omega_{0} }}} \right)$$
(11d)

Equation (10) is the main analytical result of this work. It indicates that the average intensity of a PCvChGB propagating in a turbulent atmosphere is dependent on the turbulence strength \(C_{n}^{2}\), the initial beam parameters (b, ω0, \({\kern 1pt} {\kern 1pt} \sigma_{0}\)), and the propagation distance z. By using Eq. (10), we can conveniently investigate the evolution properties of a PCvChGB in a turbulent atmosphere under different parameters conditions.

From Eq. (10), one can distinguish the following limit cases:

  • When \(C_{n}^{2} {\kern 1pt} = 0{\kern 1pt} \,{\kern 1pt}\), i.e., in the absence of turbulence, Eq. (10) will give the field of a PCvChGB propagating in free space, which is consistent with that derived in Ref. (Hricha et al. 2020b).

  • When \({\kern 1pt} {\kern 1pt} \sigma_{0} \to \infty\), Eq. (10) will give the propagation formula of a coherent vChGB in a turbulent atmosphere, which matches Eq. (12) in Ref. (Hricha et al. 2021b).

3 Numerical examples and analysis

In this section, the propagating properties of a PCvChGB in a turbulent atmosphere are illustrated numerically by using Eq. (10). As is previously reported (Hricha et al. 2020b; Lazrek et al. 2021), a PCvChGB at the initial plane is hollow dark beam-like, and can also have two types of intensity distribution depending on the value of the parameter b: for a small value of b (saying typically b = 0.1) the beam profile is a hollow Gaussian-like and for large b (typically b = 4), it becomes a four petal-like. Hence, hereafter, both initial beam profiles (i.e., the beam with a small b and a large b configuration) will be considered separately. Also, the propagation properties of the PCvChGB in free space are presented for the sake of comparison. In the numerical simulations (unless specified otherwise), the parameters are set as \(\omega_{0} = 20\,mm\), M = 1,\(\sigma_{0} = 10\,\,mm\,,\)\(\lambda = 1064\,nm\)\(C_{n}^{2} = 10^{ - 13} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\) and \(z_{r} = {{k\omega_{0}^{2} } \mathord{\left/ {\vphantom {{k\omega_{0}^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}\) is the Rayleigh length.

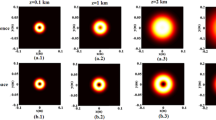
Figure 1 shows the contour graph of the normalized average intensity distribution for a PCvChGB traveling in the turbulent atmosphere at some selected propagation distances (z = 0, z = 0.1zr, 0.5 \(z_{r}\), \(z_{r}\) and 5 \(z_{r}\)), and the corresponding diagrams for the free-space propagation.

Fig. 1
figure 1

The normalized average intensity distribution for PCvChGBs (with b = 0.1 and b = 4) traveling in a turbulent atmosphere (the first and third rows) at z = 0, z = 0.1 \(z_{r}\), 0.5 \(z_{r}\)\(z_{r}\), 1, and 5 \(z_{r}\), and the corresponding diagrams for the free-space propagation (the second and fourth rows), with M = 1, \(\sigma_{0} = 10mm\) and \(C_{n}^{2} = 10^{ - 13} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\)

Full size image

One can see that the PCvChGB traveling in a turbulent atmosphere keeps its initial profile unchanged at short propagation distances, until a certain distance. As the propagation distance is further increased, the beam loses gradually its central dark region and evolves into a solid Gaussian-like beam. A comparison of the beam evolutions in a turbulent atmosphere with the free-space propagation (see the second and fourth rows) indicates that the beam spreads more rapidly and loses its initial shape faster in turbulence than in free space, e.g., it is found that for b = 0.1 and b = 4, the beam changes profile at z = 0.5 zr and z = 1.05 zr in the turbulent atmosphere and the corresponding values in free space are 0.91 zr and 1.8 zr, respectively. In addition, one can note that the distortion and rotation effect on the four lobes for a PCvChGB with large b is almost insensitive to atmospheric turbulence.

To further analyze the evolution of the central region intensity upon the beam propagation, we have depicted in Fig. 2 the variation of the on-axis intensity in a turbulent atmosphere versus the propagation distance z, for different values of the vortex charge number (M = 1, 2, and 3).

Fig. 2
figure 2

The normalized axial intensity versus propagation distance z of a PCvChGB for different vortex charges. a, b in turbulent atmosphere, and c, d in free space, with \(C_{n}^{2} = 10^{ - 13} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and \(\sigma_{0} = 10mm\)

Full size image

It can be seen that the rise of on-axis intensity distribution is faster for an initial PCvChG with the smaller b configuration. In addition, one can notice that the rise speed of the central peak intensity is slower when the vortex charge M is larger, and the on-axis intensity distribution is less sensitive to the vortex charge M for an initial beam with a large b configuration. This means that one can obtain a PCvChGB nearly non-affected by the turbulent atmosphere within a certain propagation range by property adjusting the values of the initial beam parameters M and b.

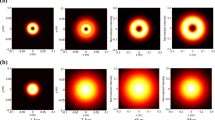
Figure 3 depicts the average intensity distribution of the perturbed PCvChGB at the planes z = 1zr and z = 5zr, for different initial coherence lengths σ0. It can be seen that for both initial beam configurations, the smaller σ0 the larger the beam spot size.

Fig. 3
figure 3

The normalized average intensity distribution of a PCvChGB (with small b and large b configurations) in a turbulent atmosphere for different values of \(\sigma_{0}\) at the planes z = 1zr and z = 5zr, with \(C_{n}^{2} = 10^{ - 14} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and M = 1

Full size image

Furthermore, one can observe from Fig. 4 that the rise speed of the central peak intensity is faster as σ0 is smaller. In other words, a PCvChGB with a small initial coherence length will be more affected by the turbulence.

Fig. 4
figure 4

The normalized axial intensity versus propagation distance z of a PCvChGB in a turbulent atmosphere for different values \(\sigma_{0}\), and for a b = 0.1 and b b = 4, with M = 1, \(\omega_{0} = 20m\,m\) \(\lambda = 1064\,\,nm\) \(C_{n}^{2} = 10^{ - 13} \,m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and

Full size image

The effect of increasing the structure constant \(C_{n}^{2}\) on the propagating PCvChGB is shown in Fig. 5. It is found that the PCvChGB is affected by the turbulence and spreads more rapidly when the structure constant is larger. Further, from Fig. 6, one can see that the conversion of the beam from a hollow profile into a solid Gaussian profile becomes quicker as the turbulence is stronger.

Fig. 5
figure 5

The normalized average intensity of PCvChGBs (with b = 0.1 and b = 4) traveling in a turbulent atmosphere at z = zr and z = 5zr, for different values \(C_{n}^{2}\), with \(\lambda = 1064nm\)\(\omega_{0} = 20m\,m\),\(\sigma_{0} = 10m\,m\) and M = 1

Full size image
Fig. 6
figure 6

The normalized on-axis average intensity versus propagation distance z of a PCvChGB in a turbulent atmosphere for different values of \(C_{n}^{2}\), and for a b = 0.1 and b b = 4, with M = 1, \(\omega_{0} = 20m\,m\) \(\sigma_{0} = 010mm\) \(\lambda = 1064\,\,nm\) and

Full size image

The influence of the wavelength λ on the propagation proprieties of the beam in the turbulent atmosphere is depicted in Figs. 7 and 8. The corresponding results of the free-space propagation are shown for comparison (see Fig. 8).

Fig. 7
figure 7

The average intensity distribution of a PCvChGB in a turbulent atmosphere at z = 0.5 zr, for different \(\lambda\), with \(C_{n}^{2} = 10^{ - 13} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\), \(\omega_{0} = 20mm\), \(\sigma_{0} = 10mm\), and M = 1. a1, b1 \(\lambda = 632.8nm\), a2, b2 \(\lambda = 1060nm\), a3, b3 \(\lambda = 1550nm\) and a4, b4 \(\lambda = 2000nm\)

Full size image
Fig. 8
figure 8

The normalized axial intensity versus propagation distance z of a PCvChGB in a turbulent atmosphere and free space for different values \(\lambda\). a, b for b = 0.1 and c, d for b = 4, with M = 1, \(\omega_{0} = 0.02\,m\), \(\sigma_{0} = 0.01\,m\) and \(C_{n}^{2} = 10^{ - 13} \,m^{{ - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}\)

Full size image

It is found that for a fixed propagation distance (z = zr), the beam size is larger and the rising speed of the central intensity is faster as λ is smaller. In addition, From Fig. 8, one can see that the beam profile changes more rapidly in a turbulent atmosphere compared to the free-space case.

The evolution properties of the PChGB which are illustrated above can be physically explained by the dynamics of the random homogeneities of the turbulent atmosphere. While the beam is propagating in the turbulent medium, the average beam energy distribution tends to concentrate around the propagation axis. The dynamic of energy conversion is larger in the intermediate propagation distance range. At larger propagation distances, the beam evolves into a nearly Gaussian averaged profile, and the initial hole intensity center is filled in the far field.

4 Conclusion

In this paper, the propagation properties of a partially coherent vortex cosine-hyperbolic-Gaussian beam (PCvChGB) are investigated. Based on the extended Huygens-Fresnel integral, the analytical expression of the average intensity for a PCvChGB propagating in a turbulent atmosphere is derived in detail. From the obtained expression, the effects of the atmospheric turbulence on the propagation properties of a PCvChGB under different beam parameters conditions are demonstrated numerically. It is shown that the beam keeps its initial hollow dark profile unchanged at short propagation distances, and then is converted into a solid Gaussian-like beam in the far-field region. The evolution of the average intensity distribution of the beam in a turbulent atmosphere is closely dependent on the incident beam parameters and structure constant. The obtained results could be beneficial for applications of PCvChGB in optical communications, remote sensing, and atom optics.