1 Introduction

The spreading of a laser beam in a turbulent atmosphere has been attracted much attention parallel to the advancement applications of laser beams. The propagation of laser beams through a turbulent atmosphere has important applications in many areas including free-space optical communications (Zhang and Yi 2009), laser radar (Cai et al. 2008), optical imaging and so-called active laser scanning (Wang et al. 2010a), and remote sensing (Wen Cheng et al. 2009). The random fluctuations in the refraction index of atmosphere cause spreading of the beam beyond that due to pure diffraction, beam wander, loss of spatial coherence, and random fluctuations in the irradiance and phase (Andrews and Phillips 2005). These effects can seriously degrade the signal-to-noise ratio of an optical heterodyne receiver. Therefore, much efforts have been devoted to a reliable theory for predicting the propagation properties of light beams in turbulent medium, and a great many achievements have been derived in the past decades (Yura 1972; Ponomarenko and Wolf 2002; Cai and He 2006a, 2006b; Cai et al. 2007; Cang et al. 2013a; Noriega-Manez and Gutiérrez-Vega 2007; Cai 2006; Kinani et al. 2011; Chu 2007).

During the last years, there are many special functions have been developed based on mathematical analytical approaches to use them as laser beam sources, such as Laguerre-Gaussian, Bessel-Gaussian and Lommel-Gaussian beams have been investigated in many studies (Wang et al. 2010b; Cang et al. 2013b; Ez-zariy et al. 2016a). Also, some special laser sources, such as Generalized spiraling Bessel and Flattened Hermite-Cosh-Gaussian propagating through an atmospheric turbulence have been investigated by many authors (Saad et al. 2017; Chib et al. 2020). Recently, Nossir et al. (2021) who are studied the behaviour of the central intensity of Generalized Humbert-Gaussian beams against the atmospheric turbulence.

Furthermore, the so-called dark hollow beams with zero central intensity have attracted great attention in the past years because of their wide applications in optical trapping particles (Kuga et al. 1997; Paterson et al. 2001). The research topics in this direction are many and varied, among them, the vortex of the flat-topped, Gaussian, Airy Gaussian, multi-hyperbolic Sine-correlated, and the Bessel-like beams (He and Lü 2011; Filimonov et al. 2016; Ez-zariy et al. 2016b; Khannous et al. 2016; Yue et al. 2019; Elmabruk and Eyyubolu 2019; Song et al. 2020; Lukin 2020).

Moreover, in two separate papers, Hricha and co-authors (2021a, 2021b) have studied the effect of the turbulent atmosphere on the propagation properties of the vortex cosine hyperbolic Gaussian and Hermite‑cosine‑hyperbolic‑Gaussian beams.

On the other hand, early Zhou (2011) has investigated the propagation of the higher-order Cosh-Gaussian beam in turbulent atmosphere. The propagation properties of a partially coherent vortex Cosh-Gaussian beam have been studied by Lazrek et al. (2021). More recently, Hricha et al. (2022) have been investigated theoretically the paraxial propagation of a partially coherent vortex cosine-hyperbolic-Gaussian beam in a turbulent atmosphere. Furthermore, we have recently investigated the propagation characteristics of a hollow higher-order Cosh-Gaussian beam in 1-Dimention (Saad et al. 2022; Ebrahim et al. 2022). However, to our knowledge, the propagation properties of such beams through the turbulent atmosphere have not been reported up to now. Therefore, the present paper is aimed to investigate the evolution and transformation properties of a GMvHchGB in both the weak and strength atmospheric turbulence conditions. This paper is organized as follows: The theoretical model has been developed in Sect. 2. Some interesting numerical results and illustrations have been given in Sect. 3. Finally, some conclusions have been outlined in Sect. 4.

2 Theoretical results

In the Cartesian coordinate system, the GMvHchGB along the x-and y-directions at the source plane (z = 0) takes the following form (Yaalou et al. 2020; Saad et al. 2022; Ebrahim et al. 2022)

$$E_{N;l} \left( {x_{0} ,y_{0} ,0} \right) = A_{0} \cosh^{N} \left( {\Omega \,x_{0} } \right)\,\cosh^{N} \left( {\Omega \,y_{0} } \right)\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{w_{0}^{2} }}} \right)\,\left( {x_{0} + i\,y_{0} } \right)^{l} \,$$
(1)

where \(A_{0}\) is the amplitude of the GMvHchGB at the origin of the source plane, \(w_{0}\) is the Gaussian waist, Ω (decentred parameter) is the parameter of the cosh part associated with the parabolic dependence of the refractive index (Lazrek et al. and (l, N) are integers and represent the hollowness and the beam-order of the considered beams, respectively. Therefore, \(E_{N;l} \left( {x_{0} ,y_{0} ,0} \right)\) can be described by a superposition of (N + 1) decentred Gaussian beams with the same waist as the fellows (Zhou and Zheng 2009)

$$\begin{gathered} E_{N;l} \left( {x_{0} ,y_{0} ,0} \right) = \frac{{A_{0} }}{{2^{2N} }}\,\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \exp \left( {a_{m}^{2} + a_{n}^{2} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left[ { - \left( {\frac{{x_{0} }}{{w_{0} }} - a_{m} } \right)^{2} } \right]\exp \left[ { - \left( {\frac{{y_{0} }}{{w_{0} }} - a_{n} } \right)^{2} } \right]\,\left( {x_{0} + iy_{0} } \right)^{l} , \hfill \\ \end{gathered}$$
(2)

where,

\(a_{m} = \left( {m - \frac{N}{2}} \right)\sqrt \delta\), and \(a_{n} = \left( {n - \frac{N}{2}} \right)\sqrt \delta\), with \(\delta = \,\Omega^{2} w_{0}^{2}\).

Recalling the binomial expansion (Gradshteyn and Ryzhik 1994)

$$\left( {x_{0} + i\,y_{0} } \right)^{l} = \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)} \,x_{0}^{s} \,\left( {iy_{0} } \right)^{l - s}$$
(3)

then, Eq. (2) can be written as

$$\begin{gathered} E_{N;l} \left( {x_{0} ,y_{0} ,\,0} \right) = \frac{{A_{0} }}{{2^{2N} }}\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)x_{0}^{s} \,\left( {iy_{0} } \right)^{l - s} \exp \left( {a_{m}^{2} + a_{n}^{2} } \right)} \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left[ { - \left( {\frac{{x_{0} }}{{w_{0} }} - a_{m} } \right)^{2} } \right]\exp \left[ { - \left( {\frac{{y_{0} }}{{w_{0} }} - a_{n} } \right)^{2} } \right]\,. \hfill \\ \end{gathered}$$
(4)

By using the extended Huygens-Fresnel diffraction integral, the output electric field component of the GMvHchGB in a turbulent atmosphere can be obtained by (Andrews and Phillips 2005; Born and Wolf 1999)

$$\begin{gathered} E_{N;l} \left( {x,y,z} \right) = - \frac{i\,k}{{2\pi \,z}}\,\exp \left( {ik\,z} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{N;l} \left( {x_{0} ,y_{0} ,\,0} \right)} } \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad\quad \times \,\exp \left\{ { - \frac{ik}{{2z}}\left[ {\left( {x_{0}^{2} + y_{0}^{2} } \right) - 2\left( {xx_{0} + yy_{0} } \right)} \right] + \psi \left( {x_{0} ,y_{0} ,x,y} \right)} \right\}\,dx_{0} dy_{0} , \hfill \\ \end{gathered}$$
(5)

where x and y are the Cartesian coordinates at the output plane z, k = 2π/λ is the wavenumber with λ being the optical wavelength and \(\psi \left( {x_{0} ,y_{0} ,x,y} \right)\) is the solution to the Rytov theory that represents the random part of the complex phase of spherical waves. Therefore, the average intensity of a GMvHchGB traveling in a turbulent atmosphere at the plane z can be expressed as

$$\begin{gathered} \left\langle {I_{N;l} \,\left( {x,y,\,{\text{z}}} \right)} \right\rangle = \frac{{\,k^{2} }}{{4\,\pi^{2} z^{2} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{N;l} \left( {x_{01} ,y_{01} ,\,0} \right)} } } } \,E_{N;l}^{ * } \left( {x_{02} ,y_{02} ,\,0} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \frac{ik}{{2z}}\left[ {\left( {x_{01}^{2} - x_{02}^{2} + y_{01}^{2} - y_{02}^{2} } \right) - 2x\left( {x_{01} - x_{02} } \right) - 2y\left( {y_{01} - y_{02} } \right)} \right]} \right\}\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\,\exp \left[ {\psi \left( {x_{01} \,,y_{01} ,x,y} \right) + \psi^{ * } \left( {x_{02} \,,y_{02} ,x,y} \right)} \right]\,} \right\rangle dx_{01} dy_{01} dx_{02} dy_{02} , \hfill \\ \end{gathered}$$
(6)

where

$$\begin{gathered} E_{N;l} \left( {x_{01} ,y_{01} ,0} \right)E_{N;l}^{ * } \left( {x_{02} ,y_{02} ,0} \right) = \frac{{A_{0}^{2} }}{{2^{4N} }}\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)\,i^{l - s} \sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} \sum\limits_{{s^{\prime} = 0}}^{l} {\left( {\begin{array}{*{20}c} l \\ {s^{\prime}} \\ \end{array} } \right)\,\left( { - i} \right)} }^{{l - s^{\prime}}} \hfill \\ \quad\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times x_{01}^{s} \,x_{01}^{{s^{\prime}}} \exp \left( { - \frac{{x_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{m} }}{{w_{0} }}x_{01} } \right)\exp \left( { - \frac{{x_{02}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{{m^{\prime}}} }}{{w_{0} }}x_{02} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \times y_{01}^{l - s} y_{02}^{{l - s^{\prime}}} \exp \left( { - \frac{{y_{01}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{n} }}{{w_{0} }}y_{01} } \right)\exp \left( { - \frac{{y_{02}^{2} }}{{w_{0}^{2} }} + 2\frac{{a_{{n^{\prime}}} }}{{w_{0} }}y_{02} } \right)\,, \hfill \\ \end{gathered}$$
(7)

and the angle brackets \(\langle \cdot \rangle\) denote the ensemble average over the medium statistics covering the log-amplitude and phase fluctuations due to the turbulent atmosphere. The asterisk means the complex conjugation. The ensemble average term is given by (Andrews and Phillips 2005)

$$\left\langle {\,\exp \left[ {\psi \left( {x_{01} \,,y_{01} ,x,y} \right) + \psi^{ * } \left( {x_{02} \,,y_{02} ,x,y} \right)} \right]\,} \right\rangle = \exp \left[ { - \frac{{\left( {x_{01} - x_{02} } \right)^{2} + \left( {y_{01} - y_{02} } \right)^{2} }}{{\rho_{0}^{2} }}} \right],$$
(8)

where \(\rho_{0} = \left( {0.545\,C_{n}^{2} k^{2} z} \right)^{{ - {\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 5}}\right.\kern-0pt} \!\lower0.7ex\hbox{$5$}}}}\) is the coherence length of a spherical wave propagating in the turbulent medium, \(C_{n}^{2}\) is the constant of refraction index structure and describes the turbulence level and z is the axial distance between the source and the output planes. Substituting Eqs. (7) and (8) into Eq. (6), after some manipulations, the average intensity of the GMvHchGB in the receiver plane can be expressed as

$$\begin{gathered} \left\langle {I_{N;l} \,\left( {x,y,\,{\text{z}}} \right)} \right\rangle = \frac{{\,A_{0}^{2} k^{2} }}{{4\,\pi^{2} B^{2} 2^{4N} }}\, \hfill \\ \times \sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)\,i^{l - s} \sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} \sum\limits_{{s^{\prime} = 0}}^{l} {\left( {\begin{array}{*{20}c} l \\ {s^{\prime}} \\ \end{array} } \right)} } i^{{l - s^{\prime}}} \,\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {x_{01}^{s} x_{02}^{{s^{\prime}}} y_{01}^{{l - s_{1} }} y_{02}^{{l - s_{2} }} } } } \,} \,\,\,\, \hfill \\ \times \exp \left[ { - \alpha_{1,x} x_{01}^{2} + 2\left( {\gamma_{1,x} + \frac{{x_{02} }}{{\rho_{0}^{2} }}} \right)x_{01} } \right]\exp \left[ { - \left( {\frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}}} \right)\,x_{02}^{2} + 2\left( {\frac{{a_{{m^{\prime}}} }}{{w_{0} }} - \frac{ikx}{{2z}}} \right)x_{02} } \right] \hfill \\ \times \exp \left[ { - \alpha_{1,y} y_{01}^{2} + 2\left( {\gamma_{1,y} + \frac{{y_{02} }}{{\rho_{0}^{2} }}} \right)y_{01} } \right]\exp \left[ { - \left( {\frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}}} \right)\,y_{02}^{2} + 2\left( {\frac{{a_{{n^{\prime}}} }}{{w_{0} }} - \frac{iky}{{2z}}} \right)y_{02} } \right]dx_{01} dx_{02} dy_{01} dy_{02} \hfill \\ \end{gathered}$$
(9)

where

$$\alpha_{1,x} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}}$$
(10a)
$$\alpha_{1,y} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}}$$
(10b)
$$\gamma_{1,x} = \frac{{a_{m} }}{{w_{0} }} + \frac{ikx}{{2z}}$$
(10c)

and

$$\gamma_{1,y} = \frac{{a_{n} }}{{w_{0} }} + \frac{iky}{{2z}}$$
(10d)

Recalling the following integrals and identities formulas (Belafhal et al. 2020; Erdelyi et al. 1954; Abramowitz and Stegun 1970)

$$\int\limits_{ - \infty }^{ + \infty } {\,x^{n} \,e^{{ - px^{2} + 2q\,x}} dx = \sqrt {\frac{\pi }{p}} \,\exp \left( {\frac{{q^{2} }}{p}} \right)\,\left( {\frac{1}{2i\sqrt p }} \right)^{n} \,H_{n} \left( {\frac{iq}{{\sqrt p }}} \right)}$$
(11a)
$$\int\limits_{ - \infty }^{ + \infty } {x^{l} \,H_{m} \left( {\alpha \,x} \right)\,e^{{ - px^{2} + 2q\,x}} \,dx} = \frac{1}{{2^{l} }}\sqrt {\frac{\pi }{p}} \,\exp \left( {\frac{{q^{2} }}{p}} \right)\,\sum\limits_{k = 0}^{{\left[ {{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} \,\left( {\frac{\alpha }{i\sqrt p }} \right)^{m + l - 2k} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right)$$
(11b)

with Re(p) > 0.

$$H_{n} \left( {x + y} \right) = \frac{1}{{2^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} }}\sum\limits_{k = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)H_{k} \left( {\sqrt 2 x} \right)} \,H_{n - k} \left( {\sqrt 2 y} \right),$$
(11c)
$$H_{n} \left( x \right) = \sum\limits_{k = 0}^{{\left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{( - 1)^{k} n!}}{k!(n - 2k)!}\left( {2x} \right)}^{n - 2k}$$
(11d)

and after skipping a lot of tedious calculations, we can deduce the analytical expression of the intensity distribution of GMvHchGB in turbulent atmosphere as the follows

$$\begin{gathered} \left\langle {I\,\left( {x,y,\,{\text{z}}} \right)} \right\rangle = \frac{{\,k^{2} }}{{4\,z^{2} }}\frac{1}{{2^{{4N + {{3l} \mathord{\left/ {\vphantom {{3l} 2}} \right. \kern-0pt} 2}}} }}\frac{1}{{\sqrt {\alpha_{1,x} \alpha_{2,x} \alpha_{1,y} \alpha_{2,y} } }}\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\times \sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)\,\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime}} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime}} \\ \end{array} } \right)} \sum\limits_{{s^{\prime} = 0}}^{l} {\left( {\begin{array}{*{20}c} l \\ {s^{\prime}} \\ \end{array} } \right)} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\times i^{{2l - s - s^{\prime}}} \exp \left( {\frac{{\gamma_{1,x}^{2} }}{{\alpha_{1,x} }} + \frac{{\gamma_{2,x}^{2} }}{{\alpha_{2,x} }}} \right)\,\left( {\frac{1}{{2i\sqrt {\alpha_{1,x} } }}} \right)^{s} \,\sum\limits_{h = 0}^{s} {\left( {\begin{array}{*{20}c} s \\ h \\ \end{array} } \right)} H_{s - h} \left( {\frac{{i\sqrt 2 \gamma_{1,x} }}{{\sqrt {\alpha_{1} } }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\times \sum\limits_{\mu = 0}^{{\left[ {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{\mu } h!}}{{\mu !\left( {h - 2\mu } \right)!}}} \,\left( {\frac{\sqrt 2 \,}{{\rho_{0}^{2} \sqrt {\alpha_{1,x} \alpha_{2,x} } }}} \right)^{{h + s^{\prime} - 2\mu }} H_{{h + s^{\prime} - 2\mu }} \left( {\frac{{i\gamma_{2,x} }}{{\sqrt {\alpha_{2,x} } }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\times \exp \left( {\frac{{\gamma_{1,y}^{2} }}{{\alpha_{1,y} }} + \frac{{\gamma_{2,y}^{2} }}{{\alpha_{2,y} }}} \right)\,\left( {\frac{1}{{2i\sqrt {\alpha_{1,y} } }}} \right)^{l - s} \,\sum\limits_{{h^{\prime} = 0}}^{l - s} {\left( {\begin{array}{*{20}c} {l - s} \\ {h^{\prime}} \\ \end{array} } \right)} H_{{l - s - h^{\prime}}} \left( {\frac{{i\sqrt 2 \gamma_{1,y} }}{{\sqrt {\alpha_{1,y} } }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad\times \sum\limits_{{\mu^{\prime} = 0}}^{{\left[ {{{h^{\prime}} \mathord{\left/ {\vphantom {{h^{\prime}} 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{{\mu^{\prime}}} h^{\prime}!}}{{\mu^{\prime}!\left( {h^{\prime} - 2\mu^{\prime}} \right)!}}} \,\left( {\frac{\sqrt 2 \,}{{\rho_{0}^{2} \sqrt {\alpha_{1,x} \alpha_{2,y} } }}} \right)^{{h^{\prime} + l - s^{\prime} - 2\mu^{\prime}}} H_{{h^{\prime} + l - s^{\prime} - 2\mu^{\prime}}} \left( {\frac{{i\gamma_{2,y} }}{{\sqrt {\alpha_{2,y} } }}} \right), \hfill \\ \end{gathered}$$
(12)

where

$$\alpha_{2,x} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - \frac{1}{{\alpha_{1,x} \rho_{0}^{4} }}$$
(13a)
$$\alpha_{2,y} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - \frac{1}{{\alpha_{1,y} \rho_{0}^{4} }}$$
(13b)
$$\gamma_{2,x} = \frac{{a_{{m^{\prime}}} }}{{w_{0} }} - \frac{ikx}{{2z}} + \frac{{\gamma_{1,x} }}{{\alpha_{1,x} \rho_{0}^{2} }}$$
(13c)

and

$$\gamma_{2,y} = \frac{{a_{{n^{\prime}}} }}{{w_{0} }} - \frac{iky}{{2z}} + \frac{{\gamma_{1,y} }}{{\alpha_{1,y} \rho_{0}^{2} }}$$
(13d)

Equation (12) is the main result of this study and represents the output field of the average intensity of the GMvHchGB in a medium turbulence atmosphere.

3 Numerical results

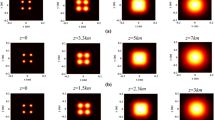
In this Section, some numerical examples of the intensity evolutions of GMvHchGB in free space and in turbulence atmosphere are carried out under the condition of Eq. (12). Figure 1 gives the transversal intesity distribution of GMvHchGB propagating in free space and in turbulence field for \({\text{C}}_{n}^{2} = 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), respectively, at different receiver planes (z = 1, 3, 6 and 8 km). The calculation parameters are set as \(\lambda = 0.8\mu m\), \(w_{0} = 0.02m\), \(l = 1\), \(n = 2\) and for small value of Ω \(\left( {\Omega = 5m^{ - 1} } \right)\). One can clearly see that the average intensity has a dark central core which propagates in free space with spreading, as propagation distance increases. However, the average intensity profile will take the form of a bright central core similar to the flat-top Gaussian profile as the GMvHchGB propagates through turbulence, as shown as in Fig. 1b. Also, it can be seen from the plots of this figure that the intensity profile unchanging its form during the propagation in either free space or atmospheric turbulence medium. These results mean that the atmospheric turbulence plays an important role in controlling the intensity distribution at the beam’s center.

Fig. 1
figure 1

Transversal intesity distribution of GMvHchGB propagating in: a Free space and b Turbulent atmosphere medium with \(C_{n}^{2} = 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\). With \(\lambda = 0.8\mu m\), \(w_{0} = 0.02m\), \(\Omega = 5\,m^{ - 1}\), \(n = 2\), l = 1

Full size image

Figure 2 displays the influence of the turbulent atmoshere on the propagation properties of the considered beam at the transverse plane, in free space and for three values of \(C_{n}^{2} \;\left( {C_{n}^{2} = 5 \times 10^{ - 16} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} ,\;C_{n}^{2} = 10^{ - 15} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} ,\;{\text{and}}\;C_{n}^{2} = 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} } \right)\) for a large value of Ω \(\left( {\Omega = 100\,m^{ - 1} } \right)\).

Fig. 2
figure 2

Transversal intesity distribution of GMvHchGB propagating in: a Free space and in turbulent atmosphere media with, b \(C_{n}^{2} = 5 \times 10^{ - 16} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), c \(C_{n}^{2} = 10^{ - 15} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\) and d \(C_{n}^{2} = 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\). With \(\lambda = 0.8\mu m\), \(w_{0} = 0.02m\), \(\Omega = 100\,m^{ - 1}\), \(n = 2\), and l = 1

Full size image

The calculation parameters are set to be the same as those in Fig. 1. One can observe that the output beam takes a shape with four individual petals at a few propagation distances (0 < z < 3 km). In the case of propagation in free-space, as in the case shown in Fig. 2a, the four petals interfere with each other to turn up into fan blades-like pattern with a dark spot at the center which gradually disappear at the large values of the propagation distances (z ≥ 8 km). In the weak atmospheric turbulence (Fig. 2b), the optical path surface of the beam gradually becomes similar to a rhombic crystal shape particularly at a large propagation distance (z = 8 km). In the strong atmospheric turbulence (Fig. 2c and d), the four lobes are evolving into a central bright spots surrounded by sqauare or round wide dimmer rings.

Moreover, a comparison of Figs.1 and 2 shows the physical nature of the decentered parameter effect, i.e., the single-lobe profile obtained for small Ω evolves into a decentered four-petal-like beam at the sufficient large values of Ω. As can be seen, if Ω = 0, the beams can be transformed into a vortex Gaussian beam but it presents an infinite power flux when Ω tends to infinity.

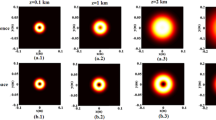
Figures 3 and 4 show the effect of the decentered, hollowness and Gaussian waist parameters on the evolution of normalized intensity distribution of GMvHchGB propagating in stronger atmospheric turbulence \(\left( {{\text{C}}_{{\text{n}}}^{{2}} = 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} } \right)\) at the plane z = 1 km.

Fig. 3
figure 3

Normalized intesity distribution of GMvHchGB propagating in a turbulent atmosphere medium with: z = 1 km, \(\lambda = 0.8\mu m\), \(w = 0,02m\), \(C_{n}^{2} = 1 \times 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\)\(n = 2\) and for: a \(l = 0\) b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), f and \(l = 5\)

Full size image
Fig. 4
figure 4

Normalized intesity distribution of GMvHchGB propagating in a turbulent atmosphere medium with: z = 1 km, \(\lambda = 0.8\mu m\), \(\Omega = 60m^{ - 1}\), \(C_{n}^{2} = 1 \times 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\)\(n = 2\) and for: a \(l = 0\), b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), f and \(l = 5\)

Full size image

The parameters of the wavelength and the beam order are the same of those to the previous figures. We can see that the GMvHchGB gradually turns into a dark hollow beam from Gaussian beam like with increase of Ω and w0, for l = 0. And for l > 0, the dark and the deep hollow area of GMvHchGB are wider with the increase of both Ω and w0 denote the spread of the beam width in free space due to diffraction. Compared with Figs. 3 and 4, one can conclude that the evolution speed of dark hollow is faster with the increase of w0.

The influence of the weak and strong values of the turbulent atmosphere on the normalized intensity of the considered beam against the x-direction illustrated in Fig. 5 for different values of the hollowness parameters (l = 0, 1, 2, 3, 4 and 5), with Ω and z are fixed at 80 cm−1 and 2 km, respectively. The normalized intensity will undergo first the dark hollow distribution and then the Gaussian-like distribution with increasing the atmospheric turbulence coefficient. We can also note that the effect of the hollowness parameter is clearly shown as the turbulence coefficient increases. It is observed that, Fig. 5a of our simulation results is consistent with the result given by Fig. 5a of Zhou (2011) which it can be regarded as a special case of the current work, when l is equal to zero. Also, one can deduce that the hollowness parameter seems much less important at the larger values of the turbulent coefficient perhaps due to the effect of the atmospheric turbulence on inner scale of the beam spreading.

Fig. 5
figure 5

Normalized intesity distribution of GMvHchGB propagating in a turbulent atmosphere medium with: z = 2 km, \(\lambda = 0.8\mu m\), \(\Omega = 80m^{ - 1}\), \(C_{n}^{2} = 1 \times 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), \(n = 2\) and for: a \(l = 0\) b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), f and \(l = 5\)

Full size image

Figure 6 displays the evolution of the normalized average intensity distribution of the GMvHchGB propagating in turbulent atmosphere \(\left( {C_{n}^{2} = 1 \times 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} } \right)\) at the plane z = 1 km.

Fig. 6
figure 6

Normalized intesity distribution of GMvHchGB propagating in a turbulent atmosphere medium with: z = 1 km, \(\lambda = 0.8\mu m\), \(\Omega = 60m^{ - 1}\), \(C_{n}^{2} = 1 \times 10^{ - 14} \,m^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), and for: a \(l = 0\), b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), f and \(l = 5\)

Full size image

We can see that the central bright region of GMvHchGB at n = l = 0 slowly turns into a dark hollow one and becomes larger as the increase of the beam order. In addition, the central dark area and its depth corresponding to beam orders are regularly increasing with the increase of the hollowness parameter l.

Finally, our numerical results show that the GMvHchGB propagating in free space/turbulent atmosphere have an almost uniform shape along the propagation axis, for small values of decentered parameter Ω. While, the output beam profile takes distinctive geometric shapes at the large values of Ω and at gradient turbulence values and finally it transforms into a flat-top Gaussian-like beam, with sufficiently large values of the propagation distances.

4 Conclusions

In this paper, based on the extended Huygens-Fresnel diffraction integral, the analytical propagation formula for the average intensity of GMvHchGB in atmospheric turbulence is derived. The expression formula shown the relationship between the output average intensity of a GMvHchGB and the beam parameters such as the beam order, hollowness, decentered, and Gaussian waist parameters. Our numerical results shown that, for small values of the decentered parameter, the beam keeps its initial profile shape unchanged at several propagation distances. Whereas, for large values of Ω, the beam changes their shapes dramatically with the increasing of the propagation distances. At large values of the turbulence, the beam converted into a flat-top Gaussian-like beam in the far-field region. The evolution of the average intensity distribution of the beam in a turbulent atmosphere is essentially dependent on incident beam parameters and the refractive index structure coefficient. Furthermore, depending on the beam parameters N and l, the GMvHchGB provides a general convenient procedure to describe the propagation characteristics to some particular beams travelling through free space/atmospheric turbulence such as a fundamental Gaussian, Cosh-Gaussian, vortex Cosh-Gaussian and higher-order Cosh-Gaussian beams. Moreover, the obtained results could be beneficial for applications of GMvHchGB in optical communications, remote sensing, and atom optics.