1 Introduction

In nonlinear science, soliton is a type of classical nonlinear wave which arises as a result of balance between nonlinearity and dispersion effects and it exhibits a kind of local state in certain direction. Taking the long wave limit of the soliton solution gives rise to a class of rational solutions which describe the lump localized in all directions in the space [1,2,3]. In particular, rational solutions are able to depict the rouge wave which additionally possesses the locality of the time [4]. Recently, a lot of lump solutions have been constructed via the direct Hirota bilinear method [5,6,7,8,9,10], in which the auxiliary function in the bilinear form is taken as the ansatz with the quadratic function. Soon later, by taking the auxiliary function as the linear combination of the quadratic function and the exponential one, it is found that such method can be used to derive the mixed solutions which indicate the lump interacting with the single stripe soliton, the stripe soliton pair and so on [11,12,13,14,15,16,17,18,19,20,21]. Starting from the bilinear form, this direct ansatz method is effective. However, is this method still valid for the multi-linear form? To the best of our knowledge, there are no relevant literatures applying this kind of method to the multi-linear form of a given nonlinear equation. In this article, we shall take a (2+1)-dimensional nonlinear integrable equation as an example to show that the above rational and rational-exponential solutions can be derived from the multi-linear form.

As an integrable extension of the Kadomtsev–Petviashvili (KP) hierarchy, the (2+1)-dimensional Date–Jimbo–Kashiwara–Miwa (DJKM) equation has been proposed [22, 23]

$$\begin{aligned}&u_{xxxxy}+4u_{xxy}u_x+2u_{xxx}u_y+6u_{xy}u_{xx}-\alpha u_{yyy}\nonumber \\&\quad -2\beta u_{xxt}=0, \end{aligned}$$
(1)

where \(\alpha \) and \(\beta \) are constants. By considering the balance between nonlinearity and dispersion, we take the dependent variable transformation with the rational form

$$\begin{aligned} u=2(\ln f)_x=2\frac{f_x}{f}. \end{aligned}$$
(2)

which leads Eq. (1) to the multi-linear form

$$\begin{aligned}&D_x[(D^3_xD_y-3\beta D_xD_t)f\cdot f]\cdot f^2 \nonumber \\&\quad +\, \frac{1}{2}D_y[ (D^4_x-3\alpha D^2_y)f\cdot f ]\cdot f^2=0. \end{aligned}$$
(3)

Here the Hirota’s bilinear operators \(D_x\),\(D_y\) and \(D_t\) are defined as [24]

$$\begin{aligned}&D^n_xD^m_yD^l_t(a\cdot b)=\bigg ( \frac{\partial }{\partial x} - \frac{\partial }{\partial x'} \bigg )^n \bigg ( \frac{\partial }{\partial y} - \frac{\partial }{\partial y'} \bigg )^m\\&\quad \times \, \bigg ( \frac{\partial }{\partial t} - \frac{\partial }{\partial t'} \bigg )^l a(x,y,t)b(x',y',t')\bigg |_{x=x',y=y',t=t'}. \end{aligned}$$

By introducing an auxiliary independent variable z, and imposing an extra constraint bilinear equation

$$\begin{aligned} (D^4_x -3\alpha D^2_y+ a D_xD_z)f\cdot f=0, \end{aligned}$$
(4)

the multi-linear form (3) can be converted to the following bilinear equation

$$\begin{aligned} \left( D^3_xD_y -3\beta D_xD_t - \frac{a}{2} D_yD_z\right) f\cdot f=0, \end{aligned}$$
(5)

where a is a constant. Equations (4) and (5) are viewed as the bilinear form of the DJKM Eq. (1), both of them are found to be nothing but the first two members of the KP hierarchy. Indeed, Eq. (4) corresponds to the bilinear form of the well-known KP equation while Eq. (5) gives the one of the (3+1)-dimensional Jimbo–Miwa equation. To investigate the complete integrability of soliton equations in the KP hierarchy, Dorizzi et al. [25] have taken Eq. (5) in isolation and tested its integrability by considering the Painlevé property, the multi-soliton criterion and the structure of symmetry group. They found that Eq. (5) is only integrable in a conditional sense. However, if Eq. (4) is considered together with Eq. (5) in lower-dimensional case, it was shown that the complete integrability conditions are satisfied. Thus, the (2+1)-dimensional DJKM Eq. (1) was established and studied [22, 23, 26, 27]. Hu and Li [23] have provided its bilinear Bäcklund transformation and proved corresponding nonlinear superposition formulae by using bilinear operator identities. With the help of the Bell polynomial theory and the Hirota bilinear method, Wang et al. [26] have derived Lax pair, infinite conservation laws and multi-shock wave solutions for the DJKM Eq. (1). Wronski and Grammi determinant solutions for the DJKM Eq. (1) have been constructed via the bilinear technique [27]. To our knowledge, the lump solution and the interaction solution between the lump and the stripe soliton for Eq. (1) have not been reported. Here we will investigate these solutions directly from the multi-linear form of the DJKM equation.

The paper is organized as follows. In Sect. 2, we derive the explicit lump solution of the DJKM equation and then analyze its local characteristics. Section 3 is devoted to finding the mixed solution between the lump and one stripe soliton via a linear combination of the quadratic function and the exponential one. The interactions including fission and fusion processes for two types of local waves are discussed in detail. In Sect. 4, we construct the rational-exponential solution consisting of the lump and the stripe soliton pair, then the dynamical analysis shows that this mixed solution exhibits a rogue wave excited from the stripe soliton pair. Conclusions and discussions are given in Sect. 5.

2 Lump solution

To construct the lump solution for the DJKM Eq. (1), we take the function f in the multi-linear form (3) as the ansatz with the following quadratic function

$$\begin{aligned} f=g^2 +h^2 +a_9, \end{aligned}$$
(6)

with

$$\begin{aligned} g= & {} a_1x+a_2 y+a_3 t+a_4,\\ h= & {} a_5x+a_6y+a_7t+a_8, \end{aligned}$$

where the real parameters \(a_i\)\((i=1,2,\ldots ,9)\) will be determined. Substituting (6) into the multi-linear form (3) and vanishing the coefficients of the variables x, y and t, we obtain a set of algebraic equations. Solving these equations gives rise to the results as follows:

$$\begin{aligned}&a_3= - \frac{\alpha \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\&a_7 = - \frac{ \alpha \left[ 2 a_1a_2a_5 \left( 3a^2_6-a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\&a_9=\frac{\left( a^2_1+a^2_5\right) ^3}{\alpha \left( a_1a_6-a_2a_5\right) ^2}. \end{aligned}$$
(7)
Fig. 1
figure 1

The lump (8) with \(a_1=-\frac{1}{8}\), \(a_2=a_5=a_6=\alpha =\beta =1\) and \(a_4=a_8=0\): a the three-dimensional plot at \(t=0\) and b the contour plots at different times

Full size image

To ensure that the function f is positive, analytical and the solution u rationally localized in all directions in the (x, y)-plane, one has to impose three constraint conditions: \(\alpha >0\), \(a^2_1+a^2_5 \ne 0\) and \(a_1a_6-a_2a_5\ne 0\). Then the solution of the DJKM Eq. (1) has the rational form

$$\begin{aligned} u=\frac{4(a_1g+a_5h)}{g^2+h^2+\frac{\left( a^2_1+a^2_5\right) ^3}{\alpha \left( a_1a_6-a_2a_5\right) ^2}}, \end{aligned}$$
(8)

with

$$\begin{aligned}&g=a_1x+a_2 y \\&\qquad - \frac{\alpha \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2} t+a_4,\\&h=a_5x+a_6y \\&\qquad - \frac{ \alpha \left[ 2 a_1a_2a_5 \left( 3a^2_6-a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2} t+a_8, \end{aligned}$$

where \(a_1,a_2,a_4,a_5,a_6\) and \(a_8\) are arbitrary real constants. At any fixed time t, when \(g^2+h^2\rightarrow +\infty \), equivalently \(x^2+y^2\rightarrow +\infty \), the rational solution u in (8) approaches to zero. Hence, the solution (8) depicts a standard lump structure. Let the partial derivatives \(u_x\) and \(u_y\) be zero, it is found that two critical points are at

$$\begin{aligned}&A \ \ \left( \frac{a_2a_8-a_4a_6+(a_2a_7-a_3a_6)t}{a_1a_6-a_2a_5} \right. \nonumber \\&\quad \left. +\, \frac{a^2_1+a^2_5}{\sqrt{\alpha }}, \frac{ a_4a_5-a_1a_8+(a_3a_5-a_1a_7)t}{a_1a_6-a_2a_5} \right) , \end{aligned}$$
(9)

and

$$\begin{aligned}&B \; \left( \frac{a_2a_8-a_4a_6+(a_2a_7-a_3a_6)t}{a_1a_6-a_2a_5} \right. \nonumber \\&\quad \left. -\,\frac{a^2_1+a^2_5}{\sqrt{\alpha }}, \frac{ a_4a_5-a_1a_8+(a_3a_5-a_1a_7)t}{a_1a_6-a_2a_5} \right) , \end{aligned}$$
(10)

which result in the maximum/minimum amplitudes \(\pm \frac{2\sqrt{\alpha } (a_1a_6-a_2a_5)}{a^2_1+a^2_5}\), respectively. Thus the lump possesses one peak at the point A and one valley at the point B, and the former’s height is equal to the latter’s depth. From the extreme points, we know that the lump moves along the route line

$$\begin{aligned}&y=\frac{a_3a_5-a_1a_7}{a_2a_7-a_3a_6}x + \frac{a_3a_8-a_4a_7}{a_2a_7-a_3a_6} \nonumber \\&\qquad \pm \,\frac{ a_1a_7-a_3a_5}{\sqrt{\alpha }(a_2a_7-a_3a_6)(a_1a_6-a_2a_5)}, \end{aligned}$$
(11)

and with the velocities

$$\begin{aligned} V_x=\frac{a_2a_7-a_3a_6}{a_1a_6-a_2a_5},\, V_y=\frac{a_3a_5-a_1a_7}{a_1a_6-a_2a_5}. \end{aligned}$$
(12)

This means that the lump’s peak and valley are symmetric with respect to the line \(y=\frac{a_3a_5-a_1a_7}{a_2a_7-a_3a_6}x + \frac{a_3a_8-a_4a_7}{a_2a_7-a_3a_6}\). Such a lump and its moving path are displayed in Fig.1. Fig. 1a shows the lump’s three-dimensional shape at time \(t=0\), and Fig. 1b displays the contour plots at different times whose moving path obeys the route line \(y=-\frac{33}{112}x\). Besides, the illustrated lump moves with the maximum/minimum amplitudes \(\pm \frac{144}{65}\), and the velocities (\(V_x=-\frac{7168}{4225}\), \(V_y=\frac{2112}{4225}\)).

Fig. 2
figure 2

The three-dimensional plots of the rational-exponential solution (15) with \(a_1=-\frac{1}{8}\), \(-a_2=a_5=a_6=\alpha =1\), \(k=-\beta =\frac{1}{10}\) and \(a_4=a_8=0\): a\(t=-\,0.8\); b\(t=0\) and c\(t=2.5\)

Full size image
Fig. 3
figure 3

The contour plots of the rational-exponential solution (15) with \(a_1=-\frac{1}{8}\), \(-a_2=a_5=a_6=\alpha =1\), \(k=-\beta =\frac{1}{10}\) and \(a_4=a_8=0\): a\(t=-0.8\); b\(t=0\) and c\(t=2.5\)

Full size image

3 Lump interacting with one stripe soliton

In this section, we will seek for the mixed solution between the lump and one stripe soliton, and further discuss their interaction property. Recall that one-soliton solution for the DJKM Eq. (1) requires the function f to be taken as \(1+e^{k_1x+l_1 y+\omega _1 t+\xi _0}\) with the dispersion relation for the coefficients \(k_1,l_1\) and \(\omega _1\). Therefore, in order to obtain the mixed lump-soliton solution, we take the function f as the ansatz with the following rational-exponential function

$$\begin{aligned} f=g^2 +h^2 +a_9 + ke^{\xi }, \end{aligned}$$
(13)

with

$$\begin{aligned} g= & {} a_1x+a_2 y+a_3 t+a_4,\ \ h=a_5x+a_6y+a_7t+a_8,\\ \xi= & {} k_1x+k_2y+k_3t, \end{aligned}$$

where the real parameters \(a_i\)\((i=1,2,\ldots ,9)\), k and \(k_i(i=1,2,3)\) will be determined. Similar to the case of the lump solution, substituting (13) into the multi-linear form (3) and vanishing the coefficients of the exponential functions and the variables x, y and t, one can get more algebraic equations. Solving these equations yields the following results:

$$\begin{aligned} a_3= & {} - \frac{\alpha \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\ a_7= & {} - \frac{ \alpha \left[ 2 a_1a_2a_5 \left( 3a^2_6 - a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\ a_9= & {} \frac{\left( a^2_1+a^2_5\right) ^3}{\alpha \left( a_1a_6-a_2a_5\right) ^2},\; k_1=\frac{\sqrt{\alpha }\left( a_1a_6-a_2a_5\right) }{a^2_1+a^2_5},\nonumber \\ k_2= & {} \frac{\sqrt{\alpha }\left( a_1a_6-a_2a_5\right) \left( a_1a_2+a_5a_6\right) }{\left( a^2_1+a^2_5\right) ^2}, \nonumber \\ k_3= & {} \frac{\alpha \sqrt{\alpha } \left( a_1a_6-a_2a_5\right) \left( a_1a_2+a_5a_6\right) \left[ \left( a_1a_2+a_5a_6\right) ^2-\left( a_1a_6-a_2a_5\right) ^2\right] }{2\beta \left( a^2_1+a^2_5\right) ^4 }.\nonumber \\ \end{aligned}$$
(14)
Fig. 4
figure 4

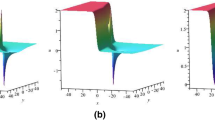
The three-dimensional plots of the rational-exponential solution (15) with \(a_1=\frac{1}{8}\), \(a_2=a_5=a_6=\alpha =1\), \(k=-\beta =\frac{1}{10}\) and \(a_4=a_8=0\): a\(t=-2.5\); b\(t=0\) and c\(t=0.8\)

Full size image
Fig. 5
figure 5

The contour plots of the rational-exponential solution (15) with \(a_1=\frac{1}{8}\), \(a_2=a_5=a_6=\alpha =1\), \(k=-\beta =\frac{1}{10}\) and \(a_4=a_8=0\): a\(t=-2.5\); b\(t=0\) and c\(t=0.8\)

Full size image

The constraint conditions: \(\alpha >0\), \(a^2_1+a^2_5 \ne 0\), \(a_1a_6-a_2a_5\ne 0\) and \(k>0\) need to be satisfied for those arbitrary constants to guarantee a well-defined function f. In this situation, the solution of the DJKM Eq. (1) is given by the rational-exponential form

$$\begin{aligned} u=\frac{4a_1g+4a_5h+ \frac{2\sqrt{\alpha }k(a_1a_6-a_2a_5)}{a^2_1+a^2_5}e^{\xi }}{g^2+h^2+\frac{(a^2_1+a^2_5)^3}{\alpha (a_1a_6-a_2a_5)^2}+ke^{\xi }}, \end{aligned}$$
(15)

with

$$\begin{aligned}&g=a_1x+a_2 y \\&\qquad -\, \frac{\alpha \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2} t+a_4,\\&h=a_5x+a_6y \\&\qquad - \,\frac{ \alpha \left[ 2 a_1a_2a_5 \left( 3a^2_6-a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2} t+a_8,\\&\xi =\frac{\sqrt{\alpha }\left( a_1a_6-a_2a_5\right) }{a^2_1+a^2_5} \left\{ x +\frac{\left( a_1a_2+a_5a_6\right) }{\left( a^2_1+a^2_5\right) }y\right. \\&\qquad \left. +\,\frac{\alpha \left( a_1a_2+a_5a_6\right) \left[ \left( a_1a_2+a_5a_6\right) ^2-\left( a_1a_6-a_2a_5\right) ^2\right] }{2\beta \left( a^2_1+a^2_5\right) ^3 }t\right\} , \end{aligned}$$

where \(a_1,a_2,a_4,a_5,a_6,a_8\) and k are arbitrary real constants.

It is known that the stripe soliton solution is expressed by the exponential function, which exhibits the exponentially localized behavior in certain direction. In contrast to a stripe soliton solution, a lump solution is a type of rational function solution which is localized in all directions in the space. Thus, the explicit solution (15) describes the interaction between the lump and one stripe soliton. The propagation process contains two kinds of phenomena: fission and fusion. To interpret the propagating properties, we analyze the solution (15) with respect to the time t directly. Specifically, assuming x and y are constants and \(k_3>0\), it is found that the exponential function \(e^{\xi }\) is the dominant term and \(u\rightarrow \frac{\sqrt{\alpha }(a_1a_6-a_2a_5)}{a^2_1+a^2_5}\) when \(t>0\), while the rational function \(g^2 +h^2 +a_9\) is the dominant term and \(u\rightarrow \frac{2a_1g+2a_5h}{g^2+h^2+\frac{(a^2_1+a^2_5)^3}{\alpha (a_1a_6-a_2a_5)^2}}\) when \(t<0\), which means that the rational lump appears. The whole evolution is the fission process. On the contrary, \(k_3<0\) leads to the fusion process. As shown in Figs. 2 and 3, one stripe wave and one lump fuse into one stripe wave gradually, which represents the fusion process. Figures 4 and 5 exhibit the fission process that one stripe wave splits into one stripe wave and one lump conversely.

Fig. 6
figure 6

The three-dimensional plots of the rational-exponential solution (18) with \(a_1=\frac{1}{10}\), \(a_2=a_5=2\), \(a_4=a_6=\alpha =1\), \(k=l=\frac{1}{20}\), \(\beta =\frac{1}{10}\) and \(a_8=0\): a\(t=-5\); b\(t=-1\); c\(t=0\); c\(t=1\) and d\(t=5\)

Full size image

4 Rogue wave excited from the stripe soliton pair

Following the idea of constructing the interaction solution between the lump and one stripe soliton, we may seek for such kind of the solution which contains the lump and a pair of stripe solitons. To this aim, we add a different exponential function to the ansatz (13) and it becomes the following form

$$\begin{aligned} f=g^2 +h^2 +a_9 + ke^{\xi } +l e^{-\xi }, \end{aligned}$$
(16)

with

$$\begin{aligned}&g=a_1x+a_2 y+a_3 t+a_4,\\&\quad h=a_5x+a_6y+a_7t+a_8,\\&\quad \xi =k_1x+k_2y+k_3t, \end{aligned}$$

where the real parameters \(a_i\)\((i=1,2,\ldots ,9)\), k, l and \(k_i(i=1,2,3)\) will be determined. Similarly, after the substitution of the function (16) into the multi-linear form (3), vanishing the coefficients of the exponential functions and the variables x, y and t yields a set of algebraic equations. By solving these equations, we obtain the results as follows:

$$\begin{aligned} a_3= & {} - \frac{\alpha \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\ a_7= & {} - \frac{ \alpha \left[ 2 a_1a_2a_5 \left( 3a^2_6 - a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] }{2\beta \left( a^2_1+a^2_5\right) ^2},\nonumber \\ a_9= & {} \frac{\left( a^2_1+a^2_5\right) ^3}{\alpha \left( a_1a_6-a_2a_5\right) ^2} + \frac{\alpha kl \left( a_1a_6-a_2a_5\right) ^2}{\left( a^2_1+a^2_5\right) ^3},\nonumber \\ k_2= & {} \frac{\sqrt{\alpha }\left( a_1a_6-a_2a_5\right) \left( a_1a_2+a_5a_6\right) }{\left( a^2_1+a^2_5\right) ^2}, \nonumber \\ k_1= & {} \frac{\sqrt{\alpha }\left( a_1a_6-a_2a_5\right) }{a^2_1+a^2_5},\nonumber \\ k_3= & {} \frac{\alpha \sqrt{\alpha } \left( a_1a_6-a_2a_5\right) \left( a_1a_2+a_5a_6\right) \left[ \left( a_1a_2+a_5a_6\right) ^2-\left( a_1a_6-a_2a_5\right) ^2\right] }{2\beta \left( a^2_1+a^2_5\right) ^4 }.\nonumber \\ \end{aligned}$$
(17)
Fig. 7
figure 7

The contour plots of the rational-exponential solution (18) with \(a_1=\frac{1}{10}\), \(a_2=a_5=2\), \(a_4=a_6=\alpha =1\), \(k=l=\frac{1}{20}\), \(\beta =\frac{1}{10}\) and \(a_8=0\): a\(t=-5\); b\(t=-1\); c\(t=0\); d\(t=1\) and e\(t=5\)

Full size image

To guarantee the well-defined function f and the appearance of the stripe soliton pair, the constraint conditions: \(\alpha >0\), \(a^2_1+a^2_5 \ne 0\), \(a_1a_6-a_2a_5\ne 0\), \(k>0\) and \(l>0\) need to be imposed. In this case, the rational-exponential solution of the DJKM Eq. (1) reads

$$\begin{aligned} u=\frac{4a_1g+4a_5h+ \frac{2\sqrt{\alpha }(a_1a_6-a_2a_5)}{a^2_1+a^2_5}(ke^{\xi }-le^{-\xi })}{g^2+h^2+\frac{(a^2_1+a^2_5)^3}{\alpha (a_1a_6-a_2a_5)^2} + \frac{\alpha kl (a_1a_6-a_2a_5)^2}{\left( a^2_1+a^2_5\right) ^3} +ke^{\xi }+le^{-\xi }}, \end{aligned}$$
(18)

with

$$\begin{aligned}&g=a_1x+a_2 y \\&\qquad -\, \frac{\alpha \left[ 2 a_1a_5a_6 (3a^2_2-a^2_6) + a_2 (a^2_2-3a^2_6)(a^2_1-a^2_5)\right] }{2\beta (a^2_1+a^2_5)^2} t\\&\qquad +\,a_4,\\&h=a_5x+a_6y \\&\qquad -\, \frac{ \alpha \left[ 2 a_1a_2a_5 (3a^2_6-a^2_2) + a_6 (3a^2_2-a^2_6)(a^2_1-a^2_5)\right] }{2\beta (a^2_1+a^2_5)^2} t\\&\qquad +\,a_8,\\&\xi =\frac{\sqrt{\alpha }(a_1a_6-a_2a_5)}{a^2_1+a^2_5} \left\{ x +\frac{(a_1a_2+a_5a_6)}{(a^2_1+a^2_5)}y\right. \\&\qquad \left. +\,\frac{\alpha (a_1a_2+a_5a_6)\left[ (a_1a_2+a_5a_6)^2-(a_1a_6-a_2a_5)^2\right] }{2\beta (a^2_1+a^2_5)^3 }t\right\} , \end{aligned}$$

where \(a_1,a_2,a_4,a_5,a_6,a_8,k\) and l are arbitrary real constants. For the solution (18), we present the simple asymptotic analysis to show that how a rogue wave arises from the stripe soliton pair. By taking x and y as constants, it can be found that

$$\begin{aligned}&\lim _{t\rightarrow \pm \infty } \frac{g^2}{h^2}\nonumber \\&= \frac{ \left[ 2 a_1a_5a_6 \left( 3a^2_2-a^2_6\right) + a_2 \left( a^2_2-3a^2_6\right) \left( a^2_1-a^2_5\right) \right] ^2}{ \left[ 2 a_1a_2a_5 \left( 3a^2_6-a^2_2\right) + a_6 \left( 3a^2_2-a^2_6\right) \left( a^2_1-a^2_5\right) \right] ^2},\end{aligned}$$
(19)
$$\begin{aligned}&\lim _{t\rightarrow \pm \infty } \frac{g^2}{ke^{\xi }+le^{-\xi }} =0,\nonumber \\&\quad \lim _{t\rightarrow \pm \infty } \frac{h^2}{ke^{\xi }+le^{-\xi }} =0, (k,l>0), \end{aligned}$$
(20)

which implies that as t tends to infinity, only the resonant stripe soliton pair appears, but as t arrives at the intermediate time \(t=0\), the rational lump emerges and attains its maximum/minimum amplitudes. This kind of the mixed solution is illustrated in Figs. 6 and 7 with three-dimensional and contour plots. The whole evolution process of the lump accords with the character of a rogue wave, hence the rational-exponential solution (18) describes the rogue wave excited from the stripe soliton pair.

5 Conclusions and discussions

In conclusion, we derive explicit rational and rational-exponential solutions of the (2+1)-dimensional DJKM equation by using the direct ansatz method. The ansatz form for the auxiliary function in the multi-linear form is taken as the quadratic function, and the different linear combinations of the quadratic function and exponential one, respectively. The dynamical analysis shows that the exact rational solution depicts the lump structure. The rational-exponential solutions are classified to two cases: (i) The first one describes the interaction between the lump and one stripe soliton, which includes fission and fusion phenomena. (ii) The second one contains the lump and the stripe soliton pair, in which the interaction process exhibits a rogue wave excited from the stripe soliton pair. Local and interaction properties for these nonlinear waves are discussed in detail.

It is worth mentioning that all our derivations start from the multi-linear form rather than the bilinear form of the objective nonlinear equation. This suggests that the direct ansatz method is also valid for the general multi-linear form. For some nonlinear equations, their bilinear forms are difficult to be derived but their multi-linear forms can be given from the truncated Painlevé expansion. Therefore, one can start directly from the multi-linear form of the nonlinear equation to seek for rational and rational-exponential solutions. Besides, if we change the functions in the ansatz into other types of functions, or consider their different linear combinations, one can obtain more different types of solutions. These solutions may be used to describe the interaction among different local waves. In addition, the lump solution and the interaction solution between the lump and the stripe soliton are provided in explicit and analytical forms. The potential applications of these mixed solutions in other nonlinear fields deserve further study.