M-lump and interactive solutions to a (3 ${+}$ 1)-dimensional nonlinear system

Abstract

This paper aims at computing M-lump solutions for the $(3+1)$-dimensional nonlinear evolution equation. These solutions in all directions decline to an identical state obtained by employing the “long wave” limit with respect to the N-soliton solutions which are got by using the direct methods. Subsequently, we discuss the dynamic properties of the M-lump solutions which describe the multiple collisions of lumps. Based on the obtained lump solutions, the lump–kink solutions are also obtained. In addition, the periodic interactive solutions are given.

1 Introduction

Lump waves in recent years have captured considerable attention in the field of the nonlinear science, due to the fact that they are identified as the advisable prototypes of rogue wave dynamics, especially in oceanography and nonlinear optics, etc. As a special localized wave, lump wave is a rationally decaying wave in all directions. Lump wave was first discovered in 1977 by Manakov et al. [1]. More importantly, the fact that the pattern of phase shifts could not be induced by the interactions of the lump waves was proved by Manakov et al. [1]. Inspired by aforementioned results, more general rational solutions of equations were studied, see [2,3,4] and the references therein. The multiple collisions of the lumps from the corresponding N-soliton solutions of the KP equation and two-dimensional nonlinear Schrödinger equation were described by Satsuma and Ablowitz [3]. Thereafter, the follow-on results indicate that lump solutions are also admitted by high-dimensional nonlinear partial differential equations. Typical examples include the Davey–Stewartson II equation, Ishimori I equation [5], Sawada–Kotera equation [6], ($2+1$)-dimensional BSK equation [7], BKP equation.

Thereupon, different methods have been applied to construct exact lump solutions of nonlinear evolution equations, such as taking limit regarding to “long wave” method [3], the inverse scattering transformation [4], Darboux transformation [5], Bäklund transformation, as well as the Hirota bilinear technique [8,9,10,11]. Notice that taking limit of the N-soliton solutions is more importance in the investigation of the M-lumps. Moreover, the interaction between lump waves and solitons of the nonlinear partial differential equation has captured considerable attention from scientists. The interaction between kink–soliton, strip–soliton and lump solution is investigated in Ref. [12, 13].

In this letter, we consider the (3 + 1)-dimensional nonlinear partial differential equation as follows:

$$\begin{aligned} \begin{aligned} -4u_{xt}+u_{xxxz}+3\alpha u_{yy}+4u_{x}u_{xz}+2u_{xx}u_z=0, \end{aligned} \end{aligned}$$

(1)

where $u=u(x,y,z,t)$. When $\alpha =1$ Eq. (1) boils down to the conventional ($3+1$)-dimensional potential-YTSF equation. Some intriguing integrable properties of the potential-YTSF equation have been explicitly discussed in the literature. Yan [14] studied the auto-Bäklund transformation and obtained its exact solutions. Multiple-soliton solutions were given in [15], and several general nontraveling wave solutions were presented in [16]. The bilinear Bäklund transformation was investigated in [17]. Hu et al. [18] constructed several new kink multi-soliton solutions by using three-wave method. We will investigate the lump solutions as well as the different interactive solutions of Eq. (1) in this paper.

With the aid of transformation $u=2(\ln f)_{x}$, then Eq. (1) is converted into the nonlinear differential equation with respect to function f as below [18]:

$$\begin{aligned} \begin{aligned}&(3\alpha D_y^2-4D_xD_t+D_x^3D_z)f\cdot f\\&\quad +4f^2\partial _x^{-1}(D_x((\ln f)_{xz}(\ln f)_{xx}))=0. \end{aligned} \end{aligned}$$

(2)

In what follows, we will construct M-lump and the interactive wave solutions of (1) by solving (2).

The outline of our paper is given by: In Sect. 2, we construct the M-lump solutions of (1). The dynamic properties of these obtained solutions describing multiple collisions of lumps are also demonstrated by some figures. By assuming f is the combination of positive quadratic, exponential and trigonometric function in Sects. 3 and 4, we investigated the lump–kink and periodic interactive solutions of Eq. (1). Finally, Sect. 5 is the conclusion.

2 M-lump solutions of Eq. (1)

In this part, we will investigate M-lump solutions of Eq. (1) by taking limit for the corresponding N-soliton solutions which can be ascertained by applying Hirota bilinear method. The solution of Eq. (2) can be given as follows:

$$\begin{aligned} f=f_{N}=\sum _{\mu =0,1}\exp \left( \sum _{i<j}^{N}\mu _i\mu _jA_{ij}+\sum _{i=1}^{N}\mu _i\eta _i\right) , \end{aligned}$$

(3)

where

$$\begin{aligned} \eta _i=k_i\left[ x+p_iy+z+\left( \frac{k_i^2}{4}+\frac{3\alpha p_i^2}{4}\right) t\right] +\eta _i^{(0)},\nonumber \\ \end{aligned}$$

(4)

and

$$\begin{aligned} \exp A_{ij}=\frac{(k_i-k_j)^2-\alpha (p_i-p_j)^2}{(k_i+k_j)^2-\alpha (p_i-p_j)^2}, \end{aligned}$$

(5)

with $k_i$, $p_i$ and $\eta _i^{(0)}$ are real constants. The notation $\sum _{\mu =0,1}$ shows summation roundly possible combinations of $\mu _i=0,1$, $(i=1,2,\ldots ,N)$; the summation $\sum _{i<j}^{(N)}$ is roundly possible combinations of the N elements with condition $i<j$. For example, the first two solutions in (3) have the form

$$\begin{aligned} \begin{aligned} f_1=&1+\exp \eta _1,\\ f_2=&1+\exp \eta _1+\exp \eta _2+\exp (\eta _1+\eta _2+A_{12}),\\ \end{aligned} \end{aligned}$$

(6)

In order to construct M-lump solutions of Eq. (1), at first, we take each $\exp (\eta _i^{(0)})=-1$ in (3). Then $f_{N}$ can be rewritten as

$$\begin{aligned} \begin{aligned} f_{N}=&\sum _{\mu =0,1}\prod _{i=1}^{N}(-1)^{\mu _i}\exp (\mu _i\xi _i) \prod _{i<j}^{N}\exp \left( \mu _i\mu _jA_{ij}\right) , \end{aligned} \end{aligned}$$

(7)

where

$$\begin{aligned} \xi _i=k_i\left[ x+p_iy+z+\left( \frac{k_i^2}{4}+\frac{3\alpha p_i^2}{4}\right) t\right] . \end{aligned}$$

Taking a limit of $k_i\rightarrow 0$ and considering all the $k_i$ to be of the same asymptotic order, we have

$$\begin{aligned} \begin{aligned} f_{N}&=\sum _{\mu =0,1}\prod _{i=1}^{N}(-1)^{\mu _i}(1+\mu _ik_i\theta _i)\\&\quad \times \prod _{i<j}^{(N)}(1+\mu _i\mu _jk_ik_jB_{ij})+O(k^{N+1}). \end{aligned} \end{aligned}$$

(8)

Considering the symmetric property of $f_{N}$ with respect to $k_i$, we find that $f_{N}$ is factorized by $\prod _{i=1}^{N}k_i$. By virtue of transformation $u=2(\ln f)_{x}$, we get a rational solution of Eq. (1). It is easily verified that $u=2(\ln \frac{f_N}{\prod _{i=1}^{N}k_i})_{x}$ is also a solution of Eq. (1). For simplicity, we omit constant factor $\prod _{i=1}^{N}k_i$ of $f_N$ and still denote it as $f_N$. The simplified $f_N$ is in the form of

$$\begin{aligned} \begin{aligned} f_{N}&=\prod _{i=1}^{N}\theta _i+\frac{1}{2}\sum _{i,j}^{(N)}B_{ij}\prod _{l\ne i,j}^{N}\theta _l\\&\quad +\frac{1}{2!2^2}\sum _{i,j,s,r}^{(N)}B_{ij}B_{sr}\prod _{l\ne i,j,s,r}^{N}\theta _l+\ldots \\&\quad +\frac{1}{M!2^M}\sum _{i,j,\ldots ,m,n}^{(N)}\overbrace{B_{ij}B_{kl}\ldots B_{mn}}^M\\&\quad \times \prod _{p\ne i,j,k,l,\ldots ,m,n}^N\theta _p+\cdots , \end{aligned} \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned}&\theta _i=x+p_iy+z+\frac{3\alpha p_i^2t}{4},\\&B_{ij}=\frac{4}{\alpha (p_i-p_j)^2}, \end{aligned} \end{aligned}$$

$\sum _{i,j,\ldots ,m,n}^{(N)}$ means the summation over all possible combinations of $i,j,\ldots ,m,n$, which are taken from $1,\ldots ,N$ and they are all different. From (9) we usually get a singular solution. However, if we choose $p_{M+i}=p_i^*$ $(i=1,2,\ldots ,M)$ for $N=2M$ with the condition $\alpha <0$, we can get a class of nonsingular rational solutions named as M-lump solutions which were confirmed by Satsuma and Ablowitz [3].

2.1 1-Lump solution of Eq. (1)

In this part, we will calculate 1-lump solutions of Eq. (1) from the corresponding 2-soliton solutions by taking $\exp (\eta _i^{(0)})=-1,~(i=1,2)$ and have

$$\begin{aligned} f_2=1-\exp \xi _1-\exp \xi _2+\exp (\xi _1+\xi _2+A_{12}),\nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} \xi _i=k_i\left[ x+p_iy+z+\left( \frac{k_i^2}{4}+\frac{3\alpha p_i^2}{4}\right) t\right] . \end{aligned}$$

(11)

Take the “long wave” limit $k_i\rightarrow 0$ for $i=1,2$ with $\frac{k_1}{k_2}=O(1)$ and $\frac{p_1}{p_2}=O(1)$. Then it yields

$$\begin{aligned} \exp A_{12}=1+\frac{4k_1k_2}{\alpha (p_1-p_2)^2}+O(k^3), \end{aligned}$$

(12)

and

$$\begin{aligned} f_2=k_1k_2(\theta _1\theta _2+\frac{4}{\alpha (p_1-p_2)^2}+O(k)). \end{aligned}$$

(13)

By virtue of the transformation $u=2(\ln f_2)_{x}$, we find that the factor $k_1k_2$ of $f_2$ can be omitted here. Thus we have

$$\begin{aligned} f_2=\theta _1\theta _2+B_{12}, \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{aligned}&\theta _i=x+p_iy+z+\frac{3\alpha p_i^2t}{4}, (i=1,2),\\&B_{12}=\frac{4}{\alpha (p_1-p_2)^2}. \end{aligned} \end{aligned}$$

By taking $p_2=p_1^*$ and $\alpha =-1$ in (14), we obtain a nonsingular solution

$$\begin{aligned} f_2=\theta _1\theta _1^*-\frac{4}{(p_1-p_1^*)^2}>0. \end{aligned}$$

(15)

Substituting (15) into $u=2(\ln f_2)_{x}$ and letting $p_1=p_R+\mathrm{i}p_I$, we obtain

$$\begin{aligned} \begin{aligned} u&=2\frac{\partial }{\partial x}\ln \left[ \left( x'+p_Ry'+z\right) ^2+p_I^2y'^2+\frac{1}{p_I^2}\right] \\&=\frac{4\left( x'+p_Ry'+z\right) }{\left( x'+p_Ry'+z\right) ^2+p_I^2y'^2+1/p_I^2}, \end{aligned} \end{aligned}$$

(16)

where

$$\begin{aligned} x'=x+\frac{3\left( p_R^2+p_I^2\right) }{4}t, \quad y'=y-\frac{3p_R}{2}t. \end{aligned}$$

Fig. 1

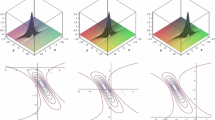
Evolution graphs of (16) by choosing $z=10, p_R=1, p_I=1$ at time a $t=-20$, b $t=0$ and c $t=20$

Fig. 2

Evolution graphs of 2-lump solution by choosing $z=10$, $p_R=1$, $p_I=1$, $h_R=1/40$ and $h_I=1/2$ at time a $t=-30$, b $t=0$ and c $t=30$

Rational solution (16) is a permanent lump solution with the condition $\alpha <0$ and this solution decaying as $O(1/x^2,1/y^2)$ for $|x|,~|y|\rightarrow \infty$ and moving with the velocity $v_x=-\frac{3(p_R^2+p_I^2)}{4}$ and $v_y=\frac{3p_R}{2}$. In Fig. 1, the evolution of this solution is drawn for a particular choice of the parameters $p_R$ and $p_I$. From the expression of solution (16), we find that $f_2$ is a positive quadratic function, which is consistent with the results in many literature [8,9,10].

2.2 Multiple-lump solutions of Eq. (1)

In this part, we will get multiple-lump solutions of Eq. (1). Taking $n=4$ and $M=2$, then (9) can be reduced to $f_4$ expressed as:

$$\begin{aligned} \begin{aligned} f_4&=\theta _1\theta _2\theta _3\theta _4+B_{12}\theta _3\theta _4+B_{13}\theta _2\theta _4 +B_{14}\theta _2\theta _3\\&\quad +B_{23}\theta _1\theta _4+B_{24}\theta _1\theta _3+B_{34}\theta _1\theta _2 \\&\quad +B_{12}B_{34}+B_{13}B_{24}+B_{14}B_{23}, \end{aligned} \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned}&\theta _i=x+p_iy+z+\frac{3\alpha p_i^2t}{4},\\&B_{ij}=\frac{4}{\alpha (p_i-p_j)^2},~ (i,j=1,2,3,4). \end{aligned} \end{aligned}$$

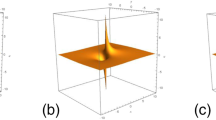
Substituting (17) into the transformation $u=2(\ln f_4)_{x}$, we obtain a nonsingular solution by taking $p_3=p_1^*,~~p_4=p_2^*$ and $\alpha =-1$. In this case, $f_4$ is a positive function composed of quartic and quadratic perfect square functions, and the obtained rational solution is a permanent 2-lump solution. In Fig. 2, the 2-lump solution is drawn for a particular choice of the parameters in $p_1=p_R+\mathrm{i}p_I,~~p_2=h_R+\mathrm{i}h_I$, and the evolution of this solution is illustrated in time.

Fig. 3

Evolution graphs of 3-lump solution by choosing $z=0$, $p_R=1/5$, $p_I=1$, $h_R=1$, $h_I=1$, $q_R=2$ and $q_I=1$ at time a $t=-\,50$, b $t=0$ and c $t=50$

Similarly, Eq. (9) can be reduced to $f_6$ by taking $n=6$ and $M=3$. The expression of $f_6$ contains 76 terms, and it is omitted here due to the limited space. Substituting $f_6$ into the transformation $u=2(\ln f_6)_{x}$, and taking $p_4=p_1^*,~~p_5=p_2^*,~~p_6=p_3^*$ and $\alpha =-\,1$, we get a nonsingular solution named as 3-lump solution of Eq. (1). Then we find that $f_6$ is a positive function composed by the complete of sextic, quartic and quadratic square functions. In Fig. 3, the solution is drawn for a particular choice of the parameters in $p_1=p_R+\mathrm{i}p_I$, $p_2=h_R+\mathrm{i}h_I$ and $p_3=q_R+\mathrm{i}q_I$.

3 Lump–kink solutions of Eq. (1)

Based on the obtained M-lump solutions, we want to study the interaction between lumps and kink solitons which is very interesting because lumps will be drowned or swallowed by the kink solitons.

3.1 Interactive solution between lump and 1-kink soliton of Eq. (1)

In this part, first we assume f as follows:

$$\begin{aligned} f=g_1^2+h_1^2+b+k\mathrm{e}^{k_1x+k_2y+k_3z+k_4t}, \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{aligned} g_1&=a_1x+a_2y+a_3z+a_4t+a_5,\\ h_1&=a_6x+a_7y+a_8z+a_9t+a_{10}, \end{aligned} \end{aligned}$$

$a_i$ $(i = 1, 2, . . . 10)$, b, k and $k_j$ $(j=1,2,3,4)$ are parameters to be setted later. Substituting (18) into Eq. (2) and eliminating coefficients of the polynomial yields a nonlinear algebraic equations which contains 120 equations and we solve it with the help of Maple and get a group of solution:

$$\begin{aligned} \Big \{a_3&=\frac{a_1a_8}{a_6},\nonumber \\ a_4&=\frac{3\alpha \left( a_1a_2^2-a_1a_7^2+2a_2a_6a_7\right) }{4\left( a_1^2+a_6^2\right) },\nonumber \\ a_7&=\frac{a_1^2k_2-a_1a_2k_1+a_6^2k_2}{k_1a_6},\nonumber \\ a_8&=-\frac{\alpha \left( a_1k_2-a_2k_1\right) ^2}{a_6k_1^4},\nonumber \\ a_9&=-\frac{3\alpha \left( 2a_1a_2a_7-a_2^2a_6+a_6a_7^2\right) }{4\left( a_1^2+a_6^2\right) },\nonumber \\ b&=-\frac{a_8\left( a_1^2+a_6^2\right) ^3}{\alpha a_6\left( a_1a_7-a_2a_6\right) ^2},\nonumber \\ k_3&=-\frac{\alpha \left( a_1k_2-a_2k_1\right) ^2}{a_6^2k_1^3},\nonumber \\ k_4&=-\frac{1}{4k_1a_6^2}\left( \alpha \left( a_1^2k_2^2-2a_1a_2k_1k_2\right. \right. \nonumber \\&\quad \left. \left. +a_2^2k_1^2-3a_6^2k_2^2\right) \right) \Big \}, \end{aligned}$$

(19)

which should be satisfied by the conditions

$$\begin{aligned} a_6\ne 0,~~a_1a_6\ne 0,~~k_1a_6\ne 0,~~a_1a_7-a_2a_6\ne 0. \end{aligned}$$

(20)

To ensure the positiveness of f and the localization of u, the following conditions should be satisfied with

$$\begin{aligned} -\frac{a_8}{\alpha a_6}>0,~~~~k>0. \end{aligned}$$

(21)

Since we can get the lump–kink solution of (1) via the transformation $u=2(\ln f)_{x}$,

$$\begin{aligned} u=\frac{4(a_1g_1+a_6h_1)+2kk_1\mathrm{e}^{k_1x+k_2y+k_3z+k_4t}}{g_1^2+h_1^2+b+k\mathrm{e}^{k_1x+k_2y+k_3z+k_4t}}. \end{aligned}$$

(22)

Fig. 4

Evolution graphs of (23) by choosing $\alpha =-1, z = 1, k = 1, k_1 = 1, k_2 = 1, a_1 =3, a_2 = 1, a_5 = 1, a_6 = 2, a_{10} = 2$ at time a $t=-80$, b $t = 0$, c $t = 80$

Through selecting appropriate values for these parameters, the dynamic graphs of interactive solution between lump and kink soliton are shown in Fig. 4. This figure shows that there are a lump and a kink soliton, with the time running lump solution begins to be swallowed by kink soliton step by step, until it is swallowed completely, these two kinds of solitons roll into a kink soliton and continue to spread.

3.2 Interactive solution between lump and 2-kink soliton

Further, in this part we want to discuss the interactive solution between lump and 2-kink soliton. We assume f is the combination of a quadratic function and two exponential functions showing as follows:

$$\begin{aligned} f=m^2+n^2+c+kg_2+k_{9}h_2+k_{10}g_2h_2, \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{aligned}&m=a_1x+a_2y+a_3z+a_4t+a_5,\\&n=a_6x+a_7y+a_8z+a_9t+a_{10}\\&g_2=\mathrm{e}^{k_1x+k_2y+k_3z+k_4t},\\&h_2=\mathrm{e}^{k_5x+k_6y+k_7z+k_8t}, \end{aligned} \end{aligned}$$

$a_i$ $(i = 1, 2,\ldots 10)$, c and $k_j$ $(j=1,2,\ldots 11)$ are parameters to be decided later. Substituting (23) into Eq. (2) and eliminating coefficients of the polynomial yields a nonlinear algebraic equations which contains 324 equations, and we solve it with Maple and obtain a group of solution as follows:

$$\begin{aligned} \Big \{a_2&=\frac{(a_1^2+a_6^2)k_2-a_6a_7k_1}{a_1k_1},\nonumber \\ a_3&=\frac{a_1a_8}{a_6},\nonumber \\ a_4&=\frac{3\alpha (a_1a_2^2-a_1a_7^2+2a_2a_6a_7)}{4(a_1^2+a_6^2)},\nonumber \\ a_8&=-\frac{\alpha (a_1k_2-a_2k_1)^2}{a_6k_1^4},\nonumber \\ a_9&=-\frac{3\alpha (2a_1a_2a_7-a_2^2a_6+a_6a_7^2)}{4(a_1^2+a_6^2)},\nonumber \\ c&=-\frac{a_8(a_1^2+a_6^2)^3}{\alpha a_6(a_1a_7-a_2a_6)^2},\nonumber \\ k&=\frac{k_{10}(a_1^2+a_6^2)}{k_5^2k_9},\nonumber \\ k_4&=-\frac{\alpha ((a_1k_2-a_2k_1)^2-3a_6^2k_2^2)}{4k_1a_6^2},\nonumber \\ k_8&=\frac{\alpha (3a_1^2k_2^2-(a_6k_2+a_7k_5)^2)}{4a_1^2k_5},\nonumber \\ k_1&=-k_5,~~k_6=-k_2\Big \}, \end{aligned}$$

(24)

which needs to satisfy the following conditions

$$\begin{aligned} \begin{aligned}&a_1\ne 0,~~a_1a_6\ne 0,~~a_1k_1\ne 0,~a_1k_5\ne 0,\\&k_5k_9\ne 0,~~a_1a_7-a_2a_6\ne 0. \end{aligned} \end{aligned}$$

(25)

To ensure that f is positive, the conditions should be further satisfied

$$\begin{aligned} c>0,~~k_{9}>0,~~k_{10}>0. \end{aligned}$$

(26)

Then we can obtain the lump–kink solution of Eq. (1) via the transformation $u=2(\ln f)_{x}$.

Fig. 5

Evolution graphs of u by choosing $z=0$, $k_4=1$, $k_5=-1$, $k_6=1$, $k_8=1$, $k_{10}=1$, $k_{11}=1$, $a_1=1$, $a_5=1$, $a_6=-1$ and $a_{10}=1$ at time a $t=-50$, b $t=-30$, c $t=-20$, d $t=0$, e $t=10$ and f $t=50$

Fig. 6

The plots of u by choosing $\alpha =-1,q=p=l=1,a_4=a_5=b_4=b_5=1,c_4=d_1=10,d_2=d_3=d_4=1$ with a $x=y=0$, b $x=10,t=1/50$ and c $y=10,t=1/50$

Figure 5 gives the dynamic graphs of interaction between a lump and a 2-kink soliton by selecting appropriate values of the parameters. From Fig. 5, we first find that there has a pair of kink solitons and a lump. With time evolving, the lump is swallowed step by step by kink solitons. Finally, these two kinds of waves roll into a 2-kink soliton and continue to spread.

Similarly, we can further discuss the interactive solution between 2-lump and 1-kink soliton as well as the interactive solution between 2-lump and 2-kink soliton, even the interactive solution between M-lump and N-kink soliton. However, for this equation the obtained interactive solution between 2-lump and 1-kink soliton is just a trivial solution, and we omitted it here.

4 Periodic interactive solutions of Eq. (1)

Periodic wave solutions of nonlinear evolution equation have attracted tremendous attention from scientists and were investigated in many literature [19,20,21].

In this part, we will discuss the periodic interactive solutions of Eq. (1). With regard to (2), we take f as follows:

$$\begin{aligned} f&=s^2+r^2+q\cos (c_1x+c_2y+c_3z+c_4t+c_5)\nonumber \\&\quad +\mathrm{e}^{d_1x+d_2y+d_3z+d_4t+d_5}+l, \end{aligned}$$

(27)

where

$$\begin{aligned} \begin{aligned} s&=a_1x+a_2y+a_3z+a_4t+a_5,\\ r&=b_1x+b_2y+b_3z+b_4t+b_5, \end{aligned} \end{aligned}$$

and $a_i$, $b_i$, $c_i$, $d_i$ $(i = 1, 2,\ldots 5)$, q and l are parameters to be decided later. Substituting (27) into Eq. (2) and eliminating coefficients of the polynomial yields a nonlinear algebraic equations which contains 279 equations, and we solve it with Maple and obtain a group of solution as follows:

$$\begin{aligned} \begin{aligned} \Bigg \{a_2&=0,~~b_2=0,~~c_2=0,~~k_2=0,~~a_3=\frac{4a_4}{d_1^2},\\ b_3&=\frac{4b_4}{d_1^2},~~c_3=-\frac{4c_4}{d_1^2},~~d_3=\frac{4d_1d_4-3\alpha d_2^2}{d_1^3}\Bigg \}, \end{aligned} \end{aligned}$$

(28)

with $d_1\ne 0$.

Then a periodic interactive solution of Eq. (1) can be obtained through the transformation $u=2(\ln f)_{x}$.

Figure 6 gives the dynamic graphs of periodic interactive solutions of Eq. (1) by selecting appropriate values of the parameters.

5 Conclusion

Lump wave solutions have attracted much attention of mathematical physicists, for these solutions may well describe rogue wave dynamics, especially in oceanography and nonlinear optics. Many papers [7,8,9,10,11] concerning 1-lump wave solutions have been reported recently. In this paper, we investigate M-lump solutions, lump–kink solutions as well as periodic interactive solutions for a ($3+1$)-dimensional nonlinear system and further discuss dynamic properties of these solutions. The method applied in this paper is universal and can be adapted to other nonlinear evolution equations. Meanwhile, readers could further construct other types of interactive wave solutions, such as peak waves and lump waves. In the near future, we will further investigate other types of interactive wave solutions of nonlinear evolution equations.