Characteristics of the solitary waves and lump waves with interaction phenomena in a (2 + 1)-dimensional generalized Caudrey–Dodd–Gibbon–Kotera–Sawada equation

Abstract

In this paper, we consider a ($2+1$)-dimensional generalized Caudrey–Dodd–Gibbon–Kotera–Sawada (gCDGKS) equation, which is a higher-order generalization of the celebrated Kadomtsev–Petviashvili (KP) equation. By considering the Hirota bilinear form of the CDGKS equation, we study a type of exact interaction waves by the way of vector notations. The interaction solutions, which possess extensive applications in the nonlinear system, are composed by lump wave parts and soliton wave parts, respectively. Under certain conditions, this kind of solutions can be transformed into the pure lump waves or the stripe solitons. Moreover, we provide the graphical analysis of such solutions in order to better understand their dynamical behavior.

1 Introduction

We all know that soliton solutions occupy a vital position in the nonlinear evolution equations (NLEEs). It is a popular topic to find exact solutions for NLEEs and has attracted a great many researchers. Over the past decade, many methods are provided to solve NLEEs, such as the Hirota bilinear method [1], inverse scattering transformation (IST) [2], and Darboux transformation (DT) [3,4,5,6,7,8]. Recently, the study of lump waves, which can be regarded as one kind of the rationally localized solutions, has become a hot topic both in the theory and experiment. Lump waves can be applied to various fields, such as nonlinear optic media, plasma, and shallow water wave [9,10,11]. Nowadays, many lump wave solutions have been found through the new direct method [12,13,14,15,16]. In addition, analyticity between lump solutions and the stripe solitons has been reported in [17,18,19,20]. Multifarious nonlinear systems in nature can be described well by the interaction solutions. Sometimes, this type of interaction solutions is used to forecast the appearance of rogue waves through analyzing the relations between rogue parts and twin-soliton parts [21].

In this work, we consider the following ($2+1$)-dimensional generalized Caudrey–Dodd–Gibbon–Kotera–Sawada (gCDGKS) equation

$$\begin{aligned} \left\{ {\begin{array}{l} 36u_{t}+\left( u_{xxxx}+15uu_{xx}+15u^{3}\right) _{x}-\alpha v_{yy} \\ \quad -\,\gamma \left( u_{xxy}+3uu_{y}+3u_{x}v_{y}\right) =0,\\ v_{x}=u, \end{array}}\right. \end{aligned}$$

(1)

where $\alpha$ and $\gamma$ are two constants and $u=u(x, y, t)$ and $v=v(x, y, t)$ are two differentiable functions with the variables x, y and t. It is a generalized form of the CDGKS equation introduced in [22], which is a higher-order generalization of the celebrated Kadomtsev–Petviashvili (KP) equation and widely employed in many physical branches. As a extended form of the KP equation, it can describe nonlinear dispersive physical phenomena well. gCDGKS Eq. (1) can be reduced to the ($2+1$)-dimensional CDGKS equation for $\alpha =\gamma =5$, which was first proposed by Konopelchenk and Dubovsky [22]. When $\alpha =\gamma =5$ and $u_{y}=0$, Eq. (1) changes into the ($1+1$)-dimensional CDGKS equation, whose N-soliton solutions and integrabilities were found in [23, 24]. The other works for the ($2+1$)-dimensional CDGKS equation were also carried out, including discussing quasiperiodic solutions and the interaction behaviors between solitons and cnoidal periodic waves [25,26,27].

To the best of our knowledge, although a great number of work have been researched about the CDGKS equation, the characteristics of the solitary waves and lump waves with interaction phenomena have not studied for gCDGKS Eq. (1). Based on the symbol calculation methods [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], the main propose of this paper is to study the lump waves based on the bilinear form and vector notations of (1). Then, we derive its one-soliton and two-soliton solutions. Furthermore, we analyze the interaction between lump waves and solitary waves. Finally, the graphical analysis of these solutions is analyzed in order to better understand their dynamical behavior.

The outline of this paper is as follows. In Sect. 2, we firstly derive the Hirota bilinear form of the generalized ($2+1$)-dimensional CDGKS equation. Then through expression (6) with (7), we construct the special form of interaction solutions (7) for the equation in the case of three variables. In Sect. 3, based on these preconditions, we obtain its lump wave solutions . In addition, in Sect. 4, one-soliton and two-soliton solutions are derived in detail. In Sect. 5, we analyze the interaction between lump wave and solitary wave of the gCDGKS equation. Furthermore, we also display some plots to depict the propagation behaviors of these solutions. In last section, some conclusions of this work are discussed.

2 Mathematical analysis

2.1 Bilinear form

Based on the previous results [46,47,48,49,50,51,52,53,54,55,56,57], the Hirota bilinear form of the gCDGKS equation can be read by

$$\begin{aligned}&B_{CDGKS}\left( f\right) \nonumber \\&\quad =\left( 36D_{x}D_{t}+D_{x}^{6}-\alpha D_{y}^{2}-\gamma D_{x}^{3}D_{y}\right) f\cdot f=0, \end{aligned}$$

(2)

under the transformations as follows

$$\begin{aligned} u=2\ln \left( f\right) _{xx}\Leftrightarrow v=2\ln \left( f\right) _{x}, \end{aligned}$$

(3)

with

$$\begin{aligned}&D_{x}^{6}f\cdot f=2\left( f_{6x}f+15f_{4x}f_{2x}-10f_{3x}^{2}-6f_{5x}f_{x}\right) ,\nonumber \\&D_{x}^{3}D_{y}f{\cdot }f{=}2\left( f_{3x, y}f{-}f_{3x}f_{y}{-}3f_{2x, y}f_{x}{+}3f_{2x}f_{x, y}\right) ,\nonumber \\&D_{x}D_{t}f\cdot f=2\left( f_{x, t}f-f_{x}f_{t}\right) ,\nonumber \\&D_{y}^{2}f\cdot f=2\left( f_{2y}f-f_{y}^{2}\right) , \end{aligned}$$

(4)

where the D-operator is denoted by

$$\begin{aligned} D_{x}^{m}D_{y}^{n}\left( f\cdot g\right) =&\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{m}\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^{n}\nonumber \\&\times f\left( x,y\right) \cdot g\left( x',y'\right) \big |_{x=x',y=y'}. \end{aligned}$$

(5)

2.2 Theories analysis for the interaction solutions

In this section, we provide the following main theorem in order to find the interaction solutions of gCDGKS Eq. (1).

Main Theorem 1

gCDGKS Eq. (1) admits the interaction solutions as follows

$$\begin{aligned} u=\varGamma \left( \partial _{x_{i}}\right) \ln f \end{aligned}$$

(6)

with

$$\begin{aligned} f&=f_{0}+\sum _{i, j=0}^{n}p_{ij}x_{i}x_{j}+\kappa _{1}{\text {e}}^{\xi }+\kappa _{2}{\text {e}}^{-\xi }\nonumber \\&=f_{0}+\chi ^{2}+\kappa _{1}{\text {e}}^{\xi }+\kappa _{2}{\text {e}}^{-\xi }, \end{aligned}$$

(7)

where $\varGamma \left( \partial _{x_{i}}\right)$ means a series of partial derivatives operations to $x_{i} \left( i= 1, 2, \ldots n-1\right)$. $\xi =\sum _{i=1}^{n}l_{i}x_{i}$, $\chi ^{2}$ is the inner product of M dimension vector $\mathbf {\chi }$ with respect to itself, and $\mathbf {\chi }=\sum _{i=0}^{n}x_{i}\mathbf {P}_{i}$, $\mathbf {P}_{i}=\left( P_{i1}, P_{i2}, \ldots , P_{iM}\right)$, wherein $x_{0}=1, x_{n}=t$, $p_{ij}=p_{ji}=\mathbf {P}_{i}\cdot \mathbf {P}_{j}=\sum _{m=1}^{M}P_{im}P_{jm} \left( i, j=0, 1, 2, \ldots n\right)$, and we have $\chi ^{2}=\sum _{m=1}^{M}\chi _{m}^{2}$ . Moreover, nandM are both positive integers, and $f_{0}, \kappa _{1}, \kappa _{2}, l_{i}$ are free scalar parameters.

The gCDGKS Eq. (1) admits the following interaction wave solutions

$$\begin{aligned}&f=f_{0}+\chi ^{2}+\kappa _{1}\text {e}^{\xi _{0}}+\kappa _{2}\text {e}^{-\xi _{0}},\nonumber \\&\xi _{0}=a_{0}x+b_{0}y+c_{0}t, \end{aligned}$$

(8)

where $\kappa _{1}, \kappa _{2}$ are free parameters, $f_{0}, a_{0}, b_{0}, c_{0}$ are arbitrary scalar parameters to be known later, and $\chi ^{2}=\mathbf {\chi }\cdot \mathbf {\chi }=\sum _{m=1}^{M}\chi _{m}^{2}$, $\mathbf {\chi }$ is a M(M is positive integers)-dimensional vector which can be expressed by the constant vectors $\mathbf {a}, \mathbf {b}, \mathbf {c}$, and $\mathbf {\lambda }$ in the following form

$$\begin{aligned} \mathbf {\chi }=x\mathbf {a}+y\mathbf {b}+t\mathbf {c}+\mathbf {\lambda }, \end{aligned}$$

(9)

where $\mathbf {a}=(a_{1}, a_{2}, \ldots , a_{M}), \mathbf {b}=(b_{1}, b_{2}, \ldots , b_{M}), \mathbf {c}=(c_{1}, c_{2}, \ldots , c_{M}), \mathbf {\lambda }=(\lambda _{1}, \lambda _{2}, \ldots , \lambda _{M})$. Next, we introduce the symbols $\varDelta _{12}=\mathbf {a}\,{\cdot }\, \mathbf {b}=\sum _{m=1}^{M}a_{m}b_{m}, \varDelta _{13}=\mathbf {a}\cdot \mathbf {c} , \varDelta _{23}=\mathbf {b}\cdot \mathbf {c}, \varDelta _{11}=a^{2}=\mathbf {a}\cdot \mathbf {a}, \varDelta _{22}=b^{2}=\mathbf {b}\cdot \mathbf {b} , \varDelta _{01}=\mathbf {a}\cdot \mathbf {\lambda }, \varDelta _{02}=\mathbf {b}\cdot \mathbf {\lambda }.$

In terms of expression (8), it denotes that the solution consists of three parts, including rational solution $f_{0}+\chi ^{2}$ (lump wave part), the exponential solution $\kappa _{1}\text {e}^{\xi _{0}}$ (soliton part), and another exponential solution $\kappa _{2}\text {e}^{-\xi _{0}}$ (soliton part), respectively. Therefore, if $\kappa _{1}=\kappa _{2}=0$, solution (3) with expression (8) turns into a pure lump. On the other hand, the solution becomes a pure soliton with $\chi ^{2}=0$. When $\kappa _{1}\ne 0, \kappa _{2}=0$, and $\xi _{0}\rightarrow +\,\infty$, the soliton solution part $\kappa _{1}\text {e}^{\xi _{0}}$ will tend to infinity, and the lump solution part and the soliton solution part $\kappa _{2}\text {e}^{-\xi _{0}}$ can be ignored. Similarly, the lump solution part is also discarded under the circumstances of $\kappa _{2}\ne 0, \kappa _{1}=0$ and $\xi _{0}\rightarrow -\,\infty$.

3 Lump wave solutions

Notably, when $\kappa _{1}=\kappa _{2}=0$, we know that Eq. (8) degenerates to the pure lump waves, which are the rational solutions and localized in all directions in space, given by

$$\begin{aligned} f=f_{0}+\chi ^{2}. \end{aligned}$$

(10)

Substituting (10) into (2), through symbolic computations with Maple, we can obtain

$$\begin{aligned} 36\varDelta _{13}-\alpha b^{2}=0,\quad \varDelta _{12}=0, \end{aligned}$$

(11)

which yields a broad categories of lump waves (3) with (10) for Eq. (1).

In order to catch the arrival place of lump waves (3) with (10), we need to obtain the critical point of lump waves. Taking $f_{x}=f_{y}=0$, we have

$$\begin{aligned}&x=x\left( t\right) =\frac{-\varDelta _{01}}{a^{2}}-\frac{\varDelta _{13}}{a^{2}}t,\nonumber \\&y=y\left( t\right) =\frac{-\varDelta _{02}}{b^{2}}-\frac{\varDelta _{23}}{b^{2}}t. \end{aligned}$$

(12)

which can represent the travel path of the lump waves.

Fig. 1

(Color online) The lump waves of Eq. (1) with parameters (19): a density plot, b three-dimensional plot at time $t=0$, c the contour plot about the progress of moving described by the straight line (16), i.e., $x=-\frac{1}{36}t, y=\frac{1}{108}t$

For presenting lump solutions specifically, we take $M=2$, and then $\mathbf {a}=(a_{1}, a_{2}), \mathbf {b}=(b_{1}, b_{2}), \mathbf {c}=(c_{1}, c_{2}), \mathbf {\lambda }=(\lambda _{1}, \lambda _{2})$. Through taking one of particular cases of (11), a series of constraining expressions for the parameters can be obtained (see [46]):

$$\begin{aligned}&a_{1}=\frac{b_{1}}{3a_{2}^{2}},\quad c_{1}=0,\quad b_{2}=-\frac{b_{1}^{2}}{3a_{2}^{3}},\nonumber \\&c_{2}=\frac{\alpha b_{1}^{2}\left( 9a_{2}^{6}+b_{1}^{2}\right) }{324a_{2}^{7}},\nonumber \\&b_{1}=b_{1},\quad \lambda _{1}=\lambda _{1},\quad a_{2}=a_{2},\quad \lambda _{2}=\lambda _{2},\quad f_{0}=f_{0}. \end{aligned}$$

(13)

where $a_{2}\ne 0$. Based on these parameters, the algebraic solutions (lump wave solutions) of Eq. (1) can be expressed in the form

$$\begin{aligned}&u=\frac{4\left( a_{2}^{2}+\frac{b_{1}^{2}}{9a_{2}^{4}}\right) }{f}\nonumber \\&\quad -\,\frac{8\left[ \left( a_{2}^{2}{+}\frac{b_{1}^{2}}{9a_{2}^{4}}\right) x{+}\frac{\alpha b_{1}^{2}\left( 9a_{2}^{6}{+}b_{1}^{2}\right) }{324a_{2}^{6}}t+\frac{b_{1}\lambda _{1}}{3a_{2}^{2}}+a_{2}\lambda _{2}\right] ^{2}}{f^{2}},\nonumber \\&v=\frac{4\left[ \left( a_{2}^{2}+\frac{b_{1}^{2}}{9a_{2}^{4}}\right) x+\frac{\alpha b_{1}^{2}\left( 9a_{2}^{6}+b_{1}^{2}\right) }{324a_{2}^{6}}t +\frac{b_{1}\lambda _{1}}{3a_{2}^{2}}+a_{2}\lambda _{2}\right] }{f}, \end{aligned}$$

(14)

with

$$\begin{aligned} f=\,&f_{0}+\left( \frac{b_{1}}{3a_{2}^{2}}x+b_{1}y+\lambda _{1}\right) ^{2}\nonumber \\&+\left( a_{2}x-\frac{b_{1}^{2}}{3a_{2}^{3}}y+\frac{\alpha b_{1}^{2}\left( 9a_{2}^{6}+b_{1}^{2}\right) }{324a_{2}^{7}}t+\lambda _{2}\right) ^{2}, \end{aligned}$$

(15)

and the travel path meets

$$\begin{aligned} x\left( t\right) =-\frac{3a_{2}^{2}\left( b_{1}\lambda _{1}+3a_{2}^{3}\lambda _{2}\right) }{b_{1}^{2}+9a_{2}^{6}}-\frac{\alpha b_{1}^{2}}{36a_{2}^{2}}t,\nonumber \\ y\left( t\right) =-\frac{3a_{2}^{3}\left( 3a_{2}^{3}\lambda _{1}-b_{1}\lambda _{2}\right) }{b_{1}\left( 9a_{2}^{6}+b_{1}^{2}\right) }+\frac{\alpha b_{1}^{2}}{108a_{2}^{4}}t, \end{aligned}$$

(16)

where $a_{2}, b_{1}, \lambda _{1}, \lambda _{2}, f_{0}$ are free scalar constants and $\alpha$ is arbitrary scalar parameters. That means the lump waves move along the straight line

$$\begin{aligned} {y=-\frac{1}{3a_{2}^{2}}x-\frac{\lambda _{1}}{b_{1}},} \end{aligned}$$

(17)

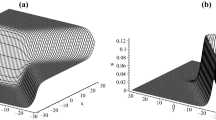
The amplitude of the lump waves should be considered, which can be obtained by solving the system $\{u_{x}=0, u_{y}=0\}$. Therefore, the amplitude of the lump waves can be given by

$$\begin{aligned} {A_\mathrm{{lump}}=\left| \frac{36a_{2}^{6} +4b_{1}^{2}}{9a_{2}^{4}f_{0}}\right| ,} \end{aligned}$$

(18)

which means that the amplitude just depends on the arbitrary constants of $a_{2}, b_{1}, f_{0}$.

To understand more about lump waves (14), the graphical analysis is plotted in Fig. 1 in order to show some behaviors of the lump waves by selecting following free parameters:

$$\begin{aligned} \alpha =b_{1}=a_{2}=f_{0}=1,\quad c_{1}=\lambda _{1}=\lambda _{2}=0. \end{aligned}$$

(19)

4 Solitary wave solutions

In order to find the solitary wave solutions for Eq. (1), we expand the function f(x, y, t) with a formal expansion parameter $\varepsilon$:

$$\begin{aligned} f\left( x, y, t\right) =1+ f^{\left( 1\right) }\varepsilon +f^{\left( 2\right) }\varepsilon ^{2} +f^{\left( 3\right) }\varepsilon ^{3}+\cdots , \end{aligned}$$

(20)

where the coefficients $f^{(i)}=f^{(i)}(x, y, t)$ $(i=1, 2,\ldots )$ are some differentiable functions to be determined. Substituting (20) into bilinear form (2), and then taking all coefficients of the same powers of $\varepsilon$ to equate zero, we have the soliton solutions of Eq. (1).

4.1 One-soliton solutions

In general, in order to seek one-solitary waves, above expansion (20) can be truncated based on $f^{\left( i\right) }=0\left( i=2, 3, 4,\ldots \right)$, and we have

$$\begin{aligned} f=1+f^{\left( 1\right) }\varepsilon =1+\text {e}^{\eta _{1}}\varepsilon , \end{aligned}$$

(21)

where $\eta _{1}=h_{1}x+\rho _{1}y+\varrho _{1}t+\theta _{1}$, and $h_{1}, \rho _{1}, \theta _{1}$ are constants. Then, putting (21) into (2), and let $\varepsilon =1$, we find

$$\begin{aligned} \varrho _{1}=\frac{\gamma h_{1}^{3}\rho _{1}+\alpha \rho _{1}^{2}- h_{1}^{6}}{36h_{1}}. \end{aligned}$$

(22)

Hence, the one-soliton solutions of Eq. (1) admit the following form

$$\begin{aligned}&u=2\left[ \ln \left( 1+\text {e}^{\eta _{1}}\right) \right] _{xx}\nonumber \\&\quad = \frac{h_{1}^{2}}{2}\text{ sech }^{2}\frac{h_{1}x+\rho _{1}y+\varrho _{1}t+\theta _{1}}{2}, \end{aligned}$$

(23)

where $h_{1}, \rho _{1}, \theta _{1}$ are real constants and $\varrho _{1}$ is denoted by $h_{1}, \rho _{1}$.

Fig. 2

(Color online) One-soliton wave (23) of Eq. (1) by selecting suitable parameters: $\alpha =2, \gamma =1, h_{1}=\rho _{1}=2, \theta _{1}=\frac{\pi }{3}$. a Perspective view of the real part of the wave $\left( t=0\right)$. b Perspective view of the real part of the wave $\left( y=0\right)$. c Perspective view of the real part of the wave $\left( x=0\right)$

4.2 Two-soliton solutions

In the same way, for getting the two-soliton solutions, expansion (20) can be truncated based on $F^{\left( i\right) }=0\left( i=3, 4, 5, \ldots \right)$, and we have

$$\begin{aligned} f=1+f^{\left( 1\right) }\varepsilon +f^{\left( 2\right) }\varepsilon ^{2}, \end{aligned}$$

(24)

where $f^{\left( 1\right) }=\text {e}^{\eta _{1}}+\text {e}^{\eta _{2}}$, $f^{\left( 2\right) }=\text {e}^{\eta _{1}+\eta _{2}+\varOmega _{12}}$, $\eta _{i}=h_{i}x+\rho _{i}y+\varrho _{i}t+\theta _{i},$ $h_{i}$, $\rho _{i}$ and $\theta _{i}$ $(i=1,2)$ are all constants. Putting (24) into (2), and taking $\varepsilon =1$, we have

$$\begin{aligned}&\varrho _{i}=\frac{\gamma h_{i}^{3}\rho _{i}+\alpha \rho _{i}^{2}- h_{i}^{6}}{36h_{i}},~~i=1, 2, \end{aligned}$$

(25)

$$\begin{aligned}&\text {e}^{\varOmega _{12}}=-\frac{\left[ \gamma \left( h_{1}-h_{2}\right) ^{3}\left( \rho _{1}-\rho _{2}\right) +\alpha \left( \rho _{1}-\rho _{2}\right) ^{2} -\left( h_{1}-h_{2}\right) ^{6}-36\left( h_{1}-h_{2}\right) \left( \varrho _{1}-\varrho _{2}\right) \right] }{\left[ \gamma \left( h_{1}+h_{2}\right) ^{3}\left( \rho _{1}+\rho _{2}\right) +\alpha \left( \rho _{1}+\rho _{2}\right) ^{2} -\left( h_{1}+h_{2}\right) ^{6}-36\left( h_{1}+h_{2}\right) \left( \varrho _{1}+\varrho _{2}\right) \right] }. \end{aligned}$$

(26)

Therefore, the two-soliton solutions of Eq. (1) have the following form

$$\begin{aligned} u=2\left[ \ln \left( 1+\text {e}^{\eta _{1}}+\text {e}^{\eta _{2}}+\text {e}^{\eta _{1} +\eta _{2}+\varOmega _{12}}\right) \right] _{xx}, \end{aligned}$$

(27)

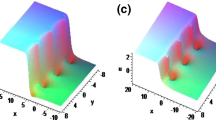
where $\eta _{i}=h_{i}x+\rho _{i}y+\varrho _{i}t+\theta _{i}\left( i=1, 2\right)$, $h_{i}, \rho _{i}, \theta _{i}$ $\varrho _{i}$ are real constants and $\varrho _{i}$ are denoted by $h_{i}, \rho _{i}.$

Fig. 3

(Color online) Two-soliton wave (27) of Eq. (1) by selecting suitable parameters: $\alpha =2, \gamma =-2.5, h_{1}=\rho _{1}=1.8, h_{2}=-\rho _{2}=1.5, \theta _{1}=\theta _{2}=0$. a Perspective view of the real part of the wave $\left( t=0\right)$. b Perspective view of the real part of the wave $\left( y=0\right)$. c Perspective view of the real part of the wave $\left( x=0\right)$

5 Interaction between lump waves and solitary waves

In this part, in order to analyze the interaction between lump waves and solitary waves, we discuss expression (8) in the case that $\kappa _{1}, \kappa _{2}$ are not all zero. Substituting interaction solutions (8) into Eq. (2), with the help of Maple, we have

$$\begin{aligned} \left\{ {\begin{array}{l}36\varDelta _{13}-\alpha b^{2}=0,\\ -a_{0}^{6}+\gamma a_{0}^{3}b_{0}+\alpha b_{0}^{2}-36a_{0}c_{0}=0, \\ \left( -6a_{0}^{5}+3\gamma a_{0}^{2}b_{0}-36c_{0}\right) \mathbf {a}\\ \quad +\left( \gamma a_{0}^{3}+2\alpha b_{0}\right) \mathbf {b}-36a_{0}\mathbf {c}=0,\\ \left( -5a_{0}^{4}+\gamma a_{0}b_{0}\right) a^{2}+\gamma a_{0}^{2}\varDelta _{12}=0,\\ \left( -\alpha b_{0}^{2}+36a_{0}c_{0}-4\gamma a_{0}^{3}b_{0}+16a_{0}^{6}\right) \kappa _{1}\kappa _{2}\\ \quad -3\gamma a^{2}\varDelta _{12}=0. \end{array}}\right. \end{aligned}$$

(28)

By considering (28) based on $\mathbf {a}\cdot \mathbf {b}=\varDelta _{12}=0$, one finds

$$\begin{aligned} b_{0}=\frac{5a_{0}^{3}}{\gamma }, \quad c_{0}=\left( \frac{25\alpha }{36\gamma ^{2}}+\frac{1}{9}\right) a_{0}^{5}, \end{aligned}$$

(29)

and

$$\begin{aligned} \mathbf {c}=\frac{5a_{0}^{4}}{36\gamma ^{2}}\left( \gamma ^{2}-5\alpha \right) \mathbf {a}+\frac{a_{0}^{2}}{36\gamma }\left( \gamma ^{2}+10\alpha \right) \mathbf {b}, \end{aligned}$$

(30)

which yield the following constraining equations

$$\begin{aligned} \frac{5a_{0}^{4}}{\gamma ^{2}}\left( \gamma ^{2}-5\alpha \right) a^{2}-\alpha b^{2}=0,\quad \varDelta _{12}=0. \end{aligned}$$

(31)

where $\alpha , \gamma$ are both parameters and $a_{0}, \mathbf {a}, \mathbf {b}$ are arbitrary constant vectors.

Fig. 4

(Color online) Three-dimensional plots and contour plots of the interaction solution for Eq. (1) with parameters (35): a, d $t={-\,400}$, b, e $t={-\,180}$, c, f $t={400}$

Fig. 5

(Color online) Three-dimensional plots and contour plots of the interaction solution for Eq. (1) with the same parameters as in (35) except for $\kappa _{2}=0.1$: a, d $t={-\,400}$ , b, e $t=0$, c, f $t={400}$

Fig. 6

(Color online) Three-dimensional plots and contour plots of the interaction solution for Eq. (1) with parameters (35): a, d $t={-\,100}$, b, e $t=0$, c, f $t={100}$

Similarly, in order to display the interaction solutions in detail, we take $M=2$ as a illustration; therefore, we have $\mathbf {a}=(a_{1}, a_{2}), \mathbf {b}=(b_{1}, b_{2}), \mathbf {c}=(c_{1}, c_{2}), \mathbf {\lambda }=(\lambda _{1}, \lambda _{2});$ then according to constraining Eqs. (31), a series of constraining expressions for the parameters can be obtained by

$$\begin{aligned}&a_{1}=a_{1},\quad a_{2}=a_{2},\quad b_{1}=-\sqrt{\frac{5}{\alpha }-\frac{25}{\gamma ^{2}}}a_{0}^{2}a_{2},\nonumber \\&b_{2}=\sqrt{\frac{5}{\alpha }-\frac{25}{\gamma ^{2}}}a_{0}^{2}a_{1},\nonumber \\&c_{1}=\frac{\alpha a_{0}^{4}}{36\gamma ^{2}}\sqrt{\frac{5\gamma ^{2}}{\alpha }-25}\nonumber \\&\qquad \times \left[ \sqrt{\frac{5\gamma ^{2}}{\alpha }-25}a_{1}-\left( \frac{\gamma ^{2}}{\alpha }+10\right) a_{2}\right] ,\nonumber \\&c_{2}=\frac{\alpha a_{0}^{4}}{36\gamma ^{2}}\sqrt{\frac{5\gamma ^{2}}{\alpha }-25}\nonumber \\&\qquad \times \left[ \sqrt{\frac{5\gamma ^{2}}{\alpha }-25}a_{2}+\left( \frac{\gamma ^{2}}{\alpha }+10\right) a_{1}\right] ,\nonumber \\&\lambda _{1}=\lambda _{1},\quad \lambda _{2}=\lambda _{2},\quad a_{0}=a_{0} ,\quad f_{0}=f_{0}, \end{aligned}$$

(32)

where $\alpha \ne 0, \gamma \ne 0$ and $\frac{5}{\alpha }-\frac{25}{\gamma ^{2}}> 0.$ According to these parameters, interaction solutions (3) with (8) for Eq. (1) can be read by

$$\begin{aligned} u=\,&\frac{2}{f}\left( 2a_{1}^{2}+2a_{2}^{2}+\kappa _{1}a_{0}^{2}\text {e}^{\xi _{0}}+\kappa _{2}a_{0}^{2}\text {e}^{-\xi _{0}}\right) \nonumber \\&-\frac{2}{f^{2}}\left( 2a_{1}\left( a_{1}x+b_{1}y+c_{1}t+\lambda _{1}\right) \right. \nonumber \\&\left. +\,2a_{2}\left( a_{2}x+b_{2}y+c_{2}t+\lambda _{2}\right) +\kappa _{1}a_{0}\text {e}^{\xi _{0}}-\kappa _{2}a_{0}\text {e}^{-\xi _{0}}\right) ^{2},\nonumber \\ v=\,&\frac{2}{f}\left( 2a_{1}\left( a_{1}x+b_{1}y+c_{1}t+\lambda _{1}\right) \right. \nonumber \\&\left. +\,2a_{2}\left( a_{2}x+b_{2}y+c_{2}t+\lambda _{2}\right) +\kappa _{1}a_{0}\text {e}^{\xi _{0}}-\kappa _{2}a_{0}\text {e}^{-\xi _{0}}\right) , \end{aligned}$$

(33)

with

$$\begin{aligned} f=\,&f_{0}+\left( a_{1}x+b_{1}y+c_{1}t+\lambda _{1}\right) ^{2}\nonumber \\&+\left( a_{2}x+b_{2}y+c_{2}t+\lambda _{2}\right) ^{2}+\kappa _{1}\text {e}^{\xi _{0}}+\kappa _{2}\text {e}^{-\xi _{0}}. \end{aligned}$$

(34)

where $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}, \lambda _{1}, \lambda _{2}, a_{0}$ are satisfied with constraining expressions (32) and $\xi _{0}$ is written as $a_{0}x+\frac{5a_{0}^{3}}{\gamma }y+\left( \frac{25\alpha }{36\gamma ^{2}}+\frac{1}{9}\right) t$.

5.1 Interaction between lump waves and line single-soliton waves

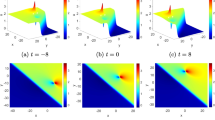
When $\kappa _{2}=0$, solution (33) implicates the interaction between lump waves and line single-soliton waves. In the following, we provide several related figures to show interaction solutions (33) by selecting following two sets of different free parameters:

$$\begin{aligned} \alpha&=0.4,\quad \gamma =3.4,\quad f_{0}=1,\quad \kappa _{1}=0.1,\quad \kappa _{2}=0,\nonumber \\ a_{0}&=0.7,\quad a_{1}=1,\quad a_{2}=-2.1,\quad \mathbf {\lambda }=0. \end{aligned}$$

(35)

Figure 4 shows the process of traveling waves for the interaction between lump waves and line single-soliton waves based on parameter selections (35). As shown in Fig. 4, the wave is composed by two part, including lump wave part and single-soliton wave part, respectively. Apparently, from Fig. 4a, d, we easily find that lump wave begins to be swallowed by single-soliton, and when $t\rightarrow -\,\infty$, the lump wave vanishes gradually, and only the soliton wave exists. The two waves collide over a period of time, exactly as the time at $t={-180}$ displayed in Fig. 4b, e; at the moment, the the lump turns to tangle with the soliton, and the amplitudes and shapes of lump wave and line single-soliton wave are changed. But when $t\rightarrow +\,\infty$, they are separated from each other and propagate along the respective directions and recover their original amplitudes and shapes, which can be explicitly observed from Fig. 4c, f. On the other hands, when we choose $\kappa _{1}=0, \kappa _{2}=0.1$ instead of $\kappa _{1}=0.1, \kappa _{2}=0$, the other parameters remain unchanged, and some similar figures can be exported from Fig. 4 through transforming (x, y, t) into $(-x, -y, -t)$.

5.2 Interaction between lump waves and line twin-soliton waves

When $\kappa _{1}\ne 0, \kappa _{2}\ne 0$, solution (33) means the interaction between lump waves and line twin-soliton waves.

Case I: Choosing the same parameters as in (35) except for $\kappa _{2}=0.1$, the interaction solution is shown in Fig. 5.

Case II: When

$$\begin{aligned} \alpha&={1},\quad \gamma ={4},\quad f_{0}=1,\quad \kappa _{1}=0.1,\quad \kappa _{2}=0.1,\nonumber \\ a_{0}&={1},\quad a_{1}={1},\quad a_{2}={2.5},\quad \mathbf {\lambda }=0, \end{aligned}$$

(36)

the interaction solution is shown in Fig. 6.

Figures 5 and 6 hold up interaction between lump waves and line twin-soliton waves. As shown in Fig. 5a, d and c, f, the lump wave turns to tangle with one of the soliton and then begins to be swallowed by ones until to be vanish with $t\rightarrow -\,\infty$ or $t\rightarrow +\,\infty$. When time comes $t=0$ in Fig. 5b, e, the lump appears with arriving its peak. The identical phenomena can be acquired in Fig. 6 based on different parameters.

6 Conclusions and discussions

In this work, gCDGKS Eq. (1) has been investigated. Based on the Hirota bilinear form of Eq. (1) and vector symbolic computations, we have obtained lump solutions (14) and interaction solutions (33). Firstly, we have provided the Hirota bilinear form of Eq. (1) and defined a type of interaction solutions (7) and given its special case (8) for Eq. (1). Then, we have indicated that interaction solutions (8) reduce to the lump waves for $\kappa _{1}=\kappa _{2}=0$ and provided the lump solutions for Eq. (1). Next, soliton solutions have been found by Hirota bilinear method. Moreover, we have calculated interaction solutions (33) based on $\mathbf {a}\cdot \mathbf {b}=0$ and analyzed the interaction phenomena between lump wave and solitary wave. In order to analyze the dynamical behaviors of these solutions (include lump waves, soliton waves, interaction solutions between lump solutions and one stripe soliton or a pair of resonance stripe solitons), we have drawn six figures with Figs. 1, 2, 3, 4, 5 and 6 under some free parameters. In this work, it is necessary to note that the dimension M of these vector can be took as 3 or some other positive integer, not just for 2. Finally, we need to emphasize that the prominent approach we employ still adapt to find some other classes of lump and interaction solutions for other models well. In the near future, more works remain to be solved for the nonlinear evolution equations in the fields of mathematical physics and engineering.