1 Introduction

It is well known that the nonlinear partial differential equations play an important role in the understanding of many nonlinear phenomena. The nonlinear partial differential equations have been investigated in many fields. The study of nonlinear partial differential equations often appears in many subjects as mathematical models. Such as quantum mechanics, heat transfer [1,2,3], mass transfer, fluid mechanics [4], nanoliquids [5,6,7,8,9,10,11], biological mathematics [12] and so on.

Recently, the interaction solutions have attracted much more attention and have already obtained many good results [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Among them, the interaction between lump and line soliton is one of the hot spot. In Ref. [16], Fokas and Pogrebkov investigated the collision of lump and line soliton in the Kadomtsev–Petviashvili I (KPI) equation, which leads to a new excitation phenomena: fusion of lumps and line solitons into line solitons. After interaction, the lumps completely immerse into the line solutions, the original solutions convert from lump–line soliton to line soliton. Thus energy transfer occurs between the lumps and line solitons in this process. In Ref. [14, 15], the authors also discussed the interaction between lumps and line solutions in the KPI equation. However, the lumps still coexist with the line solution without any changes in shapes, amplitudes, velocities after the interaction. In the process of this type of collision, there is no energy transfer between the lumps and line solitons. Very recently, Rao et al. [18] investigated the interaction of lumps and dark–dark solitons in the multi-component long-wave–short-wave resonance interaction system and exhibited various collision phenomena not been shown before, such as fusion of multi-lump into multi-soliton, fission of multi-lump from multi-soliton, partial fusion and so on.

As the \((3+1)\)-dimensional systems also play an important role in physical systems, we consider interaction between high-order lumps and line solitons in \((3+1)\)-dimensional systems. In this paper, we consider a \((3+1\))-dimensional nonlinear evolution equation (\((3+1)\)-d NEE)

$$\begin{aligned} \begin{aligned}&3q_{xz}-(2q_{t}+q_{xxx}-2qq_{x})_{y}+2(q_{x}\,\partial _{x}^{-1}q_{y})_{x}=0. \end{aligned}\!\!\!\!\nonumber \\ \end{aligned}$$
(1)

The \((3+1)\)-d NEE (1) was first introduced by Geng in the study of the algebraic geometrical solutions [28] and could be decomposed into systems of solvable ordinary differential equations with the help of the \((1+1)\)-dimensional AKNS equation. Geng and Ma studied the N-soliton solutions of the \((3+1)\)-d NEE [29]. Wazwaz [30,31,32] established the multiple soliton solutions and a variety of traveling wave solutions of the \((3+1)\)-d NEE (1). Rogue wave and some other soliton solutions were studied in Ref. [33,34,35,36]. Since the \((3+1)\)-d NEE (1) possesses the integrable properties as other integrable systems, such as possessing various kind of soliton solutions, the \((3+1)\)-d NEE is integrable. In Ref. [33, 36], the authors studied collision of first-order lump and line solitons in the \((3+1)\)-d NEE (1). They first assume the \((3+1)\)-d NEE (1) has the following solution

$$\begin{aligned} \begin{aligned} q=&-(3\log \,f)_{xx}, \end{aligned} \end{aligned}$$
(2)

with

$$\begin{aligned} \begin{aligned} f&=(a_1x+b_1y+c_1z+e_1t+k_1)^2\\&\qquad +(a_2x+b_2y+c_2z+e_2t+k_2)^2+a_0\\&\qquad +{\mathrm{e}}^{a_3x+b_3y+c_3z+e_3t+k_3}, \end{aligned} \end{aligned}$$
(3)

then substitute Eq. (2) into the \((3+1)\)-d NEE (1) and collect the power orders of \(x^{m_1}y^{m_2}t^{m_3}z^{m_4}\,(m_i\ge 0)\) and obtain a series of bilinear equations at the ascending power orders of \(x^{m_1}y^{m_2}t^{m_3}z^{m_4}\). Finally, by solving these bilinear equations with the aid of symbolic computation Maple, the values of \(a_i,b_i,c_i,e_i,k_i\) are obtained. The solution (2) exhibits the interaction phenomena of a lump fusing into a line soliton. This direct method has been applied to derive the solutions consisting of one lump and one or two line solitons to lots of nonlinear equations. However, solution describing collision of high-order lumps and line solitons cannot be obtained by this direct method, because the initial tau function f given by Eq. (3) cannot be defined in a solvable form. Until now, the solution illustrating fission and fusion collision of high-order lumps and line solitons for the \((3+1)\)-d NEE (1) has not been studied before.

The \((3+1)\)-d NEE (1) has strong relationship with the famous Kortewege–de Vries (KdV) equation. The KdV equation may be given as

$$\begin{aligned} \begin{aligned}&u_{t^{\prime }}-6u\,u_{x^{\prime }}+\,u_{x^{\prime }x^{\prime }x^{\prime }}=0\,.\\ \end{aligned} \end{aligned}$$
(4)

Taking the variable transformation

$$\begin{aligned} u(x^{\prime },t^{\prime })\rightarrow q(x,t),\quad x^{\prime }\rightarrow \frac{1}{\sqrt{3}}x,\quad t^{\prime }\rightarrow \frac{1}{6\sqrt{3}}t, \end{aligned}$$

the KdV Eq. (4) becomes the main part of the \((3+1)\)-d NEE (1) \(2q_{t}+q_{xxx}-2qq_{x}\). Thus the \((3+1)\)-d NEE (1) may be applied to model shallow water waves and short waves in nonlinear dispersive models as the KdV equation.

In this paper, we mainly focus on multiple dark soliton and the collision of high-order lumps and line solitons in the \((3+1)\)-d NEE (1). The outline of the paper is organized as follows. In Sect. 2, we obtain the multiple dark soliton solutions in determinant form to the \((3+1)\)-d NEE (1). In Sect. 3, we derive families of semi-rational solutions to the \((3+1)\)-d NEE (1) and analyze typical dynamics of the collision between lumps and line solitons in the \((3+1)\)-d NEE (1) in details. Section 4 contains a summary and discussion.

2 Multiple soliton solutions in determinant form

In this section, we will construct multiple soliton solutions to the \((3+1)\)-d NEE (1) in terms of determinant. To this end, we first transform the \((3+1)\)-d NEE (1) into the following bilinear equation

$$\begin{aligned} \begin{aligned} (3D_{x}D_{z}-2D_{y}D_{t}-D_{y}D_{x}^{3})f \cdot f =0, \end{aligned} \end{aligned}$$
(5)

by introducing the dependent variable transformation

$$\begin{aligned} \begin{aligned} q=-(3\log \,f)_{xx}, \end{aligned} \end{aligned}$$
(6)

where f is a real function with respect to variables x, y, z and t, and the operator D is the Hirota’s bilinear differential operator [37, 38] defined by

$$\begin{aligned} \begin{aligned}&P(D_{x},D_{y},D_{t},D_{z})F(x,y,t,z)\cdot G(x,y,t,z)\\&\quad =P(\partial _{x}-\partial _{x^{\prime }},\partial _{y}-\partial _{y^{\prime }}, \partial _{t} -\partial _{t^{\prime }},\partial _{z}\\&\quad \quad -\partial _{z^{\prime }})F(x,y,t,z)\\&\quad \quad G(x^{\prime },y^{\prime },t^{\prime }, z^{\prime })|_{x^{\prime }=x,y^{\prime }=y,t^{\prime }=t,z^{\prime }=z}, \end{aligned} \end{aligned}$$
(7)

and P is a polynomial of \(D_{x}\), \(D_{y}\), \(D_{t}\), \(D_{z}\).

Taking variable transformations

$$\begin{aligned}&x_1=\gamma x,\quad x_2=i\gamma y,\quad x_3=\gamma t,\nonumber \\&x_4=i\gamma z, \quad \gamma =\pm 1, \end{aligned}$$
(8)

and letting \(\tau _0=f\), then the bilinear Eq. (5) is transformed into the following bilinear equation in KP hierarchy

$$\begin{aligned} \begin{aligned} ((D^{3}_{x_{1}} + 2\,D_{x_{3}})\,D_{x_{2}}-3\,D_{x_{1}}\,D_{x_{4}})\tau _{0} \cdot \tau _{0} =0. \end{aligned} \end{aligned}$$
(9)

Based on the sato theory, the bilinear equation in the KP hierarchy

$$\begin{aligned} \begin{aligned} ((D^{3}_{x_{1}} + 2\,D_{x_{3}})\,D_{x_{2}}-3\,D_{x_{1}}\,D_{x_{4}})\tau _{n} \cdot \tau _{n}&=0, \end{aligned} \end{aligned}$$
(10)

has the following tau function [39,40,41,42]

$$\begin{aligned} \begin{aligned} \tau _{n}=\det \limits _{1\le i,j\le N} (m_{ij}^{(n)}), \end{aligned} \end{aligned}$$
(11)

where \(m_{ij}^{(n)}\) is a function of \(x_{-1},\,x_{1},\,x_{2}\) and \(x_{3}\) satisfying the following differential and difference relations

$$\begin{aligned} \begin{aligned} \partial _{x_{1}}m_{ij}^{(n)}&=\psi _{i}^{(n)}\phi _{j}^{(n)},\\ \partial _{x_{2}}m_{ij}^{(n)}&=\psi _{i}^{(n+1)}\phi _{j}^{(n)}+\psi _{i}^{(n)} \phi _{j}^{(n-1)},\\ \partial _{x_{3}}m_{ij}^{(n)}&=\psi _{i}^{(n+2)}\phi _{j}^{(n)}+ \psi _{i}^{(n+1)}\phi _{j}^{(n-1)}+\psi _{i}^{(n)}\phi _{j}^{(n-2)},\\ \partial _{x_{4}}m_{ij}^{(n)}&=\psi _{i}^{(n+3)}\phi _{j}^{(n)}+ \psi _{i}^{(n+2)}\phi _{j}^{(n-1)}+\psi _{i}^{(n+1)}\phi _{j}^{(n-2)}\\&\quad + \psi _{i}^{(n)}\phi _{j}^{(n-3)},\\ m_{ij}^{(n+1)}&=m_{ij}^{(n+1)}+\psi _{i}^{(n)}\phi _{j}^{(n+1)},\\ \partial _{x_{v}}\psi _{i}&=\psi _{i}^{(n+v)},\\ \partial _{x_{v}}\phi _{j}&=-\phi _{j}^{(n-v)}\quad (v=1,2,3,4).\\ \end{aligned} \end{aligned}$$
(12)

Here functions \(\phi _i^{(n)}\) and \(\psi _j^{(n)}\) are also functions of \(x_{-1},\,x_{1},\,x_{2}\) and \(x_{3}\). Note that the bilinear Eq. (10) would reduce to the bilinear Eq. (9) when one takes \(n=0\), namely \(\tau _n=\tau _0\).

In order to derive multiple soliton solutions, we construct functions \(m_{ij}^{(n)},\psi _{i}^{(n)}\) and \(\phi _{j}^{(n)}\) as the following forms:

$$\begin{aligned} \psi ^{(n)}_{i}= & {} p_{i}^{n}{\mathrm{e}}^{\xi _{i}},\\ \phi ^{(n)}_{j}= & {} (-q_{j})^{-n}{\mathrm{e}}^{\eta _{j}},\\ m_{ij}^{(n)}= & {} \delta _{ij}+\frac{1}{p_{i}+q_{j}}\left( -\frac{p_{i}}{q_{j}}\right) ^{n}{\mathrm{e}}^{ \xi _{i}+\eta _{j}}, \end{aligned}$$

with

$$\begin{aligned}&\xi _{i}=p_{i}x_{1}+p_{i}^2x_{2}+p_{i}^{3}x_{3}+p_{i}^{4}x_{4}+\xi _{i0},\\&\eta _{j}=q_jx_{1}-q_{j}^2x_{2}+q_{j}^{3}x_{3}-q_{j}^4x_{4}+\eta _{j0}. \end{aligned}$$

where \(\delta _{ij}=1\) when \(i=j\) and 0 elsewhere, and \(p_i,q_j,\xi _{i0},\eta _{j0}\) are arbitrarily complex constants. Furthermore, one can have

$$\begin{aligned} \begin{aligned} m_{ij}^{(n)*}=m_{ij}^{(-n)},\quad \tau _{n}^{*}=\tau _{-n}, \end{aligned} \end{aligned}$$
(13)

if constraining

$$\begin{aligned} q_j=p_j^*,\quad \xi _{i0}=\eta _{j0}^*. \end{aligned}$$

Hence, one can obtain \(\tau _{0}^{*}=\tau _{0}\), which means function \(\tau _0\) is real. By taking the variable transformations and introducing \(f=\tau _0\), general multiple soliton solutions to the \((3+1)\)-d NEE Eq. (1) is presented by the following theorem.

Theorem 1

The \((3+1)\)-d NEE Eq. (1) has multiple soliton solutions

$$\begin{aligned} \begin{aligned} u=-\,3( \mathrm{log} f)_{xx}, \end{aligned} \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned} f= |\delta _{ij}+\frac{1}{p_i+p_j^*}{\mathrm{e}}^{\xi _i+\xi _j^*}|_{N\times N} \end{aligned} \end{aligned}$$
(15)

with

$$\begin{aligned} \begin{aligned} \xi _{i}&=p_{i}\,x+ip_{i}^{2}\,y+ p_{i}^3\,t\\&\quad +ip_{i}^{4}\,z+\xi _{i0},\,1\le i\le N.\\ \end{aligned} \end{aligned}$$
(16)

Here we have taken \(\gamma =1\), and \(p_{i}\) and \(\xi _{i0}\) are arbitrary complex constants.

Fig. 1
figure 1

(Color online) Dark soliton solution to the \((3+1)\)-d NEE Eq. (1): a dark one soliton solution with parameters \(p_1=1+i,\xi _{10}=0,t=0,z=0\); b dark two solitons solution with parameters \(p_1=1+i,p_2=2+i,\xi _{10}=0,\xi _{20}=0,t=0,z=0\); c dark three solitons solution with parameters \(p_1=\frac{1}{2}+\frac{1}{2}i,p_2=\frac{2}{3}+\frac{2}{3}i,p_3=1-i,\xi _{10}=0,\xi _{20}=0,\xi _{30}=0,t=0,z=0\); d dark four solitons solution with parameters \(p_1=\frac{1}{2}+\frac{1}{2}i,p_2=\frac{2}{3}+\frac{2}{3}i,p_3=1-i,p_4=1+i,\xi _{10}=0,\xi _{20}=0,\xi _{30}=0,\xi _{40}=0,t=0,z=0\);

Full size image

Taking \(N=1\), Theorem 1 yields the following one-soliton solution to the \((3+1)\)-d NEE Eq. (1):

$$\begin{aligned} \begin{aligned} q=\left[ -3\log {\left( 1+\frac{1}{p_1+p_1^*}{\mathrm{e}}^{\xi _1+\xi _1^*}\right) }\right] _{xx}. \end{aligned} \end{aligned}$$
(17)

It is easy to find that the soliton solution is singular when \(p_{1R}<0\) and smooth when \(p_{1R}>0\), where \(p_1=p_{1R}+ip_{1I}\). When \(p_{1R}>0\), the one soliton solution would be rewritten as

$$\begin{aligned} \begin{aligned} q=-\frac{3p_{1R}^2 }{\cosh ^{2}(\widetilde{\xi _1})}, \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \begin{aligned} \widetilde{\xi _1}&=p_{1R}x-p_{1I}y+p_{1R}(p_{1R}^2-3p_{1I}^2)t\\&\qquad -4p_{1R}p_{1I}(p_{1R}^2-p_{1I}^2)+\widetilde{\xi _{10}}, \end{aligned} \end{aligned}$$
(19)

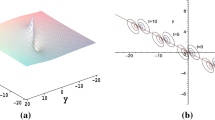
here \(\widetilde{\xi _{10}}\) is the real part of \(\xi _{10}\). The one soliton solution has amplitude \(-\frac{3p_{1R}^2}{2}<0\), thus the solution (18) is dark one soliton. Figure 1a displays the dark one soliton solution with parameters \(p_{1R}=1,p_{1I}=1,\widetilde{\xi _{10}}=0\).

Dark two solitons solution to the \((3+1)\)-d NEE Eq. (1) corresponds to \(N=2\) in Theorem 1:

$$\begin{aligned} \begin{aligned} q=-\,3( \mathrm{log} f)_{xx}, \end{aligned} \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{aligned} f&=\begin{vmatrix} 1+\frac{1}{p_1+p_1^*}{\mathrm{e}}^{\xi _1+\xi _1^*}&\frac{1}{p_1+p_2^*}{\mathrm{e}}^{\xi _1+\xi _2^*}\\ \frac{1}{p_2+p_1^*}{\mathrm{e}}^{\xi _2+\xi _1^*}&1+\frac{1}{p_2+p_2^*}{\mathrm{e}}^{\xi _2+\xi _2^*} \end{vmatrix} \\&=1+{\mathrm{e}}^{\xi _1+\xi _1^*+\rho _1}+{\mathrm{e}}^{\xi _2+\xi _2^*+\rho _2}\\&\quad +r{\mathrm{e}}^{\xi _1+ \xi _1^*+\rho _1+\xi _2+\xi _2^*+\rho _2}, \end{aligned} \end{aligned}$$
(21)

with

$$\begin{aligned} \begin{aligned} \xi _j&=p_{j}\,x+ip_{j}^{2}\,y+ p_{j}^3\,t+ip_{j}^{4}\,z+ \xi _{j0},{\mathrm{e}}^{\rho _j}\\&=\frac{1}{p_j+p_j^*},j=1,2,\\ r&=1-\frac{(p_1+p_1^*)(p_2+p_2^*)}{(p_1+p_2^*)(p_1^*+p_2)} \end{aligned} \end{aligned}$$
(22)

when \(r>0\), the dark two soliton is nonsingular. Figure 1b displays the dark two solitons solution with parameters \(p_1=1+i,p_2=2+i,\xi _{i0}=0,\xi _{20}=0\). When \(r=0\), the dark two solitons solution corresponds to resonant dark two soliton. However, the relation \(1-\frac{(p_1+p_1^*)(p_2+p_2^*)}{(p_1+p_2^*)(p_1^*+p_2)}=0\) (i.e., \(r=0\)) does not admit any solutions \(p_1,p_2\), thus resonant dark two soliton does not exist in the \((3+1)\)-d NEE Eq. (1). We also checked that dark two soliton bound state does not exist in the \((3+1)\)-d NEE Eq. (1).

With larger N, Theorem 1 yields dark N-soliton solution to the \((3+1)\)-d NEE Eq. (1). As multiple soliton solutions in the \((3+1)\)-d NEE Eq. (1) have been investigated in details in Ref. [28,29,30,31,32], we only show multiple soliton up to four solitons. Figure 1c, d illustrate dark three and four solitons with \(N=3,4\), respectively.

3 The semi-rational solutions of \((3+1)\)-d NEE equation

In this section, we will obtain semi-rational solutions to the \((3+1)\)-d NEE Eq. (1). To this end, we first construct semi-rational tau function \(\tau _n\) (11) to the bilinear Eq. (10), and select the following functions \(m_{ij}^{(n)},\psi _{i}^{(n)}\) and \(\phi _{j}^{(n)}\)

$$\begin{aligned} \begin{aligned} \psi ^{(n)}_{i}&=A_{i}p_{i}^{n}{\mathrm{e}}^{\xi _{i}},\\ \phi ^{(n)}_{j}&=B_{j}(-q_{j})^{-n}{\mathrm{e}}^{\eta _{j}},\\ m_{ij}^{(n)}&=A_{i}B_{j}\left[ \delta _{ij}+\frac{1}{p_{i}+q_{j}}\left( - \frac{p_{i}}{q_{j}}\right) ^{n}{\mathrm{e}}^{\xi _{i}+\eta _{j}}\right] , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} A_{i}&=\sum \limits _{k=0}^{n_{i}} c_{ik}(\partial _{p_{i}})^{n_{i}-k},\qquad B_{j}=\sum \limits _{l=0}^{n_{j}} d_{jl}(\partial _{q_{j}})^{n_j-l},\\ \xi _{i}&=p_{i}x_{1}+p_{i}^{2}x_{2}+p_{i}^{3}x_{3}+p_{i}^{4}x_{4},\\ \eta _{j}&=q_{i}x_{1}-q_{i}^{2}x_{2}+q_{i}^{3}x_{3}-q_{i}^{4}x_{4}. \end{aligned}$$

For simplicity, the matrix elements \(m_{ij}^{(n)}\) in Eq. (11) can be rewritten as

$$\begin{aligned} \begin{aligned} m_{i,j}^{(n)}&={\mathrm{e}}^{\xi _{i}+\eta _{j}}\left( -\frac{p_{i}}{q_{j}}\right) ^{n} \sum _{k=0}^{n_{i}}c_{ik}\left( \partial _{p_{j}}+\xi ^{\prime }\right. \\&\quad \left. + \frac{n}{p_i}\right) ^{n_{i}-k}\sum _{l=0}^{n_{j}}d_{jl} \left( \partial _{q_{j}}+\eta ^{\prime }-\frac{n}{q_j}\right) ^{n_{j}-l}\\&\qquad \frac{1}{p_{i}+q_{j}} + \delta _{ij}c_{in_{i}}d_{jn_{j}}, \end{aligned} \end{aligned}$$
(23)

where

$$\begin{aligned} \xi _{i}^{\prime }&=x_{1}+2p_{i}x_{2}+3p_{i}x_{3}+4p_{i}^{3}x_{4},\\ \eta _{j}^{\prime }&=x_{1}-2q_{j}x_{2}+3q_{j}^{2}x_{3}-4q_{j}^3x_{4}. \end{aligned}$$

here \(p_{i}\), \(q_{}j\), \(c_{ik},d_{jl}\) are arbitrary complex constants, and i, j, \(n_{i}\), N are arbitrary positive integers. Again, it is easy to obtain the following relation

$$\begin{aligned} \begin{aligned} m_{ij}^{(n)*}=m_{ij}^{(-n)},\quad \tau _{n}^{*}=\tau _{-n}, \end{aligned} \end{aligned}$$
(24)

under parametric constraint condition

$$\begin{aligned} q_j=p_j^*,\quad \xi _{i0}=\eta _{j0}^*. \end{aligned}$$

Furthermore, taking variable transformations (2) and defining \(f=\tau _0\), semi-rational solutions to the \((3+1)\)-d NEE Eq. (1) can be presented in the following theorem.

Theorem 2

The \((3+1)\)-d NEE Eq. (1) has semi-rational solutions

$$\begin{aligned} \begin{aligned} u=-\,3( \mathrm{log} f)_{xx},\\ \end{aligned} \end{aligned}$$
(25)

where

$$\begin{aligned} \begin{aligned} f= \det \limits _{1\le i,j\le N}(m_{i,j}),\\ \end{aligned} \end{aligned}$$
(26)

and the matrix elements \(m_{ij}\) are defined by

$$\begin{aligned} \begin{aligned} m_{i,j}&={\mathrm{e}}^{\xi _{i}+\xi _{j}^{*}}\left( \sum _{k=0}^{n_{i}}c_{ik}( \partial _{p_{i}}+\xi _{i}^{\prime })^{n_{i}-k}\right. \\&\qquad \left. \times \sum _{l=0}^{n_{j}}c_{jl}^{*}( \partial _{p_{j}^{*}}+\xi _{j}^{\prime *})^{n_{j}-l}\right) \frac{1}{p_{i}+p_{j}^{*}}\\&\qquad +\delta _{ij}c_{in_{i}}c^*_{jn_{j}}, \end{aligned} \end{aligned}$$
(27)

with

$$\begin{aligned} \begin{aligned}&\xi _{i}=\gamma p_{i}\,x+i\gamma \,p_{i}^{2}\,y+\gamma p_{i}^3\,t+i\gamma \,p_{i}^{4}\,z+\xi _{i0}.\\&\xi _{i}^{\prime }=\gamma p_{i}\,x+2\,i\gamma \,p_{i}\,y+3\gamma p_{i}^2\,t+4\,i\gamma p_{i}^{3}\,z. \end{aligned} \end{aligned}$$
(28)

Here \(i,j,n_{i},n_{j}\) are arbitrary positive integers, \(p_{i}\) and \(\xi _{i0}\) are arbitrary complex constants.

These semi-rational solutions demonstrate collision of lumps and line solitons, which could reveal two different types of excitation phenomena: fusion of lumps and line solitons into line solitons, and fission of line solitons into lumps and line solitons. Below, we consider dynamical features of the fission and fusion collision of lumps and line solitons in the details.

Fig. 2
figure 2

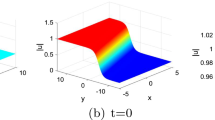
(Color online) The time evolution of semi-rational solution q (32) with parameters \(\gamma =1,\alpha =1,\beta =0,a=1,b=0,\xi _{10}=0,z=0\), which describes fusion of a lump and a line soliton into a line soliton

Full size image
Fig. 3
figure 3

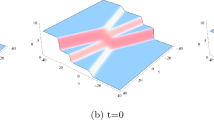
(Color online) The time evolution of semi-rational solution q (32) with parameters \(\gamma =-\,1,\alpha =1,\beta =0,a=1,b=0,\xi _{10}=0,z=0\), which describes fission of a line soliton into a lump and a line soliton

Full size image

3.1 The fission and fusion collision of one lump and one soliton

The collision of one lump and one line soliton is described by the fundamental semi-rational solutions (25) (i.e., first-order semi-rational). Taking \(N=1,\,n_{i}=1\) in Theorem 2, the fundamental semi-rational solutions of the \((3+1)\)-d NEE (1) can be given as the following form

$$\begin{aligned} \begin{aligned}&q=-(3\log {f})_{xx}, \end{aligned} \end{aligned}$$
(29)

with

$$\begin{aligned} \begin{aligned} f&={\mathrm{e}}^{\xi _1+\xi _1^*}\left( \sum _{k=0}^{1}c_{1k}(\partial _{p_{1}}+ \xi _{1}^{\prime })^{1-k}\sum _{l=0}^{1}c_{1l}^{*}(\partial _{p_{1}^{*}}+ \xi _{1}^{\prime *})^{1-l} \right) \\&\qquad \frac{1}{p_{1}+p_{1}^{*}}+\delta _{11}c_{11}c^*_{11},\\&={\mathrm{e}}^{\xi _1+\xi _1^*}(\partial _{p_{1}}+\xi ^{\prime }_{1}+c_{11})( \partial _{p^{*}_{1}}+\xi _{1}^{\prime *}+c^{*}_{11})\frac{1}{p_{1}+p_{1}^{*}}\\&\quad +\delta _{11}c_{11}c_{11}^*,\\&=\frac{{\mathrm{e}}^{\xi _1+\xi _1^*}}{p_{1}+p_{1}^{*}}\left[ (\xi _{1}^{\prime }\right. \\&\quad - \frac{1}{p_{1}+p_{1}^{*}}+c_{11})\left( \xi _{1}^{\prime *}-\frac{1}{p_{1}+p_{1}^{*}}+c_{11}^{*}\right) \\&\quad +\left. \frac{1}{(p_{1}+p_{1}^{*})^{2}}\right] +\delta _{11}c_{11}c_{11}^*, \end{aligned} \end{aligned}$$
(30)

where

$$\begin{aligned} \begin{aligned}&\xi _{1}=\gamma p_{1}\,x+i\gamma \,p_{1}^{2}\,y+\gamma p_{1}^3\,t+i\gamma \,p_{1}^{4}\,z+\xi _{10}.\\&\xi _{1}^{\prime }=\gamma p_{1}\,x+2\,i\gamma \,p_{1}\,y+3\gamma p_{1}^2\,t+4\,i\gamma p_{1}^{3}\,z, \end{aligned} \end{aligned}$$
(31)

and \(p_{1},c_{11},\xi _{10}\) are arbitrary complex parameters. We assume \(p_{1}=a+ib,c_{11}=1\) and then rewrite the above solutions as

$$\begin{aligned} \begin{aligned} q=6\frac{(l_1^2-l_2^2-l_0)+h}{(l_1^2+l_2^2+l_0+2\delta _{11}a {\mathrm{e}}^{-\xi _1-\xi _1^{*}})^2}, \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} l_1&=\gamma x-2b\gamma y+3(a^2-b^2)\gamma t\\&\qquad +4b(b^2-3a^2)\gamma z-\frac{1}{2\alpha }+1, \\ l_2&=2a\gamma y+6ab\gamma y+4a(a^2-3b^2)\gamma z,\\ h&=-\,2a[2a^{2}(l_{1}^{2}+l_{2}^{2}+l_{0})+4al_{1}+1]\delta _{11}\,{\mathrm{e}}^{-\xi _{1}-\xi _{1}^{*}}. \end{aligned} \end{aligned}$$
(33)

The semi-rational solution q defined in (29) has two different dynamic behaviors determined by the choices of the parameter \(\gamma =1\) or \(\gamma =-\,1\).

  1. (i)

    Fusion. When \(\gamma =1\), the corresponding solution q describes fusion of a lump and a line soliton into a line soliton. As shown in Fig. 2, the solution q first describes propagation of a line soliton and a lump when \(t\rightarrow -\,\infty \) (see the panel at \(t=-\,5\)). In the intermediate time, the lump immerses into the line soliton gradually (see the panels at \(t=-\,1,0\)). When \(t\rightarrow +\,\infty \), the solution q only behaves as a line soliton (see the panel at \(t=5\)). In this process, the lump gets annihilated into the line soliton.

  2. (ii)

    Fission. When \(\gamma =-\,1\), the corresponding solution q describes fission of a line soliton into a lump and a line soliton, which is opposite to the case when \(\gamma =1\). The solution is illustrated in Fig. 3. It is seen that the solution q only consists of a line soliton when \(t\rightarrow -\,\infty \) (see the panel at \(t=-\,5\)) and comprises of a lump and a line soliton when \(t\rightarrow +\,\infty \) (see the panel at \(t=5\)). In this process, a lump gets created from the line soliton.

Fig. 4
figure 4

(Color online) The time evolution of multi-semi-rational solution q (34) with parameters \(\gamma =1,p_1=\frac{4}{5},p_2=\frac{3}{4},\xi _{10}=0,z=0\), which describes fusion of two solitons and two lumps into two solitons

Full size image

3.2 The fission and fusion collision of N solitons and N lumps

The fission and fusion collision of N solitons \(\,(N \ge 2)\) and N lumps in the \((3+1)\)-d NEEs (1) are featured by the multi-semi-rational solutions. Taking \(N>1,n_{i}=1\), we can obtain multi-semi-rational solutions to the \((3+1)\)-d NEEs (1) by employing the results of Theorem 1. The multi-semi-rational solutions describe the process of fusion of N lumps and N line solitons into N line solitons or fission of N line solitons into N lumps and N line solitons, which correspond to the parameter choice of \(\gamma =-\,1\) or \(\gamma =1\). For example, setting \(N=2,n_1=n_2=1\) in Theorem 1 yields the following explicit form of the second-order semi-rational solutions

$$\begin{aligned} q=-\left( \mathrm{3log} \left( \begin{vmatrix} m_{11}&m_{12} \,\\ m_{21}&m_{22} \end{vmatrix}\right) \right) _{xx}, \end{aligned}$$
(34)

where \(m_{ij}=\frac{{\mathrm{e}}^{\xi _i+\xi _j^*}}{p_{i}+p_{j}^{*}}[(\xi _{i}^{\prime }-\frac{1}{p_{i}+p_{j}^{*}}+c_{i1})(\xi _{j}^{\prime *}-\frac{1}{p_{i}+p_{j}^{*}}+c_{j1}^{*}) +\frac{1}{(p_{i}+p_{j}^{*})^{2}}]+\delta _{ij}c_{i1}c_{j1}^*\), and \(\xi _i\) and \(\xi _i^{\prime }\) are defined in (28). The corresponding solution q also has two different dynamical behaviors:

  1. 1.

    Fusion of two line solitons and two lumps into two line solitons when \(\gamma =1\). The corresponding solution in this case is demonstrated in Fig. 4. As can be seen that the solution q consists of two line solitons and two lumps when \(t\rightarrow -\,\infty \) (see the panel at \(t=-\,10\)). In the intermediate time, these two lumps immerse into the two line solitons (see the panels at \(t=0,3\)). When \(t\rightarrow +\,\infty \), the original two line solitons and two lumps combine into two line solitons (see the panel at \(t=10\)). In this process, the original two lumps get annihilated by the two line solitons.

  2. 2.

    Fission of two line solitons into two lumps and two line solitons when \(\gamma =-\,1\). In this case, the solution q describes an opposite process to the case of \(\gamma =1\), the corresponding solution is shown in Fig. 5. It is seen that the solution only composes of two line solitons when \(t\rightarrow -\,\infty \) and consists of two line solitons and two lumps when \(t\rightarrow +\,\infty \). In a word, the ultima two lumps get created from the two line solitons.

Fig. 5
figure 5

(Color online) The time evolution of multi-semi-rational solution q (34) with parameters \(\gamma =-\,1,p_1=\frac{4}{5},p_2=\frac{3}{4},\xi _{10}=0,z=0\), which describes fission of two solitons into two lumps and two solitons

Full size image
Fig. 6
figure 6

(Color online) The time evolution of semi-rational solution q (35) with parameters \(\gamma =1,p_1=1,\xi _{10}=0,z=0\), which describes fusion of two lumps and one soliton into one soliton

Full size image

3.3 The fission and fusion collision of \(n_1\) lumps and one soliton

The fission and fusion collision of \(n_1\) lumps \((n_1\ge 2)\) and one soliton are described by the higher-order rational solutions. Taking \(N=1,n_1>1\) in Theorem 1, we can generate higher-order semi-rational solutions to the \((3+1)\)-d NEEs (1). This subclass of non-fundamental semi-rational solutions describe the process \(n_1\) lumps fusing into a single line soliton or \(n_1\) lumps fissuring from a single line soliton corresponding to the parameter choices of \(\gamma =1\) or \(\gamma =-\,1\). For example, by setting \(N=1,n_{1}=2\) in Theorem 1, the second-order semi-rational solution can be obtained from Eq. (26) as

$$\begin{aligned} \begin{aligned} q=-(3\log {f})_{xx}, \end{aligned} \end{aligned}$$
(35)

where

$$\begin{aligned} \begin{aligned} f&={\mathrm{e}}^{\xi _1+\xi _1^*}[(\partial _{p_{1}}+\xi ^{\prime }_{1})^{2}+c_{12}][( \partial _{p^{*}_{1}}+\xi ^{\prime *}_{1})^{2}\\&\quad +c^{*}_{12}]\frac{1}{p_{1}+p^{*}_{1}}+ \delta _{11}c_{12}c_{12}^*, \end{aligned} \end{aligned}$$
(36)

where \(\xi _1,\xi _{1}^{\prime }\) are defined in Eq. (28), \(p_{1}, c_{12},\xi _{10}\) are a free complex parameters. Here we have taken \(c_{10}=1,c_{11}=0\) in Eq. (25). The solution q also have two opposite dynamics behaviors:

  1. (i)

    Fusion of two lumps and one soliton into one soliton. When \(\gamma =1\), the corresponding solution describes the process of two lumps fusing into a line soliton, see Fig. 6. In this situation, the solution first consist of two lumps and a line soliton as \(t\rightarrow -\,\infty \) (see the panel at \(t=-\,7\)). In the intermediate time, these two lumps immerse into the line soliton gradually (see the panels at \(t=0,2\)). At larger time, the two lumps disappear into the single line soliton, and the solution only describes a single line soliton propagating on the constant background (see the panel at \(t=7\)). In this process, two lumps get annihilated by the single line soliton.

  2. (ii)

    Fission of one soliton into two lumps and one line soliton. When \(\gamma =-\,1\), the corresponding solution describes the process of two lumps fissuring from a line soliton, see Fig. 7. As can be seen that, the solution first describes a line soliton propagating on the constant background when \(t\ll 0\) (see the panel at \(t=-\,7\)). In the intermediate time, two lumps form on the line soliton and then separate from the line soliton (see the panel at \(t=0,3\)). When \(t\gg 0\), the corresponding solution consists of two lumps and a line soliton (see the panel at \(t=7\)). In this process, two lumps get produced from the single line soliton.

Fig. 7
figure 7

(Color online) The time evolution of semi-rational solution q (35) with parameters \(\gamma =-\,1,p_1=1,\xi _{10}=0,z=0\), which describes fission of one soliton into two lumps and one soliton

Full size image
Fig. 8
figure 8

(Color online) The time evolution of semi-rational solution q with parameters \(\gamma =1,p_1=1,\xi _{10}=0,z=0\), which describes fusion of three lumps and a line soliton into a line soliton

Full size image
Fig. 9
figure 9

(Color online) The time evolution of semi-rational solution q with parameters \(n_1=3,\gamma =-\,1,p_1=1,\xi _{10}=0,z=0\), which describes fission of a single line soliton into three lumps and a line soliton

Full size image

For larger \(n_1\), these higher-order semi-rational solutions have qualitatively similar behaviors, except that more localized lumps will fuse into or fissure from a single line soliton corresponding to parameter choice of \(\gamma =1\) or \(\gamma =-\,1\). For example, with \(n_i=3\) and parameter choices \(\gamma =1\) and \(\gamma =-\,1\) are shown in Figs. 8 and 9 respectively. As can be seen that, Fig. 8 demonstrates the process of three lumps getting annihilated by the single line soliton, which corresponds to the parameter \(\gamma =1\), while Fig. 9 illustrates the process of three lumps get produced from the single line soliton corresponding to the parameter \(\gamma =-\,1\).

4 Summary and discussion

In this paper, we obtain multiple dark soliton solutions of any order and families of semi-rational solutions to the \((3+1)\)-d NEE Eq. (1) by exploiting the Hirota’s bilinear method combined with the KP hierarchy reduction method. These semi-rational solutions describe fission and fusion collision of high-order lumps and line solitons, including one lump fusing into or fissure from one line soliton, \(N\,(N\ge 1)\) lumps fusing into or fissuring from N solitons, \(n_1\,(n_1\ge 1)\) lumps fusing into or fissuring from one soliton. After the collision, the lumps would be created or annihilated by the line solitons, which indicate that the energy exchange happens between the lumps and line solitons. It should be emphasized that fission and fusion collision in the\((3+1)\)-d NEE Eq. (1) were investigated in Ref. [33, 36], but they only discussed the collision between one lump and one soliton or two solitons. In this paper, we consider the fission and fusion collisions of lumps of any order and solitons of any order. Besides, the semi-rational solutions in Theorem 1are expressed by determinant form, whose matrix elements are given by simple algebraic expressions. Comparing with earlier results in Ref. [33, 36], our results are more general. The results would be of much importance in understanding collision phenomena of different types of nonlinear waves emerging in nonlinear systems, including water waves, optics, fluid dynamics, Bose–Einstein condensates.