1 Introduction

As a kind of special localized waves, lump waves are rationally decaying solutions in all space directions. The existence of lump waves for the Kadomtsev–Petviashvili (KP) equation was first found by Manakov et al. in Ref. [1]. It has also been found that the interactions of lump waves do not result in a pattern of phase shifts [1]. Subsequently, more general rational solutions of the KP equation were derived in many literature [2,3,4]. Thereafter, researchers have found that many high-dimensional nonlinear partial differential (NLPD) equations also admit lump solutions, such as the Davey–Stewartson II equation [3], the three-dimensional three-wave resonant interaction equation [5] and the Ishimori I equation [6]. In recent years, the subject of lump waves in nonlinear science has attracted particular attention because such waves are regarded as the appropriate prototypes to model rogue wave dynamics in both oceanography [7] and nonlinear optics [8]. Consequently, some methods have been developed to search for exact lump solutions of NPLD equations, like the inverse scattering transformation [4], the Bäcklund transformation [5], the Darboux transformation [6] and the Hirota bilinear method [9,10,11,12,13]. Among them, the Hirota bilinear method plays an important role in the study of lump solutions for NPLD equations.

In this paper, with the Hirota bilinear method, we consider the following (\(2+1\))-dimensional Sawada–Kotera equation [14,15,16,17]

$$\begin{aligned}&u_t-\left( u_{4x}+5uu_{xx}+\frac{5}{3}u^3+5u_{xy}\right) _x-5uu_y\nonumber \\&\quad +\,5\int u_{yy}dx-5u_x\int u_y dx=0, \end{aligned}$$
(1)

where u is a function of the variables x, y and t. When \(u(x,y,t)\equiv u(x,t)\), Eq. (1) reduces to the Sawada–Kotera equation [18]

$$\begin{aligned} u_t-\left( u_{4x}+5uu_{xx}+\frac{5}{3}u^3\right) _x=0. \end{aligned}$$
(2)

Up to now, many integrable properties of Eq. (1) have been studied, like the inverse scattering transform scheme [15], the Bäcklund transformation [16, 17] and the multiple soliton solutions [19].

Under the transformation \(u=6(\ln f)_{xx}\), Eq. (1) becomes the Hirota bilinear equation

$$\begin{aligned} \left( D_x^6-D_x D_t+5D_x^3D_y-5D_y^2\right) f\cdot f=0, \end{aligned}$$
(3)

where the Hirota bilinear derivatives [20] \(D_x\), \(D_t\) and \(D_y\) are defined by

$$\begin{aligned}&D_x^mD_y^kD_t^n\,(f\cdot g) = \left( \frac{\partial }{\partial x} -\frac{\partial }{\partial x'}\right) ^m\left( \frac{\partial }{\partial y} -\frac{\partial }{\partial y'}\right) ^k\nonumber \\&\quad \times \left( \frac{\partial }{\partial t} -\frac{\partial }{\partial t'}\right) ^nf(x,y,t)g(x',y',t')|_{x' = x,y'=y,\, t' =t},\nonumber \\ \end{aligned}$$
(4)

for nonnegative integers m, k and n.

Recently, a kind of generalized bilinear operators with a prime number p has been introduced in Ref. [21] as

$$\begin{aligned}&D_{p,x_1}^{n_1}\ldots D_{p,x_M}^{n_M}\left( f\cdot g\right) \nonumber \\&\quad =\prod _{i=1}^M\!\left( \!\frac{\partial }{\partial x_i} +\alpha \frac{\partial }{\partial x^{\prime }_i}\!\right) ^{n_{i}} f(x_1,\ldots ,x_M)g(x_1^{\prime },\ldots ,x^{\prime }_M) |_{x^{\prime }_1 = x_1,\ldots ,\, x^{\prime }_M=x_M}\nonumber \\&\quad =\prod _{i=1}^M\sum _{\kappa _i=0}^{n_i}\alpha ^{\kappa _i}\left( \begin{array}{c} n_i \\ \kappa _i \end{array} \right) \frac{\partial ^{n_i-\kappa _i}}{\partial x_i^{n_i-\kappa _i}} f(x_1,\ldots ,x_M)\frac{\partial ^{\kappa _i}}{\partial x_i^{\kappa _i}}g(x_1,\cdots ,x_M),\nonumber \\ \end{aligned}$$
(5)

where \(n_1, \ldots , n_M\) are arbitrary nonnegative integers, and for an integer m, the m-th power of \(\alpha \) is determined by

$$\begin{aligned}&\alpha ^m=(-1)^{r(m)},\,\, \mathrm{if}\,\, m \equiv r(m)\nonumber \\&\quad \mathrm{mod}\,\, p \,\,\,\,\mathrm{with}\,\,\, 0 \le r(m) < p. \end{aligned}$$
(6)

The choices for powers in Eq. (6) give a rule to take the signs \(+1\) or \(-1\). Obviously, when \(p=2k\), \(k\in \mathbb {N}\), all above bilinear differential operators are Hirota bilinear operators.

With a prime number p, the Hirota bilinear Eq. (3) can be generalized as

$$\begin{aligned}&\left( D_{p,x}^6-D_{p,x} D_{p,t}\right. \nonumber \\&\quad \left. +\,5D_{p,x}^3D_{p,y}-5D_{p,y}^2\right) f\cdot f=0, \end{aligned}$$
(7)

which is called the (\(2+1\))-dimensional bilinear p-Sawada–Kotera (p-SK) equation. Particularly, for the case of \(p=3\) in Eq. (7), we have the bilinear \(\mathrm{3}\)-SK equation

$$\begin{aligned}&\left( D_{3,x}^6-D_{3,x} D_{3,t}+5D_{3,x}^3D_{3,y}-5D_{3,y}^2\right) f\cdot f\nonumber \\&\quad =2\left( ff_{6x}+10f_{3x}^2\right) -2\left( f_{xt}f-f_x f_t\right) \nonumber \\&\qquad +\,30f_{xx}f_{xy}-10(ff_{yy}-f_y^2)=0. \end{aligned}$$
(8)

Under the transformations \(u=6(\ln f)_x\) and \(v=6(\ln f)_y\), which can be found based on the Bell polynomials theories [22, 23], Eq. (8) is transformed into the following nonlinear differential equation

$$\begin{aligned}&u_t-\Bigg (u_{5x}+uu_{4x}+\frac{5}{2}u_x u_{3x}+\frac{5}{12}u^2u_{3x}+\frac{10}{3}u_{xx}^2\nonumber \\&\quad +\,\frac{10}{3}u u_x u_{xx} +\frac{5}{27}u^3u_{xx}+\frac{5}{12}u_x^3+\frac{5}{8}u^2u_x^2\nonumber \\&\quad +\,\frac{25}{432}u^4u_x+\frac{11}{7776}u^6\Bigg )\nonumber \\&\quad -\,\frac{5}{72}\left( 6u_x+u^2\right) \left( 6u_y+u v \right) +5v_y=0, \end{aligned}$$
(9)

Therefore, if f solves the bilinear Eq. (3) or  (8), then \(u=6(\ln f)_{xx}\) or \(u=6(\ln f)_x\) will solve the nonlinear Eq. (1) or (9).

It is pointed out that the bilinear Eq. (7) for different values of p has the same set of positive quadratic function solutions [see the assumption in Eq. (10)]. Therefore, based on the obtained solutions, lump or lump-type solutions to the corresponding nonlinear p-SK equations can be generated under the dependent transformations.

In the present work, firstly, we will search for positive quadratic function solutions to the (\(2+1\))-dimensional bilinear p-SK Eq. (7). Then, via the dependent transformations, we will derive the lump and lump-type solutions of Eqs. (1) and (9) from the resulting quadratic function solutions. Finally, we will discuss the spatial structures of the lump waves by virtue of the extreme value theory of multivariable functions.

2 Lump solutions to the (\(2+1\))-dimensional Sawada–Kotera Eq. (1) and 3-SK Eq. (9)

In this section, we will construct positive quadratic function solutions of the bilinear Eq. (7) to generate lump solutions of Eqs. (1) and  (9).

To search for quadratic function solutions to the bilinear Eq. (7), we make the following assumption

$$\begin{aligned} f= & {} g^2+h^2+a_9, g=a_1x+a_2y+a_3t+a_4,\nonumber \\ h= & {} a_5x+a_6y+a_7t+a_8, \end{aligned}$$
(10)

where \(a_i\) \((1\le i\le 9)\) are all real parameters to be determined. Note that the function f in Eq. (10) is positive if the parameter \(a_9 > 0\). With the aid of symbolic computation, substituting Eq. (10) into (7) and eliminating the coefficients of the polynomial yield the following three sets of constraining equations on the parameters:

$$\begin{aligned}&\mathrm{I}: \left\{ a_1=a_1,\,\,a_2=a_2,\,\,a_4=a_4,\right. \nonumber \\&\quad a_5=0,\,\,a_6=a_6,\,\,a_8=a_8,\nonumber \\&\left. \quad a_3\quad =\frac{5(a_6^2-a_2^2)}{a_1},\,\,a_7=\frac{-10a_2a_6}{a_1},\,\,a_9=\frac{3a_1^3a_2}{a_6^2}\right\} \nonumber \\ \end{aligned}$$
(11)

with \(a_1a_6\ne 0\) and \(a_1a_2>0\).

$$\begin{aligned}&\mathrm{II}: \left\{ a_1=a_1,\,\,a_2=a_2,\,\,a_3=0\right. \nonumber \\&\qquad a_4=a_4,\,\,a_6=a_6,\,\,a_8=a_8,\nonumber \\&\qquad a_5=\frac{a_1(a_6^2-a_2^2)}{2a_2a_6},\,\,a_7=\frac{-10a_2a_6}{a_1},\nonumber \\&\left. \qquad a_9=\frac{3a_1^3(a_2^2+a_6^2)^3}{8a_2^5a_6^2}\right\} \end{aligned}$$
(12)

with \(a_1a_2a_6\ne 0\) and \(a_1a_2>0\).

$$\begin{aligned}&\mathrm{III}: \left\{ a_1=a_1,\,\,a_2=a_2,\right. \nonumber \\&\quad a_3=-\frac{5\left[ 2a_2a_5a_6+a_1\left( a_2^2-a_6^2\right) \right] }{a_1^2+a_5^2},\nonumber \\&\quad a_4=a_4,\,\,a_5=a_5,\nonumber \\&\quad a_7=-\frac{5\left( a_5a_6^2-a_2^2a_5+2a_1a_2a_6\right) }{a_1^2+a_5^2},\nonumber \\&\quad a_6=a_6,\,\,a_8=a_8,\nonumber \\&\left. \quad a_9=\frac{3\left( a_1^2+a_5^2\right) ^2(a_1a_2+a_5a_6)}{(a_2a_5-a_1a_6)^2}\right\} \end{aligned}$$
(13)

with \(a_1a_5\ne 0\), \(a_2a_5-a_1a_6\ne 0\) and \(a_1a_2+a_5a_6>0\).

Through the dependent variable transformation \(u=6(\ln f)_{xx}\), substituting Eqs. (11)–(13) into Eq. (10), respectively, we present three families of lump solutions for the (\(2+1\))-dimensional Sawada–Kotera Eq. (1)

$$\begin{aligned} u^{\mathrm{(I)}}= & {} \frac{12 a_1^2 \left\{ \left( a_6y -\frac{10 a_2 a_6}{a_1}t+a_8\right) ^2-\left[ a_1 x+a_2 y+\frac{5 \left( a_6^2-a_2^2\right) }{a_1}t+a_4\right] ^2+\frac{3a_2a_1^3}{a_6^2}\right\} }{\left\{ \left[ a_1 x+a_2 y+\frac{5 \left( a_6^2-a_2^2\right) }{a_1}t+a_4\right] ^2+\left( a_6 y-\frac{10 a_2a_6 }{a_1}t+a_8\right) ^2+\frac{3 a_2 a_1^3}{a_6^2}\right\} ^2}, \end{aligned}$$
(14)
$$\begin{aligned} u^{\mathrm{(II)}}= & {} \frac{3a_1^2\left\{ \frac{\left( a_2^2+a_6^2\right) ^2}{a_2^2a_6^2}f-2\left[ \frac{a_1 \left( a_2^2+a_6^2\right) ^2 }{2 a_2^2 a_6^2}x+\frac{a_6^2+a_2^2}{a_2} y+\frac{10 \left( a_2^2-a_6^2\right) }{a_1}t+2 a_4+\frac{a_8\left( a_6^2- a_2^2\right) }{a_2a_6}\right] ^2\right\} }{f^2}, \end{aligned}$$
(15)

where f is defined in Eq. (10)

$$\begin{aligned} f= & {} \left( a_1 x+a_2 y+a_4\right) ^2\\&+\left[ \frac{a_1 \left( a_6^2-a_2^2\right) }{2 a_2 a_6}x+a_6 y-\frac{10 a_2 a_6 }{a_1}t+a_8\right] ^2\\&+\frac{3 a_1^3 \left( a_2^2+a_6^2\right) ^3}{8 a_2^5 a_6^2}, \end{aligned}$$

and

$$\begin{aligned} u^{\mathrm{(III)}}= & {} \frac{12}{f^2}\left\{ \left( a_1^2+a_5^2\right) f-2 \left[ \left( a_1^2+a_5^2\right) x\right. \right. \nonumber \\&\left. \left. +(a_1a_2+a_5a_6)y-\tau t+a_1a_4+a_5a_8\right] ^2\right\} ,\nonumber \\ \end{aligned}$$
(16)

where \(\tau =\frac{20a_1a_2a_5a_6+5\left( a_6^2-a_2^2\right) (a_5^2-a_1^2)}{a_1^2+a_5^2}\) and

$$\begin{aligned}&f=\left[ a_1 x+a_2 y-\frac{5 \left( 2 a_2 a_5 a_6+a_1 \left( a_2^2-a_6^2\right) \right) }{a_1^2+a_5^2}t+a_4\right] ^2\nonumber \\&\quad ~~~~ +\left[ a_5 x+a_6 y-\frac{5 \left( -a_5 a_2^2+2 a_1 a_6 a_2+a_5 a_6^2\right) t}{a_1^2+a_5^2}+a_8\right] ^2\nonumber \\&\quad ~~~~~+\,\frac{3 \left( a_1 a_2+a_5 a_6\right) \left( a_1^2+a_5^2\right) {}^2}{\left( a_2 a_5-a_1 a_6\right) {}^2}. \end{aligned}$$
(17)

Through the transformation \(u=6(\ln f)_{x}\), we also present three families of lump solutions for the (\(2+1\))-dimensional nonlinear Eq. (9)

$$\begin{aligned} u^{\mathrm{(I)}}= & {} \frac{12 a_1 \left[ a_1 x+a_2 y+\frac{5 \left( a_6^2-a_2^2\right) }{a_1}t+a_4\right] ^2}{\left[ a_1 x+a_2 y+\frac{5 \left( a_6^2-a_2^2\right) }{a_1}t+a_4\right] ^2+\left( a_6 y-\frac{10 a_2a_6 }{a_1}t+a_8\right) ^2+\frac{3 a_2 a_1^3}{a_6^2}}, \end{aligned}$$
(18)
$$\begin{aligned} u^{\mathrm{(II)}}= & {} \frac{6a_1\left[ \frac{a_1 \left( a_2^2+a_6^2\right) ^2 }{2 a_2^2 a_6^2}x+\frac{a_6^2+a_2^2}{a_2} y+\frac{10 \left( a_2^2-a_6^2\right) }{a_1}t+2 a_4+\frac{a_8\left( a_6^2- a_2^2\right) }{a_2a_6}\right] }{\left( a_1 x+a_2 y+a_4\right) ^2+\left[ \frac{a_1 \left( a_6^2-a_2^2\right) }{2 a_2 a_6}x+a_6 y-\frac{10 a_2 a_6 }{a_1}t+a_8\right] ^2+\frac{3 a_1^3 \left( a_2^2+a_6^2\right) ^3}{8 a_2^5 a_6^2}}, \end{aligned}$$
(19)

and

$$\begin{aligned} u^{\mathrm{(III)}}= & {} \frac{12}{f}\left[ \left( a_1^2+a_5^2\right) x \right. \nonumber \\&\left. +\,(a_1a_2+a_5a_6)y-\tau t+a_1a_4+a_5a_8\right] , \end{aligned}$$
(20)

where \(\tau \) and f have been defined in Eq. (17).

Fig. 1
figure 1

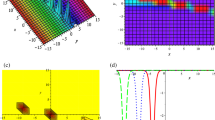
Spatial structure of the bright lump wave via the solution (14) with \(t=0\). The related parameters are, respectively, chosen as: \(a_1=1\), \(a_2=2\), \(a_4=0\), \(a_6=3\) and \(a_8=0\)

Full size image

3 Spatial structures of lump waves in Eqs. (1) and (9)

Obviously, the above-presented solution (14) has five involved parameters of \(a_1\), \(a_2\), \(a_4\), \(a_6\) and \(a_8\). If the conditions \(a_1a_6\ne 0\) and \(a_1a_2>0\) are satisfied, the quadratic function f in Eq. (10) is positive and the solution (14) is analytical and local in all space directions. Without loss of generality, we take \(a_4=a_8=0\) in solution (14). For this case, according to the extreme value theory of functions, we find that the solution (14) has three extreme value points (0, 0), \((\pm \frac{\sqrt{a_1a_2}}{a_6},0)\) on the xy-plane. The peak of the lump wave is located at the maximum point (0, 0), and two valleys are located at the minimum points \((\pm \frac{\sqrt{a_1a_2}}{a_6},0)\). The centers of the peak and valleys lie in the straight line \(y=0\) on the xy-plane, and the two valleys are symmetric with respect to the peak. Figure 1 displays the spatial structure of the lump wave, which has a peak and two valleys and algebraically decays in all space directions. Because the height of the peak is larger than the depths of the valley bottoms, the solution (14) can be called the bright lump wave solution. By a direct computation, it can be found that the amplitude of the peak is eight times as the depths of the valleys in the lump wave solution (14).

Fig. 2
figure 2

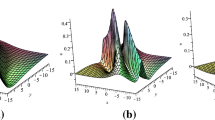
Spatial structure of the bright–dark lump wave via the solution (15) with \(t=0\). The related parameters are, respectively, chosen as: \(a_1=0.25\), \(a_2=1\), \(a_4=0\), \(a_6=0.2\) and \(a_8=0\)

Full size image

For the case of the solution (15), it can be found that there are two extreme value points \((\pm \frac{\sqrt{\frac{3}{2}a_1a_2(a_2^2+a_6^2)}}{a_2^2},0)\) on the xy-plane. The lump wave possesses only one peak at the maximum point \((\frac{\sqrt{\frac{3}{2}a_1a_2(a_2^2+a_6^2)}}{a_2^2},0)\), and one valley at the minimum point \((-\frac{\sqrt{\frac{3}{2}a_1a_2(a_2^2+a_6^2)}}{a_2^2},0)\). The peak and valley of the lump wave are symmetric with respect to the center (0, 0), as shown in Fig. 2, and so it is called the bright–dark lump wave because the height of the peak is equal to the depth of the valley bottom. Via the above similar analysis, we find that the spatial structure of the lump wave in the solution (16) is the same as that in the solution (14). In addition, for the nonlinear Eq. (9), all three families of lump wave solutions (18)–(20) have two extreme value points, and the corresponding lump waves display the one-peak and one-valley structure.

4 Conclusions

In this paper, via the generalized Hirota bilinear formulation, we have constructed positive quadratic function solutions to the (\(2+1\))-dimensional bilinear p-SK equation [ i.e., Eq. (7) ]. Under the transformation \(u=6(\ln f)_{xx}\), we have presented a class of lump solutions [namely Eqs. (14)–(16)] of the (\(2+1\))-dimensional Sawada–Kotera equation [ i.e., Eq. (1) ]. We have found that those rationally decaying solutions in all space directions can exhibit two kinds of lump waves, i.e., bright lump wave (one peak and two valleys) and bright–dark lump wave (one peak and one valley). For the nonlinear p-SK equation with \(p=3\) [ i.e., Eq. (9) ], all three families of rational solutions [namely Eqs. (18)–(20)] exhibit the bright–dark lump wave structure. Therefore, we expect that the results presented in this work will also be useful to study lump solutions in a variety of other high-dimensional nonlinear equations.