1 Introduction

The rapid progress of quantum computation and quantum computer attracts people to investigate quantum data security. Combining quantum computing method with digital image processing techniques is an effective method to solve the current image processing problems. Quantum computation has been applied in many fields of information sciences [1].

As an important form of quantum information, quantum images will make the applications of quantum computer more extensive and comprehensive. A series of methods representing quantum images have been proposed [2–7]. Le et al. proposed a flexible representation of quantum images (FRQI) [3], which captured information about colors and their corresponding positions in one image into quantum states. Meanwhile, Le designed a method on how to get the quantum states and analyzed the computational complexity of quantum image preparation. On the basis of the type proceed color transform [4], simple geometric transform [8, 9] and image watermarking [10], Zhang et al. proposed a novel enhanced quantum representation (NEQR) model for digital images [11], which improved the storage model of color information in FRQI and put not only position but also color in qubits.

Consequently, some new quantum algorithms were developed as new theoretical tools for quantum image encryption [12–25]. For instance, Liao et al. improved the efficiency of quantum steganography with noisy depolarizing channels by modifying the twirling procedure and adding quantum teleportation [13]. Hua et al. proposed a quantum image encryption algorithm based on image correlation decomposition [19], where the correlation among image pixels is established by utilizing the superposition and measurement principle of quantum states and a whole quantum image is divided into a sequence of sub-images. Gong et al. proposed a quantum image encryption algorithm based on quantum image XOR operations [25]. Jiang et al. proposed a quantum realization of Arnold and Fibonacci image scrambling [26]. After that, Jiang et al. analyzed and improved the quantum Arnold image scrambling [27], and proposed a better scheme to decrease the network complexity apparently. Zhou et al. proposed a quantum image encryption algorithm based on generalized Arnold transform and double random phase encoding [28], which scrambled the pixels by the generalized Arnold transform and the gray-level information of images was encoded by the double random-phase operations. In the field of classical image encryption, there were some good multi-image encryption algorithms [29–33]. Kong et al. presented a multi-image encryption algorithm based on optical wavelet transform and multichannel fractional Fourier transform [30] and the scheme could make full use of multi-resolution decomposition of wavelet transform and multichannel processing of multi-channel fractional Fourier transform. Liao et al. proposed reversible data hiding in encrypted images based on absolute mean difference of multiple neighboring pixels, which reduces the average extracted-bit error rate when the block size is appropriate [31].

In this paper, a quantum version of the iteration Arnold transform with parameters and a quantum multi-image encryption algorithm by combining iteration Arnold transform with parameters with quantum image correlation decomposition are designed. Due to the multi-resolution decomposition property of DWT, images are decomposed into sub-images of different frequencies and the energy of image is focused on the low-frequency part by performing DWT. Therefore, these low-frequency parts could be reassembled. Then the iteration Arnold transform with parameters is performed on the new image to scramble image by shuffling the positions of image pixels. Finally, quantum image correlation decompos ition is performed on the scrambled image. At the same time, Pauli-x gate, Pauli-z gate, phase shift gate are used to encode color information of quantum image.

The rest of this paper is organized as follows. In Section 2, the flexible representation model for quantum images and the discrete wavelet transform are reviewed. The quantum realization of image scrambling by the iteration Arnold transform with parameters is designed in Section 3. In Section 4, the quantum multi-image encryption and decryption algorithm is introduced. Section 5 is devoted to the theoretical analyses on key space, security and computational complexity. Finally, a conclusion is drawn in Section 6.

2 Flexible Representation for Quantum Images and Wavelet Transform

2.1 The Flexible Representation for Quantum Images

Classical image is represented by a matrix with the same size of the image, i.e., the number of pixels, and each pixel contains the position information and the grayscale value. Inspired by this, a quantum flexible representation for images on quantum computers capturing information about positions and grayscale values has been proposed. The flexible representation for quantum images can be expressed as:

$$ \left|M \right\rangle =\frac{1}{2^{n}}{\sum\limits_{y=0}^{2^{n}-1}} \sum\limits_{x=0}^{2^{n}-1} {\left|g(y,x) \right\rangle}\left|yx \right\rangle $$
(1)
$$ \left|g(y,x) \right\rangle =\cos \theta_{i}\left|0 \right\rangle + \sin \theta_{i}\left|1 \right\rangle $$
(2)

where \(\theta _{i} \in \left [ {0,\frac {\pi }{2}} \right ]\) (i = y x = 0,1,…,22n − 1), |0〉 and |1〉 are two-dimensional computational basis quantum states, \(\theta =\left ({\theta _{0} ,\theta _{1} ,{\ldots } ,\theta _{2^{2n}-1}} \right )\) is the vector of angles encoding colors, |g(y,x)〉 encodes the color information of the quantum image, |i〉 = |y x〉 encodes the position information of the quantum image, |x〉 = |x n−1 x n−2…x 0〉 encodes the first n-qubit along the horizontal location while |y〉 = |y n−1 y n−2…y 0〉 encodes the second n-qubit along the vertical location, and n is the number of quantum bits required for encoding.

2.2 Discrete Wavelet Transform

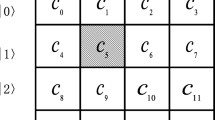
Wavelet transform is another breakthrough in mathematics after Fourier transform with profound theoretical meaning and widespread applications. Now wavelet transform plays an important role in the field of signal analysis, image processing, computer recognition, data compression, and etc. The discrete wavelet transform (DWT), a special case of wavelet transform, provides a compact representation of a signal in time and frequency domains. The energy of image is focused on the low-frequency part after DWT. In a general two-dimensional DWT, the data are decomposed into four parts firstly, shown in Fig. 1, where L L 1 and H H 1 are respectively the low-frequency and the high-frequency parts and the other two are the diagonal parts.

Fig. 1
figure 1

Discrete wavelet decomposition

Full size image

3 Realization of Iteration Arnold Transform with Parameters

3.1 Quantum Representation of Iteration Arnold Transform with Parameters

The Arnold transform, also called Arnold’s cat map, was discovered by V. I. Arnold Dyson et al. [34] and it has been used in image scrambling widely. The two-dimensional Arnold transform A in the form of matrix is defined as

$$ \left[ \begin{array}{c} {{x}^{\prime}} \\ {{y}^{\prime}} \\ \end{array} \right]=A\left[ \begin{array}{c} x \\ y \\ \end{array} \right]\left( {\bmod N} \right)=\left[ \begin{array}{cc} 1 & 1 \\ 1 & 2 \\ \end{array} \right]\left[ \begin{array}{c} x \\ y \\ \end{array} \right]\left( {\bmod N} \right) $$
(3)

The iteration Arnold transform A i with parameters in the form of matrix is defined as

$$ \left[ \begin{array}{c} {{x}^{\prime}} \\ {{y}^{\prime}} \\ \end{array} \right]=A^{i}\left[ \begin{array}{c} x \\ y \\ \end{array} \right]+\left[ \begin{array}{c} {ku} \\ {kv} \\ \end{array} \right]\left( {\bmod N} \right)=\left[ \begin{array}{cc} {f_{2i-1}} & {f_{2i}} \\ {f_{2i}} & {f_{2i+1}} \\ \end{array} \right]\left[ \begin{array}{c} x \\ y \\ \end{array} \right]+\left[ \begin{array}{c} {ku} \\ {kv} \\ \end{array} \right]\left( {\bmod N} \right) $$
(4)

where x,y,x ′,y ′∈ {0,1,…,N − 1}, f i is defined by Fibonacci spectrum as f i+2 = f i+1 + f i , f 1 = 1, f 2 = 1. x and y are the pixel coordinates of the original image, x ′ and y ′ are the pixel coordinates of the scrambled image after the iteration Arnold transform with parameters. N is the size of the original image. Generally, the original image is considered as a square image. u, v and k are the joined parameters. Its inverse transform A −i is

$$ \left[ \begin{array}{c} x \\ y \\ \end{array} \right]=A^{-i}\left[ \begin{array}{c} {{x}^{\prime}-ku} \\ {{y}^{\prime}-kv} \\ \end{array} \right]\left( {\bmod N} \right)=\left[ \begin{array}{cc} {f_{2i+1}} & {-f_{2i}} \\ {-f_{2i}} & {f_{2i-1}} \\ \end{array} \right]\left[ \begin{array}{c} {{x}^{\prime}-ku} \\ {{y}^{\prime}-kv} \\ \end{array} \right]\left( {\bmod N} \right) $$
(5)

The iteration Arnold transform with parameters in the form of pixel coordinates can be expressed as

$$ \left\{ \begin{array}{c} {{x}^{\prime}=\left( {f_{2i-1} x+f_{2i} y+ku} \right)\bmod N} \\ {{y}^{\prime}=\left( {f_{2i} x+f_{2i-1} y+kv} \right)\bmod N} \\ \end{array} \right. $$
(6)

According to the classical iteration Arnold transform with parameters, the quantum representation of the iteration Arnold transform with parameters can be described as

$$ \left\{ \begin{array}{c} |{{x}^{\prime}\rangle=| {f_{2i-1} x+f_{2i} y+ku} \rangle\bmod 2^{n}} \\ |{{y}^{\prime}\rangle=| {f_{2i} x+f_{2i-1} y+kv} \rangle\bmod 2^{n}} \\ \end{array} \right. $$
(7)

3.2 Quantum Circuit Architecture of Iteration Arnold Transform with Parameters

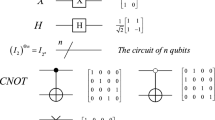
Quantum network is a device operating quantum algorithm or processing quantum information. A plain adder is used to calculate the sum of two numbers. The addition of two quantum registers |a〉 and |b〉 can be written as |a,b〉 → |a,a + b〉. The adder modulo 2n is a quantum network to calculate the sum of two numbers stored in the corresponding quantum registers. It can be written as |a,b〉 → |a,(a + b) mod 2n〉, where a, b are the inputs while (a + b) mod 2n is the output. In the iteration Arnold transform with parameters, the networks |x ′〉 and |y ′〉 for the iteration Arnold transform with parameters are independent, which can be realized by connecting several quantum ADDER-MOD 2n circuits [26]. Therefore, the quantum ADDER-MOD 2n network is basic to realize the iteration Arnold transform with parameters in quantum computer.

Assume that x, y, u and v are all n-qubit binary numbers, x = x n−1 x n−2…x 0, y = y n−1 y n−2…y 0, u = u n−1 u n−2…u 0, v = v n−1 v n−2…v 0, x i ,y i ,u i ,v i ∈ {0,1}, i = n − 1,n − 2,…,0. The realization of |x ′〉 is divided into f 2i−1 + f 2i + k steps, as shown in Fig. 2. The ADDER-MOD 2n network is used to obtain f 2i−1 x mod 2n from the first step to the (f 2i−1 − 1)-th step. In the f 2i−1-th step, x is replaced by y, and from the (f 2i−1 + 1)-th step to the (f 2i−1 + f 2i − 1)-th step, the ADDER-MOD 2n network is employed to obtain (f 2i−1 x + f 2i y) mod 2n. In the (f 2i−1 + f 2i )-th step, y is replaced by u, and from the (f 2i−1 + f 2i + 1)-th step to the last step, the ADDER-MOD 2n network is exploited to obtain (f 2i−1 x + f 2i y + k u) mod 2n.

$$\begin{array}{@{}rcl@{}} \left|x,x \right\rangle &\to& \left|x, 2x\bmod 2^{n} \right\rangle \to {\cdots} \to \left|x, f_{2i-1}x \bmod 2^{n}\right\rangle \to \left|y, f_{21-1}x \bmod 2^{n}\right\rangle \\ &\to& \left|y,(f_{2i-1}x+y)\bmod 2^{n} \right\rangle \to {\cdots} \to \left|y,(f_{2i-1}x+f_{2i}y)\bmod 2^{n} \right\rangle \\ &\to& \left|u,(f_{2i-1}x+f_{2i}y)\bmod 2^{n} \right\rangle \to {\cdots} \to \left|u,(f_{2i-1}x+f_{2i}y+ku)\bmod 2^{n} \right\rangle \end{array} $$
(8)
Fig. 2
figure 2

|x ′〉 network for the iteration Arnold transform with parameters

Full size image

The realization of |y ′〉 is divided into f 2i + f 2i−1 + k steps, as shown in Fig. 3.

$$\begin{array}{@{}rcl@{}} \left|x,x \right\rangle &\to& \left|x,2x\bmod 2^{n} \right\rangle \to {\cdots} \to \left|x,f_{2i}x\bmod 2^{n} \right\rangle \to \left|y,f_{2i}x \bmod 2^{n} \right\rangle \\ &\to& \left|y,(f_{2i}x+y)\bmod 2^{n} \right\rangle \to {\cdots} \to \left|y,(f_{2i}x+f_{2i-1}y\bmod 2^{n} \right\rangle \\ &\to& \left|v,(f_{2i}x+f_{2i-1}y)\bmod 2^{n} \right\rangle \to {\cdots} \to \left|v,(f_{2i}x+f_{2i-1}y+kv\bmod 2^{n} \right\rangle \\ \end{array} $$
(9)
Fig. 3
figure 3

|y ′〉 network for the iteration Arnold transform with parameters

Full size image

4 Quantum Multi-Image Encryption and Decryption Algorithm

4.1 Quantum Multi-Image Encryption Algorithm

Assume that the four images to be encrypted are I 1, I 2, I 3 and I 4. The proposed multi-image encryption algorithm consists of the following steps, and the encryption procedure is shown in Fig. 4.

  1. Step 1.

    By performing discrete wavelet transform on the four images of size 2n × 2n, respectively, the corresponding low frequency image L L i (i = 1,2,3,4) of size 2n−1 × 2n−1 can be obtained.

    $$ LL_{i} =\text{DWT}\left( {I_{i}} \right) $$
    (10)

    Randomly build up an image from the corresponding low frequency images. Then the new image can be expressed as:

    $$ \left|Q \right\rangle =\frac{1}{2^{n}}{\sum\limits_{y=0}^{2^{n}-1}}{\sum\limits_{x=0}^{2^{n}-1}}{\left|f(y,x) \right\rangle\left|yx \right\rangle} $$
    (11)
    $$ \left|f(y,x) \right\rangle =\cos \psi_{i}\left|0 \right\rangle +\sin \psi_{i}\left|1 \right\rangle, \psi_{i} \in \left[0, \frac{\pi}{2}\right], i= yx= 0,1,\ldots, 2^{2n}-1 $$
    (12)

    where the new image is a classical image of size 2n × 2n.

  2. Step 2.

    To obtain |Q i 〉, one performs the iteration Arnold transform with parameters on |Q〉 for i times, where |x ′〉 represents the horizontal location information and |y ′〉 represents the vertical location information of the scrambled image |Q i 〉. The quantum version of the iteration Arnold transform with parameters is defined as

    $$\begin{array}{@{}rcl@{}} \left|Q_{i} \right\rangle &=& A^{i}\left|M \right\rangle = \frac{1}{2^{n}} {\sum\limits_{y=0}^{2^{n}-1}}{\sum\limits_{x=1}^{2^{n}-1}} \left|g(y,x)\right\rangle A^{i}\left|yx\right\rangle \\ &=& \frac{1}{2^{n}} {\sum\limits_{y=0}^{2^{n}-1}}{\sum\limits_{x=0}^{2^{n}-1}} \left|g(y,x)\right\rangle A^{i}\left|y\right\rangle A^{i}\left|x\right\rangle\\ &=& \frac{1}{2^{n}} {\sum\limits_{y=0}^{2^{n}-1}}{\sum\limits_{x=0}^{2^{n}-1}} \left|g(y,x)\right\rangle \left|y^{\prime}\right\rangle \left|x^{\prime}\right\rangle \end{array} $$
    (13)

    where

    $$ \left\{ \begin{array}{c} \left|x^{\prime}\right\rangle =\left|f_{2i-1}x+f_{2i}y+ku \right\rangle \bmod 2^{n}\\ \left|y^{\prime}\right\rangle =\left|f_{2i}x+f_{2i-1}y+kv \right\rangle \bmod 2^{n} \end{array} \right. $$
    (14)
  3. Step 3.

    |Q i 〉 is divided into a range of sub-images |Q 1〉 , |Q 2〉 ,⋯ |Q l−i 〉 by performing the quantum image correlation decomposition technology [20]. Then we divide |Q i 〉 into three segments |Q i1〉 , |Q i2〉 and |Q i3〉.

  4. Step 4.

    To encode the color information of the quantum image, quantum bit gates are performed on these sub-images. Pauli-x gate, Pauli-z gate and phase shift gate are successively performed on the three segments. Pauli-x gate C j is performed on |Q i1〉. Pauli-x gate C j is controlled by a classical binary number a w , where a w ∈ {0,1}, w = 0,1,…,22n − 1. Binary sequence \(A=a_{0} a_{1} {\ldots } a_{2^{2n}-1}\) is the key. Pauli-x gate C j is used to construct a 2n + 1 qubit-based unitary transform H j .

    $$ H_{j} =\left( {C_{j}} \right)^{a_{w}} =\left\{ \begin{array}{lc} C_{j} , & a_{w} =1;\\ I, & a_{w} =0.\\ \end{array} \right. $$
    (15)
    $$ C_{j} =\left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right] $$
    (16)

    A 2n + 1 qubit-based unitary transform B j could be constructed with unitary transform H j .

    $$ B_{j} ={I\otimes \sum\limits_{y=0}^{2^{n}-1} \underset{\underset{yx\ne j}{x=0}}{\overset{2^{n}-1}{\sum}} {\left|yx \right\rangle \left\langle {yx} \right|}} +H_{j} \otimes \left|j \right\rangle \left\langle j \right| $$
    (17)

    The Pauli-x matrix B j is a unitary matrix since \(B_{j} B_{j}^{\dag } =I^{\otimes 2n+1}\). If we apply a 2n + 1 qubits unitary transform B on the quantum image |Q i1〉, then |f i1〉 will be obtained.

    $$\begin{array}{@{}rcl@{}} B\left|Q_{i1} \right\rangle &=& \prod\limits_{y=0}^{2^{n}-1}\prod\limits_{x=0}^{2^{n}-1} B_{j}\left|Q_{i1} \right\rangle \\ &&= \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1}\left( \cos \theta_{yx}\left|1 \right\rangle + \sin \theta_{yx}\left|0 \right\rangle\right)\left|yx \right\rangle \\ &&= \left|f_{i1} \right\rangle \end{array} $$
    (18)

    Pauli-z gate D m is performed on |Q i2〉. D m is controlled by a classical binary number e o , where e m ∈ {0,1}, m = 0,1,…,22n − 1. Binary sequence \(E=e_{0} e_{1} {\ldots } e_{2^{2n}-1}\) is the key. Pauli-z gate D m is used to construct a 2n + 1 qubit-based unitary transform S m .

    $$ S_{m} =\left( {D_{m}} \right)^{e_{m}} =\left\{ \begin{array}{lc} D_{m} , & e_{m} =1;\\ I, & e_{m} =0.\\ \end{array} \right. $$
    (19)
    $$ D_{m} =\left[ \begin{array}{cc} 0 & {-i} \\ i & 0 \\ \end{array} \right] $$
    (20)

    Unitary transform S m is used to construct a 2n + 1 qubit-based unitary transform R m .

    $$ R_{m} ={I\otimes \sum\limits_{y=0}^{2^{n}-1} \underset{\underset{yx\ne 0}{x=0}}{\overset{2^{n}-1}{\sum}} {\left|yx \right\rangle \left\langle {yx} \right|}} +S_{m} \otimes \left|m \right\rangle \left\langle m \right| $$
    (21)

    The Pauli-z matrix D m is a unitary matrix since \(R_{m} R_{m}^{\dag } =I^{\otimes 2n+1}\). If we apply 2n + 1 qubits unitary transform R on the quantum image |Q i2〉, then |f i2〉 will be achieved.

    $$\begin{array}{@{}rcl@{}} R\left|Q_{i2} \right\rangle &=& \prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} R_{m}\left|Q_{i2} \right\rangle \\ &&= \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1}\left( \cos \theta_{yx}\left|1 \right\rangle -\sin \theta_{yx}\left|0 \right\rangle \right)\left|yx \right\rangle \\ &&= \left|f_{i2} \right\rangle \end{array} $$
    (22)

    Phase shift gate K t is performed on |Q i3〉 and is controlled by a classical binary number l t , where l t ∈ {0,1}, t = 0,1,…,22n − 1. Binary sequence \(L=l_{1} l_{2} {\ldots } l_{2^{2n}-1}\) is the key. Phase shift gate K t is used to construct a 2n + 1 qubit-based unitary transform O t .

    $$ O_{t} =\left( {K_{t}} \right)^{l_{t}} =\left\{ \begin{array}{lc} K_{t} , & l_{t} =1;\\ I, & l_{t} =0.\\ \end{array} \right. $$
    (23)
    $$ K_{t} =\left[ \begin{array}{cc} 1 & 0 \\ 0 & {e^{i\psi}} \\ \end{array} \right] $$
    (24)

    where t = 0,1,…,22n − 1 and 𝜃 is a real number and distributed uniformly between 0 and 1. Unitary transform O t is used to construct a 2n + 1 qubit-based unitary transform P t .

    $$ P_{t} ={I\otimes \sum\limits_{y=0}^{2^{n}-1} \underset{\underset{yx\ne t}{x=0}}{\overset{2^{n}-1}{\sum}} {\left|yx \right\rangle \left\langle {yx} \right|}} +O_{t} \otimes \left|t \right\rangle \left\langle t \right| $$
    (25)

    The controlled phase matrix P t is a unitary matrix since \(P_{t} P_{t}^{\dag } =I^{\otimes 2n+1}\). By applying a 2n + 1 qubits unitary transform P on the quantum image |Q i3〉, |f i3〉 could be obtained.

    $$\begin{array}{@{}rcl@{}} P\left|Q_{i3} \right\rangle &=& \prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} P_{t}\left|Q_{i3} \right\rangle \\ &&= \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1}\left( \cos \theta_{yx}\left|0 \right\rangle + e^{j \psi}\sin \theta_{yx}\left|1 \right\rangle\right)\left| {yx} \right\rangle \\ &&= \left|f_{i3} \right\rangle \end{array} $$
    (26)
  5. Step 5.

    To obtain the quantum cipher-text image |f〉, one encrypts all of the images |f i1〉, |f i2〉 and |f i3〉 into the superposition form.

    $$ \left|f \right\rangle =a_{0} \left|f_{0} \right\rangle +a_{1}\left|f_{1} \right\rangle +{\cdots} +a_{N-1}\left|f_{N-1} \right\rangle $$
    (27)

    where a = (a 1,a 2,…,a N−1) and \({a_{0}^{2}} +{a_{1}^{2}} +{\cdots } +a_{N-1}^{2} =1\). To obtain the orthonormal basis states |M i 〉, one applies Schmidt decomposition to cipher-text image |f〉.

    $$ \left|f \right\rangle =r_{0} \left|M_{0} \right\rangle +r_{1}\left|M_{1} \right\rangle +{\cdots} +r_{N-1} \left|M_{N-1} \right\rangle $$
    (28)

    where r = (r 0,r 1,…,r N−1) and \({r_{0}^{2}} +{r_{1}^{2}} +{\cdots } +r_{N-1}^{2} =1\).

Fig. 4
figure 4

The quantum multi-image encryption algorithm procedure

Full size image

4.2 Quantum multi-image Decryption Algorithm

In the multi-image encryption algorithm, the key involves iterative times i and the classical binary sequences \(A=a_{1} a_{2}{\ldots } a_{2^{2n}-1} \), \(E=e_{1} e_{2} {\ldots } e_{2^{2n}-1} \) , \(L=l_{1} l_{2} {\ldots } l_{2^{2n}-1}\). The decryption process is as follows.

  1. Step 1.

    The cipher-text image |f〉 is obtained by making measurements on the received quantum image |f i 〉. With the projection operators |M i 〉 ,i = 0,1,…,N − 1, the projection measurement can be executed.

    $$ J=\sum\limits_{i=0}^{N-1} J_{i} \left|M_{i}\right\rangle \left\langle M_{i}\right| $$
    (29)
    $$ J_{i} =\frac{t_{i}} {t-t_{i}} $$
    (30)

    where t represents the total number of the measurements and t i is the number of the measurement result |f i 〉.

  2. Step 2.

    According to the quantum image correlation decomposition, different inverse transforms are performed to obtain the sub-images |Q 0〉 , |Q 1〉 ,…, |Q N−1〉. For |f i1〉, the decryption operation B −1 is performed with the key A.

    $$\begin{array}{@{}rcl@{}} B^{-1}\left|f_{i1} \right\rangle &=&\prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} B_{j}^{\dag} \left|f_{i1}\right\rangle \\ &&= \prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} B_{j}^{\dag}\left( \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} (\cos \theta_{yx}\left|1 \right\rangle +\sin \theta_{yx}\left|0 \right\rangle)\left|yx \right\rangle\right)\\ &&= \left|Q_{i1} \right\rangle \end{array} $$
    (31)

    where \(B_{j}^{\dag }\) is the Hermitian conjugate of B j . The decryption operation is performed on |f i2〉 with the key E.

    $$\begin{array}{@{}rcl@{}} R^{-1}\left|f_{i2} \right\rangle &=&\prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} R_{m}^{\dag}\left|f_{i2}\right\rangle \\ &=& \prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} R_{m}^{\dag} \left( \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} (\cos \theta_{yx}\left|1 \right\rangle -\sin \theta_{yx}\left|0 \right\rangle)\left|yx \right\rangle\right) \\ &=& \left|Q_{i2}\right\rangle \end{array} $$
    (32)

    where \(R_{m}^{\dag }\) is the Hermitian conjugate of R m . For |h i3〉, the decryption operation P −1 should be executed to obtain image |Q i3〉 with the key L.

    $$\begin{array}{@{}rcl@{}} P^{-1}\left|f_{i3} \right\rangle &=&\prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} P_{t}^{\dag} \left|f_{i3}\right\rangle \\ &=& \prod\limits_{y=0}^{2^{n}-1} \prod\limits_{x=0}^{2^{n}-1} P_{t}^{\dag} \left( \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} (\cos \theta_{yx}\left|0 \right\rangle +e^{j \psi}\sin \theta_{yx}\left|1 \right\rangle)\left|yx \right\rangle\right) \\ &=& \frac{1}{2^{n}} \sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} \left|g(y,x)\right\rangle \left|yx\right\rangle \\ &=& \left|Q_{i3}\right\rangle \end{array} $$
    (33)

    where P −1 is the inverse operator of P. Then the quantum image |Q i 〉 is rebuilt by these sub-images.

  3. Step 3.

    One performs the inverse iteration Arnold transform with parameters A −i on the quantum image |Q i 〉, where the quantum version of the inverse iteration Arnold transform A −i with parameters is defined as:

    $$\begin{array}{@{}rcl@{}} \left|Q \right\rangle &=& A^{-i}\left|Q_{i} \right\rangle \\ &=& \frac{1}{2^{n}}\sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} \left|g(y,x)\right\rangle A^{-i}\left|y^{\prime}x^{\prime}\right\rangle \\ &=& \frac{1}{2^{n}}\sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} \left|g(y,x)\right\rangle A^{-i}\left|y^{\prime}\right\rangle A^{-i}\left|x\right\rangle\\ &=& \frac{1}{2^{n}}\sum\limits_{y=0}^{2^{n}-1} \sum\limits_{x=0}^{2^{n}-1} \left|g(y,x)\right\rangle \left|yx \right\rangle \end{array} $$
    (34)

    where

    $$ \left\{ \begin{array}{c} {\left|x \right\rangle =A^{-i}\left|x^{\prime} \right\rangle =f_{2i+1} \left( {{x}^{\prime}-ku} \right)-f_{2i} \left( {{y}^{\prime}-kv} \right)}\\ {\left|y \right\rangle =A^{-i}\left|y^{\prime} \right\rangle =-f_{2i} \left( {{x}^{\prime}-ku} \right)+f_{2i-1} \left( {{y}^{\prime}-kv} \right)}\\ \end{array} \right. $$
    (35)
  4. Step 4.

    L L i (i = 1,2,3,4) could be obtained from the desirable image. Then the inverse discrete wavelet transform should be performed on these images.

    $$ I_{i} =\text{DWT}^{-1}\left( {LL_{i}} \right) $$
    (36)

    where DWT−1 is the inverse transform of DWT. Finally, the corresponding plaintext images I 1, I 2, I 3 and I 4 are obtained.

5 Algorithm Analyses

Practical quantum computer is still not available due to the lack of the quantum hardware, thus the quantum multi-image encryption algorithm can not be simulated. The proposed quantum multi-image encryption algorithm is limited to the theoretical analyses on key space, security and computational complexity.

5.1 Key Space

A good image encryption scheme should be as sensitive as possible to its keys, and the key space should be large enough to make brute-force attack infeasible or impossible. Assume that the key space for the iteration Arnold transform with parameters is K 1 and the key space for quantum image correlation decomposition is K 2, then the total key space of the proposed multi-image encryption algorithm is K 1 K 2. Pauli-x gate, Pauli-z gate and phase shift gate build up the quantum image correlation decomposition. The keys of the iteration Arnold transform with parameters are composed of the parameters k, u, v and the iteration times i. The key space K 1 is very large. The key space of binary sequence A is 22n, so are E and L. The key space of K 2 is 26n. With so large total key space, it is very difficult to obtain the plaintext image if the attacker doesn’t know the correct key.

5.2 Security

The performance of the proposed quantum multi-image encryption algorithm is better than that of the classical image encryption algorithm. The key space is larger and the computational complexity is lower than its classical counterparts. Hua TX et al.’s quantum image encryption scheme [19] used the corresponding parameters of the transform as the keys. If the attacker cracks the parameters, this part of the encryption scheme will fail and the information may be stolen by the attacker. The proposed multi-image encryption algorithm uses three binary sequences as the keys instead of the corresponding parameters. It increases the key space, and the key space of the proposed image encryption algorithm is larger than that of Hua TX et al.’s encryption algorithm. The image encryption algorithms based on classical Arnold transform have potential security threats due to its periodicity. If the attacker cracks the periodicity, the image will fail to be scrambled. The iteration Arnold transform with parameters in the multi-image encryption algorithm overcomes the shortcoming by the joined parameters k, u, v. The attacker cannot obtain the correct original image even if she decrypts the image with the right periodicity. Because the attacker doesn’t know the joined parameters, it can greatly improve the security. The weakness of the algorithm is that it can not be simulated and that quantum image correlation on decomposition transform is limited to theoretical analyses.

5.3 Computational Complexity

Assume I 1, I 2, I 3 and I 4 are the original images of size 2n × 2n, then there are 22n pixels in each image. The computational complexity of the proposed multi-image encryption algorithm depends on the discrete wavelet transform, iteration Arnold transform with parameters and quantum image correlation decomposition. In the quantum image correlation decomposition, the computational complexity depends on Pauli-x gate, Pauli-z gate and phase shift gate, whose computational complexities are O(n). The quantum image correlation decomposition needs to perform encryption operation on N sub-images at the same time. Therefore the computational complexity of quantum image correlation decomposition is O(N n). For the corresponding classical encryption algorithms, Pauli-x gate, Pauli-z gate and phase shift gate are performed on the image by using 22n multiplication operations, their computation complexities are O(N22n). The elementary gates of ADDER-MOD 2n are 28n − 12. The iteration Arnold transform with parameters involves 2(f 2i−1 + f 2i + k)(28n − 12) basic gates. Then the total computational complexity of the proposed multi-image encryption algorithm is O([N + 56(f 2i−1 + f 2i + k)]n) [35]. The computational complexity of the classical iteration Arnold transform with parameters is O(22n) and the total computational complexity is O((N + 1)22n). Therefore, the proposed multi-image encryption algorithm has lower computational complexity than its classical counterparts.

6 Conclusion

A quantum version of iteration Arnold transform with parameters is designed and its quantum circuit is suggested. By combining iteration Arnold transform with parameters with quantum image correlation decomposition technology, a quantum multi-image encryption algorithm is proposed. The encryption process can be realized by performing the discrete wavelet transform, the iteration Arnold transform with parameters and quantum image correlation decomposition technology on the different frequencies of images, position information and encoding color information of these sub-images, respectively. The independent parameters and three binary sequences are used as the keys, and the key space of the proposed multi-image encryption algorithm is very large. Detailed theoretical security and computational complexity analyses on the proposed multi-image encryption algorithm are given. Since the quantum image correlation decomposition technology cannot be simulated currently, the proposed multi-image encryption algorithm is in principle The quantum version of iteration Arnold transform with parameters can enlarge the key space and the scrambled image can be hardly decrypted by joined parameters. Even if the attacker knows the periodicity of the iteration Arnold transform with parameters, she also cannot obtain the correct image due to the joined parameters. The proposed multi-image encryption algorithm can encrypt multiple images at the same time, which has a higher efficiency. Moreover, the proposed multi-image encryption algorithm has lower computational complexity and larger key space than its classical counterparts.