On efficient time-dependent reliability analysis method through most probable point-oriented Kriging model combined with importance sampling

Abstract

Time-dependent reliability analysis (TRA) has attracted widespread attention due to its viability in evaluating the reliability of structures during the entire service life. However, TRA for complicated structures often leads to extremely high computational cost. To alleviate computational burden, this study develops a most probable point (MPP)-oriented Kriging model combined with the importance sampling (MPP-KIS) method for TRA. The strategy is that a comprehensive Kriging modeling method based on MPP is developed to construct the surrogate models for instantaneous performance functions discretized from the time-dependent reliability problem. A new learning function and a precise stopping criterion that take into account of the accuracy of the Kriging around MPP are contrived for updating the surrogate models. An adaptive screening strategy is introduced to identify the safe time trajectories to spare calculating the responses. The importance sampling method is integrated with the adaptive screening strategy for efficient computation of the time-dependent probability of failure. Two numerical examples and two engineering cases are exemplified to demonstrate the effectiveness and proficiency of the proposed method. The results show that the proposed MPP-KIS method achieves reliable results with substantially improved computational efficiency.

1 Introduction

Reliability analysis is a viable measure for estimating the reliability of a structure subject to uncertainties (Song et al. 2023), which can be classified into two categories: static uncertainties and dynamic uncertainties. Accordingly, reliability analyses can be divided into three types: time-independent reliability analysis, time-dependent reliability analysis (TRA), and time- and space-dependent reliability analysis. The former type of methods, like first-order reliability method (FORM) (Yang et al. 2020) and second-order reliability method (SORM) (Gong and Frangopol 2019; Wu et al. 2020a), assume that uncertainties are independent of time (Jiang et al. 2021), neglecting sources of time-dependent uncertainties, such as degradation of material properties, stochastic operating conditions, and dynamic loadings, resulting in unreliable predictions (Yang et al. 2022b). Differing from conventional time-independent reliability analysis, TRA estimates the probability that a structure, subject to time-dependent uncertainties, will operate reliably throughout its service life, which exhibits more practicality for engineering problems (Zhao et al. 2022a, 2022b). Besides, time- and space-dependent reliability analyses are also developed recently to address problems pertaining to stochastic processes, random fields, and tempo-spatial variables (Wu and Du 2023).

On the other hand, time-dependent reliability analysis is usually computationally intensive due to the involvement of time-dependent factors, such as time parameter and stochastic processes (Hu and Du 2013a; Zhou et al. 2022). To efficiently address the problem of high computational intensity for time-dependent reliability problems, researchers have developed various methods in recent years, which can be divided into three categories: outcrossing rate methods (Jiang et al. 2017), stochastic process discretization-based methods (Zhang et al. 2021a), and surrogate model-based methods (Li and Wang 2020). For the outcrossing rate methods, outcrossing rate refers to mean of the performance function outcrossing from the reliable state to the failure state per time unit (Wang et al. 2020). TRA problems are processed by integrating the outcrossing rate under assumption of independent outcrossing events (Jiang et al. 2017). Rice’s first-passage formula laid the foundation for the outcrossing rate methods, but its application is usually hindered by the relevant intricate computations (Rice 1945). Subsequently, PHI2 method was developed in response to the complexity in calculating the outcrossing rate (Andrieu-Renaud et al. 2004). However, the computational result by this method is usually not stable due to its sensitivity to the different time step size in the finite difference (Wang et al. 2016). PHI2 + method was then proposed to simplify the evaluation process and improve the stability of PHI2 method, which yields an analytical expression (Sudret 2008). Unfortunately, these methods may lead to considerable errors when attending time-dependent reliability problems that outcrossing events in different instances are highly correlated (Jiang et al. 2018). To make amendment, the joint crossing rate was employed to process the strongly correlated outcrossing events by Hu and Du (2013b). Although the performance of outcrossing rate methods has been improved significantly in recent years, proficiently deriving the outcrossing rate for problems with complex mathematical properties remains a challenge (Zhang et al. 2023).

To this gap, a number of stochastic process discretization-based methods have been developed to circumvent calculating the outcrossing rate. This new type of approach discretizes time-dependent performance functions into a series of instantaneous performance functions and operates analyses on each instantaneous performance function. Then, the series system probability of failure can be calculated utilizing the correlation between the instantaneous performance functions. A TRA method based on stochastic process discretization (TRPD) was developed by Jiang et al. (2014). TRPD method first transformed a TRA problem into a series of time-independent reliability problems at discretized time nodes. The reliability indexes of all time-independent performance functions were then calculated by FORM, which were further utilized to calculate the serial system reliability based on multivariate normal distribution. Improved TRPD (iTRPD) method was also proposed to further simplify the solution procedure and enhance the efficiency of computing for TRPD method (Jiang et al. 2018). Since these methods need to search MPP of each instantaneous performance function, they still ensue remarkably high computational expense when discretized number of the time interval is large.

To improve computational efficiency, surrogate models are applied to address TRA problems, which have attracted much attention for their superior computational efficiency without compromise of accuracy. The basic idea of surrogate model-based methods is replacing the limit state function (LSF) with a surrogate model, such as Kriging model (Hu and Du 2015), response surface (Chen et al. 2022; Gavin and Yau 2008; Roussouly et al. 2013), neural network (Zhang et al. 2022), and support vector machine (Pan and Dias 2017; Rocco and Moreno 2002; Shi et al. 2020). Kriging model is widely adopted as it predicts not only the response but also the variance of the unknown points (Hu and Mahadevan 2016). Generally, TRA methods based on Kriging model can be categorized as extreme response Kriging model-based methods, global response Kriging model-based methods (Liu et al. 2022), and MPP-informed Kriging model-based methods. Extreme response Kriging model-based methods build Kriging for the extreme value of LSF and transforms the time-dependent reliability problem into static problems (Yu and Li 2021). Since these methods should search the extreme value of LSF over the specified time domain, it usually incurs a double-loop procedure, in which extreme time is identified by performing global optimization in the inner loop, and Kriging model of extreme response is established in the outer loop (Ji et al. 2023). It thus ensues very high computational cost (Song et al. 2022). To prevent the inefficiency of double-loop method, the global response Kriging model-based methods have been brought up in recent years (Zhao et al. 2022c). Specifically, a single-loop Kriging modeling method was proposed by Hu and Mahadevan (2016), which significantly reduced computational cost of TRA. Wang and Chen (2017) developed an adaptive extreme response surface (AERS) method through improving the update procedure of Kriging model. A Kriging modeling method on the basis of failure-pursuing for identification of the most useful samples was proposed by Jiang et al. (2019) for efficient implementation of TRA. Furthermore, Jiang et al. (2020) developed an efficient TRA method in terms of misclassification probability of Kriging model. Song et al. (2022) investigated the correlation between discrete points on both the same and different time trajectories and introduced an adaptive Kriging method via variance reduction of predictions to improve the modeling efficiency of Kriging.

Recently, researchers have developed MPP-informed Kriging model-based methods to improve the accuracy and efficiency of TRA. In these methods, the MPP information is utilized to construct the Kriging model, which is then employed directly or indirectly to calculate the time-dependent probability of failure. It should be noted that this type of method is also related to other types of methods, such as TRA methods based on stochastic process discretization and TRA methods based on extreme response Kriging model. Specifically, an approximating MPP trajectory (AMPPT) method was presented by Zhang et al. (2021b) to improve the efficiency of TRA. In AMPPT, the Kriging model is established to estimate MPP trajectory in U-space. The time-dependent reliability is then computed based on estimated MPP trajectory. Since AMPPT circumvents evaluations of MPPs at all discretized time points with the help of the Kriging model, the efficiency of computing is significantly improved. Further advance was the Kriging-assisted TRPD method (K-TRPD), which used Kriging model to predict MPP trajectories for TRPD method at discretized time points, thus reducing the number of function calls for MPP evaluation (Zhang et al. 2021a). It is worth noting that the above two methods are essentially based on the combination of FORM and Kriging models to approximate MPP trajectories, where FORM actually participates in TRA and will have a significant impact on the results of TRA. It is generally understood that FORM has low computational accuracy and inadequate robustness when dealing with highly nonlinear performance functions (Meng et al. 2023; Yang et al. 2020). Therefore, the above two methods may result in significant computational errors of TRA or even nonconvergence. To avoid this deficiency of the abovementioned methods that use the Kriging model to approximate MPP trajectories, Yu and Li (2021) recently proposed an extreme response Kriging model-based method combining with Monte Carlo Simulation (MCS) for efficient implementation of TRA, where MPP information is only used as the sampling center in each iteration and does not participate in the calculation of reliability. Specifically, MPP information from the Kriging model is firstly determined as the sampling center to generate candidate samples, based on which the extreme values are evaluated. The Kriging model is then updated using a novel probabilistic model leaning function. Subsequently, MCS is used to calculate the time-dependent reliability. It should be emphasized that this method updates the Kriging model by adding many sample points at a time node instead of just one sample point without considering the variance information of the Kriging model, which may miss important sample points with high uncertainty. As a result, this may ensure inability to improve accuracy of the Kriging model to the greatest extent, thereby rendering the learning process inefficient. In addition, MCS method must extract a large number of samples to obtain convergent results, which occupies a large amount of computing memory, leading to low efficiency (Wu et al. 2020b).

From the above analysis, although advances in MPP-informed Kriging model-based TRA methods have been made, it remains a challenge to improve the computational accuracy and efficiency of Kriging model for TRA. To improve computational efficiency for TRA, this study develops an MPP-oriented Kriging model combined with the importance sampling (MPP-KIS) method. The advantages of current MPP-KIS are reflected in three aspects. Firstly, a new learning function is contrived to refine the Kriging models based on the approximate MPPs until a straightforward and effective stopping criterion is met. The constructed Kriging models can well fit the limit state functions near true MPPs as guided by updating procedure. A note of attention is that the acquisition of the approximate MPP does not require any computational cost since it is derived from Kriging model rather than the true limit state function. Secondly, an adaptive screening strategy is introduced to enhance the computational efficiency by the constructed β-surface that distinguishes safety sample points in the sample pool into two categories: inside and outside the β-surface, where the computations of the limit state function values at some sample trajectories inside the β-surface can be circumvented. Finally, to further enhance the computational efficiency of MCS method for reliability analysis and take full advantage of the derived information of MPP, the adaptive screening strategy is integrated with importance sampling (IS) method to estimate time-dependent probability of failure.

The remainder of the paper is organized as follows. Section 2 presents the fundamental concepts of Kriging model and time-dependent reliability analysis. Section 3 elaborates the proposed MPP-KIS method. Four examples are exemplified to demonstrate the proposed method in Sect. 4. Concluding remarks are drawn in Sect. 5.

2 Kriging model and time-dependent reliability analysis

2.1 Kriging surrogate modeling method

As a robust interpolation measure, Kriging model is comprised of a regression model and a stochastic process. It is usually adopted in TRA due to its exceptional fitting and predictive abilities for attending nonlinear functions (Yang et al. 2022a; Zafar et al. 2020). Given n sample points ${\mathbf{x}}_{{{\text{old}}}} = \left\{ {{\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{n} ,} \right\}$ and associated responses ${\mathbf{y}}_{{{\text{old}}}} = \left\{ {y_1 ,y_2 , \ldots ,y_n ,} \right\}$, Kriging model can predict the response for the unknown point ${\mathbf{x}}_{{{\text{new}}}}$ (Guo et al. 2020):

$$g_{{\text{K}}} \left( {{\mathbf{x}}_{{{\text{new}}}} } \right) = {{\varvec{\upbeta}}}^{{\text{T}}} {\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{new}}}} } \right) + Z\left( {{\mathbf{x}}_{{{\text{new}}}} } \right),$$

(1)

where ${{\varvec{\upbeta}}} = \left[ {\beta_{1} ,\beta_{2} , \ldots ,\beta_{k} } \right]^{{\text{T}}}$ is the vector of regression coefficients; ${\mathbf{F}}\left( {\mathbf{x}} \right) = \left[ {f_{1} \left( {\mathbf{x}} \right), \ldots ,f_{k} \left( {\mathbf{x}} \right)} \right]^{{\text{T}}}$ stands for the vector of base functions; $Z\left( {\mathbf{x}} \right)$ symbolizes a stationary Gaussian process representing the variance predicted by the regression model. The mean of $Z\left( {\mathbf{x}} \right)$ is zero, and its covariance can be expressed as

$$\mathrm{Cov}\left( {Z\left( {{\mathbf{x}}_{i} } \right),Z\left( {{\mathbf{x}}_{j} } \right)} \right) = \sigma_{Z}^{2} R_{\theta } \left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right),{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} \in {\mathbf{x}}_{{{\text{old}}}} ,$$

(2)

where $\sigma_{Z}^{2}$ represents the variance of $Z\left( {\mathbf{x}} \right)$; $R_{\theta } \left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)$ is the correlation function of $Z\left( {\mathbf{x}} \right)$ with θ as the parameter. In this study, Gaussian kernel function is identified as the correlation function:

$$R_{\theta } \left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right) = \prod\limits_{l = 1}^{d} {\exp \left( { - \theta_{l} \left| {x_{i,l} - x_{j,l} } \right|^{2} } \right)} ,$$

(3)

where $\theta_{l}\$$\left( {l = 1,2, \ldots ,d} \right)$ is correlation parameter; d is the dimensionality of input samples x. Maximum likelihood estimation method is utilized to estimate the correlation parameter:

$${\hat{\mathbf{\theta }}} = \mathop {{\text{argmin}}}\limits_{{{\varvec{\uptheta}}}} \left( {\left| {{\mathbf{M}}_{R} } \right|^{\frac{1}{n}} \sigma_{Z}^{2} } \right),$$

(4)

where ${\mathbf{M}}_{R}$ is the correlation coefficient matrix and can be expressed as

$${\mathbf{M}}_{R} \left( {i,j} \right) = R_{\theta } \left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right).$$

(5)

Via generalized least squares method, coefficients of regression β and variance $\sigma_{Z}^{2}$ can be obtained by

$${\hat{\mathbf{\beta }}} = \left( {{\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{old}}}} } \right)^{{\text{T}}} {\mathbf{M}}_{R}^{ - 1} {\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{old}}}} } \right)} \right)^{ - 1} {\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{old}}}} } \right)^{{\text{T}}} {\mathbf{M}}_{R}^{ - 1} {\mathbf{y}}_{{{\text{old}}}}$$

(6)

$$\hat{\sigma }_{Z}^{2} = \frac{1}{n}\left( {{\mathbf{y}}_{{{\text{old}}}} - {\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{old}}}} } \right){\hat{\mathbf{\beta }}}} \right)^{{\text{T}}} {\mathbf{M}}_{R}^{ - 1} \left( {{\mathbf{y}}_{{{\text{old}}}} - {\mathbf{F}}\left( {{\mathbf{x}}_{{{\text{old}}}} } \right){\hat{\mathbf{\beta }}}} \right).$$

(7)

Kriging model can be formulated for the performance function once all the coefficients have been acquired. The time-dependent probability of failure can be efficiently calculated employing constructed Kriging model. In this study, the Toolbox DACE (Lophaven et al. 2002) is utilized for the construction of Kriging model and employed to compute the responses.

2.2 Basic concept of time-dependent reliability analysis

In TRA problem, reliability is the probability that an engineering structure will operate reliably over the specified time interval, which can be represented by the probability that LSF is higher than zero throughout that time interval (Yang et al. 2024). The time-dependent reliability and probability of failure within the time interval $\left[ {t_{s} ,t_{e} } \right]$ are calculated by (Li and Wang 2022)

$$P_{s} \left( {t_{{\text{s}}} ,t_{{\text{e}}} } \right) = \Pr \left\{ {g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right) > 0,\forall t \in \left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]} \right\}$$

(8)

$$P_{f} \left( {t_{{\text{s}}} ,t_{{\text{e}}} } \right) = \Pr \left\{ {g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right) \le 0,\exists t \in \left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]} \right\},$$

(9)

where $g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right)$ represents the time-dependent performance funtion; X denotes the vector composed of random variables; ${\mathbf{Y}}\left( t \right)$ indicates the vector consisting of stochastic processes; t is time parameter. Figure 1 shows the time-dependent probability of failure by TRA and instantaneous probability of failure by time-independent reliability analysis. From Fig. 1, the time-dependent probability of failure is the accumulation of the instantaneous ones.

Fig. 1

Time-dependent and instantaneous probability of failure

2.3 Extreme value-based method

The extreme value-based method is an essential class of methods with respect to extreme value of the LSF for computing probability of failure. The extreme value is derived by minimizing the performance function within the specified time interval $\left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]$ (Wang and Chen 2017):

$$g_{\min } = \mathop {\min }\limits_{{t \in \left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]}} g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right).$$

(10)

To demonstrate the relatability between time-dependent probability of failure and the extreme value, Fig. 2 shows the realizations of a time-dependent performance function (Jiang et al. 2020). From Fig. 2, the extreme value of the i-th realization is less than zero, which implies that this realization fails. Thus, it is feasible to judge if the structure fails by the extreme value of realization. The probability for the occurrence of failure events can be determined by the extreme value:

$$\begin{gathered} P_{f} \left( {t_{{\text{s}}} ,t_{{\text{e}}} } \right) = \Pr \left\{ {g_{\min } \le 0} \right\} \\ = \Pr \left\{ {\mathop {\min }\limits_{{t \in \left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]}} g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right) \le 0} \right\}. \\ \end{gathered}$$

(11)

Fig. 2

$g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right)$ vs. time

For most TRA problems, performance functions are usually nonlinear and implicit. It is not straightforward to derive analytical solutions for Eqs. (8–11). Consequently, MCS method is commonly adopted to estimate the probability of failure. However, this simulation scheme ensues significant computational cost due to the discretization of time interval and the expansion of stochastic processes (Song et al. 2022). To perform time-dependent reliability analysis efficiently, Kriging model $g_{{\text{K}}}$ of LSF is utilized for employing MCS, and Eq. (11) can be further calculated through (Jiang et al. 2020)

$$P_{f} \left( {t_{{\text{s}}} ,t_{{\text{e}}} } \right) \approx \frac{1}{{N_{{{\text{MCS}}}} }}\sum\limits_{m = 1}^{{N_{{{\text{MCS}}}} }} {I_{t} \left( {{\mathbf{X}}_{{{\text{input}}}}^{\left( m \right)} } \right)} ,$$

(12)

where ${\mathbf{X}}_{{{\text{input}}}}$ denotes input variables of LSF except for the time parameter; $I_{t}$ is time-dependent indicator function for ${\mathbf{X}}_{{{\text{input}}}}^{\left( m \right)}$:

$$I_{t} \left( {{\mathbf{X}}_{{{\text{input}}}}^{\left( m \right)} } \right) = \left\{ \begin{gathered} 1, \, \mathop {\min }\limits_{{t \in \left[ {t_{{\text{s}}} ,t_{{\text{e}}} } \right]}} \, g_{{\text{K}}} \left( {{\mathbf{X}}_{{{\text{input}}}}^{\left( m \right)} ,t} \right) \le 0 \hfill \\ 0,{\text{ otherwise}} \hfill \\ \end{gathered} \right.$$

(13)

3 The proposed MPP-KIS method

In this section, the MPP-oriented Kriging modeling method combined with the importance sampling method, abbreviated as MPP-KIS, is proposed for solving TRA problems. The method is composed of three parts: (1) expansion optimal linear estimation of stochastic processes; (2) MPP-oriented Kriging modeling method; (3) importance sampling method integrating adaptive screening strategy.

3.1 Expansion optimal linear estimation for stochastic process

To transform performance function $g\left( {{\mathbf{X}},{\mathbf{Y}}\left( t \right),t} \right)$ in Eq. (9) into a series of instantaneous ones, N_y-dimensional stochastic process vector ${\mathbf{Y}}\left( t \right)$ should be discretized first. To this end, $\left[ {t_{s} ,t_{e} } \right]$ is uniformly discretized into ${\mathbf{t}}_{{\text{d}}} = \left[ {t_{1}^{{}} ,t_{2}^{{}} , \ldots ,t_{d}^{{}} } \right]$ for discretizing the stochastic process. Subsequently, ${\mathbf{Y}}\left( t \right)$ is expanded at $N_{t}$ interested time points ${\mathbf{t}}_{{\text{u}}} = \left[ {t_{1} ,t_{2} , \ldots ,t_{{N_{t} }} } \right]$ by expansion optimal linear estimation (EOLE) (Andrieu-Renaud et al. 2004):

$$\hat{Y}_{k} \left( {t_{i} } \right) = \mu_{k} \left( {t_{i} } \right) + \sigma_{k} \left( {t_{i} } \right)\sum\limits_{j = 1}^{r} {\frac{{\xi_{j}^{k} }}{{\sqrt {\lambda_{j} } }}{{\varvec{\Phi}}}_{j}^{{\text{T}}} {\mathbf{C}}_{{Y_{k} \left( t \right){{\varvec{\upchi}}}}} \left( {t_{i} } \right)} ,i = 1,2, \ldots ,N_{t} ,k = 1,2, \ldots ,N_{y} ,$$

(14)

where $\mu_{k} \left( t \right)$ is the mean function of $Y_{k} \left( t \right)$; $\sigma_{k} \left( t \right)$ is the standard deviation function; r is the number of truncation terms; ${{\varvec{\upchi}}} = \left[ {Y_{k} \left( {t_{1}^{{}} } \right),Y_{k} \left( {t_{2}^{{}} } \right), \ldots ,Y_{k} \left( {t_{d}^{{}} } \right)} \right]^{{\text{T}}}$ is the discretized stochastic process at ${\mathbf{t}}_{{\text{d}}}$; ${{\varvec{\upxi}}}_{k} = \left[ {\xi_{1}^{k} ,\xi_{2}^{k} , \ldots ,\xi_{r}^{k} } \right]^{{\text{T}}}$ is a group of independent variables standard normally distributed; ${\mathbf{C}}_{{Y_{k} \left( t \right){{\varvec{\upchi}}}}} \left( {t_{i} } \right)$ is the correlation coefficient of $Y_{k} \left( {t_{i} } \right)$ and ${{\varvec{\upchi}}}$; $\lambda_{j}$ and ${{\varvec{\Phi}}}_{j}$ are the solutions of the characteristic equation:

$${\mathbf{C}}_{{{\mathbf{\chi \chi }}}} {{\varvec{\Phi}}}_{j} = \lambda_{j} {{\varvec{\Phi}}}_{j} ,$$

(15)

where ${\mathbf{C}}_{{{\mathbf{\chi \chi }}}}$ can be derived by

$${\mathbf{C}}_{{{\mathbf{\chi \chi }}}} = \left\{ {\rho_{{Y_{k} }} \left( {t_{m} ,t_{n} } \right)|t_{m} ,t_{n} \in {\mathbf{t}}_{{\text{d}}} } \right\}.$$

(16)

As EOLE is truncated after the r term, its variance error can be estimated by

$${\text{Err}}_{k} \left( {t_{i} } \right) = 1 - \sum\limits_{j = 1}^{r} {\frac{1}{{\lambda_{j} }}\left[ {{{\varvec{\Phi}}}_{j}^{{\text{T}}} {\mathbf{C}}_{{Y_{k} \left( t \right){{\varvec{\upchi}}}}} \left( {t_{i} } \right)} \right]^{2} } ,i = 1,2, \ldots ,N_{t}$$

(17)

According to Eq. (17), the number of truncation terms r is directly related to the accuracy of EOLE. Too few truncation terms will lead to an excessive error in results of EOLE, where significant errors in the variance of stochastic processes exhibit. This further ensues error in the probability of failure due to the insufficient precision of input samples. Consequently, the number of truncated terms r should be specified for a low variance error of EOLE. In this study, r is set appropriately to maintain a variance error of less than 0.03 to balance accuracy against efficiency. Taking r = 8 as an example, results for a stochastic process with mean μ, variance σ², and correlation coefficient function $\rho \left( {x_{1} ,x_{2} } \right) = \exp \left( { - \left( {\left( {x_{1} - x_{2} } \right)/0.876} \right)^{2} } \right)$ are plotted in Fig. 3.

Fig. 3

Result and error of EOLE

3.2 MPP-oriented Kriging modeling method

After discretizing the random process, $N_{t}$ instantaneous performance functions $g\left( {{\mathbf{X}},{{\varvec{\upxi}}},t_{i} } \right)\$$\left( {i = 1,2, \ldots ,N_{t} } \right)$ are obtained, of which Kriging models will be established by MPP-oriented Kriging modeling method proposed in this subsection. An active learning function and a stopping criterion are developed for training Kriging based on MPP information efficiently. The specific construction process of Kriging model for the i-th performance function $g\left( {{\mathbf{X}},{{\varvec{\upxi}}},t_{i} } \right)$ is outlined as follows.

3.2.1 Construction of initial Kriging model

To start with, Rosenblatt transformation, an extensively used technique for transforming random variables into independent standard normal variables based on the information of probability distribution, is applied for the conversion of input variables X into standard normal space (Yu et al. 2022). For simplicity of presentation, $g\left( {{\mathbf{X}},{{\varvec{\upxi}}},t_{i} } \right)$ is rewritten as $g\left( {{\mathbf{Z}},t_{i} } \right)$, in which Z represents all the input variables. A training sample pool is then built to construct Kriging model for $g\left( {{\mathbf{Z}},t_{i} } \right)$. Considering that the initial training sample pool should exhibit a high level of uniformity and randomness, Latin Hypercube sampling (LHS) method is employed herein to construct initial training sample pool:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{X}}^{(1)} } & {{\mathbf{Y}}^{(1)} } & {t_{{t_{1} }} } \\ {{\mathbf{X}}^{(2)} } & {{\mathbf{Y}}^{(2)} } & {t_{{t_{2} }} } \\ \vdots & \vdots & \vdots \\ {{\mathbf{X}}^{(n)} } & {{\mathbf{Y}}^{(n)} } & {t_{{t_{n} }} } \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}c} {{\mathbf{X}}^{(1)} } & {{{\varvec{\upxi}}}^{(1)} } & {t_{{t_{1} }} } \\ {{\mathbf{X}}^{(2)} } & {{{\varvec{\upxi}}}^{(2)} } & {t_{{t_{2} }} } \\ \vdots & \vdots & \vdots \\ {{\mathbf{X}}^{(n)} } & {{{\varvec{\upxi}}}^{(n)} } & {t_{{t_{n} }} } \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{{}}^{(1)} } & {t_{{t_{1} }} } \\ {{\mathbf{Z}}_{{}}^{(2)} } & {t_{{t_{2} }} } \\ \vdots & \vdots \\ {{\mathbf{Z}}_{{}}^{(n)} } & {t_{{t_{n} }} } \\ \end{array} } \right]$$

(18)

After the calculation of response values for the initial training sample pool, the initial Kriging model of $g\left( {{\mathbf{Z}},t_{i} } \right)$ is ultimately constructed by Eq. (1) as

$$M_{i} \left( {\mathbf{Z}} \right) = g\left( {{\mathbf{Z}},t_{i} } \right).$$

(19)

3.2.2 Update strategy for initial Kriging model

When the initial Kriging model is in place, the update strategy of Kriging will be initiated. The improvement of the accuracy of Kriging is highly dependent on the information of sample points in the training sample pool, which will be obstructed if the range of the training sample pool is too extensive (Yu et al. 2022). To prevent this, the active learning sampling area is constrained by the proposed update strategy via updating the sampling center based on the location of MPP obtained approximately by Kriging models and reducing the sampling radius during the training process. Therefore, the accuracy of Kriging around MPP can be substantially improved, and the stability of active learning is ensured. The proposed update strategy is elaborated in the following steps:

First, iHL-RF algorithm (Zhang and Kiureghian 1995) with high robustness is used to locate MPP ${\mathbf{Z}}^{*}$ by solving the following problem iteratively,

$$\left\{ \begin{gathered} {\text{find}}:{\mathbf{Z}}^{*} \hfill \\ {\text{min}}:\left| {{\mathbf{Z}}^{*} } \right| \hfill \\ {\text{subject to}}:M_{i} \left( {{\mathbf{Z}}^{*} } \right) = 0 \hfill \\ \end{gathered} \right.$$

(20)

in which the procedure of the k-th iteration can be represented by

$${\mathbf{Z}}^{k + 1} = {\mathbf{Z}}^{k} + \alpha {\mathbf{d}}^{k} ,$$

(21)

where ${\mathbf{Z}}^{k}$ denotes the random variable at the k-th iterative step; ${\mathbf{d}}^{k}$ is the search direction and calculated by

$${\mathbf{d}}^{k} = \frac{{\left( {\nabla M_{i} \left( {{\mathbf{Z}}^{k} } \right)} \right)^{{\text{T}}} {\mathbf{Z}}^{k} - M_{i} \left( {{\mathbf{Z}}^{k} } \right)}}{{\left( {\nabla M_{i} \left( {{\mathbf{Z}}^{k} } \right)} \right)^{{\text{T}}} \nabla M_{i} \left( {{\mathbf{Z}}^{k} } \right)}}\nabla M_{i} \left( {{\mathbf{Z}}^{k} } \right) - {\mathbf{Z}}^{k},$$

(22)

where α is the iterative step length and can be selected by minimizing the merit function:

$$\left\{ \begin{gathered} m\left( {\mathbf{Z}} \right) = \frac{1}{2}\left\| {\mathbf{Z}} \right\| + c\left| {M_{i} \left( {\mathbf{Z}} \right)} \right| \hfill \\ c > \frac{{\left\| {\mathbf{Z}} \right\|}}{{\left\| {\nabla M_{i} \left( {\mathbf{Z}} \right)} \right\|}} \hfill \\ \end{gathered} \right.,$$

(23)

where c is the constant. In this paper, c is set as

$$c = \frac{{\left\| {\mathbf{Z}} \right\|}}{{\left\| {\nabla M_{i} \left( {\mathbf{Z}} \right)} \right\|}} + 0.5$$

(24)

After solving Eq. (20), MPP ${\mathbf{Z}}^{*}$ will be obtained and utilized to determine a new sampling region. It should be noted that a new sampling region should determine center and radius of sampling. Herein, the obtained MPP ${\mathbf{Z}}^{*}$ is selected as the sampling center, and the sampling radius is proposed as

$$r = \frac{1}{{\lambda^{p} }},$$

(25)

where p denotes the number of training times; λ represents the adjusting parameter in a range from 1 to 10 that controls the degree of reduction in the sampling range. Figure 4 illustrates the relationship between the radius r and the number of training times p for different adjusting parameters λ. From Fig. 4, radius r varies quickly when the adjusting parameter λ is close to 1 and decreases slowly if λ is too high. To achieve the dynamic balance of radius reduction as much as possible, λ = 2 is selected as an adjusting parameter in this study.

Fig. 4

Relationship between radius and number of iterations for different parameters

After obtaining the new sampling region with MPP ${\mathbf{Z}}^{*}$ as center and r as radius, the candidate sample set ${\mathbf{x}}_{{\text{c}}}$ is generated by LHS. A new learning function is then contrived to select new sample point x from candidate sample set ${\mathbf{x}}_{{\text{c}}}$. To better balance Kriging model’s error estimation of prediction value and the impact on the accuracy of model near MPP for a new point, the proposed learning function is defined as

$${\mathbf{x}}_{{{\text{new}}}} = \mathop {\arg \min }\limits_{{{\mathbf{x}} \in {\mathbf{x}}_{{\text{c}}} }} \left\{ {\frac{{1 + \exp \left( {\delta \left| {{\mathbf{x}} - {\mathbf{x}}^{*} } \right|} \right)}}{{\sigma \left( {\mathbf{x}} \right)}}} \right\},$$

(26)

where δ is utilized for the penalty effect, which is generally specified as a considerably high value. Herein, δ = 500 is adopted in this study. σ is the standard deviation of Kriging predictor. Using Eq. (26), Kriging model can be updated iteratively until the set stopping criterion is satisfied.

3.2.3 Stopping criterion

The stopping criterion is an indispensable link in the update process of Kriging model, and a proper stopping criterion can strike well trade-off for computational efficiency and accuracy. Herein, the relative error of MPP information over two successive iterations is considered as a stopping criterion for Kriging model. The stopping criterion can be specified as

$${\varepsilon}=\left|\mathbf{Z}_{n}^* - \mathbf{Z}_{o}^*\right|\leq{\varepsilon}_{M}.$$

(27)

where ${\mathbf{Z}}_{{{n}}}^{*}$ and ${\mathbf{Z}}_{{{o}}}^{*}$ denote MPP obtained in the current and the previous iterations according to the established Kriging model, respectively; $\varepsilon_{M}$ represents convergence tolerance, which is a positive number, generally taken as $1 \times 10^{ - 2}$ or lower.

After the stopping criterion is satisfied, Kriging models $M_{i} \left( {\mathbf{Z}} \right)\$ $\left( {i = 1,2, \ldots ,N_{t} } \right)$ and corresponding MPPs ${\mathbf{Z}}_{{{\text{MPP}}}}^{\left( i \right)}\$$\left( {i = 1,2, \ldots ,N_{t} } \right)$ can be obtained.

3.3 Importance sampling method integrating adaptive screening strategy

To improve the efficiency of MCS method for reliability analysis, this subsection combines the importance sampling method with an adaptive screening strategy to perform TRA on the basis of the above-constructed Kriging models.

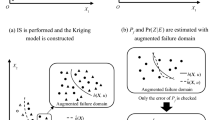
3.3.1 Adaptive screening strategy

As illustrated in Fig. 5, the sphere, which is centered at the origin of the ordinates with the reliability index as the radius, is tangent to the LSF. It is denoted as β-surface, by which the random space is divided into the failure and safe regions. It is understood that the sample points interior to β-surface are safe points whose responses of performance function are higher than 0. Therefore, the values of failure indicator function can be determined without calculating response values of these points. Accordingly, the adaptive screening strategy can be put forward as follows: (1) before calculating the values of failure indicator function, β-surface is constructed with center at the origin of the ordinates and the distance from MPP to that origin as radius; (2) sample points are checked whether they fall within β-surface. If they fall inside, they are identified as safe sample points, of which calculation of the function response is spared. Based on the above two steps, the computational efficiency will be further improved. It is worth mentioning that β-surface is straightforward to be built in view of the fact that MPPs have been derived during the update process of Kriging model.

Fig. 5

Schematic for β-surface and samples in standard normal space

3.3.2 Importance sampling method integrating adaptive screening strategy

In this subsection, the previously proposed adaptive screening strategy is integrated into the importance sampling method to circumvent computing response values of samples interior to β-surface. The steps are specified as follows:

(1) To construct the importance density function for IS method and β-surface for the adaptive screening strategy, the multivariate normal probability density function, which is denoted as $h\left( {\mathbf{Z}} \right)$, is taken as the importance density function. The mean can be calculated by

$${{\varvec{\upmu}}} = \left\{ {\left. {{\mathbf{Z}}_{{{\text{MPP}}}}^{{{\text{uni}}}} } \right|{\mathbf{Z}}_{{{\text{MPP}}}}^{{{\text{uni}}}} \left( j \right) = {\mathbf{Z}}_{{{\text{MPP}}}}^{\left( i \right)} \left( j \right),i = \mathop {{\text{argmin}}}\limits_{i} \left( {\left| {{\mathbf{Z}}_{{{\text{MPP}}}}^{\left( i \right)} \left( j \right)} \right|} \right),j = 1,2, \ldots ,d} \right\},$$

(28)

where d is the dimension of MPPs. The covariance matrix of the multivariate normal probability density is

$${{\varvec{\Sigma}}} = r{\mathbf{I}},$$

(29)

where r ranges from 1 to 2; I is the d-dimensional unit matrix. After obtaining $h\left( {\mathbf{Z}} \right)$, β-surface is constructed with the origin of the ordinates as the center, and its radius is

$$r_{\beta } = \left\| {{\mathbf{Z}}_{{{\text{MPP}}}}^{{{\text{uni}}}} } \right\|.$$

(30)

(2) LHS method is employed to generate $N_{{{\text{IS}}}}$ d-dimensional sample points ${\mathbf{Z}}_{{{\text{IS}}}} = \left[ {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( 1 \right)} ,{\mathbf{Z}}_{{{\text{IS}}}}^{\left( 2 \right)} , \ldots ,{\mathbf{Z}}_{{{\text{IS}}}}^{{\left( {N_{{{\text{IS}}}} } \right)}} } \right]$ according to the importance density function. The probability density and importance probability density of the k-th sample ${\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)}$ can then be obtained by

$$f\left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right) = \prod\limits_{j = 1}^{d} {\phi \left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} \left( j \right)} \right)}$$

(31)

$$h\left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right) = \frac{1}{{\sqrt {\left| {{\varvec{\Sigma}}} \right|\left( {2\pi } \right)^{d} } }}\exp \left( { - \frac{1}{2}\left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} - {{\varvec{\upmu}}}} \right)^{{\text{T}}} {{\varvec{\Sigma}}}^{ - 1} \left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} - {{\varvec{\upmu}}}} \right)} \right),$$

(32)

where $\phi \left( x \right)$ is probability density function of the variable that standard normally distributed.

(3) For the k-th sample ${\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)}$, as described in SubSect. 3.3.1, if $\left| {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right| \le r_{\beta }$, the sample point is identified as interior to β-surface, its failure indicator function value is 0. Otherwise, $I_{t}^{\left( k \right)}$ can be determined by

$$I_{t}^{\left( k \right)} = I_{t} \left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right) = \left\{ \begin{gathered} 1, \, \mathop {\min }\limits_{{i = 1,2, \ldots ,N_{t} }} M_{i} \left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right) \le 0 \hfill \\ 0,{\text{ otherwise}} \hfill \\ \end{gathered} \right.$$

(33)

The probability of failure can then be obtained by

$$P_{f} = \frac{1}{{N_{{{\text{IS}}}} }}\sum\limits_{k = 1}^{{N_{{{\text{IS}}}} }} {I_{t}^{\left( k \right)} \frac{{f\left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right)}}{{h\left( {{\mathbf{Z}}_{{{\text{IS}}}}^{\left( k \right)} } \right)}}} .$$

(34)

3.4 Implementation procedure

Figure 6 shows the flowchart for the proposed MPP-KIS method, and its specific implementation steps are exposited in Table 1.

Fig. 6

Flowchart for proposed MPP-KIS method

Table 1 Implementation procedure for MPP-KIS method

4 Examples and discussions

In this section, four examples are employed to validate effectiveness and proficiency of MPP-KIS. The first example is a typical mathematical example; the second is a simply supported beam; the third is RV reducer, which is an engineering case for TRA; the last is an engineering case of flexible wheel of the harmonic reducer for TRA, of which performance function is implicit. The proposed MPP-KIS method is compared with PHI2 + (Andrieu-Renaud et al. 2004), iTRPD (Jiang et al. 2018), SEVM (Meng et al. 2021), and AERS (Wang and Chen 2016). To render fair comparison, all the aforementioned methods adopt the same number of time discretization for all examples, and 10⁶ samples are taken at every time instants for MCS to guarantee accuracy. The time-dependent probability of failure approximated by MCS is considered as caliber, and the relative error is calculated through (Song et al. 2022)

$$E_{{\mathit{r}}} = \frac{{P_{f} - P_{f}^{{{\text{MCS}}}} }}{{P_{f}^{{{\text{MCS}}}} }},$$

(35)

where $E_{{\mathit{r}}}$ represents the relative error of calculation results; $P_{f}$ denotes the estimated probability of failure; $P_{f}^{{{\text{MCS}}}}$ is the computational result by MCS.

4.1 A mathematical example

The first example is a popular benchmark problem that includes a stochastic process, a set of random variables, and time parameter t. The LSF of this problem is (Meng et al. 2021)

$$g\left( {{\mathbf{x}},Y\left( t \right),t} \right) = x_{1}^{2} x_{2} - 5x_{1} \left( {1 + Y\left( t \right)} \right)t + \left( {x_{2} + 1} \right)t^{2} - 20,$$

(36)

where ${\mathbf{x}} = \, \left[ {x_{1} ,x_{2} } \right]^{{\text{T}}}$ is a vector of random variables following distribution of $N\left( {3.5,0.25^{2} } \right)$; $Y\left( t \right)$ is a stationary Gaussian process with a mean of 0 and variance of 1; time parameter t ranges from 0 to 1.

4.1.1 Effects of adjusting parameter and stopping criterion

To investigate the impacts of the adjusting parameter λ and the stopping criterion $\varepsilon_{M}$ on the performance of the proposed MPP-KIS method, parametric studies with regard to these two parameters are performed in this example. In these parametric studies, λ ranges from 1.2 to 10 and $\varepsilon_{M}$ varies from $10^{ - 4}$ to $10^{ - 1}$. The corresponding variations of probability of failure and number of functional evaluations (NOFE) are presented in Fig. 7. From Fig. 7a, the computational results of MPP-KIS approach closely to the results of MCS for the cases, where $\lambda \in \left\{ {1.2,2} \right\}$ and $\varepsilon_{M} \in \left\{ {10^{ - 4} ,10^{ - 3} ,10^{ - 2} } \right\}$, while the results by MPP-KIS with $\lambda \in \left\{ {6,10} \right\}$ or $\varepsilon_{M} = 10^{ - 1}$ exhibit a significant error. This is because larger λ ensues more rapid reduction of the sampling radius, leading the new points selected by the learning function too closer to the MPP, which further negates the prediction accuracy of the Kriging model. Besides, the accuracy of the Kriging model cannot be guaranteed if the stopping criterion is too loose. As shown in Fig. 7b, MPP-KIS with a higher adjusting parameter λ or a higher stopping criterion $\varepsilon_{M}$ can incur lower computational cost. Based on the above analysis, an optimal balance between accuracy and efficiency can be achieved by utilizing $\lambda = 2$ and $\varepsilon_{M} = 10^{ - 2}$, which are also used in other examples.

Fig. 7

Reliability analysis results of MPP-KIS with different adjusting parameters and stopping criterion

4.1.2 Comparison with other methods

The time interval $\left[ {0,1} \right]$ is equally discretized into 21 time nodes in this example. Note that AERS and the proposed method ensue 6 NOFE for the construction of each initial instantaneous Kriging model. The computational results by different methods are given in Table 2, in which time interval, NOFE, and relative error are included. From Table 2, the computational results by MPP-KIS, with a relative error less than 1%, approach more closely to counterparts of MCS than those by other methods. It indicates that MPP-KIS exhibits the highest computational accuracy compared to other methods. On the other hand, NOFE of MPP-KIS is as low as 251, which is the least among all the methods, implying the highest computational efficiency.

Table 2 Time-dependent probability of failure for example 1

To demonstrate more directly the performance of the proposed MPP-KIS method in this example, Fig. 8 plots the probability of failure throughout the time interval. From Fig. 8, curve of probability of failure by MPP-KIS is the closest to that of MCS method. Besides, probability of failure curve for PHI2 + method gradually deviates from that of MCS as the time interval expands. Furthermore, Fig. 9a depicts some parts of realizations of the LSF, and Fig. 9b shows the approximated extreme value distributions for MCS, SEVM, AERS, and MPP-KIS, which are obtained by kernel density estimation with Scott’s Rule. Since only the exact tails with extreme values less than zero are of concern when determining the probability of failure, it is of no avail that extreme value distributions of SEVM, AERS, and MPP-KIS are absolutely consistent with that of MCS throughout the entire time interval.

Fig. 8

Time-dependent probability of failure for example 1

Fig. 9

Time-dependent performance function and extreme value distribution of example 1

To further demonstrate superior model accuracy of Kriging model constructed by MPP-KIS, Table 3 compares MPP of the performance function by iHL-RF algorithm as the true value and MPP by the proposed method as the predicted value. In Table 3, the numbers outside and inside the parentheses represent values of MPP and the relative error, respectively. From Table 3, MPP by MPP-KIS is close to the true value at all the discrete time nodes. The maximum prediction error of MPP-KIS is less than 1.5%, indicating smooth convergence of the proposed method.

Table 3 Comparison of true MPP and MPP by proposed method

4.2 A simply supported beam

TRA with stochastic process load and random variables is implemented for a simply supported beam. As shown in Fig. 10, the initial rectangular cross-sectional area and length of the simple supported beam are $A_{0} = b_{0} \times h_{0}$ and L = 5 m, respectively. The entire rectangular section of this simply supported beam undergoes isotropic surface corrosion. Hence, the time-variable area is expressed as

$$A\left( t \right) = b\left( t \right) \times h\left( t \right),$$

(37)

where $b\left( t \right) = b_{0} - d_{c} \left( t \right)$ and $h\left( t \right) = h_{0} - d_{c} \left( t \right)$ are the time-variable width and length of the corroded cross-section, respectively, in which $d_{c} \left( t \right) = \kappa t$ represents the corrosion rate and $\kappa$ is the corrosion coefficient of 0.036 mm/year.

Fig. 10

Corroded simply supported beam

The simply supported beam is subjected to a dynamic load $F\left( t \right)$ in the middle and a uniformly distributed load $p = 78500b_{0} h_{0}$(N/m) over the entire beam. The beam material yield strength is denoted as $\sigma_{z}$. The structure will fail when the beam bending moment exceeds its ultimate bending moment. Therefore, the LSF of the simply supported beam can be presented as (Guo et al. 2023)

$$g\left( {{\mathbf{X}},F\left( t \right),t} \right) = \frac{F\left( t \right)L}{4} + \frac{{78500b_{0} h_{0} L^{2} }}{8} - \frac{{b\left( t \right)h\left( t \right)^{2} \sigma_{z} }}{4},$$

(38)

where $F\left( t \right)$ is the dynamic load modeled by a random process; $\sigma_{z}$, $b_{0}$, $h_{0}$ are random parameters. Table 4 shows the stats for the uncertain parameters in the simply supported beam.

Table 4 Stats for uncertain parameters in simply supported beam

In this example, the concerned time interval is [0, 10] and is equally discretized into 61 and 21 time nodes for MCS and other methods, respectively. AERS and the proposed method require NOFE of 6 to construct the initial Kriging model. Table 5 lists the computational results by all the methods, which includes time interval, NOFE, and relative error. It can be observed that the computational results by all methods except PHI2 + are close to those of MCS. The reliability analysis results by PHI2 + deviate slightly from that of MCS. In terms of computational accuracy, the relative error of the proposed MPP-KIS method is as low as 1.38%, which is lower than those of PHI2 + , iTRPD, and AERS, but slightly higher than that of SEVM. On the other hand, MPP-KIS incurs as low as 335 NOFE, which is far below those for other methods. It implies that MPP-KIS exhibits the highest computational efficiency without compromise of accuracy.

Table 5 Time-dependent probability of failure for example 2

To more directly demonstrate the advantages of the proposed MPP-KIS method, Fig. 11 depicts the curves of probability of failure over the entire time interval for all methods. From Fig. 11, the probability of failure curve for MPP-KIS is basically consistent with that of MCS over the entire time interval, while curves of other methods are slightly disparate from that of MCS. Figure 12a presents a number of realizations of the LSF, and Fig. 12b shows the approximated extreme value distributions of four methods, including SEVM, AERS, MPP-KIS, and MCS. It should be mentioned that only the accuracy of tails that the extreme value is less than zero are of interest for calculating probability of failure. From Fig. 12b, the extreme value distributions of four methods are different from each other, but the tails of AERS, MPP-KIS, and SEVM are basically similar to that of MCS method.

Fig. 11

Time-dependent probability of failure for example 2

Fig. 12

Time-dependent performance function and extreme value distribution of example 2

To further demonstrate superior model accuracy of Kriging model constructed by MPP-KIS, Table 6 compares MPP of the performance function by iHL-RF algorithm as the true value and MPP by the proposed method as the predicted value. In Table 6, the numbers outside and inside the parentheses represent values of MPP and the relative error, respectively. From Table 6, MPP by MPP-KIS is close to the true value at all the discrete time nodes. The maximum prediction error of MPP-KIS is as low as 1.3%, indicating smooth convergence of the proposed method.

Table 6 Comparison of true MPP and MPP by proposed method

4.3 RV reducer

Rotary Vector (RV) reducer is a two-stage cycloid-enclosed planetary gear transmission. As shown in Fig. 13, RV reducer consists of a planetary wheel reducer and a cycloid pinion reducer, which includes an input shaft, planetary gear, crankshaft, cycloid gear, pinion, pinion housing, roller bearing, washer, needle roller bearing, and angular contact ball bearing. RV reducer is characterized by small size, lightweight, and the high ability to achieve a wide range of transmission ratios (Yang et al. 2021). It is widely used in various industrial applications. However, due to the constantly changing external loads and the continuous degradation of material properties with time during the operation, it is susceptible to failure after long-term operation (Yang et al. 2021). Therefore, this study conducts TRA for RV reducer.

Fig. 13

Diagram for components and assembly of RV reducer (Yang et al. 2021)

4.3.1 Planetary gear

During operation, RV reducer transmits torque to the planetary gear through a motor. The following equation defines the torque output of the motor $T_{0}$,

$$T_{0} = 9550\frac{P}{n},$$

(39)

where n designates the motor rotation speed; P denotes the output power of the motor. Since the output power P varies with time in practical engineering settings, it is processed as a Gaussian process. Given number of planet gears $n_{p}$ and the unbalanced load coefficient $k_{p}$, the torque $T_{1}$ at the center axis of RV reducer can be derived as

$$T_{1} = \frac{{T_{0} }}{{n_{p} }}k_{p} .$$

(40)

Denoting the pitch circle diameter of planetary gear as d, the pitch circle circumferential force of the central wheel can be obtained as

$$F_{t} = 2\frac{T}{D} = 2000\frac{{T_{1} }}{d}.$$

(41)

According to the formula for tooth surface contacting fatigue strength of cylindrical helical gear, the calculated tooth surface contacting stress of the planetary gear can be calculated by

$$\sigma_{H} = Z_{H} Z_{E} Z_{\varepsilon } Z_{\beta } \sqrt {\frac{{K_{H} F_{t} }}{{\phi_{d} d_{1}^{2} }}\frac{u + 1}{u}} ,$$

(42)

where $Z_{H}$ is the factor of nodal area; $Z_{E}$ is the elastic coefficient; $Z_{\varepsilon }$ is the factor of contact ratio; $Z_{\beta }$ is the coefficient of helical angle; $\phi_{d} = b/d$ is the tooth width coefficient; b is the tooth width; u is the transmission ratio; $K_{H}$ the is load coefficient, which can be written as

$$K_{H} = K_{A} K_{V} K_{H\beta } K_{H\alpha } ,$$

(43)

where $K_{A}$ is the usage coefficient; $K_{V}$ is the coefficient of dynamic load; $K_{H\alpha }$ is the coefficient of load distribution between teeth; $K_{H\beta }$ is the coefficient of longitudinal load distribution.

The allowable tooth surface contact stress of the planetary gear is obtained by

$$\sigma_{H\lim j} = \sigma_{H\lim } Z_{NT} Z_{L} Z_{V} Z_{R} Z_{W} Z_{X} ,$$

(44)

where $Z_{NT}$ is the calculated life coefficient of gear’s contact strength, reflecting the load-carrying capacity of the gear in finite life; $Z_{R}$ is the tooth surface roughness factor, representing the influence of the gear’s surface roughness; $Z_{V}$ is the speed factor, indicating the influence of the circumferential linear speed of the gear nodes; $Z_{W}$ is the work hardening factor; $Z_{L}$ is the lubrication factor, representing the influence of the lubricant viscosity; $Z_{X}$ is the size factor for contact stress calculation, representing the influence of the dimensional parameters of the gear teeth on allowable contact stress; $\sigma_{H\lim }$ represents the limit of tooth surface contacting fatigue strength of test gear, which decreases with time and is given by

$$\sigma_{H\lim } = \sigma_{H\lim }^{0} e^{ - 0.002t} ,$$

(45)

where $\sigma_{H\lim }^{0}$ is initial limit of contact fatigue strength.

Based on the stress–strength interference model, the LSF of planetary wheel tooth surface contact fatigue failure can be defined according to Eqs. (44–45):

$$\begin{gathered} G = \sigma_{H\lim j} - \sigma_{H} \\ = \sigma_{H\lim } Z_{N} Z_{R} Z_{V} Z_{W} Z_{L} Z_{X} - Z_{H} Z_{E} Z_{\varepsilon } Z_{\beta } \sqrt {\frac{{1.91 \times 10^{7} k_{p} P}}{{d^{2} bn_{p} n}}\frac{u + 1}{u}K_{A} K_{V} K_{H\beta } K_{H\alpha } } \\ \end{gathered},$$

(46)

where the input power P is a Gaussian process with mean 0.4 kW, standard deviation 0.08kW, and autocorrelation coefficient function $\rho_{P} \left( {t_{1} ,t_{2} } \right) = \exp \left[ { - \left( {\left( {t_{1} - t_{2} } \right)/l} \right)^{2} } \right]$, where l = 6. The stats for the normal random variables and constants are shown in Tables 7 and 8 (Qian et al. 2020).

Table 7 Stats for random parameters of example 3.1

Table 8 Constant parameters of example 3.1

In this example, the interested time interval of is [0, 10] in year, which is equally discretized into 61 and 21 time instants for MCS and other methods, respectively. AERS and the proposed method adopt NOFE of 19 for the construction of each initial instantaneous Kriging model. The computational results by various methods are given in Table 9, in which the time interval, NOFE, and relative error are included. From Table 9, the relative error of computational results by the proposed MPP-KIS method is as low as 1.17%, which is less than those of other methods except for iTRPD. Although MPP-KIS method exhibits lower accuracy than iTRPD, its computational efficiency is the highest of all methods. Especially, it yields 73.5% reduction in NOFE compared to iTRPD, indicating a remarkably higher computational efficiency.

Table 9 Time-dependent probability of failure for example 3.1

To demonstrate more directly the performance of the proposed MPP-KIS method, Fig. 14 depicts curves of probability of failure overall time interval. According to Fig. 14, the curves of probability of failure for all the methods except for PHI2 + are close to that of MCS. The proposed MPP-KIS method exhibits the highest computational accuracy among all these methods, which proves the superiority of the proposed MPP-KIS method.

Fig. 14

Time-dependent probability of failure for example 3.1

4.3.2 Cycloid gear

In operation, the maximum contact strength at the tooth surface of RV reducer cycloid can be expressed as

$$\sigma_{H} = \sigma_{H0} \sqrt {K_{A} K_{V} K_{H} } ,$$

(47)

where $\sigma_{H0}$ is the initial contact strength; $K_{A} = 1.5$ is the service factor; $K_{V}$ is the factor of dynamic load; $K_{H}$ is the coefficient of load share between teeth. Considering that some errors are not straightforward to be assessed, the calculated coefficient $K$ is introduced to rectify the maximum tooth surface contact strength of the cycloid gear:

$$\sigma_{H} = \sigma_{H0} \sqrt {KK_{A} K_{V} K_{H} } .$$

(48)

The contacting fatigue strength of the cycloid wheel can be obtained by

$$\sigma_{H\lim s} = \sigma_{H\lim } Z_{N} Z_{L} Z_{V} Z_{R} Z_{W} Z_{X} ,$$

(49)

where $Z_{N}$ is the life factor for the contact strength calculations; $Z_{L}$ is the lubricant factor; $Z_{V}$ is the speed factor; $Z_{R}$ is the roughness factor; $Z_{W}$ is the working harden factor; $Z_{X} = 1$ is the dimensional factor; $\sigma_{H\lim }$ is the contact fatigue limit of the test gear, which decreases with time:

$$\sigma_{H\lim } = \sigma_{H\lim }^{0} e^{ - 0.003t} ,$$

(50)

where $\sigma_{H\lim }^{0}$ is the limit of initial contact fatigue of the gear.

Based on the stress–strength interference model and Eqs. (48) and (49), the LSF for cycloid gear contact fatigue failure is expressed as

$$\begin{gathered} G = \sigma_{H\lim s} - \sigma_{H} \\ = \sigma_{H\lim } Z_{N} Z_{L} Z_{V} Z_{R} Z_{W} Z_{X} - \sigma_{H0} \sqrt {KK_{A} K_{V} K_{H} } . \\ \end{gathered}$$

(51)

Stats for the distribution of normal variables in Eq. (51) are shown in Table 10 (Qian et al. 2020).

Table 10 Stats for random parameters of example 3.2

In this example, the interested time interval is [0, 10] in year, which is equally discretized into 61 and 21 time instants for MCS and other methods, respectively. It should be noted that AERS and the proposed MPP-KIS method adopt NOFE of 11 for the construction of each initial instantaneous Kriging model. Table 11 lists the calculation results by different methods, where time interval, NOFE, and relative error are included. According to Table 11, the relative error of computational results by the proposed MPP-KIS method is the lowest of 1.66% among all the methods. In contrast, the computational results by iTRPD exhibit the highest relative error. In terms of computational efficiency, the proposed MPP-KIS method ensues NOFE of 731, which is less than those for PHI2 + , SEVM, AERS, and iTRPD to register the most superior computational efficiency.

Table 11 Time-dependent probability of failure for example 3.2

To further demonstrate the superior performance of Kriging model constructed by the proposed MPP-KIS method, Fig. 15 shows the probability of failure curves in the overall time interval. According to Fig. 15, the curves by MPP-KIS and SEVM are similar to the result by MCS, while the curves by iTRPD, AERS, and PHI2 + deviate slightly from that of MCS.

Fig. 15

Time-dependent probability of failure for example 3.2

4.4 Flexible wheel case

The flexible wheel is a core transmission component of the harmonic reducer, which is one of precision reducers extensively utilized in industrial robots. It features the advantages of small volume, light weight, and superior transmission accuracy, etc. As shown in Fig. 16, the harmonic reducer is comprised of a rigid wheel, a flexible wheel, and a wave generator. The harmonic reducer incurs elastic deformation of the flexible wheel, as depicted in Fig. 17(b), by continuously rotating the wave generator, yielding a continuous cycle of engagement, meshing, disengaging, and separating between the flexible wheel and the rigid wheel via transmitting force and torque. Thus, the flexible wheel plays a pivotal role in the working process of the harmonic reducer.

Fig. 16

3D model of harmonic reducer

Fig. 17

Schematic for flexible wheel structure before and after deformation

Figure 17(a) illustrates the structure of the flexible wheel, and Table 12 tabulates the detailed relatable parameters. During operation, the influence of uncertainty factors negates the reliability of the flexible wheel to lead to premature failure. As the core driving component of the harmonic reducer, the flexible wheel’s reliability is closely related to that of the reducer, both of which govern the operational reliability and service life of industrial robots. Therefore, it is a prerequisite to evaluate the impact of uncertainty factors on the reliability of the flexible wheel. This example considers uncertain factors, such as material properties and dynamic loads, to conduct TRA with regard to the maximum equivalent stress of the flexible wheel.

Table 12 Structural parameters of flexible wheel

Figure 18 shows the equivalent stress analysis results of the flexible wheel connecting with the rigid wheel. FEM for the flexible wheel consists of 244,149 hexahedron elements and 1,013,081 nodes. The failure event can be defined as the maximum equivalent stress of the flexible wheel exceeding the allowable material strength. Accordingly, the LSF of the flexible wheel is constructed based on the stress–strength interference model:

$$G\left( t \right) = R - S\left( {{\mathbf{X}},Y\left( t \right)} \right),$$

(52)

where R represents the material strength for the flexible wheel of the harmonic reducer; $S\left( {{\mathbf{X}},Y\left( t \right)} \right)$ stands for the maximum equivalent stress that the flexible wheel is subjected to during operation. For parameterization, $S\left( {{\mathbf{X}},Y\left( t \right)} \right)$ is exported as a functional mock-up unit (FMU) file by finite element analysis software and used for reliability analysis. The expression of S can be written as

$$S\left( {{\mathbf{X}},Y\left( t \right)} \right) = S\left( {X_{1} ,X_{2} ,X_{3} ,X_{4} ,Y\left( t \right)} \right),$$

(53)

where $X_{1}$, $X_{2}$, $X_{3}$, $X_{4}$ denote tooth width, wall thickness, outside corner radius of bucket bottom, and interior corner radius of bucket bottom, respectively; $Y\left( t \right)$ is the stochastic input torque of harmonic reducer. The stats for relatable parameters are listed in Table 13.

Fig. 18

FEM equivalent stress analysis results for flexible wheel

Table 13 Stats for flexible wheel structural parameters

The time interval under consideration in this example is [0, 10] in month. The reliability analysis results including time interval, NOFE, and relative error are listed in Table 14. It should be noted that analytical methods, such as PHI2 + , SEVM, and iTRPD, cannot process this example because the LSF is implicit. From Table 14, relative error of the proposed MPP-KIS method is as low as 1.31%, which implies that the computational results of MPP-KIS are highly consistent with those by MCS. NOFE of MPP-KIS is as low as 507, which exhibits 34.8% reduction compared to that of AERS, demonstrating remarkably superior accuracy and efficiency of MPP-KIS.

Table 14 Time-dependent probability of failure for example 4

5 Conclusions

A most important point (MPP)-oriented Kriging model combined with the importance sampling (MPP-KIS) method is proposed to solve time-dependent reliability (TRA) problems. In this MPP-KIS method, surrogate models of TRA problems with high accuracy around MPP are established by the MPP-oriented Kriging modeling method, including the adaptive sampling radius formula, the learning function using approximate MPP information, and a simple and effective stopping criterion. In addition, the adaptive screening strategy is introduced into the importance sampling method to efficiently compute the time-dependent failure of probability through applying the results from the training procedure of Kriging model.

Four examples with varying complexity are employed to demonstrate performance of the proposed MPP-KIS method. It is shown that the proposed MPP-KIS method is more efficient without compromise of the solution accuracy compared to other prevailing methods when dealing with explicit and implicit time-dependent reliability problems. The established Kriging model exhibits high accuracy around its MPP, which smoothly converges toward the real performance function during the training procedure. This renders MPP-KIS a stable convergence ability. The importance sampling integrating with the adaptive screening strategy possesses good compatibility with the proposed surrogate modeling method, all of which are based on MPP.

On a whole, the proposed method can accurately and efficiently evaluate the time-dependent probability of failure. However, the computational efficiency will be negated if the time intervals are excessively discretized. In our future research, the proposed method will be expanded into the time-dependent hybrid reliability analysis to attend different sources of uncertainties. The authors will also devote to its application for time-dependent reliability-based design optimization problems considering multiple constraint functions.