An improved Kriging-based approach for system reliability analysis with multiple failure modes

Abstract

Reliability analysis with multiple failure modes is needed because more than one failure mode exists in many engineering applications. Kriging-based surrogate model is widely adopted for component reliability analysis because of its high computational efficiency. Compared with Kriging-based component reliability analysis, selecting the sample points that affect the system performance is more difficult than that of a single failure mode in system reliability analysis. Therefore, how to select suitable sample points is a key problem in system reliability analysis. Meanwhile, reducing the number of calls to the performance functions is challenging, especially for systems with time-consuming performance functions. In this paper, an improved Kriging-based system reliability analysis approach is proposed based on the two strategies. In strategy 1, the initial sample points are determined by considering only two different cases: (a) the candidate samples are selected from the safe regions only for series systems; (b) the candidate samples are selected from the failure regions only for parallel systems. Therefore, samples having little contributions to the composite performance function are avoided. In strategy 2, the sample points determined in strategy 1 will be further optimized by interpolating. From comparisons with three reported methods in numerical examples, the efficiency and accuracy of the proposed method are illustrated.

1 Introduction

Structural reliability analysis (SRA) aims to estimate the failure probability of a component or a system considering various uncertainties, such as geometric parameters and material properties. It plays an important role in ensuring the quality of the product. As a result, it has received considerable attention in many fields, including electric vehicles [1], bridges [2], robots [3], etc. In general, SRA can be divided into two categories: component reliability analysis and system reliability analysis. Because multiple failure modes exist in real engineering applications, SRA under multiple failure modes is needed.

In SRA, the failure probability $P_{{\text{f}}}$ is defined as

$$ P_{{\text{f}}} = \int_{F} {f({\varvec{x}}){\text{d}}x} , $$

(1)

where F refers to the failure region when the response value of performance function G(x) is less than 0 (G(x) < 0), and f(x) is the joint probability density function of the random variables. Generally, $P_{{\text{f}}}$ cannot be directly estimated by the integral in Eq. (1), because the form of G(x) is often complex and highly nonlinear. To address this problem, many reliability methods are reported. The Monte Carlo Simulation (MCS) with large sample size is a classical one to provide benchmark results for accuracy comparisons. However, the MCS is not appropriate if implicit performance functions are involved, because numerous simulations such as finite element analysis is extremely time-consuming [4]. To reduce computational burden, surrogate models are adopted for SRA in recent years, then, the implicit performance functions are replaced by surrogate models for reliability analysis. These surrogate models include support vector machines (SVM) [5], response surface method (RSM) [6], polynomial chaos expansion (PCE) [7], artificial neural networks (ANN) [8, 9], hybrid models [10], extended support vector regression(X-SVR) [11], and Kriging [12,13,14,15,16,17,18,19,20]. Among them, Kriging-based SRA has received more attention as it has excellent characteristics: exact interpolation and a local index of uncertainty on the prediction [12].

Many Kriging-based methods have been reported in component reliability analysis (CRAS) in recent years. Echard [12] reported an active learning reliability method combining Kriging and MCS (AK-MCS), and AK-MCS is a competitive method in CRAS; subsequently, several other approaches are reported to improve the AK-MCS, please see Refs [13, 14, 16] for detail. However, system reliability analysis (SRAS) is more difficult than CRAS, because it involves multiple failure modes. As a result, existing Kriging-based CRAS methods, in general, cannot be directly applied to SRAS efficiently. Fauriat [15] extended the AK-MCS method for system reliability; then, a useful and competitive method for system reliability analysis, i.e., AK-SYS, was reported. Based on the AK-SYS, Yun [21] refined learning function U and proposed an improved adaptive Kriging model for SRAS. Yang [16] reported an active learning Kriging model with a truncated candidate region for SRAS. Xiao [22] reported an adaptive Kriging-based efficient reliability method for structural systems with multiple failure modes and mixed variables. Gong [23] reported an important sampling-based system reliability analysis of corroding pipelines considering multiple failure modes. Perrin [32] reported an active learning surrogate model for the conception of systems with multiple failure modes. These aforementioned works are useful for SRAS. However, the applicability of them is generally lower than the AK-SYS because the latter is very easy to implement. In AK-SYS, the key idea is to construct a composite performance to select new sample points. However, some samples, which have very little contributions to the construction of composite performance function, may be selected and added to the design of experiments (DoE) [24] during the process. These useless samples may increase the number of calls to the performance and, thus, increase computation time. Because the highly applicability of AK-SYS, an improved system reliability analysis method is proposed based on AK-SYS in this paper. First, a new sampling-based strategy is employed to determine the initial candidate sample points; sample points in safe regions are considered for series systems, whereas in failure regions are for parallel systems. Then, the initial candidate sample points are further optimized in strategy 2 by interpolating. Based on these two strategies, an improved Kriging-based approach for system reliability analysis with multiple failure modes is proposed based on AK-SYS; it is termed as IK-SRA. Finally, an effective composite performance function is constructed by the proposed method; it requires generally fewer function calls compared with AK-SYS to achieve almost the same accuracy level.

The rest of the paper is organized as follows. Section 2 gives a brief review of Kriging and the system reliability analysis. Section 3 gives details of proposed method. Five numerical examples are analyzed in Sect. 4 to show the proposed method. Finally, the conclusion is summarized in Sect. 5.

2 Basic theory

2.1 Kriging theory

Kriging is one of the most used estimators for interpolation of spatial data [25,26,27]. There are several types of Kriging models, such as ordinary Kriging, simple Kriging, universal Kriging, indicator Kriging, and co-Kriging [28]. The most commonly used one is ordinary Kriging, such as in references [12, 29,30,31]. In this paper, the ordinary Kriging method is selected. Kriging possesses two main interesting characteristics: exact interpolation, and a local index of uncertainty on the prediction. The Kriging model consists of two main parts: a linear regression model and a stochastic process, which is defined as follows [33]:

$$ \hat{G}({\varvec{x}}) = f^{{\text{T}}} ({\varvec{x}})\beta + Z({\varvec{x}}), $$

(2)

where $f({\varvec{x}}) = [f_{1} (x),f_{2} (x), \ldots ,f_{p} (x)]^{{\text{T}}}$ is the vector of basic functions and $\beta$ is the vector of the regression coefficients, and $Z({\varvec{x}})$ is a stationary Gaussian process with zero mean. The covariance between any two experimental sample points is defined as follows:

$$ {\text{Cov}}(Z(x_{i} ),Z(x_{j} )) = \sigma^{2} R(x_{i} ,x_{j} ),\;i,j = 1,2, \ldots ,N, $$

(3)

where $\sigma^{2}$ is the process variance and $R(x_{i} ,x_{j} )$ is the Gaussian correlation function [34]. Gaussian correlation function is adopted in this study and is defined as follows [35]:

$$ R(x_{i} ,x_{j} ) = \exp \left( { - \sum\nolimits_{t = 1}^{n} {\theta_{t} \left| {x_{it} - x_{jt} } \right|^{2} } } \right), $$

(4)

where n is the dimensionality number of the random vector ${\varvec{x}}$,$\theta_{t}$ is the correlation parameter, and $x_{it} ,x_{jt}$ are the tth components of vectors ${\varvec{x}}_{{\varvec{i}}}$ and ${\varvec{x}}_{j}$, respectively [36]. In this study, the regression part of the Kriging model is constant. Then, the parameters $\beta$ and $\sigma^{2}$ can be computed by [37]

$$ \hat{\beta } = ({\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}})^{ - 1} {\varvec{F}}^{T} {\varvec{R}}^{ - 1} G, $$

(5)

$$ \hat{\sigma }^{2} = \frac{1}{N}(G - \, {\varvec{F}}\hat{\beta })^{T} {\varvec{R}}^{ - 1} (G - \, {\varvec{F}}\hat{\beta }), $$

(6)

where F is a vector of $f({\varvec{x}})$ and G is the vector of the response obtained at each random input variable. R is the correlation matrix, i.e.,

$$ {\varvec{R}} = \left[ {\begin{array}{*{20}c} {R(x_{1} ,x_{2} )} & \cdots & {R(x_{1} ,x_{N} )} \\ \vdots & \ddots & \vdots \\ {R(x_{N} ,x_{1} )} & \cdots & {R(x_{N} ,x_{N} )} \\ \end{array} } \right]. $$

(7)

The correlation parameter $\theta_{t}$ can be calculated using the maximum likelihood estimation:

$$ \hat{\theta } = \arg \mathop {\min }\limits_{\theta } (\det \, {\varvec{R}})^{\frac{1}{n}} \hat{\sigma }^{2} . $$

(8)

According to the Gaussian regression theory, $\hat{G}\left( { \, {\varvec{x}}} \right)$ follows a normal distribution $\hat{G}\left( { \, {\varvec{x}}} \right)\sim N\left( {\mu_{{\hat{G}}} \left( { \, {\varvec{x}}} \right),\sigma_{{\hat{G}}}^{2} \left( { \, {\varvec{x}}} \right)} \right)$, with the following expressions:

$$ \mu_{{\hat{G}}} ({\varvec{x}}) = f^{T} ({\varvec{x}})\hat{\beta } + r^{T} ({\varvec{x}}){\varvec{R}}^{ - 1} (G - F\hat{\beta }), $$

(9)

$$ \sigma_{{\hat{G}}}^{2} ({\varvec{x}}) = \sigma^{2} - [f^{T} ({\varvec{x}})r^{T} ({\varvec{x}})]\left[ {\begin{array}{*{20}c} 0 & {{\varvec{F}}^{T} } \\ {\varvec{F}} & {\varvec{R}} \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {f({\varvec{x}})} \\ {r({\varvec{x}})} \\ \end{array} } \right], $$

(10)

where $r^{T} ({\varvec{x}}) = [R({\varvec{x}},{\varvec{x}}_{1} ),...,R({\varvec{x}},{\varvec{x}}_{N} )]^{T}$ is a vector containing the covariance between x and each experimental sample. Generally, both $\mu_{{\hat{G}}} ({\varvec{x}})$ and $\sigma_{{\hat{G}}}^{2} ({\varvec{x}})$ can be evaluated by MATLAB toolbox DACE [34].

2.2 System reliability analysis

In this study, both parallel and series systems are considered. The failure probability of the parallel and series systems are defined as

$$ P_{{f_{{{\text{parallel}}}} }} = P\left\{ {\bigcap\limits_{i = 1}^{k} {g_{i} (x) < 0} } \right\} = P\left\{ {\mathop {\max }\limits_{i = 1}^{k} g_{i} (x) < 0} \right\}, $$

(11)

and

$$ P_{{f_{{{\text{series}}}} }} = P\left\{ {\bigcup\limits_{i = 1}^{k} {g_{i} (x) < 0} } \right\} = P\left\{ {\mathop {\min }\limits_{i = 1}^{k} g_{i} (x) < 0} \right\}, $$

(12)

respectively, where k is the number of failure modes, and $g_{i} ({\varvec{x}})$ is the performance function of the corresponding ith failure mode.

One of the most classical ways to address system reliability problems by surrogate models is to convert multiple performance functions into a single composite performance function. In general, the composite performance functions of parallel and series systems can be, respectively, expressed with performance function as follows:

$$ \left\{ {x:\bigcap\limits_{j = 1}^{p} {g_{j} \left( x \right) \le 0} } \right\}{ = }\left\{ {x:g_{{{\text{comp}}}} \left( x \right)\mathop \equiv \limits^{{{\text{def}}}} \mathop {\max }\limits_{j} g_{j} (x) \le 0} \right\}, $$

(13)

$$ \left\{ {x:\bigcup\limits_{j = 1}^{p} {g_{j} \left( x \right) \le 0} } \right\}{ = }\left\{ {x:g_{{{\text{comp}}}} \left( x \right)\mathop \equiv \limits^{{{\text{def}}}} \mathop {\min }\limits_{j} g_{j} (x) \le 0} \right\}. $$

(14)

3 The proposed method based on AK-SYS

In this study, to illustrate the effectiveness of the proposed method, it is compared with the classical methods AK-SYS and ALK-TCR. Herein, the two methods are briefly reviewed. Then, the two strategies of the proposed method are described in detail. Finally, the summary of the proposed method is given.

3.1 Review of AK-SYS and ALK-TCR

AK-SYS is an adaptation of the classical method AK-MCS for system reliability analysis [15]. Three different strategies were reported in AK-SYS: Component approach, composite model approach and composite criterion approach.

The composite criterion approach is more efficient than others, as shown in AK-SYS [15]. The brief introduction for the third one is made herein. In this approach, surrogate models are no longer updated simultaneously, whereas just one surrogate model is updated based on the active learning function. The active learning function is defined as

$$ U_{S} ({\varvec{x}}^{(i)} ) = \frac{{\left| {\hat{g}_{S} ({\varvec{x}}^{(i)} )} \right|}}{{\sigma_{{\hat{g}_{S} ({\varvec{x}}^{(i)} )}} }}, $$

(15)

where $\hat{g}_{s}$ is the response of performance function and $\sigma_{{\hat{g}_{s} }}$ is the standard deviation from Kriging model; s refers to the target sample points and the following are the details to determine these sample points:

For parallel systems,

$$ s_{j,i} = \arg \left\{ {\mathop {\max }\limits_{j = 1}^{k} g_{j} ({\varvec{x}}_{i} )} \right\},\;i = 1,2,...,N, $$

(16)

where k is the number of failure modes. Similarly, for series systems, it is given as follows,

$$ s_{j,i} = \arg \left\{ {\mathop {\min }\limits_{j = 1}^{k} g_{j} ({\varvec{x}}_{i} )} \right\},i = 1,2, \ldots ,N, $$

(17)

where s can be described as the following matrix:

$$ s = \left[ {\begin{array}{*{20}c} {s_{1,1} } & \cdots & {s_{{1,i_{1} }} } & \cdots & {s_{1,N} } \\ {s_{2,1} } & \cdots & {s_{{2,i_{2} }} } & \cdots & {s_{2,N} } \\ \cdots & \cdots & {s_{{j,i_{j} }} } & \cdots & \cdots \\ {s_{k - 1,1} } & \cdots & {s_{{k - 1,i_{k - 1} }} } & \cdots & {s_{k - 1,N} } \\ {s_{k,1} } & \cdots & {s_{{k,i_{k} }} } & \cdots & {s_{k,N} } \\ \end{array} } \right]_{k \times N} . $$

(18)

Then, the best added sample point can be determined by

$$ x_{j,i} \leftarrow \arg \left\{ {\mathop {\min }\limits_{j,i} U_{j,i} } \right\}. $$

(19)

The processes of AK-SYS can be described as follows [15]:

• a. Generating N samples based on MCS, and selecting N₀ samples by Latin Hypercube Sampling (LHS), ${\varvec{x}}_{i} ,i = 1, \ldots ,N_{0}$. Then, the initial DoE is generated by $(x_{i} ,\hat{g}_{j,i} (x_{i} ))$;

• b. Constructing the initial Kriging models of each failure modes, respectively. These constructed Kriging models are denoted as $M_{j} ,j = 1,2, \ldots ,k,$ and k is the number of failure modes;

• c. Determining the composite failure mode of each sample by Eqs. (16) or (17) to obtain $M_{j,i}$;

• d. Estimating the learning function values of all samples by Eq. (15);

• e. Determining the minimum value $U_{{{\text{min}}}}$ and the best candidate sample $x_{j,i}$;

• f. Judging the convergence criterion. If satisfied, proceed to (h), else to (g);

• g. Updating the DoE and corresponding surrogate model $M_{j}$. And go to (c);

• h. Estimating system probability failure $P_{{f_{{{\text{system}}}} }}$.

However, AK-SYS fails to rightly identify the insignificant component if the values of component performance functions exist large numerical difference. Therefore, Yang [16] reported a system reliability analysis method through active learning Kriging model with truncated candidate region, it is termed as ALK-TCR. The basic idea of ALK-TCR is to pay little attention to the insignificant components in the design space.

In ALK-TCR, a truncated candidate region was proposed to identify the unimportant components, such as the arc O₁C, O₁B, O₂E, and O₂D, and making the sampling near the important component, such as arc AO₁O₂F, as shown in the Fig. 1.

Fig. 1

A series system with three components [16]

The adaptive truncating region is defined as [16]

$$ \tilde{T}_{k} = \left\{ {\bigcup\limits_{i = 1}^{k - 1} {\tilde{T}_{k}^{i} } } \right\} \cup \left\{ {\bigcup\limits_{i = k + 1}^{p} {\tilde{T}_{k}^{i} } } \right\}, $$

(20)

where $\tilde{T}_{k}^{i} = \left\{ {{\varvec{x}}\left| {u_{g}^{i} ({\varvec{x}}) \le - \delta \sigma_{g}^{i} ({\varvec{x}})} \right.} \right\}$ is for a series system. For a parallel system, $\tilde{T}_{k}^{i} = \left\{ {{\varvec{x}}\left| {u_{g}^{i} ({\varvec{x}}) \ge \delta \sigma_{g}^{i} ({\varvec{x}})} \right.} \right\}.$

3.2 The proposed method

In this section, two strategies are introduced in detail. In strategy 1, based on the U learning function, a sampling strategy is proposed for series and parallel systems, respectively. To avoid selecting samples that have little contributions to the construction of composite performance function, Strategy 2 is used to further optimize the initial candidate samples.

3.2.1 Strategy 1: determining the initial candidate sample points.

A series system with three failure modes is shown in Fig. 2. The composite performance function g_comp can be obtained through Eq. (14). Therefore, the arc A₁O₁O₂B₃ is on the limit state of the composite performance function. As shown in Fig. 3, the failure and safe regions are divided by the arc A₁O₁O₂B₃. To yield accurate failure probability, it is important to have accurate composite performance function. In other words, the surrogate models should be accurate compared with arc A₁O₁O₂B₃. Furthermore, surrogate models in other regions such as: arc O₁A₂, O₁B₁, O₂A₃, and O₂B₂ are not required accurately because the samples in these regions are always less than 0.

Fig. 2

A series system with three failure modes

Fig. 3

The limit state of a composite performance function in a series system

Similarly, a parallel system with three failure modes is shown in Fig. 4. The composite performance function can be obtained through Eq. (13). It is easy to know that the arc A₃O₂B₁ divides space into failure and safe regions, as shown in Fig. 5. To yield accurate failure probability, it is important to have accurate composite performance function. In other words, the surrogate models should be accurate compared with arc A₃O₂B₁. Furthermore, surrogate models in other regions such as: arc A₁O₂, A₂B₂, and B₃O₂ are not required accurately because the samples in these regions are always greater than 0.

Fig. 4

A parallel system with three failure modes

Fig. 5

The limit state of a composite performance function in a parallel system

For a series system, the composite performance function can be described as

$$ g_{{{\text{comp}}}} = \left\{ {\begin{array}{*{20}c} { < 0,\mathop \cup \limits_{i = 1}^{k} g_{i} < 0} \\ { > 0,\mathop \cap \limits_{i = 1}^{k} g_{i} > 0} \\ \end{array} } \right., $$

(21)

where k is the number of failure modes. For a series system, the values of all performance functions are greater than 0 in the safe regions; whereas in the failure regions, at least one is less than 0. To reduce the computational burden, the surrogate model of each component in the failure region is not required to accurately constructed because most of them have almost no contributions to the failure probability. Thus, the safe regions are considered for selecting samples for series systems. Then, an improved learning function based on AK-SYS is proposed as follows:

$$ \begin{array}{*{20}l} {\min U_{S} (x^{{(i)}} ) = \frac{{\left| {\hat{g}_{S} (x^{{(i)}} )} \right|}}{{\sigma _{{\hat{g}_{S} (x^{{(i)}} )}} }},} \hfill \\ {\text{s.t.}}{\left\{ {x\left| {g_{1} (x_{i} ) \cap \cdots g_{{k - 1}} (x_{i} ) \cap g_{k} (x_{i} ) > 0} \right.} \right\},i = 1,2, \ldots ,N.} \hfill \\ \end{array} $$

(22)

For a parallel system, the composite performance function can be given by

$$ g_{{{\text{comp}}}} = \left\{ {\begin{array}{*{20}c} { < 0,\mathop \cap \limits_{i = 1}^{k} g_{i} < 0} \\ { > 0,\mathop \cup \limits_{i = 1}^{k} g_{i} > 0} \\ \end{array} } \right.. $$

(23)

For a parallel system, the values of all performance functions are less than 0 in the failure regions; whereas in the safe regions, at least one is greater than 0. As aforementioned discussions, the failure regions are considered for selecting samples for parallel system. Similarly, an improved learning function based on AK-SYS is proposed for parallel systems as follows:

$$ \begin{array}{*{20}l} {\min U_{S} (x^{{(i)}} ) = \frac{{\left| {\hat{g}_{S} (x^{{(i)}} )} \right|}}{{\sigma _{{\hat{g}_{S} (x^{{(i)}} )}} }},} \hfill \\ {\text{s.t.}} {\left\{ {x\left| {g_{1} (x_{i} ) \cap \cdots g_{{k - 1}} (x_{i} ) \cap g_{k} (x_{i} ) < 0} \right.} \right\},i = 1,2, \ldots ,N.} \hfill \\ \end{array} $$

(24)

3.2.2 Strategy 2: optimizing the initial candidate samples

Based on strategy 1, an initial candidate sample point is identified. However, it may not be the best candidate sample point because its U function value is not the global minimum according to Eq. (15). Therefore, the candidate sample points determined by strategy 1 need to be further optimized.

Herein, strategy 2 is proposed to further optimize the candidate sample points by interpolation. In strategy 2, one of the sample points is determined by strategy 1, and is called X_s1 as shown in Fig. 6. The other sample is determined by the shortest distance between X_s1 and the samples that are residing in the counterpart regions of the limit state function; this sample point is denoted as X_s2, as shown in Fig. 6. For each performance function, at least one sample point is in the failure region. The sample point X_s2 can be determined by the following:

$$ \begin{gathered} \mathop {\arg }\limits_{{X_{i} }} \left\{ {\min (D({\varvec{X}}_{i} ))} \right\} \hfill \\ D({\varvec{X}}_{i} ) = \sqrt {\sum\limits_{k = 1}^{d} {(X_{i}^{k} - X_{s1}^{k} )^{2} } } \hfill \\ \begin{array}{*{20}c} {\text{s.t.}} \\ {} \\ \end{array} \left\{ {\begin{array}{*{20}l} {g({\varvec{X}}_{i} ) \cdot g({\varvec{X}}_{s1} ) < 0} \hfill \\ {\exists g_{1} (x_{i} ) < 0,\exists g_{2} (x_{i} ) < 0, \ldots ,\exists g_{k} (x_{i} ) < 0} \hfill \\ \end{array} } \right.{ ,} \quad i = 1,2, \ldots ,N, \hfill \\ \end{gathered} $$

(25)

where d is the dimension of the variables, and X_i is the sample point that has the opposite response sign to the sample point X_s1; D is the distance between sample points X_i and X_s1. Then, N_t sample points are interpolated between these two sample points X_s1, X_s2. Finally, the next best sample point is determined by the learning function U. Mathematically, the strategy can be expressed as follows

$$ \begin{gathered} \mathop {\min }\limits_{{{\varvec{X}}_{q} }} U({\varvec{X}}_{q} ), \, q = 1,2, \ldots ,N_{t} ,N_{t} + 1,N_{t} + 2 \hfill \\ {\text{ s}}{\text{.t}}{. }{\varvec{X}}_{q} = {\varvec{X}}_{s1} (1 - t) + {\varvec{X}}_{s2} t, \, 0 \le t \le 1, \hfill \\ \end{gathered} $$

(26)

where X_q is the random interpolated sample point between sample points X_s1 and X_s2, and the number of interpolations is N_t. Then, the next best sample point can be determined by the minimum U value from these N_t + 2 samples. In this study, N_t is set as 100.

Fig. 6

The distance from the initial candidate sample point to the sample points on the other side of limit state function

The processes of abovementioned two strategies for series systems with three failure modes are shown in Fig. 7. First, the safe region is selected according to Eq. (21), as shown in the Part 1 of Fig. 7. Then, the initial best sample point X_s1 and the corresponding performance function are determined according to Eq. (22) in the selected safe region, as shown in the Part 2 of Fig. 7. Finally, optimizing the initial best sample point by interpolation between sample points X_s1 and X_s2, where X_s2 is determined according to Eq. (25), is shown in the Part 3 of Fig. 7. Similarly, the processes of the proposed method for a parallel system are shown in Fig. 8.

Fig. 7

The process of the proposed method for a series system

Fig. 8

The process of the proposed method for a parallel system

3.3 Summary of the proposed method

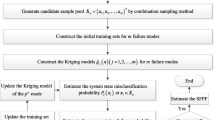
The flowchart of the proposed method is shown in Fig. 9, and the main steps are structured as follows:

• Step 1: Generating N samples based on the distributions of variables; Defining the initial DoE as the training points, the same number of initial training samples is used for the proposed method, AK-SYS and ALK-TCR. Latin hypercube sampling (LHS) method is adopted to generate these samples, and the lower bound and the upper bound of LHS are determined by $\{ \mathop {\min }\nolimits_{i = 1}^{N} {\varvec{x}}_{i} ,\mathop {\max }\nolimits_{i = 1}^{N} {\varvec{x}}_{i} \}$, respectively;

• Step 2: Constructing the Kriging model of each failure mode and predicting the responses and variances of these N samples using the constructed Kriging models;

• Step 3: Determining the initial best sample point through Eq. (15);

• Step 4: Determining the sampling regions. The failure regions are selected for parallel systems through Eq. (23), and the safe region for series systems through Eq. (21);

• Step 5: Judging the regions where the initial best sample points are located. If the sample points meet the requirements according to Eqs. (22) or (24), proceed to step 6; otherwise, remove this sample point and go back to step 3.

• Step 6: Optimizing the initial sample points. First, determining the sample point X_s2 according to Eq. (25). Then, N_t samples will be interpolated between these two sample points X_s1 and X_s2, and determining the next best sample point from the N_t + 2 samples by Eq. (26);

• Step 7: Judging the convergence. If U ≤ 2, proceed to step 8; otherwise, predicting the response of the current best sample point and go back to step 2;

• Step 8: Computing the failure probability.

Fig. 9

Flowchart of the proposed method

4 Validation and comparison with numerical examples

In this section, five numerical examples are studied, including two parallel systems and three series systems. Examples 1 and 2 are used to illustrate the efficiency and high accuracy of the proposed method; example 3 is used to illustrate the robustness of the proposed method for a parallel system with disconnected failure regions; example 4 is used to illustrate the effectiveness of the proposed method for moderate dimensions. The last example is used to illustrate the applicability of the proposed method to engineering problems with implicit performance functions. The reliability results estimated by MCS is regarded as the benchmark, and the results estimated by AK-SYS, ALK-TCR and the proposed method are compared.

4.1 Example 1 A parallel system with three failure modes

A parallel system with three failure modes, g₁, g₂ and g₃ is used [15, 16]. The performance functions are defined as follows

$$ \left\{ {\begin{array}{*{20}l} {g_{1} ({\varvec{x}}) = 8{\varvec{x}}_{2}^{2} - 8{\varvec{x}}_{1}^{2} + \left( {{\varvec{x}}_{1}^{2} + {\varvec{x}}_{2}^{2} } \right)^{2} } \hfill \\ {g_{2} ({\varvec{x}}) = 2{\varvec{x}}_{1}^{2} - 2{\varvec{x}}_{1}^{2} - \left( {{\varvec{x}}_{1}^{2} + {\varvec{x}}_{2}^{2} } \right)^{2} } \hfill \\ {g_{3} ({\varvec{x}}) = \alpha \left\{ {8{\varvec{x}}_{2}^{2} - 8{\varvec{x}}_{1}^{2} - \left( {{\varvec{x}}_{1}^{2} + {\varvec{x}}_{2}^{2} } \right)^{2} } \right\}} \hfill \\ \end{array} } \right., $$

(27)

where ${\varvec{x}}_{1}$ and ${\varvec{x}}_{2}$ follow the standard normal distribution,${\varvec{X}}\sim N({0},{1})$, and $\alpha$ is a parameter that affects the value of g₃. In this paper, to illustrate the robustness of the proposed method, the parameter $\alpha$ with two values $\alpha = 1$ and $\alpha = 1000$ is, respectively, considered.

To illustrate the effectiveness of the proposed method, three different methods, i.e., MCS, AK-SYS, and ALK-TCR, are compared. For the fair comparisons, the same number of samples, i.e., 12 sample points, generated by LHS is used and added to the initial DoE for AK-SYS, ALK-TCR and the proposed method. The number of samples used for MCS is 1×10⁵, and the candidate samples size is set as $N = 1 \times 10^{4}$ in AK-SYS, ALK-TCR and the proposed method. The result of MCS with $N_{{{\text{MCS}}}} = 1 \times 10^{5}$ samples is a benchmark for comparisons. $\varepsilon$ is the absolute value of the relative error, and $\varepsilon = \left| {\hat{P}_{{\text{f}}} - P_{{\text{f}}} } \right|/P_{{\text{f}}}$. Cov stands for the coefficients of variation.

The results obtained from different methods are listed in Table 1. To reduce the uncertainty of results, all compared methods are performed 20 times independently, and the average results are reported. The box diagram is used to show the distribution of results, as shown in Fig. 12. Also, standard deviations are given to illustrate the robustness of the method. N_calls is the number of calls to the performance function. Based on Table 1, the N_calls of proposed method IK-SRA is 85.1, and is less than both AK-SYS and ALK-TCR with 96.2 and 94.6, respectively. Therefore, the proposed method is more efficient than both in this example. Note that g₃ = 0 does not contribute to the composite performance function, as shown in Fig. 10. Therefore, evaluation on g₃ = 0 is useless for reliability analysis. Meanwhile, from Table 1, it shows that the failure probability estimated by the proposed method is more accurate than ALK-TCR, however, the relative error of AK-SYS is 0.05%, which is more accurate than that of the proposed method. The proposed method improves the efficiency of reliability analysis by reducing the number of calls to performance functions, as shown in Fig. 11, the percentage improvements in efficiency ($p = \left| {\frac{1}{{N_{{{\text{calls}}}} \left( {\text{IK-SRA}} \right)}} - \frac{1}{{N_{{{\text{calls}}}} \left( {\text{AK-SYS/ALK-TCR}} \right)}}} \right|/\frac{1}{{N_{{{\text{calls}}}} \left( {\text{AK-SYS/ALK-TCR}} \right)}}$) are 13% and 11.2% compared with AK-SYS and ALK-TCR, respectively (Fig. 12).

Table 1 Result of example 1, $\alpha = 1$

Fig. 10

The composite performance function of the numerical example 1

Fig. 11

The percentage improvement in efficiency in example 1

Fig. 12

The boxes of three methods AK-SYS, ALK-TCR and the proposed method in case 1 of example 1

Figure 13 shows the limit state function of each failure modes, the selected samples added to DoE, the selected samples by each Kriging model in the whole update process, and the constructed Kriging models of each failure mode by AK-SYS. Figure 14 shows that by ALK-TCR, and Fig. 15 shows that by IK-SRA. The converging processes of different methods are shown in Fig. 16, which shows that the proposed method converges quickly and achieves accurate results.

Fig. 13

The process of sampling in AK-SYS for $\alpha = 1$ in example 1

Fig. 14

The process of sampling in ALK-TCR for $\alpha = 1$ in example 1

Fig. 15

The process of sampling in IK-SRA for $\alpha = 1$ in example 1

Fig. 16

The convergence processes of different methods for $\alpha = 1$ in example 1

For $\alpha = 1000$, reliability results computed by MCS, AK-SYS, and ALT-TCR are listed in Table 2. Figure 17 shows the distributions of results estimated by each method in 20 runs. It shows that the proposed method IK-SRA is more effective than AK-SYS and ALK-TCR because its N_calls is 84.2, whereas AK-SYS and ALK-TCR are 105.8 and 93.7 in this case, g₃ = 0 does not contribute to the composite performance function, as shown in Fig. 10. Table 2 shows that N_calls on g₃ = 0 is almost zero in the proposed method, which improves computational efficiency in reliability analysis. The proposed method improves the efficiency of reliability analysis by reducing the number of calls to performance functions, as shown in Fig. 11, the percentage improvements in efficiency are 25.7% and 11.3% compared with AK-SYS and ALK-TCR, respectively.

Table 2 Result of example 1, $\alpha = 1000$

Fig. 17

The boxes obtained by three methods AK-SYS, ALK-TCR and the proposed method in case 2 of example 1

Figure 18 shows the limit state function of each failure modes, the selected samples added to DoE, the selected samples by each Kriging model in the whole update process, the constructed Kriging models of each failure mode by AK-SYS. Figure 19 shows that by ALK-TCR. Figure 20 shows that by IK-SRA. The converging processes of different methods are shown in Fig. 21, which shows that the proposed method has the fast convergence speed and high accuracy level.

Fig. 18

The process of sampling in AK-SYS for $\alpha = 1000$ in example 1

Fig. 19

The process of sampling in ALK-TCR for $\alpha = 1000$ in example 1

Fig. 20

The process of sampling in IK-SRA for $\alpha = 1000$ in example 1

Fig. 21

The convergence processes of different methods for $\alpha = 1{000}$ in example 1

4.2 Example 2 A series system with three failure modes

A series system with three failure modes is studied in example 2 [16]. The three failure models are defined as

$$ \left\{ {\begin{array}{*{20}l} {g_{1} ({\varvec{x}}) = \sin (2.45x_{1} ) - (x_{1}^{2} + 3.9)(x_{2} + 2)/20} \hfill \\ {g_{2} ({\varvec{x}}) = 100\sin (2.5x_{1} ) - 5(x_{1}^{2} + 4)(x_{2} + 0.5)} \hfill \\ {g_{3} ({\varvec{x}}) = 1000\sin (2.55x_{1} ) - 5(10x_{1}^{2} + 41)(x_{2} - 1)} \hfill \\ \end{array} } \right., $$

(28)

in which variable x obeys uniform distribution: $x_{1} \in [ - 4,4]$ and $x_{2} \in [ - 20,2]$. Figure 22 shows the schematic of these three failure modes. The Fig. 22 shows that the failure probability is dependent on the first failure mode g₁.

Fig. 22

A series system in example 2

For a fair comparison, 12 sample points are selected by LHS method and added to the initial DoE for all compared methods. The number of samples used for MCS is 1×10⁵, and the candidate samples size is set as $N = 1 \times 10^{{4}}$ for AK-SYS, ALK-TCR and the proposed method. The results obtained from different methods are listed in Table 3. Figure 23 shows the distributions of results estimated by each method with 20 runs. Based on Table 3, the N_calls of proposed method IK-SRA is only 72.1, and is less than both AK-SYS and ALK-TCR with109.9 and 92.8, respectively. Therefore, the proposed method is more efficient than both in this example. Note that g₂ = 0 and g₃ = 0 do not contribute to the composite performance function, as shown in Fig. 22. Therefore, evaluation on g₂ = 0 and g₃ = 0 is useless for reliability analysis. Meanwhile, from Table 3, it shows that ALK-TCR is slightly more accurate than the proposed method. The proposed method improves the efficiency of reliability analysis by reducing the number of calls to performance functions, and the percentage improvements in efficiency are 52.4% and 28.7% compared with AK-SYS and ALK-TCR, respectively.

Table 3 Result of example 2

Fig. 23

The boxes results obtained by three methods AK-SYS, ALK-TCR and the proposed method in example 2

Figure 24 shows the limit state function of each failure modes, the selected samples added to DoE, the selected samples by each Kriging model in the whole update process, and the constructed Kriging models of each failure mode by AK-SYS. Figure 25 shows that by ALK-TCR, and Fig. 26 shows that by IK-SRA. The converging processes of different methods are shown in Fig. 27.

Fig. 24

The process of sampling in AK-SYS in example 2

Fig. 25

The process of sampling in ALK-TCR in example 2

Fig. 26

The process of sampling in IK-SRA in example 2

Fig. 27

The convergence processes of different methods in example 2

4.3 Example 3 A parallel system with disconnected regions

This example is a parallel system with disconnected failure regions [16], and its failure probability is defined as

$$ P_{f} = P\left\{ {g_{1} ({\varvec{x}}) < 0 \cap g_{2} ({\varvec{x}}) < 0 \cap g_{3} ({\varvec{x}}) < 0} \right\}, $$

(29)

where the performance function of each failure mode is defined as

$$ \left\{ {\begin{array}{*{20}l} {g_{1} ({\varvec{x}}) = (4 - 2.1x_{1}^{2} + x_{1}^{4} /3)x_{1}^{2} + x_{1} x_{2} + ( - 4 + 4x_{2}^{2} )x_{2}^{2} + 0.8} \hfill \\ {g_{2} ({\varvec{x}}) = 100(4 - 2.1x_{1}^{2} + x_{1}^{4} /3)x_{1}^{2} + 100x_{1} x_{2} + 100( - 4 + 4x_{2}^{2} )x_{2}^{2} + 60} \hfill \\ {g_{3} ({\varvec{x}}) = 500(4 - 2.1x_{1}^{2} + x_{1}^{4} /3)x_{1}^{2} + 500x_{1} x_{2} + 500( - 4 + 4x_{2}^{2} )x_{2}^{2} + 250} \hfill \\ \end{array} } \right., $$

(30)

where variables x₁ and x₂ follow a normal distribution, ${\varvec{X}} \sim N(0,0.3^{2} )$. For a fair comparison, 12 sample points are selected by LHS method and added to the initial DoE. The number of samples used for MCS is 1×10⁵, and the candidate samples size is set as $N = 1 \times 10^{{4}}$ for AK-SYS, ALK-TCR and the proposed method in this case.

The results obtained from different methods are listed in Table 4. Figure 29 shows the distributions of results estimated by each method in 20 runs. Based on Table 4, the N_calls of proposed method IK-SRA is only 58.4, and is less than both AK-SYS and ALK-TCR with 100.1 and 72.2. Therefore, the proposed method is more efficient than both in this example. Note that g₂ = 0 and g₃ = 0 do not contribute to the composite performance function, as shown in Fig. 28. Therefore, evaluation on g₂ = 0 and g₃ = 0 is useless for reliability analysis. Meanwhile, from Table 4, it also shows that AK-SYS and ALK-TCR can obtain slightly more accurate result than that of the proposed method. However, the proposed method is more effective than both, and the percentage improvements in efficiency are 71.4% and 23.6% compared with AK-SYS and ALK-TCR, respectively (Fig. 29).

Table 4 Result of example 3

Fig. 28

A parallel system in example 3

Fig. 29

The box results obtained by three methods AK-SYS, ALK-TCR and the proposed method in example 3

Figure 30 shows the limit state function of each failure modes, the selected samples added to DoE, the selected samples by each Kriging model in the whole update process, the constructed Kriging models of each failure mode by AK-SYS. Figure 31 shows that by ALK-TCR and Fig. 32 shows that by IK-SRA. The converging processes of different methods are shown in Fig. 33, which shows that the proposed method achieves to true value more quickly than others.

Fig. 30

The process of sampling in AK-SYS in example 3

Fig. 31

The process of sampling in ALK-TCR in example 3

Fig. 32

The process of sampling in IK-SRA in example 3

Fig. 33

The convergence processes of different methods in example 3

4.4 Example 4 A series system with 8 variables

In this case, a roof truss structure with three failure modes is studied. Figure 34 shows the roof truss structure, it is a series system with eight variables [21].

Fig. 34

The schematic diagram of roof truss structure

In this roof structure, the top beam and the compression bars are made by concrete, and all the bottom beam and the tension bars are made by steel. The distributed loads can be transformed into points loads, $P = ql/4$. In this study, three failure modes are considered: (1) In the first failure mode, the vertical displacement $\Delta_{C}$ of node C is considered as follows

$$ \Delta_{C} = \frac{{ql^{2} }}{2}\left( {\frac{{ql^{2} }}{2} + \frac{{ql^{2} }}{2}} \right), $$

(31)

and the failure will occurs when $\Delta_{C}$ exceeds 3 cm. A_C denotes the sectional area of the concrete bars, and A_S denotes the sectional area of the steel bars; E_C denotes the elastic modulus of the concrete bars, and E_s denotes the elastic modulus of the steel bars; l denotes a dimension size; (2) In the second failure mode, the internal force of AD bar is considered, which is derived as

$$ N_{{{\text{AD}}}} = - 1.185ql, $$

(32)

and the failure occurs when N_AD exceeds the ultimate stress of this bar, which is equal to f_CA_C, where f_C denotes the compressive strength of the AD bar; (3) In the third failure mode, the internal force of EC bar is considered, which is derived as

$$ N_{{{\text{EC}}}} = 0.75ql, $$

(33)

and the failure occurs when N_EC exceeds the ultimate stress of this bar, which is equal to f_SA_S, where f_S denotes the tensile strength of the EC bar. Therefore, the three failure models are defined as follows:

$$ g_{1} = 0.03 - \frac{{ql^{2} }}{2}\left( {\frac{3.81}{{A_{C} E_{C} }} + \frac{1.13}{{A_{S} E_{S} }}} \right), $$

(34)

$$ g_{2} = f_{C} A_{C} - 1.185ql, $$

(35)

$$ g_{3} = f_{S} A_{S} - 0.75ql, $$

(36)

where the eight input variables q, l, A_S, A_C, E_S, E_C, f_S and f_C are all assumed to be lognormal variables, and their distribution parameters are shown in Table 5.

Table 5 The distribution parameters of all the variables of the roof truss structure

As this roof structure is a series system, the failure probability is formulated as follows:

$$ P_{{\text{f}}} = {\text{Prob}}\left[ {g_{1} \le 0 \cup g_{2} \le 0 \cup g_{3} \le 0} \right]. $$

(37)

The same number of samples, i.e., 32 samples, generated by LHS are used and added to the initial DoE for AK-SYS, ALK-TCR and the proposed method. The number of samples used for MCS is 7×10⁵, and the candidate samples size is set as $N = {2} \times 10^{{5}}$ in AK-SYS, ALK-TCR and the proposed method.

The results obtained from different methods are listed in Table 6. Figure 35 shows the distributions of results estimated by each method in 20 runs. Based on Table 6, the N_calls of proposed method IK-SRA is only 114.0, and is less than both AK-SYS and ALK-TCR with 120.4 and 125.1, respectively. The proposed method significantly improves the efficiency of reliability analysis by reducing the number of calls to performance functions, and the percentage improvements in efficiency are 5.6% and 9.7% compared with AK-SYS and ALK-TCR, respectively. Therefore, the proposed method is more efficient than both in this example. Table 6 also shows that the proposed method can obtain an accurate result. The converging processes of different methods are shown in Fig. 36, which shows that the proposed method converges quickly and achieves accurate results.

Table 6 Result of example 4

Fig. 35

The box results obtained by three methods AK-SYS, ALK-TCR and the proposed method in example 4

Fig. 36

The convergence process of different methods in example 4

4.5 Example 5 A planar truss structure with 7 nodes

A planar truss structure with 7 nodes [38], shown in Fig. 37, is selected as the engineering problem. This is a series system with 4 random variables. Where the fixed hinge support is at node 1 and the sliding hinge support is at node 4. The vertical loads F₁, F₂, and F₃ in the -y direction are applied for nodes 5, 6 and 7, respectively. Figure 38 shows the deformation of the truss structure after the application of load. The Young’s modulus of truss structure is 2 × 10⁵ Mpa, i.e., E = 2 × 10⁵Mpa. A is the cross-sectional area. The geometric size of bars is shown in Fig. 37. The corresponding statistical properties of these random variables are given in Table 7.

Fig. 37

A planar truss structure with 7 nodes (length unit: mm)

Fig. 38

The deformation of the truss after the application of load

Table 7 The distribution parameters of all the variables of the planar truss structure

The actual horizontal deflection of nodes 2, 4 and 6 can be expressed as $\Delta_{2}$, $\Delta_{4}$, $\Delta_{6}$, and are calculated using the FEM. They should satisfy the constraint $\Delta_{2} \le 0.0254$ mm, $\Delta_{4} \le 0.0935$ mm, $\Delta_{6} \le 0.0468$ mm. Therefore, the performance functions can be established:

$$ \left\{ {\begin{array}{*{20}c} {g_{1} (A,F_{1} ,F_{2} ,F_{3} ) = 0.0254 - \Delta_{2} ;} \\ {g_{2} (A,F_{1} ,F_{2} ,F_{3} ) = 0.0935 - \Delta_{4} ;} \\ {g_{3} (A,F_{1} ,F_{2} ,F_{3} ) = 0.0468 - \Delta_{6} .} \\ \end{array} } \right. $$

(38)

For a fair comparison, 12 samples are selected and added to the initial DoE. The result of MCS with $N_{{{\text{MCS}}}} = 1 \times 10^{6}$ samples is a benchmark for comparisons. The number of samples used for MCS is 1×10⁶, and the candidate samples size is set as $N = {1} \times 10^{{5}}$ for AK-SYS, ALK-TCR and the proposed method. The results obtained from different methods are listed in Table 8. Figure 39 is the result for different method with20 runs. Based on Table 8, the function calls of proposed method IK-SRA is only 52.9, which is less than both AK-SYS and ALK-TCR with 66.5 and 83.1. The proposed method is more effective than others, and the percentage improvements in efficiency are 25.7% and 57.1% compared with AK-SYS and ALK-TCR, respectively. Table 8 shows that the proposed method can obtain the accurate result. The converging processes of different methods are shown in Fig. 40.

Table 8 Result of example 5

Fig. 39

The box results obtained by three methods AK-SYS, ALK-TCR and the proposed method in example 5

Fig. 40

The convergence process of different methods in example 5

5 Conclusion

In this study, a new system reliability analysis method with two strategies is proposed. Selecting the candidate samples that have little contributions to the failure probability during the process of reliability analysis will increase the computing burden. To address this problem, the proposed method has two strategies. In strategy 1, a new sampling-based criterion is developed to avoid selecting these useless samples; for series systems, the safe regions are selected; for parallel systems, the failure regions are selected. In strategy 2, the initial best sample point will be further optimized by interpolating. Finally, the next best sample point is obtained based on the learning function.

Five numerical examples are investigated to illustrate the proposed method IK-SRA. The results showed that the N_call of IK-SRA is generally a bit smaller than that of AK-SYS and ALK-TCR, while maintaining high accuracy for both series and parallel systems. Moreover, the proposed method is also effective for systems with disconnected failure regions. In general, the proposed is more effective than both AK-SYS and ALK-TCR, whereas almost the same accuracy level is achieved. Furthermore, it has high applicability because it is easy to implement. Therefore, the proposed method is optimal when the accuracy requirements are met. However, the proposed method may need further refinement if the accuracy requirement is particularly high. In addition, the proposed method is difficult to use for small probability and high-dimensional problems; these are our future work.