A multi-fidelity surrogate modeling method based on variance-weighted sum for the fusion of multiple non-hierarchical low-fidelity data

Abstract

Multi-fidelity (MF) surrogate models have been widely adopted in simulation-based engineering design problems to reduce the computational cost by fusing data with diverse fidelity levels. Most of the MF modeling methods only apply to the problems with hierarchical low-fidelity (LF) models. However, the LF models obtained from different simplification approaches often vary in fidelity levels throughout the design space, namely, the multiple LF models are non-hierarchical. To address this challenge, a MF surrogate modeling method based on variance-weighted sum (VWS-MFS) is developed to flexibly handle multiple non-hierarchical LF data in this work. Firstly, each set of the non-hierarchical LF data is allocated diverse weights according to uncertainties quantified by variances of constructed Kriging models, which enables all the LF data to be fused and contribute to the trend function reflecting the response trend of the true model. Secondly, for more precise scaling factor between HF and LF models and mean square error (MSE) estimation, an improved hierarchical kriging (IHK) model is introduced to construct the MF surrogate model enabling the LF model scaled by a varied scaling factor to capture the characteristics of the HF model. The performance of the proposed VWS-MFS method is compared to three MF surrogate models through several numerical examples and one engineering case. Results show that the proposed method provides more accurate MF surrogate models under the same computational cost. Additionally, the proposed method saved the computational cost by more than 59.61% with the same model accuracy compared to the Kriging model built with HF data for the engineering case.

1 Introduction

Surrogate models have been widely adopted in the simulation-based engineering design problem as a substitute to expensive simulation models or physical experiments to alleviate the computational cost (Chatterjee et al. 2019; Jiang et al. 2019). Surrogate models are built from available samples to give predictions based on the interpolated or fitted mathematical relationships. There are many widely used surrogate models, such as polynomial response surface (PRS) (Kleijnen 2008), kriging (Zhou et al. 2015), support vector regression (Shi et al. 2020; Vafeiadis et al. 2015), radial basis function (RBF) (Tripathy 2010) and so on. Wang and Shan (2007) compared the application of these models in different scenarios. In the process of building a surrogate model, models with diverse fidelities are usually available to obtain sampling data. Taking the aerodynamic design optimization of an airfoil as an example, the fidelity levels of simulation models may vary in terms of mathematical description of models (e.g., the Euler non-cohesive equations vs the Reynolds-averaged Navier–Stokes equations), degree of discretization of the models (e.g., coarse mesh vs refined mesh), and level of resolution errors (e.g., inadequate vs iterations adequate iterations). In general, the high-fidelity (HF) model can give more accurate and reliable simulation results. However, it is time-consuming and even computational prohibitive to construct a surrogate model entirely relying on the HF model to obtain the quantity of interest (QOIs) in many cases (Xia and Shi 2018). On the other hand, the low-fidelity (LF) model is able to obtain the simulation results with a considerable lower computational demand, whereas it may lead to the inaccuracy or even distortion of the final surrogate model entirely relying on the LF model.

To relieve this problem, multi-fidelity (MF) surrogate models have increased in popularity which strike a balance between the computational cost and prediction accuracy by integrating the HF and LF data (Rokita and Friedmann 2018; Song et al. 2013). In the construction of the MF surrogate models, small amounts of HF data are used to guarantee the prediction accuracy, while large amounts of LF data are used to relieve the computational burden (Hao et al. 2020; Tao et al. 2019). The decisive condition for the successful use of MF surrogate models is an assumption that the LF model should reflect the general trend of responses given by the HF model (Liu et al. 2018). In general, the MF surrogate modeling methods can be divided into three categories according to diverse means of data fusion (Zhou et al. 2017a, b), which includes the scaling function-based method, the space-mapping method, and the Co-Kriging method.

First, in the process of scaling function-based surrogate modeling, a scaling function is built to capture the discrepancy between the HF and LF models. As a correction-based method, it calibrates the LF model according to the response of the HF model. There are three types of scaling function: the additive scaling function (Song et al. 2019; Sun et al. 2020; Wu et al. 2021; Zhou et al. 2021), the multiplicative scaling function (Liu and Collette 2014; Zhu et al. 2014), and the hybrid scaling function (Ariyarit et al. 2018; Beachy et al. 2020; Bryson and Rumpfkeil 2017; Li et al. 2016). Song et al. (2019) developed a radial basis function (RBF) and regarded it as an additive scaling function to narrow the discrepancy between the HF and LF models; Wu et al. (2021) approximated the additive scaling function by Kriging model, and then applied it to the optimization problem of missile radome; Sun et al. (2020) developed a Kriging model to fit the error between the HF and LF models to serve as an additive scaling function, and then applied it to a novel MF bi-level optimization method for the shape design problem of underwater wings; Bryson and Rumpfkeil (2017) developed a novel hybrid gradient-enhanced MF surrogate modeling method using polynomial chaos expansions, which seeks complementary multiplicative and additive corrections to LF data; Li et al. (2016) proposed a hybrid scaling method based on least squares and then applied the MF model constructed to substitute for the implicit performance function in reliability-based design optimization by using the values of HF function and its gradient at design points. On the account of its relatively simple forms which are easy to understand, the scaling function-based method is the most extensively for MF surrogate modeling.

Second, in the space-mapping method, the aim is to establish a mapping relation between the HF and LF design space, ultimately bringing about an accurate MF surrogate model which is able to reflect the behavior of the HF model. There are two ways of space-mapping according to diverse mapping space. One is input-to-input mapping which means mapping the input space of the HF model to that of the LF model. The other is output-to-output mapping which means mapping the output space of the LF model to that of the HF model. Zhou et al. (2017a, b) put forward an output-to-output space-mapping strategy based on radial basis function by integrating information obtained from models with diverse fidelity levels, in which the multiple-to-one-dimensional structures of the scaling function are transformed to a novel one-to-one-dimensional structure alleviating the burden of model-fitting; Jiang et al. (2018) proposed an output-to-output space-mapping approach based on a Gaussian process, where the LF data is regarded as prior information in the process of MF surrogate modeling; Zhang et al. (2021a) put forward a novel space-mapping-based surrogate model, in which two mapping functions are constructed to accelerate the multiphysics design for high power microwave filters; Jin et al. (2021) combined the input-to-input space-mapping method and Gaussian process auto regression, thus enabling flexible learning for the complex cross-correlations, and then developed a complementary data-fusion algorithm in order to monitor the strain of structural system. The obvious advantage of the space-mapping method lies in that it allows the HF and LF models to have different dimensions of design space.

Lastly, the Co-Kriging model is a space interpolation approach, which can be regarded as the extension of the Kriging model with multi-variable under the assistance of auxiliary or secondary information (Han et al. 2012). The Co-Kriging model is originally derived from the geo-statistics community Howarth (1979). Afterward, Han and Görtz (2012) put forward a MF surrogate modeling method called hierarchical kriging (HK), where the LF function serves as the trend of HF function and a more reasonable value of the MSE is estimated ultimately; Han et al. (2020) extended the original HK model with two-level fidelities to multi-level HK model, which can fuse the simulation data with multiple fidelity levels; Cheng et al. (2021) put forward a novel nearest-neighbor co-kriging Gaussian process, in which the nearest-neighbor Gaussian process and auto-regressive model are coupled employing augmentation ideas; Xing et al. (2021) put forward a novel additive structure for multi-level MF modeling using co-kriging, where the HF response is written in the form of the sum of model response with the lowest-fidelity and all the residuals between the responses of models with successive fidelity levels using Gaussian processes. Apart from the variation and extension of the Co-Kriging model, the Co-Kriging model is widely used in the intelligent manufacturing field (Krishna and Ganguli 2021; Yang et al. 2021), marine industry (Sun et al. 2020; Zhang et al. 2021b), aerospace field (Priyanka and Sivapragasam 2021; Wauters et al. 2020) and so on. For example, Krishnan and Ganguli (2021) adopted a co-kriging model to determine the natural frequencies of the beam by integrating the HF and LF finite element models, which belong to Timoshenko beam and Euler–Bernoulli beam separately; Yang et al. (2021) employed the HK to predict the temperature and specific energy consumption in the process of corner milling.

During the construction of the MF surrogate model, most of the work mentioned above assumed that the models available are hierarchical. However, the fidelity levels of models could not be identified and ranked distinctly in many other situations. Namely, the models are non-hierarchical that no fidelity gap exists between each other. It is a less-noticed but common-exist situation, where multiple non-hierarchical LF models are generated in different ways to simplify the HF model. For instance, it could be hard to distinguish the 3-D finite element model with coarse mesh from the 1-D finite element model with refined mesh in model fidelity. To address this issue, a MF surrogate modeling method based on variance-weighted sum (VWS-MFS) for multiple non-hierarchical LF models is proposed to make the utmost of the non-hierarchical LF data. In the proposed method, Kriging models are built for each set of non-hierarchical LF data using the Gaussian process, which gives the variance to quantify corresponding uncertainties. Specifically, the VWS-MFS method is developed by aggregating the HF data and the fused non-hierarchical LF data. In the process of fusing LF data, Kriging models are constructed for each set of non-hierarchical LF data using the Gaussian process, which can give the variance to quantify corresponding uncertainties. Then the mean and variance of the non-hierarchical LF surrogate models obtained above are fused by allocating diverse weights according to the uncertainties, which enables each set of the non-hierarchical LF data to contribute to the trend function. The weighting approach enables the fidelity of the LF data to change throughout the design space, thus relaxing the fidelity assumption of hierarchical relationships among LF models. Furthermore, the framework of an improved hierarchical kriging (IHK) model developed in our previous work (Hu et al. 2017) is extended to construct a single MF surrogate model incorporating the HF data and the fused LF data, thus making it possible to provide not only more precise scaling factor between HF and LF models but also more accurate MSE estimation. The performance of the proposed VWS-MFS method will be demonstrated through several numerical examples and one engineering case. It is expected that accurate MF surrogate models will be developed using the proposed method.

The remaining of this paper is organized as follows: In Sect. 2, a brief description of the Kriging method is provided, and the background of MF surrogate modeling is given. The details of the proposed VWS-MFS method are described in Sect. 3. In Sect. 4, several numerical examples and an engineering case are utilized to demonstrate the merits and effectiveness of the proposed VWS-MFS method in the comparison with three other MF surrogate models existed. Besides, the effects of key factors are explored. Finally, Sect. 5 concludes this paper with the summary and future work.

2 Background

In the process of the MF surrogate modeling, the Kriging technique is utilized. For the reason that Kriging is able to provide a reasonable estimation of the MSE at an untried point, which is particularly significant to obtain the prediction accuracy of the surrogate model with finite samples. In this section, a brief description of the Kriging model and the background of MF surrogate modeling are provided.

2.1 Kriging technique

Kriging technique is a surrogate modeling method with single fidelity using interpolation approach, where the model constructed goes through all the design points. Generally, the Kriging model can be expressed as:

$$\begin{gathered} \hat{y}\left( x \right) = p\left( x \right) + z\left( x \right) {\varvec{f}}\left( x \right)^{T} {\varvec{\beta}} + z\left( x \right) \hfill \\ \end{gathered}$$

(1)

where $x$ is the design variable, $p\left( x \right)$ represents a polynomial function that reflects the mean of the output performance, ${\varvec{f}}\left( x \right)$ represents a vector of functions of $x$, ${\varvec{\beta}}$ represents a vector of regression coefficients, $z\left( x \right)$ serves as a random process with zero mean whose covariance can be written as:

$$Cov\left[ {z\left( {x_{1} } \right),z\left( {x_{2} } \right)} \right] = \upsilon^{2} R\left( {x_{1} ,x_{2} } \right)$$

(2)

where $\upsilon^{2}$ indicates the process variance of $z\left( x \right)$, and $R\left( {x_{1} ,x_{2} } \right)$ is a spatial correlation function between points $x_{1}$ and $x_{2}$, which depends only on the Euclidean distance between them. The correlation functions that are commonly used include power function, exponential function, Gaussian function, linear function, and so on.

Suppose that the responses of the HF model could be approximated with the linear combination of the HF design points. Thus, the IHK predictor can be expressed as:

$$\hat{y}\left( x \right) = {\varvec{c}}^{T} {\varvec{Y}}$$

(3)

where ${\varvec{Y}}$ indicates the vector of responses, ${\varvec{c}} = \left[ {c^{1} ,c^{2} , \cdots ,c^{N} } \right]$ represents the vector of weight coefficients related to the design points, $N$ indicates the number of design points. Thus, the error between the true response and predicted response can be written as:

$$\begin{gathered} \hat{y}\left( x \right) - y\left( x \right) = {\varvec{c}}^{T} {\varvec{Y}} - y\left( x \right) {\varvec{c}}^{T} (\varvec{F\beta } + \varvec{Z}) - \left( {{\varvec{f}}\left( x \right)^{T} {\varvec{\beta}} + z\left( x \right)} \right) {\varvec{c}}^{T} {\varvec{Z}} - z + \left( {{\varvec{F}}^{T} {\varvec{c}} - {\varvec{f}}\left( x \right)} \right)^{T} {\varvec{\beta}} \end{gathered}$$

(4)

where ${\varvec{Z}} = \left[ {z_{1} \, z_{2} \, \ldots \, z_{N} } \right]$. To guarantee the unbiased prediction, it is demanded that ${\varvec{F}}^{T} {\varvec{c}} - {\varvec{f}}\left( x \right) = 0$, thus

$${\varvec{F}}^{T} {\varvec{c}} = {\varvec{f}}\left( x \right)$$

(5)

Under this condition, the mean squared error (MSE) of the predictor can be expressed as:

$$\begin{gathered} \varphi \left( x \right) = \text{E}\left[ {\left( {\hat{y}\left( x \right) - y\left( x \right)} \right)^{2} } \right] \text{E}\left[ {\left( {{\varvec{c}}^{T} {\varvec{Z}} - z} \right)^{2} } \right] {E}\left[ {z^{2} + {\varvec{c}}^{T} {\varvec{ZZ}}^{T} {\varvec{c}} - 2{\varvec{c}}^{T} {\varvec{Z}}z} \right] \upsilon^{2} \left( {1 + {\varvec{c}}^{T} {\varvec{Rc}} - 2{\varvec{c}}^{T} {\varvec{r}}} \right) \end{gathered}$$

(6)

To minimize the MSE, the Lagrangian multiplier ${\varvec{\lambda}}$ is introduced. Thus, the Lagrangian function with respect to ${\varvec{c}}$ can be expressed as:

$$L\left( {{\varvec{c}},{\varvec{\lambda}}} \right) = \upsilon^{2} \left( {1 + {\varvec{c}}^{T} {\varvec{Rc}} - 2{\varvec{c}}^{T} {\varvec{r}}} \right) - {\varvec{\lambda}}^{T} \left( {{\varvec{F}}^{T} {\varvec{c}} - {\varvec{f}}} \right)$$

(7)

The gradient of the Lagrangian function with respect to ${\varvec{c}}$ could be written as:

$$L^{\prime}_{c} \left( {{\varvec{c}},{\varvec{\lambda}}} \right) = 2\upsilon^{2} \left( {{\varvec{Rc}} - {\varvec{r}}} \right) - {\varvec{F}}{\varvec{\lambda}}$$

(8)

Considering the first-order necessary conditions for optimality, the following system of equations can be obtained:

$$\left[ {\begin{array}{*{20}c} \varvec{R} & \varvec{F} \\ {\varvec{F}^{T} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \varvec{c} \\ {\varvec{\tilde{\lambda }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \varvec{r} \\ \varvec{f} \\ \end{array} } \right]$$

(9)

where

$${\varvec{F}} = \left[ {f\left( {{\varvec{s}}_{1} } \right), \cdots ,f\left( {{\varvec{s}}_{N} } \right)} \right]^{T}$$

(10)

$$\varvec{\tilde{\lambda }} = - \frac{\varvec{\lambda }}{{2\upsilon ^{2} }}$$

(11)

$${\varvec{R}}{:} =\left( {R\left( {{\varvec{s}}_{i} ,{\varvec{s}}_{j} } \right)} \right)_{i,j} \in \text{R}^{N \times N}$$

(12)

$${\varvec{r}}: = \left( {R\left( {{\varvec{s}}_{i} ,x} \right)} \right)_{i} \in \text{R}^{N}$$

(13)

The solution to the equation above is:

$$\varvec{\tilde{\lambda }} = \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}} \right)^{ - 1} \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{Y}} - {\varvec{f}}} \right)$$

(14)

$${\varvec{c}} = {\varvec{R}}^{ - 1} \left( {{\varvec{r}} - \varvec{\tilde{\lambda }}} \right)$$

(15)

Finally, referring to Simpson et al. (2001), the Kriging predictor can be written as:

$$\begin{gathered} \hat{y}( x ) = {\varvec{f}}^{T} {\varvec{\beta}}^{*} + {\varvec{r}}^{T} {\varvec{R}}^{ - 1} ( {{\varvec{Y}} - \varvec{F\beta }^{*} } )= {\varvec{f}}^{T} {\varvec{\beta}}^{*} + r( x )^{T} {\varvec{\gamma}}^{*} \end{gathered}$$

(16)

where ${\varvec{\beta}}^{*} { = }\left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}} \right)^{ - 1} {\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{Y}}$ denotes the coefficient of the scaling factor, the matrices ${\varvec{\beta}}^{*}$ and ${\varvec{\gamma}}^{*}$ depends only on the design data which can be calculated in the process of model-fitting. For every prediction point $x$, only $f\left( x \right)$ and $r\left( x \right)$ need to be recalculated and two simple products added.

The MSE of the Kriging model for an unobserved point can be calculated by:

$$\varphi \left( x \right) = \upsilon^{2} \left[ {1 + \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{r}} - {\varvec{f}}} \right)^{T} \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}} \right)^{ - 1} \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{r}} - {\varvec{f}}} \right) - {\varvec{r}}^{T} {\varvec{R}}^{ - 1} {\varvec{r}}} \right]$$

(17)

2.2 Multi-fidelity surrogate modeling

The MF surrogate modeling technology is under the assumption that HF models are more accurate to represent the characteristics of the real physical model but require expensive computational cost, while the LF models are less accurate but considerably demand less computation. In the process of MF surrogate modeling, an LF surrogate model is calibrated with the responses of the HF model from a suitable size of design experiments. In other words, a small amount of HF data are used to modify the LF surrogate model to ensure the modeling accuracy, while more LF data are used to reflect the trend of real response. By reducing the computationally demanding of the HF model, a more high-accuracy surrogate model can be constructed at the same computational cost. In this way, the MF surrogate technology can take advantage of the merits of both HF and LF models.

In general, the MF surrogate modeling based on the interaction of the HF model and LF model can be written as follows (Qi et al. 2016):

$$\hat{F}\left( {x,{\varvec{g}}} \right) = \hat{F}\left( {f^{l} \left( x \right),{\varvec{g}}} \right) \approx F\left( x \right)$$

(18)

where $\hat{F}\left( {x,{\varvec{g}}} \right)$ represents the MF surrogate model which serves as the substitution of the actual HF model, ${\varvec{g}}$ is the vector of tuning parameters to minimize the discrepancy between HF and LF models, $F\left( x \right)$ denotes the true response of the HF model, and $f^{l} \left( x \right)$ denotes the response of the LF model. From the above definitions, the MF surrogate model tends to approach the high accuracy of the HF model with considerably less computational cost.

3 A multi-fidelity surrogate modeling method based on variance-weighted sum (VWS-MFS)

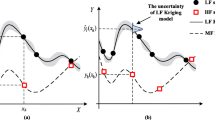
Except for the hierarchical data that exist in MF surrogate modeling, the non-hierarchical data also exist in many prediction scenarios. Namely, the LF models are non-hierarchical that no clear fidelity hierarchy exists between each other. To describe the differences between hierarchical and non-hierarchical models, a simple illustration in Fig. 1 is utilized. Figure 1 depicts the models with one high fidelity and two non-hierarchical low fidelities. The red line denotes the true model, which is usually replaced by the HF model in most cases. The black line denotes the HF model, while the yellow and blue lines denote two LF models. Obviously, the HF model can more accurately represent the true model than two LF models. However, neither of the two LF models is always closer to the true model throughout the design space.

Fig. 1

Illustration of the differences between hierarchical and non-hierarchical models

Supposing that this situation is regarded as a problem of fusing hierarchical data by ranking the fidelities among the LF models artificially. So here comes the question that the data with higher accuracy also exist in the lower-fidelity model which is artificially defined, which will result in the loss of useful information. As a result, the prediction accuracy of the MF surrogate model will inevitably decrease. Thus, the current hierarchical MF modeling method may lead to the loss of information and the reduction of prediction accuracy when applied to the situation with non-hierarchical models.

The motivation of this work is to put forward a non-hierarchical modeling method that can make the utmost of the information from non-hierarchical LF data, which is then incorporated the non-hierarchical LF data with the HF data. To this end, the VWS-MFS method is proposed, in which the uncertainty of each non-hierarchical LF model is characterized and weighted by variance enabling all the LF models to contribute to the trend function, then combined with the HF data to construct a single MF surrogate model.

In the following subsections, the details of the VWS-MFS modeling method are presented. The modeling process is demonstrated in Subsect. 3.1. Then, the correlation model and the hyperparameter tuning strategy are illustrated in Subsect. 3.2 and 3.3, respectively. Finally, the framework of VWS-MFS is shown in Subsect. 3.4.

3.1 Model solving

The process of the MF surrogate modeling consists of the fusion of non-hierarchical LF data and the integration of HF data with fused LF data. The formulation of the proposed VWS-MFS model can be expressed as:

$$\hat{y}_{H} \left( x \right) = h\left( x \right)\sum\limits_{i = 1}^{m} {\omega_{i} \hat{y}_{i,L} \left( x \right)} + z\left( x \right)$$

(19)

where $m$ denotes the number of non-hierarchical LF models, $\omega_{i}$ denotes the weights allocated to each set of LF data, $h\left( x \right)$ is a function to modify the LF model.

The details of the solving this formulation and process of constructing the VWS-MFS model are described in the following of this subsection, which can be divided into three steps. First, build the intermediate Kriging models for each set of non-hierarchical LF data with Gaussian processes, thus obtaining the mean and variance respectively to quantify the uncertainty. Second, fuse the above means and variances of the non-hierarchical LF data by weighting and summing. Third, the IHK model is employed to construct a single MF surrogate model combining the HF data and the fused LF data.

3.1.1 Establishment of intermediate models with Kriging technique

It is assumed that there are $m$ non-hierarchical LF models $l_{L}^{1} , \ldots ,l_{L}^{m}$, all mapping from the design space $x \in \text{R}^{d}$ to $\text{R}$. The LF models are evaluated with a finite number of designs, specified by the design set $D_{i} ,i = 1, \ldots ,m$, which consists of $n_{i}$ design points. The design points can be written in matrix form as ${\varvec{S}}_{L}^{i} = \left[ {{\varvec{s}}_{1,L}^{i} , \ldots ,{\varvec{s}}_{{n_{i} ,L}}^{i} } \right]^{T} \in \text{R}^{{n_{i} \times d}}$ while the corresponding $n_{i}$ response is written as ${\varvec{Y}}_{L}^{i} = \left[ {y_{1,L}^{i} , \ldots ,y_{{n_{i} ,L}}^{i} } \right]^{T} \in \text{R}^{{n_{i} }}$ with ${\varvec{s}}_{j,L}^{i} \in \text{R}^{d}$ denoting the $j{\text{th}}$ design point of the $i\text{th}$ LF model and $y_{j,L}^{i}$ denoting the corresponding response. It is noted that the design points of all LF models are consistent. The design set $D_{i}$ can be expressed as $\left( {{\varvec{S}}_{L}^{i} ,{\varvec{Y}}_{L}^{i} } \right)$.

For each design set, the Kriging technique is used to build the surrogate model. A square exponential covariance function with additive Gaussian noise is chosen, while the hyperparameters of the covariance function and noise variance are selected based on the maximum likelihood approach. For each LF model, the Kriging predictor can be expressed as a function:

$$\hat{y}_{L}^{i} \left( x \right) = m_{L}^{i} \left( x \right) + z_{L}^{i} \left( x \right)$$

(20)

where $m_{L}^{i} \left( x \right)$ is a mean function to describe the trend in the output space, $z_{L}^{i} \left( x \right)$ serves as a random process with zero mean whose covariance can be written as $\upsilon_{i}^{2} R_{i} \left( {x_{p} ,x_{q} } \right)$. And $R_{i} \left( {x_{p} ,x_{q} } \right)$ is a covariance function to encode the relationship between two points $x_{p}$ and $x_{q}$ in the design space, $\upsilon_{i}^{2}$ indicates the process variance of $z_{L}^{i} \left( x \right)$.

The hyperparameters and the noise variance depend on the design set $D_{i}$. Therefore, the covariance function $R_{i} \left( {x_{p} ,x_{q} } \right)$ varies with the different LF data sets. Finally, the Kriging predictor obtained at any prediction point $x$ in the design space consists of posterior mean and prior variance.

For any design point $x$, the posterior mean for each Kriging predictor can be explicitly calculated and serve as a surrogate model of $l_{L}^{i}$:

$$\hat{y}_{L}^{i} \left( x \right) = {\varvec{f}}_{i}^{T} {\varvec{\beta}}_{i}^{*} + {\varvec{r}}_{i}^{T} {\varvec{R}}_{i}^{ - 1} \left( {{\varvec{Y}}_{i} - {\varvec{F}}_{i} {\varvec{\beta}}_{i}^{*} } \right)$$

(21)

For each LF model, the prior variance can be computed as follows:

$$\begin{gathered} \sigma_{i}^{2} \left( x \right) = \varphi_{L}^{i} \left( x \right) = \upsilon_{i}^{2} \left[ {1 + \left( {{\varvec{F}}_{i}^{T} {\varvec{R}}_{i}^{ - 1} {\varvec{r}}_{i} - {\varvec{f}}_{i} } \right)^{T} \left( {{\varvec{F}}_{i}^{T} {\varvec{R}}_{i}^{ - 1} {\varvec{F}}_{i} } \right)^{ - 1} \left( {{\varvec{F}}_{i}^{T} {\varvec{R}}_{i}^{ - 1} {\varvec{r}}_{i} - {\varvec{f}}_{i} } \right) - {\varvec{r}}_{i}^{T} {\varvec{R}}_{i}^{ - 1} {\varvec{r}}_{i} } \right] \hfill \\ \end{gathered}$$

(22)

where the parameters share the same meaning and solution processes as those in Sect. 2.1.

3.1.2 Fusion of non-hierarchical low-fidelity data

Once the intermediate surrogate models have been built for each set of the non-hierarchical LF data, the LF information concluding all the posterior means and prior variances are available. For each set of LF information, the prior variance can serve as an indicator to quantify the uncertainty of the LF surrogate models. To describe the quantified uncertainty of each surrogate model, a simple illustration in Fig. 2 is used. Figure 2 depicts three LF surrogate models with posterior mean and prior variance. The black dots are design points, the solid line is the posterior mean $\hat{y}_{L}^{i} \left( x \right),i = 1,2,3$ of the Gaussian process, the gray shading represents plus or minus three times the prior variance $\sigma_{i}^{2} \left( x \right)$. The predicted uncertainty of each model at a certain point is represented by the probability distribution density function, shown as the colorized shading.

Fig. 2

Illustration of quantified uncertainty of surrogate models

The fused non-hierarchical LF data can be obtained by combining all the LF information available using a weighted sum of all the estimates suggested by Lam et al. (2015). The weight is inversely proportional to the prior variance. Therefore, for any area in the design space higher local fidelity the model shows, larger the weight is.

The weighting method utilizes the long-established theory of combining probability distributions. Figure 3 illustrates this method for $m = 3$ LF surrogate models. At the given design point in Fig. 2, The predicted uncertainty of each model represented by the green, yellow and blue shading is fused. The red shading denotes the distribution of the predicted response after fusion: a normally distributed random variable with mean $\overline{y}_{L} \left( x \right)$ and variance $\overline{\sigma }_{L}^{2} \left( x \right)$.

Fig. 3

Illustration of fusing uncertainty

The fused mean estimate is computed by a variance-weighted sum of posterior means:

$$\overline{y}_{L} \left( x \right) = \sum\limits_{i = 1}^{m} {\omega_{i} \hat{y}_{L}^{i} \left( x \right)}$$

(23)

$$\omega_{i} = \overline{\sigma }_{L}^{2} \left( x \right) \times \frac{1}{{\sigma_{i}^{2} \left( x \right)}}$$

(24)

where the $\overline{\sigma }_{L}^{2} \left( x \right)$ is the fused variance estimate calculated by summing the inverses of variances and then inverting the sum:

$$\overline{\sigma }_{L}^{2} \left( x \right) = \left( {\sum\limits_{i = 1}^{m} {\frac{1}{{\sigma_{i}^{2} \left( x \right)}}} } \right)^{{{ - }1}}$$

(25)

The fused non-hierarchical LF data can be expressed as $f_{L} \sim \left( {\overline{y}_{L} \left( x \right),\overline{\sigma }_{L}^{2} \left( x \right)} \right)$. Significantly, a larger prior variance indicates greater uncertainty of the corresponding model, leading to a less contribution to the trend function obtained ultimately.

3.1.3 Construction of MF surrogate model

There is a HF model $l_{H}$ with the same design space as LF models. The HF model is evaluated at $n_{H}$ designs, specified by the design set $D_{H}$. The design points can be written as ${\varvec{S}}_{H} = \left[ {{\varvec{s}}_{1,H} , \ldots ,{\varvec{s}}_{{n_{H} ,H}} } \right] \in \text{R}^{{d \times n_{H} }}$ while the corresponding $n_{H}$ response is written as ${\varvec{Y}}_{H} = \left[ {y_{1,H} , \ldots ,y_{{n_{H} ,H}} } \right]^{T} \in \text{R}^{{n_{H} }}$ with ${\varvec{s}}_{j,H} = \left[ {s_{j,H}^{1} \, s_{j,H}^{2} \, \ldots \, s_{j,H}^{d} } \right] \in \text{R}^{d}$ denoting the $j{\text{th}}$ design point and $y_{j,H}$ denoting the corresponding response. The design set $D_{H}$ can be expressed as $\left( {{\varvec{S}}_{H} ,{\varvec{Y}}_{H} } \right)$.

Then construct a single MF surrogate model using the improved hierarchical Kriging (IHK) model by combining the HF data $\left( {{\varvec{S}}_{H} ,{\varvec{Y}}_{H} } \right)$ and the fused LF data $\left( {\overline{y}_{L} \left( x \right),\overline{\sigma }_{L}^{2} \left( x \right)} \right)$. IHK is a MF surrogate modeling method suggested by Hu et al. (2017), which is an extension of the HK method. The LF design points gained from considerably less computationally demanding model is used to reflect the general trend of the true response, while the HF design points gained from the expensive-to-compute model are used to modify it. Hence, the HF function can be depicted in the form:

$$\begin{gathered} Y\left( x \right) = h\left( x \right)\overline{y}_{L} \left( x \right) + z\left( x \right) = h\left( x \right)\sum\limits_{i = 1}^{m} {\omega_{i} \hat{y}_{L}^{i} \left( x \right)} + z\left( x \right) \end{gathered}$$

(26)

where $\overline{y}_{L} \left( x \right)$ represents the fused mean estimate of LF models, which is given in Eq. (23). $z\left( x \right)$ denotes a random process with zero mean whose covariance can share the same expression with the Kriging model mentioned above $h\left( x \right)$ represents the global function of the scaling factor that reflects the correlation relationship between the responses of the fused LF model and HF model throughout the design space. In IHK, $h\left( x \right)$ is a polynomial response surface (PRS) model to map the fused LF data to the HF data whose value varies with the location of the prediction point. Thus, the LF model is scaled by a varied scaling factor to capture the characteristics of the HF model. However, the scaling factor is a constant in the HK model. By contrast, $h\left( x \right)$ is more specific to express the relationship between the fused LF model and HF model in IHK. which can be written as:

$$h\left( x \right) = \beta_{0} + \sum\limits_{i = 1}^{d} {\beta_{i} x_{i} } + \sum\limits_{1 \le j \le k \le d} {\beta_{jk} x_{j} x_{k} }$$

(27)

where $d$ denotes the dimensions of the design space, $x_{i}$, $x_{j}$, $x_{k}$ are different design variables, and $\beta_{i}$, $\beta_{jk}$ are the coefficients in front of them.

Take a two-dimensional case for example:

$$\hat{y}_{H} \left( {x_{1} ,x_{2} } \right) = \left( {\beta_{1} { + }\beta_{2} x_{1} { + }\beta_{3} x_{2} { + }\beta_{4} x_{1}^{2} { + }\beta_{5} x_{1} x_{2} { + }\beta_{6} x_{2}^{2} } \right)\overline{y}_{L} \left( {x_{1} ,x_{2} } \right) + z\left( {x_{1} ,x_{2} } \right)$$

(28)

can be written as:

$$y\left( x \right) = f\left( x \right)^{T} {\varvec{\beta}} + z\left( x \right)$$

(29)

where

$${\varvec{\beta}} = \left[ {\beta_{1} \, \beta_{2} \, \ldots \, \beta_{6} } \right]$$

(30)

$$\begin{gathered} f\left( x \right) = \left[ {f_{1} \, f_{2} \, f_{3} \, f_{4} \, f_{5} \, f_{6} } \right] = \left[ {\overline{y}_{L} \left( {x_{1} ,x_{2} } \right) \, x_{1} \overline{y}_{L} \left( {x_{1} ,x_{2} } \right) \, x_{2} \overline{y}_{L} \left( {x_{1} ,x_{2} } \right) \, } \right. \left. {x_{1}^{2} \overline{y}_{L} \left( {x_{1} ,x_{2} } \right) \, x_{1} x_{2} \overline{y}_{L} \left( {x_{1} ,x_{2} } \right) \, x_{2}^{2} \overline{y}_{L} \left( {x_{1} ,x_{2} } \right)} \right] \end{gathered}$$

(31)

Finally, the IHK predictor and the MSE can be obtained according to Eqs. (16) and (17). According to the expression of MSE, the matrix ${\varvec{f}}$ associates not only with the response of the LF model but with the location of the prediction point, indicating that the IHK model can provide more precise MSE estimation in comparison to the HK model.

3.2 Correlation model

The correlation function $R\left( {x_{1} ,x_{2} } \right)$ that depends on the Euclidean distance between points $x_{1}$ and $x_{2}$ is calculated in the process of modeling, and it is often expressed as the form:

$$R\left( {x_{1} ,x_{2} } \right) = \prod\limits_{k = 1}^{d} {R_{k} \left( {{\varvec{\tau}},x_{1}^{k} - x_{2}^{k} } \right)}$$

(32)

where ${\varvec{\tau}} = \left[ {\tau_{1} , \ldots ,\tau_{d} } \right] \in R^{d}$ are the hyperparameters to be turned which determine the decrease rate of the correlation function, and a smaller ${\varvec{\tau}}$ leads to a slower decrease. $x_{1}^{k}$ and $x_{2}^{k}$ denote the inputs of the $k{\text{th}}$ dimension of points $x_{1}$ and $x_{2}$.

The types of correlation functions can be categorized into two groups. In the first group, the correlation functions contain spline function, Gaussian function, cubic function, and so on, showing a parabolic behavior near the origin. In the second group, the correlation functions contain a linear function, exponential function, spherical function, and so on, showing a linear behavior near the origin. In general, the selection of correlation functions is up to the underlying phenomenon. The correlation function in the most popular use is the Gaussian exponential function calculated by:

$$\begin{gathered} R_{k} \left( {{\varvec{\tau}},x_{1}^{k} - x_{2}^{k} } \right) = \exp \left( { - \tau_{k} \left| {x_{1}^{k} - x_{2}^{k} } \right|^{{p_{k} }} } \right) R\left( {{\varvec{\tau}},x_{1}^{k} ,x_{2}^{k} } \right) = \prod\limits_{k = 1}^{d} {\exp \left( { - \tau_{k} \left| {x_{1}^{k} - x_{2}^{k} } \right|^{{p_{k} }} } \right)} \, , \, 1 \le p_{k} \le 2 \end{gathered}$$

(33)

Considering the correlation matrix of Gaussian exponential function is relatively large thus leading to a singular matrix easily, a cubic spline correlation (Lophaven et al. 2002) is also utilized in the modeling process. The cubic spline correlation is not only second-order differentiable all the time but also maintains a good balance between smoothness and robustness of the function. The function is calculated by:

$$R_{k}\, \left( {{\varvec{\tau}},x_{1}^{k} - x_{2}^{k} } \right) = \left\{ \begin{gathered} 1 - 15\xi_{k}^{2} + 30\xi_{k}^{3} \, \text{for}\, \, 0 \le \xi_{k} \le 0.2 1.25\left( {1 - \xi_{k} } \right)^{3} \, \text{for} \, 0.2 \le \xi_{k} \le 1 0 \, \text{for}\, \, \xi_{k} \ge 1 \end{gathered} \right.$$

(34)

where $\xi_{k} = \tau_{k} \left| {x_{1}^{k} - x_{2}^{k} } \right|$.

3.3 Hyperparameter tuning strategy

In the proposed method, the hyperparameters ${\varvec{\tau}} = \left[ {\tau_{1} , \ldots ,\tau_{d} } \right]$ are needed to be estimated in the process of model construction. Generally, the unknown hyperparameters ${\varvec{\tau}}$ are calculated using the maximum likelihood estimation (MLE). The likelihood function could be written as:

$$L\left( {{\varvec{\beta}}^{*} ,\upsilon^{2} ,{\varvec{\tau}}} \right) = \frac{1}{{\sqrt {\left( {2\pi \upsilon^{2} } \right)^{n} \left| {\varvec{R}} \right|} }}\exp \left( { - \frac{{\left( {{\varvec{Y}} - {\varvec{F\beta }}^{*} } \right)^{T} {\varvec{R}}^{ - 1} \left( {{\varvec{Y}} - {\varvec{F\beta }}^{*} } \right)^{T} }}{{2\upsilon^{2} }}} \right)$$

(35)

The corresponding MLE of the coefficient ${\varvec{\beta}}^{*}$ and the variance $\upsilon^{2}$ can be obtained by maximizing the above equation.

$$\beta^{*} = \left( {{\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}} \right)^{ - 1} {\varvec{F}}^{T} {\varvec{R}}^{ - 1} {\varvec{F}}$$

(36)

$$\upsilon ^{2} = \frac{1}{d}\left( {\varvec{Y} - \varvec{F\beta }^{*} } \right)^{T} \varvec{R}^{{ - 1}} \left( {\varvec{Y} - {\varvec{F\beta}}^{*} } \right)$$

(37)

Substitute Eq. (36) and Eq. (37) into Eq. (35) and then take the logarithm, the following expression is obtained to be maximized:

$$\begin{gathered} \max \, f\left( \Theta \right) = - n\ln \upsilon^{2} \left( {\varvec{\tau}} \right) - \ln \left| {R\left( {\varvec{\tau}} \right)} \right| \hfill \\ \text{s.t.} \Theta \text{ > 0} \\ \end{gathered}$$

(38)

where $\Theta$ is the vector of ${\varvec{\tau}}$, $\upsilon$ and $R$ are functions of $\Theta$. The optimization problem is difficult to be solved analytically. In terms of this issue, a modified version of the direct search of the Hooke and Jeeves algorithm can be used.

3.4 The framework of VWS-MFS

The framework of the proposed method is shown in Fig. 4. It is the integration algorithm of a non-hierarchical LF data fusing method and IHK. Considering the non-hierarchical LF models, the uncertainty is characterized and weighted by variance so that the fidelity of each set of LF data can change throughout the design space. Furthermore, IHK is chosen to combine the HF data with the fused LF data to provide a more precise MSE estimation. The specific steps are shown as the flow chart below follows:

Fig. 4

Flow diagram of the modeling based on VWS-MFS

Step 1::

Use Latin hypercube sampling (LHS) to generate a certain number of LF design points enabling that the points are uniformly distributed in the design space.

Step 2::

Based on the LF design points given in step 1, run simulations or conduct physical experiments for each LF model to obtain the responses of the LF design points respectively.

Step 3::

For each design set, a Gaussian process modeling approach is used to build the surrogate model, thus obtaining all the posterior mean and prior variance of LF models.

Step 4::

Fused the above non-hierarchical LF data available by combining all the LF information available using a weighted sum of all the estimates, giving the fused mean and variance of LF models.

Step 5::

Use LHS to generate a smaller number of HF design points.

Step 6::

Based on the LF design points given in step 5, run simulations or conduct physical experiments to obtain the responses of the HF model at the HF design points.

Step 7::

Considering that IHK can provide better MSE estimation, construct a single MF surrogate model using the IHK by combining the fused LF data obtained in Step 4 and the HF data obtained in Step 6.

4 Experimental study

In this section, the proposed VWS-MFS is verified using multiple numerical test examples and one engineering case. First, a one-dimensional numerical example with three LF models is utilized to demonstrate the details of the proposed VWS-MFS model. Then, eight numerical test examples of different dimensions and numbers of LF models are utilized to verify the merits and effectiveness of the proposed method. In addition, explore the effects of key VWS-MFS factors employing one two-dimensional numerical example and one ten-dimensional numerical example. In the end, the proposed method is applied to the engineering case of a cylinder pressure vessel.

For comparison, model the examples above with three other MF surrogate models available: (1) the VWS-HK model developed by combining two exiting methods from Han and Görtz (2012) and Lam et al. (2015), (2) the linear regression multi-fidelity surrogate (LR-MFS) from Zhang et al. (2017), (3) the extended Co-Kriging construction with multi-level multi-fidelity (MLMF-CK) from Xiao et al. (2018).

Two different error metrics are adopted to evaluate the accuracy of the surrogate model obtained by each method: (1) maximum absolute error (MAE) that reveals the local accuracy, (2) root mean square error (RMSE) that reveals the global accuracy. The smaller the value of MAE/RMSE is, the better prediction performance the surrogate model owes. These two metrics can be expressed as:

$$\begin{gathered} \text{MAE} = \max \left| {y_{i} - \hat{y}_{i} } \right| \, , \, i = 1, \ldots ,N \text{RMSE} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } } \, , \, i = 1, \ldots ,N \end{gathered}$$

(39)

where $N$ represents the number of test points, $y_{i}$ and $\hat{y}_{i}$ denote the true value and the prediction value of response at the $i^{th}$ test point, respectively.

4.1 Demonstration example

To verify the proposed VWS-MFS framework above, a one-dimensional numerical example with three LF models is adopted to demonstrate the details and test the prediction performance. In this example, the HF function is taken from Forrester et al. (2007). The expression of the HF model and three LF models are as follows:

$$\begin{gathered} y^{H} = \left( {6x - 2} \right)^{2} \sin \left( {12x - 4} \right) y_{1}^{L} = \left( {3x^{2} - 0.1x - 1.3} \right)y^{H} - \left( {x + 8} \right) y_{2}^{L} = \left( {x^{3} + x^{2} - 0.1x + 0.5} \right)y^{H} - \left( {x + 8} \right) y_{3}^{L} = \left( { - 2x + 4} \right)y^{H} - \left( {x + 8} \right) x \in \left[ {0,1} \right] \end{gathered}$$

(40)

Figure 5 shows the true value of models and correlation coefficients between the HF model and every LF model in each interval. The black line is the HF model, while the others are LF models. It can be seen that none of the three LF models always hold a better correlation to the true model throughout the design space, which means that there is no clear level of fidelity among the data of LF models. Besides, the correlation coefficients between the HF model and every LF model are calculated from each interval which divides the design space into 10 equal sections. It can be observed that the values of correlation coefficients in most intervals for every LF model are large enough to reflect the trend of the response of the HF model. Moreover, the correlation coefficient between the HF model and every LF model varies in each interval, thus the three LF models rank variably in fidelity. The data of LF models are non-hierarchical.

Fig. 5

Illustration of HF and LF models and correlation coefficient

The numbers of design points of the HF model and LF models are six and ten, respectively. To avoid the situation the design point is located too close to the global maximum or minimum of the function, the HF design points are selected manually. The design points of the HF model are ${\varvec{S}}_{H} = \left[ {0,0.2,0.4,0.6,0.9,1.0} \right]$, while the design points of LF models are ${\varvec{S}}_{L} = \left[ {0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0} \right]$.

Figure 6 illustrates the results of weighting and summing LF variances. The red solid line in the left graph indicates the fused variance, while the other three lines in different colors indicate the variances of the three LF models. In addition, the right graph gives the corresponding weights throughout the design space, which are computed by variances. It can be noted that the variances obtained in different areas of design space change in magnitude, resulting in variable weights of different LF models. In any area of the design space, a larger prior variance indicates greater uncertainty of the corresponding LF model, leading to a smaller weight to the fused mean and a less contribution to the trend function obtained ultimately.

Fig. 6

Illustration of weighting and summing LF variances

The result of fusing LF surrogate models is given in Fig. 7, in which the black line represents the LF model, while the red line represents the fused LF surrogate model based on the three LF surrogate models drawn in different styles and colors. The fused responses namely the estimates of fused mean are computed by the variance-weighted sum of the three LF responses. It can be concluded that the fused LF surrogate model can reflect the trend of the HF model well in most areas of the design space.

Fig. 7

Illustration of fusing LF surrogate models

Figure 8 shows the comparison results of different modeling methods mentioned above. And the three methods for comparison share the same HF and LF design points with the proposed VWS-MFS method. Besides, the IHK model is also constructed for comparison, which is based on the data from the HF model and LF model 1. To keep the same total budget, the data to construct the IHK model consist of 6 HF design points sharing the same locations with the proposed VWS-MFS model and 3 × 10 LF design points selected uniformly in the design space. The black line represents the HF model which can be regarded as the true model, the filled stars represent the HF design points. The red solid line represents the result using the proposed VWS-MFS model to fit this function, and the brown dashed line represents the result using the IHK model. Besides, the other three lines in different styles and colors denote the approximated functions using VWS-HK, MR-MFS, and MLMF-CK, respectively using the same design points. It can be concluded that the VWS-MFS model constructed by fusing the data from one HF model and three LF models achieves great improvement in accuracy compared to the IHK model with only one LF model taken into consideration. In addition, the proposed VWS-MFS model outperforms the other three MF surrogate models in most areas of design space. Besides, the proposed VWS-MFS model is closer to the true value than the VWS-HK model verifying that IHK can provide better MSE estimation to obtain prediction values of higher accuracy.

Fig. 8

Comparison results of different modeling methods

In this example, 2000 test points are generated randomly to calculate the values of error metrics. Table 1 shows the values of different modeling methods. It can be concluded that the MAE and RMSE of the proposed method are both smaller than the others. It is also proved that the proposed VWS-MFS model performs better in local accuracy and global accuracy.

Table 1 Accuracy comparison of different modeling methods

4.2 Additional test examples

4.2.1 Experiments of a series of numerical examples

To demonstrate the effectiveness and merits of the VWS-MFS model, eight numerical examples with different dimensions of design space and numbers of LF models are also tested. Table 2 summarizes in the features of the eight numerical test examples, including the dimension, number of LF models, nonlinear degree, and sampling configurations for the HF model and each LF model. The expressions of the eight examples are listed in Appendix A. There are two types of strategies to select samples for MF surrogate modeling methods: the one-shot sampling approach (Jones 2001) and the sequential sampling approach (Hao et al. 2018, 2020; Peng et al. 2021). The research of sampling approach for MF models are is out of the scope of this work. For each test problem, the HF and LF data are randomly and uniformly generated using Latin hypercube sampling. The number of data for constructing the MF surrogate model depends on the dimension and characteristics of the problems. Generally, the problem with a higher dimension, a higher degree of nonlinearity, and a larger number of LF models deserve more sample data. Besides, the selection of the number of samples concluding HF data and LF data is obtained from our previous experience. Precisely, the number of high-fidelity data is about 5d–20d, where d is the dimension of the input design space. And the number of LF data for each model is about 4–6 times that of HF data.

Table 2 Features of the eight numerical test examples

Each numerical example is duplicated 100 times at the same number of design points to avoid the influence of the distribution of design points on the prediction accuracy. For each test example, 2000 test points are selected randomly to calculated the values of two error metrics. The boxplots of the values of MAE and RMSE for different modeling methods are shown in Fig. 9. The upper (75%) and lower (25%) quartile values are included in the boxes. And the solid lines that extend from the top and bottom of the box indicate 1.5 times the inter-quartile range.

Fig. 9

Boxplots of the values of MAE and RMSE for different modeling methods

As observed in Fig. 9, there are also a few outliers that lie out of the range among the results. To make a fair comparison, the average values of MAE and RMSE shown as horizontal solid lines in the boxes are summarized after removing the outliers. The specific values are list in Table 3 with the smallest one in bold.

Table 3 Accuracy comparison of different modeling methods

As can be seen from Table 3, the results of the VWS-MFS model have the smallest values of both MAE and RMSE in the eight numerical test examples, namely, the proposed method shows the best prediction performance in both global accuracy and local accuracy. In general, the proposed VWS-MFS model method can be promising and effective in most function problems.

4.2.2 Effect of the cost ratio of LF to HF models

In this subdivision, the effect of the cost ratio of the LF models to the HF model is explored employing a two-dimensional example, Example 3. It is under the assumption that the total budget of generating points for the design of experiments (DoE) is fixed. Besides, the cost of generating one HF design point is fixed as well, while the cost of generating one LF design point varies with the cost ratio. For a single-fidelity surrogate model, the number of total HF design points is set to be $k \times d$, where $d$ is the dimension of the design space and $k$ is a self-defined constant. To construct a MF surrogate model, the number of HF design points is assumed to be $l \times d\left( {l < k} \right)$ and $l$ is a self-defined constant, and the remaining $\left( {k - l} \right) \times d$ simulations are allocated to generating more LF design points. It is noted that the value of $k$ and $l$ are obtained from experience. The total cost ratio of LF to HF models is $\theta_{0}$. Thus the number of total LF design points is $\left( {k - l} \right) \times {d \mathord{\left/ {\vphantom {d {\theta_{0} }}} \right. \kern-\nulldelimiterspace} {\theta_{0} }}$. It is assumed that the cost ratio is the same for each LF model. Therefore, the number of LF design points is $\left( {k - l} \right) \times {d \mathord{\left/ {\vphantom {d \theta }} \right. \kern-\nulldelimiterspace} \theta }$ for each LF model, where $\theta = m \times \theta_{0}$ denotes the cost ratio of each LF model to the HF model and $m$ indicates the number of LF models.

In addition, 4/5 of the total budget is allocated to HF design points, while the remaining 1/5 of the total budget is allocated to LF design points. And the value of $k$ is set to be 5, thus the total budget is going to be 10 to keep the same with the number of HF design points in subsection 4.2.1 ensuring enough design points to construct the MF surrogate model. In other words, the total number of HF design points is 10 for a single-fidelity surrogate model. In the process of constructing a MF surrogate model for Example 3, the number of HF design points is 8, while the number of LF design points is ${2 \mathord{\left/ {\vphantom {2 \theta }} \right. \kern-\nulldelimiterspace} \theta }\left( {\theta = m \times \theta_{0} } \right)$ for each LF model. To better explore the effect of cost ratio $\theta_{0}$ on the prediction performance of the MF surrogate model, eight values of $\theta_{0}$ are compared, and the values of $\theta$ are 0.25, 0.2, 0.1, 0.05, 0.04, 0.025, 0.02, and 0.01. Thus, the corresponding values of $\theta_{0}$ are 0.083, 0.067, 0.033, 0.016, 0.013, 0.0083, 0.0067 and 0.0033. The detailed sampling configurations of the HF model and each LF model for different values of cost ratio for Example 3 are listed in Table 4.

Table 4 Sampling configurations for Example 3

Figure 10 shows the effect of different cost ratios on the prediction performance of the proposed VWS-MFS model for Example 3 employing two error metrics. It can be observed that the values of MAE and RMSE go down as the cost ratio $\theta_{0}$ decreases from 0.083 to 0.013. In addition, when the cost ratio $\theta_{0}$ continues decreasing after less than 0.013, the MAE and RMSE tend to be constant values. That is, with the cost ratio $\theta_{0}$ decreasing, the number of LF design points is increasing, which enables more LF information provided to VWS-MFS to reflect the trend of real response. Thus, the accuracy of VWS-MFS is improved gradually. It hits the peak when $\theta_{0} = 0.013$. And then the reduction of the cost ratio $\theta_{0}$ cannot make the performance to be better.

Fig. 10

Comparison of different cost ratios

To better evaluate the LF information provided, Fig. 11 illustrates the maximum values of MAE and RMSE for all the three LF models when only LF design points are used. It can be observed that when the cost ratio $\theta_{0}$ decreases from 0.083 to 0.013 which means the number of LF design points of each LF model increases from 8 to 50, the maximum values of MAE and RMSE go down and the decline is becoming more and more gentle until they reach constant values. It means that when the number of LF design points of each LF model reaches 50, the LF information available becomes saturated and the surrogate model built only by LF design points is close enough to the real LF models. No more LF information can be provided by increasing the number of LF design points. That explains why the performance of the MF surrogate model cannot be improved anymore when the cost ratio $\theta_{0}$ decreases after less than 0.013.

Fig. 11

Maximum values of MAE and RMSE for LF models

It can be concluded that when the total budget of generating points and the allocation to the HF model are fixed, the decrease of the cost ratio $\theta_{0}$ in a certain range contributes to providing more useful LF information, obtaining an ultimate improvement in the performance of VWS-MFS.

4.2.3 Effect of the diverse combinations of HF and LF design points

In this subdivision, the effect of diverse combinations of HF and LF design points is explored employing a two-dimensional example and a ten-dimensional example, Examples 3 and8. It is under the same assumption as the last subdivision that the total budget of generating design points is limited. And the value of $k$ is set to be 5 for Examples 3 and 20 for Example 8. For better illustration of the effect of diverse combinations of HF and LF design points, the value of the cost ratio $\theta$ is set to be 0.125 and the $\theta_{0}$ is set to be 0.042.

For Example 3, the allocation cases of the total budget for generating HF design points of the single-fidelity surrogate is named “3-2”, “3.5-1.5”, “4-1”, “4.5-0.5”, respectively. The total budget for Example 3 can run 5d = 10 HF simulations. The case “3-2” means that the 3/5 budget is allocated to generate the HF design points, while the remaining 2/5 budget is allocated to generate the LF design points. In other words, the number of HF and LF design points for each model are 6 and 32, respectively. The same goes for the other cases. For Example 8, the nine allocation cases of the total budget for generating HF design points of the single-fidelity surrogate is named “4-6”, “4.5-5.5”, “5-5”, “5.5-4.5”, “6-4”, “6.5-3.5”, “7-3”, “7.5-2.5”, “8-2”, respectively. The total budget for Example 3 can run 20d = 200 HF simulations. The case “4-6” means that the 4/10 budget is allocated to generate HF design points, with the remaining 6/10 budget allocated to generate LF design points. In other words, the number of HF and LF design points for each model are 80 and 960, respectively. The same goes for the other cases. Tables 5 and 6 summarized the detailed allocations of samples for diverse combinations of design points for the HF model and each LF model in Example 3 and 8, respectively.

Table 5 Sampling configurations for Example 3

Table 6 Sampling configurations for Example 8

Figure 12 shows the effect of diverse combinations of HF and LF design points on the prediction performance of the proposed VWS-MFS model for Example 3 and 8 using MAE and RMSE to indicate the variation of accuracy.

Fig. 12

Comparison of diverse combinations of HF and LF design points

For Example 8, VWS-MFS performs better with the number of the HF design points increasing from 80 to 120, and the decline is becoming more and more gentle. During this stage, the increasing HF design points provide more HF data to modify the LF approximation model to ensure the modeling accuracy. Although the number of LF design points decreases, the negative impact on the accuracy is much smaller than the positive impact brought by the HF data. However, this leads to the decline more and more gentle.

Ultimately, when the number of HF design points reaches 120, the performance of VWS-MFS becomes worse as the number of HF design points increases and the number of LF design points decreases. This is because the negative impact brought by decreasing LF design points becomes larger than the positive impact brought by the increasing HF design points. During the stage where the number of HF design points is larger than 120, the fewer LF data maybe not enough to reflect the trend of real response, or the HF information available may begin to be saturated. Thus, this results in poor accuracy of VWS-MFS.

For Example 3, VWS-MFS performs better with the number of the HF design points increasing from 6 to 8 but worse when it increases to 9, which shows the same trend with Example 8. The performance of VWS-MFS hits the best when the number of HF design points and LF design points is 8 and 16, respectively. In this case, the HF data to ensure the modeling accuracy and the LF data to reflect the trend of real response achieve the balance.

The black dot dash lines in Fig. 12 indicate the single-fidelity surrogate model built only by HF design points using the Kriging model. The number of HF design points for Examples 3 and 8 are 8 and 100 in the same total budget as the VWS-MFS model. Obviously, VWS-MFS performs better than the HF Kriging model except for the first case.

It can be concluded that when the total budget of generating points is fixed, an appropriate combination of HF and LF design points can strike a balance between them, ultimately improve the performance of VWS-MFS to the maximum extent.

4.3 Engineering case

In this subsection, the implementation of the proposed VWS-MFS is demonstrated on the prediction problem of a long cylinder pressure vessel for the compressed natural gas from Zhou et al. (2016) to verify the engineering applicability. The corresponding geometry, model parameters, and loading force of the long cylinder pressure vessel are shown in Fig. 13.

Fig. 13

Schematic diagram of the long cylinder pressure vessel

In the design process of the cylinder pressure vessel for the compressed natural gas, the less total consumption of the manufacturing material, the better. There are five independent design variables: the inside diameter of end part $r_{1}$, the inside diameter of body part $r_{2}$, the thickness of end part $t_{1}$, the thickness of body part $t_{2}$, and the height of end part $h_{1}$. And the respective range of the above five design variables is list in Table 7, while other parameters are preset and maintain unchanged. The long cylinder pressure vessel is subject to the action of an evenly distributed loading force $P = 23\text{MPa}$. The Poisson’s ratio and Young’s modulus are $\mu = 0.3$ and $E = 207\text{MPa}$, respectively. The total consumption of the manufacturing material $f$ can be computed using the following mathematical equation:

$$\begin{gathered} f = 2\pi h_{1} t_{1} \left( {t_{1} + 2r_{1} } \right) + \pi t_{2} \left( {t_{2} + 2r_{2} } \right)\left( {6000 - \sqrt {r_{2}^{2} - t_{1}^{2} } - h_{1} } \right) + \frac{2}{3}\pi \left\{ {\left[ {2\left( {r_{2} + t_{2} } \right)^{2} { + }\left( {r_{1} + t_{1} } \right)^{2} } \right]\sqrt {\left( {r_{2} + t_{2} } \right)^{2} - \left( {r_{1} + t_{1} } \right)^{2} } - \left( {2r_{1}^{2} + r_{2}^{2} } \right)\sqrt {r_{2}^{2} - r_{1}^{2} } } \right\} \end{gathered}$$

(41)

Table 7 Sampling configurations for the long cylinder pressure vessel

However, the Von Mises stress will change according to the five design parameters. In addition, the maximum Von Mises stress is limited by the maximum allowable stress with the value $\sigma_{\max } = 250\text{MPa}$. The stress constraint can be expressed in the following form:

$$\, \sigma \le \sigma_{\max }$$

(42)

However, the maximum Von Mises stress $\sigma$ of the long cylinder pressure vessel cannot be calculated analytically. Therefore, the proposed VWS-MFS is employed to approximate the relationship between the design variables and the stress response. In this study, ANSYS 18.0 is used as a simulation tool to obtain the stress response. In addition, MATLAB R2017a is utilized to change the values of five design variables in the source file to call the simulations.

In this prediction problem, one HF model and two LF models are available. Considering the symmetry shape of the long cylinder pressure vessel, the axial symmetry 3-D finite element model with Hexahedral meshes with 5 mm mesh size is chosen as the HF model, while the mesh size is set as 40 mm for the first LF model. And the second LF model is a 1-D finite element model with 10 mm mesh size. The grid models and corresponding simulation analysis results are depicted in Fig. 14, respectively.

Fig. 14

HF and LF models of the cylinder pressure vessel

For comparison, the VWS-HK, LR-MFS, and MLMF-CK are also constructed to integrate data from the simulation models. In this engineering case, one simulation for 3-D HF model took approximately 25.5008 s on a Inter(R) CORE(TM) i9-9820X CPU (3.3 GHz) computer, while 3.9923 s for the 3-D LF model and 3.8836 s for the 1-D LF model. The cost ratios are both approximately 6.5. The numbers of HF and LF design points are 25 and 50, respectively. And 25 test points are chosen randomly to calculate the error metrics MAE and RMSE of the four MF surrogate models. The VWS -HK, LR-MFS, and MLMF-CK share the same HF and LF design points. Table 8 lists the accurate results of the values of two error metrics for the different methods. It is found that the proposed VWS-MFS method provides the most accurate surrogate model, in which both the values of MAE and RMSE are the smallest. To keep the same total budget, the number of design points for the Kriging model with single fidelity constructed only based on HF data is (25 + ((100/6.5)), which approximately equals to be 40. It can be observed that the proposed VWS-MFS method performs better than the Kriging model with single fidelity, which verified the usefulness of the LF information. In addition, the values of MAE and RMSE for the Kriging model obtained by 100 design points are 7.7131 and 2.0539 respectively, which still show a little bit of distance to reach the same accuracy with the proposed VWS-MFS method. Compared to the Kriging model with single fidelity, the VWS-MFS method can save the computational cost by more than 59.61%.

Table 8 Accuracy comparison of different modeling methods

Take the MAE and RMSE of MLMF-CK as the reference values, the percentages of improvement in corresponding local and global accuracy for each surrogate model can be obtained as relative values to reflect the performance more intuitively. The relative values of accuracy improvement for the other three methods are illustrated in Fig. 15. The column filled with an orange dense pattern indicates the percentage of improvement in local accuracy which is calculated by the value of MAE. And the green one indicates the improvement of global accuracy calculated by the value of RMSE. It can be concluded that the proposed method achieves the maximum improvement with the local accuracy improved by 82.71% and the global accuracy improved by 81.29%.

Fig. 15

Relative percentages of improvement in local and global accuracy

The HF simulation responses and prediction responses of test points based on different MF modeling methods are shown in Fig. 16. The dashed line denotes the ideal prediction responses, where the prediction responses are equal to the HF simulation responses at test points. The points with diverse colors and symbols indicate the prediction responses of diverse MF surrogate models. The prediction response is closer to the HF simulation result as the point is nearer to the dashed line, which indicates the MF surrogate model with more accurate prediction performance. It can be concluded that the proposed VWS-MFS performs better than the other methods at most points, which has verified its engineering applicability as well.

Fig. 16

True and predicted responses at the validation points

5 Conclusion

In this work, the VWS-MFS method is developed to construct the MF surrogate model by incorporating the multiple non-hierarchical LF data with HF data, in which the available information is fully utilized. Since the uncertainties of non-hierarchical LF data are characterized and weighted by variance, the proposed method enables the fidelity of the LF data to change throughout the design space, which relaxes the fidelity assumption of hierarchical relationships among LF models. In addition, the IHK model is adopted to fuse the HF data making it possible to provide a more precise estimation.

The performance of the proposed VWS-MFS method is demonstrated and explored using nine numerical test examples with different properties, where three different MF surrogate models (VWS-HK, LR-MFS, and MLMF-CK) are utilized for comparison. Several conclusions can be drawn from the above comparisons: (1) Given the same number of design points, the proposed VWS-MFS method shows the best prediction performance for both local accuracy and global accuracy verifying the effectiveness. The values of error metrics have been reduced by 50% or more in most function problems. (2) With the total budget and allocation to the HF model fixed, the decrease of the cost ratio in a certain range contributes to providing more useful LF information, obtaining an ultimate improvement in the prediction performance. The accuracy of the MF surrogate model achieved the best when the cost ratio $\theta_{0}$ is approximately equal to 0.013 for the two-dimension numerical example above. (3) With the total budget of generating points and the cost radio fixed, an appropriate combination of HF and LF design points can strike a balance between them, ultimately improve the performance to the maximum extent. Finally, the prediction problem of a long cylinder pressure vessel, with the stress responses of the HF model and two LF models obtained from finite element models with different mesh sizes and dimensions, demonstrated that the accuracy of VWS-MFS improved by 80% around compared to the MLMF-CK method existed, which proved that the proposed VWS-MFS method is an efficient and feasible approach in support of the design of engineering products. It is expected to work under more given prediction problems of engineering cases.

It is noted that the proposed method is based on the assumption that the LF models are independently neglecting the covariance between LF models. The main reason is that compared to the covariance between HF and LF models, the effects of covariance among LF models have less effect on the prediction performance of the MF surrogate model. However, the effect of covariance among LF models is not always small enough to be ignored in some cases. Under these circumstances, the ignorance of the covariance may result in the loss of some important information of LF data, leading to the deterioration of the accuracy of the MF surrogate model. As part of the future work, the proposed method will consider the correlation between LF models.

Appendix A

The expressions of eight examples used in Subsect. 4.2 are listed.

Example 1

$$\begin{gathered} y^{H} = 2\sin \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} 5}} \right. \kern-\nulldelimiterspace} 5}} \right) y_{1}^{L} = {{x\left( {x - 5} \right)\left( {x - 12} \right)} \mathord{\left/ {\vphantom {{x\left( {x - 5} \right)\left( {x - 12} \right)} {30}}} \right. \kern-\nulldelimiterspace} {30}} y_{2}^{L} = {{\left( {x + 2} \right)\left( {x - 5} \right)\left( {x - 10} \right)} \mathord{\left/ {\vphantom {{\left( {x + 2} \right)\left( {x - 5} \right)\left( {x - 10} \right)} {30}}} \right. \kern-\nulldelimiterspace} {30}} 0 \le x \le 10 \end{gathered}$$

Example 2

$$\begin{gathered} y^{H} = 4x_{1}^{2} - 2.1x_{1}^{4} + {{x_{1}^{6} } \mathord{\left/ {\vphantom {{x_{1}^{6} } 3}} \right. \kern-\nulldelimiterspace} 3} + x_{1} x_{2} - 4x_{2}^{2} + 4x_{2}^{4} y_{1}^{L} = y^{H} \left( {0.7x_{1} ,0.7x_{2} } \right) + x_{1} x_{2} - 65 y_{2}^{L} = y^{H} \left( {0.8x_{1} ,0.6x_{2} } \right) + x_{1}^{4} + 32 x_{1} ,x_{2} \in \left[ { - 2,2} \right] \end{gathered}$$

Example 3

$$\begin{gathered} y^{H} = - \sin x_{1} - e^{{{{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {100}}} \right. \kern-\nulldelimiterspace} {100}}}} + 10 + {{x_{2}^{2} } \mathord{\left/ {\vphantom {{x_{2}^{2} } {10}}} \right. \kern-\nulldelimiterspace} {10}} y_{1}^{L} = - \sin \left( {0.9x_{1} } \right) - e^{{{{9x_{1} } \mathord{\left/ {\vphantom {{9x_{1} } {1000}}} \right. \kern-\nulldelimiterspace} {1000}}}} + 9.7 + {{x_{1}^{2} } \mathord{\left/ {\vphantom {{x_{1}^{2} } {10}}} \right. \kern-\nulldelimiterspace} {10}}0 + {{x_{2}^{2} } \mathord{\left/ {\vphantom {{x_{2}^{2} } {10}}} \right. \kern-\nulldelimiterspace} {10}} \hfill \\ y_{2}^{L} = - \sin x_{1} - e^{{{{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {100}}} \right. \kern-\nulldelimiterspace} {100}}}} + 10.3 + 0.03\left( {x_{1} - 0.3} \right){{^{2} + \left( {x_{2} - 1} \right)^{2} } \mathord{\left/ {\vphantom {{^{2} + \left( {x_{2} - 1} \right)^{2} } {10}}} \right. \kern-\nulldelimiterspace} {10}} y_{3}^{L} = - \sin \left( {0.9x_{1} } \right) - e^{{{{9x_{1} } \mathord{\left/ {\vphantom {{9x_{1} } {1000}}} \right. \kern-\nulldelimiterspace} {1000}}}} + 10 + 0.64{{x_{2}^{2} } \mathord{\left/ {\vphantom {{x_{2}^{2} } {10}}} \right. \kern-\nulldelimiterspace} {10}} x_{1} ,x_{2} ,x_{3} \in \left[ {0,1} \right] \end{gathered}$$

Example 4

$$\begin{gathered} y^{H} = {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {2\left( {\sqrt {1 + \left( {x_{1} + x_{3}^{2} } \right){{x_{4} } \mathord{\left/ {\vphantom {{x_{4} } {x_{1}^{20} }}} \right. \kern-\nulldelimiterspace} {x_{1}^{20} }}} - 1} \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {\sqrt {1 + \left( {x_{1} + x_{3}^{2} } \right){{x_{4} } \mathord{\left/ {\vphantom {{x_{4} } {x_{1}^{20} }}} \right. \kern-\nulldelimiterspace} {x_{1}^{20} }}} - 1} \right)}} + \left( {x_{1} + 3x_{4} } \right)e^{{\left( {1 + \sin x_{3} } \right)}} \hfill \\ y_{1}^{L} = 0.79\left( {1 + \sin {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {10}}} \right. \kern-\nulldelimiterspace} {10}}} \right)y^{H} - 2x_{1} + x_{2}^{2} + x_{3}^{2} + 0.5 \hfill \\ y_{2}^{L} = y^{H} + e^{{{{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {100}}} \right. \kern-\nulldelimiterspace} {100}} \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ {0.5,1} \right] \hfill \\ \end{gathered}$$

Example 5

$$\begin{gathered} y^{H} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - x_{3} } \right) \hfill \\ y_{1}^{L} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - 0.75x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - 0.75x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - 0.75x_{3} } \right)^{2} \hfill \\ y_{2}^{L} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - 1.25x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - 1.25x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - 1.25x_{3} } \right)^{2} \hfill \\ y_{3}^{L} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2.25x_{2}^{2} - x_{1} } \right)^{2} + 3\left( {3.25x_{3}^{2} - x_{2} } \right)^{2} + 4\left( {4.25x_{4}^{2} - x_{3} } \right)^{2} \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ { - 10,10} \right] \hfill \\ \end{gathered}$$

Example 6

$$\begin{gathered} y^{H} = [100\left( {x_{2} - x_{1}^{2} } \right)^{2} + \left( {x_{1} - 1} \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + \left( {x_{2} - 1} \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} \hfill \\ \, {{ + \left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} ]} \mathord{\left/ {\vphantom {{ + \left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} ]} {100000}}} \right. \kern-\nulldelimiterspace} {100000}} \hfill \\ y_{1}^{L} = [100\left( {x_{2} - x_{1}^{2} } \right)^{2} + 4\left( {x_{1} - 1} \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + 4\left( {x_{2} - 1} \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} \hfill \\ \, {{ \, + 4\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + 4\left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + 4\left( {x_{5} - 1} \right)^{2} ]} \mathord{\left/ {\vphantom {{ \, + 4\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + 4\left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + 4\left( {x_{5} - 1} \right)^{2} ]} {100000}}} \right. \kern-\nulldelimiterspace} {100000}} \hfill \\ y_{2}^{L} = [80\left( {x_{2} - x_{1}^{2} } \right)^{2} + \left( {x_{1} - 1} \right)^{2} + 80\left( {x_{3} - x_{2}^{2} } \right)^{2} + \left( {x_{2} - 1} \right)^{2} + 80\left( {x_{4} - x_{3}^{2} } \right)^{2} \hfill \\ \, {{ + \left( {x_{3} - 1} \right)^{2} + 80\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 80\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} ]} \mathord{\left/ {\vphantom {{ + \left( {x_{3} - 1} \right)^{2} + 80\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 80\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} ]} {100000}}} \right. \kern-\nulldelimiterspace} {100000}} \hfill \\ y_{3}^{L} = [100\left( {x_{2} - x_{1}^{2} } \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} \hfill \\ \, {{ + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} ]} \mathord{\left/ {\vphantom {{ + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} ]} {100000}}} \right. \kern-\nulldelimiterspace} {100000}} \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} \in \left[ { - 5,10} \right] \hfill \\ \end{gathered}$$

Example 7

$$\begin{gathered} y^{H} = \frac{{2\pi x_{3} \left( {x_{4} - x_{6} } \right)}}{{\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-\nulldelimiterspace} {x_{1} }}} \right)\left[ {1 + {{2x_{7} x_{4} } \mathord{\left/ {\vphantom {{2x_{7} x_{4} } {\left( {\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-\nulldelimiterspace} {x_{1} }}} \right)x_{1}^{2} x_{8} } \right) + {{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } {x_{5} }}} \right. \kern-\nulldelimiterspace} {x_{5} }}}}} \right. \kern-\nulldelimiterspace} {\left( {\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-\nulldelimiterspace} {x_{1} }}} \right)x_{1}^{2} x_{8} } \right) + {{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } {x_{5} }}} \right. \kern-\nulldelimiterspace} {x_{5} }}}}} \right]}} \hfill \\ y_{1}^{L} = 0.4y^{H} + x_{1}^{2} x_{8} + {{x_{1} x_{7} } \mathord{\left/ {\vphantom {{x_{1} x_{7} } {x_{3} }}} \right. \kern-\nulldelimiterspace} {x_{3} }} + {{x_{1} x_{6} } \mathord{\left/ {\vphantom {{x_{1} x_{6} } {x_{2} }}} \right. \kern-\nulldelimiterspace} {x_{2} }} + x_{1}^{2} x_{4} \hfill \\ y_{2}^{L} = 0.6y^{H} + {{10x_{1} x_{5} } \mathord{\left/ {\vphantom {{10x_{1} x_{5} } {x_{2} }}} \right. \kern-\nulldelimiterspace} {x_{2} }} + {{x_{1} x_{8} } \mathord{\left/ {\vphantom {{x_{1} x_{8} } {x_{4} }}} \right. \kern-\nulldelimiterspace} {x_{4} }} + x_{1}^{3} x_{7} \hfill \\ x_{1} \in \left[ {0.05,0.15} \right];x_{2} \in \left[ {100,50000} \right];x_{3} \in \left[ {63070,115600} \right]; \hfill \\ x_{4} \in \left[ {990,1110} \right];x_{5} \in \left[ {63.1,116} \right];x_{6} \in \left[ {700,820} \right]; \hfill \\ x_{7} \in \left[ {1120,1680} \right];x_{8} \in \left[ {9855,12045} \right] \hfill \\ \end{gathered}$$

Example 8

$$\begin{gathered} y^{H} = \sum\limits_{i = 1}^{10} {x_{i}^{3} } + \left( {\sum\limits_{i = 1}^{10} {0.5ix_{i} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{10} {0.5ix_{i} } } \right)^{4} \hfill \\ y_{1}^{L} = \sum\limits_{i = 1}^{10} {x_{i}^{3} } + \left( {\sum\limits_{i = 1}^{10} {2ix_{i} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{10} {3ix_{i} } } \right)^{4} \hfill \\ y_{2}^{L} = \sum\limits_{i = 1}^{10} {x_{i}^{3} } + \left( {\sum\limits_{i = 1}^{10} {3ix_{i} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{10} {4ix_{i} } } \right)^{4} \hfill \\ y_{3}^{L} = \sum\limits_{i = 1}^{10} {x_{i}^{3} } + \left( {\sum\limits_{i = 1}^{10} {ix_{i} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{10} {2ix_{i} } } \right)^{4} \hfill \\ x_{i} \in \left[ { - 5,10} \right] \hfill \\ \end{gathered}$$