Abstract
Robust design optimization (RDO) has been eminent, ascertaining optimal configuration of engineering systems in presence of uncertainties. However, computational aspect of conventional RDO can often get computationally intensive as neighborhood assessments of every solution are required to compute the performance variance and ensure feasibility. Surrogate assisted optimization is one of the efficient approaches in order to mitigate this issue of computational expense. However, the performance of a surrogate model plays a key factor in determining the optima in multi-modal and highly non-linear landscapes, in presence of uncertainties. In other words, the approximation accuracy of the model is principal in yielding the actual optima and thus, avoiding any misguide to the decision maker on the basis of false or, local optimum points. Therefore, an extensive survey has been carried out by employing most of the well-known surrogate models in the framework of RDO. It is worth mentioning that the numerical study has revealed consistent performance of a model out of all the surrogates utilized. Finally, the best performing model has been utilized in solving a large-scale practical RDO problem. All the results have been compared with that of Monte Carlo simulation results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The presence of uncertainty is inevitable in the life cycle analysis and design optimization of an industrial output. In order to illustrate its omnipresence, manufacturing variations can be considered as a classical example of one of the major sources of uncertainties inherently associated with a product [1]. Deterministic approaches may not always converge to the desired optima, especially when the design solution is highly sensitive to such variations. In such critical situations, it could lead to either unsafe or over safe outcomes. Therefore, incorporating uncertainty in product analysis and design is necessary to yield economically viable solutions.
Robust design optimization (RDO) is one of the most popular approaches which take into account the effect of uncertainties into the design optimization formulation [2,3,4]. RDO has been observed to improve product quality significantly, and yield insensitive solutions, even in real time industrial applications [5, 6]. Over the last two decades, it has gained much attention across various domains, such as, telecommunications and electronics [7,8,9], aerospace [10,11,12], automobile [13,14,15], ship design [16,17,18], structural mechanics [19,20,21], structural dynamics and vibration control [22, 23] and fatigue analysis [24,25,26].
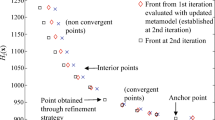
RDO establishes a mathematical framework for optimization motivated to minimize the propagation of input uncertainty to output responses [27, 28]. A graphical representation presented in Fig. 1 illustrates the concept of RDO. Out of the two optimal solutions, \({x_2}\) is more robust as compared to \({x_1},\) since the former does not affect the objective function \(f\left( x \right)\) much, and hence is less sensitive. Broadly, the problem formulations of RDO generally constitute of maximizing the performance, minimizing the performance variance, or both. For the details and insight of RDO formulation, the reader is referred to the following literatures [2, 29, 30]. Since RDO attempts to resolve sensitive design solutions in a random environment, it suffers from computational issues as an obvious consequence. Despite the advances in computer configuration and speed, the mammoth computational costs of running such complex simulation codes have prohibited their usage.
Therefore, in order to avoid running such high fidelity simulations, various approximation schemes have emerged [31]. These techniques, also known as surrogate modelling, have been observed to resolve the computational expenses significantly by approximating the underlying model in a sample space [32, 33]. Various such techniques have been developed till date, such as least square approximation [34], moving least square [35], polynomial chaos expansion [36], anchored ANOVA decomposition [37], Kriging [38], radial basis function [39], artificial neural network [40], support vector machines [41] and multivariate adaptive regression splines [42].
Such techniques have been successfully utilized in design optimization for engineering applications. A comprehensive review of the use of approximation models in mechanical and aerospace systems, and multidisplinary design optimization can be found in [12, 43, 44]. However, in context to optimization, such efficient paradigms have found their use primarily in deterministic frontier. To further illustrate the gap in research in this particular area, it may be justified to reveal that application of approximation models in RDO is quite limited in number and content [1]. A possible explanation for the lack of investigation in this area can be derived from the fact that the performance output is likely to be vulnerable and unstable in presence of uncertainties in an optimization framework. Additionally, solutions of constrained RDO problems can easily move to infeasible regions, if they are located close to constraint boundaries [45]. Thus, accuracy of the method to capture the original model is the governing factor to yield stable results satisfying feasible bounds, as the optima is highly sensitive to the convergence of each iteration.
Thus, the primary motivation of this paper lies in investigating most of the popular surrogate models and study their performance in the framework of RDO. Considering the lack of relevant literature in surrogate assisted RDO, an extensive review and thorough comparative assessment of various surrogate models in RDO has been felt as the need of the hour by the authors. This work is expected to serve as the guiding and selection application of the appropriate approximation models for the solution of high-fidelity computationally expensive stochastic optimization problems. Six benchmark RDO examples have been solved by utilizing as many as eleven popular surrogate models. Finally, a practical problem has been realistically modelled and solved by utilizing the most consistently performing model. To be specific, the dimensionality of the problems in terms of the number of stochastic variables vary from 2 to 48. The robust optimal solutions obtained have been validated with that of Monte Carlo simulation (MCS).
The paper has been organized in the following sequence. The theoretical development of the surrogate models employed for this study has been illustrated in Sect. 2. Section 3 explains the framework of surrogate assisted RDO technique. Numerical study has been carried out in Sect. 4 in order to illustrate the efficiency and accuracy of the various surrogate assisted RDO frameworks. A practical engineering RDO problem has been efficiently addressed in Sect. 5. Finally, conclusion has been drawn by discussing potentiality of the surrogate models in RDO framework on the basis of the results obtained from the study.
2 Surrogate Modelling
In this section, various surrogate models have been explained along with brief description of their mathematical formulations, which would provide complete insight to the readers.
2.1 Anchored ANOVA Decomposition
Various methods approximate multivariate functions in such a way that the component functions of the approximation are ordered starting from a constant and gradually approaching to multivariance as one proceeds along first order, second order and so on. An example of such method is ANOVA decomposition [37, 46,47,48] which is a general set of quantitative model assessment and analysis tool for mapping the high dimensional relationships between input and output model variables. It is an efficient formulation of the system response, if higher order co-operative effects are weak, allowing the physical model to be captured by the lower order terms. Practically for most well-defined physical systems, only relatively low order co-operative effects of the input variables are expected to have a significant effect on the overall response. ANOVA decomposition utilizes this property to fit an accurate hierarchical representation of the physical system. The fundamental concepts of generalized ANOVA decomposition has been discussed henceforth.
Let, \({\mathbf{x}}=\left( {{x_1},{x_2}, \ldots ,{x_P}} \right) \in {\mathbb{R}^P}\) and consider that \(\eta ={\mathbb{L}^2}\left( {{\mathbb{R}^P},{P_X}} \right).\) The generalized ANOVA decomposition expresses \(\eta \left( {\mathbf{x}} \right)=\eta \left( {{x_1},{x_2}, \ldots ,{x_P}} \right)\) as the sum of the hierarchical correlated function expansion in terms of the variables [37, 48] as
The expansion (1) exists and is unique under one of the hypothesis:
where \({\eta _0}\) is constant term representing the zeroth order component function or the mean response. The function \({\eta _i}\left( {{x_i}} \right),\) referred to as first order component function representing the independent effect. Similarly, \({\eta _{i,j}}\left( {{x_i},{x_j}} \right)\) is termed as second-order component function and represents co-operative effect of two-variables acting at a time. The higher-order terms indicate higher order co-operative effect with \({\eta _{1, \ldots ,\,P}}\left( {\mathbf{x}} \right)\) denoting the effect of all the variables acting together.
Moreover, each term \({\eta _u}\) in the model function \(Y=\eta \left( {\mathbf{X}} \right)\) [in Eq. (1)] can be solved explicitly by integration and is given by [49],
The conditional expectation \({\text{E}}\left( {{Y \mathord{\left/ {\vphantom {Y {X_{u} }}} \right. \kern-\nulldelimiterspace} {X_{u} }}} \right)\) effectively reduces a P dimensional function \(\eta \left( {{x_1},{x_2}, \ldots ,{x_P}} \right)\) to a linear sum of following smaller α(<P) dimensional functions [50]:
Over a \(\left( {P - \alpha } \right)\) dimensional rectangular grid \(\prod\nolimits_{{u \ne i,j, \ldots ,i_{\alpha } }} {x_{u}^{{\mu _{u} }} ,{\text{ }}} \mu _{u} = 1,2, \ldots ,K_{u}\)
Remark
In this study, second order anchored ANOVA decomposition has been utilized for approximating actual functions. To generate the approximation of any function, initially a reference point \({\mathbf{\bar x}}=\left( {{{\bar x}_1},{{\bar x}_2}, \ldots ,{{\bar x}_P}} \right),\) has to be defined in the variable space. In practice, the choice of the reference point \({\mathbf{\bar x}}\) is essential, especially only if the first few terms, i.e., first and second order, in Eq. (1) are considered. The reference point \({\mathbf{\bar x}}\) at the middle of the input domain appears to be the ideal choice [51].
Based on the above formulation presented, a step-by-step procedure for approximation by utilizing anchored ANOVA decomposition has been provided in algorithm 1.

2.2 Polynomial Chaos Expansion
The polynomial chaos expansion (PCE) is an efficient technique for obtaining the responses of stochastic systems. This has been introduced by Wiener [52] and hence, known as ‘Wiener Chaos expansion’. The generalized results have been presented by Xiu and Karniadakis [53] for various continuous and discrete system from the so called Askey-scheme and further stated the \({\mathcal{L}_2}\) convergence in the corresponding Hilbert space.
Assuming \({\mathbf{i}}=\left( {{i_1},{i_2}, \ldots ,{i_n}} \right) \in \mathbb{N}_{0}^{n}\) be a multi-index with \(\left| {\mathbf{i}} \right|={i_1}+{i_2}+ \cdots +{i_n},\) and let \(N \ge 0\) be an integer. The Nth order PCE of g(Z) can be stated as:
where \(\{ a_{{\mathbf{i}}} \}\) are unknown coefficients which are to be determined. \({\Phi _{\mathbf{i}}}\left( Z \right)\) are n-dimensional orthogonal polynomials with maximum order of N and satisfies the following relation
here \({\delta _{{\mathbf{ij}}}}\) denotes the multivariate kronecker delta function. It is to be noted that if \(\varpi \left( z \right)\) is Gaussian, the orthogonality relation in Eq. (6) yields Hermite polynomial as the optimal polynomial. The correspondence of the type of orthogonal polynomial and type of random variable has been presented in Table 1 [53].
Since the emergence of generalised PCE [53], discrete variants of PCE have been developed. It is worth mentioning that each of the variants of PCE are based on Eq. (5). However, the uniqueness resides in the algorithm utilized to determine the unknown coefficients associated with the bases. The Weiner-Askey PCE, proposed by Xiu and Karniadakis [53] is based on the Galerkin projection. In this method, Galerkin projection has been utilized to decompose the governing stochastic partial differential equation into a system of coupled differential equations. Furthermore, it has been demonstrated that PCE based on Galerkin approach yields excellent results and provide exponential convergence with increase in order of PCE. However, the method, being intrusive in nature, requires knowledge regarding the governing partial differential equation of the system. Consequently, it is not applicable to real-life problems with unknown governing differential equation. In order to address this issue, special attention has been provided to develop non-intrusive PCE. The most popular non-intrusive PCE is the one based on least square method [54, 55]. In this method, the least square technique is implemented to determine the unknown coefficients associated with the bases. Least square based PCE is easy to implement and applicable for systems with unknown governing differential equations. Other alternatives that have been investigated for determining the unknown coefficients associated with the bases are quadrature method [56, 57] and collocation approach [58, 59]. However, all the variants of PCE discussed above are only suitable for small scale problems. This is because, the number of unknown coefficients associated with PCE increases factorially with increase in number of variables. This renders application of PCE to large scale problems infeasible.
Blatman and Sudret [60, 61] proposed two adaptive sparse PCE for solving high-dimensional problems. The purpose of the methods is to determine, in an iterative manner, the components/variables that significantly contributes to the response of interest. The number of unknown coefficients associated with the bases are reduced by eliminating the components/variables having no or less effect on the output response. While the first approach [60] utilizes change in coefficient of determination (R2) to identify the significant components, the second approach utilizes least angle regression scheme [61] to identify the less important components. Moreover, it has been demonstrated that the proposed adaptive sparse PCE is capable of treating systems having number of variables as large as 500. However, only problems governed by elliptical partial differential equations have been investigated as part of the above works.
Due to its superior performance, PCE has found wide applications is various domains. PCE has been utilized for solving the stochastic steady state diffusion problem by Xiu and Karniadakis [62] and the stochastic Navier–Stokes equation [63]. Further, PCE has been utilized for sensitivity analysis by Sudret [64]. A reduced PCE has been developed for stochastic finite element analysis by Pascual and Adhikari [65, 66]. In each of the above mentioned applications, PCE has been found to yield excellent results. However, there are few issues regarding PCE that are yet to be answered. Firstly, PCE is only applicable to systems involving independent random variables. If the system under consideration involves correlated variables, ad hoc transformations, such as, Nataf transformation, needs to be employed to transform the dependent variables into independent variables. Secondly, PCE involves determining orthogonal polynomials for a system. However, orthogonal polynomials are known only for a few random variables as shown in Table 1. Hence, if the system under consideration involves variable(s), orthogonal polynomial(s) for which is not known, implementation of PCE may become tedious.
2.3 Multivariate Adaptive Regression Splines (MARS)
MARS [42] is governed by a set of bases which are selected for approximating the output response through a forward or backward iterative approach. The functional form of MARS is represented as:
with
where \({\alpha _k}\) and \(H_{k}^{f}({x_i})\) are the coefficient of the expansion and the basis functions, respectively. The basis function can be represented as
where \({i_k}\) is the order of interaction in the kth basis function and \({z_{i,k}}= \pm 1.\)\({x_{j(i,k)}}\) in Eq. (9) is the jth variable with \(1 \le j\left( {i,k} \right) \le n.\)\({t_{i,k}}\) represents the knot location on each of the corresponding variables. \(H_{k}^{f}({x_i})\) in Eq. (9) represents the multivariate spline basis function and is represented as the product of univariate spline basis functions \({z_{i,k}},\) which is either of order one or cubic, depending on the degree of continuity of the approximation. The notation “tr” denotes the function is a truncated power function.
Each function is piecewise linear with a knot tr at every \({X_{(i,k)}}.\) MARS models the function by allowing the basis function to bend at the knots. The maximum number of knots considered, the minimum number of observations between knots, and the highest order of interaction terms are to be determined. Automated variable screening is performed within MARS by using the generalized cross-validation (GCV) model fit criterion, which has been developed by Craven and Wahba [67]. The location and number of spline bases needed is determined by a (a) over-fitting a spline function through each knot and (b) removing the knots that have least contribution to the overall fit of the model as determined by the modified GCV criterion. The following equation shows the lack-of-fit (LOF) criterion used by MARS:
where
MARS has been utilized by Sudjianto et al. [68] to emulate a conceptually intensive complex automotive shock tower model in fatigue life durability analysis. A comparative assessment of MARS as compared to linear, second-order and higher-order regression models has been carried out by Wang et al. [69]. MARS has been utilized by Friedman [42] to approximate behaviour of performance variables in a simple alternating current series circuit. The primary advantage of MARS is its computational efficiency. Moreover, MARS model is capable of handling large data and almost no data preparation is required for building it. However, accuracy of MARS model is lower as compared to other surrogate techniques. Additionally, MARS is incapable of predicting the confidence bound of prediction and additional sample points are required for its validation. This, in turn, reduces the computational efficiency of the MARS model.
2.4 Radial Basis Function
Radial basis function (RBF) is another surrogate model which is quite popular among researchers. RBF is often used to perform the interpolation of scattered multivariate data [70,71,72]. The metamodel appears in a linear combination of Euclidean distances, which may be expressed as
where n is the number of sampling points, \({w_k}\) is the weight determined by the least-squares method and \({\varphi _k}(X,{x_k})\)is the k-th basis function determined at the sampling point \({x_k}.\) Various symmetric radial functions are used as basis function. The radial functions for RBF model are illustrated as,
It is to be noted that unlike PCE and response surface method (RSM), RBF is not a regression technique. Rather, RBF may be broadly considered as an interpolation technique. As a result, RBF, unlike regression techniques, yields exact result at the sample points.
Till date, RBF has found wide application in the domain of structural reliability and uncertainty quantification. A dynamic surrogate model based on stochastic RBF has been developed by Volpi et al. [73] for uncertainty quantification. The method has been equipped with auto-tuning scheme based on curvature, adaptive sampling scheme, parallel infill and multi-response criterion. It has also been illustrated that the surrogate based on stochastic RBF outperforms popular surrogate such as Kriging. A hybridized RBF has been proposed by Dai et al. [74] for structural reliability analysis. To be specific, the hybridized RBF has been formulated by replacing the learning network of RBF with support vector algorithm. As a consequence, it has been possible to exploit the advantages of support vector algorithm, such as good generalization and global optimization. Comparative assessment illustrated that the method proposed outperform both RBF and support vector algorithm. Other works on RBF include, but are not limited to, development of performance measure approach based reliability analysis technique using RBF [75] and integration of RBF into the FORM algorithm [76]. However, RBF yields satisfactory results only for problems that are linear and/or, weakly non-linear.
2.5 Artificial Neural Network
Artificial neural networks (ANNs) are a family of surrogate model inspired by biological functioning of brain and nervous system. ANNs are generally presented as a system of interconnected ‘neuron’. The neurons in ANN, often termed as nodes, consists of some primitive functions. All the connections have numeric weight that are tuned based on input data. A typical structure of ANN has been illustrated in Fig. 2. The network is represented as a function \(\Phi\) obtained by combining the primitive functions \(f_{1} {\text{, }}f_{2} ,{\text{ }}f_{3} {\text{ and }}f_{4}.\)\({\alpha _1}{,}{\alpha _2}, \ldots ,{\alpha _5}\) are termed as weights and determined by employing some learning algorithm. Based on the above points, it should be clear that three elements govern the formation of an ANN, namely the primitive function associated with the node, topology of the network (single layer or multilayer) and the learning algorithm used to determine the weights associated with the connections. Based on these criteria, multiple variants of ANN have evolved over the years.
Multilayer feed-forward neural network (MFFNN) [77] is the most popular and widely used ANN. Here, the neurons are arranged in three layers, namely input layer, hidden layer and output layer. It is worthwhile to mention that the number of hidden layers in feed-forward neural network may be more than one. Therefore, it is necessary to perform convergence study to determine the optimum number of layers. Moreover, the number of neurons/nodes in each hidden layer should also be determined by using some appropriate convergence criterion. Each neuron/node consists of a transfer function that expresses the internal activation level of the neuron. A transfer function may either of linear or nonlinear. An account of popular transfer functions has been provided in Table 2.
Another popular ANN scheme is the well-known back-propagation algorithm based ANN [78]. In this scheme, the errors in prediction are propagated backward to the inputs. Based on the errors received, the weights associated with the connections are further updated. The process is repeated until errors at the output layer is less than a specified threshold.
Due to its high accuracy level, ANN has found wide application in uncertainty quantification and reliability analysis. ANN based response surface method has been presented by Shu and Gong [79] for reliability analyses of c-phi slopes. The soil properties have been assumed to be having spatial randomness and hence modelled as random field. It has been observed that the proposed approach yield accurate estimation of failure probability. A multi-wavelet neural network based response surface method has been proposed by Dai et al. [80] for structural reliability analysis. It has been illustrated that the proposed algorithm outperforms the well-known multilayer perceptron based response surface method. Other works which utilized neural network in the field of uncertainty quantification and reliability analysis include [40, 81, 82].
2.6 Support Vector Regression
Support vector regression (SVR) is a variant of the Support Vector Machine (SVM) utilized for regression analysis. SVR uses a subset of data samples, support vectors, in order to construct an approximation model that has a maximum deviation of \(\varepsilon\) from the function value corresponding to each training data. For a linear mapping, the SVR model may be represented as
where \(\hat g({\varvec{X}})\) is the approximate value of the objective function at \(x,\)W represents a vector of weights, b is the bias term, and \(\left\langle \cdot \right\rangle\) denotes the inner product. Equation (18) may be further expressed as a convex optimization problem as
where \({g_i}\left( {{X_i}} \right)\) represent the responses at the sample points. It should be noted that there might not be a function that satisfies the condition in Eq. (19). Hence, introducing slack variables \({\xi _i},\xi _{i}^{*},\) Eq. (19) can be rewritten as:
where \(n\) is the number of sample points. The regularization parameter, C, determines the trade-off between the model complexity and the degree for which deviation larger than \(\varepsilon\) is allowed in Eq. (20). The formulation discussed corresponds to dealing with a \(\varepsilon\)-insensitive loss function, as proposed by [83]
Next introducing a Lagrange multiplier as:
It is to be noted that the dual variables in Eq. (22) should satisfy the positivity constraints, i.e., \({\alpha _i},\alpha _{i}^{*},{\eta _i},\eta _{i}^{*} \ge 0.\) Furthermore, it can be shown that Eq. (22) has a saddle point with respect to the primary and dual variables at the optimal solution [84]. Hence,
where \(\alpha _{i}^{{\left( * \right)}}\) includes both \({\alpha _i}\) and \(\alpha _{i}^{*}.\) Similarly, \(\eta _{i}^{{\left( * \right)}}\) also includes both \({\eta _i}\) and \(\eta _{i}^{*}.\) Substituting Eqs. (23)–(25) into Eq. (22) yields
It should be noted that variables \({\eta _i}\) and \(\eta _{i}^{*}\) are not present in Eq. (26). Additionally using Eq. (24),
In order to compute b, the so-called Karush–Kuhn–Tucker (KKT) condition has been utilized. According to the KKT condition,
and
From Eq. (29), important remarks can be presented. First, \(\left( {C - \alpha _{i}^{{\left( * \right)}}} \right)=0\) only if the samples lie outside the \(\varepsilon\)-insensitive zone. Secondly, \({\alpha _i}\alpha _{i}^{*}=0,\) i.e., either \({\alpha _i}\) or \(\alpha _{i}^{*}\) should always be zero. Finally, for \(\alpha _{i}^{{\left( * \right)}} \in \left( {0,C} \right),\)\(\xi _{i}^{{\left( * \right)}}=0.\) Hence, the second factor in Eq. (28) vanishes. Therefore,
Similar to the procedure described above, a non-linear regression can be achieved by replacing the \(\left\langle \cdot \right\rangle\) in Eq. (18) with a kernel function, K, [83] as
All other operations will be applicable as discussed previously.
SVR, of late, has found wide application in uncertainty quantification and reliability analysis. Least square based SVR has been utilized [85] for reliability analysis. It has been illustrated that the structural risk associated with SVR is inherently minimized and therefore, suitable as a surrogate model for reliability analysis. Bootstrap technique has been integrated into the framework of SVR by Lins et al. [86] for obtaining confidence and prediction interval using SVR. The bootstrap based SVR has been utilized for a large scale problem involving component degradation of offshore oil industry. A novel dynamic-weighted probabilistic SVR has been proposed by Liu et al. [87]. The approach developed has been utilized for a real case study on reactor coolant pump governed by 20 failure scenarios. Other significant work on SVR include [88, 89].
Tuning the parameters for obtaining optimum performance is an important aspect associated with SVR. A hybrid method (APSO-SVR) based on the particle swarm optimization and analytical selection for tuning of parameters in SVR has been developed by Zhao et al. [90]. It has been demonstrated that APSO-SVR outperforms the conventional SVR is terms of convergence. Other significant contribution to parameter tuning of SVR include work by Zhao et al. [91] and Coen et al. [92].
2.7 Kriging
Kriging is a surrogate model which is based on Gaussian process modelling. The basic idea of Kriging is to incorporate interpolation, governed by prior covariances, in order to obtain responses at unknown points [93, 94]. In this method, the functional response characteristics is illustrated as:
where \(\hat {\varvec{g}}\left( {\varvec{X}} \right)\) is the response function of interest, \({\varvec{X}}\) is an N dimensional vector (N design variables), \({y_0}({\varvec{X}})\) is the known approximation (usually polynomial) function and Z(x) represents is the realization of a stochastic process with mean zero, variance, and non-zero covariance. In the model, the local deviation at an unknown point (X) is expressed using stochastic processes. The sample points are interpolated with the help of Gaussian as the correlation function to estimate the trend of the stochastic processes [95, 96].
Consider, \({\mathbf{X}}={\left\{ {{X_1},{X_2}, \ldots ,{X_N}} \right\}^T} \in {\Re ^N}\) be the vector of basic random variables and \(g\left( {\mathbf{X}} \right)\) be the system response output. In universal Kriging, \({y_0}({\varvec{X}})\) is represented by using a multivariate polynomial as:
where \({b_i}\left( {\varvec{X}} \right)\) represents the ith basis function and \({a_i}\) denotes the coefficient associated with the ith basis function. The primary idea behind such a representation is that the regression function captures the variance in the data (the overall trend) and the Gaussian process interpolates the residuals. Suppose \(X=\left\{ {{X^1},{X^2}, \ldots ,{X^n}} \right\}\) represents a set of n samples. Also, assume \(g=\left\{ {{g_1},{g_2}, \ldots ,{g_n}} \right\}\) to be the responses at training points. Therefore, the regression part can be written as a n × p model matrix F,
whereas, the stochastic process is defined using a n × n correlation matrix \(\Psi\)
where \(\psi \left( { \cdot , \cdot } \right)\) is a correlation function, parameterised by a set of hyperparameters \(\theta.\) The hyperparameters are further identified by maximum likelihood estimation (MLE). A detailed account of MLE in the context of Kriging can be found in [38]. The prediction mean and variance can be obtained as:
and
where \(M=\left( {\begin{array}{*{20}{c}} {{b_1}\left( {{X_p}} \right)}& \ldots &{{b_p}\left( {{X_p}} \right)} \end{array}} \right)\) is the modal matrix of the predicting point \({X_p},\)
is a p × 1 vector consisting of the unknown coefficients determined by generalised least squares regression and
is an 1 × n vector denoting the correlation between the prediction point and the sample points. The process variance \({\sigma ^2}\) is given by
It is worthwhile to mention that the universal Kriging, as formulated above, is an interpolation technique. This can be easily validated by substituting the ith sample point in Eq. (36) and considering that \(r\left( {{X^i}} \right)\) is the ith column of \(\Psi:\)
One issue associated with the universal Kriging is selection of the optimal polynomial order. Conventionally, the order of the polynomial is selected empirically. However, such non-adapted framework may render the modelling inefficient. Recent works [97,98,99,100,101,102,103,104] have addressed these issues.
An essential feature associated with Kriging is selection of appropriate covariance function [105,106,107]. Mostly, the covariance functions used with Kriging surrogate are stationary and can be expressed in the following form:
The correlation function defined in Eq. (42) has two desirable properties. Firstly, the correlation function for multivariate functions can be represented as product of one dimensional correlations. Secondly, the correlation is stationary and depends only in the distance between two points. Few standard stationary covariance functions, which have been investigated are namely, (a) exponential correlation function, (b) generalised exponential correlation function (c) Gaussian correlation function (d) linear correlation function (e) spherical correlation function (f) cubic correlation function and (g) spline correlation function. The mathematical forms of the above correlation functions are provided below:
-
i.
Exponential correlation function:
$$\psi _{j} \left( {\theta ;\,d_{j} } \right) = \exp \left( { - \theta _{j} \left| {d_{j} } \right|} \right)$$(43) -
ii.
Generalised exponential correlation function:
$${\psi _j}\left( {\theta ;\,{d_j}} \right)=\exp \left( { - {\theta _j}{{\left| {{d_j}} \right|}^{{\theta _{n+1}}}}} \right),\,{ }0<{\theta _{n+1}} \le 2$$(44) -
iii.
Gaussian correlation function:
$${\psi _j}\left( {\theta ;\,{d_j}} \right)\,=\,\exp \left( { - {\theta _j}{d_j}^{2}} \right)$$(45) -
iv.
Linear correlation function:
$${\psi _j}\left( {\theta ;\,{d_j}} \right)\,=\,\max \left\{ {0,1 - {\theta _j}\left| {{d_j}} \right|} \right\}$$(46) -
v.
Spherical correlation function:
$${\psi _j}\left( {\theta ;\,{d_j}} \right)=1 - 1.5\,{\xi _j}\,+\,0.5\,\xi _{j}^{2},\,{ }{\xi _j}\,=\,\min \left\{ {1,\,{\theta _j}\left| {{d_j}} \right|} \right\}$$(47) -
vi.
Cubic correlation function:
$${\psi _j}\left( {\theta ;\,{d_j}} \right)=1 - 3\,\xi _{j}^{2}\,+\,2\,\xi _{j}^{3},\,{ }{\xi _j}=\min \left\{ {1,\,{\theta _j}\left| {{d_j}} \right|} \right\}$$(48) -
vii.
Spline correlation function:
$$\psi _{j} \left( {\theta ;d_{j} } \right) = \left\{ {\begin{array}{*{20}l} {1 - 5\xi _{j}^{2} + 30\xi _{j}^{3} ,\,\,\,\,\,\,\,\,\,\,\,0 \le \xi _{j} \le 0.2} \\ {1.25\left( {1 - \xi _{j}^{3} } \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,0.2 \le \xi _{j} \le 1} \\ {0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\xi _{j}> 1} \\ \end{array} } \right.$$(49)
where \({\xi _j}={\theta _j}\left| {{d_j}} \right|.\)
For all the correlation functions described above, \({d_j}={x_i} - {x_i}^{\prime }.\)
2.8 Locally Weighted Polynomials
An approach for the pointwise estimation of the unknown function from known samples based upon Taylor’s series expansion has been proposed by Cleveland [108]. This idea was further extended into a statistical framework for model approximation. Later, these methods have been generalized into kernel regression approach [109, 110].
Locally weighted polynomial (LWP) regression is one such form of instance-based algorithm for learning continuous non-linear mappings [111]. Basically, it is a non-parametric regression approach that combine multiple models in a k-nearest-neighbor based metamodel [112]. A low-order weighted least square model is fitted at each training point. Let the input–output mapping be represented as,
where \(\varepsilon _{j} \sim N\left( {0,1} \right){\text{ and }}\sigma ^{2} \left( {x_{j} } \right)\) is the variance of \(Y_{j} {\text{ at }}x_{j}.\) For cases where homoscedastic variance is assumed, \({\sigma ^2}\left( x \right)={\sigma ^2}.\)\(M\left( x \right)\) can be obtained by solving the followinsg for \(\alpha\)
where \({K_b}\left( \cdot \right)\) controls the weights and b controls the size of neighbourhood around \({x_0}\). Equation (51) can be rewritten as
where W is a diagonal matrix of weights, \({W_{ii}}={K_b}\left( {{x_j} - {x_0}} \right).\) Coefficient vector α can be obtained by the following expression
Thus, there are three principal parameters whose selection may have an effect on the approximation, which are bandwidth (b), the order of polynomial (p), and the kernel or weight function (Kb) [113]. A natural way to select the bandwidth and calibrate the tradeoff is to minimize the mean squared error [114]. In this context, a variable bandwidth selector for kernel regression which can be extended for local linear regression has been proposed in [115]. An adaptive method has been proposed by Fan and Gijbels [116] for selecting the appropriate order of polynomials based on local factors, allowing p to range through various points within the support. In context to choose Kb, it has been established in [113], that the constant for the Epanechnikov kernel is the smallest and hence optimal in terms of integrated mean squared error. However, the difference between the kernels is negligible, so the selection may depend upon the user’s preference at large.
Expressions for the asymptotic bias and variance of an estimate have been presented in [117]. The local linear model using the Epanechnikov kernel has been proven to optimize the linear minimax risk [118], which is a criterion to benchmark the efficiency of an estimator in terms of sample size required for obtaining a certain level of accuracy in results. Later, these results were extended to LWP in [119]. LWP is observed to perform well near the boundary of support of the data, unlike most of non-parametric models in which rate of convergence is slow [110]. However, the basis of slow convergence has been explained as lower number of training points were utilized for estimators near the boundary. It has been illustrated in [120], that no linear estimator can prove to be superior on the boundary in a minimax sense in terms of mean squared error in comparison to LWP. Further details can be found in [109]. Few references in which computational efficiency of LWP has been improved upon are [121,122,123]. Some recent extensions of LWP include [124,125,126].
After an extensive literature review of popular surrogate models, the following section has been attributed to demonstrate the utilization of any of the above models in RDO framework.
3 Surrogate Assisted RDO Framework
This section discusses that how the surrogate models will be employed to address the issue of computational expense of robust optimization. The objective and/or constraint functions in RDO involve mean and standard deviation of stochastic responses, which is the main reason for making the computational platform cumbersome. This is due to large number of simulations required to approximate the statistical quantities of responses during each optimization iteration. It is worth mentioning that, generally there are two ways to introduce efficiency in an RDO approach, which are,
-
To avoid expensive original function/FE evaluation within an optimization iteration,
-
To reduce the number of optimization iterations by preserving the elite solutions.
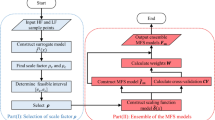
The scope of the present study is limited so as to address the first point discussed above, in order to present a comparative assessment of efficient surrogate assisted RDO tools. Therefore, instead of simulating original objective and constraint functions, the functions are approximated by surrogate models, which have been utilized within the optimization routine. This efficient surrogate based framework of RDO assists the computation to be limited to nominal costs, especially in case of large scale finite-element based models. A flow diagram of the entire steps involved in the surrogate assisted RDO approach has been depicted in Fig. 3 for better understanding.
During the evaluation of objective and constraint functions in Fig. 3, it is to be noted that in order to compute the response statistics, simulations are carried out based upon the model generated by the surrogate. This renders significant level of computational efficiency in comparison to MCS performed on the actual FE model. Moreover, since simulations have to be carried out in each of the optimization iteration, computational savings can be achieved in each of such iterations, until convergence of the optima.
Thus, the computational efficiency of surrogates as compared to simulation based RDO framework can be realized as an obvious matter of fact, however, approximation accuracy of the former is a crucial factor yet to be investigated. Therefore, various surrogate models as described in Sect. 2 have been employed in solving few typical non-linear analytical examples in the following section.
4 Numerical Examples
In order to illustrate the efficiency and accuracy of the various surrogate models in RDO platform, six benchmark examples have been considered in this section. In example 1, a test function has been investigated. A two bar plane truss has been studied in example 2. Conceptual design of a bulk carrier is of great concern in shipping industry, which is considered in example 3. Design of a welded beam has been taken up as the fourth example. A speed reducer problem has been investigated in example 5. Side impact crashworthiness of a car has been considered in example 6. Each of the optimization problems deal with single objective and multiple constraint functions. The sequence of examples has been placed in accordance to the increasing number of stochastic variables and hence, increasing complexity. Results obtained have been compared with that of Monte Carlo simulations (MCS) based RDO solutions.
In this paper, the computational platform has been MATLAB® version 8.1 R2013a. MATLAB® toolbox fmincon has been utilized as the optimization search engine. Grid sampling has been utilized for generating training points for constructing anchored ANOVA model. While the other surrogate models have been trained by utilizing latin-hypercube sampling [127]. For the comparison of computational effort, the number of original actual function evaluations is chosen as the primary index tool. This is due to the fact that the number of function evaluations indirectly indicates the CPU time usage.
The surrogates employed in order to solve the examples have been illustrated in Table 3. The abbreviations of the surrogate models mentioned in Table 3, have been utilized throughout the remaining paper.
4.1 Example 1: Test Function [21]
The first example considered is RDO of a test function [21]. The description of the problem has been stated as:
The objective is to minimize the standard deviation of f with a probabilistic constraint on g. \(\sigma _{f}^{*}\) and k have been adopted to be 15 and 3, respectively. The design variables \(x_{1} {\text{ and }}x_{2}\) follow normal distribution with standard deviation 0.4.
The number of sample points utilized for comparison of various methods have been presented in Table 4. The corresponding robust optimal solutions obtained have been reported in Table 5. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 4.
Comparative assessment of the surrogate models for example 1 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.2 Example 2: Two Bar Planar Truss [21]
RDO of a planar two bar truss [21] has been considered as the second example. The problem consists of two design variables, which are the cross sectional area \({x_1}\) and the horizontal span of each truss\({x_2}.\) The density of bar material \(\rho,\) the magnitude of the applied load \(Q,\) and the material’s tensile strength \(S\) are the other parameters of the problem. The objective is to minimize the volume of structure subject to constraints on axial strength of each of the members. The description of the deterministic optimization can be stated as:
The values of the other parameters \(\rho ,{\text{ }}Q{\text{ and }}S\) are \(10^{4} {\text{ kg/m}}^{{\text{3}}} ,{\text{ }}800{\text{ kN and }}1050{\text{ MPa}},\) respectively. The RDO formulation has been presented in Eq. (56).
The weighing factors \(w_{1} {\text{ and }}w_{2}\) have been adopted to be 0.5. \(\mu _{f}^{*} ,{\text{ }}\sigma _{f}^{*} {\text{ and }}k\) have been set as 10, 2 and 3, respectively. The description of the random variables has been presented in Table 6. The coefficient of variation of the two design variables is 0.02.
The number of sample points utilized for comparison of various methods have been presented in Table 7. The corresponding robust optimal solutions obtained have been reported in Table 8. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 5.
Comparative assessment of the surrogate models for example 2 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.3 Example 3: Bulk Carrier Design [16]
The third example considered is that of an RDO of a bulk carrier [16]. The basic cost function of the optimization problem has been considered to be the unit transportation cost. The six design variables have been described in Table 9. The formulation involves some design constraints and have been constructed based on geometry, stability and model validity.
The mathematical model of the cost function has been discussed briefly.
With the help of Eq. (66), \({V_k}\) has units of \({\text{m/s}}\) and \(g = 9.8065{\text{ m/s}}^{2}\) in Eq. (65).
The unit transportation cost has been adopted to be the objective function of the optimized conceptual design of a bulk carrier and can be evaluated using Eq. (83). Since the design problem incorporates several environmental factors and involves detailed modelling, large number of parameters have been involved. Therefore, to maintain disambiguity, all parameters required for evaluating Eq. (83) have been well defined in Eqs. (57)–(82). The constraints pertaining to the optimization problem have been defined in Eqs. (84)–(91).
where \(KB,BMT{\text{ and }}KG\) have been defined in Eqs. (92)–(94), respectively.
The description of random variables have been provided in Table 10. Two case studies have been performed for different configurations of objective function as presented in Table 11. The number of sample points utilized for comparison of various methods have been presented in Table 12. The robust optimal solutions corresponding to the case studies undertaken have been reported in Tables 13 and 14. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 6.
Comparative assessment of the surrogate models for example 3 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions, corresponding to case 1 of Table 11, (c) number of iterations (d) number of function calls, required in yielding the optimal solutions, corresponding to case 2 of Table 11. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.4 Example 4: Welded Beam Design [128]
The fourth example considered is that of a welded beam design [128]. The objective is to minimize the cost of the beam subject to constraints on shear stress, bending stress, buckling load, and end deflection. There are four continuous design variables, namely, beam thickness \({x_1}\), beam width \({x_2}\), weld length \({x_3}\), and weld thickness \({x_4}\).
The problem description can be stated as follows:
where
For the RDO formulation of the problem, each of the design variables have been assumed to be normally distributed with standard deviation to be 5%. Case study has been performed considering objective function to be: \({\text{mean}}\left( {f\left( {\mathbf{x}} \right)} \right) + {\text{SD}}\left( {f\left( {\mathbf{x}} \right)} \right),\) where SD is standard deviation.
The number of sample points utilized for comparison of various methods have been presented in Table 15. The corresponding robust optimal solutions obtained have been reported in Table 16. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 7.
Comparative assessment of the surrogate models for example 4 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.5 Example 5: Speed Reducer [129]
The fifth example considered is that of speed reducer, which is a standard optimization problem. The details of theoretical formulation can be found elsewhere [129]. The problem consists of seven design variables and eleven constraint functions. The mathematical description of the problem has been presented below.
The variable bounds have been presented in Eq. (111).
For the RDO formulation of the problem, each of the design variables have been assumed to be normally distributed with standard deviation to be 5%. Case studies have been performed considering various objective functions as shown in Table 17.
The number of sample points utilized for comparison of various methods have been presented in Table 18. The corresponding robust optimal solutions obtained have been reported in Tables 19 and 20. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 8.
Comparative assessment of the surrogate models for example 5 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions, corresponding to case 1 of Table 17, (c) number of iterations (d) number of function calls, required in yielding the optimal solutions, corresponding to case 2 of Table 17. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.6 Example 6: Side Impact Crashworthiness of Car [130]
The sixth example considered is that of an RDO of side impact crashworthiness of car [130]. This example has been reformulated as a robust optimization problem. The problem consists of eleven stochastic variables and nine variables out of them are design variables. The description of the stochastic and design variables have been provided in Tables 21 and 22.
The optimization problem formulation can be stated as:
The functional forms of the objective and constraint functions have been provided in Eqs. (114)–(124).
Case studies have been performed considering various objective functions as shown in Table 23. The number of sample points utilized for comparison of various methods have been presented in Table 24. The corresponding robust optimal solutions obtained have been reported in Tables 25 and 26. The number of iterations and function calls required for yielding the optimal solutions have been presented in Fig. 9.
Comparative assessment of the surrogate models for example 6 in terms of (a) number of iterations (b) number of function calls, required in yielding the optimal solutions, corresponding to case 1 of Table 23, (c) number of iterations (d) number of function calls, required in yielding the optimal solutions, corresponding to case 2 of Table 23. The number of function calls refer to the number of function evaluations in the optimization loop. The results obtained by MCS are also provided
4.7 Results and Discussion
The results obtained for each of the six problems by utilizing the surrogate models have been discussed in this section. This discussion has been presented in order to provide guidance to the users about the appropriateness of a particular surrogate model to be utilized in a specific problem. For each of the case studies performed, the best performing surrogate model (in terms of closeness to MCS based solutions) has been marked in bold.
Firstly, in case of example 1, ANOVA-D performs excellently, almost exactly matching the MC based optimal solutions. Apart from ANN and SVM, all other models exhibit acceptable performance in terms of approximation accuracy. ANOVA-D and the PCE based models have been observed to converge in less number of iterations and function calls, in comparison to the other surrogate models. In example 2, ANOVA-D, FK, RBF and the PCE based approaches yield strikingly similar results as compared to MCS based RDO. Also, the above models yield results in relatively less number of iterations as compared to the other models, which probably experience delayed convergence due to some false optima at intermediate iterations. In example 3, excellent similar results have been obtained by ANOVA-D and UK as compared to MC based solutions, both in terms of accuracy and rate of convergence. Models such as, RBF, LWP, ANN and MARS yield slightly inaccurate results, however, in relatively less number of iterations as compared to the above ones. In example 4, ANOVA-D, PCE-OLS and PCE-LAR achieve almost exact results as that of MCS, in relatively less number of iterations and function calls as compared to other surrogate models. Excellent results in terms of similarity to MCS have been obtained by ANOVA-D, PCE-OLS and PCE-LAR in example 5. The above models outperform the other surrogates not only in response approximation but also in terms of rate of convergence. FK has also achieved decent and satisfactory results, however, it requires significantly higher number of iterations to converge. It is also worth mentioning that PCE-Q did not achieve convergence due to the lack of ability to accurately approximate the response functions in presence of multiple constraints. Exactly same results have been achieved by ANOVA-D as compared to MC based solutions in example 6. However, other models such as, UK, PCE-LAR, LWP, ANN and MARS have performed very well both in terms of approximation accuracy and rate of convergence. It is also worth mentioning that PCE-Q and PCE-OLS did not achieve convergence due to the lack of ability to accurately approximate the response functions in multiple constrained environment.
The results of each of the examples as discussed above illustrate that performance of a surrogate model is very sensitive in an RDO framework, and may easily lead to an incorrect optima. In all of the above examples carried out, only one surrogate model i.e., ANOVA-D, has been consistent in accurately capturing the non-linearity and multi-modal landscapes in presence of constraints. It is also worth mentioning that PCE-LAR, being an adaptive sparse model, has achieved good results in most of the problems. Rest of the models have been observed to perform well in few problems and found unsuitable for other complex non-linear problems. Thus, on the basis of the above results, it is recommended to employ ANOVA-D as a surrogate model for highly complex problems whose response landscapes are difficult to capture and additionally comprising of multiple non-linear constraints. Since ANOVA-D has been observed to perform in a superior manner not only in terms of accuracy but also in convergence rate, therefore, it has been employed to solve a large-scale practical engineering problem in the next section.
5 Practical Problem: RDO of a Hydroelectric Dam Model
Electricity generation using a hydroelectric dam is primarily governed by the hourly water supplied through the turbine and the water level in the reservoir. It is quite obvious that due to environmental variations, large amount of uncertainties are associated with a hydroelectric dam. Moreover, cost of energy is also influenced by various factors. Hence, it is of utter importance to consider the presence of uncertainties while optimizing (maximizing) the overall revenue of a hydroelectric dam.
The hydroelectric dam considered in this study as presented in Fig. 10, is such that the water in the reservoir may either leave through the spillway or turbine. It is obvious that the water leaving through the turbine will be utilized in producing electricity. The primary objective of designing a hydroelectric dam is to maximize the revenue generated by selling the electricity. Conventional optimization of the above mentioned hydroelectric dam can be found in [131].
Various uncertainties are associated with any hydroelectric dam. For instance, the flow through spillway and turbine are generally controlled by some machine operated gates. However, it is not possible to exactly control the flow with such machineries and this results in some uncertainties. On the other hand, the in-flow to the reservoir is uncontrolled and hence large sources of uncertainties is associated with this. Moreover, market price of electricity depends on various factors and is highly uncertain. It is to be noted that flow through spillway, flow through turbine, in-flow and market price are generally monitored on an hourly basis. In the present study, the simulation is run for 12 h and hence, the system under consideration involves 48 random variables. A detailed account of the involved uncertain variables have been provided in Table 27.
The electricity produced in a hydroelectric dam depends on two primary parameters, namely amount of water owing through the turbine and the reservoir storage level. The storage of reservoir again depends on the three factors: (a) in-flow, (b) flow through turbine and (c) flow through spillway. As the flow through turbine increases, the water in the reservoir decreases. Therefore, it is necessary to compute the optimum flow through the turbine and spillway that maximizes the electricity production. Moreover, certain constraints needs to be considered while solving the optimization problem. First, both reservoir level and downstream flow rates should be within some specified limit. Secondly, maximum flow through the turbine should not exceed the turbine capacity. Finally, the mean reservoir level at the end of the simulation should be same as that at the beginning. This ensures that the reservoir is not emptied at the end of the optimization cycle. The RDO problem has been stated as:
where \(\mu \left( \cdot \right){\text{ and }}\sigma \left( \cdot \right)\) denote mean and standard deviation, respectively. R denotes the revenue generated and S denotes the storage of the reservoir. \(f_{t} {\text{ and }}f_{s}\) in Eq. (125) represent the flow through turbine and spillway, respectively. \(\beta\) is the weightage factor. The objective is to determine \(f_{t} {\text{ and }}f_{s}\) that minimizes the objective function as defined in Eq. (125).
The RDO results have been obtained for \(\beta =0.5,\) i.e., equal weightage has been assigned to the mean and standard deviation of the revenue generated. The number of sample points required for training the anchored ANOVA decomposition (ANOVA-D) model is 4609. The results obtained by ANOVA-D have been validated with that of MCS (104 samples) for each optimization iteration. The robust optimal solutions obtained by utilizing ANOVA-D as presented in Table 28 and Fig. 11 has achieved excellent similarity with benchmark MCS solutions. This illustrates high approximation accuracy of ANOVA-D. Additionally, ANOVA-D has utilized significantly less number of sample points as compared to MCS, which illustrates its computational efficiency. Overall, the performance of ANOVA-D is acknowledgeable in such high-dimensional problem as this present one.
After carrying out an extensive numerical study by utilizing few surrogate models in RDO framework (Sect. 4) and also, addressing a practical engineering problem in an efficient manner (Sect. 5), the study has been summarized briefly in the next section.
6 Summary and Recommendations
An extensive survey has been carried out in this study illustrating the performance of surrogate models in RDO framework. As previously illustrated, the approximation accuracy of a surrogate model is a crucial factor in stochastic optimization as a slight deviation from the results of any intermediate iterations may easily deviate to yield a false or local optima. Therefore, the motivation of the study has been to access the performance of available surrogate models in terms of their approximation potential while solving typical non-linear RDO problems. This study would also serve as a guiding handbook for the selection of a suitable surrogate model for addressing a problem of a particular level of complexity. In this context, few salient points have been highlighted on the basis of the results achieved by various surrogate models:
-
First and foremost, ANOVA-D has outperformed the other models investigated for solving typical non-linear RDO examples. It has proven its consistency and robustness in accurately approximating the response functions in all examples, unlike the other models. It is highly recommended for use in future applications of stochastic optimization.
-
Secondly, performance of least angle regression based PCE is noteworthy both in terms of yielding accurate solutions and rate of convergence, except in the third example. After ANOVA-D, PCE-LAR has achieved the second ranking among the models utilized and thus, recommended to be utilized and further improved.
-
Thirdly, ordinary least square and quadrature based PCE do not achieve convergence in examples 5 and 6. Thus, they are not recommended to be utilized for relatively high-dimensional non-linear problems with multiple constraints. However, they may be considered to be suitable for low-dimensional problems.
-
Fourthly, performance of models such as, Kriging, RBF, LWP, ANN and MARS have been observed to vary in different problems and thus, found to be inconsistent. It is highly recommended to validate the results obtained by using these above models with benchmark solutions, if available.
-
Lastly, SVM has yielded unacceptable results due to its lack of capability to accurately capture the non-linearity in functional space and thus, gets deviated from the true optima in presence of constraints.
Thus, after identifying high reliability of ANOVA-D in complex landscapes, it has been employed to solve a practical large-scale hydroelectric dam model. As expected, ANOVA-D has yielded similar results as compared to MCS based RDO solutions, by utilizing limited number of training points, considering the scale of the problem. Thus, the study illustrates the resilience of anchored ANOVA decomposition is note-worthy and encouraging for applications in further complex engineering systems.
References
Jin R, Du X, Chen W (2003) The use of metamodeling techniques for optimization under uncertainty. Struct Multidiscip Optim 25:99–116
Zang C, Friswell MI, Mottershead JE (2005) A review of robust optimal design and its application in dynamics. Comput Struct 83:315–326
Beyer H-G, Sendhoff B (2007) Robust optimization: a comprehensive survey. Comput Methods Appl Mech Eng 196:3190–3218
Chen W, Allen J, Tsui K, Mistree F (1996) Procedure for robust design: minimizing variations caused by noise factors and control factors. J Mech Des Trans ASME 118:478–485
Du X, Chen W (2000) Towards a better understanding of modeling feasibility robustness in engineering design. J Mech Des Trans ASME 122:385–394
Huang B, Du X (2007) Analytical robustness assessment for robust design. Struct Multidiscip Optim 34:123–137
Phadke M (1989) Quality engineering using robust design. Prentice Hall, Englewood Cliffs, NJ
Taguchi G (1987) System of experimental design: engineering methods to optimize quality and minimize costs, vol 1, UNIPUB/Kraus International Publications, White Plains, NY
Taguchi G (1986) Quality engineering through design optimization. Krauss International Publications, White Plains, NY
Alexandrov N, Lewis R (2002) Analytical and computational aspects of collaborative optimization for multidisciplinary design. AIAA J 40:301–309
Hicks R, Henne PA (1978) Wing design by numerical optimization. J Aircr 15:407–412
Sobieszczanski-Sobieski J, Haftka R (1997) Multidisciplinary aerospace design optimization: survey of recent developments. Struct Optim 14:1–23
Fang J, Gao Y, Sun G, Li Q (2013) Multiobjective reliability-based optimization for design of a vehicle door. Finite Elem Anal Des 67:13–21
Hwang K, Lee K, Park G (2001) Robust optimization of an automobile rearview mirror for vibration reduction. Struct Multidiscip Optim 21:300–308
Sun G, Li G, Zhou S, Li H, Hou S, Li Q (2010) Crashworthiness design of vehicle by using multiobjective robust optimization. Struct Multidiscip Optim 44:99–110
Diez M, Peri D (2010) Robust optimization for ship conceptual design. Ocean Eng 37:966–977
Hart CG, Vlahopoulos N (2009) An integrated multidisciplinary particle swarm optimization approach to conceptual ship design. Struct Multidiscip Optim 41:481–494
Parsons M, Scott R (2004) Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods. J Sh Res 48:61–76
Doltsinis I, Kang Z (2004) Robust design of structures using optimization methods. Comput Methods Appl Mech Eng 193:2221–2237
Lagaros ND, Plevris V, Papadrakakis M (2007) Reliability based robust design optimization of steel structures. Int J Simul Multidiscip Des Optim 1:19–29
Lee SH, Chen W, Kwak BM (2009) Robust design with arbitrary distributions using Gauss-type quadrature formula. Struct Multidiscip Optim 39:227–243
Cheng J, Liu Z, Wu Z, Li X, Tan J (2014) Robust optimization of structural dynamic characteristics based on adaptive Kriging model and CNSGA. Struct Multidiscip Optim 51:423–437
Roy BK, Chakraborty S (2015) Robust optimum design of base isolation system in seismic vibration control of structures under random system parameters. Struct Saf 55:49–59
Lee T, Jung J (2006) Metamodel-based shape optimization of connecting rod considering fatigue life. Key Eng Mater 211:306–308
Li F, Meng G, Sha L, Zhou L (2011) Robust optimization design for fatigue life. Finite Elem Anal Des 47:1186–1190
McDonald M, Heller M (2004) Robust shape optimization of notches for fatigue-life extension. Struct Multidiscip Optim 28:55–68
Lee I, Choi KK, Du L, Gorsich D (2008) Dimension reduction method for reliability-based robust design optimization. Comput Struct 86:1550–1562
Ramakrishnan B, Rao S (1996) A general loss function based optimization procedure for robust design. Eng Optim 25:255–276
Schuëller GI, Jensen HA (2008) Computational methods in optimization considering uncertainties—an overview. Comput Methods Appl Mech Eng 198:2–13
Bhattacharjya S (2010) Robust optimization of structures under uncertainty, Ph.D. Thesis, Department of Civil Engineering. Bengal Engineering and Science University, Shibpur
Kleijnen JPC (1987) Statistical tools for simulation practitioners. Marcel Dekker Inc., New York
Jin R, Chen W, Simpson T (2001) Comparative studies of metamodeling techniques under multiple modeling criteria. Struct Multidiscip Optim 23:1–13
Sudret B (2012) Meta-models for structural reliability and uncertainty quantification. In: Proc. 5th Asian-Pacific Symp. Stuctural Reliab. Its Appl. (APSSRA, 2012), Singapore, pp 53–76
Kim S-H, Na S-W (1997) Response surface method using vector projected sampling points. Struct Saf 19:3–19
Kang S-C, Koh H-M, Choo JF (2010) An efficient response surface method using moving least squares approximation for structural reliability analysis. Probabilistic Eng Mech 25:365–371
Jacquelin E, Adhikari S, Sinou J, Friswell MI (2014) Polynomial chaos expansion and steady-state response of a class of random dynamical systems. J Eng Mech 141:04014145
Rabitz H, Aliş ÖF (1999) General foundations of high-dimensional model representations. J Math Chem 25:197–233
Kaymaz I (2005) Application of kriging method to structural reliability problems. Struct Saf 27:133–151
Deng J (2006) Structural reliability analysis for implicit performance function using radial basis function network. Int J Solids Struct 43:3255–3291
Mareš T, Janouchová E, Kučerová A (2016) Artificial neural networks in the calibration of nonlinear mechanical models. Adv Eng Softw 95:68–81
Richard B, Cremona C, Adelaide L (2012) A response surface method based on support vector machines trained with an adaptive experimental design. Struct Saf 39:14–21
Friedman JH (1991) Multivariate adaptive regression splines. Ann Stat 19:1–67
Simpson T, Mauery T, Korte J, Mistree F (1998) Comparison of response surface and kriging models for multidisciplinary design optimization. In: 7th AIAA/USAF/NASA/ISSMO Symp. Multidiscip. Anal. Optim, St. Louis, MO, pp 381–391
Giunta A, Watson L, Koehler J (1998) A comparison of approximation modeling techniques: polynomial versus interpolating models. In: Proc. Seventh AIAA/USAF/NASA/ISSMO Symp. Multidiscip. Anal. Optim. AIAA-98-4758. pp 1–13
Ray T, Smith W (2006) A surrogate assisted parallel multiobjective evolutionary algorithm for robust engineering design. Eng Optim 38:997–1011
Chowdhury R, Rao BN, Prasad AM (2008) High dimensional model representation for piece-wise continuous function approximation. Commun Numer Methods Eng 24:1587–1609
Chowdhury R, Rao BN, Prasad AM (2009) High-dimensional model representation for structural reliability analysis. Commun Numer Methods Eng 25:301–337
Alis ÖF, Rabitz H (2001) Efficient implementation of high dimensional model representations. J Math Chem 29:127–142
Chastaing G, Gamboa F, Prieur C (2011) Generalized hoeffding-sobol decomposition for dependent variables-application to sensitivity analysis. Electron J Stat 6:2420–2448
Ho T-S, Rabitz H (2003) Reproducing kernel Hilbert space interpolation methods as a paradigm of high dimensional model representations: application to multidimensional potential energy surface construction. J Chem Phys 119:6433
Sobol IM (1993) Sensitivity estimates for nonlinear mathematical models. Math Model Comput Exp 1:407–414
Wiener N (1938) The homogeneous Chaos. Am J Math 60:897. doi:10.2307/2371268
Xiu D, Karniadakis GE (2002) The Wiener–Askey polynomial Chaos for stochastic differential equations. SIAM J Sci Comput 24:619–644
Hampton J, Doostan A (2015) Coherence motivated sampling and convergence analysis of least squares polynomial chaos regression. Comput Methods Appl Mech Eng 290:73–97
Filomeno Coelho R, Lebon J, Bouillard P (2011) Hierarchical stochastic metamodels based on moving least squares and polynomial chaos expansion. Struct Multidiscip Optim 43:707–729
Madankan R, Singla P, Patra A, Bursik M, Dehn J, Jones M et al (2012) Polynomial chaos quadrature-based minimum variance approach for source parameters estimation. Procedia Comput Sci 9:1129–1138
Zheng Zhang TA, El-Moselhy IM, Elfadel L, Daniel (2014) Calculation of generalized polynomial-chaos basis functions and Gauss quadrature rules in hierarchical uncertainty quantification. IEEE Trans Comput Des Integr Circuits Syst 33:728–740
Zhao F, Tian Z (2012) Gear remaining useful life prediction using generalized polynomial chaos collocation method. In: Pham H (ed), Proc. 18TH ISSAT Int. Conf. Reliab. Qual. Des. pp 217–221
Hosder S, Walters RW, Balch M (2012) Point-collocation nonintrusive polynomial chaos method for stochastic computational fluid dynamics. AIAA J 48:2721–2730
Blatman G, Sudret B (2010) An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng Mech 25:183–197
Blatman G, Sudret B (2011) Adaptive sparse polynomial chaos expansion based on least angle regression. J Comput Phys 230:2345–2367
Xiu D, Karniadakis GE (2002) Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput Methods Appl Mech Eng 191:4927–4948
Xiu D, Karniadakis GE (2003) Modeling uncertainty in flow simulations via generalized polynomial chaos. J Comput Phys 187:137–167
Sudret B (2008) Global sensitivity analysis using polynomial chaos expansions. Reliab Eng Syst Saf 93:964–979
Pascual B, Adhikari S (2012) A reduced polynomial chaos expansion method for the stochastic finite element analysis. Sadhana-Acad Proc Eng Sci 37:319–340
Pascual B, Adhikari S (2012) Combined parametric-nonparametric uncertainty quantification using random matrix theory and polynomial chaos expansion. Comput Struct 112:364–379
Craven P, Wahba G (1978) Smoothing noisy data with spline functions. Numer Math 31:377–403
Sudjianto A, Juneja L, Agrawal H, Vora M (1998) Computer aided reliability and robustness assessment. Int J Reliab Qual Saf Eng 05:181–193
Wang X, Liu Y, Antonsson EK (1999) Fitting functions to data in high dimensionsal design space. In: ASME Des. Eng. Tech. Conf., Las Vegas, p DETC99/DAC-8622
Krishnamurthy T (2003) Response surface approximation with augmented and compactly supported radial basis functions. In: 44th AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf., American Institute of Aeronautics and Astronautics, Reston, Virigina
Hardy RL (1971) Multiquadric equations of topography and other irregular surfaces. J Geophys Res 76:1905–1915
Buhmann MD (2000) Radial basis functions. Acta Numer 9:1–38
Volpi S, Diez M, Gaul NJ, Song H, Iemma U, Choi KK et al (2015) Development and validation of a dynamic metamodel based on stochastic radial basis functions and uncertainty quantification. Struct Multidiscip Optim 51:347–368
Dai HZ, Zhao W, Wang W, Cao ZG (2011) An improved radial basis function network for structural reliability analysis. J Mech Sci Technol 25:2151–2159
Chau MQ, Han X, Jiang C, Bai YC, Tran TN, Truong VH (2014) An efficient PMA-based reliability analysis technique using radial basis function. Eng Comput 31:1098–1115
Chau MQ, Han X, Bai YC, Jiang C (2012) A structural reliability analysis method based on radial basis function. C Comput Mater Contin 27:128–142
Kriesel D (2010) A brief introduction to neural network
Hagan MT, Demuth HB, Beale MH, Jesús OD (2008) Neural network design, 2nd edn. Cengage Learning, New Delhi
Shu S, Gong W (2016) An artificial neural network-based response surface method for reliability analyses of c-φ slopes with spatially variable soil, China. Ocean Eng 30:113–122
Dai H, Zhang H, Wang W (2015) A multiwavelet neural network-based response surface method for structural reliability analysis. Comput Civ Infrastruct Eng 30:151–162
Peng W, Zhang J, You L (2015) The hybrid uncertain neural network method for mechanical reliability analysis. Int J Aeronaut Sp Sci 16:510–519
Zio E (2006) A study of the bootstrap method for estimating the accuracy of artificial neural networks in predicting nuclear transient processes. IEEE Trans Nucl Sci 53:1460–1478
Vapnik VN (1998) Statistical learning theory. Wiley, New York
Goldstein H (1986) Classical mechanics. Addison-Wesley, Reading, MA
Z. Guo, G. Bai, Application of least qquares support vector machine for regression to reliability analysis. Chin J Aeronaut 22 (2009) 160–166
Lins ID, Droguett EL, das Chagas Moura M, Zio E, Jacinto CM (2015) Computing confidence and prediction intervals of industrial equipment degradation by bootstrapped support vector regression. Reliab Eng Syst Saf 137:120–128
Liu J, Vitelli V, Zio E, Seraoui R (2015) A novel dynamic-weighted probabilistic support vector regression-based ensemble for prognostics of time series fata. IEEE Trans Reliab 64:1203–1213
Gunn SR (1997) Support vector machines for classification and regression, Technical report, image speech and intelligent systems research group. Southampton, UK
Xiao M, Gao L, Xiong H, Luo Z (2015) An efficient method for reliability analysis under epistemic uncertainty based on evidence theory and support vector regression. J Eng Des 26:340–364
Zhao W, Tao T, Zio E, Wang W (2016) A novel hybrid method of parameters tuning in support vector regression for reliability prediction: particle Swarm optimization combined With analytical selection. IEEE Trans Reliab 1–13
Zhao W, Tao T, Zio E (2013) Parameters tuning in support vector regression for reliability forecasting. Chem Eng Trans 33:523–528
Coen T, Saeys W, Ramon H, De Baerdemaeker J (2006) Optimizing the tuning parameters of least squares support vector machines regression for NIR spectra. J Chemom 20:184–192
Olea RA (2011) Optimal contour mapping using Kriging. J Geophys Res 79:695–702
Warnes JJ (1986) A sensitivity analysis for universal kriging. Math Geol 18:653–676
Krige DG (1951) A Statistical approach to some basic mine valuation problems on the witwatersrand. J Chem Metall Min Soc South Africa 52:119–139
Krige DG (1951) A statisitcal approach to some mine valuations and allied problems at the Witwatersrand. University of Witwatersrand
Joseph VR, Hung Y, Sudjianto A (2008) Blind Kriging: a new method for developing metamodels. J Mech Des 130:031102
Hung Y (2011) Penalized blind kriging in computer experiments. Stat Sin 21:1171–1190
Couckuyt I, Forrester A, Gorissen D, De Turck F, Dhaene T (2012) Blind Kriging: implementation and performance analysis. Adv Eng Softw 49:1–13
Kennedy M, O’Hagan A (2000) Predicting the output from a complex computer code when fast approximations are available. Biometrika 87:1–13
Wang B, Bai J, Gea HC (2013) Stochastic Kriging for random simulation metamodeling with finite sampling. In: Vol. 3B 39th Des. Autom. Conf., ASME, p V03BT03A056. doi:10.1115/DETC2013-13361
Qu H, Fu MC (2014) Gradient extrapolated Stochastic Kriging. ACM Trans Model Comput Simul 24:1–25
Kamiński B (2015) A method for the updating of stochastic kriging metamodels. Eur J Oper Res 247:859–866
Bhattacharyya B (2017) A critical appraisal of design of experiments for uncertainty quantification. Arch Comput Methods Eng. doi:10.1007/s11831-017-9211-x
Rivest M, Marcotte D (2012) Kriging groundwater solute concentrations using flow coordinates and nonstationary covariance functions. J Hydrol 472–473:238–253
Putter H, Young GA (2001) On the effect of covariance function estimation on the accuracy of Kriging predictors. Bernoulli 7:421–438
Biscay Lirio R, Camejo DG, Loubes J-M, Muñiz Alvarez L (2013) Estimation of covariance functions by a fully data-driven model selection procedure and its application to Kriging spatial interpolation of real rainfall data. Stat Methods Appt 23:149–174
Cleveland W (1979) Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc 74:829–836
Hastie T, Loader C (1993) Local regression: automatic kernel carpentry (with discussion). Stat Sci 8:120–143
Fan J, Gijbels I (1992) Variable bandwidth and local linear regression smoothers. Ann Stat 20:196–216
Cleveland W, Devlin S (1988) Locally weighted regression: an approach to regression analysis by local fitting. J Am Stat Assoc 83:596–610
Cleveland W, Devlin S, Grosse E (1988) Regression by local fitting. J Econom 37:87–114
M. Wand, M. Jones (1995) Kernel smoothing, CRC Press, Boca Raton, FL
Fan J, Gijbels I (1996) Local polynomial modelling and its applications, Chapman and Hall
Schucany W (1995) Adaptive bandwidth choice for kernel regression. J Am Stat Assoc 90:535–540
Fan J, Gijbels I (1995) Adaptive order polynomial fitting: bandwidth robustification and bias reduction. J Comput Graph Stat 4:213–227
Lall U, Moon Y, Kwon H, Bosworth K (2006) Locally weighted polynomial regression: parameter choice and application to forecasts of the Great Salt Lake. Water Resour Res 42
Fan J (1993) Local linear regression smoothers and their minimax efficiencies. Ann Stat 21:196–216
Fan J, Gasser T, Gijbels I, Brockmann M, Engel J (1997) Local polynomial regression: optimal kernels and asymptotic minimax efficiency. Ann Inst Stat Math 49:79–99
Cheng M, Fan J, Marron J (1997) On automatic boundary corrections. Ann Stat 25:1691–1708
Fan J, Marron J (1994) Fast implementations of nonparametric curve estimators, J Comput Graph Stat 3:35–56
Hall P, Wand M (1996) On the accuracy of binned kernel density estimators. J Multivar Anal 56:165–184
Seifert B, Brockmann M, Engel J, Gasser T (1994) Fast algorithms for nonparametric curve estimation. J Comput Graph Stat 3:192–213
Seifert B, Gasser T (2000) Data adaptive ridging in local polynomial regression. J Comput Graph Stat 9:338–360
Li Q, Lu X, Ullah A (2003) Multivariate local polynomial regression for estimating average derivatives. J Nonparametr Stat 15:607–624
Kai B, Li R, Zou H (2010) Local composite quantile regression smoothing: an efficient and safe alternative to local polynomial regression, J R Stat Soc Ser B-Stat Methodol 72:49–69
McKay MD, Beckman RJ, Conover WJ (1979) A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2:239–245
Deb K (2001) Multi-objective optimization using evolutionary algorithms. Wiley, Chichester
Regis RG (2014) Evolutionary programming for high-dimensional constrained expensive black-box optimization using radial basis functions. IEEE Trans Evol Comput 18:326–347
Deb K, Gupta S, Daum D, Branke J, Mall AK, Padmanabhan D (2009) Reliability-Based Optimization Using Evolutionary Algorithms. IEEE Trans Evol Comput 13:1054–1074
DeLand S (2012) Solving large-scale optimization problems with MATLAB: A hydroelectric flow example
Acknowledgements
TC acknowledges the support of MHRD, Government of India and RC acknowledges the support of CSIR via Grant No. 22(0712)/16/EMR-II.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all the authors, the corresponding author states that there is no conflict of interest.
Rights and permissions
About this article
Cite this article
Chatterjee, T., Chakraborty, S. & Chowdhury, R. A Critical Review of Surrogate Assisted Robust Design Optimization. Arch Computat Methods Eng 26, 245–274 (2019). https://doi.org/10.1007/s11831-017-9240-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-017-9240-5