1 Introduction

Computational analysis and design of structural crashworthiness often involve multiple materials, strong nonlinearity and complicated contact, which require significant numerical effort and high computational cost. In this scenario, the conventional sensitivity-based optimization that typically necessitates a large number of analysis iterations to converge to an optimal design may be of limited practical value. In many cases it is extremely (if not impossible) to formulate a mathematical relationship between design objectives/constraints and design variables, making the sensitivity based approaches less feasible. To ease the mathematical and computational burden, one of effective alternatives is to construct a surrogate model based on a limited number of finite element analyses, which enables to formulate an explicit relationship between the objective/constraint functions and design variables with relatively simple expressions for optimization.

To date, substantial efforts have been devoted to apply specific surrogate models for different design problems (Hussain et al. 2002; Simpson et al. 2004; Lee and Kang 2007; Marzbanrad and Ebrahimi 2011; Lanzi et al. 2004; Acar et al. 2011; Kaya and Ozturk 2010; Jin et al. 2001; Yang et al. 2000, 2005a, b; Yang and Gu 2004; Viana et al. 2009; Song et al. 2010; Liao et al. 2008). It must be pointed out that these different surrogate models often provide rather different modeling accuracy (Viana et al. 2009), gradient information and design outcomes (Wang et al. 2011). It is unclear which surrogate model is most suitable for a particular case. Sometimes justification of a surrogate model itself may not be sound without comparing it with other models. Often researchers must make use of their past experience and/or literature data in order to choose a suitable surrogate model. To account for uncertainties in predictions, a simple and preferable way is to attempt different surrogate models, from which the best can be selected based upon the relative fitting accuracy (Viana et al. 2009; Wang et al. 2011). Nevertheless, it may not guarantee that such a surrogate model with the best global fitness (or the lowest modeling errors) would necessarily lead to the best optimal results. Hence a comparative study on different surrogate techniques for both modeling accuracy and design optimization often becomes essential. Unfortunately, systematic studies on this issue, particularly across different types of surrogate modeling techniques, have been rather limited thus far (Viana et al. 2009; Wang et al. 2011; Zhao and Xue 2010; Yang and Gu 2004).

As one of most typical energy absorbers, thin-walled structures have been widely used in automobile, aerospace and transportation engineering for their high ratio of energy absorption induced by progressive axial folding to structural weight. The early investigations of thin-walled structures were concentrated on the straight columns with circular, square, rectangular and/or multi-corner cross-sections using analytical, numerical (Liu 2008) and experimental methods (Abramowicz and Jones 1986). In addition to straight columns, experimental (Alghamdi 2002) and numerical (Nagel and Thambiratnam 2004a) studies were also conducted for tapered structures under axial or oblique loads (Ahmad et al. 2010). Compared with straight tubes, taper tubes have been considered more preferable because they can more likely provide a desired constant mean load-deflection response and are capable of withstanding oblique and axial loads (Nagel and Thambiratnam 2004b). Furthermore, tapered tubes are less likely to fail in a global buckling, thereby avoiding an undesirable crushing (Hou et al. 2011).

To increase the energy absorption without sacrificing too much weight, recent attention has been paid to cellular materials such as sawdust, honeycomb, foam, et al., filled in straight (Santosa et al. 2000; Seitzberger et al. 1997; Borvik et al. 2003) and tapered (Mirfendereski et al. 2008; Ahmad and Thambiratnam 2009a, b) thin-walled structures. Of these cellular filler materials, foam has proven particularly ideal for its large deformation at nearly constant load (Hou et al. 2009). To gain further insights into the effects of foam filling on the energy absorption characteristics of thin-walled tubes, the substantial experimental (e.g. Mamalis et al. 2008) and numerical studies (e.g. Bi et al. 2010) were conducted. New interest has been given to taper structures filled with foams for its superior balance of crashing stability and energy absorption capacity (Hou et al. 2011). From design perspective, foam-filled taper structures are more sophisticated and a single response model may not be adequate. But how to more properly relate the design variables to crashworthiness criteria remains questionable.

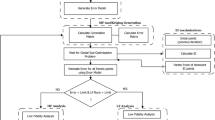
Unlike most of traditional crashworthiness designs involving single response model, the present study concerns four typical surrogate models, namely polynomial response surface (PRS), Kriging (KRG), support vector regression (SVR) and radial basis function (RBF), for optimizing foam-filled taper column. Any of these four surrogate models, as long as its modeling errors meet the accuracy requirements, will be used for the design optimization using both gradient based and non-gradient based algorithms. The final optimum will be selected through a comparative assessment of all the optimal solutions. This case study is expected to shed some light in advocating a more proper way of justifying adoption of surrogate models.

2 Numerical analysis of foam-filled taper structure

2.1 Crashworthiness criteria

To systematically study the crashworthiness of foam-filled tapered thin-walled structures and optimize the performance, it is essential to define the crashworthiness criteria. There have been many different indicators available to evaluate the crush characteristics and energy absorption capabilities of different structures (Sun et al. 2010b; Guler et al. 2010). Of these indicators, specific energy absorption (SEA) is widely used to estimate the energy absorption capabilities of absorbers with different materials and weights, and will be used in this study. SEA denotes the specific energy absorbed per unit mass of the absorber, as formulated below:

$$ \emph{SEA}=\frac{E_{\emph{absorbed}}}{M} $$
(1)

where M is the total mass of foam-filler and thin-walled structure, and E absorbed is the total absorbed energy during crashing, which can be calculated as:

$$ E_{\it absorbed} =\int_0^\delta {F({\bf x})dx} $$
(2)

where F is the crushing force in axial direction and δ the crashing displacement. Obviously, a higher SEA value indicates a higher capability of energy absorption.

Another indictor to energy absorption capacity is mean crash force F avg which is defined as the total energy absorption divided by the corresponding crushing displacement, given as:

$$ F_{\it avg} =\frac{E_{\it absorbed} }{\delta } $$
(3)

In automotive applications, the peak impact force represents other critical indicator to the occupant survival rate when impact occurs. A large peak impact force often leads to a high deceleration and may cause severe injury or even death of occupant (Liao et al. 2008b). In typical thin-walled structures, the initial peak force F peak is usually the same as the global peak force F global (Fig. 1a). However, in a foam-filled tapered thin-walled structure they can be different (Fig. 1b). Therefore, both F peak and F global can be used as the force indicators to evaluate the crashworthiness characteristics of the foam-filled thin-walled structures. In this study, we constrain F peak and F global to the predefined levels.

Fig. 1
figure 1

Axial impact force vs deformation in thin-walled structure. a Typical hollow thin-walled structure. b Foam-filled tapered thin-walled structure

Full size image

2.2 Finite element modeling

The structure analyzed herein is a foam-filled tapered thin-wall column with square cross-section subjected to an axial impact load, as shown in Fig. 2a. The length of the column is h = 300 mm, the small end of the tapered tube remains unchanged as a square of a × a = 50 mm × 50 mm. The dimension of the big square end of the tapered tube is obtained by varying taper angle θ. The foam-filled taper column impacts onto the rigid wall from the smaller end at an initial velocity of v = 15 m/s. To generate enough kinetic energy as applied in vehicle crashing, an additional mass block of 400 kg is attached to the big end (Fig. 2a).

Fig. 2
figure 2

a Schematic of the tapered square column with foam-filler. b finite element model

Full size image

In this study, finite element models were developed using commercial code LS-DYNA. The Belytschko-Lin-Tsay reduced integration shell elements were employed to model the column wall. To model the foam materials, the eight-node brick elements with one integration point were adopted. Stiffness-based hourglass control was employed to avoid spurious zero energy deformation modes and reduced integration was used to avoid volumetric locking.

Since the foam-filled taper tube involves two materials, different contact algorithms in LS-DYNA can be used. The interface between the foam and inner wall of column was modeled as an “automatic surface to surface” contact. While “automatic single surface” contact was applied to the column wall itself to avoid interpenetration of folding generated during axial collapse. To account for contact between the rigid bodies, foam and tube, “node to surface” and “automatic surface to surface” contacts were defined with static and dynamic coefficients of friction of 0.2 and 0.3, respectively (Seitzberger et al. 1997). These two kinds of stiffness were defined such that neither interpenetration nor instability commonly resulted from inappropriate stiffness is encountered.

The materials of the thin wall column used here is aluminum alloy AA6061-T4 with density ρ = 2700 kg/m3, Poisson’s ratio ν = 0.28, Young’s modulus E = 64.75 GPa, and yielding stress σ y  = 71 MPa. The post collapse response of column was defined using the true static stress-strain curve of the aluminum that was obtained from a standard tensile test (Kim 2002). As the aluminum is insensitive to the strain rate, the rate-dependent effect is neglected in the FE modeling (Hou et al. 2009).

The foam was modeled as proposed by Deshpande and Fleck (2000), in which the yield criterion of foam material is defined as follows:

$$ \Phi =\hat{\sigma }-\sigma_y \le 0 $$
(4)

where σ y is the yield stress and the equivalent stress \(\hat{{\sigma }}\) is given as:

$$ \hat{{\sigma }}^2=\frac{1}{\left[ {1+( {\alpha / 3} )^2} \right]}\left[\sigma_e^2 +\alpha^2\sigma_m^2 \right] $$
(5)

where σ e is the von Mises effective stress and σ m the mean stress. Parameter α controlling the shape of the yield surface is a function of the plastic Poisson’s ratio ν p given as:

$$ \alpha^2=\frac{9(1-2\nu_p )}{2(1+\nu_p )} $$
(6)

It is easily derived from (6) that α = 2.12 when ν p  = 0.

The strain hardening rule is implemented in this material model as:

$$ \sigma_y =\sigma_p +\gamma \frac{\hat{\varepsilon }}{\varepsilon_D }+\alpha_2 \ln \left[ {\frac{1}{1-\left( {{\hat{\varepsilon }} \mathord{\left/ {\vphantom {{\hat{\varepsilon }} {\varepsilon_D }}} \right. \kern-\nulldelimiterspace} {\varepsilon_D }} \right)^\beta }} \right] $$
(7)

where \(\hat{\varepsilon }\) is equivalent strain, σ p , α 2, γ, β and ε D are the material parameters and can be related to the foam density as

$$ \left\{{{\begin{array}{@{}r@{\,\,\,}c@{\,\,\,}l} \left( {\sigma_p ,\alpha_2 ,\gamma ,\dfrac{1}{\beta },E_p } \right)&=&C_0 +C_1 \left( {\dfrac{\rho_f }{\rho_{f0} }} \right)^\kappa \\\\ \varepsilon_D &=&-\ln \left( {\dfrac{\rho_f }{\rho_{f0} }} \right)\\ \end{array}}} \right. $$
(8)

where ρ f is the foam density and ρ f0 the density of the base material. C 0, C 1 and κ are the constants as listed in Table 1. Note that the Young’s modulus of foam material E p is also a function of ρ f as shown in (8) (Hanssen et al. 2002).

Table 1 Material constants for aluminum foam (Hanssen et al. 2002; Reyes et al. 2003)
Full size table

In order to decide the size of elements, a convergence test was carried out to minimize the effect of mesh refinement on the accuracy of the numerical results. It is found that the optimal mesh sizes for the tube and foam are 5 × 5 mm2 and 3 × 3 × 3 mm3, respectively, as in Fig. 2b, which was used throughout the study.

Figure 3 plots the kinetic, internal, total and hourglass energies during the deformation process of a foam-filled taper column under dynamic loading. It is easily seen that the decrease in kinetic energy is almost equal to the increase of the internal energy, and the total energy remains nearly unchanged. The hourglass energy is less than 1% of the system internal energy. Note that the amount of hourglass energy is also a good indicator to estimate the mesh quality, which typically should be less than 5% of the internal energy of the system to overcome the hourglass problem (Mirfendereski et al. 2008). Therefore, the mesh sizes used here are considered adequate to capture the crashing details of the foam filled thin-walled column. Figure 4 plots the force versus time of the structure (ρ = 0.32 g/cm3, θ = 6.6°, t = 1.5 mm) as well as its deformation at five different time frames.

Fig. 3
figure 3

Kinetic, internal, total and hourglass energy of the foam-filled column

Full size image
Fig. 4
figure 4

Axial crushing behaviour of foam-filled taper tube

Full size image

3 Optimization with multiple surrogate models

3.1 Surrogate models

The surrogate models provide an effective alternative to mathematical formulation of the relation between the design variables and sophisticated responses, which facilitate design optimization with relatively low computational cost. In this study, four different surrogate models, namely, cubic polynomial response surface method (PRS) (Myers and Montgomery 1995), Kriging (KRG) (Sacks et al. 1989), support vector regression (SVR) (Smola and Scholkopf 2004), and radial basis function (RBF) (Gutmann 2001; Sun et al. 2010c, 2011; Regis and Shoemaker 2005; Mullur and Messac 2006; Zhao and Xue 2010) are considered herein to approximate functional responses. There have been substantial studies on the key characteristics of these individual surrogate models (Hussain et al. 2002), and a brief list about the parameters and functions used in this study is provided in Table 2.

Table 2 Parameters and functions of four surrogate models
Full size table

3.2 Optimization formulation

As aforementioned, a high SEA is expected for crashworthiness design because it indicates high capacity of energy absorption for the same weight of materials. Therefore, maximizing SEA is considered as the design objective herein. Different constraints have been prescribed in literature. In this study characteristic forces in terms of F avg , F peak and F global are constrained to avoid severe damage.

Wall thickness t, taper angle θ and the foam density ρ (Fig. 2a) are taken as the design variables herein, which range from 0.5 mm to 2 mm for t, from 0° to 12° for θ, and from 0.2 g/cm3 to 0.6 g/cm3 for ρ, respectively.

As a result, the optimization problem can be formulated mathematically as follows:

$$ \left\{ {{\begin{array}{@{}r@{\quad}l} \textit{Maximize} & {\emph{SEA}=f(t,\;\theta ,\;\rho )} \\ {s.t.} & {\left\{ {{\begin{array}{@{}l} {F_{\it global} (t,\;\theta ,\;\rho )\le \mathrm{240~kN}} \\ {F_{\it peak} (t,\;\theta ,\;\rho )\le \mathrm{80~kN}} \\ {F_{\it avg} (t,\;\theta ,\;\rho )\ge \mathrm{120~kN}} \\ {0.5~\mathrm{mm}\le t\le 2~\mathrm{mm}} \\ {0^{\circ}\le \theta \le 12^{\circ}} \\ {0.2~\mathrm{g/cm}^3\le \rho \le 0.6~\mathrm{g/cm}^3} \\ \end{array} }} \right.} \\ \end{array} }} \right. $$
(9)

3.3 Design of Experiments (DOE)

To formulate the objective and constraint functions, sample points are needed to explore the design space. A typical way to generate sample points is to adopt design of experiments (DOE). Of many different DOE methods available, Latin hypercube sampling (LHS) is considered rather effective on reducing computational cost (Olsson et al. 2003). In this study, totally 30 sample points are generated using LHS approach, which are considered adequate to evaluate 20 coefficients of a cubic PRS involving the three design variables. Figure 5 exhibits the sample points and validation points (for the following sections) in the 3D design domain.

Fig. 5
figure 5

Sampling points (30) and validation points (20)

Full size image

3.4 Error analysis of the surrogate models

To assess the modeling accuracy of these four different surrogate schemes, use of the sampling points themselves may not be appropriate. Especially, KRG and RBF can go through the sample point themselves, making the tested values at the sampling points meaningless. For this reason, new validation points are needed to evaluate the models against the performance metrics. In this study, additional 20 validation points (see Fig. 5) are generated to verify the accuracy of surrogate models. Three numerical estimators, namely R-square (R2), Root-Mean-Square-Error (RMSE) and Maximum-Absolute-Percentage-Error (MAPE) are used to validate the accuracy of these surrogate models, as given in (10)–(12), respectively.

$$ \mathrm{R}^2=1-\frac{\sum\limits_{i=1}^m {(y_i -\hat{y}_i )^2} }{\sum\limits_{i=1}^m {(y_i -\overline y_i )^2} } $$
(10)
$$ \mathrm{RMSE} = \sqrt{\frac{1}{m}\sum\limits_{\mathrm{i}=1}^m \left(\!{\kern3pt}y_{i}^{{\kern-6pt}\tiny \smallfrown}-y_i\right) } $$
(11)
$$ \mathrm{MAPE}=\max \left( {\frac{\left| {\hat{y}_i -y_i } \right|}{y_i }} \right) $$
(12)

where m = 20 is the number of newly created validation points, y i is the true FEA values on the validation points, \({\kern3pt}\tiny\smallfrown{y}_{i}^{{\kern-6pt}}\) the corresponding approximate surrogate values, and \(\overline {y}_{i} \) the mean of function over these m validation points. The values of these performance metrics show the prediction accuracy and capability of the surrogate models at the new points. In general, the R2 and RMSE metrics indicate the overall accuracy of an approximation model, while the MAPE metrics indicate a local metrics, which describes the error in a sub-region of the design space. Overall, the closer the value of R2 to unity and/or the smaller the values of RMSE and MAPE, the better the accuracy.

4 Results

4.1 Error analysis of surrogate models

To compare the performance of these surrogate models explicitly, multiple bar-charts are provided in Fig. 6 together with Table 3. It can be seen clearly that in general these four models approximate four different responses rather well. Specifically, the SVR model performs best in the approximation of SEA and F avg , while the RBF model presents the best for F peak , and the PRS model the best for F global .

Fig. 6
figure 6

Error comparison of the four different surrogate models. a Error for SEA. b Error for F peak . c Error for F avg . d Error for F global

Full size image
Table 3 Error assessment of the four surrogate models
Full size table

In Fig. 7, the 3D contours of SEA are plotted to gain more insights into these four models. In each plot the density is set to be in between 0.4 g/cm3 and 0.5 g/cm3 only. It can be seen that the contours with PRS, KRG and RBF models are rather similar and change almost monotonically, while that from SVR differs somewhat and appears more complicated. The overall consistency indicates the minimum errors given in Table 3 and Fig. 6.

Fig. 7
figure 7

Surface plots of SEA responses for the four different surrogate models. a PRS model. b KRG model. c RBF model. d SVR model

Full size image

The comparison actually shows that each of these four models is sufficiently accurate for the prediction of SEA, F avg , F peak and F global (e.g. all the R2 values are fairly close to 1.0). Nevertheless, there is no clear best yet of these four surrogate models for this particular goal. Each surrogate model has its cons and pros in practical applications. Besides, a best or satisfactory error estimate and surface contour may not necessarily imply a best surrogate for the design process because optimization typically relies on the gradient information to search an optimum. Thus we will use all of them for solving the optimization problem defined in (9), respectively, and then compare which might provide the best solution to this case.

4.2 Optimization and validation

To obtain the optimal design of the foam-filled tapered square column, both the Sequential Quadratic Program (SQP) and Particle Swarm Optimization (PSO) (Sun et al. 2010a) are used herein. Since SQP is a gradient-based approach and searching for the global optimum may rely on the initial point, the optimization was solved through 40 random initial design points and the best solution will be chosen as a quasi-global optimum. On contrary, PSO is a derivative-free global optimum algorithm and one run could lead to a global optimum.

The final optimization results are plotted in Fig. 8 for these four different surrogate models, respectively, in which the contours show the distribution of SEA. Note that the three color lines in each plot represent these three constraints, respectively. In each plot, the small triangular region enclosed by these three constrains defines the feasible domain for the optimization. The red dot is the minimum point obtained from the SQP and PSO procedures for each surrogate model, which implies that these two optimum search algorithms result in the same global optimum.

Fig. 8
figure 8

Optimum design with different surrogate models (ρ = 0.6 g/cm3). a Optimization based on the PRS model. b Optimization based on the KRG model. c Optimization based on the RBF model. d Optimization based on the SRV model

Full size image

In addition to the difference of the SEA contours approximated by these four surrogate models, it can be seen that the constraint functions F avg and F global play an active role in the optimization when using the PRS model. Specifically, the optimum point is found at their intersection. While constraints F avg and F peak play predominant role in the optimization when using other three surrogate models and the optimum points appear at the intersection of F avg and F peak .

Table 4 summarizes the optimized design variables together with the values of objective function. For design variables t and θ, it shows that the RBF model and SVR model lead to the fairly close results, while the PRS and KRG models result in different values. Interestingly, the optimal value of density ρ (0.6 g/cm3) is confirmed no matter what kind of surrogate model is used. This is to say that a higher density of foam will absorb more crashing energy under the same condition, which is due to the higher foam resistance to the inward buckle of the thin wall during plastic deformation and densification. Note that the optimal density of 0.6 g/cm3 is just the best within the given range, which may not be the best for the foam within a lower (e.g. Hou et al. 2009 from 0.027 to 0.27 g/cm3) or a higher range (e.g. Bi et al. 2010 from 0.34 g/cm3 to 0.82 g/cm3). The previous studies have exhibited that the SEA dependency on density may not necessarily be monotonic (Hou et al. 2009). An overly high foam density may sacrifice SEA and significantly increase the peak force (Hou et al. 2011).

Table 4 Results of constrained optimization for the four surrogate models
Full size table

Obviously, from the perspective of predicting optimum results, SVR is the best model that leads to the greatest SEA value, while PRS appears the worst. Note that the difference in the optimized SEA is over 10% between the best and worst surrogate models.

In addition, the optimum results without these three constraints (i.e. F global  ≤ 240 kN, F peak  ≤ 80 kN, and F avg  ≥ 120 kN) are also shown in Fig. 8 for comparison. The blue dots in Fig. 8 represent the optimum subject to the unconstrained optimization, where the optimal density is equal to the maximum value of 0.6 g/cm3. Interestingly, the optimum wall thickness t varies significantly with the different surrogate models, and taper angle θ of 0° is found to be the optimum in the other models than SVR. The unconstrained results indicate that SEA can be improved by adjusting the wall thickness appropriately, and decreasing the taper angle to 0°. In other words, the wall of column should be neither too thin nor too thick, and straight foam-filled structures have higher energy absorption capability per unit mass than tapered structures under the same crushing conditions.

Table 5 and Fig. 9 compare the predicted optimum designs and the real FEA results based on the optimal design variables obtained in Table 3. The errors of the PRS model for SEA, F avg , F peak and F global are 6.71%, 7.8%, 0.75% and 22.14%, respectively. The errors of the KRG model are 7.31%, 11.32%, −4.04% and 9.67%, respectively, the negative value −4.04% herein implies the violation of constraint F peak . The errors of the RBF model are 2.56%, −2.36%, 0.35% and 2.51%, respectively, again the negative value of −2.36% implies the violation of constraint F avg . The errors of the SVR model are 0.89%, 0.92%, 0.71% and 1.24%, respectively.

Table 5 Comparison of predicted optimum design and validation FEAs
Full size table
Fig. 9
figure 9

Errors between optimized results and re-calculated FEA results

Full size image

As far as the design error is concerned, the RBF model and SVR model perform better than the other two models, which is consistent with the results in the previous primary error analysis (Section 4.1). Note that from the FE re-analysis of optimized variables, the PRS model generates the highest SEA value of 15.94 kJ/kg with all satisfied constraints even the error is slightly higher than those of the SVR and RBF models. Following this, the SVR model yields the second best SEA of 15.69 kJ/kg with all satisfied constraints. It is found that the KRG and RBF models predict infeasible solutions due to the violation of constraints. The results once again prove that the surrogate model with the best primary fitness (e.g. SVR was the best for SEA in this case from Table 3) may not necessarily be the best model for the design optimization (Table 5). Therefore, simultaneous tests of multiple surrogate models are important to find the real optimum design, especially for computationally expensive simulation such as the design of foam-filled tapered thin-walled structure.

It should be noticed that many factors, such as the sampling scheme, the number of sample points and the response itself as well as many parameters used in each surrogate model, contribute on the accuracy of the constructed surrogate model. However, a generalized comparison of these four surrogate models for complex engineering problems appears to be difficult and depends on the nature of problems. In other words, the effort made in this study was not aimed to verify which surrogate model is best for any crashworthiness optimization problem of foam-filled thin-walled structure in terms of the error analysis. On contrary, it attempted to reveal how these different surrogate models could lead to different optimal designs, thereby demonstrating how to improve the accuracy of design optimization by using different surrogate models simultaneously instead of optimizing a single model. The comparative study indicated that use of multiple surrogate models should be advocated for more precise design optimization, which may avoid the possibility that an overall accurate surrogate model may lead to the non best optimum.

5 Conclusions

In this paper, the comparative study on these four surrogate models, namely polynomial response surface (PRS), Kriging (KRG), radial basis function (RBF) models and support vector regression (SVR) was conducted for the design optimization of foam-filled taper structure. To understand the performance of different surrogate models a comparative study was conducted to assess the primary modeling accuracy of objective and constraint functions as well as their performance in design optimization. Firstly, it is confirmed that all these four models can yield good primary fitness of the real functions based on the error analysis with the validation FEAs, though there is no single best available to approximate all functions consistently in this problem. Secondly, the optimization was conducted by means of a gradient approach of sequential quadratic program (SQP) method and a non-gradient approach of Particle Swarm Optimization (PSO) method for each surrogate model. In the SQP method, the multiple initial points could lead to a quasi-global optimum that is consistent with PSO approach. It is found that the optimal results are affected by the characteristics of specific surrogate functions and the difference of optimal objective can be over 10% in this design problem.