1 Introduction

For aircraft and aerospace structures, composite material has been increasingly used in the load-carrying components (Wang et al. 2002; Zhu et al. 2016). Due to the limitation of traditional manufacturing process, straight fiber paths are commonly utilized in the practical design of aircraft and aerospace structures, like fuselage, rocket interstage, fuel tank, etc. Buckling is the main failure consideration for thin-walled structures under axial or other combined loads (Bourada et al. 2016; Hao et al. 2016b; Wang et al. 2014; Hao et al. 2017b). The buckling behavior is highly dependent on stacking sequences for composite structures, and thus many studies were devoted to the stacking sequence optimization for maximum buckling load. In general, due to the inherent feature of multiple local optima, heuristic methods were employed to find the global optimum (Le and Haftka 1993; Soremekun et al. 2001; Liu et al. 2000; Karakaya and Soykasap 2009). Blending constraint (Liu et al. 2011; Kristinsdottir et al. 2001), patch constraint (Zehnder and Emanni 2006) and other manufacturing constraints (Wang and Costin 1992; Sørensen and Lund 2013) were considered for ease of manufacturing. Because the buckling analysis of thin-walled structures is time-consuming, surrogate model has been adopted in order to release the high computational burden (Rikards et al. 2004; Abouhamze and Shakeri 2007).

As a promising structural concept, variable-stiffness composite panels with curvilinear fiber path can tailor the in-plane stiffness for improving the loading path and stress distribution. According to the previous studies (Van den Brink et al. 2012; Gürdal et al. 2008), an improvement of buckling load ranging from 35% to 67% can be achieved by using a variable-stiffness design compared to traditional constant-stiffness design with straight fiber path, and this can be attributed to the redistribution of in-plane loads from critical regions to relatively stiff regions. Due to this advantage, the design and optimization of variable-stiffness panels have attracted much attention in recent years (Madeo et al. 2017; Wu et al. 2015; Peeters et al. 2015; Rouhi et al. 2017). To start with, several representation functions of curvilinear fiber path were developed, including linear variation function (Gürdal et al. 2008), quadratic and cubical functions (Muc and Ulatowska 2010), trigonometric function (Blom et al. 2009), etc. For these methods, a reference path is defined firstly, and then a shifting criterion is specified, finally, the fiber angle in arbitrary region can be expressed explicitly. In general, linear variation function is the simplest method to describe the fiber path, in which only two design variables are involved, and thus it has been extensively investigated in the previous studies. However, the design space of variable-stiffness panels is also highly restricted for this rough representation. Besides, level set method was also used to represent a series of continuous equally spaced fiber paths, and an optimization for the minimal compliance was performed to find the optimum fiber path (Brampton et al. 2015). In addition, a specific scalar function corresponding to the cocurrent and equipotential lines in the flow field was used to define a set of fiber angles within one ply (Niu et al. 2016), and the fiber path can be guaranteed to be continuous and non-intersect. Moreover, since a pair of cocurrent and equipotential lines passing through arbitrary point are orthogonal to each other, the other function can be determined if one is defined, which means that the fiber paths of two adjacent plies can be obtained simultaneously. Based on these representation methods, the optimization of variable-stiffness panels can be carried out. Obviously, for the design of variable-stiffness panels, the total number of design variables would be very large, even if linear variation function is used. Assuming that n r is the number of design variables for each ply, the total number of design variables would be N t  = n r  × n p , where n p is the number of independent ply. For high-dimension optimization problems, a multi-step framework was established by Rouhi et al. (2017), and its basic idea is to narrow the design space according to the optimum results in previous steps. Jing et al. (2015) proposed a global shared-layer blending method for solving the tailoring problem of tapered composite structure, which can successfully avoid delamination at ply-drop location and generate manufacturable structures with maximum blending property. Considering multiple manufacturing constraints, Jing et al. (2016) further developed a multi-level optimization framework based on a sequential permutation table method, and a high design efficiency is achieved compared to traditional methods. For curvilinear fiber path, several specific manufacturing constraints were also considered in the optimization process, such as curvature constraint, parallelism constraint (Lozano et al. 2016; Montemurro and Catapano 2017).

As a type of promising numerical method for structural analysis, IGA proposed by Hughes et al. (2005) can provide exact modeling of structures with complex geometry and boundary condition, by which CAD and CAE can be integrated together due to the utilization of smooth spline basis functions. Compared to traditional FEA, IGA can produce accurate solution with less computational cost, because only less degree of freedom is required for the IGA to achieve similar accuracy. More importantly, IGA can provide analytical sensitivity expression, which is particularly suitable for the optimization of variable-stiffness panels.

Due to the complex characteristic of curvilinear fiber path, the optimization of variable-stiffness panels is still very challenging, because the design space is highly non-convex, which results in the fact that traditional gradient-based optimization methods may trapped into local optima. In this case, heuristic methods can guarantee the global optimization capacity but is computationally inefficient. Surrogate model is a powerful tool for the global optimization of complex problems with relatively small computational cost (Hao et al. 2012, 2013). A detailed comparison of different surrogate models was reported by Nik et al. (2014) for the optimum design of variable-stiffness composite panels. Due to the inherent multi-local-optima feature, the fidelity of surrogate model is difficult to ensure, even if a large number of training samples are used. In order to improve the prediction accuracy of surrogate model, there have been plenty of related studies on the construction and dynamic updating of surrogate model. It has been demonstrated that adding one single point at a time may not be efficient when the main concern is wall-clock time (rather than number of simulations) and simulations can run in parallel (Viana et al. 2013). Thus, various multiple points infilling criterions have been developed, and the most famous one is known as Efficient Global Optimization (EGO) method (Jones et al. 1998), where the expected improvement (EI) is used to balance the prediction uncertainty and objective value. Then, many improved algorithms were developed to balance the exploration and exploitation, including the weighted EI (Sóbester et al. 2005), generalized EI (Sasena et al. 2002), augmented EI (Huang et al. 2006), modified EI (Rehman et al. 2014). The EGO method was adopted in the optimization of stiffened composite panels (Haftka et al. 2016), and a feasible optimal structure was obtained with a low computational cost (Todoroki and Sekishiro 2008). Recently, Li et al. (2016) proposed an expected improvement and mutual information (EI&MI) infilling criterion, which employs the entropy to precisely quantify the uncertainty of surrogate model, and then balances the global exploration and local exploitation when adding new samples.

For traditional surrogate model, only exact function values of design points are used to establish the surrogate model, thus plenty of sampling points must be calculated in the design of experiment to guarantee the approximation quality of surrogate model. However, additional information such as gradient/sensitivity is not fully utilized (Han and Görtz 2012), whereas it can be obtained analytically for the IGA. In order to improve the prediction accuracy of surrogate model, and also reduce the number of required sampling points, gradient-enhanced Kriging (GEK) model was developed to incorporate gradient or sensitivity information into the construction of surrogate model (Chung and Alonso 2002; Yamazaki et al. 2010; Yamazaki and Mavriplis 2013; Ulaganathan et al. 2015), including direct GEK and indirect GEK, respectively (Chung and Alonso 2002). For the direct GEK developed by Morris et al. (1993), gradient/sensitivity information is directly used to establish Kriging model by expanding the correlation function and correlation vector. Laurent et al. (2013) compared the direct GEK and Kriging model by mechanical functions, and it is found that the direct GEK can lead to a significant decrease in the number of required sample points. This is due to the fact that, additional points in the vicinity of real sample points with small distance, are approximated by using the gradient information. Unlike the direct GEK, the indirect GEK employs the same correlation function as the one of Kriging, and the samples include the real sample points and additional points. According to the works by Laurenceau and Sagaut (2008), the direct and indirect GEK show a same fitting accuracy with identical parameters, when the step size is small enough, though it is difficult to be determined. Moreover, (Yamazaki et al. 2010; Yamazaki and Mavriplis 2013) developed a gradient/Hessian-enhanced Kriging (HGEK) model using the second-order gradient information, which is particularly suitable for high-dimensional complex problems. It can be expected that once the GEK model is combined with IGA, the optimization efficiency of variable-stiffness panels would be improved significantly, because the advantages of exact modelling, analysis and analytical sensitivity can be fully explored.

In this study, an efficient optimization framework is developed for the design of variable-stiffness panels by combination of IGA method, GEK method and multiple points infilling criterion. This paper is organized as follows. In Section 2, the basic formulas of isogeometric buckling analysis for variable-stiffness panels is introduced. In Section 3, gradient-enhanced kriging model is presented, and a new multiple points infilling criterion is developed based on EI&MI, i.e. expected improvement with Gauss distance (EIGD). In Section 4, an optimization framework is proposed for the design of variable-stiffness panels based on GEK. In Section 5, the proposed method is compared with several existing optimization methods. Finally, conclusions are drawn, and results show that the proposed method can find a better optimum design in a more efficient manner, which can significantly improve the computational efficiency of variable-stiffness panels for aerospace industry.

2 Sensitivity derivation based on isogeometric analysis

For the linear buckling analysis of variable-stiffness panels, the governing equation can be expressed as

$$ \left(\mathbf{K}-\lambda {\mathbf{K}}_G\right){\mathbf{a}}^i=0\kern2em i=1,2,\dots, r $$
(1)

where K is the global stiffness matrix, K G is the geometric matrix. λ is the buckling factor, and the buckling load can be obtained by multiplying the buckling factor with the predefined load. ai is the ith buckling mode, and r is the total number of degrees of freedom.

During the optimization process, the buckling factor λ (usually defined as optimization objective) will change due to the variation of design variables a, and the change of design variables a is summed up to the sensitivity. The main process of the sensitivity derivation is given herein. The derivative of the objective function λ with respect to the design variable a can be expressed as

$$ \frac{\partial \lambda }{\partial a}=\frac{1}{{\mathbf{d}}^{\mathrm{T}}{\mathbf{K}}_G\mathbf{d}}\left[{\mathbf{d}}^{\mathrm{T}}\frac{\partial \mathbf{K}}{\partial a}\mathbf{d}-\lambda {\mathbf{d}}^{\mathrm{T}}\frac{\partial {\mathbf{K}}_G}{\partial a}\mathbf{d}\right] $$
(2)

where d is the instability waveform.

As is evident from (2), \( \frac{\partial \mathbf{K}}{\partial a} \) and \( \frac{\partial {\mathbf{K}}_G}{\partial a} \) should be obtained. The global stiffness matrix K can be expressed as

$$ \mathbf{K}=\sum \limits_{n=1}^{numele}{\mathbf{k}}_n $$
(3)

where k n is the element stiffness matrix, and numele represents the element number. The element stiffness matrix can be calculated through the loop in Gaussian points

$$ {\mathbf{k}}_n=\sum \limits_{m=1}^{numgas}{\mathbf{B}}^{\mathrm{T}}\overline{\mathbf{Q}}\mathbf{B}{w}_1{w}_2\left|\mathbf{J}\right| $$
(4)

where B is the strain matrix, w1 and w2 are two weighted coefficients. |J| denotes the Jacobian matric, \( \overline{\mathbf{Q}} \) is the global plane-stress stiffness, numgas represents the number of Gaussian points. Similarly, the geometric stiffness matrix can also be obtained through the loop in Gaussian points

$$ {\mathbf{k}}_{gn}=\sum \limits_{m=1}^{numgas}{\mathbf{G}}^{\mathrm{T}}\left[\boldsymbol{\upsigma} \right]\mathbf{G}{hw}_1{w}_2\left|\mathbf{J}\right| $$
(5)

where [σ] is the initial stress matrix, G is the derivative matrix of shape function, and h is the lamination thickness.

$$ \frac{\partial {\mathbf{k}}_{gn}}{\partial a}=\sum \limits_{m=1}^{numgas}{\mathbf{G}}^{\mathrm{T}}\frac{\partial \left[\boldsymbol{\upsigma} \right]}{\partial a}\mathbf{G}{hw}_1{w}_2\left|\mathbf{J}\right| $$
(6)

where

$$ \boldsymbol{\upsigma} ={\mathbf{DBu}}^e $$
(7)

in which D is the material elastic matrix, ue is the nodal displacement. In this case, the derivation only needs to concern about [σ]. According to the chain rule, \( \frac{\partial \boldsymbol{\upsigma}}{\partial a} \) can be rewritten as

$$ \frac{\partial \boldsymbol{\upsigma}}{\partial a}=\frac{\partial \mathbf{D}}{\partial a}{\mathbf{Bu}}^e+\mathbf{DB}\frac{\partial {\mathbf{u}}^e}{\partial a} $$
(8)

3 Gradient-enhanced kriging model assisted by multiple points infilling criterion

3.1 Gradient-enhanced kriging model

In essence, the Kriging model is a statistical prediction method containing two components

$$ Y\left(\boldsymbol{x}\right)=\beta +Z\left(\boldsymbol{x}\right) $$
(9)

where β is the regression coefficient, Z(x) is the stochastic process with a mean of zero and a variance of σ2.

Kriging model can predict the response values in arbitrary design space by the following equation

$$ \widehat{y}(x)=\beta +{\boldsymbol{r}}_{\left(\boldsymbol{x}\right)}^T{\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\beta \boldsymbol{F}\right) $$
(10)

where Y is the column vector of response data of known design samples, R is the matrix of correlation function specified by user, r is the correlation vector, F is the regression vector, which is a unit matrix for constant regression.

For the indirect GEK (Liu and Batill 2002), gradient information is used to calculate additional points by the first-order Taylor approximation as

$$ {\displaystyle \begin{array}{l}{\boldsymbol{x}}_{add}^i={\boldsymbol{x}}^i+\Delta \boldsymbol{x}\\ {}\mathbf{y}\left({\boldsymbol{x}}_{add}^i\right)=\mathbf{y}\left({\boldsymbol{x}}^i\right)+\Delta {\boldsymbol{x}}^T\left[\frac{\partial y\left({\boldsymbol{x}}^i\right)}{\partial \boldsymbol{x}}\right]\end{array}} $$
(11)

In the direct GEK, the gradient information is used to establish the matrix of R. The matrix of samples and values are

$$ {\displaystyle \begin{array}{l}S={\left[{\boldsymbol{x}}^1,{\boldsymbol{x}}^2,\cdots, {\boldsymbol{x}}^n,{\boldsymbol{x}}^1\cdots {\boldsymbol{x}}^1,{\boldsymbol{x}}^2\cdots {\boldsymbol{x}}^2,\cdots, {\boldsymbol{x}}^n\cdots {\boldsymbol{x}}^n\right]}^T\in {\mathrm{\Re}}^{\left(n+n\times \mathit{\dim}\right)\times \mathit{\dim}}\\ {}Y={\left[y\left({\boldsymbol{x}}^1\right)\cdots y\left({\boldsymbol{x}}^n\right),\frac{\partial y\left({\boldsymbol{x}}^1\right)}{x_1^1}\cdots \frac{\partial y\left({\boldsymbol{x}}^1\right)}{x_d^1},\cdots, \frac{\partial y\left({\boldsymbol{x}}^n\right)}{x_1^n}\cdots \frac{\partial y\left({\boldsymbol{x}}^n\right)}{x_{dim}^n}\right]}^T\in {\mathrm{\Re}}^{n+n\times \mathit{\dim}}\end{array}} $$
(12)

where n denotes the number of samples, dim is the number of dimensions. The detailed derivation process of R and r can be found in the Appendix.

$$ {\displaystyle \begin{array}{l}\widehat{y}(x)=\beta +{\boldsymbol{r}}_{\left(\boldsymbol{x}\right)}^T{\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\beta \boldsymbol{F}\right)\\ {}\beta ={\left({\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}\boldsymbol{F}\right)}^{-1}{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}\boldsymbol{Y}\end{array}} $$
(13)

It should be noted that there is no additional sample point, thus the matrix calculation is much better. In this paper, the direct GEK is utilized.

3.2 EI&MI multiple points infilling criterion

In order to fully explore the design space, some infilling criterions are used to search for new samples and then update the surrogate model, until convergence is achieved. The infilling criterions can be divided into single point criterion and multiple points criterion. As an important improvement of EI criterion, a multiple points infilling criterion named EI&MI was developed by Li et al. (2016). The EI&MI adopts the entropy to precisely measure the uncertainty of Kriging model, and then balances the global exploration and local exploitation of multiple points infilling sampling criteria. Only the key process of EI&MI is introduced herein, and the detail information can be found in Ref. (Li et al. 2016).

In any given step-loop, S ⊂ Ω denotes the evaluated design points. According to the principle of maximum entropy, the global exploration of infilled samples should be achieved as follows

$$ H\left({\mathbf{Y}}_{\mathbf{X}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)=-\int p\left({\mathbf{Y}}_{\mathbf{X}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)\ln \left[\int p\left({\mathbf{Y}}_{\mathbf{X}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)\right]d{\mathbf{Y}}_{\mathbf{X}} $$
(14)

For the parallel points added, in order to avoid the high dimensional infilling criterion, we suggest to select the infilled samples one by one. Assuming that the number of selected infilled samples is k − 1, the kth sample can be selected by

$$ {\displaystyle \begin{array}{l} Find\ {\mathbf{x}}_{\mathrm{k}}\\ {}\mathit{\operatorname{Maximize}}\ H\left({\mathbf{Y}}_{{\mathbf{X}}_{\mathrm{k}}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)\\ {} Subject\ to:{\mathbf{x}}_k\in \Omega \end{array}} $$
(15)

where x k denotes the kth infilled sample. Here, we would like to balance the two objectives in (15) into one function. The new function should maintain the good searching ability of the serial infilling criterion such as EI. Thus, \( H\left({\mathbf{Y}}_{{\mathbf{X}}_{\mathrm{k}}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right) \) is decomposed as

$$ H\left({\mathbf{Y}}_{{\mathbf{X}}_{k-1}}|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)+H\left(y\left({\mathbf{x}}_k\right)|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right)-\mathrm{MI}\left({\mathbf{Y}}_{{\mathbf{X}}_{k-1}},y\left({\mathbf{x}}_k\right)|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right) $$
(16)

where MI is the mutual information. Consequently, the multiple points infilling criterion of EI&MI is obtained

$$ {\displaystyle \begin{array}{l} Find\ {\mathbf{x}}_k\\ {}\mathit{\operatorname{Maximize}}\ \mathrm{EIMI}\left({\mathbf{x}}_k\right)=E\left[I\left({\mathbf{x}}_k\right)\right]\exp \left\{-\rho \mathrm{MI}\left[{\mathbf{Y}}_{{\mathbf{X}}_{k-1}},y\left({\mathbf{x}}_k\right)|{\mathbf{Y}}_{\mathbf{S}}=\mathbf{Y}\right]\right\}\\ {}\kern9.25em \Rightarrow E\left[I\left({\mathbf{x}}_k\right)\right]{M}^{\rho}\left({\mathbf{x}}_k,{\mathbf{X}}_{k-1}\right)\\ {} Subject\ to:{\mathbf{x}}_k\in \Omega \end{array}} $$
(17)

where

$$ \mathrm{M}\left({\mathbf{x}}_{\mathrm{k}},{\mathbf{X}}_{k-1}\right)=1-{\widehat{\mathrm{R}}}_{x_k{X}_{k-1}}{{\widehat{\mathrm{R}}}^{-1}}_{X_{k-1}{X}_{k-1}}{\widehat{\mathrm{R}}}_{X_{k-1}{x}_k} $$
(18)

The range of M is 0 ≤ M(x k , Xk − 1) ≤ 1. M(x k , Xk − 1) = 0 when x k  ∈ Xk − 1, and M(x k , Xk − 1) = 1 when \( {\widehat{\mathrm{R}}}_{{\mathrm{x}}_k,{\mathrm{X}}_{k-1}}=0 \). It implies that when x k is close to any former point x i (i < k), M is close to zero. Therefore, EI&MI will keep the infilled samples away from each other.

3.3 Multiple points infilling criterion: EIGD

As introduced in the last section, EI&MI was proposed to prevent the distance among points to be too close by maximizing the entropy principle. However, the expression of M(xk, Xk − 1) is so complicated that limits the applicability for engineering problems. In order to simplify the implementation process, a new multiple points infilling criterion named expected improvement with Gauss distance (EIGD) is developed in this section. The EIGD adopts the Gauss function to balance the distance among multiple points, and the implementation process can be greatly simplified. In addition, other kernel functions can also be used to keep the distance, as shown in Table 1.

Table 1 Typical kernel functions
Full size table

In each updating loop, once surrogate model is established, EI will be known at any design space. When the first infilling point is obtained based on EI, the next point should be keep a distance away from its location. In view of this point, Gauss function can be adapted to describe the influence of the infilling points added.

$$ {\displaystyle \begin{array}{l} Find\ {\mathbf{x}}_k\\ {}\mathit{\operatorname{Maximize}}\ EIGD\left({\mathbf{x}}_k\right)=E\left[I\left({\mathbf{x}}_k\right)\right]{\left[\prod \limits_{i=1}^{k-1}\left(1- Gauss\left({\mathbf{x}}_k,{\mathbf{x}}_i,\alpha \right)\right)\right]}^{\rho}\\ {} Subject\ to:{\mathbf{x}}_k\in \Omega \kern0.75em k=1,2,\cdots, n\end{array}} $$
(19)

where x k is the kth infilling point, and k-1 points have been filled.

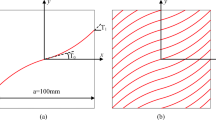
Herein, a benchmark mathematical problem (i.e. six-hump camel-back function shown as Fig. 1) is adapted to demonstrate the effectiveness of EIGD.

$$ f(x)=\left(4-2.1{x}_1^2+\frac{1}{3}{x}_1^4\right){x}_1^2+{x}_1{x}_2+\left(4{x}_2^2-4\right){x}_2^2,{x}_1\in \left[-2,2\right],{x}_2\in \left[-1,1\right] $$
(20)
Fig. 1
figure 1

3D surface and contour map for six-hump camel-back function. a 3D surface b Contour map

Full size image

For this benchmark example, 9 original sample points are used to establish the GEK model, and two infilling points are added to the training set in each loop. The Gauss distance can be obtained when dimension is one as

$$ GD={\left(1- Gauss\left({\mathbf{x}}_k,{\mathbf{x}}_i,\alpha \right)\right)}^{\rho }={\left(1-\exp \left(-\alpha {\left|d\right|}^2\right)\right)}^{\rho } $$
(21)

where d is the distance between xk and xi, α and ρ are two parameters. In order to get the parameters rationally, the influences of α and ρ are investigated, as shown in Fig. 2. The value of GD should nearly be zero when the two points are near, and quickly to be one when the distance is large. As is evident from Fig. 2a and b, the red line meets the requirements. When α is more than 100 and ρ is less than 0.3, the GD function is steep. Similarly, when α is less than 100 and ρ is more than 0.3, the GD function is so flat that the area affected is too large. Thus, we set α = 100, ρ = 0.3 in this study. The updating loops of six-hump camel-back function are shown in Fig. 3, in which the yellow point is the first one to add, and the red point is the second one. When the first point is to infill, EIGD equals to EI. When the second point is to infill, EIGD around the infilled points will times the coefficient of less than one, so the second point will away from the infilled points by searching the maximal EIGD. In this way, more than one peak can be found by EIGD criterion.

Fig. 2
figure 2

The influence of parameters to GD function. a GD function with ρ = 0.3 b GD function with α = 100

Full size image
Fig. 3
figure 3

Updating loops of six-hump camel-back function with infilling points added by EIGD. a First loop b Second loop

Full size image

The proposed EIGD can control the distance among the infilling points in each loop, moreover, it is more convenient for implementation compared to EI&MI. Although EI&MI or EIGD can be used to add multiple points to find not only one local optimum, the computational cost of EIGD is much cheaper than that of EI&MI, especially when the number of infilling points is large.

4 Surrogate-based optimization framework of variable-stiffness panels considering manufacturing constraints

As already mentioned in the abstract, the Automated Tape Laying (ATL) and Automated Fiber Placement (AFP) technology allow the designer to find more flexible fiber path, which significantly increases the load-carrying potential and design space of composite components (Hao et al. 2016a). Also, it has been demonstrated that IGA can provide accuracy prediction of buckling factor with less computational cost compared to FEA method (Hao et al. 2017a). However, new types of constraints may be raised in the manufacturing process of variable-stiffness panels, and it should be considered in the design optimization to guarantee the manufacturability of the optimum design. In this section, two typical manufacturing constraints (Huang et al. 2016) are introduced for the AFP process, including curvature constraint and parallelism constraint.

Once the curvature of an innermost tow of a course becomes too severe, the compressed side would exhibit local buckling or wrinkle modes (Kahya 2016). For variable-stiffness panels, the curvature of fiber path at arbitrary point can be expressed as

$$ cur\left(x,y\right)=\frac{\left|{y}^{{\prime\prime}}\right|}{{\left|1+{y^{\prime}}^2\right|}^{\frac{3}{2}}} $$
(22)

where y′ is the derivative of y on x, and y″ is the derivative of y′ on x.

To eliminate the phenomenon of gaps and overlaps, the fiber orientations along the normal should not change excessively, as shown in Fig. 4. The parallelism constraint is defined as

$$ par\left(x,y\right)=\left|\frac{\partial \theta }{\partial \boldsymbol{n}}\right| $$
(23)
Fig. 4
figure 4

Illustration of fiber parallelism

Full size image

A surrogate-based optimization framework is proposed in Fig. 5, by which the advantages of IGA including exact modelling, analysis and analytical sensitivity can be fully utilized. Fiber orientation angles are optimized with the objective of maximizing the buckling load. In the framework, various functions can be utilized to represent a family of curvilinear fiber path. The optimization problem can be formulated as

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Maximize}}:\lambda \\ {} Subject\ to:\left\{\begin{array}{c} cur\left(x,y\right)\le {c}_m\\ {} par\left(x,y\right)\le {p}_m\\ {}{X}_i^l\le {X}_i\le {X}_i^u,i=1,2,\cdots, n\\ {}\left(x,y\right)\in \Omega \end{array}\right.\end{array}} $$
(24)

where λ is the buckling factor, Ω is the design domain of the panel, c m and p m are the threshold values of fiber curvature and parallelism, X i is the ith design variable to control the curvilinear fiber path, \( {X}_i^l\le {X}_i\le {X}_i^u,\kern0.5em i=1,2,3,4 \) and \( {X}_i^l\le {X}_i\le {X}_i^u,\kern0.5em i=1,2,3,4 \) are the lower and upper bounds of the ith design variable. A set of sample points is generated in the process of design of experiment (DOE) to establish the surrogate model, e.g. Optimal Latin Hypercube Sample (OLHS). Due to the inherent feature of multimodal search problems, evolutionary algorithm (like Genetic Algorithm, GA) is used to find the optimum stacking sequence. In each updating loop, based on multiple infilling points criterions, several points that satisfy the constraints evaluated by IGA are added in each updating loop. If the convergence criterion is not satisfied, another new surrogate model will be built. Herein, the convergence criterion is set as: EI < 10−4 and no improvement in three loops. For the proposed framework, both the global optimization capacity and optimization efficiency can be guaranteed.

Fig. 5
figure 5

The proposed optimization framework of variable-stiffness panels based on GEK

Full size image

5 Optimization of variable-stiffness panels with manufacturing constraints

5.1 Model description

For the linear variation path, the function of fiber orientation angle is along the x axis, which is assumed to be centered along the length l of the panel and can be defined as

$$ {\theta}^i(x)=\frac{2\left({T}_1^i-{T}_0^i\right)}{l}\left|x\right|+{T}_0^i $$
(25)

where \( {T}_0^i \) is the fiber orientation angle at the panel center of the ith layer, \( {T}_1^i \) is the fiber orientation angle at the panel boundary of the ith layer, θi(x) is the fiber orientation angle of the ith layer. The reference fiber path is shown in Fig. 6.

Fig. 6
figure 6

Variable-stiffness panel based on linear variation function. (a) Definition of reference fiber path (b) Fiber path

Full size image

In the following sections, a square panel with a length of 254 mm is investigated. A 20-ply balanced symmetric laminate is used and the fiber angles of two adjacent plies are opposite. The lamina properties are set as E1 = 181.0 GPa, E2 = 10.27 GPa, G12 = G13 = 7.17 GPa, G23 = 3.78 GPa, υ12 = 0.28, and the ply thickness is 0.15 mm.

5.2 Loading and boundary conditions

For aircraft panels, combined compression-shear load is a common design condition. Because the combined loading condition may cause complicated mode shapes with coupling pattern, complex loading path is required to increase the resistance to buckling. In this study, non-uniform loading is considered, and the amplitude of axial compression is P = sin(4πy/l + π/3), as shown in Fig. 7. This further highlights the load-carrying gain of variable-stiffness panels, which can tailor the in-plane stiffness by varying the fiber path. Besides, the boundary condition has a substantial influence on the buckling behavior and mode shape. A typical boundary condition (i.e. four loading edges simply supported, SSSS) is investigated in this study. The linear buckling analysis is performed based on IGA, and quadratic NURBS elements are used for IGA. Both the analysis procedure and sensitivity derivation are programed in MATLAB.

Fig. 7
figure 7

Loading and boundary conditions of variable-stiffness panel

Full size image

5.3 Optimization results

The proposed framework is used to conduct the optimization of variable-stiffness panels based on linear variation function, and the optimization formulations in each step can be found in Section 4. Due to the constraint of symmetric laminates, only 5 plies need to be designed. The involved design variables include the fiber orientation angle at the panel center and boundary. Therefore, a total number of 10 variables are involved in the optimization. The ranges of each variable are defined as follows

$$ {X}_{i\cdot j}={T}_j^i\in \left[{0}^{{}^{\circ}},{90}^{{}^{\circ}}\right],i=1,2,\cdots, 5,\kern0.5em j=1,2 $$
(26)

We normalize the variables in the optimization, in order to guarantee the convergence rate of surrogate-based optimization. Then, the buckling optimization of variable-stiffness panels is performed.

5.3.1 Optimization without manufacturing constraints

A set of 50 sample points is generated by the OLHS to establish the surrogate model firstly. In the updating process of surrogate model, several infilling criterions are compared, including EI&MI, EIGD and EI. For multiple infilling points criterions, 4 points evaluated by IGA are added in each updating loop. In the surrogate model method, genetic algorithm (GA) is used to search the maximum of EI or other infilling criterions. The algorithm parameters in GA are set as: population size = 200, max generations = 1000, crossover fraction = 0.8, mutation rate = 0.01, function tolerance =10−6. The iteration history is also shown in Fig. 8. The optimum values of design variables in each ply are listed in Table 2, where the column of DOE means the best result in Design of Experiment, and the row of improvement % means the percentage of improvement over DOE.

Fig. 8
figure 8

Iterations histories of buckling factor by different optimizations

Full size image
Table 2 Optimum variable values of linear variation fiber path without manufacturing constraints
Full size table

As is evident from Table 2, the number of required iterations for GEK with EI is much fewer than the original Kriging with EI. Moreover, the performance of optimum design by GEK is better, which demonstrates that the GEK method including gradient information is more efficient. Furthermore, comparing the infilling criterions based on GEK method, the EI&MI and EIGD criterions show higher computational efficiency than EI. Due to the fact that parallel computing method can be used in the multiple points infilling criterion, even if the number of points is increased, the computational cost for infilling points remains almost unchanged, thus the GEK with EIGD criterion can be regarded as the most promising method.

To illustrate the computational efficiency and optimization capacity of proposed method, GA is also used to perform the global optimization directly (named as direct GA), and thus numerous function calls are involved in the optimization process. For this example, the total computational cost of direct GA is about 70 h, using a work station with a CPU of 2.20 Hz and 32G RAM, while the one is only 20 h for the optimization using GEK. The time of calculating buckling factor for each sample is about 20 s, and if the gradient information is required, the time will increase to 108 s. For direct GA, each population should be calculated by IGA, and about 20 s × 200 population × 60 iter ≈ 70 h. For GEK method, only 50 + 4 × 10 iter = 90 points need to be calculated by IGA, and the CPU time is about 90 × 108 s ÷ 4 parallel = 40 min. In each loop, the time to establish GEK is 24 min in average. And GA is used to search the maximum of EIGD, the time of calculating EIGD for one sample is about 22 min, and the total time will be 40 min + 24 min × 10 iter +22 min × 4 points × 10 iter ≈ 20 h, which is lower than the one based on EI&MI. Similarly, for Kriging method, the time cost on establishing model is 6 min in average, the time of calculating EI for one sample is about 20 min and the total time is 6 min × 38 iter +20 min × 38 iter ≈ 17 h.

In addition, Figs. 9, 10, 11, and 12 show the optimum fiber paths without manufacturing constraints for different methods. As is evident, the phenomenon of fiber enrichment can be found, and thus manufacturing constraints should be considered during the optimization process. After the optimization by GEK with EIGD, the buckling factor λ of curvilinear fiber path without manufacturing constraints increases from 113.6 to 129.6, with an improvement of 14.08%.

Fig. 9
figure 9

Optimum fiber paths without manufacturing constraints (GEK-EI&MI). a Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image
Fig. 10
figure 10

Optimum fiber paths without manufacturing constraints (GEK-EIGD). a Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image
Fig. 11
figure 11

Optimum fiber paths without manufacturing constraints (GEK-EI). a Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image
Fig. 12
figure 12

Optimum fiber paths without manufacturing constraints (Kriging-EI). (a)Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image

5.3.2 Optimization considering manufacturing constraints

In the above optimization, it is found that the linear variation fiber path is more flexible, and results indicate that the load-carrying capacity of variable-stiffness panel can be remarkably improved. However, the phenomenon of fiber enrichment can be found in the optimum design. For example, when the fiber orientation angle at the panel center or at the boundary of panel is close to π/2 or the change of local fiber angle is too sharp, the phenomenon of fiber enrichment can be found, as shown in Fig. 13, which greatly challenges the existing manufacturing technologies such as ATL and AFP.

Fig. 13
figure 13

Optimum linear variation function path without manufacturing constraints

Full size image

In order to satisfy the practical manufacturing requirements, the fiber curvature constraint and parallelism constraint are introduced as typical manufacturing constraints during the optimization process (Huang et al. 2016). In this study, the upper limit of fiber curvature c m is set to be 0.1, and the parallelism p m is set to be π/6 for Constraint (1) and π/30 for Constraint (2), respectively. For the linear variation function, the value of y coordination of the ith layer can be calculated from the fiber path function.

$$ {y}^i(x)=\frac{l}{2\left({T}_1^i-{T}_0^i\right)}\left\{-\ln \left[\cos \left({T}_0^i+\frac{2\left({T}_1^i-{T}_0^i\right)}{l}\left|x\right|\right)\right]+\ln \left[\cos \left({T}_0^i\right)\right]\right\} $$
(27)

And the curvature function can be written as:

$$ {\displaystyle \begin{array}{l} cur\left(x,{y}^i\right)=\frac{\left|{y}^{i\hbox{'}\hbox{'}}\right|}{{\left|1+{y}^i{\hbox{'}}^2\right|}^{\frac{3}{2}}}=\left|\frac{2\left({T}_1^i-{T}_0^i\right)}{l}\cos \left({\phi}_x^i\right)\right|\le {c}_m\\ {}\Rightarrow \left|\cos \left({\phi}_x^i\right)\right|\le \left|\frac{l}{2\left({T}_1^i-{T}_0^i\right)}\right|{c}_m\end{array}} $$
(28)

where, \( {\phi}_x^i={T}_0^i+\frac{2\left({T}_1^i-{T}_0^i\right)}{l}\left|x\right| \) is the fiber orientation angle of the ith layer. For the linear variation path function, the curvature constraint is usually satisfied, when the panel size is not too small.

Similarly, the parallelism function can be expressed as

$$ par\left(x,{y}^i\right)=\left|\frac{\partial \theta }{\partial \boldsymbol{n}}\right|=\left|\frac{\partial \theta }{\partial x}{n}_1+\frac{\partial \theta }{\partial {y}^i}{n}_2\right|=\left|\frac{4\left({T}_1^i-{T}_0^i\right)}{l\cdot \cos \left({\phi}_x^i\right)\tan \left(2{\phi}_x^i\right)}\right|\le {p}_m $$
(29)

Note that (29) achieves the maximal value when \( {\phi}_x^i \) is close to 0 or π/2, which means that the maximum par can only appear at the center of the panel or the boundary of the panel. Therefore, an easy way to avoid the condition of par(x, yi) > p m is to limit the range of fiber variation. On this basis, the optimization of curvilinear fiber path is carried out based on GEK with EIGD. Taking the SSSS boundary condition for example, the iteration history of buckling factor λ is shown in Fig. 14. The optimum values of design variables are listed in Table 3, and the buckling modes are listed in Table 4.

Fig. 14
figure 14

Iteration histories of buckling factor for linear variation fiber paths by using GEK with EIGD

Full size image
Table 3 Optimum variable values of linear variation fiber path considering/without manufacturing constraints
Full size table
Table 4 Buckling modes of different optimum designs based on straight and linear variation fiber paths
Full size table

When the Constraint (1) is taken into account, the buckling factor λ of curvilinear fiber path increases from 113.6 to 128.6, with an improvement of 13.20%. And for the Constraint (2), the constraint is tighter, and thus the buckling factor λ only increases to 128.1, with an improvement of 12.76%.

To further investigate the influence of manufacturing constraints, the optimum fiber paths considering curvature constraint and parallelism constraint are shown in Figs. 15 and 16. As can be observed, the constraint is not active for Constraint (1), thus the fiber enrichment occurs. Instead, when the constraint is tightened for Constraint (2), the fiber enrichment is well eliminated, and the curvilinear fiber path becomes smooth. In general, the arrangement of fiber satisfies the requirement of stiffness distribution to avoid stress concentration. This will allow for a better understanding of load redistribution mechanism, which can be responsible for a significantly increased buckling load. Moreover, the AFP technology is adequate for manufacturing this type of composite panels, and this can be attributed to the curvature constraint and parallelism constraint.

Fig. 15
figure 15

Optimum fiber paths with manufacturing constraint (1) (GEK-EIGD). a Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image
Fig. 16
figure 16

Optimum fiber paths with manufacturing constraint (2) (GEK-EIGD). a Ply-1/2/19/20 b Ply-3/4/17/18 c Ply-5/6/15/16 d Ply-7/8/13/14 e Ply-9/10/11/12

Full size image

Besides, in order to illustrate the excellent performance of curve fiber, the optimization of straight fiber is also compared. For straight fiber, the stacking sequence of initial design is [±0°, ±22.5°, ±45°, ±67.5°, ±90°, ±90°, ±67.5°, ±45°, ±22.5°, ±0°]s. After performing linear buckling analysis, the buckling factor λ is obtained as 82.7 for the SSSS boundary condition. Then, GA is adopted to perform the optimization. The iteration history of buckling factor is shown in Fig. 8. After 56 iterations, the optimum buckling factor λ of panel is 114.3, with an improvement of 38.2%. By comparing the optimum designs of straight fiber path and curvilinear fiber path, the buckling factor increases from 114.3 to 130.7 for the curvilinear fiber path, with an improvement of 14.35%.

6 Conclusions

In this paper, an efficient optimization framework is developed for the design of variable-stiffness panels by combination of IGA method, GEK method and multiple points infilling criterion, where IGA can provide analytical gradient information and accuracy prediction of buckling factor with less computational cost compared to FEA method, moreover, GEK can use the gradient information to improve the accuracy of surrogate model. These characteristics make the combination of IGA and GEK become an efficient method. Furthermore, on the basis of EI&MI criterion, a new multiple points infilling criterion named EIGD is developed, which can enhance the global optimization capacity of GEK and simplify the implementation of EI&MI.

A square panel with linear variation fiber path is served as illustrative example. The performance of proposed method is compared with original Kriging, GEK with EI, GEK with EI&MI. The fiber paths and buckling modes as well as buckling factors of the optimum designs are examined in detail. It can be found that the GEK exhibits better performance than original Kriging method in terms of both global optimization capacity and computational efficiency. Moreover, using multiple points infilling criterion can further increase the optimization efficiency of EI infilling criterion, and the computing cost of EIGD in each iteration is cheaper than EI&MI. Besides, the effects of manufacturing constraints are investigated. It can be concluded that the phenomenon of fiber enrichment can be well eliminated by an appropriate selection of curvature constraint and parallelism constraint. In summary, the combination of GEK, IGA and EIGD is a promising optimization framework, which can significantly improve the load-carrying efficiency of variable-stiffness panels for future aerospace and aircraft industries.