A novel multi-fidelity surrogate modeling method for non-hierarchical data fusion

Abstract

Multi-fidelity (MF) surrogate model has been widely used in simulation-based engineering design processes to reduce the computational cost, with a focus on cases involving hierarchical low-fidelity (LF) data. However, accurately identifying and sorting the fidelity of LF models is challenging when dealing with non-hierarchical cases. In this paper, we propose a novel non-hierarchical MF surrogate framework called weighted multi-bi-fidelity (WMBF) to solve this problem. The proposed WMBF has both the advantage of two non-hierarchical frameworks, the weighted sum (WS) and parallel combination (PC) techniques, leveraging an entropy-based weight to include multiple-moments statistical information. It offers not only a weight with more information but also a more individualized scaling function within the weighted-sum framework, additionally a more individualized discrepancy function compared with existing methods. Moreover, it provides the idea of exploiting Kullback–Leibler (KL) divergence (an entropy-based metric) to characterize uncertainty for calculating weight within the WS framework. To validate the performance of the WMBF, we conduct evaluations using several numerical test functions and one engineering case. The result demonstrates that the WMBF achieves both accurate and robust predictions with minimal computational cost.

1 Introduction

Surrogate models have been widely used to replace some time-consuming simulations in engineering for their low computational cost, such as Kriging [1], polynomial response surface (PRS) [2], polynomial chaos expansion [3], support vector machine [4], and radial basis function (RBF) [5]. They assist in constructing accurate mathematical models and generating predictions using available design samples. The surrogate model constructed by the data from the high-fidelity (HF) model generates more accurate predictions than the one constructed from the low-fidelity (LF) model, but it also has a higher computational cost. Hence, the multi-fidelity (MF) surrogate model was proposed to balance the prediction accuracy and the computational cost [6], which has been applied in engineering optimization; see [7,8,9,10] and the reference therein.

The main concept of MF surrogate model involves the correction of LF models using HF models in different ways, including space mapping, multiplicative correction, additive correction, and comprehensive correction [11]. The space mapping correction can be considered as correcting the input or output variables of HF model to LF model, allowing different dimensions of LF and HF design space. Several works are devoted to space mapping based on Gaussian [12, 13] and RBF [14, 15]. In addition, the multiplicative (or additive) correction has been widely studied in aerospace [16,17,18] and manufacturing material [19,20,21]. It corrects the LF model response by constructing a surrogate model of the ratio (or difference) between the HF and LF model, known as the scaling (or discrepancy) function.

Moreover, comprehensive correction is the combination of these two corrections. One may intuitively set the multiplicative factor as a constant and build a surrogate model of the additive correction. The co-Kriging was presented based on it in [22], and it was regarded as a general extension of Kriging under the assistance of auxiliary variables or secondary information [23]. It was applied to computational simulation in [24] called KOH model, which has been broadly applied to aerospace field [25] and intelligent manufacturing field [26]. The KOH model provides both predicted values and its mean-squared error (MSE), but it has high computational complexity and low robustness. Therefore, Han et al. developed the hierarchical Kriging (HK) [23] to improve KOH with a more reasonable estimated MSE and less computational complexity. Multiple researches have been presented to make variations and extensions of HK since it was proposed [27,28,29]. For example, the improved hierarchical Kriging (IHK) [27] was proposed by using the PRS to map the LF model to the HF data, which leads to a more accurate MF surrogate model. Another comprehensive correction method is the hybrid method developed in [19], where the additive and multiplicative correction based on the Kriging model were summed by using a weighting function based on adaptive hybrid method. A similar hybrid method also has been combined with RBF scaling function [30], and applied to Bayesian optimization [31].

When there are more than two LF models, the fusion of MF models becomes a significant research problem. Currently, most MF surrogate methods focus on hierarchical cases. These methods assume that model fidelity increases progressively from LF to HF, allowing approximation through step-by-step modeling by hierarchical MF surrogate model. However, this solution may not be suitable for non-hierarchical cases in practice. In certain scenarios, it is challenging to identify and rank the fidelity of LF models intuitively due to the various ways of simplifying the HF model. For instance, a 3-D finite element model with a coarse mesh and a 1-D finite element model with a refined mesh are both simplified versions (i.e., LF models) of a 3-D finite element model with a refined mesh (i.e., HF model). However, it is difficult to determine which LF model is closer to the HF model. Therefore, it is necessary and promising to investigate the non-hierarchical MF surrogate model.

To deal with the non-hierarchical MF cases, the weighted-sum (WS) method has been proposed and investigated to enhance the performance of MF surrogate model in recent literature [32,33,34,35]. Zhang et al. developed the linear regression multi-fidelity surrogate (LRMF) within the WS framework, utilizing the PRS to model the discrepancy function [33]. Additionally, Zhang et al. proposed the non-hierarchical low fidelity co-Kriging (NHLF), which assigned scaling factors to all non-hierarchical LF models and combined them as the trend function within the WS framework [34]. Moreover, the variance-weighted sum multi-fidelity surrogate (VWS-MFS) employed the WS framework for data fusion as well, which first fused all LF data based on variance-weight and then built MF model between the LF fusion data and HF data [35].

However, the individualization of the discrepancy function between each LF and HF data has not been considered in these WS-based methods. Different from the WS method, another approach called parallel combination (PC) regarded the HF model as the sum of each LF model and its corresponding discrepancy function separately [32]. To this end, we propose a novel method based on the combination of the WS and PC methods when constructing a non-hierarchical MF surrogate model in this paper. Moreover, as for the weight calculation method in the WS framework, we provide an entropy-based weight that contains more moment information compared with the variance-based weight in VWS-MFS. Therefore, we develop a weighted multi-bi-fidelity (WMBF) framework that utilizes the bi-fidelity surrogate model to describe the relationship between each LF and HF data, and then fuses them for the final prediction with the weight using Kullback–Leibler (KL) divergence (an entropy-based metric) within the WS framework. Except for achieving the individualization of the discrepancy function, the proposed method also owns a weight with more information and a more individualized scaling function in the WS framework compared with VWS-MFS. The effectiveness of the proposed method is illustrated by several numerical examples and one engineering case.

The remaining of this paper is organized as follows: the background of bi-fidelity surrogate models and the weighted-sum MF surrogate method are given in Sect. 2. Section 3 describes the details of the proposed WMBF method. In Sect. 4, several numerical examples and an engineering case are exploited to demonstrate the superiority and effectiveness of the proposed WMBF method by comparing it with other existing surrogate models. The effects of the main factors are also discovered in Sect. 4. The conclusion and future work are given in Sect. 5.

2 Background

The background of BF surrogate models and the weighted-sum MF surrogate method are introduced in this section.

2.1 Hierarchical Kriging and improved hierarchical Kriging for bi-fidelity surrogate model

In this study, we focus on the relationship between HF and each LF data. Since it can be explored through bi-fidelity (BF) surrogate model, here we provide a brief introduction to hierarchical methods for building a d-dimension BF surrogate model between HF data set,

$$\begin{aligned} D_{{\textrm{H}}}:= \left\{ \left( {\textbf{X}}_{{\textrm{H}}},{\textbf{y}}_{{\textrm{H}}}\right) | {\textbf{X}}_{{\textrm{H}}} \in {\mathbb {R}}^{n_{{\textrm{H}}} \times d}, {\textbf{y}}_{{\textrm{H}}} \in {\mathbb {R}}^{n_{{\textrm{H}}}}\right\} , \end{aligned}$$

and LF data set,

$$\begin{aligned} D_{{\textrm{L}}}:= \left\{ \left( {\textbf{X}}_{{\textrm{L}}},{\textbf{y}}_{{\textrm{L}}}\right) | {\textbf{X}}_{{\textrm{L}}} \in {\mathbb {R}}^{n_{{\textrm{L}}} \times d}, {\textbf{y}}_{{\textrm{L}}} \in {\mathbb {R}}^{n_{{\textrm{L}}}}\right\} , \end{aligned}$$

including HK and IHK. Here, $n_{{\textrm{L}}}$ and $n_{{\textrm{H}}}$ are respectively the number of LF and HF sampling points; the pair $\left( {\textbf{X}}_{{\textrm{H}}},{\textbf{y}}_{{\textrm{H}}}\right)$ denotes the HF sampled data sets in the vector space. Similarly the LF model is assumed to sample at $n_{{\textrm{L}}}$ points ${\textbf{X}}_{{\textrm{L}}}$ with corresponding responses ${\textbf{y}}_{{\textrm{H}}}$.

Han et al. presented the HK to reduce the computational complexity of co-Kriging [23]. To build a BF surrogate model between $D_{{\textrm{H}}}$ and $D_{{\textrm{L}}}$, HK first builds a Kriging surrogate model ${\hat{y}}_{{\textrm{L}}}({\textbf{x}})$ for the LF model, and then models the discrepancy function between ${\hat{y}}_{{\textrm{L}}}({\textbf{x}})$ and the HF model as a stationary random process $z({\textbf{x}})$:

$$\begin{aligned} {y}_{{\textrm{H}}_{1}}({\textbf{x}}) = \beta _{0}{\hat{y}}_{{\textrm{L}}}({\textbf{x}})+z({\textbf{x}}). \end{aligned}$$

(1)

where $\beta _{0}$ is a scaling factor indicating the correlation between LF and HF models. It finally gives the prediction of response of the untried point as

$$\begin{aligned} {\hat{y}}_{{\textrm{H}}_{1}}({\textbf{x}}) = \beta _{0} {\hat{y}}_{{\textrm{L}}}({\textbf{x}}) + {\textbf{r}}^{\top }({\textbf{x}}) {\textbf{R}}^{-1} ({\textbf{y}}_{{\textrm{H}}} - \beta _{0} {\textbf{F}}_{{\textrm{HK}}}), \end{aligned}$$

(2)

where ${\textbf{R}} \in {\mathbb {R}}^{n_{{\textrm{H}}} \times n_{{\textrm{H}}}}$ is the spatial correlation matrix among the HF observed points; ${\textbf{F}}_{{\textrm{HK}}} = \left[ {\hat{y}}_{{\textrm{L}}}({\textbf{x}}_{1}),\ldots ,{\hat{y}}_{{\textrm{L}}}({\textbf{x}}_{n_{{\textrm{H}}}}) \right] ^{\top }$ is the design vector, ${\textbf{r}} \in {\mathbb {R}}^{n_{{\textrm{H}}}}$ is the correlation vector between the untried point and the HF observed points. Also, we can obtain $\beta _{0} = ({\textbf{F}}_{{\textrm{HK}}}^{\top } {\textbf{R}}^{-1} {\textbf{F}}_{{\textrm{HK}}})^{-1} {\textbf{F}}_{{\textrm{HK}}}^{\top }{\textbf{R}}^{-1} {\textbf{y}}_{{\textrm{H}}}$. Moreover, the MSE of the HK prediction can be calculated by:

$$\begin{aligned} \begin{aligned}&\sigma ^{2} \left\{ 1 - {\textbf{r}}^{\top }{\textbf{R}}^{-1}{\textbf{r}} + [{\textbf{r}}^{\top }{\textbf{R}}^{-1}{\textbf{F}}_{{\textrm{HK}}}-{\hat{y}}_{{\textrm{L}}}({\textbf{x}})]\right. \\&\left. ({\textbf{F}}_{{\textrm{HK}}}^{\top }{\textbf{R}}^{-1}{\textbf{F}}_{{\textrm{HK}}})^{-1} [{\textbf{r}}^{\top }{\textbf{R}}^{-1}{\textbf{F}}_{{\textrm{HK}}}-{\hat{y}}_{{\textrm{L}}}({\textbf{x}})]^{\top } \right\} \end{aligned} \end{aligned}$$

(3)

where $\sigma ^{2}$ is the variance of $z({\textbf{x}})$. This MSE estimator performs more precise than the traditional Kriging because the approximated LF model ${\hat{y}}_{{\textrm{L}}}({\textbf{x}})$ is contained. Meanwhile, instead of modeling the “cross correlation” between HF and LF data in co-Kriging, only the individual correlation of HF and LF data is modeled in HK, which reduces the model complexity.

The IHK used a PRS function to map the LF function to the HF data, leading to a more accurate MF model compared with HK [27]. Specifically, the BF surrogate model between $D_{{\textrm{H}}}$ and $D_{{\textrm{L}}}$ can be formulated as

$$\begin{aligned} {y}_{{\textrm{H}}_{2}}({\textbf{x}}) = h({\textbf{x}}) {\hat{y}}_{{\textrm{L}}}({\textbf{x}}) +z({\textbf{x}}), \end{aligned}$$

(4)

where $h({\textbf{x}})$ is a response surface model with the expression of

$$\begin{aligned} h({\textbf{x}}) = \beta _{0} + \sum \limits ^{d}_{l=1}{\beta _{l}{x}_{l}} + \sum \limits _{1 \le j \le k \le d}{\beta _{{jk}}{x}_{j}{x}_{k}}. \end{aligned}$$

(5)

Taking the two-dimensional case for example, then (4) can be expressed as:

$$\begin{aligned} {y}_{{\textrm{H}}_{2}}({\textbf{x}})=f({\textbf{x}})^{\top }\varvec{\beta } +z({\textbf{x}}), \end{aligned}$$

(6)

where $\varvec{\beta } = [\beta _{1},\beta _{2},\beta _{3},\beta _{4},\beta _{5},\beta _{6}]$ and

$$\begin{aligned} \begin{aligned} f({\textbf{x}})&= [f_{1},f_{2},f_{3},f_{4},f_{5},f_{6}]\\&= [1, x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}]{\hat{y}}_{{\textrm{L}}}(x_{1},x_{2}). \end{aligned} \end{aligned}$$

(7)

Using a similar solving procedure to HK, IHK produces results that have a similar form to (2) and (3), but with a different design matrix ${\textbf{F}}_{{\textrm{IHK}}}=[f({\textbf{x}}_{{\textrm{H}}}^{1}),\ldots , f({\textbf{x}}_{{\textrm{H}}}^{n_{{\textrm{H}}}})]^{\top }$ and thus a different scaling factor $\beta ^{\star } = ({\textbf{F}}_{{\textrm{IHK}}}^{\top }{\textbf{R}}^{-1}{\textbf{F}}_{{\textrm{IHK}}})^{-1}{\textbf{F}}_{{\textrm{IHK}}}^{\top }{\textbf{R}}^{-1}{\textbf{y}}_{{\textrm{H}}}$. Since f incorporates both the LF model and predictor location information, IHK achieves a superior MSE estimation compared with HK.

2.2 Multi-model fusion framework and variance-weighted sum multi-fidelity surrogate

Chen et al. presented a non-hierarchical multi-model fusion framework with two main fusion methods: weighted-sum (WS) and parallel combination (PC) [32].

The WS approach models the true physical response $y^{{\textrm{t}}}({\textbf{x}})$ as a linear combination of simulation models $y^{{\textrm{s}}}({\textbf{x}})$ together with a single discrepancy function $\delta ({\textbf{x}})$, i.e.,

$$\begin{aligned} y^{{\textrm{t}}}({\textbf{x}})= y^{{\textrm{s}}}({\textbf{x}})\varvec{\rho }+\delta ({\textbf{x}}), \end{aligned}$$

(8)

where $\varvec{\rho } = [\rho ^{1},\ldots ,\rho ^{M}]^{\top }$ denotes the weight parameters with each entry corresponding to one simulation model (M is the number of simulation models). $\delta ({\textbf{x}})$ is the residual function that captures the discrepancy between the weighted sum and the true response.

The PC approach models the true physical response $y^{{\textrm{t}}}({\textbf{x}})$ as the sum of a simulation model $y^{{\textrm{m}}_{i}}({\textbf{x}})$ and its corresponding discrepancy function $\delta ^{{i}}({\textbf{x}})$, i.e.,

$$\begin{aligned} y^{{\textrm{t}}}({\textbf{x}})= y^{{\textrm{m}}_{i}}({\textbf{x}}) + \delta ^{{i}}({\textbf{x}}) (i=1,\ldots ,M). \end{aligned}$$

(9)

In MF case, the above framework (8) and (9) can be applied to model the relationship between LF and HF data. Hence, different MF surrogate methods were proposed under the WS framework, proving the superiority of WS [28, 33]. For example, Cheng et al. proposed a MF surrogate modeling method called VWS-MFS (VWS) based on the variance-weighted sum, which can make the utmost of the information from non-hierarchical LF data [35]. Its formulation can be expressed as:

$$\begin{aligned} {y}_{{\textrm{H}}}({\textbf{x}}) = g({\textbf{x}})\sum \limits _{i=1}^{M}{\omega _{i}{\hat{y}}_{i,\textrm{L}}({\textbf{x}})} +z({\textbf{x}}), \end{aligned}$$

(10)

where $\omega _{i}$ denotes the weights allocated to each set of LF data, $g({\textbf{x}})$ is a function to modify the LF model.

The process of constructing the model can be divided into three steps. Firstly, the Kriging model is built for each LF data set, obtaining the mean ${\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})$ and variance $\sigma _{i}^{2}({\textbf{x}})$ respectively. Secondly, the above means and variances are used for weighted summation. Specifically, the fused mean of the design point is estimated by:

$$\begin{aligned} {\bar{y}}_{{\textrm{L}}}({\textbf{x}})=\sum \limits _{i=1}^{M}{\omega _{i}{\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})} =\sum \limits _{i=1}^{M}{\frac{{\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})}{\sigma _{i}^{2}({\textbf{x}}) \sum _{j=1}^{M}{1/\sigma _{j}^{2}({\textbf{x}})}}}. \end{aligned}$$

(11)

Fig. 1

Comparison of frameworks between VWS and WMBF

Thirdly, the IHK model is used to construct the MF surrogate model combining the HF data and the fused LF data. Finally, the prediction result and its MSE are obtained by the IHK predictor.

One can easily verify that (10) can be rewritten in the form of (8). The term $\omega _{i}g({\textbf{x}})$ can be regarded as the correction of HF data for each LF data, where $\omega _{i}$ is the weight calculated by the single Kriging model built on each LF data, and $g({\textbf{x}})$ is a PRS model severing as the scaling function to map the fused LF data to the HF data.

3 The proposed WMBF method

In this section, the details of the proposed WMBF method will be presented, including the MF construction framework, the entropy-based weight calculation method and the overall WMBF construction flowchart.

3.1 The MF construction framework

Most existing non-hierarchical MF methods have been proposed and investigated within the WS framework. Motivated by the separated discrepancy functions in the PC approach, we propose a novel non-hierarchical MF framework called weighted multi-bi-fidelity (WMBF). The WMBF framework integrates both the WS and PC methods, which is formulated as

$$\begin{aligned} \begin{aligned} {\hat{y}}_{{\textrm{H}}}({\textbf{x}})&= \sum \limits _{i=1}^{M}{\omega _{i}\left[ g_{i}({\textbf{x}}){\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}}) + Z_{i}({\textbf{x}}) \right] }\\&= \sum \limits _{i=1}^{M}{\omega _{i}g_{i}({\textbf{x}}){\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})} + \sum \limits _{i=1}^{M}{\omega _{i}Z_{i}({\textbf{x}})}, \end{aligned} \end{aligned}$$

(12)

where M indicates the number of non-hierarchical LF models, ${\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})$ is the single Kriging surrogate model of each LF data, $\omega _{i}, g_{i}({\textbf{x}}), Z_{i}({\textbf{x}})$ stand for the weight, scaling function, and discrepancy function of each BF model, respectively.

On the one hand, the term $\sum _{i=1}^{M}{\omega _{i}Z_{i}({\textbf{x}})}$ is a weighted summation of multiple independent Gaussian progress derived from the BF surrogate models. It can be regarded as a single Gaussian progress, enabling to express (12) in the form of the WS framework (8). On the other hand, the term $g_{i}({\textbf{x}}){\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})+ Z_{i}({\textbf{x}})$ is in line with the idea of separated discrepancy in the PC framework (9), which will be modeled by BF surrogate model in the proposed method. In this way, the WMBF integrates the idea of both WS and PC approaches to enhance the accuracy of the non-hierarchical MF surrogate model, as illustrated in Fig. 1.

Figure 1 also demonstrates the difference between the WMBF and VWS. Specifically, the term $\omega _{i}g_{i}({\textbf{x}})$ in (12) is treated as the multiplicative correction between each LF and HF data, where $\omega _{i}$ and $g_{i}({\textbf{x}})$ are calculated based on the uncertainty and the scaling function of the BF model built on each LF and HF data. Compared with VWS, WMBF offers a more reasonable weight $\omega _{i}$ by utilizing information from the BF model instead of relying solely on the single-fidelity (SF) model. Meanwhile, WMBF provides distinct scaling functions $g_{i}({\textbf{x}})$ to capture the correlation between each LF and HF data, whereas VWS employs a common scaling function $g({\textbf{x}})$ for all LF models.

Moreover, the proposed WMBF framework stands out from other WS methods due to the individualization of the discrepancy between each LF and HF data, aligning with the principle of PC. Specifically, the discrepancy function $Z_{i}({\textbf{x}})$ are computed by the BF model and then fused based on their corresponding uncertainty weight $\omega _{i}$.

3.2 The entropy-based weight calculation methods

The weight coefficient in the WS framework should adhere to the rule that a high weight signifies a strong correlation between the individual LF and HF data, further representing the LF’s significant contribution to the overall MF surrogate model.

The existing WS-based methods still focus on obtaining weight coefficients through MF surrogate methods such as HK, Co-Kriging, etc., which may involve complex calculations, especially using Co-Kriging in high input dimensions will cause “the curse of dimensionality”. Weights based on the accuracy or uncertainty of the corresponding surrogate models do not have such drawbacks. Considering the uncertainty, Lam gave a novel definition of fidelity in terms of a variance metric and used it to fuse into the non-hierarchical MF surrogate model [36]. VWS-MFS utilized the same variance metric to characterize the uncertainty of each LF data and accomplish the LF data fusion [35]. However, due to the deficiency of variance in describing uncertainty, the metric of weight within the WS framework can be improved accordingly. Inspired by the multiple-moment statistical information brought by entropy, we introduce a novel metric of weight coefficient based on entropy within the WMBF framework.

In information theory, the entropy is the measure of the amount of missing information, also known as Shannon entropy [37]. It is defined in terms of a continuous set of probabilities p(x) as follows:

$$\begin{aligned} H(X)=-\int _{X} p(x) \ln {p(x)} dx.. \end{aligned}$$

(13)

It is found that entropy is a superior measure of uncertainty compared with variance because of its ability to capture multi-moment information. Moreover, entropy is extended to the mutual information to quantify information flow between two distributions, such as the Kullback–Leibler (KL) divergence, expressed as follows:

$$\begin{aligned} D_{\text {KL}}(P||Q)=\int _{x \in X}p(x)log({\frac{p(x)}{q(x)}})dx, \end{aligned}$$

(14)

where P and Q are two distributions respectively with probability density function p(x) and q(x) [38]. Notably, when P and Q are Gaussian (i.e., $P \sim {\mathcal {N}}(\mu _{1},\sigma ^{2}_{1}),Q \sim {\mathcal {N}}(\mu _{2},\sigma ^{2}_{2})$), then (14) can be expressed as

$$\begin{aligned} D_{\text {KL}}(P||Q)= \ln {\frac{\sigma _{2}}{\sigma _{1}}} - \frac{1}{2} +\frac{\sigma _{1} + (\mu _{1} - \mu _{2})^{2}}{2 \sigma ^{2}_{2}}. \end{aligned}$$

(15)

It is found from (15) that the KL divergence involves not only the natural logarithm of the variance but also the mean values, enabling the provision of more information and greater nonlinear insights compared with the variance alone. Moreover, the decreasing KL divergence suggests a convergence between the two distributions, P and Q, indicating their increasing similarity and decreasing uncertainty. This makes it a suitable metric for quantifying the relationship between the two distributions.

Thus, we propose a novel weight in the WMBF framework based on (15), which utilizes the KL divergence $D_{\text {KL}}^{i}(P||Q)$ between each LF and BF model to characterize their uncertainty and correlationship (given a total of M BF models), expressed as:

$$\begin{aligned} \omega _{i} = \frac{(1+(D_{\text {KL}}^{i}(P||Q))^{\alpha _{i}})^{-1}}{\sum _{j=1}^{M} (1+(D_{\text {KL}}^{j}(P||Q))^{\alpha _{j}})^{-1}}, \end{aligned}$$

(16)

where $\alpha _{i} = {(\log _{10}{\max (D_{\text {KL}}^{i})} - \log _{10}{\min (D_{\text {KL}}^{i})})}^{-1}$ is a scalar for regulating the magnitude.

As the divergence between each LF and BF model increases, its weight in the final MF surrogate model decreases. This indicates that the BF model, relying on corresponding LF data with lower consistency with HF data, will contribute less to the final surrogate model. By incorporating multiple-moment information between each LF and HF data, this weight provides a more accurate estimation for the MF surrogate model than VWS-MFS.

Considering that the poor BF model on some points may introduce interference to the surrogate model, then model with small weight on a certain point needs to be discarded. To this end, the dropout mechanism is employed to polish the above weight. Specifically, we refined the weight function by incorporating an indicator function, which determines whether a given BF model is significant enough at a particular point. By introducing a threshold denoted as $\epsilon$, the refined weight is calculated as follows:

$$\begin{aligned} \omega _{r_{i}} = \omega _{i} \times {\mathbb {I}}(\omega _{i} > \epsilon ), \end{aligned}$$

(17)

where the indicator function is defined as:

$$\begin{aligned} {\mathbb {I}}(\omega _{i}> \epsilon ) = \left\{ \begin{aligned} {1,}&\quad {\omega _{i} > \epsilon }\\ {0,}&\quad {\textrm{else}}\\ \end{aligned},\right. \end{aligned}$$

(18)

(17) reveals that, a BF model at a specific point with a weight smaller than the threshold is deemed insufficiently effective to contribute to the final surrogate model, thus its weight is set to zero. On the contrary, if the weight surpasses the threshold, it retains its original weight. However, setting a weight to zero raises a concern about the normalization of weights. To address this, we add the original weight of the eliminated model on the largest remaining weight. This ensures that the sum of all BF models’ weights at a certain point equals one. In this way, the proposed weight calculation method integrates multiple BF models by discarding less pertinent information through the dropout mechanism, facilitating an adaptive selection process.

Fig. 2

Construction flowchart of WMBF

3.3 The overall WMBF construction flowchart

The proposed WMBF construction flowchart is shown in Fig. 2. Specifically, we start with building individual SF surrogate model for each set of LF data using ordinary Kriging. Then, the IHK is applied to construct the BF model between each LF and HF data. The uncertainty between each LF and BF model is quantified using the KL divergence. Finally, the integration of all BF models is accomplished by utilizing their respective weights in a summation procedure. The detailed process is described in this section.

3.3.1 Step 1: Generate LF and HF sampling set

Assume that there are M non-hierarchical LF models $S_{{\textrm{L}}}^{1},\ldots ,S_{{\textrm{L}}}^{M}$ mapping from design space $x \in {\mathbb {R}}^{d}$ to ${\mathbb {R}}$. For each LF model $S_{{\textrm{L}}}^{i}$, a sampling set ${\textbf{X}}_{{\textrm{L}}}^{i}=[{\textbf{x}}_{{\textrm{L}}}^{i,1},\ldots ,{\textbf{x}}_{{\textrm{L}}}^{i,n_{i}}] ^{\top }\in {\mathbb {R}}^{n_{i}\times d}$ is generated using the Latin Hypercube Sampling (LHS) method with a relatively large number of sample points $n_{i}$ ($n_{i}$ is equal for each i). As for the HF model $S_{{\textrm{H}}}$, LHS is also used for generating sampling set ${\textbf{X}}_{{\textrm{H}}}=[{\textbf{x}}_{{\textrm{H}}}^{1},\ldots ,{\textbf{x}}_{{\textrm{H}}}^{n_{{\textrm{H}}}}] ^{\top }\in {\mathbb {R}}^{n_{{\textrm{H}}}\times d}$ with a relatively small number of sample points $n_{{\textrm{H}}}$. In this construction process, non-nested sampling is considered. Specifically, it means the HF sample set is sampled outside of the LF sample set as ${\textbf{X}}_{{\textrm{H}}}\cap {\textbf{X}}_{{\textrm{L}}} = \emptyset$, thus the non-nested ${\textbf{X}}_{{\textrm{H}}}$ is generated with some new sample points.

3.3.2 Step 2: Run LF and HF simulations to collect LF and HF response values

With the sampling set ${\textbf{X}}_{{\textrm{L}}}^{i}$ in Step 1, the corresponding response set $Y_{{\textrm{L}}}^{i} = [y_{{\textrm{L}}}^{i,1},\ldots ,y_{{\textrm{L}}}^{i,n_{i}}]^{\top } \in {\mathbb {R}}^{n_{i}}$ is collected by running the LF simulation. Thus, the LF design set $D_{{\textrm{L}}_{i}}=\{({\textbf{X}}_{{\textrm{L}}}^{i},Y_{{\textrm{L}}}^{i})\} (i=1,\ldots ,M)$ with $n_{i}$ design points is obtained. With the sampling set ${\textbf{X}}_{{\textrm{H}}}$ in Step 1, the corresponding response set $Y_{{\textrm{H}}} = [y_{{\textrm{H}}}^{1},\ldots ,y_{{\textrm{H}}}^{n_{{\textrm{H}}}}]^{\top } \in {\mathbb {R}}^{n_{{\textrm{H}}}}$ is collected by running the HF simulation. Thus, the HF design set $D_{{\textrm{H}}}=\{({\textbf{X}}_{{\textrm{H}}},Y_{{\textrm{H}}})\}$ with $n_{{\textrm{H}}}$ design points is obtained.

3.3.3 Step 3: Build bi-fidelity surrogate models for HF and each LF data

For each LF model $S_{{\textrm{L}}}^{i}$, an ordinary Kriging model will be built as an SF surrogate model based on its corresponding design set $D_{{\textrm{L}}_{i}}$ as follow:

$$\begin{aligned} {y}_{{\textrm{L}}}^{i}({\textbf{x}}) = s_{{\textrm{L}}}^{i}({\textbf{x}}) + z_{{\textrm{L}}}^{i}({\textbf{x}}), \end{aligned}$$

(19)

where $s_{{\textrm{L}}}^{i}({\textbf{x}})$ is the mean function describing the overall trend of LF model, and $z_{{\textrm{L}}}^{i}({\textbf{x}})$ is the random process with zero mean and variance $\sigma _{{\textrm{L}},i}^{2}$, its covariance function is given by $\sigma _{{\textrm{L}},i}^{2}{\textbf{R}}_{{\textrm{L}},i}({\textbf{x}}_{p},{\textbf{x}}_{q})$. The correlation function ${\textbf{R}}_{{\textrm{L}},i}({\textbf{x}}_{p},{\textbf{x}}_{q})$ quantifies the relationship between two design points ${\textbf{x}}_{p}$ and ${\textbf{x}}_{q}$, which is defined using different types of functions, with the Gaussian exponential function chosen in this paper (i.e., ${\textbf{R}}(\theta ,{\textbf{x}}_{p},{\textbf{x}}_{q})=\exp (-\theta {|{{\textbf{x}}_{p}-{\textbf{x}}_{q}}|}^{2})$). The hyper-parameters $\theta$ will be estimated using the maximum log-likelihood method based on the LF design set $D_{{\textrm{L}}_{i}}$. Details of the Kriging method can be found in [1]. With the same solving process, we get the surrogate of each LF model $S_{{\textrm{L}}}^{i}$, so that given any design point ${\textbf{x}}$ the predicted value is calculated as

$$\begin{aligned} {\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}}) = f_{i}^{\top } \beta _{i} + r_{{\textrm{L}},i}^{\top } {\textbf{R}}_{{\textrm{L}},i}^{-1} ({\textbf{Y}}_{i} - {\textbf{F}}_{i}) \beta _{i}, \end{aligned}$$

(20)

meanwhile with the MSE as

$$\begin{aligned} \begin{aligned} {\hat{\sigma }}_{{\textrm{L}},i}^{2}({\textbf{x}})&= \sigma _{{\textrm{L}},i}^{2} [1 + ({\textbf{F}}_{{\textrm{L}},i}^{\top } {\textbf{R}}_{{\textrm{L}},i}^{-1} r_{{\textrm{L}},i} - f_{{\textrm{L}},i})^{\top } ({\textbf{F}}_{{\textrm{L}},i}^{\top } {\textbf{R}}_{{\textrm{L}},i}^{-1} {\textbf{F}}_{{\textrm{L}},i})^{-1}\\&\quad ({\textbf{F}}_{{\textrm{L}},i}^{\top } {\textbf{R}}_{{\textrm{L}},i}^{-1} r_{{\textrm{L}},i} - f_{{\textrm{L}},i}) - r_{{\textrm{L}},i}^{\top } {\textbf{R}}_{{\textrm{L}},i}^{-1} r_{{\textrm{L}},i}]. \end{aligned} \end{aligned}$$

(21)

Since the SF surrogate model ${\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}})$ is obtained, then the BF surrogate model between HF and each LF data can be built based on the BF methods mentioned in Sect. 2.1. Here, WMBF prefers the IHK considering its accurate prediction performance. The HK is also exploited for comparison in the Experiment part referred to as WMBF-HK. Therefore, the BF surrogate model between $D_{{\textrm{H}}}$ and each $D_{{\textrm{L}}_{i}}$ can be formulated as

$$\begin{aligned} {y}_{{\textrm{H}}}^{i}({\textbf{x}}) = g_{i}({\textbf{x}}) {\hat{y}}_{{\textrm{L}}}^{i}({\textbf{x}}) +z_{i}({\textbf{x}}), \end{aligned}$$

(22)

where $g_{i}({\textbf{x}})$ is a scaling function (i.e., in WMBF it is a response surface model while in WMBF-HK it is a constant scalar). For the sake of clarity, we will only focus on the inference based on IHK in the following part. The predictor of IHK is obtained at any design point ${\textbf{x}}$:

$$\begin{aligned} \begin{aligned} {\hat{y}}_{{\textrm{H}}}^{i}({\textbf{x}})&= {f^{i}}^{\top }\beta _{i}^{\star }+r_{i}^{\top }{\textbf{R}}_{i}^{-1}({\textbf{Y}}_{{\textrm{H}}}-{\textbf{F}}_{i}\beta _{i}^{\star })\\&= f^{i}({\textbf{x}})^{\top }\beta _{i}^{\star }+r_{i}({\textbf{x}})^{\top }\gamma ^{\star }, \end{aligned} \end{aligned}$$

(23)

where $\beta _{i}^{\star } = ({\textbf{F}}_{i}^{\top }{\textbf{R}}_{i}^{-1}{\textbf{F}}_{i})^{-1}{\textbf{F}}_{i}^{\top }{\textbf{R}}_{i}^{-1}{\textbf{Y}}_{i}$ is the coefficient of the scaling factor, ${\textbf{F}}_{i}=[f^{i}({\textbf{x}}_{{\textrm{H}}}^{1})\dots f^{i}({\textbf{x}}_{{\textrm{H}}}^{n_{{\textrm{H}}}})]^{\top }$ is the design matrix, ${\textbf{R}}_{i}:=({\textbf{R}}_{i}({\textbf{x}}_{p},{\textbf{x}}_{q}))_{p,q} \in {\mathbb {R}}^{n_{{\textrm{H}}} \times n_{{\textrm{H}}}}$ and $r:=({\textbf{R}}({\textbf{x}}_{p},{\textbf{x}}))_{p}\in {\mathbb {R}}^{n_{{\textrm{H}}}}$ are the covariance function. The corresponding MSE is estimated as:

$$\begin{aligned} \begin{aligned} \varphi _{i}^{2}({\textbf{x}})&=\sigma _{i}^{2}[1+({\textbf{F}}_{i}^{\top }{\textbf{R}}_{i}^{-1}r_{i}-f^{i})^{\top } ({\textbf{F}}_{i}^{\top }{\textbf{R}}_{i}^{-1}{\textbf{F}}_{i})^{-1}\\&\quad ({\textbf{F}}_{i}^{\top }{\textbf{R}}_{i}^{-1}r_{i}-f^{i}) -r_{i}^{\top }{\textbf{R}}_{i}^{-1}r_{i}]. \end{aligned} \end{aligned}$$

(24)

3.3.4 Step 4: Fuse multiple BF surrogate models to MF surrogate model using weighted-sum

During the construction of the LF and BF surrogate models, their mean and variance are given by the Kriging and IHK method. Specifically, each LF model $y_{\text {L}}^{i} \sim {\mathcal {N}}({\hat{y}}_{{\textrm{L}}}^{i},{\hat{\sigma }}_{{\textrm{L}},i}^{2})$ and each BF model $y_{\text {H}}^{i}\sim {\mathcal {N}}({\hat{y}}_{{\textrm{H}}}^{i},\varphi _{i}^{2})$. According to (15), the KL divergence between $y_{\text {L}}^{i}$ and $y_{\text {H}}^{i}$ is calculated as follow:

$$\begin{aligned} D_{\text {KL}}^{j}(y_{\text {L}}^{i}||y_{\text {H}}^{i}) =\ln {\frac{\varphi _{i}}{{\hat{\sigma }}_{{\textrm{L}},i}}} - \frac{1}{2}+\frac{{\hat{\sigma }}_{{\textrm{L}},i} + ({\hat{y}}_{{\textrm{L}}}^{i} - {\hat{y}}_{{\textrm{H}}}^{i})^{2}}{2 \varphi _{i}^{2}}. \end{aligned}$$

(25)

Thus, the MF surrogate model is built by fusing multiple ${\hat{y}}_{H}^{i}({\textbf{x}})$ into a weighted summation as follow:

$$\begin{aligned} {\hat{y}}_{{\textrm{H}}}({\textbf{x}}) = \sum \limits _{i=1}^{M} {\omega _{r_{i}} {\hat{y}}_{{\textrm{H}}}^{i}({\textbf{x}})}, \end{aligned}$$

(26)

The weight $\omega _{r_{i}}$ is calculated as (17) expressed where $\epsilon$ is set as 0.1 (since its sensitivity analysis proves that it has little influence on the modeling effect). The weight of each BF model $\omega _{i}$ is calculated by:

$$\begin{aligned} \omega _{i} = \frac{(1+(D_{\text {KL}}^{i}(y_{\text {L}}^{i}||y_{\text {H}}^{i}))^{\alpha _{i}})^{-1}}{\sum _{j=1}^{M} (1+(D_{\text {KL}}(y_{\text {L}}^{i}||y_{\text {H}}^{i}))^{\alpha _{j}})^{-1}}, \end{aligned}$$

(27)

where $\alpha _{i} = {(\log _{10}{\max (D_{\text {KL}}^{i})} - \log _{10}{\min (D_{\text {KL}}^{i})})}^{-1}$.

The MSE-based weight is also considered for comparison in Experiment part referred to as WMBF-MSE, where the weight of each BF model $\omega _{i}$ is calculated as follow:

$$\begin{aligned} \omega _{i} = \frac{1}{\varphi _{i}^{2}({\textbf{x}})\sum _{j=1}^{M} 1/\varphi _{j}^{2}({\textbf{x}})}. \end{aligned}$$

(28)

3.3.5 Step 5: Evaluation of MF surrogate model

Measurements that describes the error between the surrogate model prediction and the ground truth are adopted to evaluate the accuracy of the surrogate models as follows:

• maximum absolute error (MAE) is a metric revealing the local accuracy.

• mean relative error (MRE) is a metric revealing the overall confidence degree of accuracy.

• root mean square error (RMSE) is a metric revealing the global accuracy.

Fig. 3

Figures of the ground truth of Example 3. Left figure shows the true value curves of the HF and LF models. Right figure shows the absolute correlations between HF and each LF model in intervals

Table 1 Errors of different surrogate methods for Example 3

These three metrics can be calculated for N test points by:

$$\begin{aligned} \begin{aligned} \textrm{MAE}&= \max \vert {y_{i}-{\hat{y}}_{i}}\vert ,\\ \textrm{MRE}&= \sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}\frac{\vert {y_{i}-{\hat{y}}_{i}}\vert }{\vert {y_{i}}\vert }},\\ \textrm{RMSE}&= \sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}(y_{i}-{\hat{y}}_{i})^{2}}, \end{aligned} \end{aligned}$$

(29)

where $y_{i}$ and ${\hat{y}}_{i}$ represent the true value and the predicted value of response at the $i^{{\textrm{th}}}$ test point, respectively.

4 Experiment

4.1 Demonstration example

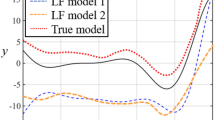
To illustrate the entire process of the proposed WMBF, we use a 1-d test function (refer to Example 3 in “Appendix 1”) with 2 LF models as an example and present the corresponding results during the procedure.

The left figure in Fig. 3 displays the true value curves of HF and LF models, suggesting no hierarchical difference between each LF and HF model. On the other hand, the right figure in Fig. 3 presents the absolute correlations between each LF and HF model in the small interval, illustrating the unstable correlations between each LF and HF model throughout the whole design space. Therefore, Fig. 3 clearly demonstrates the non-hierarchical nature of this test function, necessitating the use of a specific non-hierarchical surrogate method.

Fig. 4

Curves of weights of different surrogate models. The left figure indicates the weight curves of LF models changing with x in VWS-MFS. The middle figure indicates the MSE-based weight curves of multiple BF models changing with x in WMBF. The right figure indicates the KL-divergence-based weight curves of multiple BF models changing with x in WMBF

Fig. 5

Curves of MSE of each BF model and LF model. The left figure indicates the MSE curves of each BF model changing with x in WMBF. The right figure indicates the MSE curves of each LF model changing with x in VWS-MFS

In this demonstration, we manually choose the HF and LF design points to prevent the nonuniform distribution resulting from random sampling. The design points of the HF and LF model are chosen as $S_{{\textrm{H}}}=[0.18,0.27,0.5,0.73,0.82]$ and $S_{{\textrm{L}}}=[0,0.2,0.4,0.6,0.8,1]$. We then use different surrogate methods with the same design samples to test their effect. Particularly for the BF method (i.e., IHK), the number of design points is kept the same as others(i.e., HF design points are still $S_{{\textrm{H}}}$ and LF design points are $S_{{\textrm{L}}'}$ which consists of $2\times 6$ design points uniformly chosen within the design space).

Several surrogate methods, including SF method (i.e., Kriging), BF method (i.e., IHK [27]) and MF methods (i.e., LRMF [33], VWS [35], NHLF [34], WMBF-MSE and WMBF-KL), are used to predict this example. Specifically, WMBF-MSE exploits the MSE-based weight [referred to (28)] within the proposed WMBF framework, while WMBF-KL utilizes KL-divergence-based weight within the WMBF framework (i.e., the proposed method). Their prediction errors are calculated using 1000 randomly generated test points, as presented for comparison in Table 1. The results show that WMBF-KL achieves the lowest error among all methods, further confirming its superior performance.

The proposed WMBF method not only constructs a non-hierarchical MF surrogate model in a novel framework but also employs an innovative weight calculation method based on entropy. To demonstrate its superiority within both the novel framework and the weight calculation, we provide the illustrations in Figs. 4 and 5.

On the one hand, Fig. 4 showcases the weight curves corresponding to the design point x for three methods: VWS, WMBF-MSE, and WMBF-KL. It is found that the weight curves of VWS remain constant with respect to x, whereas those within WMBF vary in magnitude with x. This finding clarifies that the proposed WMBF framework outperforms VWS in its strong adaptability to unknown inputs, enabling it to derive more appropriate weights than VWS. More specifically, Fig. 5 displays the MSE curves of each BF model and LF model, respectively, from WMBF-MSE and VWS. Evidently, the MSE curves of LF models coincide, resulting in constant weights of 0.5 in VWS, rendering these weight coefficients meaningless. In contrast, the MSE curves of BF models exhibit some discrepancies near the interval’s boundary, which corresponds to the original function’s behavior in Fig. 3. This indicates the superiority of the WMBF framework in exploiting the BF information instead of the LF’s to calculate weight, thereby enhancing information utilization. Moreover, the weight curves in Fig. 4 when using different metrics to characterize uncertainty in the WMBF framework, demonstrate similar changing trends. Their varying trends better align with the ground truth or correlation curves shown in Fig. 4, emphasizing the WMBF’s superior ability to characterize the true model compared with VWS.

On the other hand, the respective weight curves based on MSE and KL divergence within WMBF in Fig. 4 also exhibit some differences. As indicated in (26), the weight in WMBF signifies the contribution of each BF model to the final surrogate model. Therefore, it should ideally correspond to the correlation between each LF and HF model, as displayed in Fig. 3. In this regard, the WMBF-KL outperforms the WMBF-MSE. In addition, in terms of numerical values, the MSE values are zero at the known points. Conversely, KL divergence value is zero only when two distributions are identical, resulting in non-zero values for the KL divergence between each BF and LF model. The utilization of zero as the denominator in weight calculations is theoretically unsound. In contrast, adopting KL divergence mitigates this concern, highlighting its merits in capturing uncertainty.

4.2 Numerical examples

In this part, more numerical examples involving various design space dimensions are presented to illustrate the effectiveness of the proposed WMBF. On the one hand, the effectiveness and robustness of surrogate methods are discussed for method comparison in the first part using the fixed sample size. On the other hand, the impact of the sample size and sample budget, which are regarded as two key factors influencing the results of the surrogate method, are also explored in the following parts to further verify the superiority of WMBF over the existing methods.

Fig. 6

Boxplots of different test functions with different surrogate methods. Each subfigure presents the performance of the test function indicated as its subtitle. The boxes in each figure include the error values between the lower (25%) and upper (75%) quartiles. The y-coordinate axis is log-scaled, considering the significant difference in the order of magnitude between the errors

Table 2 Average errors of different surrogate methods after removing outliers for Example 1–9

4.2.1 Effectiveness and robustness

We test nine test functions (see “Appendix 1”) using the proposed WMBF (both WMBF-MSE and WMBF-KL) and other non-hierarchical MF surrogate methods (i.e., LRMF [33], VWS-MFS [35] and NHLF [34]) with the fixed sample size provided in “Appendix 2”. They are decided by the preliminary experiment to make the model sufficiently accurate. Columns in Table 8 respectively represent the total sample size N, the sample size ratio $p_0$, the HF and each LF sample size $N_{\text {HF}}|N_{\text {LF}}$ and the number of LF models M.

By randomly setting the seed of the initial LHS designs, the surrogate modeling procedure is run 50 times for each method and test function. Their errors (MAE, RMSE and MRE) are shown as the boxplots in Fig. 6. Specifically, for all test functions, the WMBF-based methods achieve smaller errors compared with others, proving the WMBF’s effectiveness. To compare the size of the boxes, we quantify the number of vertical grids inside them due to the log-scaled y-axis. The robustness of the WMBF framework is evident from their relatively smaller boxes compared with other methods across all test functions, attributed to the variance reduction achieved by the ensemble of multiple BF models. Since there are some outliers outside the boxes, we exclude these outliers and average the remaining values for a fairer comparison. The results in Table 2 show that the WMBF-based methods exhibit smaller errors for all test functions. To support this finding statistically, the one-sided t-test is performed on the repeated prediction errors between WMBF-KL and each method. The corresponding results are reflected in Table 2, with errors underscored once if the p-value is less than 0.05, and doubly underscored if the p-value is less than 0.1. The statistical tests affirm that the proposed WMBF-KL significantly outperformed others in most cases. Some results for WMBF-MSE are not statistically significant, possibly due to the substantial performance improvement introduced by the WMBF framework in comparison to existing methods.

As the conclusion of this part, the proposed method exhibits a relatively robust performance while ensuring the prediction accuracy across all test functions. Notably, the WMBF framework emerges as the dominant role, with the KL divergence demonstrating its effectiveness in enhancing performance.

Table 3 The lowest error of each method in their optimal sample size and ratio for Example 5

Fig. 7

Errors curves of different surrogate models varying with N while $p_{0}$ is fixed as the optimal for Example 5. The y-coordinate axis is log-scaled, considering the significant difference in the order of magnitude between the errors

Fig. 8

Errors curves of different surrogate models varying with $p_{0}$ while N is fixed as the optimal for Example 5. The y-coordinate axis is log-scaled, considering the significant difference in the order of magnitude between the errors

4.2.2 The effect of sample size and its rate

The sample size plays a crucial role in surrogate modeling as it directly reflects the computational cost. Meanwhile, in MF cases, the sample size ratio between LF and HF models also matters, which determines the allocation of total samples. An ideal surrogate model should effectively utilize the sampling design points while minimizing cost. In this part, we conduct experiments to demonstrate the advantage of WMBF concerning these aspects, using a two-dimensional test function (i.e., Example 5 in “Appendix 1”).

Assume a total sample size of N, with a portion pN being LF samples, and the remaining $(1-p)N$ being HF samples. In this study, there exists more than one LF model, and each LF model’s sample size is assumed to be $p_{0}N$, where $p=M p_0$ represents the sample size rate of the LF model and is constrained to $0.5<p<1$ (M indicates the number of LF models). Additionally, we define the sample size ratio between LF and HF model as $\gamma = \frac{pN}{(1-p)N}$. Since $\gamma$ changes with p, we will only investigate the variation in N and $p_0$ in the following experiment to maintain simplicity.

The variation range of N and $p_0$ is influenced by two factors. Firstly, the total sample size range is bounded by the minimum requirement for the HF sample size, denoted as $N_{{\textrm{HF}}}$, which must satisfy $N_{{\textrm{HF}}}\ge {(d+1)(d+2)}/{2}$ (d represents the dimensionality of the input variables) required in the IHK modeling procedure (see [27] for more details). Secondly, it is commonly understood that the sample size of LF exceeds that of HF, thus yielding the condition ${p_{0}}/{1-Mp_{0}}>1$. Consequently, the range of $p_0$ is restricted to ${1}/{M+1}< p_0 < {1}/{M}$, where $M=2$ in Example 5. Furthermore, considering $N_{{\textrm{HF}}} = (1-M p_0)N \ge {(d+1)(d+2)}/{2}$, the final range of $p_0$ is given by

$$\begin{aligned} \frac{1}{M+1}< p_0 < \frac{2N-(d+1)(d+2)}{2NM}. \end{aligned}$$

(30)

In light of the revealed latent relationship between N and $p_0$, we conduct experiments on their feasible combinations within respective ranges. Specifically, the assessment of the surrogate model involves quantifying the errors between the ground truth and the prediction of the model constructed based on the corresponding parameter combinations. To guarantee both non-redundancy of $\gamma$ and the uniform coverage across the sampling domain, we compose the series of N, consisting of twelve values uniformly distributed within a range limited to more than five times the lower bound of $N_{{\textrm{HF}}}$. Correspondingly, the $p_0$ series is constituted by six equidistant values, ensuring uniform distribution within the bounds defined by (30).

Six different MF surrogate modeling methods (i.e., LRMF, NHLF, VWS-MFS, VWS-HK, WMBF-HK and WMBF) are used for comparison. Table 3 presents the lowest error achieved by each method. Our approach generally outperforms others with the smallest error. The error curves are plotted as N and $p_{0}$ are increased, respectively, while keeping another parameter at its optimal value, as shown in Figs. 7 and 8.

Figure 7 illustrates that the general error trend decreased as N increased. This suggests that as the sample size increases, the effect of surrogate models improves when the sample size rate is fixed. Significantly, the curves of the proposed WMBF consistently remain at the bottom, proving its better effectiveness and cost-saving ability compared with other methods. Methods using model uncertainty to calculate weight within WS framework including VWS-based and WMBF-based methods exhibit better performance than LRMF and NHLF. It reveals the fact that the large sample size improves VWS and WMBF well, as increased samples contribute to a reduction in uncertainty.

In Fig. 8, it is evident that the error curves exhibit a general upward trend as $p_{0}$ increases, indicating that the surrogate model would perform better as the HF sample size getting larger. Because the less effective information leads to a decrease in modeling accuracy. All methods show this trend except LRMF, which indicates that it is relatively insensitive to variations in sample proportion. Probably because the ordinary least square method it used to solve the coefficients does not strictly require a large sample size. Additionally, the polynomial response surface LRMF used to model the discrepancy function has an obvious disadvantage compared to the Gaussian process in terms of modeling accuracy. Moreover, IHK-based methods outperform HK-based methods when p0 is small, but the trend reverses when p0 is large. This is because IHK requires more coefficients to be solved, which requires sufficient sample information. Overall, the proposed WMBF is the most effective when there is enough sample information, as shown by its lower position in most cases, confirming its effectiveness and cost-efficiency. A notable observation is the significant fluctuation in VWS-MFS’s curves, which is absent in WMBF’s. That means that WMBF demonstrates a more stable performance than VWS-MFS.

4.2.3 The effect of sample budget ratio

In this part, we perform experiments considering the cost and budget, which also gauge the cost-saving ability of the surrogate model. The budget and cost ratios assigned for sampling one design point between the single LF model and the HF model are denoted as $b_{0}$ and $c_{0}$, respectively. In engineering applications, the cost ratio $c_{0}$ is generally straightforward to determine but challenging to manually control. While the budget ratio $b_{0}$ remains elastic, allowing flexible adjustment of the sampling budget allocation between LF and HF models. Thus in this experiment, we focus on the effect of the surrogate models under a fixed $c_{0}$ and a sequence of values for $b_{0}$, using a two-dimensional test function (i.e., Example 5 in “Appendix 1”).

The experimental procedure is similar to that of Sect. 4.2.2, involving the calculation of errors between the ground truth and the prediction of the model built by different combinations of $c_{0}$ and $b_{0}$. Notably, when the total budget is fixed, variations in $c_{0}$ and $b_{0}$ will ultimately affect the sample size ratio between M LF models and 1 HF model, denoted as $\gamma$ in Sect. 4.2.2 where $\gamma > 1$. It is evident that $\gamma _{0} = {b_{0}}/{c_{0}}$, where $\gamma _{0} = {\gamma }/{M}$ represents the sample size ratio of a single LF and HF model. Hence, we have $\gamma _{0} > {1}/{M}$ (in this experiment $\gamma _{0}$ falls within the range of [1, 5]). In this way, exploring the effect of surrogate models under different $b_{0}$ with a fixed $c_{0}$ is equivalent to investigating the impact of surrogate models under different $\gamma _{0}$, effectively reflecting the influence of $b_{0}$. Specifically, in this experiment, the total sample size $N= 200$, and the fixed cost ratio $c_{0}={1}/{200}$, while $b_{0}$ is constrained within the range of $b_{0} = \gamma _{0} \times c_{0} \in [c_{0},5c_{0}]$. A sequence of 12 $b_{0}$ values is sampled within this range, considering the non-redundant $\gamma _{0}$ and the uniform sampling coverage. Since the $c_{0}$ and $b_{0}$ values are determined, the surrogate model is constructed using the corresponding $\gamma _{0} = {b_{0}}/{c_{0}}$, and the errors are calculated.

Table 4 The lowest error of each method in their optimal sampling budget ratio with non-nested and nested sampling for Example 5

Fig. 9

Errors curves of different surrogate models varying with $b_{0}$ under the fixed $c_{0}(1/200)$ for Example 5. The y-coordinate axis is log-scaled, considering the significant difference in the order of magnitude between the errors

Six different MF surrogate modeling methods (i.e., LRMF, NHLF, VWS-MFS, VWS-HK, WMBF-HK and WMBF) are tested for comparison. The lowest error of each method is listed in Table 4, where the proposed WMBF demonstrates advantages in minor errors compared with others.

Figure 9 depicts the error curves varying with $b_{0}$ under a fixed $c_{0}$ value of $\frac{1}{200}$. Among these curves, NHLF and LRMF exhibit smooth changes, demonstrating that their performance may be less affected by the variations in $b_{0}$. However, their relatively higher values compared with the other curves indicate their weak effectiveness. The error curves for the remaining models show a clear trend: as $b_{0}$ increases, the surrogate performance worsens. This phenomenon implies that a smaller budget ratio between LF and HF should be adopted, allocating more budgets to the HF model and fewer to the LF model, thereby ensuring a better performance of the MF surrogate model. Besides, the WMBF method demonstrates the best performance at small $b_{0}$, as indicated by its consistently lower error curves across [0.004, 0.016]. Notably, comparing the curves of WMBF and VWS-MFS reveals significant fluctuations in the VWS-MFS curves around $b_{0}=0.01$, which are absent in the WMBF curves. This suggests that WMBF shows a more stable performance than VWS-MFS under varying budget ratios $b_{0}$.

Fig. 10

Errors bar of WMBF varying with $N_{H}$ and $N_{L}$ for Example 5. The y-coordinate axis is log-scaled, considering the significant difference in the order of magnitude between the errors. The corresponding $N_{L}$ and $N_{H}$ is fixed as 20 and 10

The above experiments reveal a significant impact of the sample size ratio between LF and HF models on the surrogate model. Consequently, further investigation into the influence of HF and LF samples on the performance of the proposed WMBF is conducted. This is achieved by maintaining a constant number of LF (or HF) samples while varying the HF (or LF) samples in Example 5. The resulting error bars are illustrated in Fig. 10. Both of the varying bar plots indicate that the overall errors of WMBF decrease as HF (or LF) sample size increases. Moreover, when the sample size comes to a certain range, the errors tend to be constant. This phenomenon demonstrates that increasing the HF (or LF) sample size provides WMBF with more information for modeling, thereby enhancing its performance. However, once the sample size reaches a point indicating sufficiency for modeling, its further augmentation contribute small additional information. Thus, the future exploration in sequential sampling is necessary.

4.2.4 Discussion of the numerical experiment

The above numerical experiments are analyzed for the influential elements to the model performance in this part.

From the methodology perspective, the weighted-sum framework integrates multiple models through the ensemble mechanism, reducing variance and enhancing robustness. The VWS and WMBF framework, which leverage uncertainty for weight calculation in the ensemble process, demonstrate superior performance compared to methods that prioritize individual modeling. The refined BF model IHK also improves performance when information is sufficient. The proposed WMBF emphasizes the relationship between LF and HF data compared with VWS, focusing on richer information in characterizing individual BF. Consequently, WMBF outperforms VWS in accuracy.

From the sampling perspective, the effective information amount from samples significantly impacts model performance. This is influenced by three factors: total sample size, sample proportion, and sample location. The changes in total sample size and sample proportion were discussed in Sects. 4.2.2 and 4.2.3, specifically exploring N, $p_0$, and $b_0$. Controlling them to eventually increase the effective information improves model performance. However, once enough effective information is obtained for an accurate model, further sampling has a small impact. In this paper, the sample location is determined by LHS, which can be further optimize in our future work incorporated with sequential sampling to find the minimum effective information for the most accurate model.

4.3 Engineering case: the NACA0012 airfoil

In this part, we verify the practicability of the proposed method by applying it to an engineering case involving a CFD-based problem. Specifically, we solve the Euler equation for the NACA0012 airfoil under fixed freestream conditions (i.e., pressure = 101,325 Pa, temperature = 273.15 K). Various state-of-the-art solvers under different mechanisms, corresponding to the non-hierarchical case discussed in this work, are available to address this problem in practice. We utilize two computational tools: the open-source CFD code called SU2 [39] and a self-developed software called Foilflow [40].

The inputs to the problem are the Mach number (Uniform, [0.6, 0.8]) and angle of attack (Uniform, [${-}$10, 10]), while the coefficients of lift (CL) and coefficients of drag (CD) are the random outputs. The ratio of these two coefficients, known as the lift-drag ratio (LDR), is a significant parameter for evaluating aerodynamics and aerodynamic efficiency of aircraft. Hence, predicting it accurately holds great importance for aircraft design and aerodynamic control. In this experiment, we construct two surrogate models: one for CL and another for CD, and then calculate LDR based on their predictions.

Fig. 11

Convergence behavior of outputs from SU2 at a specific design point. The top and bottom subfigures exhibit the convergence behavior of CD and CL respectively, where the blue line depicts the convergence curves and the red point locates the LF partially-converged simulation

Table 5 Three simulations at the same design point for engineering case

Fig. 12

The mesh figures of two simulations. The left figure shows the mesh figure of SU2 provided for HF and LF1 models. The right figure shows the mesh figure of Foilflow provided for LF2 model

Table 6 Details of different sampling cases for engineering case experiment

Table 7 Errors of surrogate models of CL, CD and LDR for different sampling cases

Fig. 13

The true and predicted LDR values of the validation points. The black line represents the regression of $y=x$. The star, diamond and square types represent the prediction results of Kriging, HK and WMBF, respectively

In this case, a fully-converged simulation with fine mesh from SU2 is regarded as the HF simulation, while the partially-converged simulation with fine mesh from SU2 (denoted by LF1) and the 1fully-converged simulation with coarse mesh from Foilflow (denoted by LF2) are regarded as two non-hierarchical LF simulations, respectively. On the one hand, the partially-converged simulation of SU2 (LF1) is obtained by retaining one decimal place of significant digits from the fully-converged solution. Figure 11 shows the convergence behavior of the outputs from SU2 at a specific design point, which indicates the LF point is indeed partially converged. On the other hand, the fine mesh used in SU2 (HF and LF1) consisted of 10,216 triangular cells (i.e., 5233 points), while the coarse mesh used in Foilflow (LF2) consists of 6144 cells. Figure 12 illustrates the mesh figures of simulations from these two solvers, clearly indicating that SU2 employs a finer grid compared with Foilflow. Table 5 presents the relationship between these three simulations (i.e., HF, LF1 and LF2) at the same design point. The differences between HF simulation with LF1 and LF2 cannot be contrasted directly. Thus, the non-hierarchical MF methods are necessary for this engineering case. In this engineering case, one HF simulation by SU2 costs around 15 s on a Intel(R) Core (TM) i5-1135G7 (2.42 GHz) computer, while 7 s for one partial-converged LF simulation by SU2 and 7 s for one LF simulation by Foilflow. Therefore, the cost ratios between each LF and HF model are both 0.4667.

Similar to the previous numerical examples, here we also perform the experiment using non-nested LHS samples. We compare the performance of three cases: SF, BF and MF, considering four sampling sources. The specific details are listed in Table 6, where $N,p_{0},m$ are consistent with their definitions in Sect. 4.2.2. The ordinary Kriging and the IHK are applied to SF and BF cases, respectively, while four MF surrogate methods (WMBF, VWS, NHLF and LRMF) are employed in MF cases. Table 7 lists the MAE, RMSE and MRE of these surrogate models, which are calculated using 100 randomly generated validation points. Based on the errors of CD and CL, the errors of LDR are calculated by adding them up together as total errors.

Fig. 14

Error curves of surrogate models varying with the number of HF sampling. The MAE, MRE and RMSE curves of LDR, CD and CL are depicted under different surrogate models (SF, MF and BF), as indicated by its subtitle

The results presented in Table 7 illustrate that the proposed WMBF outperforms others, with smaller errors in most cases. Notably, since the MAE of the proposed method for CL prediction does not rank as the absolute best, it does reveal a limitation in local performance. Nevertheless, its MAE remains commendably low, at 1%, underscoring its overall effectiveness.

Besides, Fig. 13 shows the true and predicted LDR values of the validation points using different surrogate methods. The proximity of the scatter points to the black line indicates the accuracy of the predictions. The results suggest that the WMBF has a better performance than BF and SF methods. Furthermore, Fig. 14 displays the error curves of different surrogate models (i.e., SF, BF and MF) varying with the number of HF samples. The overall trend of these curves clearly demonstrates the superiority of MF over BF and SF, providing strong evidence that the surrogate model’s performance improves with the incorporation of higher-fidelity information.

In summary, the proposed WMBF exhibits great performance in the context of this engineering case, surpassing other commonly used surrogate methods, which proves its strong suitability in engineering applications. Moreover, leveraging higher-fidelity data to construct the surrogate model significantly enhances its effectiveness.

5 Conclusion

In this paper, we propose a novel framework named weighted multi-bi-fidelity (WMBF) to deal with the non-hierarchical case in MF surrogate modeling. The proposed WMBF demonstrates several advantages over the existing methods. As a WS-based method, it utilizes the uncertainty of each LF and BF model to analyze their relationship, resulting in a weight that incorporates more information and a more individualized scaling function than VWS-MFS. Meanwhile, it includes the concept of PC, which provides a more individualized discrepancy function compared with the existing WS-based methods. Besides, it offers a novel weight to character uncertainty with entropy, which contains more statistical moment information compared with the variance-based weight.

The effectiveness of the proposed method is demonstrated using nine numerical test functions, where several MF surrogate approaches (VWS, LRMF and NHLF) are used for comparison. The conclusions can be summarized as follows:

(1) The proposed WMBF exhibits excellent robustness and great effectiveness in repeated experiments across most test functions with a fixed sample size. Notably, the WMBF framework plays a major role, while the KL-divergence-based weight is demonstrated effective. (2) Taking a two-dimensional test function as an example, considering the sample size rate and budget ratio, the proposed WMBF outperforms other surrogate models in terms of saving sampling costs. On the one hand, under identical sampling conditions, WMBF surpasses other surrogate models by owing the lowest error curves among all. (3) On the other hand, when the sampling cost ratio is fixed, the performance of the surrogate models deteriorates with an increase in the budget ratio. However, the proposed WMBF shows the highest level of stability, indicating that it is the most cost-saving option. (4) The effective information provided by samples is the essentially control factor in sampling aspect. Once sufficient effective information is achieved by enough samples, further sampling contribute small to enhancing model performance. Finally, the proposed method is applied to solve the prediction problem of an airfoil in the real world, demonstrating its efficiency and feasibility in engineering problems.

The construction of the non-hierarchical LF data fusion framework is the initial step. However, to improve the surrogate model’s performance, additional refinements and optimizations are essential. Specifically, we intend to investigate the integration of the proposed MF surrogate modeling framework with a sequential sampling strategy in our future work. Furthermore, we will explore alternative frameworks for non-hierarchical MF surrogate models, such as the methods involving Artificial Neural Networks (ANNs).

Appendices

Appendix 1: The numerical example expressions

Example 1

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= \sin {x}\\ y_{{\textrm{L1}}}&= y_{H} + 0.1(x-\pi )^{2}\\ y_{{\textrm{L2}}}&= 1.2y_{H} + 0.1(x-\pi )^{2} - 0.2 \\ 0&\le x \le 2\pi \end{aligned} \end{aligned}$$

(31)

Example 2

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= (6x-2)^{2}\sin {12x-4}\\ y_{{\textrm{L1}}}&= 0.5y_{H} +10(x-0.5)+5\\ y_{{\textrm{L2}}}&= 0.4y_{H} -x-1 \\ y_{{\textrm{L3}}}&= 0.3y_{H} 10x +6\\ 0&\le x \le 1 \end{aligned} \end{aligned}$$

(32)

Example 3

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= 2\sin {\pi x/5}\\ y_{{\textrm{L1}}}&= x(x-5)(x-12)/30 \\ y_{{\textrm{L2}}}&= (x+2)(x-5)(x-10)/30 \\ 0&\le x \le 10 \end{aligned} \end{aligned}$$

(33)

Example 4

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= 4 x_{1}^{2}-2.1x_{1}^{4}+x_{1}^{6}/3 +x_{1}x_{2} -4x_{2}^{2}+4x_{2}^{4}\\ y_{{\textrm{L1}}}&= y_{H}(0.7x_{1},0.7x_{2})+x_{1}x_{2}-65\\ y_{{\textrm{L2}}}&= y_{H}(0.8x_{1},0.6x_{2})-x_{1}^{4}+32\\ x_{1},x_{2}&\in [-2,2] \end{aligned} \end{aligned}$$

(34)

Example 5

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&=-\sin {x_{1}}- \exp (x_{1}/100)+x_{2}^{2}/10\\ y_{{\textrm{L1}}}&=-\sin {x_{1}}- \exp (x_{1}/100)+10.3\\ {}&\qquad +0.03(x_{1}-0.3)^{2}+(x_{2}-1)^{2}/10\\ y_{{\textrm{L2}}}&=-\sin {0.9x_{1}}- \exp (0.9x_{1}/100)+10+0.64x_{2}^{2}/10\\ x_{1},x_{2}&\in [0,1] \end{aligned} \end{aligned}$$

(35)

Example 6

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= x_{1}/2\left( \sqrt{1+(x_{1}+x_{3}^{2})x_{4}/x_{1}^{20}} -1 \right) \\ {}&\qquad +(x_{1}+3x_{4})e^{(1+\sin {x_{3}})}\\ y_{{\textrm{L1}}}&= 0.79(1+sin{x_{1}}/10)y^{H} -2x_{1}+x_{2}^{2}+x_{3}^{2}+0.5\\ y_{{\textrm{L2}}}&= y_{H}+e^{x_{3}/2}-x_{1}/10\\ x_{1},x_{2},&x_{3},x_{4} \in [0.5,1] \end{aligned} \end{aligned}$$

(36)

Example 7

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= \left[ 100(x_{2} - x_{1}^{2})^{2} + (x_{1} -1 )^{2} +100(x_{3}-x_{2}^{2})^{2} \right. \\&\qquad \left. +(x_{2}-1)^{2} + 100(x_{4}-x_{3}^{2})^{2} +(x_{3}-1)^{2} \right. \\ {}&\qquad \left. +100(x_{5}-x_{4}^{2})^{2} +(x_{4}-1)^{2} + 100(x_{6}-x_{5}^{2})^{2} \right. \\ {}&\qquad \left. +(x_{5}-1)^{2}\right] /100000\\ y_{{\textrm{L}}1}&= \left[ 100(x_{2} - x_{1}^{2})^{2} + 4(x_{1} -1 )^{2} +100(x_{3}-x_{2}^{2})^{2} \right. \\&\qquad \left. +4(x_{2}-1)^{2} + 100(x_{4}-x_{3}^{2})^{2} +4(x_{3}-1)^{2} \right. \\ {}&\qquad \left. +100(x_{5}-x_{4}^{2})^{2} +4(x_{4}-1)^{2} + 100(x_{6}-x_{5}^{2})^{2} \right. \\ {}&\qquad \left. +4(x_{5}-1)^{2}\right] /100000\\ y_{{\textrm{L}}2}&= \left[ 80(x_{2} - x_{1}^{2})^{2} + (x_{1} -1 )^{2} +80(x_{3}-x_{2}^{2})^{2} \right. \\&\qquad \left. +(x_{2}-1)^{2} + 80(x_{4}-x_{3}^{2})^{2} +(x_{3}-1)^{2} \right. \\ {}&\qquad \left. +80(x_{5}-x_{4}^{2})^{2} +(x_{4}-1)^{2}+ 80(x_{6}-x_{5}^{2})^{2} \right. \\ {}&\qquad \left. +(x_{5}-1)^{2}\right] /100000\\ y_{{\textrm{L}}3}&= \left[ 100(x_{2} - x_{1}^{2})^{2} +100(x_{3}-x_{2}^{2})^{2} + 100(x_{4}-x_{3}^{2})^{2} \right. \\&\qquad \left. +100(x_{5}-x_{4}^{2})^{2}+ 100(x_{6}-x_{5}^{2})^{2} \right] /100000\\ x_{i}&\in [-5,10], i=1,\ldots ,6 \end{aligned} \end{aligned}$$

(37)

Example 8

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= \frac{2\pi x_{3}(x_{4}-x{6})}{\ln {(x_{2}/x{1})\left[ 1+2x_{7}x_{4}/ \left( \ln {(x_{2}/x_{1})}x_{1}^{2} x_{8}\right) + x_{3}/x_{5}\right] }}\\ y_{{\textrm{L}}1}&= 0.4y_{{\textrm{H}}}+ x_{1}^{2} x_{8} + x_{1}x_{7}/x_{3} + x_{1}x_{6}/x_{2} + x_{1}^{2}x_{4}\\ y_{{\textrm{L}}2}&= 0.6y_{{\textrm{H}}} + 10 x_{1}x_{5}/x_{2} + x_{1}x_{8}/x_{4} + x_{1}^{3}x_{7}\\ x_{1}&\in [0.05,0.15];x_{2} \in [100,50000];x_{3} \in [63070,115600];\\ x_{4}&\in [990,1110];x_{5} \in [63.1,116];x_{6} \in [700,820];\\ x_{7}&\in [1120,1680];x_{8} \in [9855,12045]; \end{aligned} \end{aligned}$$

(38)

Example 9

$$\begin{aligned} \begin{aligned} y_{{\textrm{H}}}&= \sum \limits _{i=1}^{10}{x_{i}^{3}} +\left( \sum \limits _{i=1}^{10}{0.5 i x_{i}} \right) ^{2} + \left( \sum \limits _{i=1}^{10}{0.5 i x_{i}} \right) ^{4}\\ y_{{\textrm{L}}1}&= \sum \limits _{i=1}^{10}{x_{i}^{3}} +\left( \sum \limits _{i=1}^{10}{2 i x_{i}} \right) ^{2} + \left( \sum \limits _{i=1}^{10}{3 i x_{i}} \right) ^{4}\\ y_{{\textrm{L}}2}&= \sum \limits _{i=1}^{10}{x_{i}^{3}} +\left( \sum \limits _{i=1}^{10}{3 i x_{i}} \right) ^{2} + \left( \sum \limits _{i=1}^{10}{4 i x_{i}} \right) ^{4}\\ y_{{\textrm{L}}3}&= \sum \limits _{i=1}^{10}{x_{i}^{3}} +\left( \sum \limits _{i=1}^{10}{i x_{i}} \right) ^{2} + \left( \sum \limits _{i=1}^{10}{2 i x_{i}} \right) ^{4}\\ x_{i}&\in [-5,10], i=1,\ldots ,10 \end{aligned} \end{aligned}$$

(39)

Appendix 2: The sample size in Sect. 4.2.1

The fixed sample size and rate used in Sect. 4.2.1 are listed in Table 8, which are determined according to the mode of the optimal combinations of all methods.

Table 8 The fixed sample size and ratio used in Sect. 4.2.1