Compact Stars of Emending Class One in f(T) Gravity

Abstract

In this paper, we study the spherically symmetric anisotropic compact stars of emending class one in f(T) (where T being the torsion of the spacetime) gravity. For this purpose, we have used a particular form of the metric functions to solve the modified equation of motion in f(T) gravity for static anisotropic fluid source. The constructed models represent the class of anisotropic stars like $SAX J 1808.4-3658 (SS1)$, $Her X - 1, Vela X-12, PSR J1614-2230$ and $Cen X -3$. We have calculated the physical parameters of the stars such as pressure, density, regularity and anisotropy. We have also discussed the stability of formulated models and proved that in f(T) theory of gravity (with diagonal tetrad) these models of the stars are unstable.

1 Introduction

The current cosmological observations (Riess et al. 1998; Perlmutter et al. 1999; Bennett et al. 2003) demonstrate that our universe encounters the phase of accelerated expansion. In spite of the fact that the very easy approach to clarify this fact is the inclusion of a cosmological constant (Peebles and Ratra 2003), but the challenges like fine-tuning issue connected with cosmological constant have drawn the attention of some authors to consider more realistic choices to handle the issue of expansion of the universe. Among all the possible choices, one is to discuss the dark energy paradigm, which can be originated from various fields, such as a scalar field (Ratra and Peebles 1988; Wetterich 1988) and a phantom field. A second heading is to modify the theory of gravity, such as f(R) (R is Ricci scalar) (Sotiriou and Faraoni 2010; De Felice and Tsujikawa 2010), higher derivatives in the activity (Nojiri and Odintsov 2005), brane world augmentations (Cai et al. 2006), string theory (Tsujikawa 2010), holographic properties (Hsu 2004; Li 2004; Huang and Li 2004; Ito 2005), UV modifications (Horava 2009; Calcagni 2009; Kiritsis and Kofinas 2009; Lu et al. 2009; Saridakis 2010) and so forth. As of late, another technique showen up in the literature (Ferraro and Fiorini 2007; Bengochea and Ferraro 2009; Linder 2010) is f(T) gravity. It depends on the old thought of the teleparallelequivalent of General Relativity (TEGR) (Hayashi and Shirafuji 1979, 1982; Myrzakulov 2011), which instead of utilizing the curvature can be defined via the Levi-Civita connection, with Weitzenböck connection that is free of curvature, and just depends on torsion (Caldwell 2002; Feng et al. 2005; Einstein 1928). As depicted in (Myrzakulov 2011) the Lagrangian density can then be developed from this torsion tensor under the presumptions of invariance under general coordinate transformations, global Lorentz transformations and the parity operation, along with requiring the Lagrangian density to be second order in the torsion tensor.

As compared to f(R) gravity with fourth-order nonlinear differential equations, f(T) theory of gravity has second-order field equations. This fact has enhanced the interest among the researchers to study the accelerated expansion of the universe (Bengochea and Ferraro 2009; Linder 2010) and one can reproduce a cosmological phenomena (Dent et al. 2011; Yerzhanov et al. unpublished) that include a scalar field (Wu and Yu 2010a) and constrain the model parameters (Wu and Yu 2010b) to investigate the dynamical behavior of the universe (Myrzakulov 2011). A lot of work (Jamil et al. 2012a, b, c, d, 2013a; Bamba et al. 2013; Jamil et al. 2013b; Yesmkhanova et al. 2012; Houndjo et al. 2012, 2015 Chattopadhyay et al. 2014; Rudra et al. 2012; Momeni et al. 2015; Aslam et al. 2013; Rodrigues et al. 2013; Momeni and Myrzakulov 2014) related to cosmological attractor solutions, cosmological models, reconstruction and entropy corrections in f(T) gravity has been done.

Currently, the study of compact stars and massive objects has become the subject of keen interest in general relativity as well as in modified theories of gravity (Abbas et al. 2014, 2015b, c, d, e; Zubair et al. 2016a, b; Zubair and Abbas 2016a, b; Yousaf et al. 2016a, b; Yousaf and Bhatti 2016). The astrophysical compact objects having small radii and large densities may produce very strong gravitational effects in their surrounding. In this present article, we have formulated the equations of motion for static anisotropic emending class one compact object in f(T) theory. We have investigated the physical behavior of the compact objects in the framework of f(T) gravity.

We have arranged the paper as follows: Sect. 2 investigates the matter components and equation of state parameters. The regularity conditions, anisotropic parameter and stability of the compact stars are presented in Sect. 3. Finally, we discuss the results of the paper in the last section.

2 Equations of Motion in Generalized Telleparallel Gravity

We begin with static spherically symmetric spacetime which is given by

$$\begin{aligned} ds^{2}=e^{a(r)}dt^{2}-e^{b(r)}dr^{2}-r^{2}(d\theta ^{2}+sin^{2}(\theta )d\phi ^{2}). \end{aligned}$$

(1)

We take the matter as anisotropic fluid for which energy-momentum tensor is

$$\begin{aligned} \mathcal {T}_{\mu }^{\nu }=(\rho +p_{t})u_{\mu }u^{\nu }-p_{t}\delta _{\mu }^{ \nu }+(p_{r}-p_{t})v_{\mu }v^{\nu }, \end{aligned}$$

(2)

where $u^{\mu }$ and $v^{\mu }$ are the four-velocity and radial-four vectors, respectively. Further, $p_r$ and $p_t$ are pressures along radial and transverse directions.

The tetrad matrix for metric (1) is

$$\begin{aligned}[e_{\mu }^{i}]=diag[e^{\frac{a(r)}{2}},e^{\frac{b(r)}{2} },r,rsin(\theta )]. \end{aligned}$$

(3)

Also, $e=det[e_{\mu }^{i}]=e^{\frac{(a+b)}{2}}r^{2}sin(\theta )$, and using the results of (Abbas et al. 2015a), we get

$$\begin{aligned} T(r)& = \frac{2e^{-b}}{r}(a^{^{\prime }}+\frac{1}{r}), \end{aligned}$$

(4)

$$\begin{aligned} T^{^{\prime }}(r)& = \frac{2e^{-b}}{r}(a^{^{\prime \prime }}+\frac{1}{r^{2}} -T(b^{^{\prime }}+\frac{1}{r})), \end{aligned}$$

(5)

where the prime means differentiations with respect to r. The modified field equations (Abbas et al. 2015a) for fluid source are

$$\begin{aligned} 4\pi \rho& = \frac{f}{4}-\frac{f_{T}}{2}\left( T-\frac{1}{r^{2}}-\frac{e^{-b} }{r}(a^{^{\prime }}+b^{^{\prime }})\right) , \end{aligned}$$

(6)

$$\begin{aligned} 4\pi p_{r}& = \frac{f_{T}}{2}\left( T-\frac{1}{r^{2}}\right) -\frac{f}{4}, \end{aligned}$$

(7)

$$\begin{aligned} 4\pi p_{t}& = \left[ \frac{T}{2}+e^{-b}\left( \frac{a^{^{\prime \prime }}}{2} +\left(\frac{a^{^{\prime }}}{4}+\frac{1}{2r}\right)\left(a^{^{\prime }}-b^{^{\prime }}\right)\right) \right] \frac{f_{T}}{2}-\frac{f}{4}, \end{aligned}$$

(8)

$$\begin{aligned} \frac{cot\theta }{2r^{2}}T^{^{\prime }}f_{TT}& = 0. \end{aligned}$$

(9)

Also, Eq. (9) yields

$$\begin{aligned} f(T)=\beta T+{\beta }_{1}, \end{aligned}$$

(10)

where $\beta$ and ${\beta }_{1}$ are integration constants; the solutions are new if $\beta \ne 1$ and ${\beta }_{1}\ne 0$; otherwise, solutions corresponds to GR. We take the following form of metric function Karmarkar (1948); Tolman (1939):

$$\begin{aligned} e^{a(r)}=B\left( 1+Cr^{2}\right) ^{4},\quad \quad e^{b(r)}=1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}, \end{aligned}$$

(11)

where B, C and F are arbitrary constants that can be determined on some physical background. Now using Eq. (11), field equations leads to

$$\begin{aligned} \rho& = \frac{-\left[ 8Cr^{2}+\left( 1+Cr^{2}\right) \right] \beta }{8\pi r^{2} \left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] \left( 1+Cr^{2}\right) }\nonumber \\&+\frac{8Cr\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2} \right] }{8\pi r\left( 1+Cr^{2}\right) \left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{2}}\nonumber \\&+\frac{128B^{2}C^{2}Fr\left( 1+Cr^{2}\right) ^{3}+256B^{2}C^{3}Fr^{3}\left( 1+Cr^{2}\right) ^{2}\beta }{8\pi r\left( 1+Cr^{2}\right) \left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{2}}+\frac{\beta }{8\pi r^{2}}-\frac{\beta _{1}}{16\pi }, \end{aligned}$$

(12)

$$\begin{aligned} p_{r}=\frac{\left[ 8Cr^{2}+\left( 1+Cr^{2}\right) \right] \beta }{8\pi r^{2} \left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] \left( 1+Cr^{2}\right) }-\frac{\beta }{8\pi r^{2}}-\frac{\beta _{1}}{16}, \end{aligned}$$

(13)

$$\begin{aligned} p_{t}& = \frac{\left[ 8C\left( 1+Cr^{2}\right) -16C^{2}r^{2}\right] \beta }{ 8\pi \left( 1+Cr^{2}\right) ^{2}\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] } \\&+\frac{\left[ 8Cr\left\{ \left( 8Cr^{2}\left( 1+Cr^{2}\right) \right) +2\left( 1+Cr^{2}\right) \right\} \left\{ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right\} \right] \beta }{32\pi r\left( 1+Cr^{2}\right) ^{2}\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{3}} \nonumber \\&-\frac{\left[ \left( 8Cr^{2}\left( 1+Cr^{2}\right) \right) +2\left( 1+Cr^{2}\right) \right] }{\left( 1+Cr^{2}\right) }\times \frac{\left[ 128B^{2}C^{2}Fr\left( 1+Cr^{2}\right) ^{3}\right] \beta }{32\pi r\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{3}} \nonumber \\&-\frac{\left[ \left( 8Cr^{2}\left( 1+Cr^{2}\right) \right) +2\left( 1+Cr^{2}\right) \right] }{\left( 1+Cr^{2}\right) }\times \frac{\left[ 256B^{2}C^{3}Fr^{3}\left( 1+Cr^{2}\right) ^{2}\right] \beta }{32\pi r\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{3}}-\frac{{\beta }_{1}}{ 16\pi }, \nonumber \end{aligned}$$

(14)

The equation of state (EOS) parameters are

$$\begin{aligned} {\omega }_{r}(r)& = \frac{\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] \beta \left[ 1-\beta +8BCF\left( 1+Cr^{2}\right) ^{2}\right] ^{-1}}{\left[ Cr^{2}(8-7\beta )+2B\left( 1+Cr^{2}\left( 1+\left( 2+32CF\left( 1+Cr^{2}\right) ^{3}\right) \beta \right) \right) \right] } \nonumber \\&-\frac{\left[ 1-\beta +8BCF\left( 1+Cr^{2}\right) ^{2}\right] ^{-1}\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] \left( 8BCF\left( 1+Cr^{2}\right) ^{3}\right) \beta }{\left[ Cr^{2}(8-7\beta )+2B\left( 1+Cr^{2}\left( 1+\left( 2+32CF\left( 1+Cr^{2}\right) ^{3}\right) \beta \right) \right) \right] }\end{aligned}$$

(15)

$$\begin{aligned} {\omega }_{t}(r)& = \frac{(-3+C(-r^{2}(3+4Cr^{2})\beta (2(1+Cr^{2})^{-1}\left[ 1+64BC^{2}Fr^{2}(1+Cr^{2})^{2}\right] ^{-1}}{\left[ 1-\beta +8BCF(1+Cr^{2})^{2}(Cr^{2}+2B(1+Cr^{2}(1+(2+32CF(1+Cr^{2})^{3})\beta )))\right] } \nonumber \\&+\frac{64BCF(r+Cr^{3})^{2}(5+Cr^{2}+4Cr^{4})\beta (2(1+Cr^{2})^{-1}\left[ 1+64BC^{2}Fr^{2}(1+Cr^{2})^{2}\right] ^{-1}}{\left[ 1-\beta +8BCF(1+Cr^{2})^{2}(Cr^{2}+2B(1+Cr^{2}(1+(2+32CF(1+Cr^{2})^{3})\beta )))\right] } \nonumber \\&+\frac{16B^{2}F(1+Cr^{2})^{3}(1+Cr^{2}(7+4Cr^{2}(3+128CF(-1+C^{2}r^{4})))) }{\left[ 1-\beta +8BCF(1+Cr^{2})^{2}(Cr^{2} +2B(1+Cr^{2}(1+(2+32CF(1+Cr^{2})^{3})\beta )))\right] } \end{aligned}$$

(16)

Fig. 1

Left, middle and right plots show density for SAX J 1808.4-3658(SS1), PSR J1614-2230 and Vela X-12, respectively

Fig. 2

Left, middle and right plots show the behavior of the radial pressure for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

Fig. 3

Left, middle and right plots show the behavior of the transverse pressure for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

Fig. 4

Left, middle and right plots show the behavior of EOS parameter ${ \omega }_{r}$ for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

Fig. 5

Left, middle and right plots show the behavior the EOS parameter ${ \omega }_{t}$ for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

3 Physical Analysis of Model

This section deals with the physical properties of the proposed model like regularity, anisotropic behavior and stability.

3.1 Anisotropic Behavior

Using Eqs. (12) and (13), we get

$$\begin{aligned} \frac{d\rho }{dr}& = \frac{2C^{2}r\left[ 1-\beta +16BCF(1+Cr^{2})^{2}(4+2B(-1+128C^{2}Fr^{2}(1+Cr^{2})(1+4Cr^{2}) \right] }{\pi (1+Cr^{2})^{2}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{3}} \nonumber \\&+\frac{Cr^{2}(20-21\beta )-5\beta -2B(1+2C(r^{2}+8F(1+Cr^{2})^{2}(-1+Cr^{2}(8+33Cr^{2}))))\beta }{\pi (1+Cr^{2})^{2}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{3}} \nonumber \\&+\frac{128CF(B+BCr^{2})^{2}(1+Cr^{2}(3+\beta +2C(r^{2}+2(r^{2}+4F(1+Cr^{2})^{4})\beta )))}{\pi (1+Cr^{2})^{2}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{3}} \end{aligned}$$

(17)

$$\begin{aligned} \frac{dp_{r}}{dr}=\frac{2C^{2}r\left[ -1+16BCF\left( 1+Cr^{2}\right) ^{2}\left( -5-17Cr^{2}+32BCF\left( 1+Cr^{2}\right) ^{4}\right) \right] \beta }{\pi \left( 1+Cr^{2}\right) ^{2}\left[ 1+64BC^{2}Fr^{2}\left( 1+Cr^{2}\right) ^{2}\right] ^{2}} \end{aligned}$$

(18)

The above results lead to following equations:

$$\begin{aligned} \frac{d^{2}\rho }{dr^{2}}& = \nonumber \\&\frac{2C^{2}(-1+\beta +C(-3r^{2}(-1+\beta )+32B^{2}F(1+Cr^{2})^{3}))}{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&+\frac{ -32B^{2}F(1+Cr^{2})^{3}(-Cr^{2}(3+128CF(1+Cr^{2})(2+Cr^{2}(5+39Cr^{2}))))}{ \pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&+\frac{-\beta +2C(-3r^{2}+8F(1+Cr^{2})(1+Cr^{2}(31+75Cr^{2}+333C^{2}r^{4})))\beta )}{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&-\frac{ \begin{array}{c} 2048B^{3}CF^{2}(1+Cr^{2})^{4}(-(1+Cr^{2})(-1+3Cr^{2}(-6+Cr^{2}(-11+ \\ 128CF(1+Cr^{2})(1+Cr^{2}(5+12Cr^{2})))))) \end{array} }{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&+\frac{ 2Cr^{2}(4+C(25r^{2}+33Cr^{4}+16F(1+Cr^{2})^{2}(-1+Cr^{2}(16+Cr^{2}(77+156Cr^{2})))))\beta ) }{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&+\frac{ \begin{array}{c} 131072B^{4}C^{3}F^{3}r^{2}(1+Cr^{2})^{6}(5+Cr^{2}(22+Cr^{2}(35+18Cr^{2})+3 \beta + \\ 3C(16F(1+Cr^{2})^{5}+r^{2}(5+12Cr^{2}))\beta )) \end{array} }{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \nonumber \\&-\frac{16BF(1+Cr^{2})^{2}(4-5\beta +Cr^{2}(44-48\beta +3Cr^{2}(-8+7\beta )))}{\pi (1+Cr^{2})^{3}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{4}} \end{aligned}$$

(19)

$$\begin{aligned} \frac{d^{2}p_{r}}{dr^{2}}& = -\frac{\left[ 2C^{2}(1+C(-3r^{2}+16BF(1+Cr^{2})^{2}(5+Cr^{2}(44-9Cr^{2})\right] \beta }{ \pi (1+Cr^{2})^{3}\left[ 1+64BC^{2}Fr^{2}(1+Cr^{2})^{2}\right] ^{3}} \nonumber \\&-\frac{6144B^{2}C^{3}F^{2}r^{2}(1+Cr^{2})^{7}\beta }{\pi (1+Cr^{2})^{3}\left[ 1+64BC^{2}Fr^{2}(1+Cr^{2})^{2}\right] ^{3}} \nonumber \\&+\frac{ 32BCF(1+Cr^{2})^{2}(1+Cr^{2}(41+Cr^{2}(163+315Cr^{2})))\beta }{\pi (1+Cr^{2})^{3}\left[ 1+64BC^{2}Fr^{2}(1+Cr^{2})^{2}\right] ^{3}} \end{aligned}$$

(20)

Fig. 6

Here only data of Her X-1 have been used

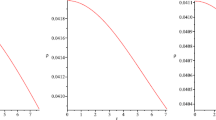
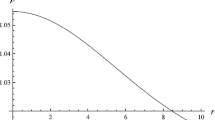
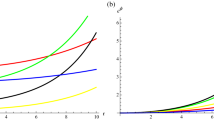
From Fig. 6, it is clear that at $r=0$, $\frac{d\rho }{dr}=0,~~ \frac{dp_{r}}{dr}=0$ and $\frac{d^{2}\rho }{dr^{2}}<0,~~\frac{d^{2}p_{r}}{ dr^{2}}<0$, while at this point $\rho$ and $p_{r}$ have maximum values (see Figs. 1, 2). The regularity and physical behavior of $p_t$ in Fig. 3). Also, from Figs. 4 and 5, it is clear that $0<\omega _{r}(r)<1$ and $0<\omega _{t}(r)$. It is concluded that stars are composed of ordinary matter and dark energy due to the effects of f(T) term. The anisotropy in this model, i.e., $\Delta =\frac{2}{r}(p_{t}-p_{r})$ is obtained as follows:

$$\begin{aligned} \Delta& = -\frac{\left( 1+9Cr^{2}\right) }{4\pi r^{3}(1+Cr^{2})(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})}+\frac{1}{4\pi r^{3}} \nonumber \\&-\frac{ 4C(-3+C(-r^{2}(3+4Cr^{2})-64BCF(r+Cr^{3})^{2}(5+Cr^{2}+4C^{2}r^{4})))\beta }{ 4\pi r(1+Cr^{2})^{2}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{3}} \nonumber \\&+\frac{16B^{2}F(1+Cr^{2})^{3}(1+Cr^{2}(7+4Cr^{2}(3+128CF(-1+C^{2}r^{4})))) \beta }{4\pi r(1+Cr^{2})^{2}(1+64BC^{2}Fr^{2}(1+Cr^{2})^{2})^{3}} \end{aligned}$$

(21)

It is clear from the Fig. 7 that for our model $\Delta >0$ a repulsive force is present which allows the formation of super massive star.

Fig. 7

Left, middle and right plots show the behavior of anisotropy $\Delta$ for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

3.2 Matching Conditions

Here, we discuss the matching of spacetime (1) to the vacuum exterior metric given by

$$\begin{aligned} ds^{2}=-\left( 1-\frac{2m}{r}\right) dt^{2}+\left( 1-\frac{2m}{r}\right) ^{-1}dr^{2}+r^{2}(d\theta ^{2}+sin^{2}(\theta )d\phi ^{2}). \end{aligned}$$

(22)

The matching conditions at $r=R$ yield the following results (Bhar et al. 2016):

$$\begin{aligned} 1-\frac{2m}{R}& = B\left( 1+CR^{2}\right) ^{4}, \end{aligned}$$

(23)

$$\begin{aligned} 1+64BC^{2}FR^{2}\left( 1+CR^{2}\right) ^{2}& = \left( 1-\frac{2m}{ R}\right) ^{-1}, \end{aligned}$$

(24)

$$\begin{aligned} 8BC\left( 1+CR^{2}\right) ^{3}& = \frac{2m}{R^{3}}. \end{aligned}$$

(25)

The above equations can be simplified to the following form

$$\begin{aligned} B=\frac{\left( 1-\frac{9m}{4R}\right) ^{4}}{\left( 1-\frac{2m}{R} \right) ^{3}} \end{aligned}$$

(26)

$$\begin{aligned} C=\frac{1}{4}\frac{m}{R^{3}}\left( 1-\frac{9m}{4R}\right) ^{-1} \end{aligned}$$

(27)

$$\begin{aligned} F=\frac{1}{2}\left( \frac{m}{R^{3}}\right) ^{-1}. \end{aligned}$$

(28)

For the values of M and R for a given star, the constants B, C and F can be specified as in Table 1.

Table 1 Values of constants for given Masses and Radii of Stars (Bhar et al. 2016)

3.3 Stability

In our anisotropic model, we define sound speeds as

$$\begin{aligned} \upsilon _{sr}^{2}= \frac{dp_{r}}{d\rho }\equiv&-\left[ \Big ( 1+64BC^{2}Fr^{2}( 1+Cr^{2}) ^{2}\Big )\Big ( -1+16BCF( 1+Cr^{2}) ^{2} \right. \nonumber \\&\left. \Big ( -5-17Cr^{2}+32BCF( 1+Cr^{2}) ^{4}\Big ) \Big ) \beta \right] \times \Big [ 1-\beta +16BCF \nonumber \\&( 1+Cr^{2}) ^{2}\Big \{ 4+2B( 1+Cr^{2}) \Big ( -1+128C^{2}Fr^{2}( 1+Cr^{2}) \nonumber \\&( 1+4Cr^{2}) \Big ) +Cr^{2}(20-21\beta )-5\beta -2B\Big ( 1+2C\Big ( r^{2}+8F \nonumber \\&( 1+Cr^{2}) ^{2}\Big ( -1+Cr^{2}( 8+33Cr^{2}) \Big ) \Big ) \Big ) \beta +128CF( B+BCr^{2}) ^{2} \nonumber \\&\Big ( 1+Cr^{2}\Big ( 3+\beta +2C\Big ( r^{2}+2( r^{2}+4F( 1+Cr^{2}) ^{4}) \beta \Big ) \Big ) \Big ) \Big \} \Big ]^{-1} , \end{aligned}$$

(29)

$$\begin{aligned} \upsilon _{st}^{2} =\frac{dp_{t}}{d\rho }\equiv&\frac{1}{\text {28}\pi ( 1+Cr^{2}) ^{3}\Big ( 1+64BC^{2}Fr^{2}( 1+Cr^{2}) ^{2}\Big ) ^{4}} \nonumber \\&\times C^{2}r\Big [ -3 +C\Big \{ 5r^{2}+32BF( 1+Cr^{2}) ^{2}\Big ( -8-8Cr^{2}\Big ( 8 +Cr^{2}( 5 \nonumber \\&+6Cr^{2}) \Big ) -B( 1+Cr^{2}) \Big ( 4+Cr^{2}\Big ( 19+768CF+18C \nonumber \\&(1+320CF)r^{2}+7168C^{3}Fr^{4}+5248C^{4}Fr^{6}+3072C^{5} \nonumber \\&Fr^{8}\Big ) \Big ) +32B^{2}CF\Big ( 1+Cr^{2}) ^{3}\Big ( 3+Cr^{2}\Big ( 22+Cr^{2}\Big ( 61+8C \nonumber \\&( 9r^{2}+64F( 1+Cr^{2}) \Big ( -1+Cr^{2}( -5+4Cr^{2})\Big ) \Big ) \Big ) \Big ) \Big ) \Big ) \Big \}\Big ] \beta . \end{aligned}$$

(30)

The above equations lead to

$$\begin{aligned} \upsilon _{st}^{2}-\upsilon _{sr}^{2}& = \frac{1}{\text {28}\pi ( 1+Cr^{2}) ^{3}\Big ( 1+64BC^{2}Fr^{2}( 1+Cr^{2}) ^{2}\Big ) ^{4}} \nonumber \\&\times C^{2}r\Big [ -3 +C\Big \{ 5r^{2}+32BF( 1+Cr^{2}) ^{2}\Big ( -8-8Cr^{2}\Big ( 8 +Cr^{2}( 5 \nonumber \\&+6Cr^{2}) \Big ) -B( 1+Cr^{2}) \Big ( 4+Cr^{2}\Big ( 19+768CF+18C \nonumber \\&(1+320CF)r^{2}+7168C^{3}Fr^{4}+5248C^{4}Fr^{6}+3072C^{5} \nonumber \\&Fr^{8}\Big ) \Big ) +32B^{2}CF\Big ( 1+Cr^{2}) ^{3}\Big ( 3+Cr^{2}\Big ( 22+Cr^{2}\Big ( 61+8C \nonumber \\&( 9r^{2}+64F( 1+Cr^{2}) \Big ( -1+Cr^{2}( -5+4Cr^{2})\Big ) \Big ) \Big ) \Big ) \Big ) \Big ) \Big \}\Big ] \beta +\nonumber \\&\left[ \Big ( 1+64BC^{2}Fr^{2}( 1+Cr^{2}) ^{2}\Big )\Big ( -1+16BCF( 1+Cr^{2}) ^{2} \right. \nonumber \\&\left. \Big ( -5-17Cr^{2}+32BCF( 1+Cr^{2}) ^{4}\Big ) \Big ) \beta \right] \times \Big [ 1-\beta +16BCF \nonumber \\&( 1+Cr^{2}) ^{2}\Big \{ 4+2B( 1+Cr^{2}) \Big ( -1+128C^{2}Fr^{2}( 1+Cr^{2}) \nonumber \\&( 1+4Cr^{2}) \Big ) +Cr^{2}(20-21\beta )-5\beta -2B\Big ( 1+2C\Big ( r^{2}+8F \nonumber \\&( 1+Cr^{2}) ^{2}\Big ( -1+Cr^{2}( 8+33Cr^{2}) \Big ) \Big ) \Big ) \beta +128CF( B+BCr^{2}) ^{2} \nonumber \\&\Big ( 1+Cr^{2}\Big ( 3+\beta +2C\Big ( r^{2}+2( r^{2}+4F( 1+Cr^{2}) ^{4}) \beta \Big ) \Big ) \Big ) \Big \} \Big ]^{-1} \end{aligned}$$

(31)

By using the cracking concept (introduced by Herrera (1992)) we found that the region where ${\upsilon _{sr}}>\upsilon _{st}\upsilon_{sr}>\upsilon _{st}$ is potentially stable; otherwise, unstable. In present case, Fig. 8 indicates that there is no change of sign for the term $\upsilon _{st}^{2}-\upsilon _{sr}^{2}$ within the interior of star, so proposed models are unstable.

Fig. 8

Left, middle and right plots show the behavior of $\upsilon _{st}^{2}-\upsilon _{sr}^{2}$ for SAX J 1808.4-3658, PSR J1614-2230 and Vela X-12, respectively

4 Summary

This paper deals with the modeling of spherical compact stars of emending class one in f(T) gravity with diagonal tetrad field. In this case, the assumption of diagonal tetrad field leads to linear form of function f(T) in T from the equations of motion. In order to solve the field equations analytically, we have assumed the particular form of the metric components, which is compatible with the stars of embedding class one. This form of the metric functions involves some unknown constants which can be determined by matching the interior fluid source with the vacuum exterior solution. This matching is smooth as in both geometries metric tensor components are continuous. Further, both the theories, standard GR and modified f(T) theory, have equations of motion upto second order so both are compatible for smooth matching of interior and exterior solutions. We apply the observed masses and radii of some compact stars in order to determine the constant in the metric potential functions.

Further, we have investigated the explicit expression for matter density and pressure components as given in Eqs. (12)–(13). It is clear from the expression of metric functions that these are regular at $r=0$; further density as well as pressures is non-singular at $r=0$ shown in Figs. 1, 2, 3. The EOS ${\omega }_r$ and ${\omega }_t$ are less than one and greater than one (see Figs. 4, 5), which indicates that matter has been modified from ordinary to exotic form. Figure 6 implies the maximality of radial pressure at center $r=0$. The anisotropic parameter $\Delta$ is positive (as shown in Fig. 7) at all points inside the star that explains the repulsive behavior of force and plays a key role to produce more mass of the stars. We have presented the stability of the compact as given in Fig. 8; this figure shows that our proposed strange star models are unstable. This work can be extended by using the non-trivial tetrad and electromagnetic field explicitly.