1 Introduction

Accelerated expansion of the current universe is well established through observational studies (Perlmutter et al. 1999; Bennett et al. 2003; Spergel et al. 2003; Tegmark et al. 2004; Abazajian et al. 2004, 2005; Allen et al. 2004). It is believed that this expansion is due to missing energy component, also dubbed as Dark Energy (DE) characterized by negative pressure. Reviews on DE include Padmanabhan (2005), Li et al. (2011) and Bamba et al. (2012), Nojiri and Odintsov (2007a, 2007b). The ΛCDM model, the simplest DE candidate, is consistent very well with all observational data. However, it has the following two weak points: The Λ has fine tuning amount and good marginal adoption with cosmological observations in large scales. This motivates the researchers in proposing the wide range of more complex generalized cosmological models of DE which have been discussed in Bamba et al. (2012), Bamba (2012).

In recent years, the holographic dark energy (HDE) (Li 2004; Li et al. 2011), is based on holographic Universe idea and it is one of the interesting and powerful candidates for the DE. and its density is given by (Li 2004)

$$\begin{aligned} \rho_{\varLambda}=3c^2m_p^2L^{-2} \end{aligned}$$
(1)

where L is the IR cutoff, m p =(8πG)−1/2 is the reduced Planck mass. IR cut-offs L parameter is considered in various ways in numerous articles: the Hubble horizon H −1, particle horizon, the future event horizon, the Ricci scalar curvature radius. Also it was proposed a generalization of holographic models in which the cut-off parameter has a more general form (Nojiri and Odintsov 2006). The last generalized holographic dark energy scenario has been investigated from different point of the views,specially the stability under small perturbations. In all of these models, the cut-off length scale is proportional to the causal length that considered to the perturbations of the flat spacetime. Further more, it is suggested that phenomenon of matter collapse can be avoided through the existence of appropriate repulsive force. In the present set up of cosmological scenario, this can be only prevented through phantom-like DE which contains enough repulsive force. Different attempts have been made in this way, e.g., reduction of BH mass though phantom accretion phenomenon (Babichev et al. 2004, 2008; Martin-Moruno 2008; Jamil et al. 2008, 2011; Jamil 2009; Jamil and Qadir 2011; Sharif and Abbas 2011; Bhadra and Debnath 2012; Sharif and Jawad 2013c) and the avoidance of event horizon in the presence of phantom-like DE (Sharif and Jawad 2014).

Moreover, it is predicted that phantom DE with strong negative pressure can push the universe towards the big rip singularity where all the physical objects lose the gravitational bounds and finally dispersed. This prediction supports the phenomenon of the avoidance of BH formation and motivated Wei (2012) in constructing PDE model. He pointed out different possible theoretical and observational ways to make the BH free phantom universe with Hubble horizon through PDE parameter. Further, Sharif and Jawad (2013a, 2013b, 2014) have analyzed this proposal in detail by choosing different IR cutoffs through well-known cosmological parameters in flat and non-flat universes. This model has also been in different modified gravities (Sharif and Zubair 2014). Another direction that one can follow to explain the acceleration is to modify the gravitational sector itself, acquiring a modified cosmological dynamics. However, note that apart from the interpretation, one can transform from one approach to the other, since the crucial issue is just the number of degrees of freedom beyond General Relativity and standard model particles (Kofinas et al. 2014; Sahni and Starobinsky 2006). Detailed review in this modified gravity approach is available in references like Nojiri and Odintsov (2007a, 2007b), Tsujikawa (2010), Cai et al. (2010) and Clifton et al. (2012). In the majority of modified gravitational theories, one suitably extends the curvature based Einstein-Hilbert action of General Relativity. However, an interesting class of gravitational modification arises when one modifies the action of the equivalent formulation of General Relativity based on torsion (Kofinas and Saridakis 2014). Inspired by the f(R) modifications of the Einstein-Hilbert Lagrangian, f(T) modified gravity has been proposed by extending T to an arbitrary function (Ferraro and Fiorini 2007). Different aspects of the f(T) has been investigated in the literature (Aslam et al. 2013; Bamba 2012; Bamba and Odintsov 2014; Bamba et al. 2012, 2013a, 2013b, 2013c, 2014a, 2014b, 2014c; Farooq et al. 2013; Houndjo et al. 2012, 2013; Jamil et al. 2012a, 2012b, 2012c, 2012d, 2012e, 2012f, 2012g, 2012h, 2012i, 2013a, 2013b; Cai et al. 2011; Momeni and Setare 2011; Momeni et al. 2012; Rodrigues et al. 2013a, 2013b; Setare and Momeni 2011). The simplest modified gravity is obtained by replacing R→f(R), is so called f(R) gravity. This kind of the modified gravities have several interesting extensions (for a recent review see Nojiri and Odintsov 2014). The next modification is inspired from the string theory. It comes from the Gauss- Bonnet term G and widely investigated in the literature (Capozziello et al. 2009, 2013; Nojiri and Odintsov 2003, 2005a, 2005b, 2006, 2007a, 2007c, 2008, 2011; Nojiri et al. 2002, 2005, 2006a, 2006b, 2007, 2009, 2010; Bamba et al. 2008, 2010a, 2010b; Cognola et al. 2006, 2007, 2008, 2009; Lidsey 2002a, 2002b; Cvetic et al. 2002).

The main motivation to consider GB models is they are motivated from the string theory. In low limit of string theory these higher order curvature corrections appeared. Motivated by f(R) gravity, we can introduce the f(G) gravity, proposed by Nojiri and Odintsov (2005a). This modification of the Einstein gravity unified dark matter and dark energy (Cognola et al. 2006) in a same scenario and in a consistent way and also in relation to the gauge/gravity proposal (Lidsey 2002a, 2002b). To include the higher GB terms in f(T) gravity and motivated from the f(R,G) model, recently f(T,T G ) has been constructed on the basis of T (old quadratic torsion scalar) and T G (new quartic torsion scalar T G that is the teleparallel equivalent of the Gauss-Bonnet term) (Kofinas and Saridakis 2014). This theory also belongs to a novel class of gravitational modification. Cosmological applications for this gravity have also been presented in detailed. To realize the role of DE in modified gravity, a very useful technique proposed by Nojiri and Odintsov (2005a, 2006) and it extended for several cosmological scenarios. Consider the first Friedmann equation of a type of modified gravity in the following form:

$$\begin{aligned} \kappa^2\rho_{DE}=\sum_{\sum n_{i}=n} A(R,G,\ldots) \frac{\partial^n f(R,G,\ldots)}{\partial R^{n_1} \partial G^{n_2}\cdots} \end{aligned}$$
(2)

In the above equation, f(R,G,…) stands for the modified gravity action. For a model of DE, for example the holographic DE, in general \(\rho_{DE}=\rho_{DE}(H,\dot{H},\ldots)\). Also, implicitly we able to write it as ρ DE =ρ DE (R,G,…). So, if we can solve the following partial differential equations for f(R,G,…), indeed we reconstructed the modified gravity for this type of DE. Also, the reconstruction scheme works if we assume that in any cosmological epoch, a(t) is given. Our aim in this work is to reconstruct f(T,T G ) for PDE in flat FRW Universe.

Here, we also check cosmological aspects of this theory in flat FRW universe. It is interesting to mention that we provide the correspondence scenario of newly proposed gravity theory as well as dynamical DE model (PDE).

The plan of the paper is given as follows: Next section contains the reconstruction scheme. We provide the construction of reconstructed \(f(T, T_{G})=\tilde{f}\) models and corresponding EoS parameter with respect to PDE parameter (s). In Sect. 2, we have reported a reconstruction approach through power-law form of scale factor. In Sect. 3, we present reconstruction scheme with a choice of Hubble rate H leading to unification of matter and dark energy dominated universe. In Sect. 4, we choose the scale factor in the “intermediate” form and reconstruct f and subsequently w DE . A bouncing scale factor in power law form is considered in Sect. 5 and a reconstruction scheme is reported. An analytic form of f is assumed in Sect. 6 and Hubble parameter is reconstructed without any choice of scale factor. The paper is concluded in Sect. 7.

2 Reconstruction scheme for f(T,T G ) through power-law scale factor

A new and valid generalization of f(T) in the modified gravity models as f(T,T G ) based on T and equivalent to Gauss-Bonnet term T G in the teleparallel, is quite different from their counterparts f(T) and f(R,G) in Einstein gravity (Kofinas et al. 2014). In f(T,T G ) gravity

$$\begin{aligned} S =\frac{1}{2}\int d^{4} x\,e\,F(T,T_G)+ \int d^{4} x\,e\,\mathcal{L}_m, \end{aligned}$$
(3)

where in “God-given natural units” c=1, κ 2≡8πG=1 and \(\mathcal{L}_{m}\) is Lagrangian of the matter fields. For a spatially flat cosmological FRW metric

$$ ds^{2}=- dt^{2}+a^{2}(t) (d\vec{x}\cdot d\vec{x} ), $$
(4)

we obtain:

$$\begin{aligned} &{T=6H^2} \end{aligned}$$
(5)
$$\begin{aligned} &{T_G=24H^2\bigl(\dot{H}+H^2\bigr)} \end{aligned}$$
(6)

where \(H=\dot{a}/a\) is the Hubble parameter and dots denote differentiation with respect to t. Friedmann equations in the usual form are

$$\begin{aligned} &{H^2=\frac{1}{3}(\rho_m+\rho_{DE})} \end{aligned}$$
(7)
$$\begin{aligned} &{\dot{H}=-\frac{1}{2}(\rho_m+\rho_{DE}+p_m+p_{DE})} \end{aligned}$$
(8)

Kofinas et al. (2014) modified Eqs. (7) and (8) by defining the energy density and pressure of the effective dark energy sector as

$$\begin{aligned} \rho_{DE} =&\frac{1}{2} \bigl(6H^2-f+12H^2f_T+T_G~f_{T_G}-24H^3 \dot {f}_{T_G} \bigr) \end{aligned}$$
(9)
$$\begin{aligned} p_{DE} =&\frac{1}{2} \biggl[-2 \bigl(2\dot{H}+3H^2 \bigr)+f-4\bigl(\dot{H}+3H^2\bigr)f_T \\ &{}-4H\dot {f}_T-Tf_{T_G}+\frac{2}{3H}T_G\dot{f}_{T_G}+8H^2 \ddot{f}_{T_G} \biggr] \end{aligned}$$
(10)

Standard matter and dark energy are conserved separately, i.e. the evolution equations are

$$\begin{aligned} &{\dot{\rho}_m+3H(\rho_m+p_m)=0} \end{aligned}$$
(11)
$$\begin{aligned} &{\dot{\rho}_{DE}+3H(\rho_{DE}+p_{DE})=0} \end{aligned}$$
(12)

The first property of PDE is

$$\begin{aligned} \rho_{\varLambda}\gtrsim m_p^2 L^{-2} \end{aligned}$$
(13)

To implement Eq. (13), Wei (2012) set PDE in the simplest way as

$$\begin{aligned} \rho_{\varLambda}=3n^2 m_p^{4-s}L^{-s} \end{aligned}$$
(14)

where n and s are both dimensionless constants. From Eqs. (13) and (14) we have \(L^{2-s}\gtrsim m_{p}^{s-2}=l_{p}^{2-s}\), where l p is the reduced Planck length. Since L>l p , one requires

$$\begin{aligned} s \leq2 \end{aligned}$$
(15)

Another requirement for PDE is that it is to be phantom-like (Wei 2012) i.e.

$$\begin{aligned} w_{\varLambda}<-1 \end{aligned}$$
(16)

It was stated in Wei (2012) that to obtain the EoS for PDE, we should choose a particular cut-off L and the simplest cut-off is the Hubble horizon L=H −1.

The PDE mentioned above would now be studied in f(T,T G ) gravity proposed recently by Kofinas et al. (2014). As we are going to consider PDE in f(T,T G ) gravity in Eq. (9) we use (L=1/H)

$$\begin{aligned} \rho_{DE}=\rho_{\varLambda}=3n^2 m_p^{4-s} \biggl(\frac{t}{m} \biggr)^{-s} \end{aligned}$$
(17)

Reconstruction scheme is a way to solve the following second order partial differential equation for f(T,T G ):

$$\begin{aligned} \begin{aligned}[b] \rho_{DE}(T,T_G) &=\frac{T}{2}- \frac{1}{2}f(T,T_G) +T{\frac{\partial}{\partial T}}f(T,T_G) \\ &\quad {}+\frac{1}{2}\,G{\frac{\partial}{\partial G}}f(T,T_G)\\ &\quad {}-\frac{1}{2}\,A ( T,T_G ) {\frac{\partial^{2}}{\partial{G}^{2}}}f ( T,T_G ) \\ &\quad {}-\frac{1}{2}B ( T,T_G ) { \frac{\partial ^{2}}{\partial T \partial T_G}}f ( T,T_G ) \end{aligned} \end{aligned}$$
(18)

There is no simple solution for this partial differential equation for a given set of functions {A,B}. But sometimes for a choice of scale factor a(t) we can solve it.

We consider the scale factor in the form

$$ a(t)=a_0 t^m $$
(19)

where m>0. Subsequently Hubble parameter H and its time derivative \(\dot{H}\) are

$$\begin{aligned} &{H=\frac{m}{t},\qquad \dot{H}=-\frac{m}{t^2}} \end{aligned}$$
(20)
$$\begin{aligned} &{ \begin{aligned}[c] T&=\frac{6 m^2}{t^2},\qquad T_G=\frac{24 (-1+m) m^3}{t^4}\\ \dot{T}&=-\frac{12 m^2}{t^3};\qquad \dot{T}_G=-\frac{96 (-1+m) m^3}{t^5} \end{aligned}} \end{aligned}$$
(21)

Considering Eqs. (9), (17) and (21) we get the following differential equation

$$\begin{aligned} &{\biggl(\frac{t^{2+s} }{4-4 m} \biggr)\frac{d^2f}{dt^2}+t^{1+s} \frac{5}{4} \biggl(\frac{m-2}{m-1} \biggr) \frac{df}{dt}+t^s f} \\ &{\quad {}-6 m^2 t^{-2+s}+6 m^s n^2=0} \end{aligned}$$
(22)

This differential equation has an exact solution given by the following expression:

$$\begin{aligned} f (t) =& {C_2} {t}^{\frac{5}{2}m-\frac{9}{2}+\frac{1}{2}\sqrt{65-74m+25{m}^{2}}} \\ &{} +{C_1 } {t}^{\frac{5}{2}m-\frac{9}{2}-\frac{1}{2}\sqrt{65-74m+25{m}^{2}}} \\ &{} + \frac{120 ( -\frac{8}{5}{m}^{1+s}+\frac{3}{5} {m}^{2+s}+{m}^{s} ) n^{2}{t}^{2-s}}{15{t}^{2} ( ( s-\frac{4}{5} ) m+\frac{1}{5}{s}^{2}+\frac{4}{5}-\frac {9}{5}s ) ( -\frac{5}{3}+m ) } \\ &{}- \frac{60( ( s-\frac{4}{5} ) m +\frac{1}{5}{s} ^{2}+\frac{4}{5}-\frac{9}{5}s ) ( m-1 ) m^{2}}{15{t}^{2} ( ( s-\frac{4}{5} ) m+\frac{1}{5}{s}^{2}+\frac{4}{5}-\frac {9}{5}s ) ( -\frac{5}{3}+m ) } \end{aligned}$$
(23)

It is possible to write f(T,T G ) in the following form:

$$\begin{aligned} &{f(T,T_G)} \\ &{\quad =\, C_2 \biggl( {\frac{2{T}^{3/2}\sqrt{6}}{3G-2{T}^{2}}} \biggr) ^{{\frac{-5{T}^{2}}{3T_G-2{T}^{2}}}-9/2+1/2\sqrt{65+{\frac{148{ T}^{2}}{3T_G-2{T}^{2}}}+{\frac{100{T}^{4}}{ ( 3T_G-2 {T}^{2 } ) ^{2}}}}}} \\ &{\qquad +\, C_1 \biggl( {\frac{2{T}^{3/2}\sqrt{6}}{3 T_G{-}2{T}^{2}}} \biggr) ^{{\frac{-5{T}^{2}}{3T_G-2{T}^{2}}}-9/2- 1/2\sqrt{65+{\frac{148{T}^{2}}{3T_G-2{T}^{2}}}+{\frac{100{T }^{4}}{ ( 3T_G-2{T}^{2}) ^{2}}}}}} \\ &{\qquad -\,32805 \bigl( T_G-2/3{T}^{2}\bigr)^{4} \bigl( T_G-2/3 {T}^{2} \bigr) ^{4}} \\ &{\qquad \times\,\biggl[ 3/5 \biggl( {\frac{-2{T}^{2}}{3T_G-2 {T}^{2} }} \biggr) ^{2+s}-8/5 \biggl( {\frac{-2{T}^{2}}{3T_G-2 {T}^{2}}} \biggr) ^{1+s}} \\ &{\qquad +\, \biggl( { \frac{-2{T}^{2}}{3T_G-2{T}^{2}}} \biggr) ^{s} \biggr] n^{2} \biggl( 2{ \frac{T^{3/2}\sqrt{6}}{3 T_G-2 {T}^{2}}} \biggr) ^{2-s}} \\ &{\qquad +\,{\frac{2}{45}}\bigl(\bigl( -2/3 s^{2}+8/3s \bigr) T^{2}+T_G\bigl( -9s+4+{s}^{2} \bigr) T^{4}T_G \bigr) } \\ &{\qquad \times\, \bigl( 3T_G-2{T}^{2}\bigr) ^{-4}\bigl( 8{T}^{2}s+3{s}^{2}T_G-2{s}^{2}{T}^{2}} \\ &{\qquad +\,12T_G-27sT_G \bigr) ^{-1}\bigl( -4{T}^{2}+15T_G \bigr) ^{-1}{T}^{-3}} \end{aligned}$$
(24)

Based on the choice of the scale factor we have \(\dot{H}<0\) is valid in the whole cosmic history. Hence, considering \(w_{\varLambda}=-1-\frac{s\dot{H}}{3H^{2}}<-1\) as required by PDE, we need s<0. It was clearly established in Wei (2012) that for PDE

  • EoS w Λ goes asymptotically to −1 in the late;

  • w Λ <−1;

  • w Λ never crosses the phantom divide w=−1 in the whole cosmic history.

In order to verify whether consideration of PDE in the f(T,T G ) gravity, which is a class of modified gravity, leads to results consistent with that of Wei (2012) we consider both 0<s≤2 as well as s<0. In particular we consider s=2 and s=−2. Solving Eq. (22) for the said two cases we have two solutions for f(t) as:

$$\begin{aligned} \tilde{f}(s=2) =&\frac{12(-1+m)m^2 (-1+n^2 )}{(-5+3m) t^2} \\ &{}+t^{\frac{1}{2} (-9+5m-\sqrt{65+m(-74+25 m)} )} \\ &{}\times \bigl[C_2+C_1t^{\sqrt{65+m(-74+25m)}} \bigr] \end{aligned}$$
(25)

and

$$\begin{aligned} \tilde{f}(s=-2) =&\frac{12(-1+m) (\frac{m^4}{5-3m}+\frac{n^2 t^4}{13-7m} )}{m^2t^2} \\ &{}+t^{\frac{1}{2} (-9+5 m+\sqrt{65+m(-74+25m)} )} \\ &{}\times \bigl[C_3+C_4 t^{-\sqrt{65+m(-74+25m)}} \bigr] \end{aligned}$$
(26)

It may be noted that from now onwards \(\tilde{f}\) would denote the reconstructed f. Using solution (25) in Eq. (10) we get the modified p DE for s=2 as function of t

$$\begin{aligned} &{p_{DE}(s=2)} \\ &{\quad {}=\frac{1}{192(-1+m)m(-5+3m)}t^{\frac{1}{2}(-11-\xi)}} \\ &{\qquad {}\times \bigl[m^5 \bigl(-1728n^2t^{\frac{7+\xi}{2}}-750C_1t^{\frac{5 m}{2}+\xi} \bigr)} \\ &{\qquad {}+384 m^4 t^{\frac{5+\xi}{2}} \bigl(-2+4t+n^2(2+11t) \bigr)} \\ &{\qquad {}-192m^3t^{\frac{5+\xi }{2}} \bigl(-8+16t+n^2(8+15t) \bigr)} \\ &{\qquad {} +25C_1m^4t^{\frac{5 m}{2}+\xi}(158+45t-18 \xi)} \\ &{\qquad {}+ 5C_1t^{\frac{5 m}{2}+\xi}(-9+\xi) \bigl(-6-53t+4(2+t)\xi} \\ &{\qquad {}+(-2+t)\xi^2 \bigr)+3C_1m^3t^{\frac{5m}{2}+\xi} \bigl(t(-1884+65 \xi)} \\ &{\qquad {}-10\bigl(254+3(-22+\xi)\xi\bigr)\bigr)} \\ &{\qquad {}-C_1 mt^{\frac{5m}{2}+\xi} \bigl(2382-2\xi\bigl(962+\xi(-179+8\xi)\bigr)} \\ &{\qquad {}+t\bigl(8396+\xi\bigl(-957+\xi(-50+3\xi)\bigr)\bigr)\bigr)} \\ &{\qquad {}-C_2(-5+3m)t^{5m/2} \bigl(250m^4-75m^3\bigl(5t+2(6+\xi)\bigr)} \\ &{\qquad {}-(9+\xi) \bigl(-2(1+\xi) (3+\xi)+t\bigl(-53+(-4+\xi ) \xi\bigr)\bigr)} \\ &{\qquad {}+m^2\bigl(t(1259+65\xi)+10\bigl(104+\xi(41+3\xi)\bigr)\bigr)} \\ &{\qquad {}+m\bigl(-2(6+\xi) \bigl(37+\xi(22+\xi )\bigr)} \\ &{\qquad {}+t\bigl(-1393+\xi(-138+7\xi)\bigr)\bigr) \bigr)} \\ &{\qquad {} +m^2 \bigl(384t^{\frac{5+\xi}{2}} \bigl(-2+4t+n^2(2+t) \bigr)} \\ &{\qquad {}-C_1t^{\frac{5 m}{2}+\xi}\bigl(-6532+2\xi\bigl(1532+3(-53+\xi)\xi \bigr)} \\ &{\qquad {}+t\bigl(-10474\xi (739+21\xi)\bigr)\bigr) \bigr) \bigr]} \end{aligned}$$
(27)

Using solution (26) in Eq. (10) we get the modified p DE for s=−2 as function of t

$$\begin{aligned} &{p_{DE}(s=-2)} \\ &{\quad {}=\frac{t^{\frac{1}{2}(-11-\xi)}}{192(-1+m)m^3(-5+3m) (-13+7m)}} \\ &{\qquad {}\times \bigl[-5250C_3m^8t^{\frac{5 m}{2}+\xi}+25344 m^5t^{\frac{5+\xi}{2}}(-1+2t)} \\ &{\qquad {}-20736m^6t^{\frac{5+\xi}{2}}(-1+2t)+5376m^7t^{\frac{5+\xi }{2}}(-1+2t)} \\ &{\qquad {}+5760n^2t^{\frac{13+\xi}{2}}(-10+7t)-576mn^2t^{\frac{13+\xi}{2}}} \\ &{\qquad {}\times(-260+97t) -192m^4t^{\frac{5+\xi}{2}} \bigl(-52+104t+63n^2t^5 \bigr)} \\ &{\qquad {}+ 25 C_3 m^7 t^{\frac{5 m}{2}+\xi}(1496+315t-126 \xi)} \\ &{\qquad {}+m^2 \bigl(-576n^2t^{\frac{13+\xi}{2}}(220+17t)-65C_3t^{\frac{5m}{2}+\xi}} \\ &{\qquad {}\times (-9+\xi) \bigl(-6-53t+4(2+t) \xi+(-2+t)\xi ^2 \bigr) \bigr)} \\ &{\qquad {}+C_3m^6t^{\frac{5m}{2}+\xi} \bigl(3t(-18063+455\xi)} \\ &{\qquad {}-10\bigl(10469+9\xi(-219+7\xi)\bigr) \bigr)-C_3m^5t^{\frac {5m}{2}+\xi}} \\ &{\qquad {}\times\bigl(-144784 + 2\xi\bigl(23594+3\xi(-566+7\xi)\bigr)} \\ &{\qquad {}+t\bigl(-146794+ \xi(7708+147\xi )\bigr)\bigr)-C_3m^4t^{\frac{5 m}{2}+\xi}} \\ &{\qquad {}\times \bigl(10\bigl(10159+\xi\bigl(-5330+(664-19\xi)\xi\bigr) \bigr)} \\ &{\qquad {}+t\bigl(194934+\xi\bigl(-16306+7\xi (-89+ 3\xi)\bigr)\bigr)\bigr)} \\ &{\qquad {}-C_4 m^2 \bigl(65+m(-74+21m)\bigr)t^{5m/2} \bigl(250m^4} \\ &{\qquad {}-75m^3 \bigl(5t+2(6+\xi)\bigr)- (9+\xi) \bigl(-2(1+\xi) (3+\xi)} \\ &{\qquad {}+t\bigl(-53+(-4+\xi)\xi \bigr)\bigr)+m^2\bigl(t(1259+65\xi)} \\ &{\qquad {}+10\bigl(104+\xi(41+3\xi)\bigr)\bigr)+m\bigl(-2(6+ \xi) } \\ &{\qquad {}\times \bigl(37+\xi(22+\xi)\bigr)+t\bigl(-1393+\xi (-138+7\xi)\bigr)\bigr) \bigr)} \\ &{\qquad {}+m^3 \bigl(2880n^2t^{\frac{13+\xi }{2}}(12+13t)+C_3t^{\frac{5 m}{2}+\xi} \bigl(32856} \\ &{\qquad {}-2\xi\bigl(13871+\xi (-2782+139 \xi)\bigr)} \\ &{\qquad {}+t\bigl(125843+\xi \bigl(-15556+\xi(-825+74\xi)\bigr)\bigr)\bigr) \bigr) \bigr]} \end{aligned}$$
(28)

where \(\xi=\sqrt{65+m (-74+25 m)}\). Using Eqs. (27) and (28) the EoS for PDE i.e. \(w_{DE}=\frac{p_{DE}}{3n^{2} m_{p}^{4-s} (\frac{t}{m} )^{-s}}\) is obtained through reconstructed \(\tilde{f}\) for s=2 and s=−2 respectively as

$$\begin{aligned} &{w_{DE}(s=2)} \\ &{\quad {}=\frac{1}{72m^3(-5+3m)n^2}t^{-\frac{1}{2} (7+\xi )} \bigl[130C_1\xi t^{\frac{5m}{2}+\xi}} \\ &{\qquad {}-333C_1m\xi t^{\frac{5m}{2}+\xi}+278C_1m^2\xi t^{\frac{5m}{2}+\xi}} \\ &{\qquad {} -75C_1m^3\xi t^{\frac{5m}{2}+\xi}+15C_1\xi t^{1+\frac{5m}{2}+\xi}} \\ &{\qquad {}-34C_1m\xi t^{1+\frac{5m}{2}+\xi}+15C_1m^2\xi} \\ &{\quad {}=t^{1+\frac{5m}{2}+\xi}+C_2(-5+3m)t^{5 m/2} \bigl(218-125m^3+26\xi} \\ &{\qquad {}+ (19+3\xi )t+5m^2- (88+5\xi+5t)-m \bigl(533+51\xi} \\ &{\qquad {}+ (52+5\xi ) t \bigr) \bigr)+C_1(-5+3m)t^{\frac{5m}{2}+\xi} \bigl(218+ 19t} \\ &{\qquad {} +m\bigl(-13(41+4t) +5m(88-25m+5t)\bigr)\bigr)} \\ &{\qquad {}-24 m^2t^{\frac{1}{2} (5+\xi )}\bigl(-4+8t+9m^2n^2 t+2n^2(2+t)} \\ &{\qquad {}-m \bigl(-4+8t+n^2(4+13t) \bigr)\bigr) \bigr]} \end{aligned}$$
(29)

and

$$\begin{aligned} &{w_{DE}(s=-2)} \\ &{\quad {}=\frac{1}{72 m \xi^2 n^2}t^{\frac{1}{2} (-15-\xi )} \bigl[-1690 C_3 m^2 \xi t^{\frac{5 m}{2}+\xi}} \\ &{\qquad {}+5239 C_3 m^3 \xi t^{\frac{5 m}{2}+\xi}-5945 C_3 m^4\xi t^{\frac{5 m}{2}+\xi}} \\ &{\qquad {}+2921 C_3 m^5 \xi t^{\frac{5 m}{2}+\xi}-525 C_3 m^6 \xi t^{\frac{5 m}{2}+\xi}} \\ &{\qquad {}-195 C_3 m^2 \xi t^{1+\frac{5 m}{2}+\xi}+547C_3 m^3 \xi t^{1+\frac{5 m}{2}+\xi}} \\ &{\qquad {}-433 C_3 m^4 \xi t^{1+\frac{5 m}{2}+\xi}+105 C_3 m^5 \xi t^{1+\frac{5 m}{2}+\xi}} \\ &{\qquad {}-24 t^{\frac{1}{2} (5+\xi )} \bigl(4 (-1+m) m^4 (-13+7 m)-8 (-1+m)} \\ &{\qquad {}\times m^4 (-13+7 m) t-60 \bigl(5+m (-8+ 3 m)\bigr)n^2t^4} \\ &{\qquad {}+3 (-5+3 m) \bigl(-14+m (-3+7 m)\bigr) n^2 t^5 \bigr)} \\ &{\qquad {}-C_3m^2 \bigl(65+m(-74+ 21 m)\bigr) t^{\frac{5 m}{2}+\xi}\bigl(-218-19 t} \\ &{\qquad {}+m \bigl(533+5 m (-88+25 m-5 t)+52 t\bigr)\bigr)} \\ &{\qquad {}-C_4 m^2\bigl(65+m(-74+21m)\bigr)t^{5m/2} \bigl(-218+125m^3} \\ &{\qquad {}-26\xi- (19+3\xi ) t-5m^2(88+5\xi+5 t)} \\ &{\qquad {}+m \bigl(533+51\xi+ (52+5\xi )t \bigr) \bigr) \bigr]} \end{aligned}$$
(30)

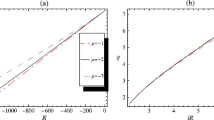
Firstly we include the discussion of reconstructed f models corresponding to PDE parameter s=2,−2, respectively. We plot f(s=2,−2) versus cosmic time as well as cosmic scale factor m>1 as shown in Figs. 1 and 2. In Fig. 1, it is observed that \(\tilde{f}(s=2)\) shows decreasing behavior from very high value and approaches to zero versus cosmic time in the range 2≤m≤2.3. However, for m>2.3, it shows decreasing behavior initially, becomes flat for a short interval of time, and then exhibits increasing behavior. Figure 2 indicates that \(\tilde{f}(s=-2)\) increases with cosmic time from very low value, becomes flat for a glimpse of time interval and then decreases for 2≤m≤2.2. For 2.2<m≤2.5, it increases but approaches to zero after short interval of time. For 2.5<m, f(s=−2) increases with cosmic time from very low value, becomes flat for a glimpse of time interval and then increases.

Fig. 1
figure 1

Plot of reconstructed f (Eq. (25)) from PDE taking s=2 and m>1. Also, n=3, C 1=0.5, C 2=0.2

Full size image
Fig. 2
figure 2

Plot of reconstructed f (Eq. (26)) from PDE taking s=−2 and m>1. Also, n=3, C 3=0.2, C 4=0.5

Full size image

We also plot EoS parameter versus cosmic time corresponding to the same values of PDE parameter for three different values of m as shown in Figs. 3 and 4. It can be observed from Fig. 3 that EoS parameter starts from dust-like matter, passes the quintessence-like and vacuum DE era and then goes towards phantom DE era. The w DE crosses phantom boundary at t≈0.5 and transits from quintessence to phantom i.e. behaves like quintom. This plot also represents that EoS parameter attains more reliable phantom era which possesses the ability for prevention of BH formation. Figure 4 represents that EoS parameter remains in the phantom DE era forever. The trajectories of EoS parameter corresponding to different values of m starts from higher phantom values and goes towards less phantom values. Also, it is observed that it never meets or crosses the −1 boundary and hence the EoS behaves like phantom. It is worthwhile to mention here that EoS parameter corresponding to both cases of PDE parameter correspond to phantom era of the universe which is a favorable sign to PDE conjecture. However, the reconstructed model corresponding to s=2 is more attractive as compare to s=−2 because of more aggressive phantom era. However, taking into account the fact as stated in Wei (2012) that for PDE w DE <−1 always and it never crosses the phantom divide w DE =−1 in the whole cosmic history, it is interpreted that EoS resulting from s=−2 is in complete agreement with it as in this case w DE <−1, →−1 and never crosses −1. Moreover, s=−2 is a choice that is in agreement with the prescription of Wei (2012), which states that if \(\dot{H}<0\) (a requirement for cosmic acceleration and holds for our choice of scale factor) s<0. Hence, it is observed that the results stated for PDE in Einstein gravity are in close agreement with those in the framework of modified gravity under consideration.

Fig. 3
figure 3

Plot of the reconstructed EoS parameter (Eq. (29)) for s=2

Full size image
Fig. 4
figure 4

Plot of the reconstructed EoS parameter (Eq. (30)) for s=−2

Full size image

3 Reconstruction scheme for unification of matter dominated and accelerated phases

We consider that the Hubble rate H is given by (Nojiri and Odintsov 2006)

$$ H(t)=H_0+\frac{H_1}{t}, $$
(31)

that leads to \(a(t)=C_{1} e^{H_{0} t}t^{H_{1}}\) and due to this choice of Hubble parameter, the PDE takes the form

$$ \rho_{\varLambda}=3n^2 t^{-s} (H_0 t+H_1 )^{s} $$
(32)

When t≪t 0, in the early Universe and \(H(t)\sim\frac{H_{1}}{t}\), the Universe was filled with perfect fluid with EOS parameter as \(w=-1+\frac{2}{3H_{1}}\). On the other hand, when t≫t 0 the Hubble parameter H(t) is constant H→H 0 and the Universe seems to be de-Sitter. So, this form of H(t) provides transition from a matter dominated to the accelerating phase. In Eq. (9) we use (31) and we get the following

$$\begin{aligned} \rho_{DE} =&\frac{1}{2} \bigl[-f[t]+ \bigl((H_1+H_0t) \\ &\times\, \bigl(-t^3\bigl(10H_1^2\bigl(2+(-3 +H_1)H_1\bigr) \\ &+\,H_0H_1\bigl(21+H_1(-73+40H_1) \bigr)t \\ &+\, H_0^2 \bigl(5-56H_1+60H_1^2 \bigr)t^2+H_0^3 (-13+40H_1)t^3 \\ &+10H_0^4t^4 \bigr)f'[t]\,{+}\,(H_1\,{+}\,H_0t) \bigl(2H_1^2H_0t({-}1\,{+}\,2H_0t) \\ &+\,H_1(-2+4H_0 t) \bigr) \bigl(12H_1 \bigl(2H_1^2+H_0t(-1+2H_0t) \\ &+\,H_1(-2+4H_0 t) \bigr) \bigr) \bigr) + t^4f''[t] \bigr) \\ &\times\, \bigl\{ 2H_1t^2 \bigl(2H_1^2 +H_0t(-1+2H_0t) \\ &+\,H_1(-2+4H_0t) \bigr)^2 \bigr\} ^{-1} \bigr]. \end{aligned}$$
(33)

In the above as well as in the subsequent differential equations f′[t] and f″[t] denote the first and second order derivatives of f respectively with respect to t. If we consider ρ Λ =ρ DE as available in Eqs. (32) and (33), we get a differential equation that can not be solved analytically for f. Hence, we solve it numerically to have f graphically. Using the same approach as in the previous section, we have reconstructed EoS parameter and showed it graphically. In Figs. 5 and 6, we have plotted \(\tilde{f}\) for s=2 and −2, respectively. In case of s=2, we have taken n=0.91, H 1=2 (red), 2.2 (green), 2.3 (blue) and H 0=0.5. For s=−2, we have taken n=4, H 1=3 (red), 3.1 (green), 3.2 (blue) and H 0=0.89.

Fig. 5
figure 5

Plot of reconstructed \(\tilde{f}\) taking s=2 for \(H(t)=H_{0}+\frac{H_{1}}{t}\)

Full size image
Fig. 6
figure 6

Plot of reconstructed \(\tilde{f}\) taking s=−2 for \(H(t)=H_{0}+\frac{H_{1}}{t}\)

Full size image

For s=2, we have observed increasing pattern of \(\tilde{f}\) and in case of s=−2, it is exhibiting decreasing pattern. We have plotted the EoS parameters corresponding to s=−2 and 2 in Figs. 7 and 8, respectively. In case of s=2, the EoS parameter is ≥−1 and hence it is behaving like quintessence. However, for s=−2, the EoS parameter is crossing −1 boundary for H 1=3.2 and hence it is behaving like quintom. Hence, it is understood that reconstructed f(T,T G ) through consideration of PDE can attain phantom era when s=−2. This is consistent with the behavior of PDE that leads to purely phantom era when considered in Einstein gravity with s=−2. However, in f(T,T G ) gravity, it can go beyond phantom for our choice \(H(t)=H_{0}+\frac{H_{1}}{t}\).

Fig. 7
figure 7

Plot of the reconstructed EoS parameter for s=2

Full size image
Fig. 8
figure 8

Plot of the reconstructed EoS parameter for s=−2

Full size image

3.1 On unification of inflation with DE in f(T,T G )

In this short subsection our aim is to realize f(T,T G ) to unify the early inflationary epoch with the late time de-Sitter era. We mention here that the unification of inflation with DE in modified gravities firstly examined for f(R) gravity. It was proposed in Nojiri-Odintsov model (Nojiri and Odintsov 2003), which was subsequently generalized to more realistic versions (Nojiri and Odintsov 2007c; Cognola et al. 2008). One important problem in early Universe is singularity and it investigated later (Nojiri and Odintsov 2008). Indeed it has been shown that there is a class of non-singular exponential gravity to unify the early- and late-time accelerated expansion of the Universe (Elizalde et al. 2011).

For our f(T,T G ) case, if we consider the inflationary solution for \(H=\frac{H_{1}}{t}\) then we have an exact solution of f as

$$ \tilde{f}=\frac{1}{t^7} \biggl[\frac{48 n^2 (-t)^{7-s}}{8+(-14+s) s}-3 t^5+C_1t^{-\sqrt{41}} +C_2t^{\sqrt{41}} \biggr] $$
(34)

This is an inflationary solution. We denote by j=7−s>5, \(\ell=\frac{48 n^{2} }{8+(-14+s) s}\), so we obtain:

$$ \tilde{f}=\frac{1}{t^7} \bigl[\ell t^j-3 t^5+C_1t^{-\sqrt{41}} +C_2t^{\sqrt{41}} \bigr] $$
(35)

At inflationary (early) Universe, when t≪t 0, the dominant part of the \(\tilde{f}\) is written as follows:

$$ \tilde{f}\sim C_1t^{-(7+\sqrt{41})} . $$
(36)

Since in this limit,

$$\begin{aligned} T\sim\frac{6H_1^2}{t^2},\qquad T_G\sim\frac{24H_1^3(H_1-1)}{t^4} \end{aligned}$$
(37)

So, the reconstructed f(T,T G ) for inflationary era is written as the following:

$$ f(T,T_G)= C_1 \biggl[-\frac{T_G}{24}\sqrt{ \frac{6}{T}} \biggr]^{7+\sqrt{41}} . $$
(38)

So, f(T,T G ) produces also the inflationary (phantom) solutions as well.

At late time, i.e. in the de-Sitter epoch when H(t)∼H 0, we use of this fact that:

$$ \begin{aligned}[c] &T\sim6H_0^2,\qquad T_G\sim24 H_0^4 ,\\ &\dot{f}_{T_G}=\dot{T}_G f_{T_G,T_G}+\dot{T}f_{T_G,T}|_{H=H_0}=0 \end{aligned} $$
(39)

so the reconstruction scheme gives us:

$$ f(T,T_G)= \sqrt{T}F \biggl(\frac{T_G}{\sqrt{T}} \biggr)-T+ \frac {6^{1-s/2}n^2m_p^{4-s}}{s-1}T^{s/2} $$
(40)

where F denotes an arbitrary function. The above f(T,T G ) reproduces de-Sitter (late time) epoch.

4 Reconstruction scheme for intermediate scale factor

Next, we consider the following scale factor (Barrow et al. 2006)

$$\begin{aligned} a(t)=\exp\bigl(At^m\bigr),\quad 0<m<1. \end{aligned}$$
(41)

The scale factor and Hubble parameter is suitably chosen so that it is consistent with the intermediate expansion:

$$\begin{aligned} H(t)=Amt^{m-1}. \end{aligned}$$
(42)

The scale factor is necessary to perform the analysis and therefore working with a hypothetical scale factor may not be consistent with the inflationary scenario. Hence we picked the intermediate scale factor which is also consistent with astrophysical observations (Barrow et al. 2006). Subsequently we have the following differential equation

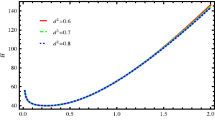
$$\begin{aligned} &{3 n^2 \biggl(\frac{t^{1-m}}{A m} \biggr)^{-s}} \\ &{\quad {}= \frac{1}{2} \biggl(6A^2m^2t^{-2+2m}-f[t]+ \frac{t f'[t]}{-1+m}} \\ &{\qquad {}+\frac{t (-1+m+Amt^m )f'[t]}{(-1+m) (-4+m (3+4At^m ) )}} \\ &{\qquad {}+ \frac{t (20+m^2 (9+16At^m )-m (27+20A t^m ) )f'[t]}{(-1+m) (-4+m (3+4At^m ) )^2} } \\ &{\qquad {}- \frac{t^2 (-4+m (3+4At^m ) ) f''[t] }{(-1+m) (-4+m (3+4At^m ) )^2} \biggr)} \end{aligned}$$
(43)

Solving Eq. (43) numerically and plotting reconstructed \(\tilde{f}\) in Figs. 9 and 10 for s=−2 and s=2. We observe that for s=2 as well as s=−2, the reconstructed f(T,T G ) model is displaying decreasing pattern. It is noted from Fig. 11 (for s=2) that the reconstructed w DE crosses phantom boundary at t≈1.15 and hence behaves like quintessence. However, in Fig. 12 (for s=−2), we observe that the EoS parameter w DE <−1 which indicates an aggressively phantom-like behavior. Hence, for intermediate scale factor, the PDE in modified gravity f(T,T G ) pertains to phantom era of the universe and hence it is consistent with the behavior of PDE in Einstein gravity for s=−2. It may be noted (for s=2 case) that we have taken n=0.9, A=10 and red, green and blue lines correspond to m=0.33,0.35,0.40 respectively. On the other hand, for s=−2, we have taken n=4, A=0.6 and red, green and blue lines correspond to m=0.20,0.25,0.30 respectively.

Fig. 9
figure 9

Plot of reconstructed \(\tilde{f}\) taking s=2 for intermediate scale factor

Full size image
Fig. 10
figure 10

Plot of reconstructed \(\tilde{f}\) taking s=−2 for intermediate scale factor

Full size image
Fig. 11
figure 11

Plot of the reconstructed EoS parameter for s=2 for intermediate scale factor

Full size image
Fig. 12
figure 12

Plot of the reconstructed EoS parameter for s=−2 for intermediate scale factor

Full size image

5 Reconstruction scheme for bouncing scale factor

Inflation is a solution for flatness problem in big-bang cosmology. Bouncing scenario predicts a transitionary inflationary Universe, in which the Universe evolves from a contracting epoch (H<0) to an expanding epoch (H>0). It means the scale factor a(t) reaches a local minima. So the cosmological solution is non-singular. In GB gravity, bouncing solutions widely studied in literature (Bamba et al. 2014a, 2014b; Odintsov et al. 2014; Makarenko et al. 2014; Amorós et al. 2013; Nojiri et al. 2003; Lidsey 2002a, 2002b).

This scale factor takes the following form (Myrzakulov and Sebastiani 2014)

$$ \begin{aligned}[c] &a(t)=a_0+\alpha(t-t_0)^{2n},\\ &H (t)= \frac{2n\alpha (t-t_0)^{2n-1}}{a_0+\alpha(t-t_0)^{2n}},\quad n=1,2,3\ldots \end{aligned} $$
(44)

where a 0, α are positive (dimensional) constants and n is a positive natural number. The time of the bounce is fixed at t=t 0. When t<t 0, the scale factor decreases and we have a contraction with negative Hubble parameter. At t=t 0, we have the bounce, such that a(t=t 0)=a 0, and when t>t 0 the scale factor increases and the universe expands with positive Hubble parameter. It should be mentioned that for sake of simplicity (without any loss of generality) we have taken n in the power law form as well as in the PDE density (Eq. (14)). For this choice of scale factor, we get the following differential equation

$$\begin{aligned} &{\frac{1}{4} \biggl[\frac{48 n^2 (t-t_0)^{-2+4n}\alpha^2}{ (a_0+(t-t_0)^{2 n}\alpha )^2}+\frac{(t-t_0) (a_0+(t-t_0)^{2 n}\alpha )f'[t]}{a_0(-2+3n)-2(t-t_0)^{2n}\alpha}} \\ &{\qquad {}- \frac{2(t-t_0) (a_0+(t-t_0)^{2 n}\alpha )f'[t]}{a_0-2a_0n+(t-t_0)^{2 n}\alpha}} \\ &{\qquad{} - 2 f[t] \bigl((t-t_0) \bigl( \bigl(a_0^2(-2+3n) (-5+6n)} \\ &{\qquad{}-a_0 \bigl(-20+3n(9+2n)\bigr) (t-t_0)^{2n}\alpha} \\ &{\qquad {}+10(t-t_0)^{4n}\alpha^2 \bigr)f'[t]-(t-t_0) \bigl(a_0(-2+3n)} \\ &{\qquad {}-2(t-t_0)^{2n}\alpha \bigr) \bigl(a_0+(t-t_0)^{2n}\alpha\bigr)f''[t] \bigr) \bigr) } \\ &{\qquad {}\times \bigl((-1+2n)\bigl(a_0(2-3n)+2(t-t_0)^{2n}\alpha \bigr)^2\bigr)^{-1} \biggr]} \\ &{\quad {}=32^sn^2 \biggl(\frac{(t-t_0)^{1-2n} (a_0+(t-t_0)^{2n}\alpha )}{n\alpha} \biggr)^{-s}.} \end{aligned}$$
(45)

Solving Eq. (45) numerically and plotting reconstructed \(\tilde{f}\) in Figs. 13 and 14, we observe that the reconstructed f(T,T G ) is displaying increasing pattern for s=2. However, for s=−2, the reconstructed f(T,T G ) is displaying increasing pattern and is tending to 0 at late stage of the universe. It is also noted from Fig. 15 (for s=2) that the reconstructed w DE →−1 from w DE >−1. However, it never crosses phantom boundary and hence behaves like quintessence throughout. However, in Fig. 16, it can be observed that for s=−2 the EoS parameter w DE <−1 and this indicates aggressive phantom-like behavior. Hence, with s=−2 for bounce with power-law scale factor, PDE in modified gravity f(T,T G ) pertains to phantom era of the universe and hence it is consistent with the behavior of PDE in Einstein gravity for s=−2. It may be noted that for both of the cases, we have taken n=2, A=10 and red, green and blue lines correspond to m=0.33,0.35,0.40 respectively. On the other hand, for s=−2 we have taken n=4, a 0=10.5, α=10.1 and red, green and blue lines correspond to n=6,7,8 respectively.

Fig. 13
figure 13

Plot of reconstructed \(\tilde{f}\) taking s=2 for bounce with power-law scale factor

Full size image
Fig. 14
figure 14

Plot of reconstructed \(\tilde{f}\) taking s=−2 for bounce with power-law scale factor

Full size image
Fig. 15
figure 15

Plot of the reconstructed EoS parameter for s=2 for bounce with power-law scale factor

Full size image
Fig. 16
figure 16

Plot of the reconstructed EoS parameter for s=−2 for bounce with power-law scale factor

Full size image

6 Reconstruction through a semi analytic form of f

We assume that f(T,T G ) realizes the form

$$ f(T,T_G) \equiv f=b_0+b_1 t+b_2 t^2+b_3 t^3+\cdots $$
(46)

For this choice of f, Eq. (9) takes the form

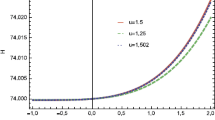
$$\begin{aligned} \rho_{DE} =&\frac{1}{2} \biggl[-b_0-b_1 t-b_2 t^2-b_3 t^3+6 H^2 \\ &+\,\frac {(b_1+t (2 b_2+3 b_3 t)) H}{H'} \\ &+\,\frac{(b_1+t (2 b_2+3 b_3 t)) H (H^2+H' )}{2 H' (2 H^2+H' )+H H''} \\ &-\,\frac{48H (b_2+3 b_3 t) H (2 H' (2 H^2+H' )+H H'' )}{24 (2 H' (2 H^2+H' )+H H'' )^2} \\ &-\,24 \bigl(b_1+t (2 b_2+3 b_3 t)\bigr) \\ &\times\,\frac{H(2 H^{\prime3}\,{+}\,4 H^3 H''\,{+}\,6 H H' H''\,{+}\,H^2 (12 H^{\prime2}\,{+}\,H^3 ) ) }{24 (2 H' (2 H^2\,{+}\,H' )\,{+}\,H H'' )^2} \biggr] \end{aligned}$$
(47)

which, on setting equal to ρ Λ gives rise to a differential equation on H that is solve numerically to generate the reconstruction of H and subsequently EoS parameter \(w_{DE}=-1-\frac{2\dot{H}}{3 H^{2}}\) that are plotted in Figs. 17, 18, 19 and 20. We have set the coefficients of the polynomial as b 0=0.8, b 1=0.6, b 2=0.5, b 3=0.2. In this reconstruction through an assumed polynomial form of f, the Hubble parameter H has been reconstructed and the reconstructed \(\tilde{H}\) has been examined for its first time derivative and it is observed that \(\dot{\tilde{H}}<0\) throughout for s=±2 and w DE <−1 for s=±2. Negative time derivative of Hubble parameter is consistent with the accelerated expansion of the universe and the aggressive phantom-like behavior of w DE is consistent with the basic property of pilgrim dark energy.

Fig. 17
figure 17

Plot of reconstructed \(\tilde{H}\) for s=2

Full size image
Fig. 18
figure 18

Plot of reconstructed \(\tilde{H}\) for s=−2

Full size image
Fig. 19
figure 19

Plot of the reconstructed EoS parameter for s=2

Full size image
Fig. 20
figure 20

Plot of the reconstructed EoS parameter for s=−2

Full size image

7 Concluding remarks

Pilgrim dark energy (PDE) model is studied in this paper and Hubble horizon has been used as an IR cutoff. The basic assumption of this model is that phantom acceleration prevents the formation of the BH. The said PDE is considered in a modified gravity f(T,T G ), which has been constructed by Kofinas and Saridakis (2014) on the basis of T (old quadratic torsion scalar) and T G (new quartic torsion scalar T G that is the teleparallel equivalent of the Gauss-Bonnet term). We have compiled our work in two phases: Firstly, we have assumed different scale factors such as a(t)=a 0 t m, \(H=H_{0}+\frac{H_{1}}{t}\), a(t)=exp(At m) and a(t)=a 0+α(t−t 0)2n. We have reconstructed f and subsequently w DE in this scenario. Secondly, we have assumed analytic function such f=b 0+b 1 t+b 2 t 2+b 3 t 3 and reconstructed Hubble parameter and w DE without any choice of scale factor.

Throughout the study, we have considered s=−2 and s=2, separately. We have observed that s=−2, as described in PDE (Wei 2012), seems more realistic choice for s than s=2 and this outcome of the present reconstruction work is consistent with Wei (2012). Moreover, it has been observed that the reconstructed w DE , irrespective of choices of scale factor or a choice of f, exhibit a more aggressive phantom-like behavior for s=−2 than s=2. This result also matches the study of Wei (2012). Hence, it is finally concluded that PDE, when considered in f(T,T G ) gravity is capable of attaining the phantom phase of the universe.