1 Introduction

It is validly known that a huge number of scientists of modern age agree to accept the fact that the gravitational effects can be described in scientific way by Einstein general relativity (GR) theory. But this theory have a gap of communication at small scales as scales of magnitude of the Planck’s length, where one can describes the spacetime structure quantum mechanically (Hehl et al. 1976, 1995; Mikhail and Wanas 1977; Möller 1978; Hayashi and Shirafuji 1979). Also, the problem of late time cosmic acceleration of the universe, lake of a unsatisfactory theory for dark energy and dark matter, are the main problem for modifications of GR. These modifications have appeared in the form of f(R), f(G), f(T), f(R,T), theories etc. (Haghani et al. 2013; Sharif and Zubair 2013a, 2013b), but here we consider only f(T) gravity theory, in this theory order of differential equations is two like GR, while all the other theories are 4th order in nature. Therefore, as compared to other theories of gravity, it is easy to make an exact analogy between GR and f(T).

Since GR has the similarity with f(T), therefore this theory would be the alternative form of the generalization of GR, namely the f(R) theory of gravity. This newly proposed f(T) theory is the modification of TT, for which Riemann tensors is zero. Recently, there has been an extensive interest to study the f(T) gravity (Bengochea and Ferraro 2009; Linder 2010; Myrzakulov 2011; Bamba et al. 2011; Wu and Yu 2011). It has been investigated that f(T) gravity has not exactly the same dynamical behavior as teleparallel equivalent of general relativity (TEGR) (Yang 2011). For the general application of this theory to astrophysical objects many observational restrictions had been studied (Bengochea 2011; Wu and Yu 2010; Zhang et al. 2011; Wei et al. 2011). Recently, many authors (Li et al. 2011a, 2011b; Dent et al. 2011; Chen et al. 2011; Zheng and Huang 2011; Cai et al. 2011) discuss the large scale structure and perturbation problems in theoretical cosmology using the formulation of f(T) gravity. The static solutions and the existence of relativistic stars have been explored in f(T) gravity (Deliduman and Yapiskan 2011; Rodrigues et al. 2013; Daouda et al. 2012).

The famous theorem about the static spherically symmetric vacuum solution that is Birkhoffs theorem, has been studied in f(T) gravity in Meng and Wang (2011). The static non-rotating solutions with spherical symmetry in f(T) theories have been investigated in Wang (2011). The theoretical models of relativistic stars and accelerated expansion of universe explored in detail in f(T) gravity in f(T) gravity. It had been proved that the Lagrangian and the equations of motion of f(T) gravitational theories does not hold the local Lorentz transformations (Li et al. 2011a, 2011b; Farajollahi and Ravanpak 2011). In f(R) gravity the equation of motions are fourth order differential equations while in f(T) gravity the order of differential equations is two (second order differential equations like GR). Therefore the equations of motion of f(T) theories are different from those of f(R) theories (Sotiriou et al. 2011; Nojiri and Odintsov 2007; Elizalde et al. 2008; Nojiri et al. 2009; Cognola et al. 2009; Wu and Yu 2010; Yang 2011; Ferraro and Fiorini 2011). Due to this property, it has been believed that f(T) theory may be much interesting than f(R) gravity for the modification of GR. The non-locality of f(T) theories, reveal the fact that there is more degrees of freedom in f(T) as compared to other theories of gravity (Ferraro and Fiorini 2007, 2008).

Recently, Abbas and his collaborators have studied the models of anisotropic compact in GR, f(R), f(G) and f(T) theories in diagonal tetrad case (Abbas et al. 2014, 2015a, 2015b; Zubair and Abbas 2015). The present paper is devoted to find analytic spherically symmetric solution with anisotropic quintessence source in the f(T) gravity. In Sect. 2, a brief review of the f(T) gravitational theory along with physical properties of the solution, i.e., the anisotropy, stability and redshift is provided in Sect. 3. The last section deals with the conclusion of the paper.

2 f(T) theory of gravity

The Teleparallel theory of gravity seemed to be an equivalent theory of gravity to the GR (Zhang et al. 2011; Wei et al. 2011; Li et al. 2011a, 2011b). Here, we will explain the basic concepts of the f(T) theory, for this purpose, we define the notation of the Latin indices that are related to tetrad field and the Greek one that are related to space-time coordinates. The line element of the manifold is given by

$$ ds^{2}=g_{\mu\nu}dx^{\mu}dx^{\nu}. $$
(1)

This spacetime can be transformed to a Minkowskian form by the matrix transformation so called tetrad field, as follows:

$$\begin{aligned} &dS^{2}=g_{\mu\nu}dx^{\mu}dx^{\nu}= \eta_{ij}\theta^{i}\theta^{j}, \end{aligned}$$
(2)
$$\begin{aligned} &dx^{\mu}=e_{i}^{\mu}\theta^{i},\quad \theta^{i}=e^{i}_{{\mu}}dx^{\mu}, \end{aligned}$$
(3)

where η ij =diag[1,−1,−1,−1] and \(e_{i}^{\mu}e_{i}^{\nu}=\delta _{\nu}^{\mu}\) or \(e_{i}^{\mu}e_{j}^{\nu}= \delta_{i}^{j}\).

The root of the metric determinant is given by \(\sqrt{-g }=\mathit{det}[e_{\mu}^{i}]=e\).

For a manifold in which the Riemann tensor part without the torsion terms is null and only the non-zero torsion terms exist, the Weitzenbock’s connection components are defined as:

$$ \varGamma^{\alpha}_{\mu\nu}=e_{i}^{\alpha} \partial_{\nu}e_{\mu}^{i}. $$
(4)

We define the torsion and the contorsion tensor as follows:

$$\begin{aligned} &T^{\alpha}_{\mu\nu}=\varGamma^{\alpha}_{\nu\mu}- \varGamma^{\alpha}_{\mu\nu}=e_{i}^{\alpha}\bigl( \partial_{\mu}e_{\nu}^{i}-\partial_{\nu}e_{\mu}^{i} \bigr), \end{aligned}$$
(5)
$$\begin{aligned} &K^{\mu\nu}_{\alpha}=-\frac{1}{2}\bigl(T^{\mu\nu}_{\alpha}-T^{\nu\mu }_{\alpha}-T^{\mu\nu}_{\alpha} \bigr), \end{aligned}$$
(6)

and the components of the tensor \(S_{\alpha}^{\mu\nu}\) is defined as

$$ S_{\alpha}^{\mu\nu}=\frac{1}{2}\bigl(K^{\mu\nu}_{\alpha}+ \delta^{\mu}_{\alpha}T^{\beta\nu}_{\beta}- \delta^{\nu}_{\alpha}T^{\beta\mu}_{\beta}\bigr), $$
(7)

one can write the torsion scalar as

$$ T=T^{\alpha}_{\mu\nu}S_{\alpha}^{\mu\nu}. $$
(8)

Now, similarly to the f(R) theory, one defines the action of f(T) theory as follows:

$$ S\bigl[e_{\mu}^{i}, \varPhi_A\bigr]=\int d^4 x e\biggl[\frac{1}{16\pi}f(T)+\mathcal{L}_{\mathit{Matter}}( \varPhi_A)\biggr], $$
(9)

where we used G=c=1 and Φ A is matter fields. Variation of above action yields the following form of equations of motion (Zhang et al. 2011; Wei et al. 2011)

$$\begin{aligned} &S_{\mu}^{\nu\rho}\partial_{\rho}T f_{TT}+ \bigl[e^{-1}e^{i}_{\mu}\partial_{\rho} \bigl(ee_i^{\alpha}S_{\alpha}^{\nu\rho} \bigr)+T^{\alpha}_{\lambda\mu} S_{\alpha}^{\nu\lambda} \bigr]f_T+\frac{1}{4}\delta^{\nu}_{\mu}f \\ &\quad =4\pi \mathcal{T}_{\mu}^{\nu}, \end{aligned}$$
(10)

where \(\mathcal{T}_{\mu}^{\nu}=\mathcal{M}_{\mu}^{\nu}+{\zeta}_{\mu}^{\nu}\) is the energy momentum tensor. Here, \(\mathcal{M}_{\mu}^{\nu}\) and \({\zeta}_{\mu}^{\nu}\), are energy momentum tensors of ordinary matter and quintessence filed which is specified by the parameter ω q with −1<ω q <−1/3. The components of \({\zeta}_{\mu}^{\nu}\) be written as (Bhar 2014) \({\zeta}_{t}^{t}={\zeta}_{r}^{r}=-\rho_{q}\), \({\zeta}_{\theta}^{\theta}={\zeta}_{\phi}^{\phi}=\frac{1}{2}(3\omega +1)\rho_{q}\).

Let us consider that the matter content is an anisotropic fluid, such that the energy-momentum tensor is given by

$$ \mathcal{T}_{\mu}^{\nu}=(\rho+p_{t})u_{\mu}u^{\nu}-p_{t} \delta_{\mu}^{\nu}+(p_{r}-p_{t})v_{\mu}v^{\nu}, $$
(11)

where u μ is the four-velocity, v μ radial four vector, ρ the energy density, p r is the radial pressure and p t is transverse pressure.

3 Model of anisotropic quintessence stars in generalized teleparallel gravity

We assume that the manifold possesses a stationary and spherical symmetry for which the metric can be written as

$$ dS^{2}=e^{a(r)}dt^{2}-e^{b(r)}dr^{2}-r^{2} \bigl(d\theta^{2}+\sin^{2}(\theta)d\phi^{2}\bigr). $$
(12)

In order to re-write the line element (12) into the invariant form under the Lorentz transformations, we define the tetrad matrix as

$$ {}\bigl[ e_{\mu}^{i}\bigr]=\mathit{diag}\bigl[e^{\frac{a(r)}{2}},e^{\frac {b(r)}{2}},r,r\sin( \theta)\bigr]. $$
(13)

Using (13), one can obtain \(e=\mathit{det}[e_{\mu}^{i}]=e^{\frac {(a+b)}{2}}r^{2}\sin(\theta)\), and with (4)–(8), we determine the torsion scalar and its derivative in terms of r as

$$\begin{aligned} &T(r) = \frac{2e^{-b}}{r}\biggl(a^{\prime}+\frac{1}{r}\biggr), \end{aligned}$$
(14)
$$\begin{aligned} &T^{\prime}(r) = \frac{2e^{-b}}{r}\biggl(a^{\prime\prime}+ \frac{1}{r^{2}}-T\biggl(b^{\prime}+\frac{1}{r}\biggr)\biggr), \end{aligned}$$
(15)

where the prime ′ denotes the derivative with respect to the radial coordinate r. One can now re-write the equations of motion (10) for an anisotropic fluid as

$$\begin{aligned} &4\pi( \rho+\rho_{q} ) = \frac{f}{4}- \biggl( T-\frac{1}{r^{2}}-\frac{e^{-b}}{r}\bigl(a^{\prime}+b^{\prime} \bigr) \biggr) \frac{f_{T}}{2}, \end{aligned}$$
(16)
$$\begin{aligned} &4\pi( p_{r}-\rho_{q} ) = \biggl( T-\frac{1}{r^{2}} \biggr) \frac{f_{T}}{2}-\frac{f}{4}, \end{aligned}$$
(17)
$$\begin{aligned} &4\pi\biggl( p_{t}+\frac{3\omega_{q+1}}{2}\rho_{q} \biggr) \\ &\quad = \biggl[ \frac{T}{2}+e^{-b} \biggl( \frac{a^{\prime\prime}}{2}+\biggl( \frac{a^{\prime}}{4}+\frac{1}{2r}\biggr) \bigl(a^{\prime}-b^{\prime} \bigr) \biggr) \biggr] \frac{f_{T}}{2}-\frac{f}{4}, \end{aligned}$$
(18)
$$\begin{aligned} &\frac{\cot\theta}{2r^{2}}T^{\prime}f_{TT} = 0. \end{aligned}$$
(19)

We used Eq. (16), which arises from the non-diagonal components θ−r of the equation of motion. We would like to mention that this set of equations exists only due to diagonal tetrad field. Further, Eq. (16), does not appear in the static case of the GR, from this equation, we get only the following form of f(T) function

$$ f(T)=\beta T+{\beta}_{1}, $$
(20)

where β and β 1 are integration constants, for simplicity we assume β 1=0. We parameterize the metric as follows (Krori and Barua 1975):

$$ b(r)=Ar^{2},\qquad a(r)=Br^{2}+C, $$
(21)

where A, B and C are some arbitrary constants which will be determined later using some physical conditions. Now one can note that we have four unknowns namely ρ, p r , ρ q , p t . To solve the above system of equations let us assume that the radial pressure p r is proportional to the matter density ρ i.e.,

$$ p_{r}=\alpha p\quad 0< \alpha< 1, $$
(22)

where α is the equation of state parameter. Now using Eqs. (14)–(22), one can obtain

$$\begin{aligned} &\rho=\frac{A+B}{4\pi ( 1+\alpha ) }\beta e^{-Ar^{2}}, \end{aligned}$$
(23)
$$\begin{aligned} &p_{r}=\frac{\alpha ( A+B ) }{4\pi ( 1+\alpha ) }\beta e^{-Ar^{2}}, \end{aligned}$$
(24)
$$\begin{aligned} &\rho_{q}=\frac{e^{-Ar^{2}}}{8\pi} \biggl[ 2A\beta-\frac{\beta}{r^{2}}- \frac{2(A+B)\beta}{1+\alpha} \biggr] +\frac{\beta}{8\pi r^{2}}+\frac {{\beta}_{1}}{16\pi} \end{aligned}$$
(25)
$$\begin{aligned} &p_{t}=\frac{e^{-Ar^{2}}}{8\pi} \bigl[ B\beta(B-A)r^{2}+\beta (2B-A) \bigr] -\frac{3\omega_{q}+1}{8\pi} \\ &\phantom{p_{t}=} \times\biggl[ e^{-Ar^{2}} \biggl\{ 2A-\frac{1}{r^{2}}- \frac{2(A+B)}{1+\alpha} \biggr\} +\frac{1}{r^{2}} \biggr] \end{aligned}$$
(26)
$$\begin{aligned} &p_{t}=\omega_{t}=\frac{p_{t}}{\rho}=\frac{1+\alpha}{2(A+B)}\bigl[ B(B-A)r^{2}+(2B-A) \bigr] \\ &\phantom{p_{t}=\omega_{t}=\frac{p_{t}}{\rho}=} -\frac{3\omega_{q}+1}{4}\biggl[ e^{-Ar^{2}} \biggl\{ 2A\beta-\frac{\beta}{r^{2}} \\ &\phantom{p_{t}=\omega_{t}=\frac{p_{t}}{\rho}=} -\frac{2(A+B)\beta}{1+\alpha} \biggr\} +\frac{\beta}{r^{2}}+\frac {{\beta}_{1}}{2} \biggr] . \end{aligned}$$
(27)

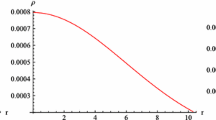
The behavior of energy density ρ, radial pressure p r and transverse pressure p t are given by Figs. 1–3. These graphs show that these quantities are decreasing functions and have maximum values at center r=0. The value for β=1 corresponds to GR as given in Bhar (2014) while β=2,3 corresponds to f(T) gravity. These values can be verified by Tables 2–4.

Fig. 1
figure 1

This figure represents the variation of ρ versus r (km)

Full size image

3.1 Anisotropic behavior

In this section, we have analyzed the anisotropic behavior of the model.

From Eqs. (23) and (24), we have

$$\begin{aligned} &\frac{d\rho}{dr}=-\frac{\beta Are^{-Ar^{2}}}{2\pi ( 1+\alpha )}< 0, \end{aligned}$$
(28)
$$\begin{aligned} &\frac{dp_{r}}{dr}=-\frac{\alpha\beta Are^{-Ar^{2}}}{2\pi ( 1+\alpha) }< 0. \end{aligned}$$
(29)

The above results lead to following equations

$$\begin{aligned} &\frac{d^{2}\rho}{dr^{2}} = -\frac{\beta A}{2\pi ( 1+\alpha ) }< 0, \\ &\frac{d^{2}p_{r}}{dr^{2}} = -\frac{\alpha\beta A}{2\pi ( 1+\alpha) }< 0. \end{aligned}$$

From the above equations, we conclude that at r=0, \(\frac{d\rho}{dr}= 0\), \(\frac{dp_{r}}{dr}=0\) and \(\frac{d^{2}\rho}{dr^{2}}<0\), \(\frac {d^{2}p_{r}}{dr^{2}}<0\), while at center ρ and p r have maximum values (see Figs. 1 and 2). This indicate maximality of central density and central radial pressure. From Fig. 4 it is clear that, for β=1 like normal matter distribution, the bound on the effective EOS in this case is given by 0<ω t (r)<1, while for β=2,3 EOS behaves as dark energy. Also, from Fig. 5, it is clear that ω q is changes its values from negatives to positive. This indicates that fact that compact stars are constituted by the combination of ordinary matter and effect of f(T) term. The measure of anisotropy, \(\Delta =\frac{2}{r}(p_{t}-p_{r})\) in this model is obtained as follows:

$$\begin{aligned} \Delta =&\frac{2}{r} \biggl[ \frac{e^{-Ar^{2}}}{8\pi} \biggl[ B\beta(B-A)r^{2}+\beta(2B-A) \\ &{}-\frac{2\alpha(A+B)}{1+\alpha} \biggr] -\frac {3\omega_{q}+1}{16\pi}\biggl[ e^{-Ar^{2}} \biggl\{ 2A\beta-\frac{\beta}{r^{2}} \\ &{}-\frac{2(A+B)\beta}{1+\alpha} \biggr\} +\frac{\beta}{r^{2}}+\frac {{\beta}_{1}}{2} \biggr] \biggr] . \end{aligned}$$
(30)

It is apparent from Fig. 6 that for our model that a repulsive(anisotropic) force would exists as Δ>0 which allows the construction of more massive distributions.

Fig. 2
figure 2

This figure represents the variation of p r versus r (km)

Full size image
Fig. 3
figure 3

This figure represents the variation of p t versus r (km)

Full size image
Fig. 4
figure 4

This figure represents the variation of ρ q versus r (km)

Full size image
Fig. 5
figure 5

This figure represents the variation of ω t versus r (km)

Full size image
Fig. 6
figure 6

This figure represents the variation of Δ versus r (km)

Full size image

3.2 Matching conditions

In this section, the exterior geometry corresponding to our interior solution is described by the Schwarzschild solution given by the line element

$$\begin{aligned} ds^{2} =&- \biggl( 1-\frac{2M}{r} \biggr) dt^{2}+\biggl( 1-\frac{2M}{r} \biggr) ^{-1}dr^{2} \\ &{}+r^{2}\bigl(d\theta^{2}+\sin^{2}(\theta)d\phi^{2}\bigr). \end{aligned}$$
(31)

The continuity of metric components g tt , g rr and \(\frac{\partial g_{tt}}{\partial r}\) at the boundary surface r=R yield,

$$\begin{aligned} &A = -\frac{1}{R^{2}}\ln \biggl( 1-\frac{2M}{R} \biggr) , \end{aligned}$$
(32)
$$\begin{aligned} &B = \frac{M}{R^{3}}{{ \biggl( 1-\frac{2M}{R} \biggr) }^{-1}} \end{aligned}$$
(33)
$$\begin{aligned} &C = \ln \biggl( 1-\frac{2M}{R} \biggr) -\frac{M}{R}{{ \biggl( 1- \frac{2M}{R} \biggr) }^{-1}} \end{aligned}$$
(34)

For the values of M and R for a strange stars, the constants A and B can be specified as in Table 1.

Table 1 Values of constants for given Masses and Radii of Stars (Li et al. 1999; Lattimer and Steiner 2014)
Full size table

3.3 Stability

In our anisotropic model, we define sound speeds as

$$\begin{aligned} &V^2 _{sr}=\frac{dp_{r}}{d\rho}\equiv\alpha, \end{aligned}$$
(35)
$$\begin{aligned} &V^2 _{st}=\frac{dp_{t}}{d\rho}\equiv-\frac{2\pi (1+\alpha ) [ B(B-A)e^{-Ar^{2}}r-+Ae^{-Ar^{2}}r(2B-A+B(B-A)r^{2}) ]-\frac{3\omega_{q}+1}{4\pi} }{A ( A+B ) r\alpha e^{-Ar^{2}}} \\ &\phantom{V^2 _{st}=\frac{dp_{t}}{d\rho}\equiv} \times\biggl[ Ae^{-Ar^{2}}r \biggl\{ 2A-\frac{1}{r^{2}}-\frac{2(A+B)}{1+\alpha} \biggr\} -\frac{2\beta}{r^{3}}+\frac{e^{-Ar^{2}}}{r^{3}}+ \frac{{\beta}_{1}}{2} \biggr]. \end{aligned}$$
(36)

The above equations lead to

$$\begin{aligned} &V^2 _{st}-V^2 _{sr}=\biggl[-\frac{2\pi(1+\alpha ) [ B(B-A)e^{-Ar^{2}}r-+Ae^{-Ar^{2}}r(2B-A+B(B-A)r^{2}) ] -\frac{3\omega_{q}+1}{4\pi} }{A ( A+B ) r\alpha e^{-Ar^{2}}} \\ &\phantom{V^2 _{st}-V^2 _{sr}=} \times\biggl[ Ae^{-Ar^{2}}r \biggl\{ 2A-\frac{1}{r^{2}}-\frac{2(A+B)}{1+\alpha} \biggr\} -\frac{2\beta}{r^{3}}+\frac {e^{-Ar^{2}}}{r^{3}}+\frac{{\beta}_{1}}{2} \biggr] \biggr]-\alpha \end{aligned}$$
(37)

According to Herrera (1992) cracking concept if radial speed of sound is greater than the transverse speed of sound i.e., \(V^{2} _{st}-V^{2} _{sr}>0\), in a region then such a region is a potentially stable region, otherwise unstable region. Figure 7 implies that \(V^{2}_{st}\) is decreasing function of radial coordinate r. In our case, Fig. 8, shows that our strange star model is stable.

Fig. 7
figure 7

This graph represents the variation of V 2 st versus r (km)

Full size image
Fig. 8
figure 8

This figure represents the variation of V 2 st −V 2 sr versus r (km)

Full size image

3.4 Surface redshift

The compactness of the star is given by

$$ u=\frac{M}{b}=\frac{ ( A+B ) \beta}{A ( 1+m ) } \biggl( \frac {1}{2}\sqrt{ \frac{\pi}{A}}\frac{Erf[ \sqrt{A}r] }{r}-e^{-Ar^{2}} \biggr). $$
(38)

The surface redshift (Z s ) resulting from the compactness u is obtained as

$$ 1+Z_{s}=[1-2u]^{\frac{-1}{2}}, $$
(39)

where

$$ 1+Z_{s}= \biggl[ 1-\frac{ ( A+B ) \beta}{A ( 1+m ) } \biggl( \frac {1}{2}\sqrt{ \frac{\pi}{A}}\frac{erf[\sqrt{A}r] }{r}-e^{-Ar^{2}} \biggr) \biggr] ^{\frac{-1}{2}}. $$
(40)

The maximum value of the surface redshift for the compact stars is shown in Fig. 9.

Fig. 9
figure 9

This figure represents the variation of Z s versus r (km)

Full size image

4 Concluding remarks

In this paper, we have constructed the model of anisotropic Quintessence stars in generalized Teleparallel gravity using the Krori and Barua (1975) ansatz. To this end, the anisotropic perfect fluid energy momentum tensor is coupled to quintessence field which can be specified by the parameter ω q such that −1<ω q <−1/3. Motivated by the present cosmological observation that our universe is accelerating due to quintessence dark energy, we have considered such field in the modeling of the anisotropic star in f(T) gravity. We have found that for diagonal tetrad matrix of static spacetime, anisotropic quintessence field yield the linear form of a f(T), with two arbitrary constant of integration namely β 1 and β. It has been found the for β 1→0 and β→1, the results for GR can be recovered, while for the other values of these parameters we have the results for f(T). We can say that if f(T)=βT, then this theory can be considered as re-scaling of GR. The unknown constants in Krori and Barua metric can be obtained by matching the interior static metric with static vacuum Schwarzschild solution. This matching is suitable in this case as f(T) and GR both involve second order derivative terms in the equations of motion and we have continuity of metric coefficients up to first order derivatives.

We have calculated the energy density, radial and transverse pressures, quintessence energy density and anisotropic parameter of the model. Using the observational data of SAXJ1808.4-3658(SS1) (radius=7.07 km), 4U1820-30 (radius=10 km), Vela X-12 (radius=9.99 km), PSR J 1614-2230 (radius=10.3 km), we have formulated the energy density, at center at r=0 and r=R and pressure at r=0. All these results have been shown in Tables 2–4, for β=1,2,3, it is interesting to note that Table 2 corresponding to β=1 matches exactly to GR results (Bhar 2014), while Tables 3, 4 are extension of GR. We have plotted the graphs only for the data of PSR J 1614-2230 (radius=10.3 km). The first and second derivatives of density and pressures, indicate that these quantities have maximum values at the center and minimum values at boundary. The behavior of quintessence density ρ q does not change in f(T) theory of gravity as compared to GR, but one can note the deviation in numerical values for β=2,3 as shown in Fig. 4. The EoS parameter ω t has same values as GR for β=1, but for β=2,3 it exhibit dark energy behavior as shown in Fig. 5. We have investigated that for our model Δ>0 (as shown in Fig. 6) and a repulsive force due to anisotropy results to the formation of more massive stars. We have shown that \(0<\upsilon_{sr}^{2}, \upsilon_{st}^{2}<1\) and \(\upsilon _{st}^{2}>\upsilon_{sr}^{2}\), hence our model is potentially stable. We would like to mention that concept of stability independent of f(T) gravity for the particular choice of the model f(T)=βT. It is not true in general for the arbitrary f(T) model. The range of surface redshift Z s for compact star candidate PSR J 1614-2230 (radius=10.3 km) is shown in Fig. 9.

Table 2 Calculated values of the parameter from the model by taking α=0.11 and β=1
Full size table
Table 3 Calculated values of the parameter from the model by taking α=0.11 and β=2
Full size table
Table 4 Calculated values of the parameter from the model by taking α=0.11 and β=3
Full size table

5 Conflict of interest

The authors declare that they have no conflict of interest.