1 Introduction

On the basis of Einstein’s proposal for the investigation of a new version to General Relativity (GR) (Unzicker and Case 2005), an alternative theory of gravitation, termed as Teleparallel Theory (TT) has been adopted many years later from the original formulation of GR. However, the analogy between GR and TT has been tackled once again on the basis of postulates defined by Moller (Moller 1961; Pellegrini and Plebanski 1963; Moller 1978; Hayashi and Nakano 1967; Hayashi 1973, 1977). According to GR the gravitational effects due to a gravitating source can be described by the curvature of that source. In general it is true that a spacetime may posses curvature and torsion (as in case of Cartan space), one can distinguish all the terms resulting from torsion of spacetime as Riemann tensor, connection, etc. Therefore, one can remark that the theory that accounts gravity as an action of curvature of spacetime (resulting from the Riemann tensor without either torsion or antisymmetric connection) can be considered as a theory that consists of only torsion with null contribution from Riemann tensor without torsion (Capozziello and Faraoni 2011).

On the basis of current expanding paradigm and existence of exotic energy component named as dark energy, various modifications of GR have been proposed. The unified theories of gravitation in low-energy scales involves the terms R 2,R μν R μν and R μναβ R μναβ , in their effective actions. In such candidates f(R) has gained great interest (Sharif and Shamir 2009; Shamir 2010; Shamir et al. 2012; Shamir and Raza 2014, 2015) and it agrees with the cosmological and astrophysical observational data (Nojiri and Odintsov 2011). In f(R) gravity, the dynamical equations are of the fourth order differential equations, so it becomes more difficult to solve these equations as compared to GR (Nojiri and Odintsov 2007). As the GR has the similarity with Teleparallel theory, a theory namely f(T) (where T is a torsion scalar) has been used. Such theory would be the alternative form of the generalization of GR, namely the f(R) theory of gravity. This newly proposed f(T) theory is the modification of TT, which is free of curvature and Riemann tensors resulting from the terms without torsion.

In the relativistic cosmology, f(T) theory has been employed to discuss the inflation of the universe (Ferraro and Fiorini 2007). Since then there has been growing interest to study the various aspects of cosmology in f(T) theory of gravity. Many authors (Hayashi 1977; Capozziello and Faraoni 2011; Nojiri and Odintsov 2007, 2011; Ferraro and Fiorini 2007; Bayin 1982; Linder 2011; Bamba et al. 2011; Zubair 2015; Zubair and Waheed 2015), investigated that this theory can be utilized as a handy candidate for the accelerated expansion of the universe without the inclusion of dark energy. In the astronomy and astrophysics, the f(T) theory was initially used to drive the BTZ black hole solutions (Dent et al. 2011). Bamba et al. (2011) and Miao et al. (2011) shown that first of black hole thermodynamics does not hold in f(T) theory. Recently, some static spherically symmetric solutions with Maxwell term have been found in f(T) theory (Wang 2011). Boehmer et al. (2011) and Daouda et al. (2011) investigated the existence of relativistic stars in f(T) theory developing the various static perfect fluid solutions.

People (Bhar et al. 2014; Kalam et al. 2013; Maurya et al. 2014; Rahaman et al. 2012) have discussed the analytical models of compact strange stars in the framework of Einstein gravity. In this paper, we formulate the models of anisotropic compact objects in f(T) theory, without using the equation of state. We have discussed the various properties of the compact objects. This paper is organized as follows: The brief review of Weitzenbock’s geometry and equation of motion of f(T) gravity will be presented in Sect. 2. Section 3, deals with the geometry of the source and physical significance of matter component. The physical analysis of the proposed model is presented in Sect. 4. Finally, we discuss the summary of results in the last section.

2 f(T) theory of gravity

Recently, it has been proved that TT is equivalent theory to the GR (Bayin 1982; Linder 2011; Rehaman et al. 2010). Here, we briefly introduce the basic concept of TT, for this purpose, it is assumed that Latin and Greek indices are related to the tetrad fields and spacetime coordinates, respectively. In this case metric of spacetime is defined as follows:

$$ ds^{2}=g_{\mu\nu}dx^{\mu}dx^{\nu}, $$
(1)

The above metric can be transformed to Minkowskian description by the tetrad matrix, defined by

$$\begin{aligned} &{dS^{2}=g_{\mu\nu}dx^{\mu}dx^{\nu}= \eta_{ij}\theta^{i}\theta^{j},} \end{aligned}$$
(2)
$$\begin{aligned} &{dx^{\mu}=e_{i}^{\mu}\theta^{i}, \theta^{i}=e^{i}_{{\mu}}dx^{\mu},} \end{aligned}$$
(3)

where \(\eta_{ij} = \operatorname{diag}[1,-1,-1,-1]\) and \(e_{i}^{\mu}e_{i}^{\nu} = \delta_{\nu}^{\mu}\) or  \(e_{i}^{\mu}e_{j}^{\nu} = \delta_{i}^{j}\).

The root of the metric determinant is given by \(\sqrt{-g}=\det[e_{\mu}^{i}]=e\). The Weitzenbock’s connection components for vanishing Riemann tensor part and non-vanishing torsion term are defined as

$$ \varGamma^{\alpha}_{\mu\nu}=e_{i}^{\alpha} \partial_{\nu}e_{\mu}^{i}=-e_{i}^{\mu} \partial_{\nu}e_{i}^{\alpha} $$
(4)

The torsion and the contorsion are defined by

$$\begin{aligned} &{T^{\alpha}_{\mu\nu}=\varGamma^{\alpha}_{\nu\mu}- \varGamma^{\alpha}_{\mu\nu}=e_{i}^{\alpha}\bigl( \partial_{\mu}e_{\nu}^{i}-\partial_{\nu}e_{\mu}^{i} \bigr)} \end{aligned}$$
(5)
$$\begin{aligned} &{K^{\mu\nu}_{\alpha}=-\frac{1}{2}\bigl(T^{\mu\nu}_{\alpha}-T^{\nu\mu}_{\alpha}-T^{\mu\nu}_{\alpha} \bigr)} \end{aligned}$$
(6)

and the components of the tensor \(S_{\alpha}^{\mu\nu}\) as

$$ S_{\alpha}^{\mu\nu}=\frac{1}{2}\bigl(K^{\mu\nu}_{\alpha}+ \delta^{\mu}_{\alpha}T^{\beta\nu}_{\beta}- \delta^{\nu}_{\alpha}T^{\beta\mu}_{\beta}\bigr). $$
(7)

Here, torsion scalar is

$$ T=T^{\alpha}_{\mu\nu}S_{\alpha}^{\mu\nu} $$
(8)

Analogous to f(R) gravity, the action for f(T) gravity is

$$ S\bigl[e_{\mu}^{i}, \varPhi_A\bigr]=\int d^4 x e\biggl[\frac{1}{16\pi}f(T)+\mathcal{L}_{Matter}( \varPhi_A)\biggr], $$
(9)

in the above action G=c=1 have been used and the \(\mathcal{L}_{Matter}(\varPhi_{A})\) is matter field. The variation of the above action provide the following field equations in f(T) gravity (Dent et al. 2011)

$$\begin{aligned} &{S_{\mu}^{\nu\rho}\partial_{\rho}T f_{TT}+ \bigl[e^{-1}e^{i}_{\mu}\partial_{\rho} \bigl(ee_i^{\alpha}S_{\alpha}^{\nu\rho} \bigr)+T^{\alpha}_{\lambda\mu} S_{\alpha}^{\nu\lambda} \bigr]f_T+\frac{1}{4}\delta^{\nu}_{\mu}f} \\ &{\quad =4\pi \mathcal{T}_{\mu}^{\nu},} \end{aligned}$$
(10)

where \(\mathcal{T}_{\mu}^{\nu}\) is matter. In the present case, we take the matter as anisotropic fluid for which energy-momentum tensor is

$$ \mathcal{T}_{\mu}^{\nu}=(\rho+p_{t})u_{\mu}u^{\nu}-p_{t} \delta_{\mu}^{\nu}+(p_{r}-p_{t})v_{\mu}v^{\nu}, $$
(11)

where u μ and v μ are the four-velocity and radial-four vectors, respectively. Further, p r and p t are pressures along radial and transverse directions.

3 Model of anisotropic compact stars in generalized teleparallel gravity

We assume the geometry of star in the form of static spherically symmetric spacetime which is given by

$$ ds^{2}=e^{a(r)}dt^{2}-e^{b(r)}dr^{2}-r^{2} \bigl(d\theta^{2}+\sin^{2}(\theta)d\phi^{2}\bigr). $$
(12)

We introduce the tetrad matrix for (12) as follows:

$$ \bigl[e_{\mu}^{i}\bigr]=\operatorname{diag} \bigl[e^{\frac{a(r)}{2}},e^{\frac{b(r)}{2}},r,r \sin(\theta)\bigr]. $$
(13)

Using Eq. (13), one can obtain \(e=\det[e_{\mu}^{i}]=e^{\frac{(a+b)}{2}}r^{2}\sin (\theta)\), and with (4)–(8), torsion scalar and its derivative are determined in terms of r as

$$\begin{aligned} &{ T(r)=\frac {2 e^{-b}}{r}\biggl(a^{'}+\frac {1}{r} \biggr),} \end{aligned}$$
(14)
$$\begin{aligned} &{ T^{'}(r)=\frac {2 e^{-b}}{r}\biggl(a^{''}+ \frac {1}{r^{2}}-T\biggl(b^{'}+\frac{1}{r}\biggr)\biggr),} \end{aligned}$$
(15)

where prime represents derivative with respect to r. The set of equations for an anisotropic fluid as

$$\begin{aligned} &{ 4\pi\rho=\frac {f}{4}-\frac{f_{T}}{2} \biggl(T- \frac{1}{r^{2}}-\frac { e^{-b}}{r}\bigl(a^{'}+b^{'}\bigr) \biggr) ,} \end{aligned}$$
(16)
$$\begin{aligned} &{ 4\pi p_{r}=\frac{f_{T}}{2} \biggl(T-\frac{1}{r^{2}} \biggr)-\frac {f}{4},} \end{aligned}$$
(17)
$$\begin{aligned} &{ 4\pi p_{t}= \biggl[\frac{T}{2}+e^{-b} \biggl(\frac{a^{''}}{2}+\biggl(\frac {a^{'}}{4}+\frac {1}{2r}\biggr) \bigl(a^{'}-b^{'}\bigr) \biggr) \biggr]\frac {f_{T}}{2}- \frac {f}{4},} \\ \end{aligned}$$
(18)
$$\begin{aligned} &{ \frac {\cot\theta}{2r^{2}}T^{'}f_{TT}=0,} \end{aligned}$$
(19)

In Eqs. (16)–(18), Eq. (19), has been used. Further, Eq. (19) leads to the following linear form of f(T):

$$ f(T)=\beta T+{\beta}_{1}, $$
(20)

where β and β 1 are integration constants. We parameterize the metric as the following:

$$\begin{aligned} b(r)=Ar^2,\quad a(r)=Br^2+C \end{aligned}$$
(21)

where arbitrary constants A, B and C can be evaluated by using some physical matching conditions. Now using Eqs. (20), (21), we get following form of matter components:

$$\begin{aligned} &{ \rho=-\frac{e^{-Ar^{2}}\beta}{8\pi r^{2}}+\frac{\beta_{1}}{16\pi}+\frac{\beta}{8\pi r^{2}}+ \frac{e^{-Ar^{2}}A\beta}{4\pi},} \end{aligned}$$
(22)
$$\begin{aligned} &{ p_{r}=\frac{e^{-Ar^{2}}B\beta}{4\pi}+\frac{e^{-Ar^{2}}\beta}{8\pi r^{2}}- \frac{\beta}{8\pi r^{2}}-\frac{{\beta}_{1}}{16\pi},} \end{aligned}$$
(23)
$$\begin{aligned} &{ p_{t}=\frac{e^{-Ar^{2}}B\beta}{4\pi}+\frac{e^{-Ar^{2}}\beta r^{2}B^{2}}{8\pi}- \frac{AB\beta r^{2}e^{-Ar^{2}}}{8\pi}} \\ &{\phantom{p_{t}=} - \frac{e^{-Ar^{2}}A\beta}{8\pi}-\frac{{\beta}_{1}}{16\pi},} \end{aligned}$$
(24)

Also, the equation of state (EOS) parameters can be written as

$$\begin{aligned} &{ {\omega}_{r}(r)=\frac{4r^{2}B\beta e^{-Ar^{2}}+2\beta e^{-Ar^{2}}-2\beta-r^{2}{\beta}_{1}}{-2\beta e^{-Ar^{2}}+r^{2}{\beta}_{1}+2\beta+4r^{2}A\beta},} \end{aligned}$$
(25)
$$\begin{aligned} &{ {\omega}_{t}(r)=\frac{r^{2}B\beta+2r^{4}B^{2}\beta e^{-Ar^{2}}-2\beta ABr^{4}+2r^{2}A\beta e^{-Ar^{2}}-4r^{2}{\beta}_{1}}{e^{-Ar^{2}} +2{\beta}_{1}r^{2}+\beta+2r^{2}A\beta e^{-Ar^{2}}},} \end{aligned}$$
(26)

4 Analysis of the proposed model

Here, we discuss the following properties of the proposed model:

4.1 Anisotropic behavior

Using Eqs. (22) and (23), we get

$$\begin{aligned} &{ \frac{d\rho}{dr}=\frac{\beta Ae^{-Ar^{2}}}{4\pi r}+\frac{\beta e^{-Ar^{2}}}{4\pi r^{3}}- \frac{\beta}{4\pi r^{3}}-\frac {A^{2}\beta re^{-Ar^{2}}}{2\pi},} \end{aligned}$$
(27)
$$\begin{aligned} &{ \frac{dp_{r}}{dr}=-\frac{\beta ABre^{-Ar^{2}}}{2\pi}-\frac{\beta Ae^{-Ar^{2}}}{4\pi r}- \frac{\beta e^{-Ar^{2}}}{4\pi r^{3}}+\frac {\beta}{4\pi r^{3}}.} \end{aligned}$$
(28)

The above results lead to following equations

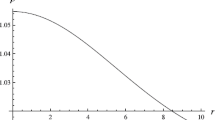
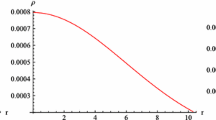
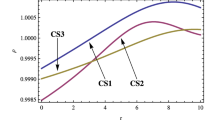
$$\begin{aligned} \frac{d^{2}\rho}{dr^{2}} =&\frac{\beta A^{2}e^{-Ar^{2}}}{2\pi}-\frac{\beta Ae^{-Ar^{2}}}{4\pi r^{2}}- \frac{\beta Ae^{-Ar^{2}}}{2\pi r^{2}}-\frac {3\beta e^{-Ar^{2}}}{4\pi r^{4}} \\ &{}+\frac{3\beta}{4 \pi r^{4}}-\frac {\beta A^{2}e^{-Ar^{2}}}{2\pi}+\frac{\beta A^{3}r^{2}e^{-Ar^{2}}}{\pi}, \\ \frac{d^{2}p_{r}}{dr^{2}} =&-\frac{\beta ABe^{-Ar^{2}}}{2\pi}+\frac{\beta A^{2}Br^{2}e^{-Ar^{2}}}{\pi}+ \frac{\beta Ae^{-Ar^{2}}}{\pi r^{2}} \\ &{}+\frac {\beta A^{2}e^{-Ar^{2}}}{2\pi}+\frac{3\beta e^{-Ar^{2}}}{4 \pi r^{4}}+\frac {\beta Ae^{-Ar^{2}}}{4\pi r^{2}}-\frac{3\beta}{4\pi r^{4}}. \end{aligned}$$

The ρ and p r have maximum values (see Figs. 1 and 2). This implies that density and pressure have maximum value at the center of the star (r=0). Figure 3 indicates that transverse pressure is decreasing function of radial coordinate. From Figs. 4 and 5, it can be see that effective EOS is given by 0<ω i (r)<1, (i=r,t) similar to normal matter distribution. This indicates the fact that compact stars are composed of ordinary matter and contribution of f(T) terms. The measure of anisotropy, \(\varDelta =\frac{2}{r}(p_{t}-p_{r})\) in this model is obtained as follows:

$$\begin{aligned} \varDelta =&\frac{\beta B^{2}re^{-Ar^{2}}}{4\pi}-\frac{\beta ABre^{-Ar^{2}}}{4\pi}-\frac{\beta Ae^{-Ar^{2}}}{4\pi r}- \frac {\beta e^{-Ar^{2}}}{4\pi r^{3}} \\ &{}+\frac{\beta}{2\pi r^{3}}. \end{aligned}$$
(29)

It is well known that anisotropy will be directed outward when p t >p r i.e., Δ>0, and inward when p t <p r i.e., Δ<0. From Fig. 6, we conclude that at r=0, \(\frac{d\rho}{dr}=0, \frac{dp_{r}}{dr}=0\), and \(\frac{d^{2}\rho}{dr^{2}}<0, \frac{d^{2}p_{r}}{dr^{2}}<0\). Figure 7 shows that in this model a repulsive (anisotropic) force would exists as (Δ>0) (for smaller values of r) which permits the formation of super massive star, while for larger values of r, Δ=0, where a star comes to the equilibrium position.

Fig. 1
figure 1

First, second and third graphs represent the density variation of Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image
Fig. 2
figure 2

First, second and third graphs represent the radial pressure variation of Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image
Fig. 3
figure 3

First, second and third graphs represent the transverse pressure variation of Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image
Fig. 4
figure 4

First, second and third graphs represent the EOS parameter ω r variation of Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image
Fig. 5
figure 5

First, second and third graphs represent the EOS parameter ω t variation of Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image
Fig. 6
figure 6

All these graphs has been plotted only for the data of 4U 1820-30

Full size image
Fig. 7
figure 7

First, second and third graphs represent the variation of anisotropy Δ for Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image

4.2 Matching conditions

In this section, we discuss the smooth matching of spacetime (12) to the vacuum exterior spherically symmetric metric given by

$$\begin{aligned} ds^2 =& \biggl(1-\frac{2M}{r} \biggr)dt^2- \biggl(1- \frac{2M}{r} \biggr)^{-1}dr^2 \\ &{}-r^{2} \bigl(d\theta^{2}+\sin^{2}(\theta)d\phi^{2}\bigr). \end{aligned}$$
(30)

The continuity of metric components g tt , g rr and \(\frac{\partial g_{tt}}{\partial r}\) at the boundary surface r=R yield,

$$\begin{aligned} A =&-\frac{1}{R^2}\ln \biggl(1-\frac{2M}{r} \biggr), \end{aligned}$$
(31)
$$\begin{aligned} B =&\frac{M}{R^3}{{ \biggl(1-\frac{2M}{r} \biggr)}^{-1}} \end{aligned}$$
(32)
$$\begin{aligned} C =&\ln \biggl(1-\frac{2M}{r} \biggr)-\frac{M}{R}{{ \biggl(1- \frac{2M}{r} \biggr)}^{-1}} \end{aligned}$$
(33)

For the values of M and R for a given star, the constants A and B can be specified as in Table 1.

Table 1 Values of constants for given masses and radii of stars
Full size table

4.3 Stability

For this anisotropic model, the sound speeds are defined as

$$\begin{aligned} \upsilon^{2}_{sr} =&\frac{dp_{r}}{d\rho }\equiv \frac{-2ABr^{4}e^{-Ar^{2}}-Ar^{2}e^{-Ar^{2}}-e^{-Ar^{2}}+1}{-2A^{2}r^{4}e^{-Ar^{2}} +Ar^{2}e^{-Ar^{2}}+e^{-Ar^{2}}-1}, \\ \end{aligned}$$
(34)
$$\begin{aligned} \upsilon^{2}_{st} =&\frac{dp_{t}}{d\rho }\equiv \frac{B^{2}r^{4}e^{-Ar^{2}}-AB^{2}r^{6}e^{-Ar^{2}}+4A^{2}Br^{6} +A^{2}r^{4}e^{-Ar^{2}}}{Ar^{2}e^{-Ar^{2}}+e^{-Ar^{2}}-2A^{2}r^{4}e^{-Ar^{2}}-1}. \end{aligned}$$
(35)

The above equations lead to

$$\begin{aligned} \upsilon^{2}_{st}-\upsilon^{2}_{sr} =& \bigl\{ -2ABr^{4} +B^{2}r^{4}-AB^{2}r^{6}+4A^{2}Br^{6}e^{Ar^{2}} \\ &{}+A^{2}r^{4}+(r^{2} A+1)-e^{-Ar^{2}}\bigr\} \\ &{}\times\bigl\{ Ar^{2}+1-2A^{2}r^{4}-e^{Ar^{2}}\bigr\} ^{-1} \end{aligned}$$
(36)

Few years ago, Herrera (1992) published a new proposal to check the stability of anisotropic gravitating source. Currently, this technique is termed as cracking concept which states that if radial speed of sound is greater than the transverse speed of sound in a region then such a region is a potentially stable region, otherwise unstable region. In our case, Fig. 8 indicates that there is change of sign for the term v 2 st −v 2 sr within the particular configuration. Hence, we find that our strange star model is unstable.

Fig. 8
figure 8

First, second and third graphs represent the variation of v 2 st −v 2 sr for Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image

4.4 Surface redshift

The compactness of the star is given by

$$\begin{aligned} u=\frac{M}{b}=\frac{2b\sqrt{A}\pi\beta+\sqrt{\pi}\beta(\pi-2A\pi r^{2})\operatorname{erf}[\sqrt{A}b]+b \pi r^{2}\beta_{1}\sqrt{A}}{4\pi\sqrt{A}} \end{aligned}$$
(37)

The surface redshift (Z s ) resulting from the compactness u is obtained as

$$ 1+Z_{s}=[1-2u]^{\frac{-1}{2}}, $$
(38)

where

$$\begin{aligned} 1+Z_{s} =& \bigl[1- \bigl(\bigl\{ 2b\sqrt{A}\pi\beta+\sqrt{\pi}\beta(\pi-2A\pi r^{2})\operatorname{erf}(\sqrt{A}b) \\ &{}+b \pi r^{2}\beta_{1}\sqrt{A}\bigr\} \bigl\{ 4\pi\sqrt{A}\bigr\} ^{-1} \bigr) \bigr]^{\frac{-1}{2}}. \end{aligned}$$
(39)

The maximum value of the surface redshift for the compact stars is shown in Fig. 9.

Fig. 9
figure 9

First, second and third graphs show the evolution of surface redshift Z s for Strange star candidates Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30, respectively

Full size image

5 Concluding remarks

Recently, there has been growing interest to study gravitational field as the effect of torsion of the underlying geometry, which was originally introduced in parallel to curvature description of gravity. This concept was developed in several years as teleparallel equivalence of GR. The black hole (BH) are extremely compact astrophysical objects which store information about the entropy on the BH horizon. In the modified TEGR, f(T) gravity posses many interesting feature. Recent observations from solar system orbital motions in order to constrain f(T) gravity have been made and interesting results have been found. The conditions for the existence and non-existence of relativistic stars have been studied in f(T) gravity (Nojiri and Odintsov 2007; Ferraro and Fiorini 2007). It is important to model the compact stars in f(T) using the diagonal tetrad field.

In this paper, we have constructed the model of compact stars in f(T) gravity. The interior of the stars has been taken as static spherically symmetric with anisotropic gravitating source. The equations of motions have been obtained by using the diagonal tetrad field. In this case the f(T) appears as a linear function of T. The explicit form of matter density, radial pressure, transverse pressure and EOS parameters have been calculated. The anisotropy, regularity and energy conditions have been discussed in detail. The observed values of masses and radii of compact stars have been used to specify the values of unknown constants of the interior metric. By using the fist and second derivatives of density and pressures, we have found that these quantities have maximum values at the center and vanish at boundary.

It is clear from Fig. 7 that in this model a repulsive (anisotropic) force would exists as (Δ>0) which indicates the formation of more massive distributions. Using the cracking concept, we have found that radial speed of sound is greater than the transverse speed of sound in a region. It is clear from Fig. 8 that there is change of sign for the term v 2 st −v 2 sr within the specific configuration. Hence, we conclude that our strange star model is unstable. The range of surface redshift Z s for Strange star candidate Her X-1, SAX J 1808.4-3658(SS1) and 4U 1820-30 is shown in Fig. 9.